Enhancing Dynamic Performance in K-Rb-21Ne Co-Magnetometers through Atomic Density Optimization
Abstract
1. Introduction
2. Theory
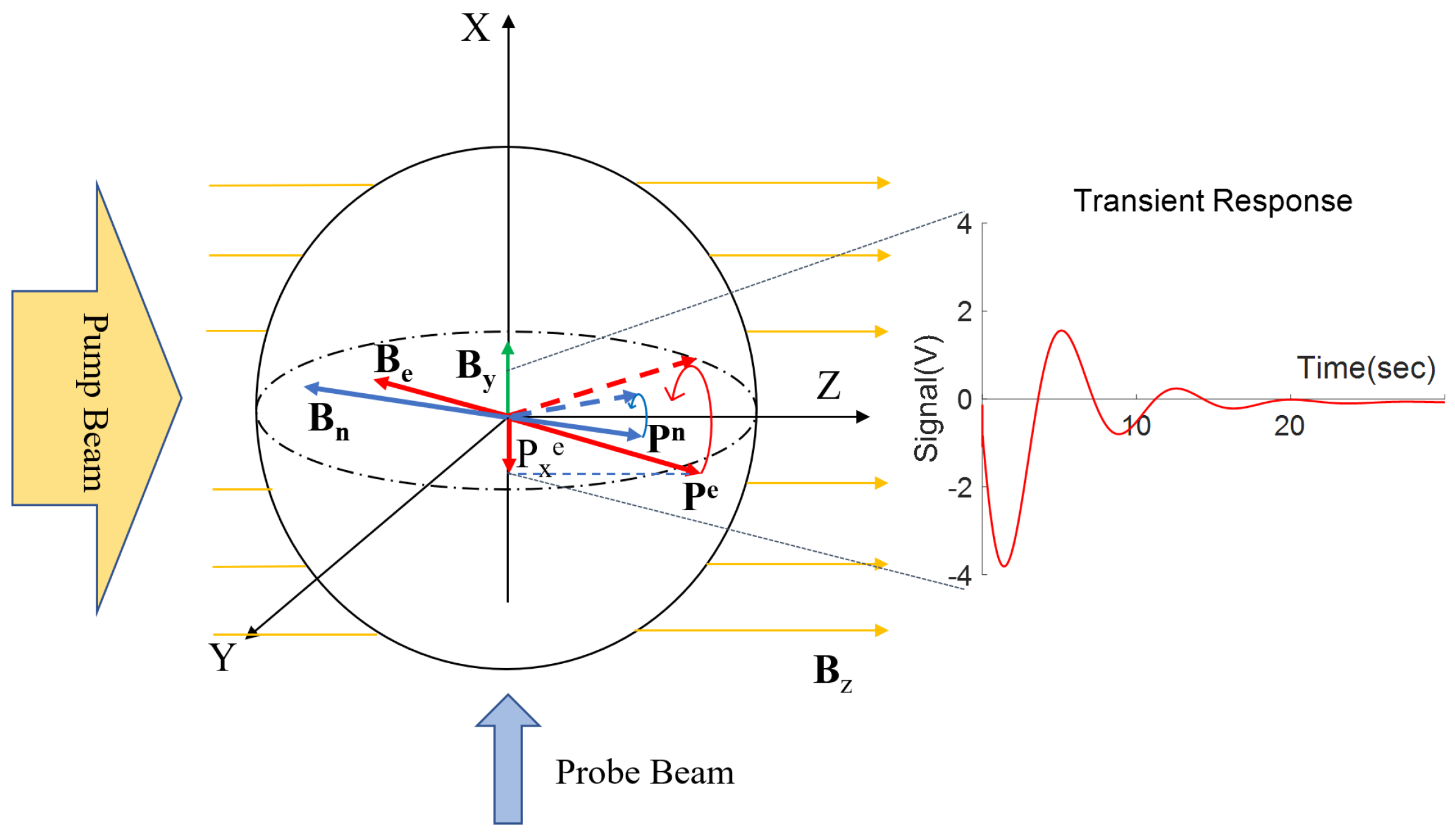
2.1. Basic Principle
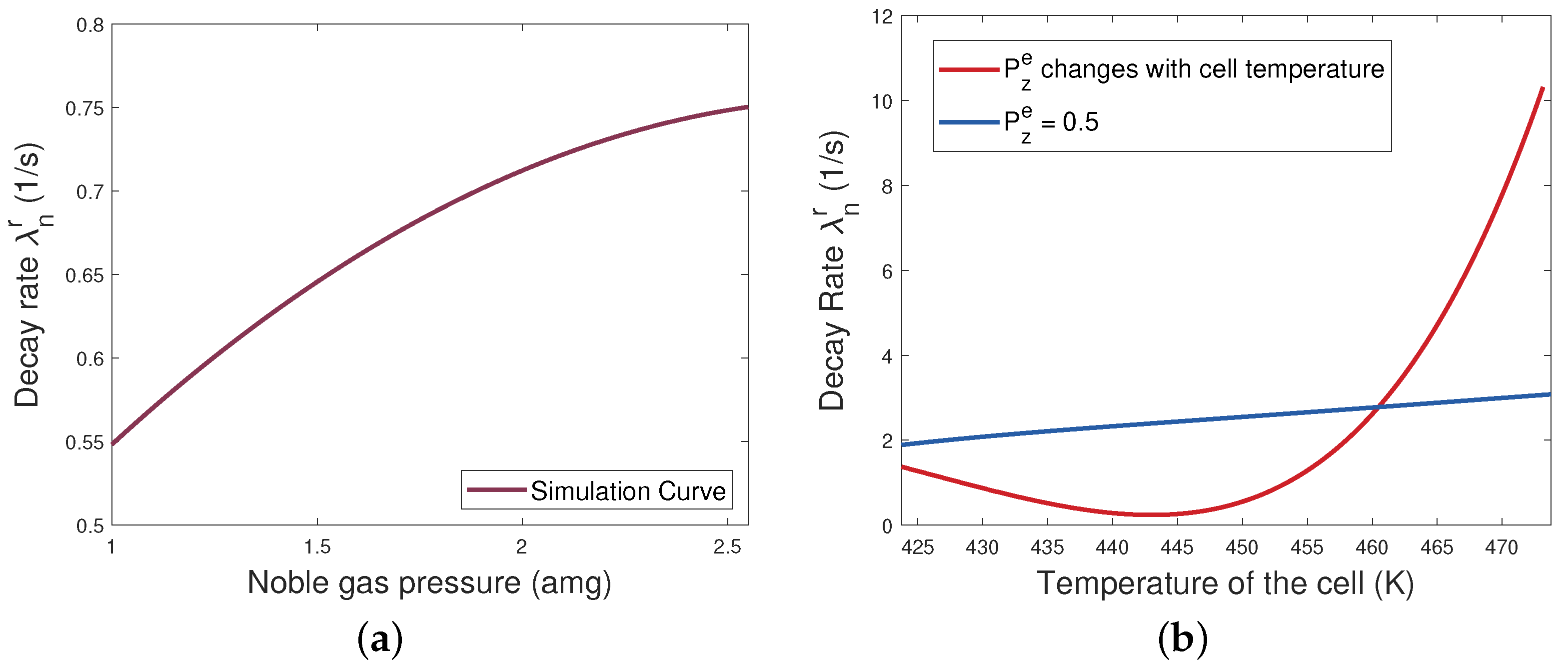
2.2. Simulation
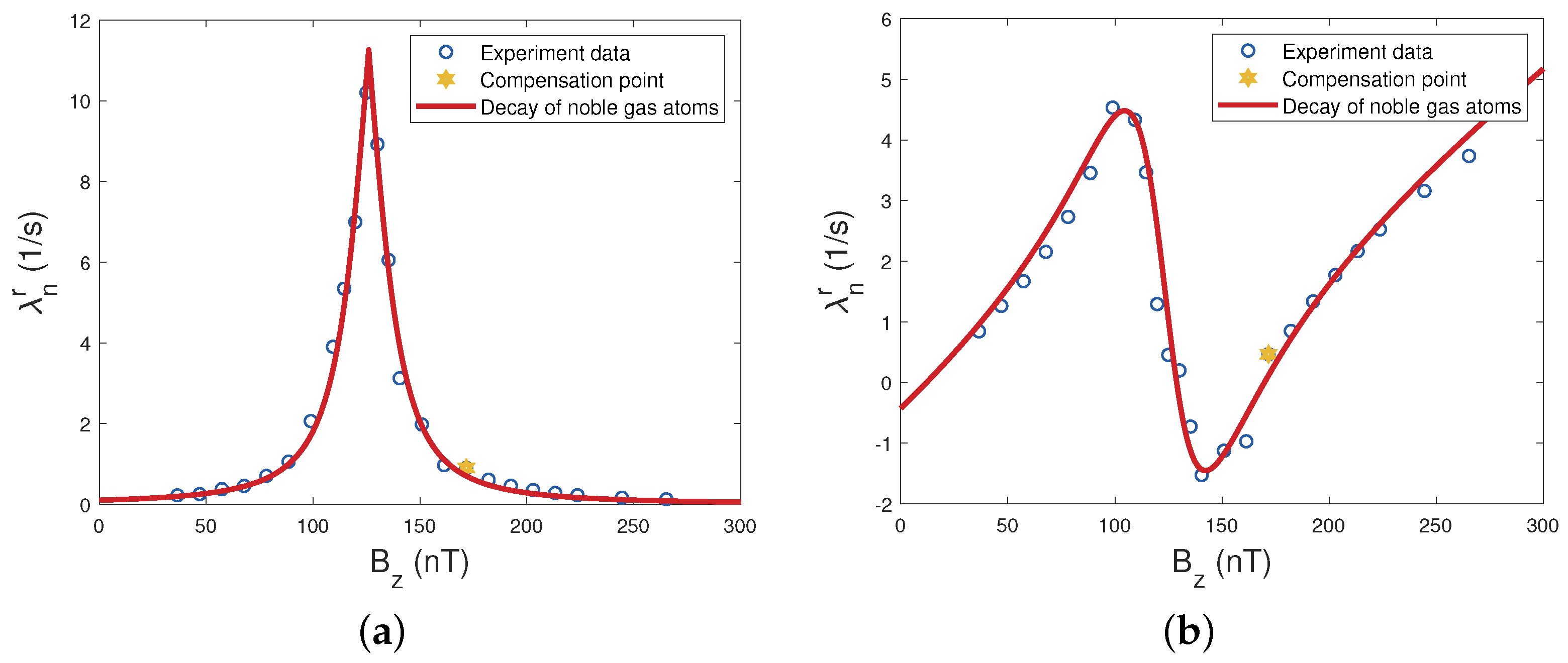
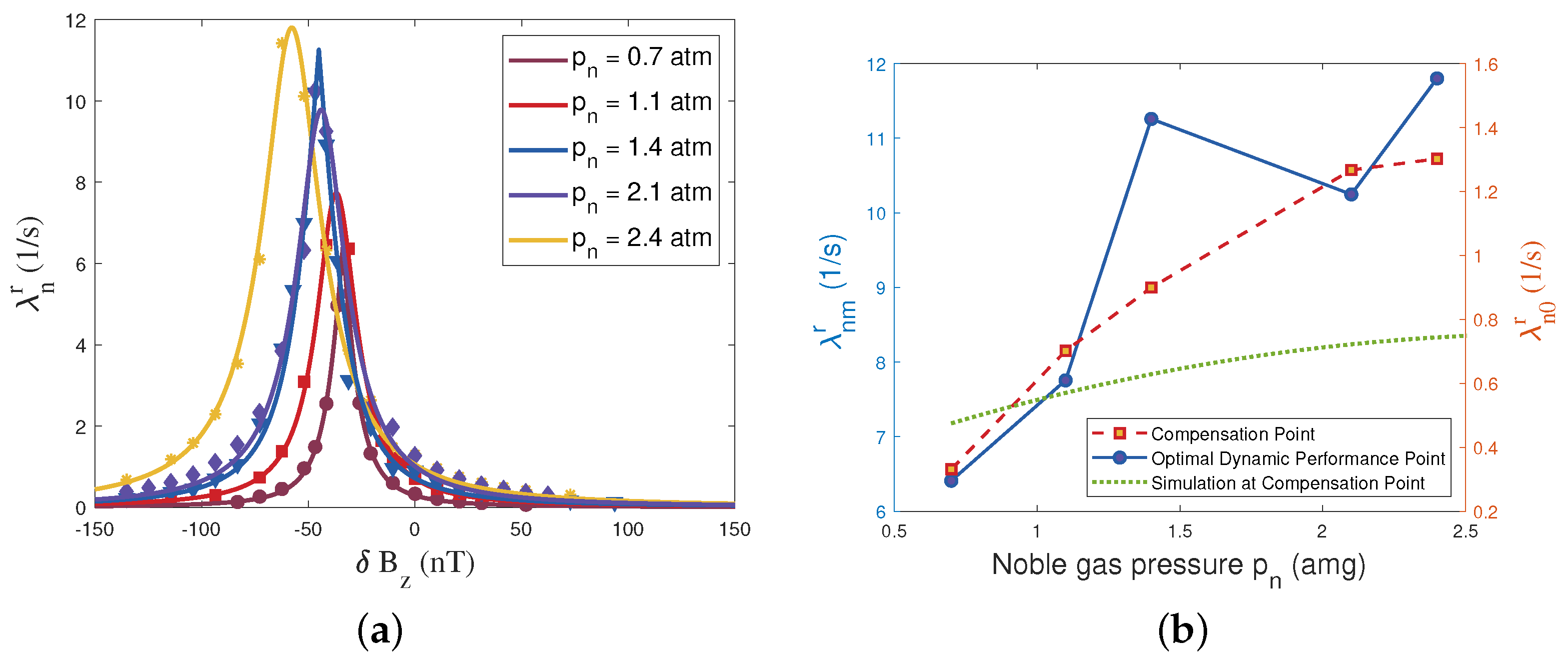
3. Experimental Results and Discussion
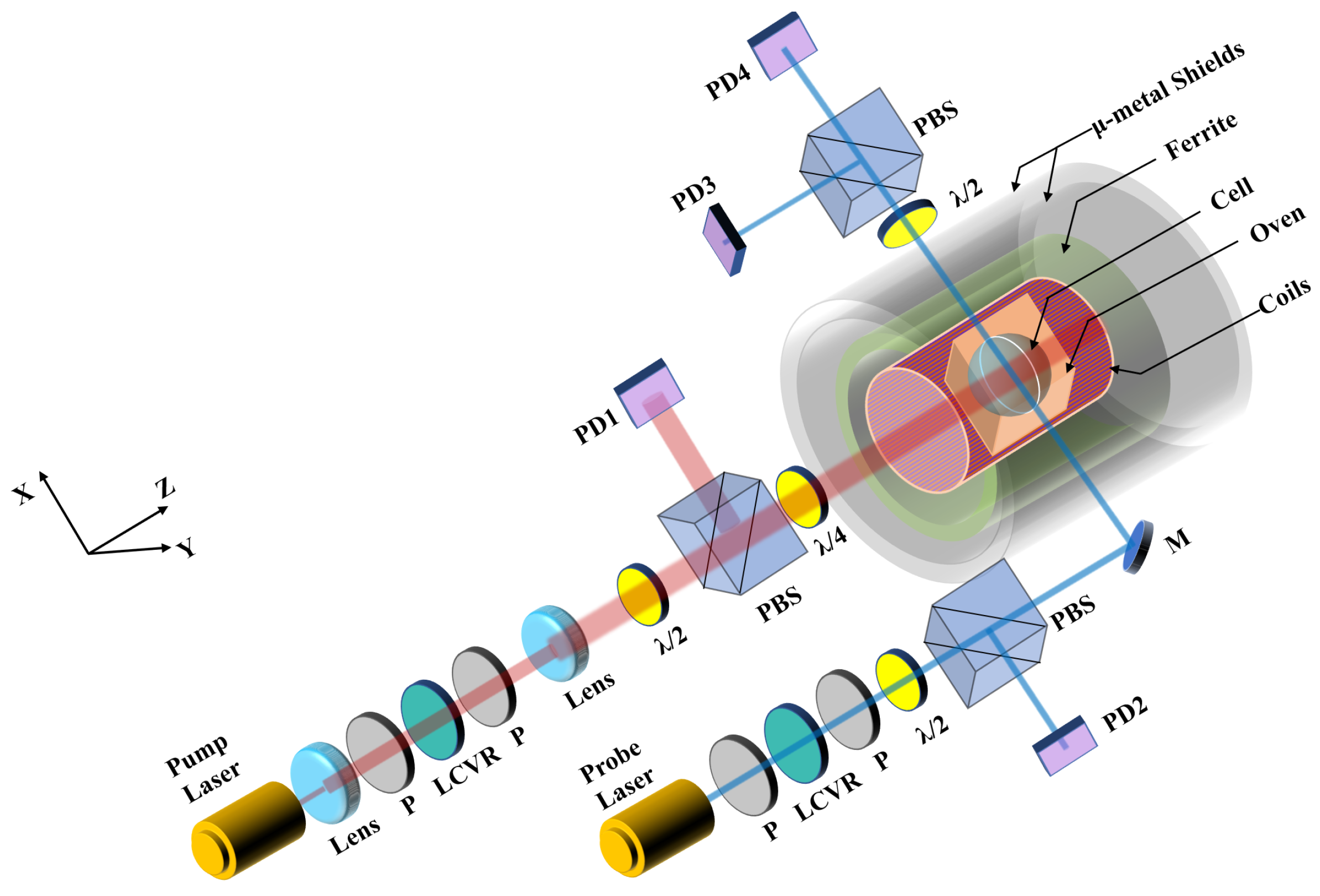
3.1. Experimental Setup
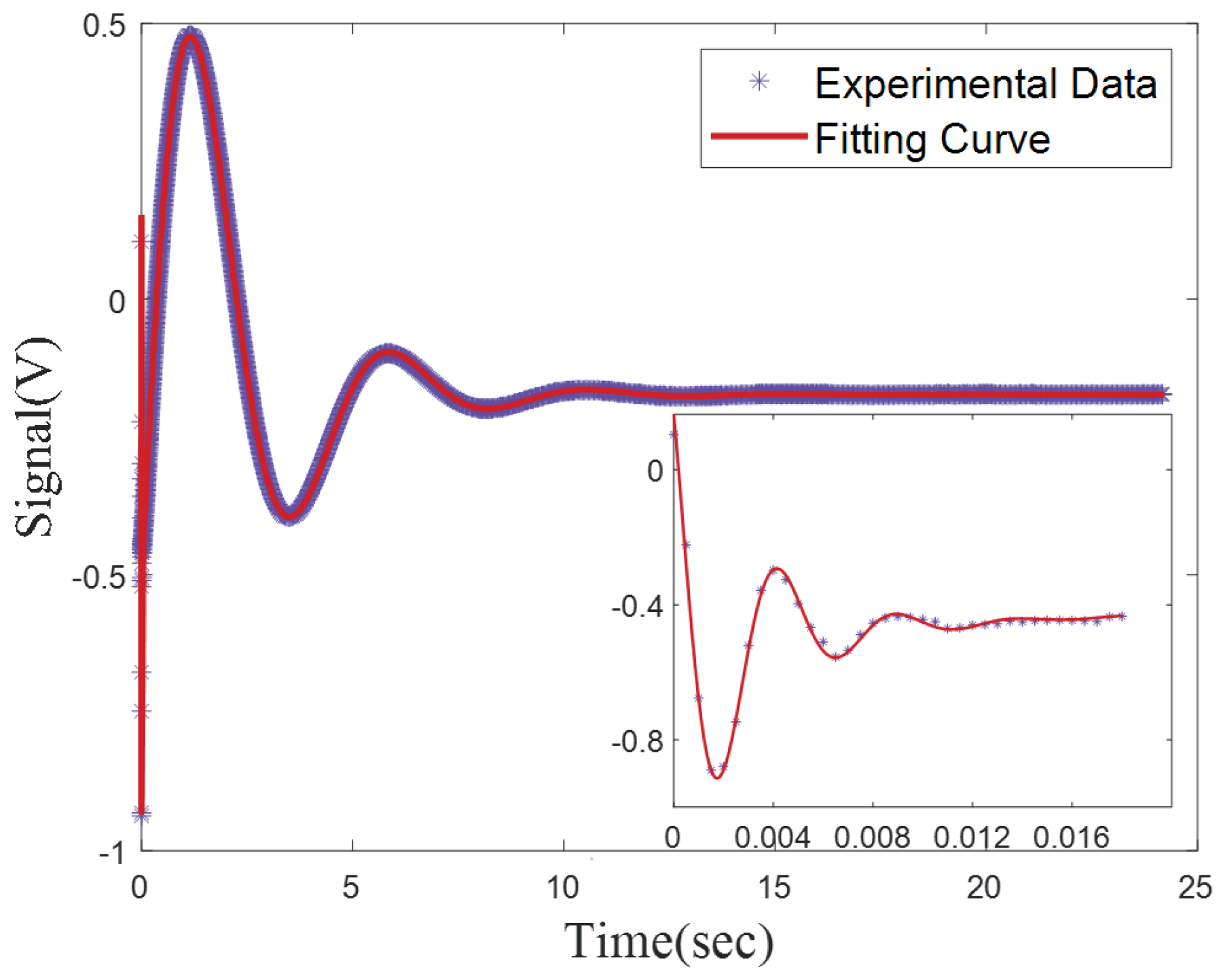
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Budker, D.; Romalis, M. Optical magnetometry. Nat. Phys. 2007, 3, 227–234. [Google Scholar] [CrossRef]
- Fang, J.; Wan, S.; Yuan, H. Dynamics of an all-optical atomic spin gyroscope. Appl. Opt. 2013, 52, 7220–7227. [Google Scholar] [CrossRef]
- Limes, M.; Sheng, D.; Romalis, M.V. He 3–Xe 129 comagnetometery using Rb 87 detection and decoupling. Phys. Rev. Lett. 2018, 120, 033401. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Z.; Zhai, Y. In-Situ Detection for Atomic Density in the K-Rb-21Ne Co-Magnetometer via an Optical Heterodyne Interferometry. Photonics 2023, 10, 1091. [Google Scholar] [CrossRef]
- Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Muñoz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S.; et al. Moving magnetoencephalography towards real-world applications with a wearable system. Nature 2018, 555, 657–661. [Google Scholar] [CrossRef]
- Allmendinger, F.; Schmidt, U.; Heil, W.; Karpuk, S.; Scharth, A.; Sobolev, Y.; Tullney, K.; Zimmer, S. New limit on Lorentz and CPT violating neutron spin interactions using a free precession 3He-129Xe co-magnetometer. Phys. Rev. Lett. 2014, 85, 110801. [Google Scholar] [CrossRef]
- Bear, D.; Stoner, R.; Walsworth, R.; Kosteleckỳ, V.A.; Lane, C.D. Limit on Lorentz and CPT violation of the neutron using a two-species noble-gas maser. Phys. Rev. Lett. 2000, 85, 5038. [Google Scholar] [CrossRef]
- Ledbetter, M.; Savukov, I.; Romalis, M. Nonlinear amplification of small spin precession using long-range dipolar interactions. Phys. Rev. Lett. 2005, 94, 060801. [Google Scholar] [CrossRef] [PubMed]
- Vasilakis, G.; Brown, J.; Kornack, T.; Romalis, M. Limits on new long range nuclear spin-dependent forces set with a K- He 3 comagnetometer. Phys. Rev. Lett. 2009, 103, 261801. [Google Scholar] [CrossRef] [PubMed]
- Wei, K.; Ji, W.; Fu, C.; Wickenbrock, A.; Flambaum, V.V.; Fang, J.; Budker, D. Constraints on exotic spin-velocity-dependent interactions. Nat. Commun. 2022, 13, 7387. [Google Scholar] [CrossRef] [PubMed]
- Walker, T.G.; Happer, W. Spin-exchange optical pumping of noble-gas nuclei. Rev. Mod. Phys. 1997, 69, 629. [Google Scholar] [CrossRef]
- Kornack, T.; Romalis, M. Dynamics of two overlapping spin ensembles interacting by spin exchange. Phys. Rev. Lett. 2002, 89, 253002. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Liu, Y.; Wei, K.; Xie, H.; Mu, T.; Fang, X.; Xu, Z.; Zhai, Y. Ultra-sensitive all-optical comagnetometer with laser heating. J. Phys. D Appl. Phys. 2022, 55, 165103. [Google Scholar] [CrossRef]
- Wei, K.; Zhao, T.; Fang, X.; Xu, Z.; Liu, C.; Cao, Q.; Wickenbrock, A.; Hu, Y.; Ji, W.; Fang, J.; et al. Ultrasensitive atomic comagnetometer with enhanced nuclear spin coherence. Phys. Rev. Lett. 2023, 130, 063201. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Wei, K.; Zhao, T.; Cao, Q.; Liu, Y.; Hu, D.; Zhai, Y. Fast dynamic frequency response-based multiparameter measurement in spin-exchange relaxation-free comagnetometers. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Kornack, T.; Ghosh, R.; Romalis, M.V. Nuclear spin gyroscope based on an atomic comagnetometer. Phys. Rev. Lett. 2005, 95, 230801. [Google Scholar] [CrossRef]
- Fang, J.; Qin, J. Advances in atomic gyroscopes: A view from inertial navigation applications. Sensors 2012, 12, 6331–6346. [Google Scholar] [CrossRef]
- Shi, M. Investigation on magnetic field response of a 87 Rb-129 Xe atomic spin comagnetometer. Opt. Express 2020, 28, 32033–32041. [Google Scholar] [CrossRef]
- Babcock, E.; Nelson, I.; Kadlecek, S.; Driehuys, B.; Anderson, L.; Hersman, F.W.; Walker, T.G. Hybrid Spin-Exchange Optical Pumping of He 3. Phys. Rev. Lett. 2003, 91, 123003. [Google Scholar] [CrossRef] [PubMed]
- Smiciklas, M.; Brown, J.; Cheuk, L.; Smullin, S.; Romalis, M.V. New Test of Local Lorentz Invariance Using a Ne 21-Rb-K Comagnetometer. Phys. Rev. Lett. 2011, 107, 171604. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Chen, Y.; Zou, S.; Liu, X.; Hu, Z.; Quan, W.; Yuan, H.; Ding, M. Low frequency magnetic field suppression in an atomic spin co-magnetometer with a large electron magnetic field. J. Phys. At. Mol. Opt. Phys. 2016, 49, 065006. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.J.; Cai, H.W.; Ding, M.; Fang, J.C. Optimization of the alkali-metal density ratio in a hybrid optical pumping atomic magnetometer. Meas. Sci. Technol. 2018, 30, 015005. [Google Scholar] [CrossRef]
- Lancor, B.; Walker, T.G. Polarization limits in K-Rb spin-exchange mixtures. Phys. Rev. A 2011, 83, 065401. [Google Scholar] [CrossRef]
- Wei, K.; Zhao, T.; Fang, X.; Li, H.; Zhai, Y.; Han, B.; Quan, W. Simultaneous Determination of the Spin Polarizations of Noble-Gas and Alkali-Metal Atoms Based on the Dynamics of the Spin Ensembles. Phys. Rev. Appl. 2020, 13, 044027. [Google Scholar] [CrossRef]
- Tang, J.; Yin, Y.; Zhai, Y.; Zhou, B.; Han, B.; Yang, H.; Liu, G. Transient dynamics of atomic spin in the spin-exchange-relaxation-free regime. Opt. Express 2021, 29, 8333–8343. [Google Scholar] [CrossRef]
- Ghosh, R.K.; Romalis, M.V. Measurement of spin-exchange and relaxation parameters for polarizing 21Ne with K and Rb. Phys. Rev. A 2010, 81, 043415. [Google Scholar] [CrossRef]
- Stone, N. Table of nuclear magnetic dipole and electric quadrupole moments. At. Data Nucl. Data Tables 2005, 90, 75–176. [Google Scholar] [CrossRef]
- Yang, L.; Pang, H.; Wei, Y.; Quan, W. Optimizing noble gas pressure for enhanced self-compensation in spin-exchange relaxation-free comagnetometers. Opt. Express 2023, 31, 33274–33286. [Google Scholar] [CrossRef]
- Brown, J.; Smullin, S.; Kornack, T.; Romalis, M. New limit on lorentz-and C P T-violating neutron spin interactions. Phys. Rev. Lett. 2010, 105, 151604. [Google Scholar] [CrossRef]
- Ruan, J.; Duan, L.; Fu, Y.; Fan, W.; Quan, W. Effects of pump laser intensity on the cell temperature working point in a K-Rb-21 Ne spin-exchange relaxation-free co-magnetometer. Opt. Express 2023, 31, 8342–8351. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Gyromagnetic ratio of the electron spin | Hz/nT |
| Gyromagnetic ratio of the electron spin | Hz/nT |
| Fermi contact enhancement factor between Rb and 21Ne atoms | [26] |
| Permeability of vacuum | N/A2 |
| Bohr magneton | J/T |
| Nuclear spin magnetic moment | J/T [27] |
| Number density of Rb atoms at 180 °C | cm−3 |
| Transverse relaxation rate of electron spin at 180 °C | 1466.51 1/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Pang, H.; Quan, W. Enhancing Dynamic Performance in K-Rb-21Ne Co-Magnetometers through Atomic Density Optimization. Photonics 2024, 11, 182. https://doi.org/10.3390/photonics11020182
Yang L, Pang H, Quan W. Enhancing Dynamic Performance in K-Rb-21Ne Co-Magnetometers through Atomic Density Optimization. Photonics. 2024; 11(2):182. https://doi.org/10.3390/photonics11020182
Chicago/Turabian StyleYang, Lv, Haoying Pang, and Wei Quan. 2024. "Enhancing Dynamic Performance in K-Rb-21Ne Co-Magnetometers through Atomic Density Optimization" Photonics 11, no. 2: 182. https://doi.org/10.3390/photonics11020182
APA StyleYang, L., Pang, H., & Quan, W. (2024). Enhancing Dynamic Performance in K-Rb-21Ne Co-Magnetometers through Atomic Density Optimization. Photonics, 11(2), 182. https://doi.org/10.3390/photonics11020182





