Upconversion Photonic Doppler Velocimetry Based on Stimulated Brillouin Scattering

Abstract

Optical up-conversion photonic Doppler velocimetry (PDV) based on stimulated Brillouin Scattering (SBS) with an all-fiber link structure is proposed in this article. Because SBS limits the laser power transmitted by a fiber over long distances, the probe does not have enough outgoing light to reach the measured surface and cannot receive the signal light. Traditionally, SBS is avoided, but it is a phase-conjugated light and shifts down relative to the source light, so it can be used as a reference light in the laser interference structure to achieve up-conversion heterodyne velocimetry. Compared with general homodyne velocimetry (DPS), SBS-PDV naturally upconverts and has more interference fringes and higher resolution at low-speed measurement. In the gas multiple reflection impact compression experiment, the velocity measurement results of SBS-PDV and dual-laser heterodyne Velocimetry (DLHV) are basically consistent, and the accuracy is better than 0.8%. Due to its coaxial heterodyne optical path, this kind of photonic Doppler velocimetry is suitable for low-velocity and long-distance practical applications in the field of shock wave physics.

1. Introduction

Velocity measurements are very important for the study of transient physical states in shock wave physics experiments [1]. By measuring stress wave propagation in materials, such as shock wave velocity and particle velocity, the pressure and density can be revealed using Hugoniot conservation equations [2,3]. Since the propagation of shock waves is a high-speed process, high time-resolved continuous velocity measurement techniques are needed for these more sophisticated studies [4].

Optical velocimetry with high time resolution and accuracy, such as PDV (photonic Doppler velocimetry) [5], DPS (Doppler pins system) [6], and DISAR (displacement interferometer system for any reflector) [7], has become routine in shock physics experiments. According to the different reference light frequencies, the laser interferometry velocimetry structure can be divided into homodyne and heterodyne, according to whether the velocity signal starts from zero frequency. Conventional velocity measurement systems use a homodyne optical path structure (such as DPS) because of its simplicity and the fact that reference light comes directly from the reflected light from the probe end face. However, because the frequency of the low-speed signal is close to the zero line of the spectrum, the velocity resolution is generally not high and the direction of motion cannot be determined. In the past two decades, heterodyne structures have developed rapidly due to their fundamental frequency migration and higher velocity resolution. A series of PDV structures, such as quadrature PDV [8], can be reconstructed by phase shift to resolve low-velocity transients. Recently, Pinghan Chu used time-lens photon Doppler velocimetry to expand the dynamic range for the use of lower-bandwidth electronics [9]. Typical heterodyne velocimetry [10], such as DLHV (dual-laser heterodyne velocimetry) [11], and frequency-shifted PDV [12] are sensitive to low velocity and direction, and are suitable for some special scenarios. For example, when the free plane jumps from zero under shock wave impacts, the ascent velocity is relatively low. Alternatively, under multiple reflected shock loadings, the velocity curve has multiple steps to represent multiple physical states [13]. However, the heterodyne optical path structure requires a different frequency of the reference light than the signal light, which means that it is achieved either by a frequency modulator or by using two lasers [14]. Regardless of which structure is adopted, two frequencies of light are required to meet the conditions of the interference principle, but the reference light at this time cannot be coaxial with the signal light. The non-coaxial optical path may be affected by external temperature or vibration, which may reduce the signal-to-noise ratio. In addition, in some long-distance measurement scenarios, where the distance between the velocimeter and the probe is often several kilometers, nonlinear effects in the fiber must be considered, such as SBS (stimulated Brillouin scattering), which limits the input power and long transmission distance of the fiber. For example, a fiber of 1 km has a maximum transmitting laser power of 200 mW. This results in a probe with low reception efficiency (not higher than −40 dB) and not enough detection light to reach the surface being measured. Therefore, the output power of the laser must be reduced to avoid the generation of SBS, whether it is a homodyne or heterodyne structure. This results in having to increase the complexity of the system and sacrifice the convenience of remote measurement. In addition, the scattering amplification characteristics of Brillouin light have also been applied to the generation of magnetic lasers and optomagnonic frequency combs [15,16].

This work mainly proposes another heterodyne velocimetry, namely SBS-PDV (stimulated Brillouin scattering–photonic Doppler velocimetry), which uses a single laser to realize up-shifted PDV with ~11 GHz base frequency through stimulated Brillouin scattering light as the reference light in optical interferometry, while retaining low-velocity transient and directional information in the remote measurement. In addition, it has a natural coaxial optical path structure, which can eliminate the influence of the environment on the transmission optical path. According to the principle of optical interference, the total light field is obtained by the superposition of SBS light and Doppler-shifted light. Therefore, the relationship between the frequency of interference fringes and the motion speed will be obtained. Through experiments, it is proved that SBS-PDV has a higher velocity resolution and is more efficient than DPS for low-speed measurements. Additionally, it can save twice the laser power and improve environmental adaptability, especially in long-distance measurement by heterodyne velocity measurement technology.

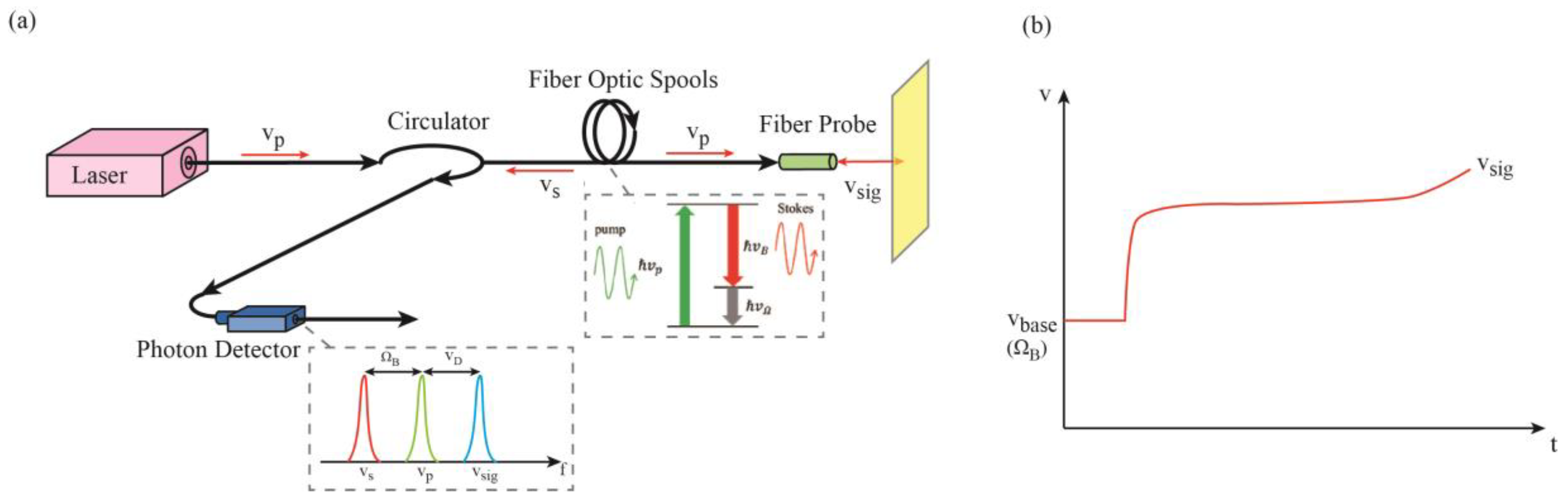
2. Theoretical analysis

The construction of laser interferometry velocity measurement with a homodyne optical path structure is shown in Figure 1a. The laser passes through a circulator to the probe, which emits detection light to illuminate the moving object and receive a signal light with a Doppler shift. The signal light is superimposed onto the reference light returned by the probe end face and enters the detector, and the electrical signal after heterodyning is output and recorded. The signal frequency is calculated by using the Fourier transform, and the velocity information is finally obtained. Usually, the relationship between velocity (u) and Doppler frequency (v_D) is u = λ_pv_D/2. However, when using all-fiber PDV measurements, the transmission power in the fiber is affected by the SBS effect, especially in long-distance measurement. SBS is a nonlinear process that can occur in optical fibers at much lower input power levels because of its lower threshold [17]. It manifests through the generation of a backward-propagating Stokes wave that carries most of the input power, once the Brillouin threshold is reached [18]. As the optical power increases, the efficiency of the reflection increases and effectively limits the amount of optical power that can be transmitted through the fiber. Usually, the input power should not be too high when producing SBS for this reason, but it may not avoid the losses incurred with low-efficiency probes. As we know, SBS manifests through the generation of a Stokes wave (an acoustic wave), whose frequency is downshifted from that of the incident light by an amount set by the nonlinear medium [19]. The acoustic wave produces density modulations that in turn modulate the refractive index of the medium. In a single-mode fiber, SBS occurs only in the backward direction with the Brillouin shift, which is a function of the core material, the fiber length, and the core diameter [20]. This Brillouin shift can be given by

$$v_B={\Omega }_B/2\pi =2n_p{v}_A/{\lambda }_p$$

(1)

where n_p is the effective mode index at the pump wavelength λ_p. If we use v_A = 5.96 km/s and n_p = 1.45, the values appropriate for silica fibers, v_B ≈ 11.1 GHz at λ_p = 1.55 μm.

Then, we derive the relationship between velocity and beat frequency, considering the Brillouin frequency shift. In the process of SBS, the acoustic wave driven by a pump produces density modulations, and the scattered k-vector also has essentially the same length as the incident one. This property allows us to use SBS as an optical reference light for up-conversion. Therefore, a method is proposed to change the process of eliminating SBS to using SBS to design the interference structure of PDV (as shown in Figure 1a). Keeping the homodyne optical path structure unchanged, the pump light is used to excite the back-transmitted Brillouin light in the fiber-optic spools. For the Brillouin process to phase match, the relationship $\left|{\overrightarrow{k}}_{scattered}\right|\approx \left|{\overrightarrow{k}}_{inc}\right|$ dictates the Brillouin acoustic k-vector length and, hence, the Brillouin frequency shift [21].

As both the energy and the momentum must be conserved during each scattering event, the frequencies, and the wave vectors of the three waves are related by

$${\Omega }_B=v_p-v_s, k_A=k_p-k_s$$

(2)

where v_p and v_s. are the frequencies, and k_p and k_s are the wave vectors, of the pump and Stokes waves, respectively.

The total intensity I (R, t) of the pump light and SBS light has the form of the traveling wave

$$I\left(R,t\right)={\left|E\left(R,t\right)\right|}^2={\left|E_P\right|}^2+{\left|E_S\right|}^2+2\left|E_P{E}_S\right|\cos \left({\Omega }_{B}t-q\cdot R+\varphi \right)$$

(3)

$$q=k_P-k_S, \varphi =\arg E_s-\arg E_P$$

(4)

As shown in the dotted box in Figure 1a, the total light field consists of three frequencies of light: pump light (v_s), SBS light (v_B), and signal light with Doppler shift (v_sig). Due to the high-frequency cut-off characteristics of the detector, only differential frequency electrical signals can be obtained. This difference in frequency consists of two parts: the Doppler frequency shift of the motion information and the frequency shift of the Brillouin reference light. The Doppler frequency is what needs to be obtained and changes over time. However, the Brillouin shift is stable when the length of the optical fiber is fixed, and the intensity I (R, t) is the sum signal with up-shifted Ω_B frequency. The difference signal can be obtained by using time–frequency analysis methods, such as the short-time Fourier transform. The relationship between the velocity of an object and the frequency of the Doppler signal is as follows:

$$\mathrm{u}=\frac{{\lambda }_0}{2}\left(v_D-{\Omega }_B\right)$$

(5)

where v_D is the frequency of the Doppler signal. Ω_B is thefrequency corresponding to the fundamental frequency v_base in Figure 1b.

3. Experimental Setup and Results

This section begins with an introduction to the optical path of the velocimetry system, verifying the optical coherence and measuring the threshold and line width. By designing speed measurement experiments with different speeds, the speed measurement accuracy and time-resolution performance of SBS-PDV are compared with the current homodyne velocimetry (DPS) and heterodyne velocimetry (DLHV).

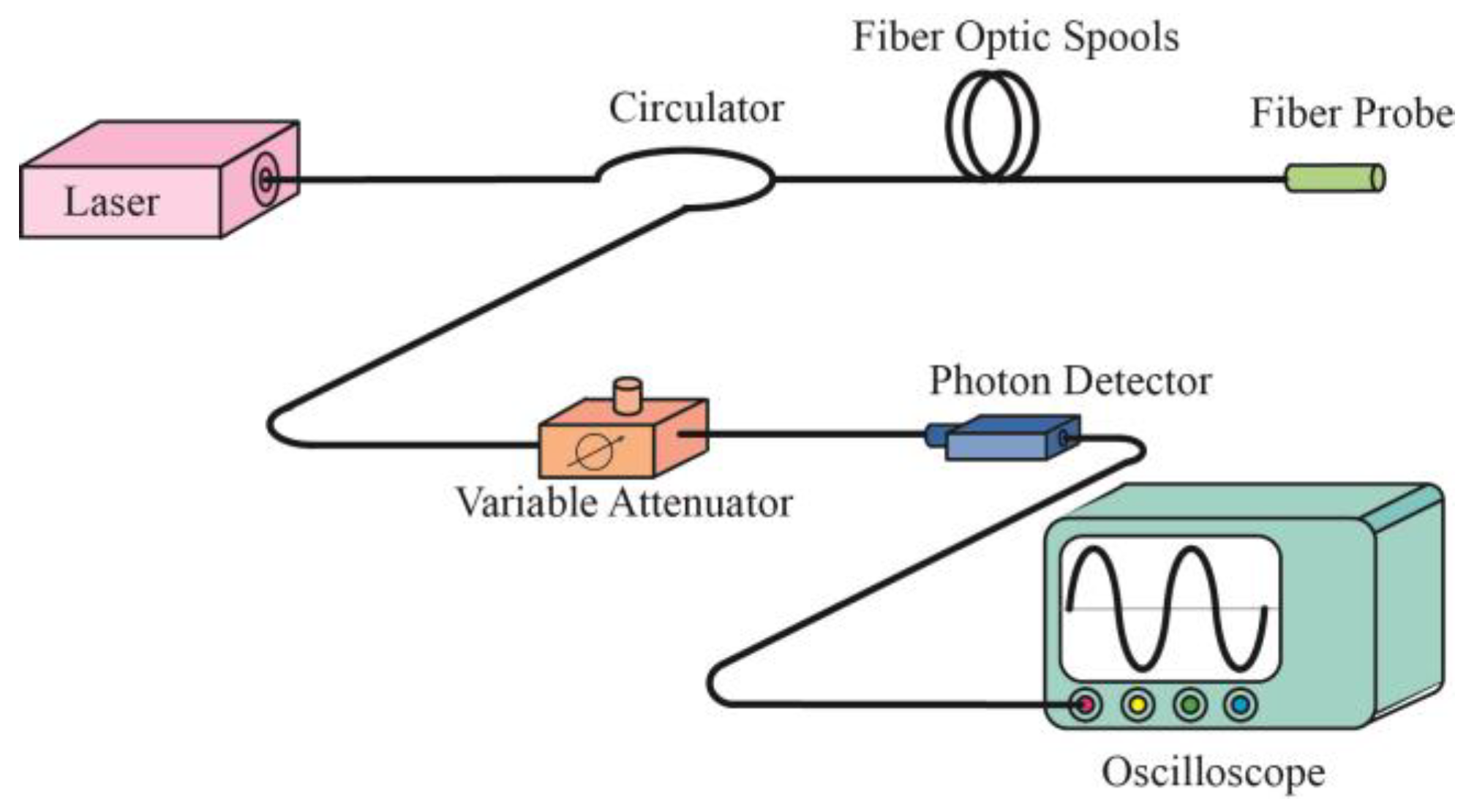
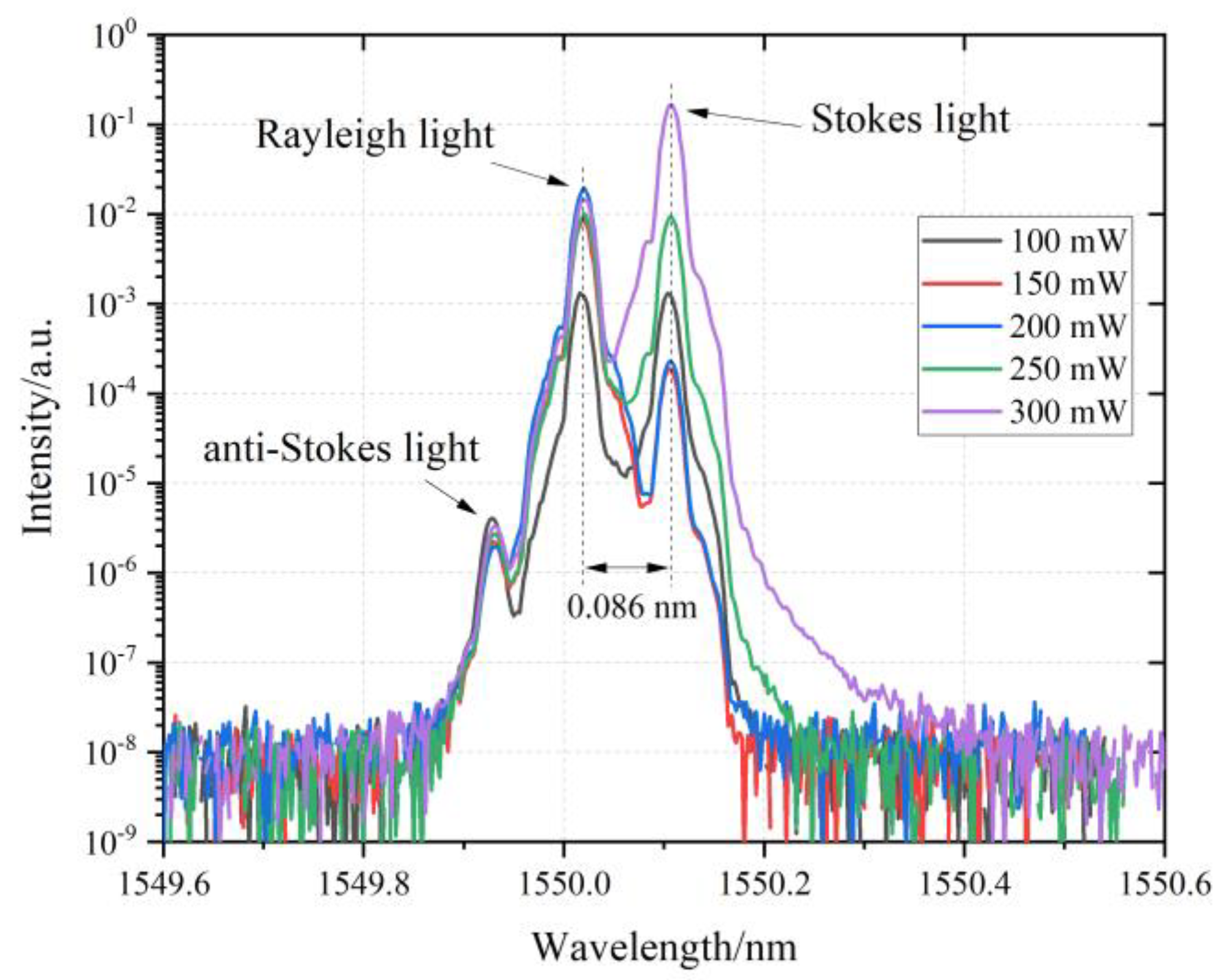
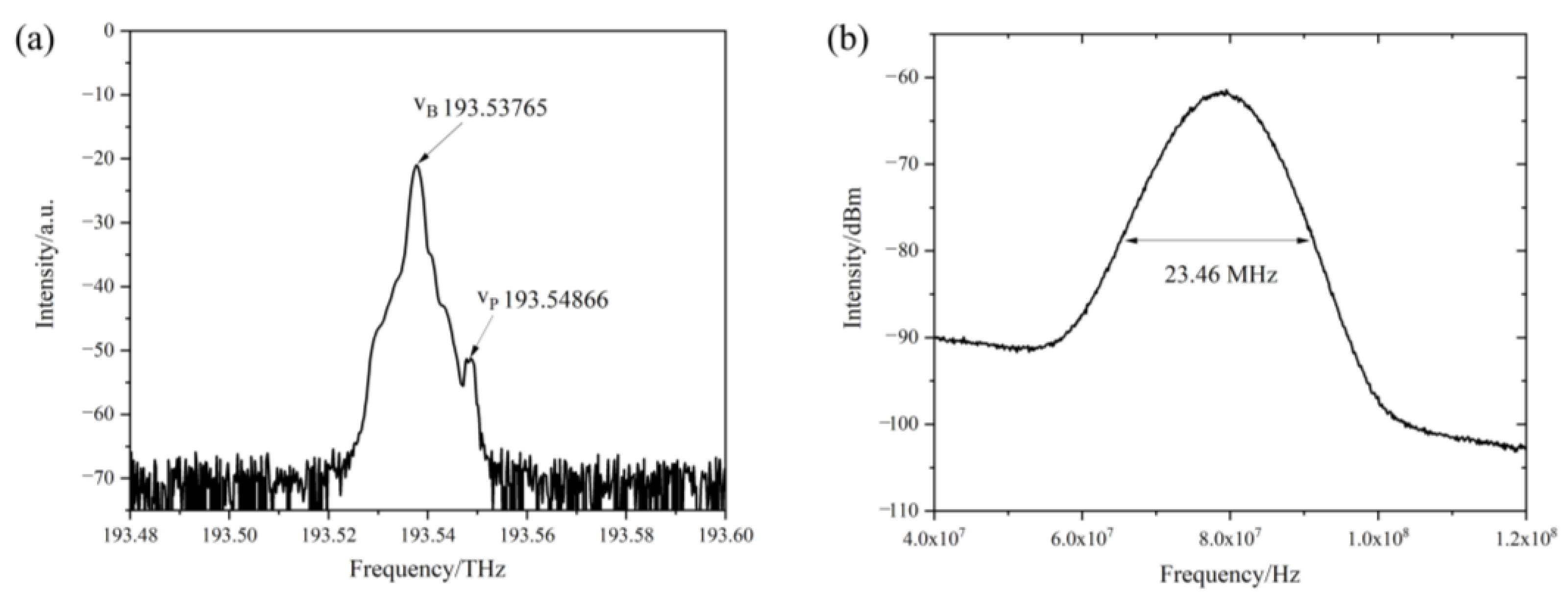
3.1. Optical Setup and System Characterization

According to the optical path structure shown in Figure 1a, a heterodyne laser interferometry velocimeter based on Brillouin scattered light can be set up as shown in Figure 2. The interference phenomenon of Brillouin scattering light and signal is described in this section.

The optical setup consists of a single-frequency laser (wavelength: 1549.90 nm, maximum output power: 1 W), which enters fiber optical spools (several kilometers) through a fiber circulator, which generate the Brillouin scattering light backward to the circulator. Meanwhile, a large proportion of forward-propagating light detects the moving surface through the fiber probe. The light containing the Doppler signal from the moving surface mixes with the reference light from the Brillouin scattering, which generates the interference fringes detected by the spectrum analyzer as shown in Figure 2. The Doppler-shifted signal is then combined with the SBS to achieve a beat frequency, which is ~11 GHz because the SBS has a lower frequency than the incident light. To avoid saturating the photoelectric detector, the optical variable attenuator should be inserted and the total signal power should be carefully guided to the detector.

Figure 3 shows the 1000 m long optical-fiber spools, which are fed with different power pump light to produce Stokes light and Rayleigh light. The wavelength difference between the two kinds of light is 0.086 nm, that is, a frequency difference of 10.75 GHz. The peak power of SBS light increases gradually with the increase in the pump power. This result confirms that this is the appropriate input power to adjust the power of the SBS light as the reference light.

The threshold of SBS can be estimated by the following formula:

$$P_{th}=G\frac{A_{eff}}{g_0{L}_{eff}},L_{eff}=\left[1-e^{-\alpha L}\right]/\alpha$$

(6)

where A_eff is the effective core area, G is the gain factor of SBS, g₀ is the gain peak of SBS, L_eff is the effective length of the fiber, and α is the loss per kilometer. From the above equation, the Stokes light intensity increases exponentially with the enhancement of pump light. Figure 4 illustrates the change in SBS threshold and power as the input power increases. With the increase in input power, the SBS power increases exponentially. When using a 1000 m fiber, an input power of 150 mW can produce about 120 μW of SBS light. At the same time, it can ensure that enough light is emitted to the surface of the test object through the fiber-optic probe. Generally, the receiving efficiency of the probe is not higher than −40 dB, and the signal light intensity drops sharply in dynamic experiments, so it is necessary to set the power of the reference light (hundreds of microwatts) higher to ensure the contrast of the interference fringes. Therefore, the input power needs to be adjusted to the appropriate value to ensure that the SBS optical power is in the hundreds of microwatts as a reference light, and the forward transmission of light to the probe has enough power, that is, in the tens of microwatts, for detection.

When the detecting target is static relative to the probe, the laser is directly reflected from the surface back to the probe into the circulator. Brillouin scattering light is stimulated when the power of the laser reaches the threshold. Therefore, the light from the fiber laser and Brillouin scattering can be observed after the third port of the circulator by the spectrograph (1 MHz frequency resolution), as shown in Figure 5a. After the baseline subtraction, the peak position was found and the peak fitting process was performed. The frequency of Brillouin scattering light at about 193.53765 THz (with the standard error of 1.07959 × 10⁻⁴) is lower than the main laser (193.54866 THz with the standard error of 1.93466 × 10⁻⁴) by 11.01 GHz, which is a frequency shift caused by the stimulated effect, and the bandwidth of Brillouin is about 23.46 MHz, as shown in Figure 5b. Because the reference light by Brillouin scattering is lower than the detecting laser, the base frequency is ~11 GHz and heterodyne velocimetry is upshifted, which indicates that positive Doppler shifts increase the beat frequency. The advantage of upshifted PDV is that it starts with a non-zero beat frequency, which preserves low-velocity transient and directional information.

According to the optical path built in Figure 2, the base frequency linewidth after the interference between SBS light and detection light is about ~24 MHz. The velocity resolution corresponding to this linewidth is 20 m/s. Since the base frequency is about 11 GHz, the time resolution corresponds to a half-cycle of 90 ps. The upper limit of the velocity measurement is related to the bandwidth of the oscilloscope and detector. The input laser power is related to the SBS threshold, however, and is limited by the receiving efficiency of the probe. As can be seen from Figure 5, when the input power is 150 mW, the SBS power is 120 μW, and the output power of the probe is 80 mW, which can satisfy the requirements of the probe’s receiving efficiency.

3.2. Low-speed Validation Experiments

Doppler Pins System (DPS) and Photonic Doppler Velocimetry (PDV) have been widely used in shockwave physics experiments as a common velocity measurement technology, which are both homodyne interference. The two speed measurement technologies of SBS-PDV and DPS were compared and tested for the low-speed movement process (usually within the hundreds of meters per second), such as one-stage light-gas gun or Hopkinson bar experiment. The first-stage light-gas gun uses high-pressure compressed gas to drive metal flyer to hit metal targets at a speed of hundreds of meters per second to produce a high-pressure and high-temperature state, as shown in Figure 6a. In this experiment, a copper flyer is used to hit a steel target, and the back surface of the steel moves under the impact, and the fiber probes of two technologies are used to measure the change in the velocity of the free surface, as shown in Figure 6b. The optical path structure of the two is basically the same, as shown in Figure 1a, but the difference is the return loss value of the probe, for which the SBS-PDV is −60 dB and the DPS is −20 dB.

In low-speed measurement experiments, SBS-PDV uses a probe with no return loss compared to DPS, so that more optical power can be used to detect the measured surface, which means a stronger signal received. Both velocimetry techniques measure speeds in a range of 200 m/s in 1 μs. In addition, SBS-PDV has manymore interference fringes per unit of time than DPS on the time-domain signal due to its up-conversion measurement, as shown in Figure 7a. As a result, there are more data points per unit of time of SBS-PDV on frequency domain signals, especially in low-speed processes, as shown in Figure 7b. The time resolution of SBS-PDV can reach 5 ns, which is 3 times higher than the time resolution of 16 nanoseconds of DPS. The motion start time interpreted by SBS-PDV is 26 ns earlier than the time judged by DPS. In addition, when the movement speed reaches its first peak, the SBS-PDV is 213 m/s, while the DPS is only 199 m/s, a difference of 14 m/s. In this way, higher time and velocity resolution can be obtained by SBS-PDV, especially when it is necessary to determine the time of motion jump. This is also the unique advantage of up-conversion heterodyne technology compared with homodyne technology.

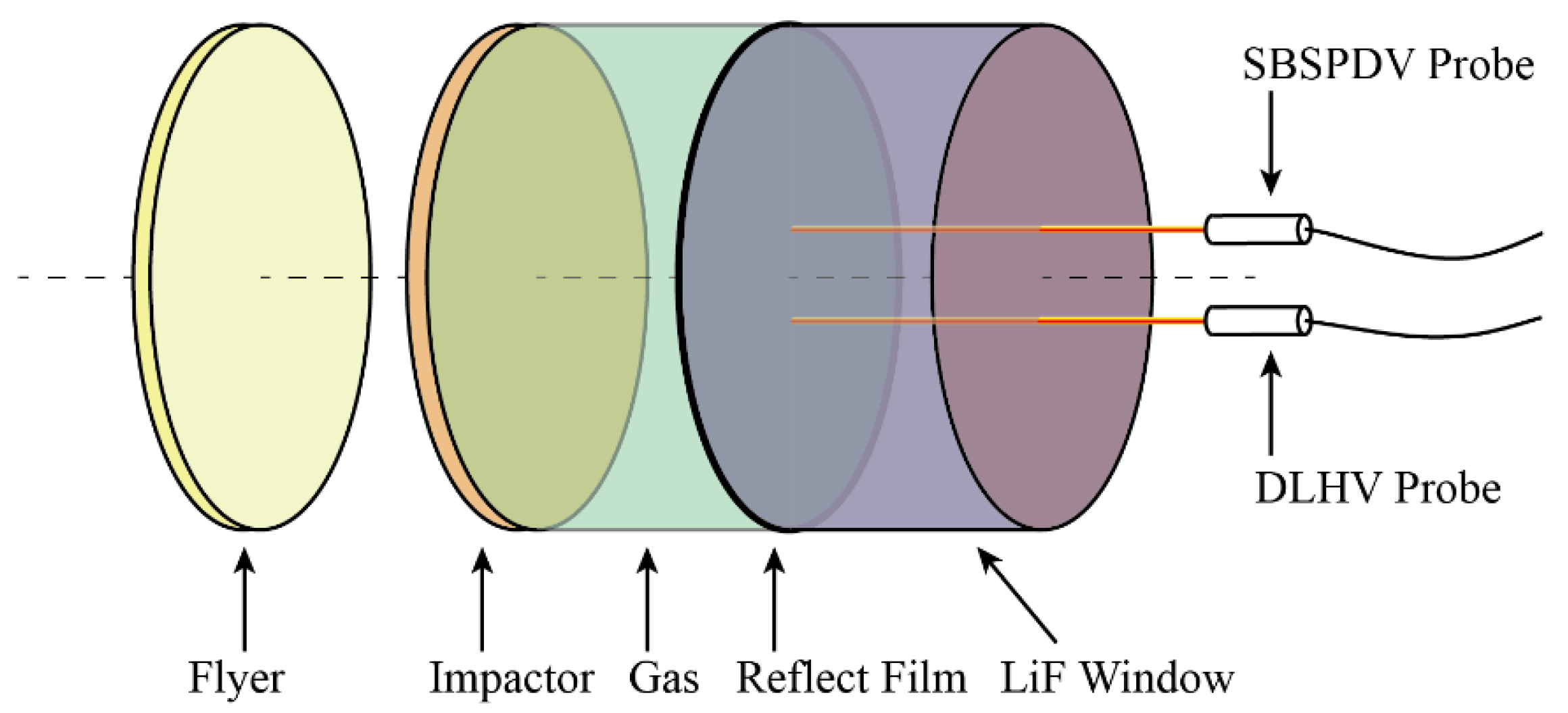
3.3. High-Speed Validation Experiments

Dual-Laser Heterodyne Velocimetry (DLHV) can be used for multiplexing as a heterodyne velocity measurement technique, which is a non-coaxial optical path. SBS-PDV and DLHV technology were compared in terms of measuring high-speed motion processes on the two-stage light-gun. The complex loading path experiment is designed to lead to the complexity of the velocity curve to be measured, so as to verify the measurement ability of SBS-PDV technology for complex velocity. The multiple reflection impact compression technology can effectively improve the compression ratio of substances, which provides a reference for the study of dynamic compression characteristics of substances. The experimental target device has a sandwich structure composed of high-impedance materials at both ends and an intermediate sample cavity, which generates a shock wave through the external action of the high-impedance layer at one end, transmits into the sample cavity, and compresses the sample. When the shock wave propagates to the interface between the sample chamber and the high-impedance layer at the other end, the shock wave will be reflected to the sample chamber and the sample will be compressed again according to the principle of wave system. In this repeated cycle, the shock wave propagates repeatedly in the cavity, and the sample undergoes multiple reflections and compression until it stabilizes to a final state.

Astrosphere structure evolution and the confinement fusion process both concern the thermodynamic state of material in extreme conditions. In many aspects of the dynamic process, the equation of the state of warm dense matter (WDM) at high temperatures and high pressures plays an important role. The state diagnosis of opaque plasma generated by multiple reverberation shock compression is a key problem. The particle velocity profile history of the interface between gas and window was measured by DLHV and SBS-PDV, as shown in Figure 8.

To test and verify each other, DLHV and SBS-PDV use the same probe, which is distributed on the two symmetrical sides. Because reference light is emitted from another laser or Brillouin scattering light, the return loss of the above-mentioned probe is −60 dB, which means that there is no reflected light from the end face of the probe.

The experimental results of SBS-PDV were compared with DLHV, which is another heterodyne technique. Warm dense gas was compressed at a certain pressure and density and enclosed in a target cavity before the experiment. A flyer was driven by a two-stage light-gas gun at several km/s velocity and a stroke impactor to generate a shock wave. The particle velocity of the interface between the sample and the LiF window was measured by using DLHV and SBS-PDV. When the shock wave reached the interface for the first time, the interface would reflect the shock wave to compress the sample and meanwhile transmit the shock wave to compress the window. Therefore, the particle velocity of the interface would change incrementally, as shown in Figure 9b.

An example of the particle velocity of the interface was obtained in a two-stage light-gas gun experiment in which the light from the DLHV and SBS-PDV probes passed through lithium fluoride (LiF) windows to the Ta surface. Each turn of the velocity curve in the spectrum reflects the process by which the gas is once again compressed by the shock wave. The resulting spectrogram of SBS-PDV, presented in Figure 9a, shows that every step of the profile is in accordance with the characteristic line of transmission shown in Figure 9b. In this case, the beat wave form was recorded at a sample rate of 100 GS/s for 10 μs. The start positions of beat frequency on the vertical axis were ~2.4 GHz and ~11 GHz for DLHV and SBS-PDV, respectively.

As can be seen from the Figure 9b, when the shock wave enters the sample, the measurement signal shows the characteristics of a plateau (between t₁ and t₂) that rises rapidly and then tends to be stable, indicating that the affected gas undergoes a process from thin to thick. The signal platform means that the primary impact temperature of the gas tends to be stable. Subsequently, the shock wave propagates by transmission to the interface of the two LiF windows (point t₃). Point t₄ corresponds to multiple reflections of shock waves in the sample into the window and re-impact on the interface of the two LiF windows.

Both velocimetry techniques measure speeds of 2000 m/s in 1 μs, as shown in Figure 10. The velocity time histories measured by DLHV and SBS-PDV were matched well with each other, with a typical characteristic inflection and time report process under multiple reverberation shock compression, as shown in Figure 10. Both velocity profiles also provided shock arrival data with sub-nanosecond precision, especially for SBS-PDV with higher base frequency. The velocity accuracy of SBS-PDV is within 0.8% of the accuracy of DLHV.

4. Conclusions

Based on stimulated Brillouin scattering effect in optical fibers, a heterodyne mixing velocimetry technology, SBS-PDV, is proposed, which has the advantages of single laser and coaxial optical path structure, especially suitable for long-distance measurement. Firstly, the structure of the interference optical path still adopts the characteristics of homodyne interference and the coaxial optical path, which is both simple and resistant to environmental factors. The base frequency linewidth is about ~24 MHz and the velocity resolution is ~20 m/s. Secondly, heterodyne velocimetry originally needs two different wavelengths of light to generate non-zero origin of frequency difference. Stimulated Brillouin scattering–PDV with only one laser realized upshifted heterodyne velocimetry and can also measure over long distances due to fiber spools running to many kilometers in length. Finally, due to the need to excite Brillouin scattered light, the input laser power can be increased to ensure that the probe has enough light for detection, just at the right balance point to meet the fringe contrast.

In conclusion, SBS-PDV has more data points and 3 times temporal resolution than DPS in low-speed measurement, which facilitates the judgment of the motion start time. It has also demonstrated a reliable SBS-PDV for shock wave velocity measurements compared directly to DLHV. SBS-PDV is single-laser upshifted heterodyne velocimetry, so it can achieve heterodyne measurement much more easily. Furthermore, the time and velocity resolutions are both higher than those of DPS and DLHV because of SBS-PDV’s higher base frequency. The temporal resolution can be within 100 picoseconds, while the velocity resolution can reach 20 m/s. Compared to DLHV, the velocity accuracy can be better than 0.8%. Therefore, SBS-PDV is a coaxial heterodyne velocity measurement technology with simple structure and high accuracy.