Associations between Ocular Biometry, Refractive Error, and Body Characteristics
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Procedure
2.3. Data Processing
2.3.1. Refractive Components
2.3.2. Height Percentile
2.4. Statistical Analysis
3. Results
3.1. Correlations between Refractive Parameters, AL, Body Height, and Age
3.2. Correlations between Refractive Parameters, AL, and Age Based on Sex
3.3. Differences in Body Height and SE Based on AL
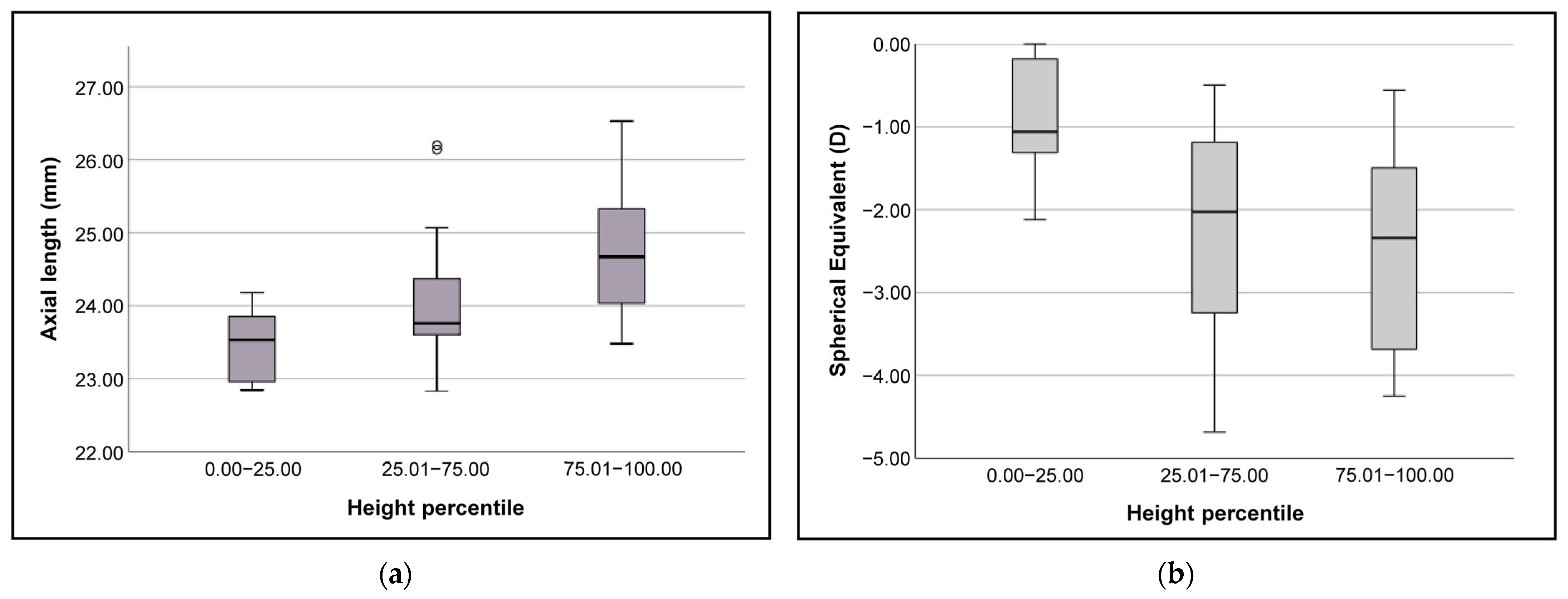
3.4. Differences in AL and SE Based on Body Height Percentile
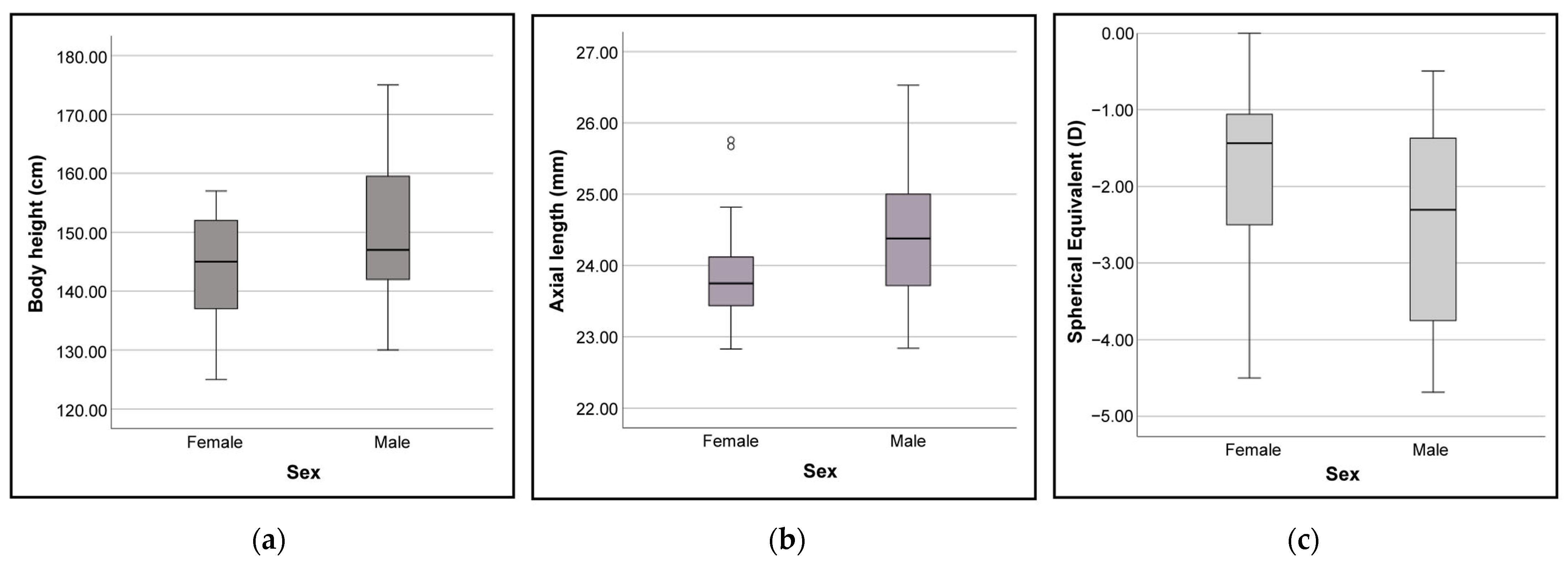
3.5. Differences in Body Height, AL, and SE Based on Sex
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holden, B.A.; Fricke, T.R.; Wilson, D.A.; Jong, M.; Naidoo, K.S.; Sankaridurg, P.; Wong, T.Y.; Naduvilath, T.J.; Resnikoff, S. Global Prevalence of Myopia and High Myopia and Temporal Trends from 2000 through 2050. Ophthalmology 2016, 123, 1036–1042. [Google Scholar] [CrossRef]
- Mohd-Ali, B.; Low, Y.C.; Shahimin, M.M.; Arif, N.; Abdul Hamid, H.; Wan Abdul Halim, W.H.; Mokri, S.S.; Baseri Huddin, A.; Mohidin, N. Ocular Dimensions, Refractive Error, and Body Stature in Young Chinese Children with Myopia in Kuala Lumpur, Malaysia. Clin. Optom. 2022, 14, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Wnekowicz-Augustyn, E.; Teper, S.; Wylegala, E. Preventing the Progression of Myopia in Children—A Review of the Past Decade. Medicina 2023, 59, 1859. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Xiao, F.; Cheng, W. Eye exercises for myopia prevention and control: A comprehensive systematic review and meta-analysis of controlled trials. Eye 2023. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.; Si, J.; Wang, X.; Lu, X.; Bi, H. Orthokeratology for Slowing Myopia Progression in Children: A Systematic Review and Meta-Analysis of Randomized Controlled Trials. Eye Contact Lens 2023, 49, 404–410. [Google Scholar] [CrossRef] [PubMed]
- Kaiti, R.; Shyangbo, R.; Sharma, I.P.; Dahal, M. Review on current concepts of myopia and its control strategies. Int. J. Ophthalmol. 2021, 14, 606–615. [Google Scholar] [CrossRef] [PubMed]
- Rozema, J.; Dankert, S.; Iribarren, R. Emmetropization and nonmyopic eye growth. Surv. Ophthalmol. 2023, 68, 759–783. [Google Scholar] [CrossRef] [PubMed]
- Dirani, M.; Islam, A.; Baird, P.N. Body stature and myopia-The Genes in Myopia (GEM) twin study. Ophthalmic Epidemiol. 2008, 15, 135–139. [Google Scholar] [CrossRef] [PubMed]
- Yip, V.C.; Pan, C.W.; Lin, X.Y.; Lee, Y.S.; Gazzard, G.; Wong, T.Y.; Saw, S.M. The relationship between growth spurts and myopia in Singapore children. Investig. Ophthalmol. Vis. Sci. 2012, 53, 7961–7966. [Google Scholar] [CrossRef]
- Tao, L.; Wang, C.; Peng, Y.; Xu, M.; Wan, M.; Lou, J.; Yu, X. Correlation Between Increase of Axial Length and Height Growth in Chinese School-Age Children. Front. Public Health 2021, 9, 817882. [Google Scholar] [CrossRef]
- Ojaimi, E.; Morgan, I.G.; Robaei, D.; Rose, K.A.; Smith, W.; Rochtchina, E.; Mitchell, P. Effect of stature and other anthropometric parameters on eye size and refraction in a population-based study of Australian children. Investig. Ophthalmol. Vis. Sci. 2005, 46, 4424–4429. [Google Scholar] [CrossRef] [PubMed]
- Kearney, S.; Strang, N.C.; Cagnolati, B.; Gray, L.S. Change in body height, axial length and refractive status over a four-year period in caucasian children and young adults. J. Optom. 2020, 13, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, H.; Pakzad, R.; Khabazkhoob, M.; Yekta, A.; Emamian, M.H.; Fotouhi, A. Ocular biometrics as a function of age, gender, height, weight, and its association with spherical equivalent in children. Eur. J. Ophthalmol. 2021, 31, 688–697. [Google Scholar] [CrossRef] [PubMed]
- Tricard, D.; Marillet, S.; Ingrand, P.; Bullimore, M.A.; Bourne, R.R.A.; Leveziel, N. Progression of myopia in children and teenagers: A nationwide longitudinal study. Br. J. Ophthalmol. 2022, 106, 1104–1109. [Google Scholar] [CrossRef] [PubMed]
- Rudnicka, A.R.; Kapetanakis, V.V.; Wathern, A.K.; Logan, N.S.; Gilmartin, B.; Whincup, P.H.; Cook, D.G.; Owen, C.G. Global variations and time trends in the prevalence of childhood myopia, a systematic review and quantitative meta-analysis: Implications for aetiology and early prevention. Br. J. Ophthalmol. 2016, 100, 882–890. [Google Scholar] [CrossRef] [PubMed]
- Villarreal, M.G.; Ohlsson, J.; Abrahamsson, M.; Sjostrom, A.; Sjostrand, J. Myopisation: The refractive tendency in teenagers. Prevalence of myopia among young teenagers in Sweden. Acta Ophthalmol. Scand. 2000, 78, 177–181. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Zhao, Z.; Wei, N.; Qi, X.; Ding, G.; Li, X.; Li, J.; Song, L.; Zhang, Y.; et al. School-based epidemiology study of myopia in Tianjin, China. Int. Ophthalmol. 2020, 40, 2213–2222. [Google Scholar] [CrossRef]
- Enthoven, C.; Haarman, A.E.G.; Swierkowska, J.; Tideman, W.; Polling, J.R.; Verhoeven, V.J.; Klaver, C.C.W. Gender predisposition to myopia shifts to girls in the young generation. Investig. Ophthalmol. Vis. Sci. 2021, 62, 2331. [Google Scholar]
- Morgan, P.B.; McCullough, S.J.; Saunders, K.J. Estimation of ocular axial length from conventional optometric measures. Contact Lens Anterior Eye 2020, 43, 18–20. [Google Scholar] [CrossRef]
- Queiros, A.; Amorim-de-Sousa, A.; Fernandes, P.; Ribeiro-Queiros, M.S.; Villa-Collar, C.; Gonzalez-Meijome, J.M. Mathematical Estimation of Axial Length Increment in the Control of Myopia Progression. J. Clin. Med. 2022, 11, 6200. [Google Scholar] [CrossRef]
- Moore, M.; Lingham, G.; Flitcroft, D.I.; Loughman, J. Myopia progression patterns among paediatric patients in a clinical setting. Ophthalmic Physiol. Opt. 2024, 44, 258–269. [Google Scholar] [CrossRef]
- Güemes-Villahoz, N.; Gómez de Liano, R.; Porras Ángel, P.; Talavero González, P.; Bella Gala, R.; Martín García, B.; Burgos Blasco, B.; Hernández García, E.; Chamorro Herrera, M.; Hernández-Verdejo, J.L.; et al. Lifestyle Factors in Myopic Spanish Children. Children 2024, 11, 139. [Google Scholar] [CrossRef]
- Atchison, D.A.; Jones, C.E.; Schmid, K.L.; Pritchard, N.; Pope, J.M.; Strugnell, W.E.; Riley, R.A. Eye shape in emmetropia and myopia. Investig. Ophthalmol. Vis. Sci. 2004, 45, 3380–3386. [Google Scholar] [CrossRef] [PubMed]
- Cooper, J.; Tkatchenko, A.V. A Review of Current Concepts of the Etiology and Treatment of Myopia. Eye Contact Lens 2018, 44, 231–247. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Lai, Y.; Sun, L.; Li, S.; Ding, X. High Myopia is Common in Patients with X-Linked Retinopathies: Myopic Maculopathy Analysis. Retina 2024, 44, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Kraus, C.L.; Trivedi, R.H.; Wilson, M.E. Intraocular lens exchange for high myopia in pseudophakic children. Eye 2016, 30, 1199–1203. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Queiruga, J.; Pena-Verdeal, H.; Sabucedo-Villamarin, B.; Giraldez, M.J.; Garcia-Resua, C.; Yebra-Pimentel, E. A cross-sectional study of non-modifiable and modifiable risk factors of dry eye disease states. Contact Lens Anterior Eye 2023, 46, 101800. [Google Scholar] [CrossRef] [PubMed]
- Noya-Padin, V.; Nores-Palmas, N.; Giraldez, M.J.; Yebra-Pimentel, E.; Pena-Verdeal, H. Comparison between Ocular Biometric Parameters and Intraocular Pressure with and without Contact Lenses. Eye Contact Lens 2023, 49, 464–470. [Google Scholar] [CrossRef] [PubMed]
- Davies, L.N.; Mallen, E.A.; Wolffsohn, J.S.; Gilmartin, B. Clinical evaluation of the Shin-Nippon NVision-K 5001/Grand Seiko WR-5100K autorefractor. Optom. Vis. Sci. 2003, 80, 320–324. [Google Scholar] [CrossRef] [PubMed]
- Kuo, Y.C.; Wang, J.H.; Chiu, C.J. Comparison of open-field autorefraction, closed-field autorefraction, and retinoscopy for refractive measurements of children and adolescents in Taiwan. J. Formos. Med. Assoc. 2020, 119, 1251–1258. [Google Scholar] [CrossRef]
- Sabur, H.; Takes, O. Agreement of axial length and anterior segment parameters measured with the MYAH device compared to Pentacam AXL and IOLMaster 700 in myopic children. Int. Ophthalmol. 2023, 43, 475–482. [Google Scholar] [CrossRef]
- Thibos, L.N.; Wheeler, W.; Horner, D. Power vectors: An application of Fourier analysis to the description and statistical analysis of refractive error. Optom. Vis. Sci. 1997, 74, 367–375. [Google Scholar] [CrossRef]
- Flegal, K.M.; Cole, T.J. Construction of LMS parameters for the Centers for Disease Control and Prevention 2000 growth charts. In National Health Statistics Reports; U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Center for Health Statistics: Hyattsville, MD, USA, 2013; pp. 1–3. [Google Scholar]
- Services, F.I. Percentiles de Estatura para la Edad Según los CDC en Chicos (de 2 a 20 años). Available online: https://www.msdmanuals.com/medical-calculators/CDCHeightForAgeBoys-es.htm (accessed on 26 December 2023).
- Services, F.I. Percentiles de Estatura para la Edad Según los CDC en Chicas (de 2 a 20 años). Available online: https://www.msdmanuals.com/medical-calculators/CDCHeightForAgegirls-es.htm (accessed on 26 December 2023).
- Armstrong, R.A.; Davies, L.N.; Dunne, M.C.; Gilmartin, B. Statistical guidelines for clinical studies of human vision. Ophthalmic Physiol. Opt. 2011, 31, 123–136. [Google Scholar] [CrossRef]
- Dunn, G. Design and Analysis of Reliability Studies: The Statistical Evaluation of Measurement Errors; Edward Arnold Publishers: New York, NY, USA; Oxford University Press: London, UK, 1989. [Google Scholar]
- Armstrong, R.A. When to use the Bonferroni correction. Ophthalmic Physiol. Opt. 2014, 34, 502–508. [Google Scholar] [CrossRef] [PubMed]
- Truckenbrod, C.; Meigen, C.; Brandt, M.; Vogel, M.; Sanz Diez, P.; Wahl, S.; Jurkutat, A.; Kiess, W. Longitudinal analysis of axial length growth in a German cohort of healthy children and adolescents. Ophthalmic Physiol. Opt. 2021, 41, 532–540. [Google Scholar] [CrossRef] [PubMed]
- Simpson, S.H. Creating a Data Analysis Plan: What to Consider When Choosing Statistics for a Study. Can. J. Hosp. Pharm. 2015, 68, 311–317. [Google Scholar] [CrossRef] [PubMed]
- Chaves, R.; Baxter-Jones, A.; Souza, M.; Santos, D.; Maia, J. Height, weight, body composition, and waist circumference references for 7- to 17-year-old children from rural Portugal. Homo 2015, 66, 264–277. [Google Scholar] [CrossRef] [PubMed]
- Selovic, A.; Juresa, V.; Ivankovic, D.; Malcic, D.; Selovic Bobonj, G. Relationship between axial length of the emmetropic eye and the age, body height, and body weight of schoolchildren. Am. J. Hum. Biol. 2005, 17, 173–177. [Google Scholar] [CrossRef]
- Okabe, N.; Takahashi, A.; Shigemoto, Y.; Kogure, C.; Ooka, T.; Shinohara, R.; Otawa, S.; Kobayashi, A.; Horiuchi, S.; Kushima, M.; et al. Refractive Error and Axial Length and Their Related Factors in 8-Year-Old Japanese Children: The Yamanashi Adjunct Study of the Japan Environment and Children’s Study (JECS). J. Clin. Med. 2023, 12, 5929. [Google Scholar] [CrossRef]
- Lu, T.L.; Wu, J.F.; Ye, X.; Hu, Y.Y.; Wu, H.; Sun, W.; Guo, D.D.; Wang, X.R.; Bi, H.S.; Jonas, J.B. Axial Length and Associated Factors in Children: The Shandong Children Eye Study. Ophthalmologica 2016, 235, 78–86. [Google Scholar] [CrossRef]
- Bikbov, M.M.; Kazakbaeva, G.M.; Gilmanshin, T.R.; Zainullin, R.M.; Arslangareeva, I.I.; Salavatova, V.F.; Bikbova, G.M.; Panda-Jonas, S.; Nikitin, N.A.; Zaynetdinov, A.F.; et al. Axial length and its associations in a Russian population: The Ural Eye and Medical Study. PLoS ONE 2019, 14, e0211186. [Google Scholar] [CrossRef]
- Mlakar, M.; Gradisek, A.; Lustrek, M.; Jurak, G.; Soric, M.; Leskosek, B.; Starc, G. Adult height prediction using the growth curve comparison method. PLoS ONE 2023, 18, e0281960. [Google Scholar] [CrossRef]
- Wang, D.; Ding, X.; Liu, B.; Zhang, J.; He, M. Longitudinal changes of axial length and height are associated and concomitant in children. Investig. Ophthalmol. Vis. Sci. 2011, 52, 7949–7953. [Google Scholar] [CrossRef]
- Mutti, D.O.; Mitchell, G.L.; Jones, L.A.; Friedman, N.E.; Frane, S.L.; Lin, W.K.; Moeschberger, M.L.; Zadnik, K. Axial growth and changes in lenticular and corneal power during emmetropization in infants. Investig. Ophthalmol. Vis. Sci. 2005, 46, 3074–3080. [Google Scholar] [CrossRef]
- Gonzalez Blanco, F.; Sanz Fernandez, J.C.; Munoz Sanz, M.A. Axial length, corneal radius, and age of myopia onset. Optom. Vis. Sci. 2008, 85, 89–96. [Google Scholar] [CrossRef]
- Jong, M.; Sankaridurg, P.; Naduvilath, T.J.; Li, W.; He, M. The Relationship between Progression in Axial Length/Corneal Radius of Curvature Ratio and Spherical Equivalent Refractive Error in Myopia. Optom. Vis. Sci. 2018, 95, 921–929. [Google Scholar] [CrossRef]
- Schappi, J.; Stringhini, S.; Guessous, I.; Staub, K.; Matthes, K.L. Body height in adult women and men in a cross-sectional population-based survey in Geneva: Temporal trends, association with general health status and height loss after age 50. BMJ Open 2022, 12, e059568. [Google Scholar] [CrossRef] [PubMed]
- Harb, E.N.; Wildsoet, C.F. Nutritional Factors and Myopia: An Analysis of National Health and Nutrition Examination Survey Data. Optom. Vis. Sci. 2021, 98, 458–468. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, H.; Jafarzadehpur, E.; Ghaderi, S.; Yekta, A.; Ostadimoghaddam, H.; Norouzirad, R.; Khabazkhoob, M. Ocular components during the ages of ocular development. Acta Ophthalmol. 2015, 93, e74–e81. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Median [IQR] | Range |
|---|---|---|
| Sphere power (D) | −1.68 [2.10] | −4.50 to −0.12 |
| Cylindrical power (D) | −0.37 [0.47] | −1.50 to 0.00 |
| SE (D) | −1.84 [2.17] | −4.69 to −0.12 |
| J0 vector | 0.00 [0.20] | −0.75 to 0.62 |
| J45 vector | 0.00 [0.20] | −0.43 to 0.68 |
| AL (mm) | 23.86 [1.01] | 22.83 to 26.53 |
| Body height (cm) | 146.00 [15.75] | 125 to 175 |
| Height percentile | 53.18 [41.39] | 4.46 to 99.04 |
| Sph Power | Cyl Power | Cyl Axis | SE | J0 | J45 | AL | Height | ||
|---|---|---|---|---|---|---|---|---|---|
| AL | rs | −0.558 * | −0.150 | 0.119 | −0.571 * | −0.138 | −0.080 | ||
| p | <0.001 | 0.208 | 0.321 | <0.001 | 0.248 | 0.506 | |||
| Height | rs | −0.303 * | −0.157 | −0.004 | −0.315 * | −0.276 * | 0.012 | 0.283 * | |
| p | 0.010 | 0.188 | 0.973 | 0.007 | 0.019 | 0.923 | 0.016 | ||
| Age | rs | −0.134 | −0.096 | 0.008 | −0.145 | −0.219 | 0.008 | 0.143 | 0.839 * |
| p | 0.260 | 0.423 | 0.949 | 0.223 | 0.065 | 0.950 | 0.231 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noya-Padin, V.; Nores-Palmas, N.; Garcia-Queiruga, J.; Giraldez, M.J.; Pena-Verdeal, H.; Yebra-Pimentel, E. Associations between Ocular Biometry, Refractive Error, and Body Characteristics. Photonics 2024, 11, 165. https://doi.org/10.3390/photonics11020165
Noya-Padin V, Nores-Palmas N, Garcia-Queiruga J, Giraldez MJ, Pena-Verdeal H, Yebra-Pimentel E. Associations between Ocular Biometry, Refractive Error, and Body Characteristics. Photonics. 2024; 11(2):165. https://doi.org/10.3390/photonics11020165
Chicago/Turabian StyleNoya-Padin, Veronica, Noelia Nores-Palmas, Jacobo Garcia-Queiruga, Maria J. Giraldez, Hugo Pena-Verdeal, and Eva Yebra-Pimentel. 2024. "Associations between Ocular Biometry, Refractive Error, and Body Characteristics" Photonics 11, no. 2: 165. https://doi.org/10.3390/photonics11020165
APA StyleNoya-Padin, V., Nores-Palmas, N., Garcia-Queiruga, J., Giraldez, M. J., Pena-Verdeal, H., & Yebra-Pimentel, E. (2024). Associations between Ocular Biometry, Refractive Error, and Body Characteristics. Photonics, 11(2), 165. https://doi.org/10.3390/photonics11020165








