Deep Learning for Polarization Optical System Automated Design
Abstract
1. Introduction
2. The Basic Principle
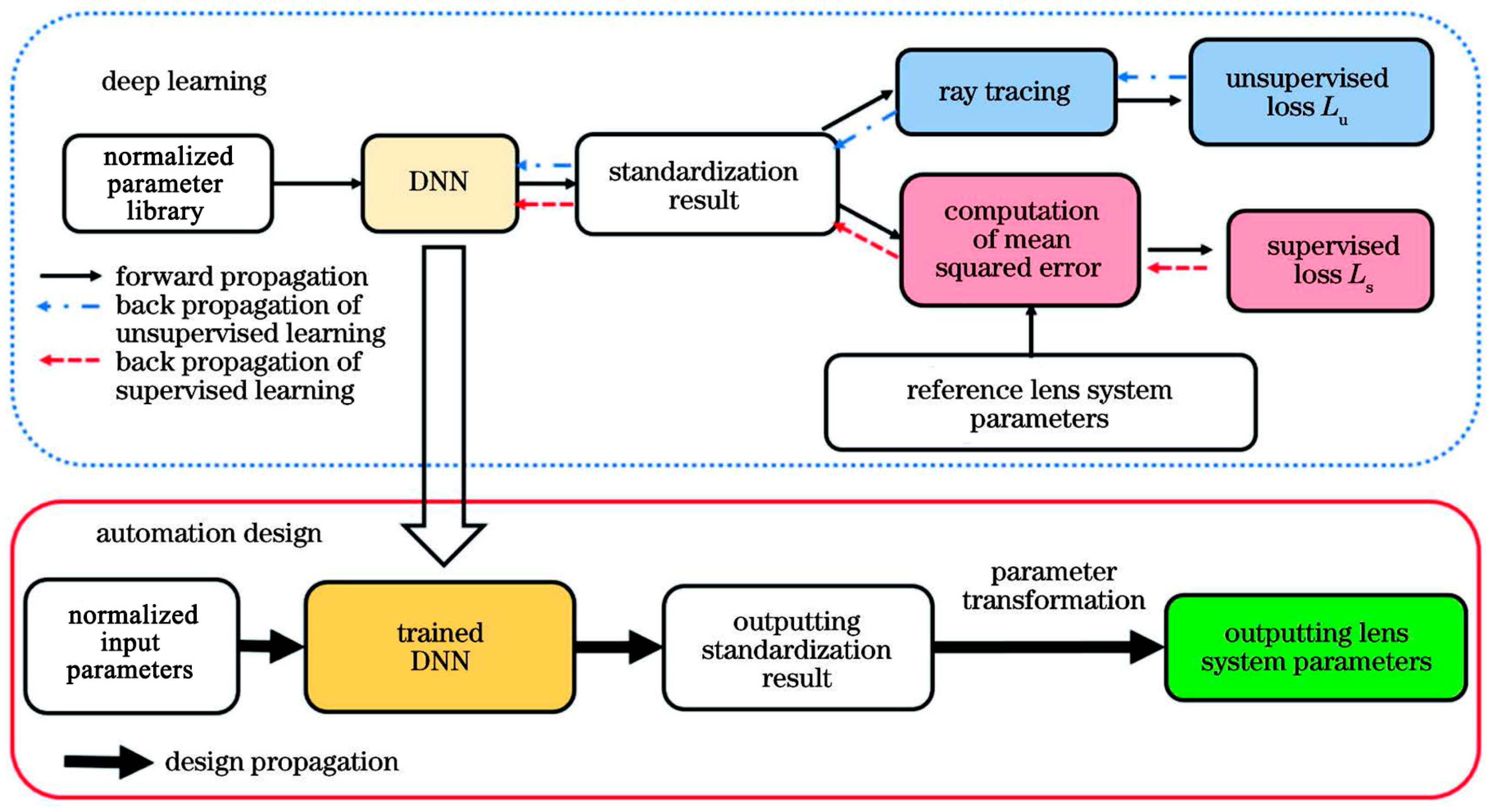
2.1. Design Process of Refractive Optical System Based on Deep Learning
2.2. Network Model Selection
2.3. Verification of Ray Tracing Algorithm
2.4. Loss Function Based on Polarized Ray Tracing
2.5. Network Model Training Based on Polarized Light Tracing
3. Analysis and Discussion
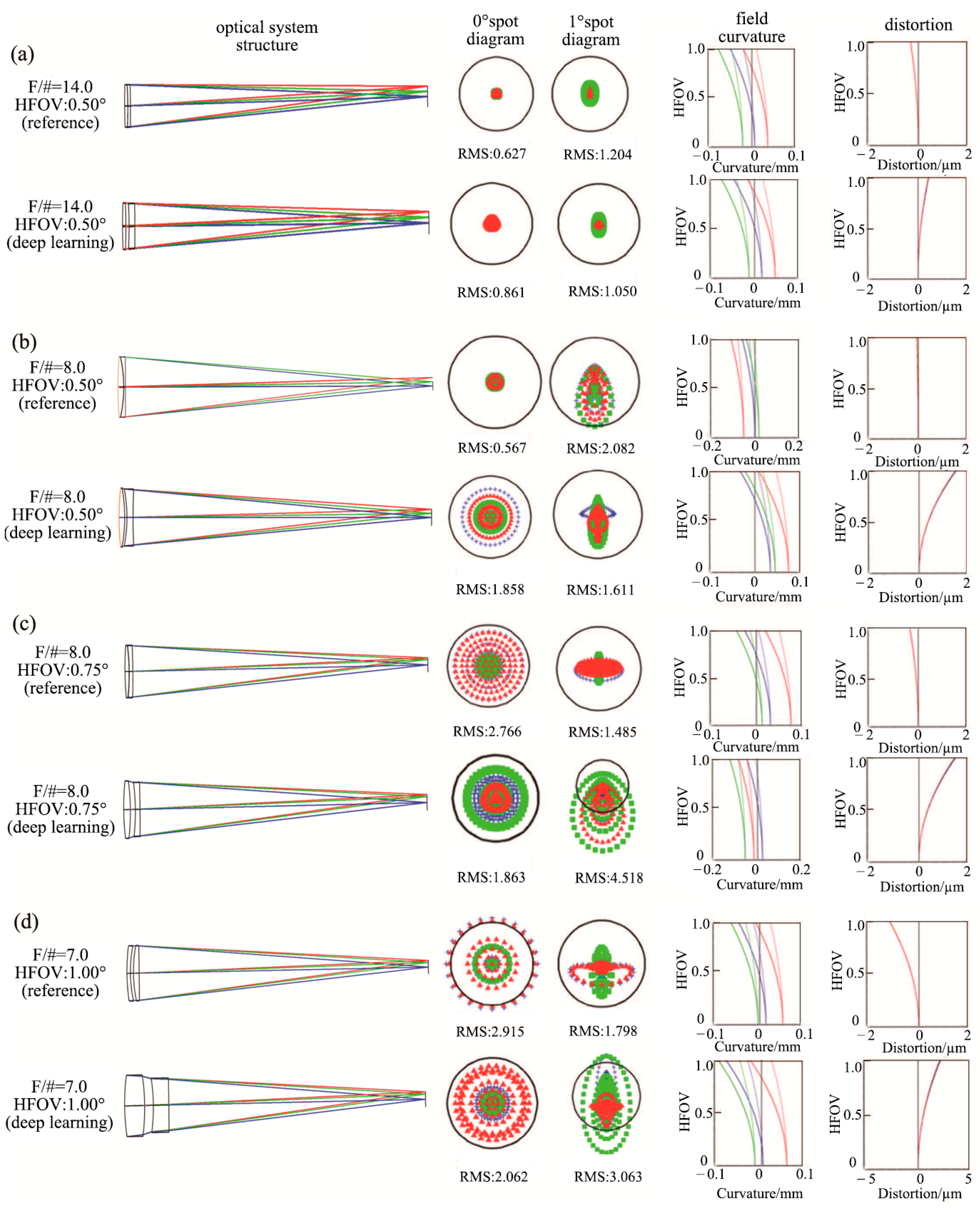
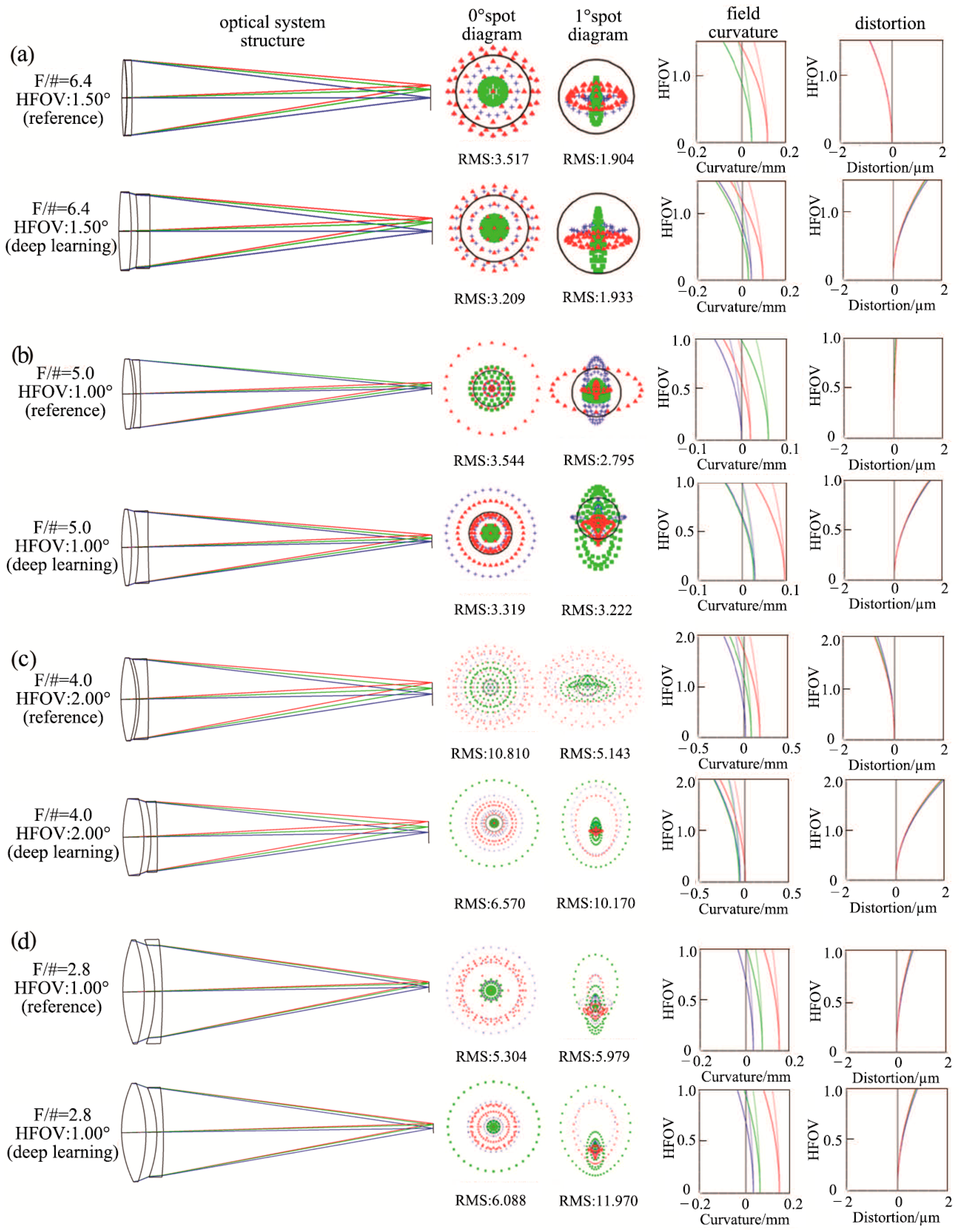
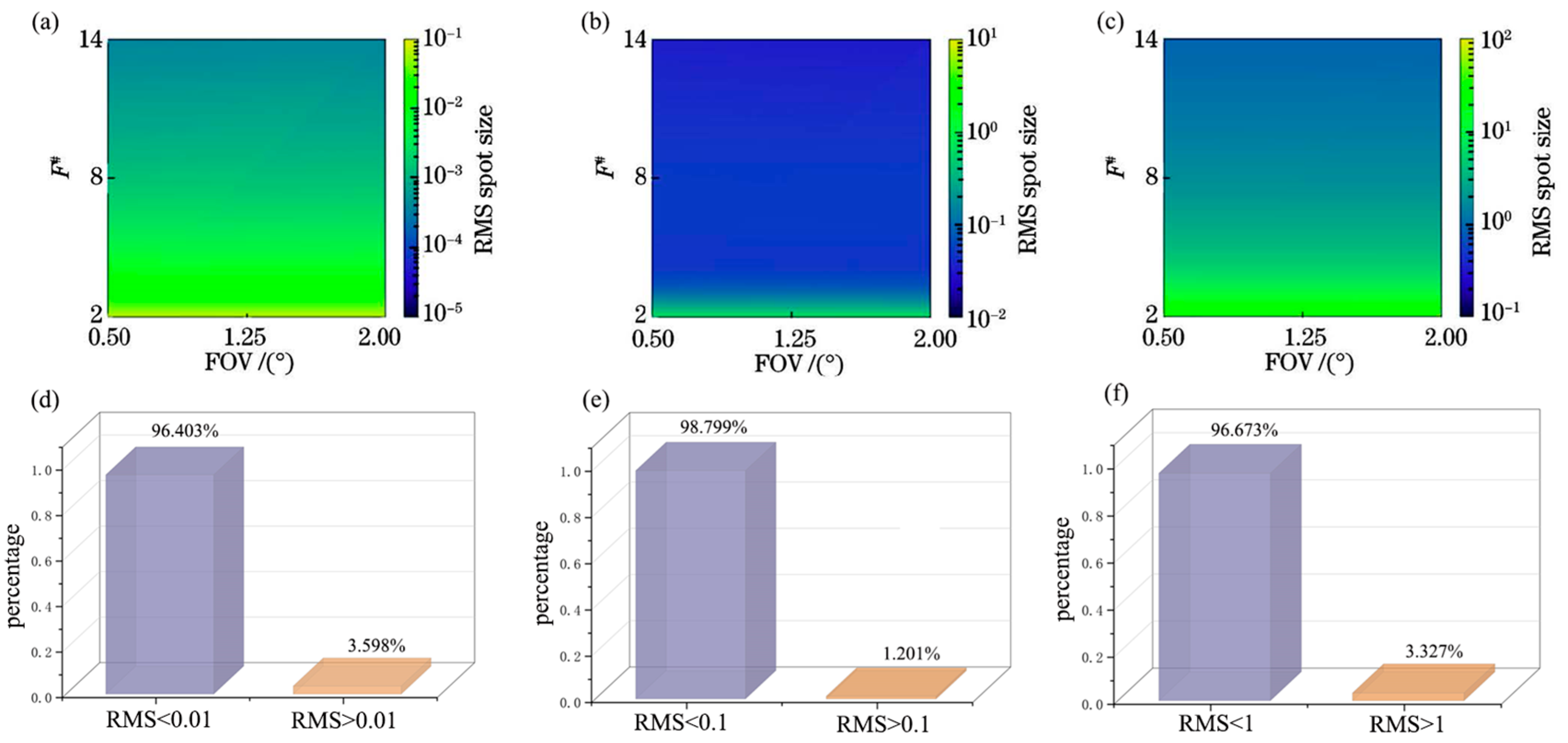
3.1. Optical Image Quality Analysis
3.2. Tolerance Analysis of Optical Systems
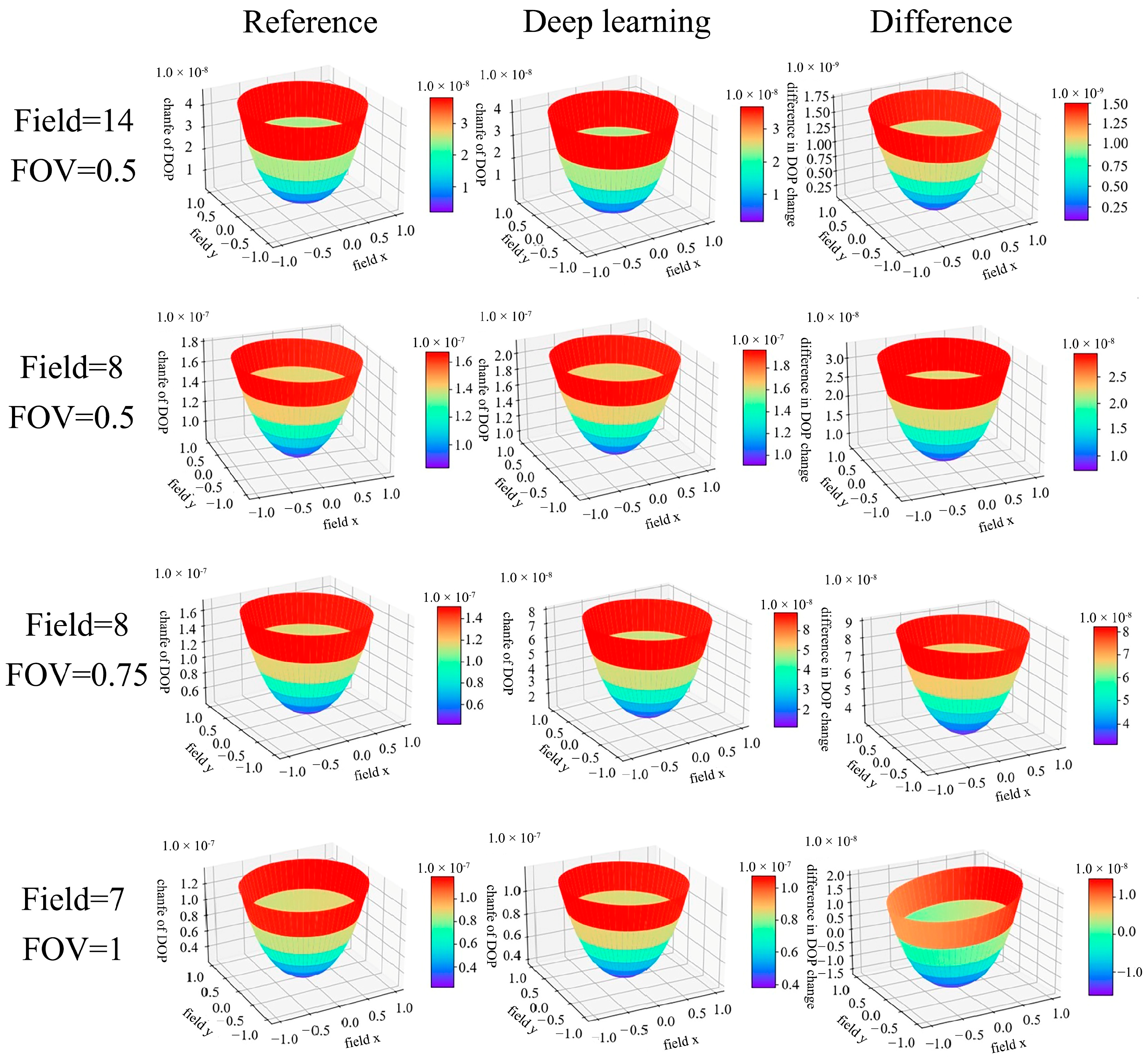
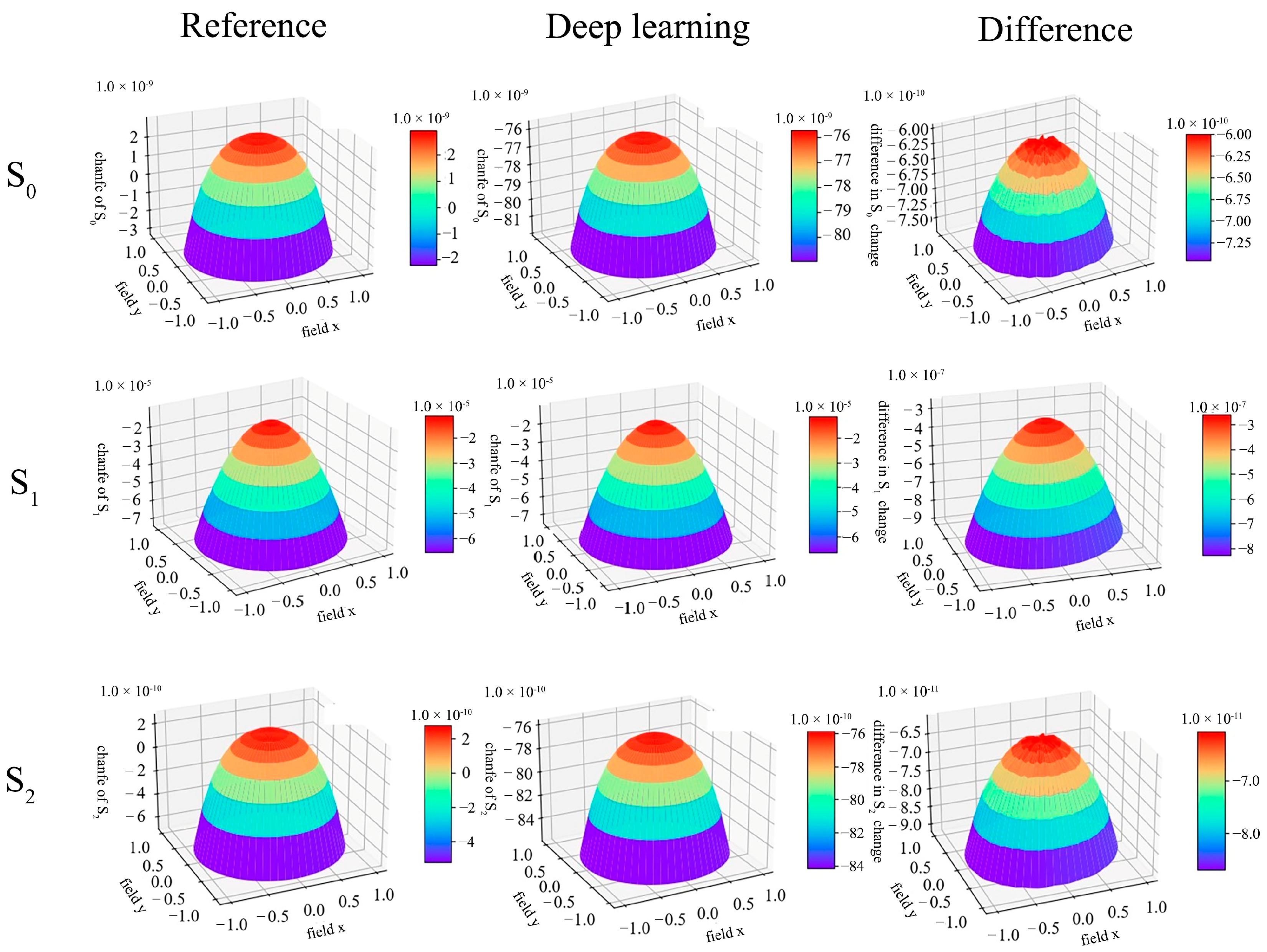
3.3. Polarization Aberration Verification
- Polarization degree change
- 2.
- Stokes vector contrast
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, W.J. Modern Lens Design; McGraw Hill Professional: New York, NY, USA, 2004. [Google Scholar]
- Meiron, J. Damped Least-Squares Method for Automatic Lens Design. J. Opt. Soc. Am. 1965, 55, 1105–1109. [Google Scholar] [CrossRef]
- Sun, J.F.; Li, X. Automatic design of machine vision lens based on improved genetic algorithm and damped least squares. In Proceedings of the Optical Design and Testing XI, Nantong, China, 10–12 October 2021; COS Photonics Asia. Volume 11895, pp. 188–202. [Google Scholar]
- Glatzel, E.; Wilson, R. Adaptive automatic correction in optical design. Appl. Opt. 1968, 7, 265–276. [Google Scholar] [CrossRef] [PubMed]
- Forbes, G.W.; Jones, A.E.W. Towards global optimization with adaptive simulated annealing. In Proceedings of the 1990 International Lens Design Conference, Monterey, CA, USA, 1 January 1990; SPIE Optical Systems Design. Volume 1354, pp. 144–153. [Google Scholar]
- Höschel, K.; Lakshminarayanan, V. Genetic algorithms for lens design: A review. J. Opt. Soc. 2018, 48, 463–470. [Google Scholar] [CrossRef]
- Isshiki, M.; Ono, H.; Hiraga, K.; Ishikawa, J.; Nakadate, S. Lens Design: Global Optimization with Escape Function. Opt. Rev. 1995, 2, 463–470. [Google Scholar] [CrossRef]
- Menke, C. Application of particle swarm optimization to the automatic design of optical systems. In Proceedings of the Optical Design and Engineering VII, Frankfurt, Germany, 14–17 May 2018; SPIE Optical Systems Design. Volume 10690, pp. 1–10. [Google Scholar]
- Yang, T.; Jin, G.-F.; Zhu, J. Automated design of freeform imaging systems. Light Sci. Appl. 2017, 6, 17081. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Cheng, D.; Wang, Y. Direct generation of starting points for freeform off-axis three-mirror imaging system design using neural network based deep-learning. Opt. Express 2019, 27, 17228. [Google Scholar] [CrossRef] [PubMed]
- Gannon, C.; Liang, R. Using machine learning to create high-efficiency freeform illumination design tools. arXiv 2019, arXiv:1903.11166. [Google Scholar]
- Côté, G.; Lalonde, J.-F.; Thibault, S. Extrapolating from lens design databases using deep learning. Opt. Express 2019, 27, 28279–28292. [Google Scholar] [CrossRef] [PubMed]
- Côté, G.; Zhang, Y.; Menke, C.; Lalonde, J.-F.; Thibault, S. Inferring the solution space of microscope objective lenses using deep learning. Opt. Express 2022, 30, 6531–6545. [Google Scholar] [CrossRef] [PubMed]
- Anche, R.M.; Sen, A.K.; Anupama, G.C.; Sankarasubramanian, K.; Skidmore, W. Analysis of polarization introduced due to the telescope optics of the Thirty Meter Telescope. J. Astron. Telesc. Instrum. Syst. 2018, 4, 018003. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, H.; Jiang, H. Polarization Aberration of a Non-Rotationally Symmetric Optical System with Freeform Surfaces. IEEE Access 2022, 10, 145538–145553. [Google Scholar] [CrossRef]
- Berthelot, D. MixMatch: A Holistic Approach to Semi-Supervised Learning. In Proceedings of the Advances in Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]

| Network | Network Structure | Apply |
|---|---|---|
| DNN | Input layer, hidden layer, active layer, output layer | Complex nonlinear fitting, complex classification problems, simple image recognition |
| CNN | Convolution layer, pooling layer, fully connected layer | Image recognition, image classification, image segmentation, speech recognition |
| RNN | Input layer, hidden layer, output layer, hidden state | Speech recognition, machine translation, text and music generation |
| Contrast Parameter | Optical Path Calculation of Actual Optical System | This Study Compiled the Algorithm Calculation | Error Value |
|---|---|---|---|
| Paraxial ray image distance | 97.009 | 97.0092 | 0.0002 |
| Paraxial image square aperture Angle | 0.100104 | 0.1002 | 0.000096 |
| Second paraxial ray ideal image height distance | 5.22816 | 5.2282 | 0.0004 |
| Off-axis point meridian plane main ray distance | 0.8052 | 0.8052 | 0 |
| Off-axis point image square aperture Angle | −0.052 | −0.0523 | 0.0003 |
| Optical System | Probability | MTF for Deep Learning Systems | Reference Lens MTF | The Absolute Value of the Difference |
|---|---|---|---|---|
| F = 14 HFOV = 0.5 | 90% | 0.6657 | 0.6552 | 0.0105 |
| 50% | 0.6780 | 0.6777 | 0.0003 | |
| 10% | 0.6862 | 0.6876 | 0.0014 | |
| F = 8 HFOV = 0.5 | 90% | 0.3047 | 0.2540 | 0.0506 |
| 50% | 0.4696 | 0.4186 | 0.0509 | |
| 10% | 0.6867 | 0.6324 | 0.0543 | |
| F = 8 HFOV = 0.75 | 90% | 0.5596 | 0.7114 | 0.1517 |
| 50% | 0.6917 | 0.76545 | 0.0737 | |
| 10% | 0.7585 | 0.79743 | 0.0388 | |
| F = 7 HFOV = 1 | 90% | 0.5484 | 0.6983 | 0.1499 |
| 50% | 0.6767 | 0.7841 | 0.1074 | |
| 10% | 0.7929 | 0.8187 | 0.0258 | |
| F = 6.4 HFOV = 1.5 | 90% | 0.6245 | 0.6116 | 0.0129 |
| 50% | 0.7159 | 0.7120 | 0.0038 | |
| 10% | 0.7702 | 0.7902 | 0.0199 | |
| F = 5 HFOV = 1 | 90% | 0.4197 | 0.3961 | 0.0236 |
| 50% | 0.6082 | 0.5933 | 0.0149 | |
| 10% | 0.7473 | 0.7618 | 0.0144 | |
| F = 4 HFOV = 2 | 90% | 0.2304 | 0.2178 | 0.0126 |
| 50% | 0.3351 | 0.3349 | 0.0002 | |
| 10% | 0.4386 | 0.4084 | 0.0302 | |
| F = 2.8 HFOV = 1 | 90% | 0.2108 | 0.2015 | 0.0093 |
| 50% | 0.3064 | 0.3508 | 0.0444 | |
| 10% | 0.4797 | 0.4994 | 0.0197 |
| Type | Value |
|---|---|
| Radius of curvature (fringe) | 1 |
| Surface irregularity (fringe) | 0.2 |
| Thickness (mm) | 0.1 |
| Surface tilt (degree) | 0.1 |
| Refractive index | 0.001 |
| Abbe number | 0.1 |
| Type | Value |
|---|---|
| Thickness (mm) | 0.1 |
| Surface eccentricity (mm) | 0.02 |
| Surface tilt (degree) | 0.1 |
| F = 14 HFOV = 0.5 | F = 8 HFOV = 0.5 | F = 8 HFOV = 0.75 | F = 7 HFOV = 1 | F = 6.4 HFOV = 1.5 | F = 5 HFOV = 1 | F = 4 HFOV = 2 | F = 2.8 HFOV = 1 |
|---|---|---|---|---|---|---|---|
| 4.753% | 12.349% | 10.071% | 10.001% | 4.166% | 15.625% | 23.45% | 23.75% |
| 0.00912% | 1.67% | 0.00913% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Fan, R.; He, C.; Wang, J.; Yang, S.; Xu, M.; Sun, H.; Li, Y.; Fu, Q. Deep Learning for Polarization Optical System Automated Design. Photonics 2024, 11, 164. https://doi.org/10.3390/photonics11020164
Shi H, Fan R, He C, Wang J, Yang S, Xu M, Sun H, Li Y, Fu Q. Deep Learning for Polarization Optical System Automated Design. Photonics. 2024; 11(2):164. https://doi.org/10.3390/photonics11020164
Chicago/Turabian StyleShi, Haodong, Ruihan Fan, Chunfeng He, Jiayu Wang, Shuai Yang, Miao Xu, Hongyu Sun, Yingchao Li, and Qiang Fu. 2024. "Deep Learning for Polarization Optical System Automated Design" Photonics 11, no. 2: 164. https://doi.org/10.3390/photonics11020164
APA StyleShi, H., Fan, R., He, C., Wang, J., Yang, S., Xu, M., Sun, H., Li, Y., & Fu, Q. (2024). Deep Learning for Polarization Optical System Automated Design. Photonics, 11(2), 164. https://doi.org/10.3390/photonics11020164





