Research on Ground Object Echo Simulation of Avian Lidar
Abstract
1. Introduction
- The beam constraint and light-energy constraint are determined based on the narrow beam of lidar and the lowest responsive light-energy level. In ground object echo simulation, these constraints can significantly enhance the efficiency of effective light screening and reduce the hardware calculation performance required by the simulation method.
- The proposed collision detection scheme enables the simultaneous detection of all rays within the narrow lidar beam, thereby significantly reducing the time required for collision detection in the ray-tracing process.
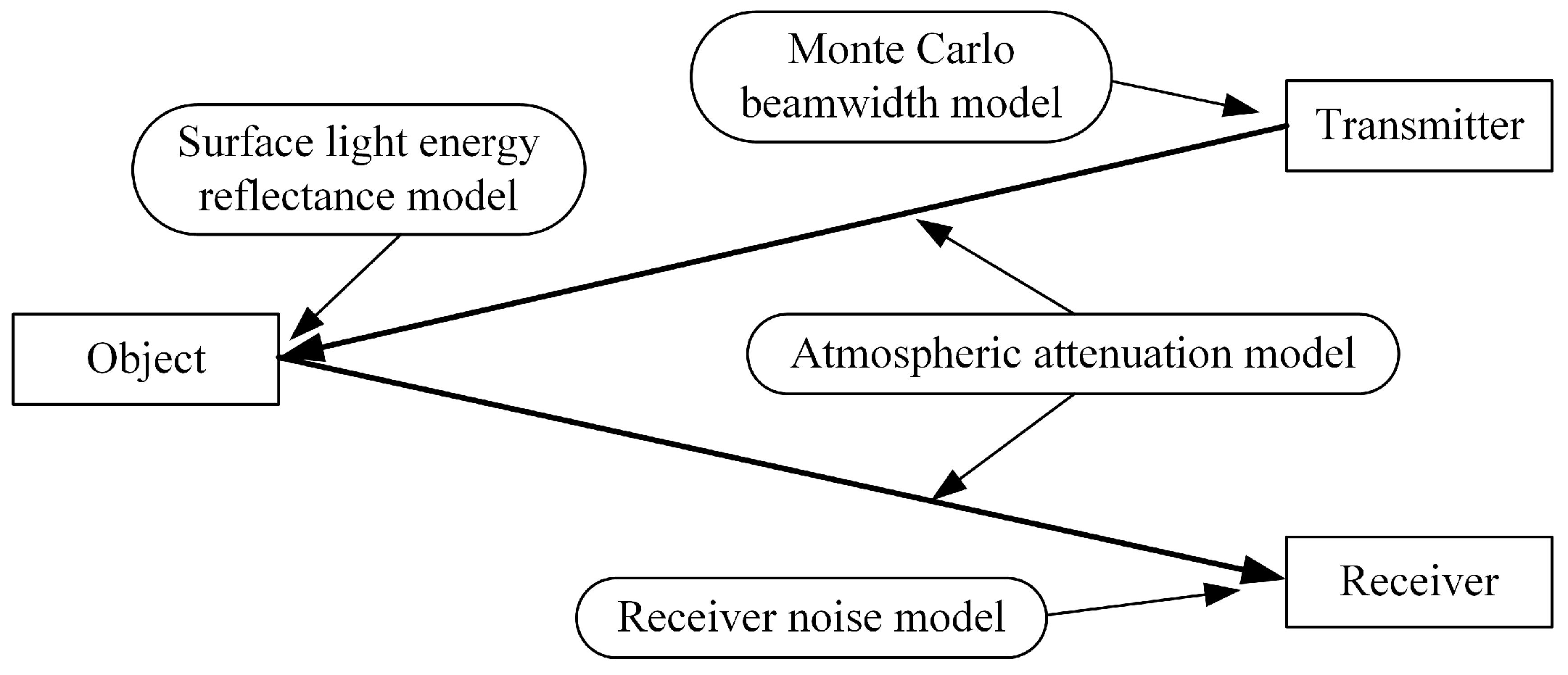
2. Associated Models of Ray-Tracing Method
2.1. Monte Carlo Beamwidth Model
2.2. Surface Light Energy Reflectance Model
2.3. Atmospheric Attenuation Model
2.4. Receiver Noise Model
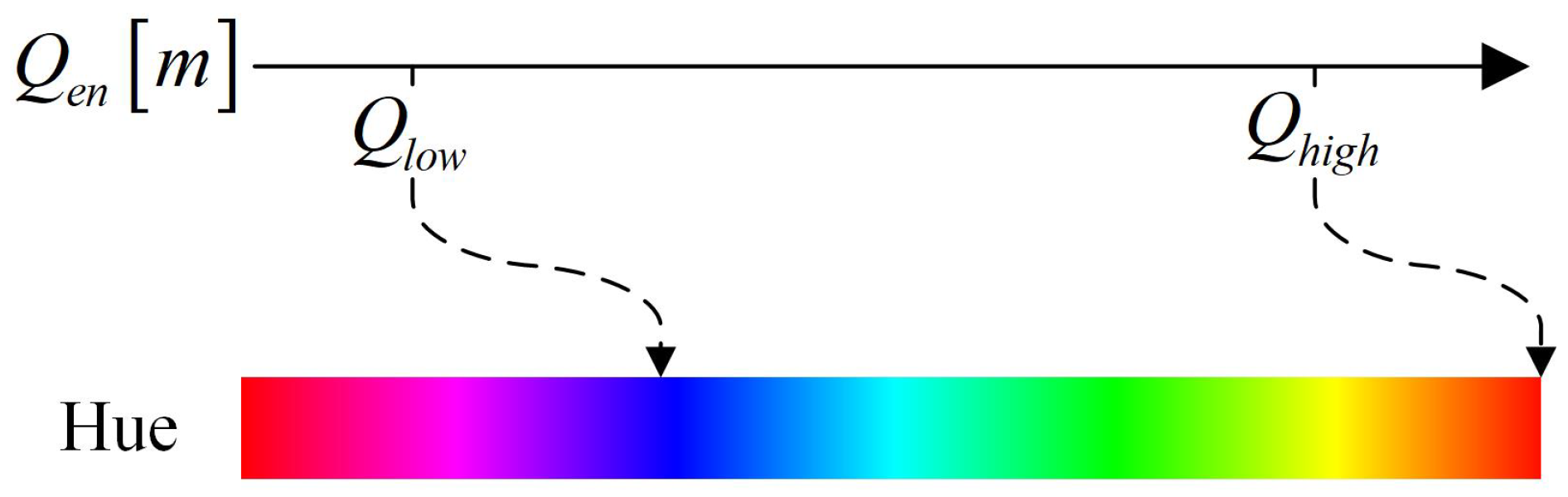
2.5. Received Light Energy Presentation Model
3. Collision Detection Scheme
3.1. Construction of Collision Detection Tree
| Algorithm 1 Construction of the collision detection tree. |
|
3.2. Intersection of Beam and Bounding Volume
3.3. Intersection between Ray and Triangular Surface
3.4. The Problem of Secondary Reflection
4. Proposed Simulation Method
| Algorithm 2 Proposed simulation method |
|
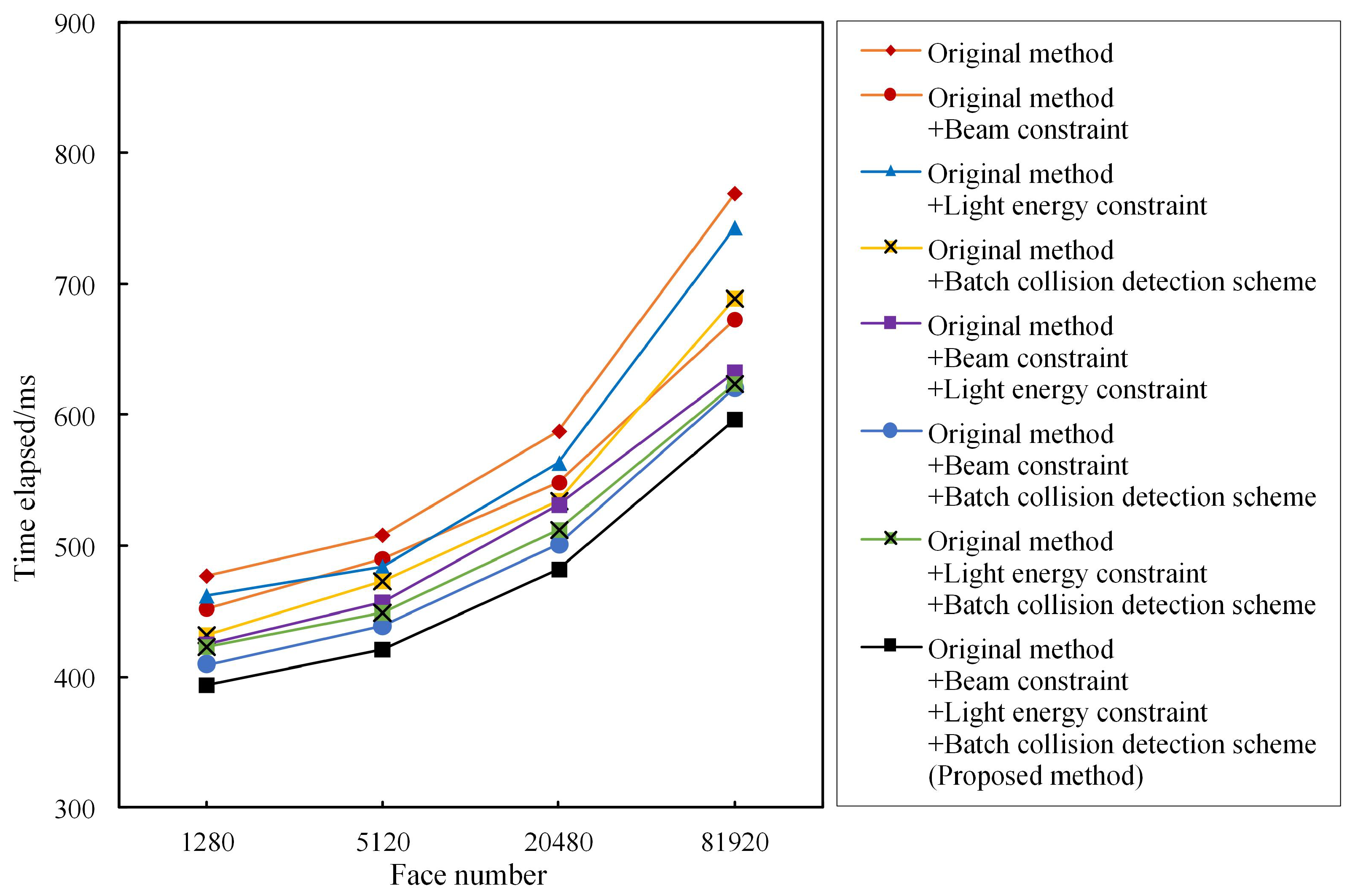
5. Simulation Results
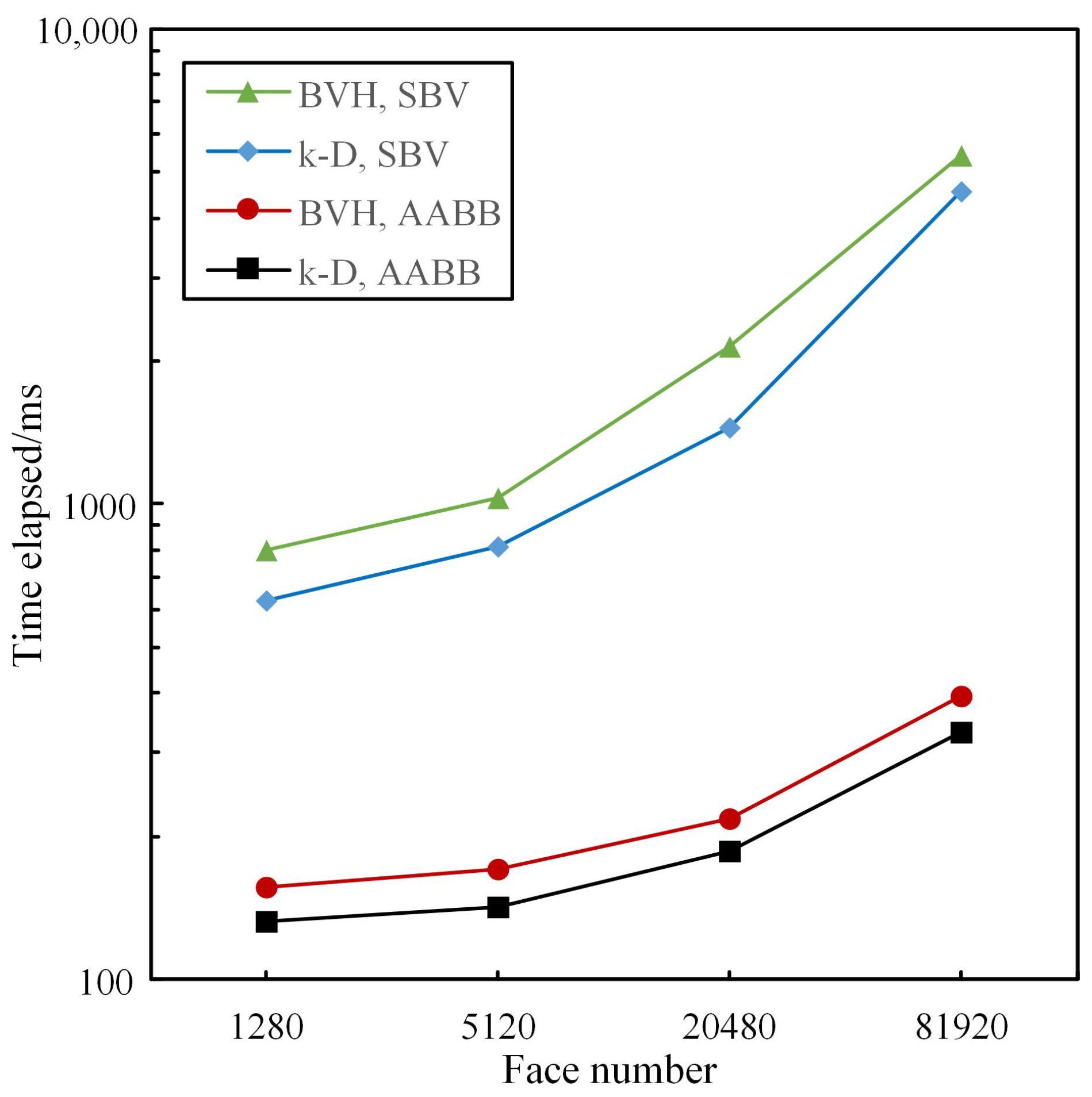
5.1. Selection of Bounding Volume Type and Collision Detection Tree Structure
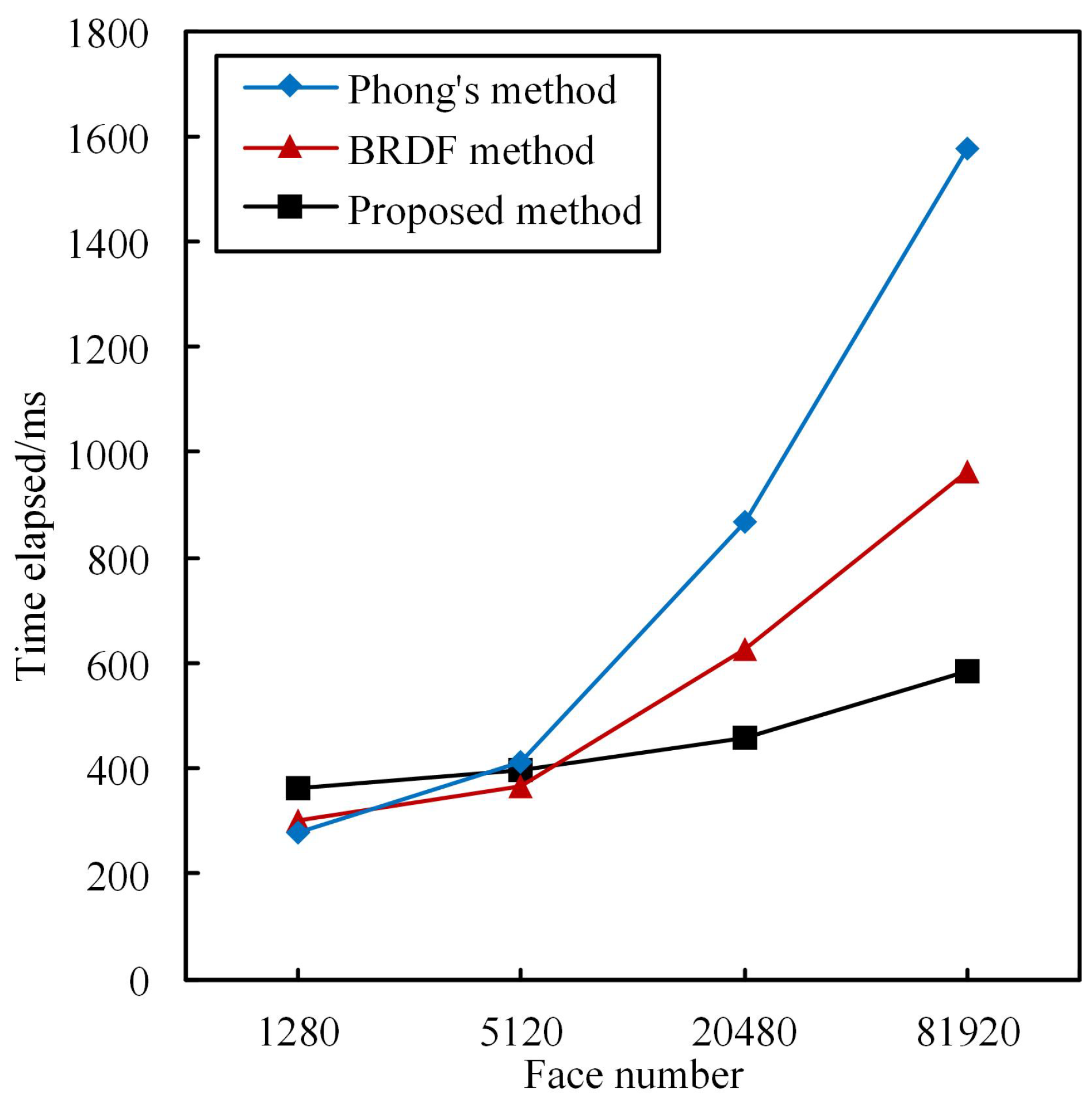
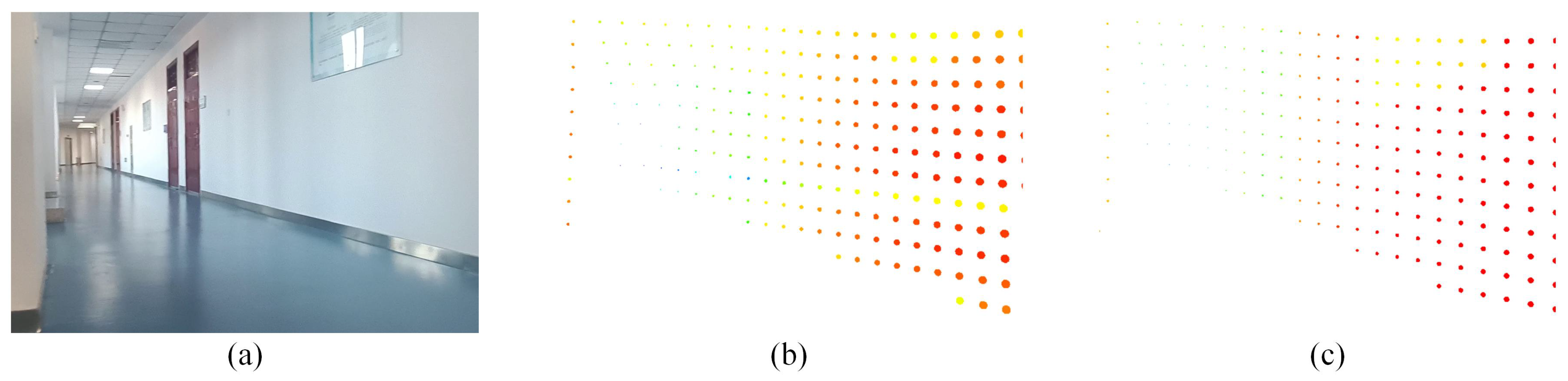
5.2. Simulation Results of Simple Small Scene
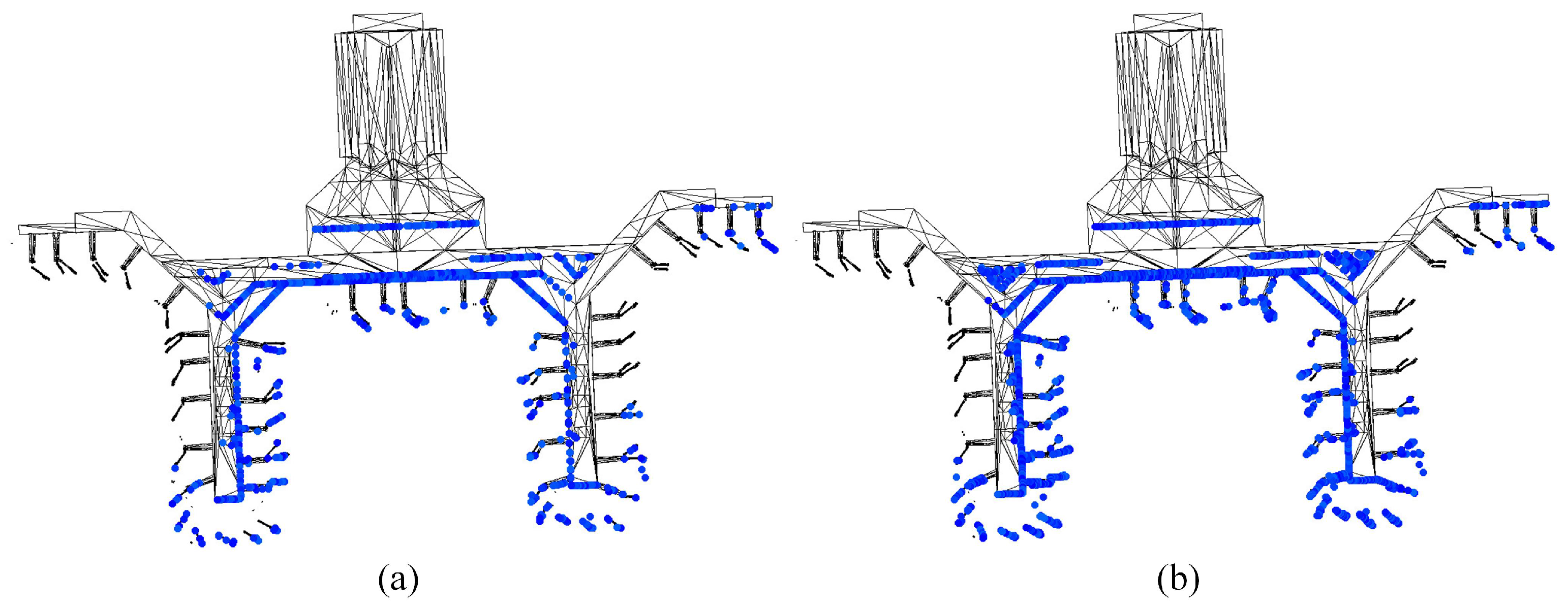
5.3. Simulation Results of Complex Large Scene
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GPU | Graphic Processing Unit |
| CUDA | Compute Unified Device Architecture |
| 3-D | Three-dimensional |
| HSB | Hue–Saturation–Brightness |
| AABB | Axis-Aligned Bounding Box |
| OBB | Oriented Bounding Box |
| SBV | Sphere Bounding Volume |
| BVH | Bounding Volume Hierarchy |
| BSP | Binary Space Partitioning |
| k-D | k-dimensional |
| 2-D | Two-dimensional |
References
- Zhao, J.; Li, Y.; Zhu, B.; Deng, W.; Sun, B. Method and Applications of Lidar Modeling for Virtual Testing of Intelligent Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2990–3000. [Google Scholar] [CrossRef]
- Rougeron, G.; Garrec, J.L.; Andriot, C. Optimal positioning of terrestrial LiDAR scanner stations in complex 3D environments with a multiobjective optimization method based on GPU simulations. ISPRS J. Photogramm. Remote Sens. 2022, 193, 60–76. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Li, G.; Zhuang, P.; Hou, G.; Zhang, Q.; Li, C. GACNet: Generate Adversarial-Driven Cross-Aware Network for Hyperspectral Wheat Variety Identification. IEEE Trans. Geosci. Remote Sens. 2023, 62, 5503314. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Sun, H.H.; Zhang, Q.; Zhuang, P.; Li, C. SSTNet: Spatial, spectral, and texture aware attention network using hyperspectral image for corn variety identification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, W.; Li, J.; Zhuang, P.; Sun, H.; Xu, Y.; Li, C. CVANet: Cascaded visual attention network for single image super-resolution. Neural Netw. 2024, 170, 622–634. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Wang, Y.; Yin, T.; Wang, C.; Lauret, N.; Regaieg, O.; Xi, X.; Gastellu-Etchegorry, J.P. Comprehensive LiDAR simulation with efficient physically-based DART-Lux model (I): Theory, novelty, and consistency validation. Remote Sens. Environ. 2022, 272, 112952. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Yin, T.G.; Lauret, N.; Grau, E.; Rubio, J.; Cook, B.D.; Morton, D.C.; Sun, G.Q. Simulation of satellite, airborne and terrestrial LiDAR with DART (I): Waveform simulation with quasi-Monte Carlo ray tracing. Remote Sens. Environ. 2016, 184, 418–435. [Google Scholar] [CrossRef]
- Esmorís, A.M.; Yermo, M.; Weiser, H.; Winiwarter, L.; Höfle, B.; Rivera, F.F. Virtual LiDAR Simulation as a High Performance Computing Challenge: Toward HPC HELIOS++. IEEE Access 2022, 10, 105052–105073. [Google Scholar] [CrossRef]
- Linnhoff, C.; Rosenberger, P.; Winner, H. Refining Object-Based Lidar Sensor Modeling—Challenging Ray Tracing as the Magic Bullet. IEEE Sens. J. 2021, 21, 24238–24245. [Google Scholar] [CrossRef]
- Chai, G.; Zhang, J.; Huang, X.; Guo, B.; Tian, L. Study of the dynamic scenes model for laser imaging radar simulation. Xi’an Dianzi Keji Daxue Xuebao/J. Xidian Univ. 2014, 41, 107–113. [Google Scholar] [CrossRef]
- Yang, J.S.; Li, T.J. Simulation of Space-Based Space Target Scene Imaging. Laser Optoelectron. Prog. 2022, 59, 253–260. [Google Scholar]
- Neumann, T.; Kallage, F. Simulation of a Direct Time-of-Flight LiDAR-System. IEEE Sens. J. 2023, 23, 14245–14252. [Google Scholar] [CrossRef]
- Winiwarter, L.; Esmorís Pena, A.M.; Weiser, H.; Anders, K.; Martínez Sánchez, J.; Searle, M.; Höfle, B. Virtual laser scanning with HELIOS++: A novel take on ray tracing-based simulation of topographic full-waveform 3D laser scanning. Remote Sens. Environ. 2022, 269, 112772. [Google Scholar] [CrossRef]
- López, A.; Ogayar, C.J.; Jurado, J.M.; Feito, F.R. A GPU-Accelerated Framework for Simulating LiDAR Scanning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3000518. [Google Scholar] [CrossRef]
- Richa, J.P.; Deschaud, J.-E.; Goulette, F.; Dalmasso, N. AdaSplats: Adaptive Splatting of Point Clouds for Accurate 3D Modeling and Real-Time High-Fidelity LiDAR Simulation. Remote Sens. 2022, 14, 6262. [Google Scholar] [CrossRef]
- Tan, K.; Cheng, X. Specular reflection effects elimination in terrestrial laser scanning intensity data using Phong model. Remote Sens. 2017, 9, 853. [Google Scholar] [CrossRef]
- Matusik, W.; Pfister, H.; Brand, M.; McMillan, L. A Data-Driven Reflectance Model. ACM Trans. Graph. (TOG) 2003, 22, 759–769. [Google Scholar] [CrossRef]
- Ceolato, R.; Berg, M.J. Aerosol light extinction and backscattering: A review with a lidar perspective. J. Quant. Spectrosc. Radiat. Transf. 2021, 262, 107492. [Google Scholar] [CrossRef]
- Liang, B.; Niu, J.; He, S.; Liu, H.; Qin, C. Tunnel lighting calculation model based on bidirectional reflectance distribution function: Considering the dynamic changes in light transmittance in road tunnels. Tunn. Undergr. Space Technol. 2023, 140, 105313. [Google Scholar] [CrossRef]
- Xing, Y.S.; Liu, X.P.; Xu, S.P. Efficient collision detection based on AABB trees and sort algorithm. In Proceedings of the 2010 8th IEEE International Conference on Control and Automation (ICCA 2010), Xiamen, China, 9–11 June 2010; pp. 328–332. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, J.; Li, W. Fitting oriented bounding box algorithm for accurate positioning of transformer wiring terminals. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; pp. 4058–4061. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, S.; Zhou, L.; Huang, L. A hybrid algorithm for the minimum bounding sphere problem. Oper. Res. Lett. 2022, 50, 150–154. [Google Scholar] [CrossRef]
- Gu, Y.; He, Y.; Fatahalian, K.; Blelloch, G. Efficient BVH construction via approximate agglomerative clustering. In Proceedings of the—High-Performance Graphics 2013, HPG 2013, Anaheim, CA, USA, 19–21 July 2013; pp. 81–88. [Google Scholar] [CrossRef]
- Ize, T.; Wald, I.; Parker, S.G. Ray tracing with the BSP tree. In Proceedings of the RT’08-IEEE/EG Symposium on Interactive Ray Tracing 2008, Proceedings, Los Angeles, CA, USA, 9–10 August 2008; pp. 159–166. [Google Scholar] [CrossRef]
- Shan, Y.X.; Li, S.; Li, F.X.; Cui, Y.X.; Li, S.; Zhou, M.; Li, X. A Density Peaks Clustering Algorithm With Sparse Search and K-d Tree. IEEE Access 2022, 10, 74883–74901. [Google Scholar] [CrossRef]
- Liu, K.; Ma, H.; Zhang, L.; Cai, Z.; Ma, H. Strip Adjustment of Airborne LiDAR Data in Urban Scenes Using Planar Features by the Minimum Hausdorff Distance. Sensors 2019, 19, 5131. [Google Scholar] [CrossRef]
- Chen, J.H.; Zhao, D.; Zheng, Z.J.; Xu, C.; Pang, Y.; Zeng, Y. A clustering-based automatic registration of UAV and terrestrial LiDAR forest point clouds. Comput. Electron. Agric. 2024, 217, 108648. [Google Scholar] [CrossRef]










| Material | p | ||
|---|---|---|---|
| Wall | 0.146 | 0.054 | 112 |
| Glass | 0.020 | 0.852 | 8046 |
| Metal | 0.075 | 0.634 | 6803 |
| Wood | 0.107 | 0.100 | 82 |
| Notation | Explanation | Value |
|---|---|---|
| Half-beamwidth | rad | |
| N | Total number of random rays within beam | 100 |
| Atmospheric attenuation coefficient | ||
| Noise photon rate | kHz | |
| h | Planck constant | J · s |
| Frequency of the laser | Hz | |
| Energy of the emitted laser pulse | J | |
| Receiver upper energy limit | J | |
| Receiver lower energy limit | J |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z.; Sang, L.; Hao, J.; Han, B.; Wang, Y.; Ge, P. Research on Ground Object Echo Simulation of Avian Lidar. Photonics 2024, 11, 153. https://doi.org/10.3390/photonics11020153
Su Z, Sang L, Hao J, Han B, Wang Y, Ge P. Research on Ground Object Echo Simulation of Avian Lidar. Photonics. 2024; 11(2):153. https://doi.org/10.3390/photonics11020153
Chicago/Turabian StyleSu, Zhigang, Le Sang, Jingtang Hao, Bing Han, Yue Wang, and Peng Ge. 2024. "Research on Ground Object Echo Simulation of Avian Lidar" Photonics 11, no. 2: 153. https://doi.org/10.3390/photonics11020153
APA StyleSu, Z., Sang, L., Hao, J., Han, B., Wang, Y., & Ge, P. (2024). Research on Ground Object Echo Simulation of Avian Lidar. Photonics, 11(2), 153. https://doi.org/10.3390/photonics11020153





