Experimentation and Analysis of Intra-Cavity Beam-Splitting Method to Enhance the Uniformity of Light in the Powersphere

Abstract

The powersphere is a spherical enclosed receiver composed of multiple photovoltaic cells. It serves as a replacement for traditional photovoltaic panels in laser wireless power transmission systems for optoelectronic conversion. The ideal powersphere aims to achieve a uniform distribution of light within the cavity through infinite reflections, reducing energy losses in the circuit. However, due to the high absorption rate of the photovoltaic cells, the direct irradiation area on the inner surface of the powersphere exhibits a significantly higher light intensity than the reflected area, resulting in a suboptimal level of light uniformity and certain circuit losses. To address the aforementioned issues, a method of intra-cavity beam splitting in the powersphere is proposed. This solution aims to increase the area of direct illumination and reduce the intensity difference between direct and reflected lights, thereby improving the light uniformity on the inner surface of the powersphere. Utilizing the transformation matrix of Gaussian beams, the q parameters for each optical path with beam splitting were calculated, and the equality of corresponding q values was demonstrated. Further, based on the q parameter expression for the electric field of Gaussian beams, the intensities for each optical path were calculated, and it was demonstrated that their values are equal. Additionally, an optical software was utilized to establish a model for intra-cavity beam splitting in the powersphere. Based on this model, a beam-splitting system was designed using a semi-transparent and semi-reflective lens as the core component. The light uniformity performance of the proposed system was analyzed through simulations. To further validate the effectiveness of the calculations, design, and simulations, multiple lenses were employed to construct the beam-splitting system. An experimental platform was set up, consisting of a semiconductor laser, monocrystalline silicon photovoltaic cells, beam expander, Fresnel lens, beam-splitting system, and powersphere. An experimental verification was conducted, and the results aligned with the theoretical calculations and simulated outcomes. The above theory, simulations, and experiments demonstrate that the intra-cavity beam-splitting method effectively enhances the optical uniformity within the powersphere.

1. Introduction

The laser wireless power transmission (WPT) is a WPT technology using laser as the power transmission medium, and the transmission distance can reach several kilometers, with a small loss, a high transmission efficiency, and a compact transmission device [1,2,3,4,5]. Owing to these advantages, it is widely used in long-endurance unmanned aerial vehicles, unmanned boats, unmanned submarines, robotic fish, and other mobile electric facilities and has become a popular field of competing research [6,7,8,9,10,11].

Traditional laser wireless power transmission systems typically use photovoltaic panels as receivers for optoelectronic conversion [12,13,14]. However, photovoltaic panels are designed for solar energy applications and require a high level of uniformity in incident light. On the other hand, laser beams exhibit a Gaussian distribution, with a higher intensity at the center and a weaker intensity at the edges [15,16]. When a laser is irradiated onto a photovoltaic panel, the currents and voltages generated by the cells at different positions are not equal, and they gradually decrease from the center of the spot towards the edges. Therefore, a large number of cells with small output values will become loads, consuming the output power generated by the remaining photovoltaic cells, and causing the cells to heat up and likely even causing a fire [17,18]. This problem can be solved in many ways, and the best way is to improve the uniformity of light on the receiving surface to ensure that the luminous fluxes on the photovoltaic cells are equal [19,20,21,22,23,24,25,26,27,28].

In order to address the problem of nonuniform laser irradiation and reduce light reflection losses, U. Ortabasi et al. proposed a closed spherical photovoltaic receiver called the “powersphere” in 2004 [29]. By substituting an enclosed spherical receiver for an open photovoltaic panel, the laser can be “imprisoned” in the sphere. When the photovoltaic cells are irradiated by the laser, most of the reflected laser is transmitted to other cells on the spherical receiver except the part of the laser that is absorbed. When the input laser power is large enough, the above process is repeated continuously, and the laser power absorbed by each cell on the photovoltaic receiving surface can be equal, and the output powers after photoelectric conversion are also equal. Due to material and process limitations, the actual effectiveness of the powersphere in practical usage falls short of theoretical expectations. In order to enhance the uniformity of light within the powersphere, the literature suggests the utilization of a TIR (Total Internal Reflection) extractor rod to convert light into a point source [29]. However, the TIR extractor rod is a complex optical device that is challenging to manufacture and expensive.

In 2007, U. Ortabasi et al. proposed the use of a Lambertian reflector to improve uniformity and developed a 250 mm diameter powersphere capable of handling input power ranging from 200 to 300 W [30]. However, one limitation of this method is that the Lambertian reflector occupies a significant area, which limits the number of photovoltaic cells that can be incorporated into the system. To address the need for a higher output power, Tiefeng HE et al. explored a different solution. A large-sized powersphere with a diameter of 1000 mm consisting of full photovoltaic cells was studied. This solution aimed to take advantage of the inherent light uniformity and high-power input capability of a large-sized sphere, thus increasing the input power to 3000 W [31]. However, due to the high absorption rate of the photovoltaic cells, the direct irradiation area on the inner surface of the powersphere exhibits a significantly higher light intensity than the reflected area, resulting in a suboptimal level of light uniformity [32].

In order to improve the output power of the powersphere, this paper explores the research on the uniformity of light within the powersphere. A method of intra-cavity beam splitting is proposed to reduce the intensity discrepancy between a direct irradiation area and reflected regions. The validity of this approach is theoretically verified through calculations using a complex radius. Using optical software as a tool, a model of the powersphere based on the beam-splitting system is established. The light intensity distribution within the powersphere without and with beam splitting is simulated and analyzed. A beam-splitting system is constructed using semi-transmissive and semi-reflective lenses. Based on this system, an experimental platform is built to conduct experimental validations.

2. System Design and Analysis

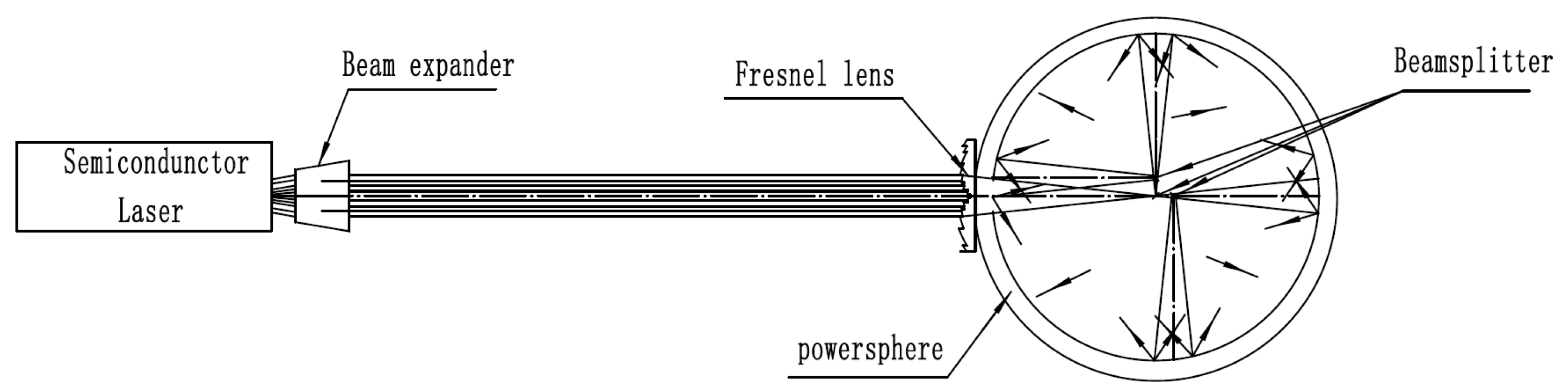
2.1. System Design

To achieve more uniform illumination, increasing the directly irradiated area is a good approach. On the one hand, it reduces the intensity of direct light, and on the other hand, it increases the area with the same light intensity distribution. The best way to increase the directly illuminated area is to divide the incident laser into several identical beams and direct them to different positions on the powersphere. Although, in theory, the number of beams should be equal to the number of photovoltaic cells for optimal results, there are practical considerations such as losses in beam splitting, the complexity and cost of the optical system increasing with more beams, the bulkiness of the beam-splitting system, and the limited installation space. At the same time, taking into account the symmetry of the sphere, a beam-splitting system consisting of three beam splitters was designed. It divides the incident laser into four identical beams, each illuminating a different part of the sphere (top, bottom, left, and right). The configuration of the beam-splitting system is shown in Figure 1.

In Figure 1, the laser transmitted to the beam-splitting system is divided into two output lights with the same power by the first beam splitter. One output is the transmission light (output₁), and the other output is the reflected light (output₂). The transmission light will continue to propagate along the original optical path until it encounters the next beam splitter and is divided into two output lasers of the same power again, forming two output lights, output₁₁ and output₁₂, in the positive direction of the Z axis and the negative direction of the Y axis. The two output lights irradiate the photovoltaic cells in the right area and below the inner surface of the powersphere. The reflected laser is deflected by 90° and propagates on the Y axis until it encounters the third beam splitter. The third beam splitter, again, divides the laser into two output lights of the same power, which are output₂₁ and output₂₂. The two outputs propagate in the negative direction of the Z axis and the positive direction of the Y axis and irradiate the photovoltaic cells in the left area and above the inner surface of the powersphere, respectively.

In this way, the incident laser becomes four outputs of equal power, and the direct irradiation area becomes 4 times of the original. Nevertheless, the power of the irradiated laser is reduced to 1/4 of the original. The combined power of the four outputs is equal to the power of the input laser without beam splitting. Hence, the beam-splitting system does not reduce the total input power, but the light is more uniformly distributed on the inner surface of the powersphere. When the divergence angle is sufficiently large, each photovoltaic cell in the powersphere is directly irradiated by the laser, which reduces the light intensity difference between direct and reflected lights. This condition can eliminate the area that cannot be directly irradiated. Each reflection can radiate to each photovoltaic cell, which improves the light uniformity effect of the powersphere. The principle of this kind of beam splitting based on a semitransparent and semireflective mirror is simple. The processing of the beam splitter is relatively conventional, and the cost is low. The splitting process presents a low loss and high efficiency. The number of beam splitters can also be increased in accordance with the divergence angle and radiation area of the laser to ensure that each area in the powersphere can be directly irradiated by the laser. On the basis of the above analysis, the optical system of the laser WPT was designed, as shown in Figure 2.

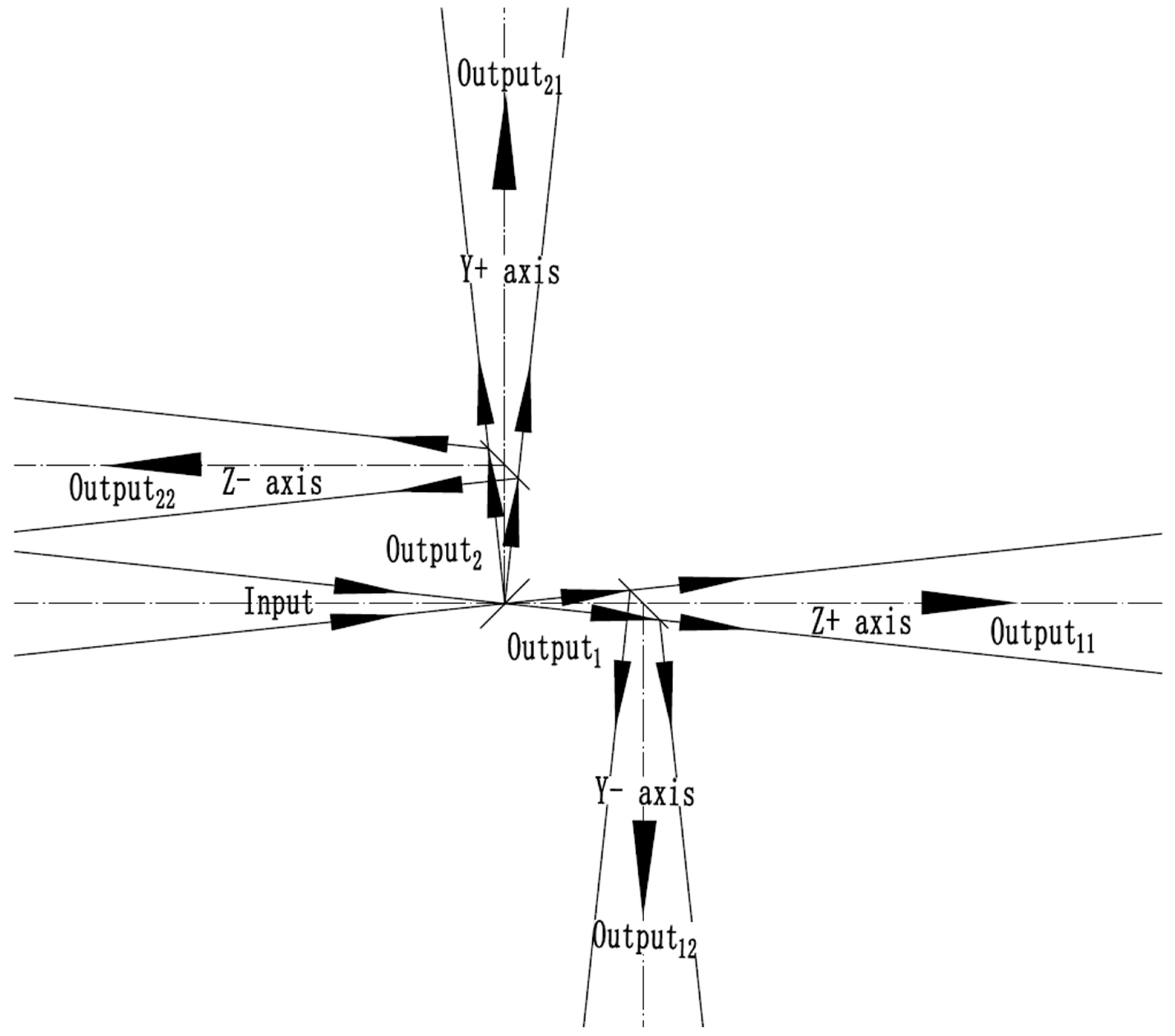
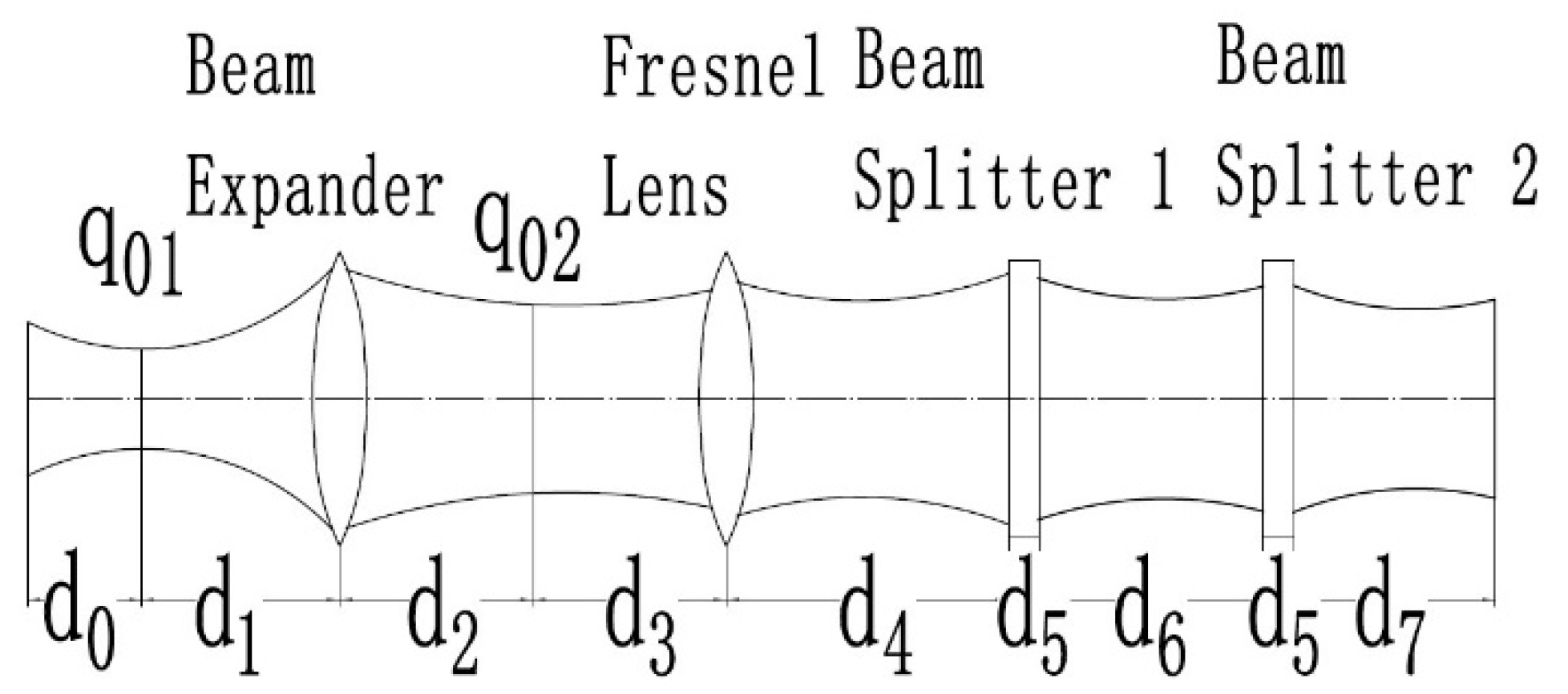
2.2. Optical Path Theory

Figure 3 is the ideal optical path diagram of the Gaussian beam for the optical system shown in Figure 2. In the diagram, the distance from the output end of the laser to the input waist of the beam expander is denoted as d₀. The distance from the input waist of the beam expander to the input surface of the beam expander is denoted as d₁. The distance from output surface of the beam expander to the output waist of the beam expander is denoted as d₂. The beam expansion factor is represented by β. The focal lengths of the input and output lenses of the beam expander are denoted as f₁ and f₂, respectively. The distance from the output waist of the beam expander to the surface of the Fresnel lens is denoted as the input surface of d₃. The distance from the surface of the Fresnel lens to beam splitter 1 is denoted as d₄. The focal length of the Fresnel lens is denoted as f₃. Due to the beam splitter’s dual functionality of reflection and refraction, it can be decomposed into a parallel plate with a refractive index of n and a thickness of d₅, acting as a refracting element, and a plane mirror with zero thickness, serving as a reflecting element. The parallel plate induces refraction in the optical path, representing the transmissive path. In contrast, the plane mirror only changes the direction of light transmission, resulting in a zero optical path length when light passes through the plane mirror. The distance from beam splitter 1 to beam splitter 2 is denoted as d₆, and the distance from beam splitter 2 to the receiving surface is denoted as d₇. This results in four different combinations of optical paths: parallel plate to parallel plate, parallel plate to plane mirror, plane mirror to parallel plate, and plane mirror to plane mirror. Then, the corresponding optical path length for these combinations are (2d₅)/n + d₆ + d₇, d₅/n + d₆ + d₇, d₅/n + d₆ + d₇, and d₆ + d₇, respectively.

So, the ABCD matrix for the beam before passing through the beam splitter is given as:

$$M_1=\left[\begin{array}{cc}1& {\mathrm{d}}_4\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ -\frac{1}{{\mathrm{f}}_2}& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{d}}_3\\ 0& 1\end{array}\right]\left[\begin{array}{cc}-\mathrm{\beta }& {\mathrm{f}}_1^{\text{'}}+{\mathrm{f}}_2^{\text{'}}-{\mathrm{d}}_1\mathrm{\beta }-\frac{{\mathrm{d}}_2}{\mathrm{\beta }}\\ 0& -\frac{1}{\mathrm{\beta }}\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{d}}_0\\ 0& 1\end{array}\right]$$

(1)

Perform matrix calculation on the above equation to obtain the following:

$$M_1=\left|\begin{array}{cc}\frac{\mathrm{\beta }({\mathrm{d}}_4-{\mathrm{f}}_3)}{{\mathrm{f}}_3}& \frac{({\mathrm{d}}_4-{\mathrm{f}}_3)\left[\left({\mathrm{d}}_0+{\mathrm{d}}_1\right){\mathrm{\beta }}^2-\left({\mathrm{f}}_1^{\text{'}}+{\mathrm{f}}_2^{\text{'}}\right)\mathrm{\beta }+{\mathrm{d}}_3-{\mathrm{d}}_2\right]-{\mathrm{d}}_4{\mathrm{f}}_3}{\mathrm{\beta }{\mathrm{f}}_3}\\ \frac{\mathrm{\beta }}{{\mathrm{f}}_3}& \frac{\left[\left({\mathrm{d}}_0+{\mathrm{d}}_1\right){\mathrm{\beta }}^2-\left({\mathrm{f}}_1^{\text{'}}+{\mathrm{f}}_2^{\text{'}}\right)\mathrm{\beta }+{\mathrm{d}}_3-{\mathrm{d}}_2\right]-{\mathrm{f}}_3}{\mathrm{\beta }{\mathrm{f}}_3}\end{array}\right|$$

(2)

Let $E=\left[\left({\mathrm{d}}_0+{\mathrm{d}}_1\right){\mathrm{\beta }}^2-\left({\mathrm{f}}_1^{\prime }+{\mathrm{f}}_2^{\prime }\right)\mathrm{\beta }+{\mathrm{d}}_3-{\mathrm{d}}_2\right]$; then, the above equation can be expressed as:

$$M_1=\left|\begin{array}{cc}\frac{\mathrm{\beta }({\mathrm{d}}_4-{\mathrm{f}}_3)}{{\mathrm{f}}_3}& \frac{({\mathrm{d}}_4-{\mathrm{f}}_3)E-{\mathrm{d}}_4{\mathrm{f}}_3}{\mathrm{\beta }{\mathrm{f}}_3}\\ \frac{\mathrm{\beta }}{{\mathrm{f}}_3}& \frac{E-{\mathrm{f}}_3}{\mathrm{\beta }{\mathrm{f}}_3}\end{array}\right|$$

(3)

There are four optical paths from beam splitter 1 to the receiving surface; then, the corresponding ABCD matrices of the receiving surface are as follows:

(1)

Transmitted and transmitted optical paths

$$M_2=\left[\begin{array}{cc}1& {\mathrm{d}}_7\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& \frac{{\mathrm{d}}_5}{\mathrm{n}}\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{d}}_6\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& \frac{{\mathrm{d}}_5}{\mathrm{n}}\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}1& \frac{2{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7\\ 0& 1\end{array}\right]$$

(4)

(2)

Transmitted and reflected optical paths

$$M_3=\left[\begin{array}{cc}1& {\mathrm{d}}_7\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{d}}_6\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& \frac{{\mathrm{d}}_5}{\mathrm{n}}\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}1& \frac{{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7\\ 0& 1\end{array}\right]$$

(5)

(3)

Reflected and transmitted optical paths

$$M_4=\left[\begin{array}{cc}1& {\mathrm{d}}_7\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& \frac{{\mathrm{d}}_5}{\mathrm{n}}\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{d}}_6\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}1& \frac{{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7\\ 0& 1\end{array}\right]$$

(6)

(4) Reflected and reflected optical paths

$$M_5=\left[\begin{array}{cc}1& {\mathrm{d}}_7\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{d}}_6\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}1& {\mathrm{d}}_6+{\mathrm{d}}_7\\ 0& 1\end{array}\right]$$

(7)

So, M₂M₁, M₃M₁, M₄M₁, and M₅M₁ represent the total ABCD matrices from the laser output end to the photovoltaic receiver surface, and the values are as follows:

(1)

The total ABCD matrix of transmitted and transmitted optical path;

$$M_2{M}_1=\left[\begin{array}{cc}\frac{\mathrm{\beta }({\mathrm{d}}_4-{\mathrm{f}}_3+\frac{2{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7)}{{\mathrm{f}}_3}& \frac{({\mathrm{d}}_4-{\mathrm{f}}_3)E-{\mathrm{d}}_4{\mathrm{f}}_3+\left(\frac{2{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7\right)\left(E-{\mathrm{f}}_3\right)}{\mathrm{\beta }{\mathrm{f}}_3}\\ \frac{\mathrm{\beta }}{{\mathrm{f}}_3}& \frac{E-{\mathrm{f}}_3}{\mathrm{\beta }{\mathrm{f}}_3}\end{array}\right]$$

(8)

(2)

The total ABCD matrix of transmitted and reflected optical paths

$$M_3{M}_1=\left[\begin{array}{cc}\frac{\mathrm{\beta }({\mathrm{d}}_4-{\mathrm{f}}_3+\frac{{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7)}{{\mathrm{f}}_3}& \frac{({\mathrm{d}}_4-{\mathrm{f}}_3)E-{\mathrm{d}}_4{\mathrm{f}}_3+\left(\frac{{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7\right)\left(E-{\mathrm{f}}_3\right)}{\mathrm{\beta }{\mathrm{f}}_3}\\ \frac{\mathrm{\beta }}{{\mathrm{f}}_3}& \frac{E-{\mathrm{f}}_3}{\mathrm{\beta }{\mathrm{f}}_3}\end{array}\right]$$

(9)

(3)

The total ABCD matrix of reflected and transmitted optical paths

$$M_4{M}_1=\left[\begin{array}{cc}\frac{\mathrm{\beta }({\mathrm{d}}_4-{\mathrm{f}}_3+\frac{{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7)}{{\mathrm{f}}_3}& \frac{({\mathrm{d}}_4-{\mathrm{f}}_3)E-{\mathrm{d}}_4{\mathrm{f}}_3+\left(\frac{{\mathrm{d}}_5}{\mathrm{n}}+{\mathrm{d}}_6+{\mathrm{d}}_7\right)\left(E-{\mathrm{f}}_3\right)}{\mathrm{\beta }{\mathrm{f}}_3}\\ \frac{\mathrm{\beta }}{{\mathrm{f}}_3}& \frac{E-{\mathrm{f}}_3}{\mathrm{\beta }{\mathrm{f}}_3}\end{array}\right]$$

(10)

(4)

The total ABCD matrix of reflected and reflected optical paths

$$M_5{M}_1=\left[\begin{array}{cc}\frac{\mathrm{\beta }({\mathrm{d}}_4-{\mathrm{f}}_3+{\mathrm{d}}_6+{\mathrm{d}}_7)}{{\mathrm{f}}_3}& \frac{({\mathrm{d}}_4-{\mathrm{f}}_3)E-{\mathrm{d}}_4{\mathrm{f}}_3+\left({\mathrm{d}}_6+{\mathrm{d}}_7\right)\left(E-{\mathrm{f}}_3\right)}{\mathrm{\beta }{\mathrm{f}}_3}\\ \frac{\mathrm{\beta }}{{\mathrm{f}}_3}& \frac{E-{\mathrm{f}}_3}{\mathrm{\beta }{\mathrm{f}}_3}\end{array}\right]$$

(11)

From Equations (8)–(11), it is evident that the values of C and D in the four matrices are identical. Furthermore, when d₅ = 0, that is, the lens is a thin lens, parameters A and B in the four matrices are also exactly equal. Consequently, the complex radius of the Gaussian beam can be represented as follows:

$${\mathrm{q}}_2=\frac{A{\mathrm{q}}_1+\mathrm{B}}{\mathrm{C}{\mathrm{q}}_1+\mathrm{D}}$$

(12)

Since parameters A, B, C, and D in the four matrices are all equal, and the incident laser originates from the same source, the complex radius of the four beam-splitting paths are equal. Consequently, the irradiation areas of the laser on the powersphere are all equal. Additionally, utilizing a partially transmitting and partially reflecting lens for beam splitting ensures that the laser powers of the four beam paths are equal. Thus, the incident laser light can be divided into four paths of light with equal areas and powers to irradiate the inner surface of the powersphere through the light-splitting system.

For the optical path of the system that does not use light splitting, the distance from the Fresnel lens to the receiving surface should be d₄ + d₆ + d₇. Substituting this distance into Equation (3) yields the same values for A, B, C, and D as the beam-splitting optical system. This implies that the complex radius for both the non-beam-splitting system and the beam-splitting system are equal. Therefore, under the condition of unchanged parameters, the beam-splitting system increases the irradiation area by a factor of four compared to the non-beam-splitting system. This theoretical analysis demonstrates the feasibility of the beam-splitting system.

Due to the electric field of the fundamental mode, the Gaussian beam can be expressible as follows [18,33,34]:

$${\psi }_{00}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\frac{\mathrm{c}}{\mathrm{\omega }\left(\mathrm{z}\right)}{\mathrm{e}}^{-\mathrm{i}\mathrm{k}\frac{{\mathrm{r}}^2}{2}\left[\frac{1}{\mathrm{R}\left(\mathrm{z}\right)}-\mathrm{i}\frac{\mathrm{\lambda }}{\mathrm{\pi }{\mathrm{\omega }}^2\left(\mathrm{z}\right)}\right]}{\mathrm{e}}^{-\mathrm{i}\left[\mathrm{k}\mathrm{z}-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{\mathrm{z}}{\mathrm{f}}\right]}$$

(13)

In the equation, c is a constant factor, k is a proportionality coefficient, λ is the wavelength, f is the confocal parameter of the Gaussian beam, R(z) is the radius of curvature of the equiphase surface, W(z) is the beam radius on the equiphase surface, and Z is the propagation distance of the beam along the optical axis, r² = x² + y².

And the q parameter is defined as:

$$\frac{1}{\mathrm{q}(\mathrm{z})}=\frac{1}{\mathrm{R}\left(\mathrm{z}\right)}-\mathrm{i}\frac{\mathrm{\lambda }}{\mathrm{\pi }{\mathrm{w}}^2\left(\mathrm{z}\right)}$$

(14)

Therefore, the electric field of the Gaussian beam can be expressed as:

$${\psi }_{00}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\frac{\mathrm{c}}{\mathrm{\omega }\left(\mathrm{z}\right)}{\mathrm{e}}^{-\mathrm{i}\mathrm{k}\frac{{\mathrm{r}}^2}{2}\frac{1}{\mathrm{q}\left(\mathrm{z}\right)}}{\mathrm{e}}^{-\mathrm{i}\left[\mathrm{k}\mathrm{z}-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{\mathrm{z}}{\mathrm{f}}\right]}$$

(15)

So, for each optical path with beam splitting, the electric field of the Gaussian beam can be expressed as:

$${\psi }_{00}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\frac{\mathrm{c}}{\mathrm{\omega }\left(\mathrm{z}\right)}{\mathrm{e}}^{-\mathrm{i}\mathrm{k}\frac{{\mathrm{r}}^2}{2}\frac{1}{{\mathrm{q}}_2\left(\mathrm{z}\right)}}{\mathrm{e}}^{-\mathrm{i}\left[\mathrm{k}\mathrm{z}-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{\mathrm{z}}{\mathrm{f}}\right]}$$

(16)

From Equation (12), it can be seen that q₂ is determined by matrices A, B, C, and D, and q₁. Since the four beams come from the same source, q₁ is equal for all beams. As previously demonstrated, A, B, C, and D are equal for the four beams. This implies that the electric fields in the four paths are equal. According to the intensity formula:

$$I\propto {\mathrm{\Psi }}_{00}^2(\mathrm{x},\mathrm{y},\mathrm{z})$$

(17)

So, the intensities of the four optical paths are also equal. Similarly, it can be demonstrated that the illuminance values of the four beams incident on the powersphere are equal, according to the illuminance formula [31]:

$$E=\frac{\mathrm{\rho }{E}_{\mathrm{B}}{\mathrm{S}}_1}{4\mathrm{\pi }{\mathrm{R}}^2}$$

(18)

In the equation, E is the total illuminance of the optical path, E_B is the illuminance at any point, $\mathrm{\rho }$ is the absorption efficiency of the photovoltaic cell, R is the radius of the powersphere, and S₁ represents the laser irradiation area.

Therefore, when $\mathrm{\rho }$, E_B and R are both equal, and the illuminated area is 1/4 of the original; the illuminance becomes 1/4 of the original value. If, during the beam-splitting process, some light deviates from the ideal optical path due to positional factors or changes in the angle, resulting in some light not illuminating the corresponding photovoltaic cell, i.e., S₁ becomes smaller, then the illuminance is correspondingly reduced.

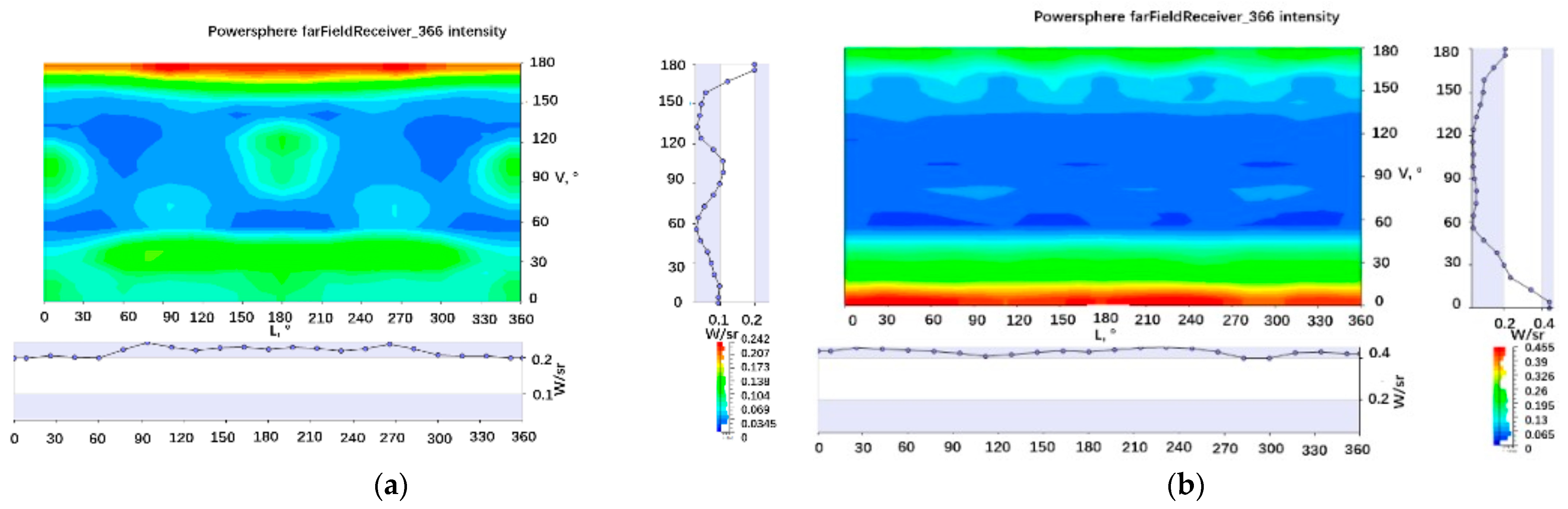
3. Modeling and Simulation Analysis

In order to more accurately study the energy distribution within the powersphere cavity with beam splitting, evaluate the performance of the beam-splitting system, and predict key parameters such as the photoelectric conversion efficiency, the optical software Lighttools was used to establish a laser wireless energy transmission model, in which the powersphere was the receiver, as shown in Figure 4. In this transmission model, an 808 nm semiconductor laser with a diameter of 400 μm and a divergence angle of 25 degrees was employed as the light source. The laser underwent collimation through a beam expander and was then focused onto the powersphere using a Fresnel lens. And, eventually, it was transmitted to the inner surface of the powersphere, where the photovoltaic cells on the inner surface undergo photovoltaic conversion to generate electricity. When conducting beam-splitting simulations, beam splitters can be added inside the model of the powersphere so that the laser is split by the partially transmitting and partially reflecting beam splitter, transforming into multiple identical beam paths, which are then directed onto the photovoltaic cells on the inner surface of the power sphere for photoelectric conversion.

Figure 5a is a ray-tracing diagram, with three semi-transparent and semi-reflective lenses added at the center of the sphere. The position of the beam splitters is shown in Figure 1. And the red objects in the figure are the semi-transparent and semi-reflective lenses. Figure 5b [32] is the ray-tracing diagram without adding three beam splitters at the center of the sphere. Comparing the two figures, it can be clearly seen that after adding a semi-transparent and semi-reflective lens, the ray density on the inner surface of the powersphere is significantly improved. A comparison between the two figures reveals that the introduction of a semi-transparent and semi-reflective lens results in a noticeable enhancement in ray density on the inner surface of the powersphere. Consequently, there are no large areas of light attenuation, and the direct irradiation area is enlarged. However, the overall distribution trend of the two diagrams remains consistent. The light intensity of the direct irradiation area is significantly higher than that of the reflection irradiation area. Among them, the illuminance on the right end of the powersphere, as shown in Figure 5, is the strongest, and it is the region directly illuminated by light. Next is the left side of the powersphere, which is the region illuminated by the first reflected light. Finally, there are the upper and lower parts of the powersphere, and they are the regions illuminated by multiple reflected lights.

Figure 6a is the light intensity distribution diagram with three semi-transparent and semi-reflective lenses added at the center of the sphere, and Figure 6b [32] is the light intensity distribution diagram without a beam splitter at the center of the sphere. The V coordinate in the figure is the Z-axis of the incident light, where 0° on the V-axis corresponds to the center of the light spot irradiating the powersphere. Hence, 180° represents the center of the light spot on the powersphere’s entrance aperture. The L-axis is perpendicular to the incident light, that is, the X or Y axis on the optical path diagram, and it is a concentric circle with the incident light spot. On the same V axis, the light intensity on the L axis basically does not change much.

Comparing the two diagrams in Figure 6, it can be found that the maximum light intensity in Figure 6a is 0.242 W/sr, the strongest area is located within 0°–15°, and it occupies 1/12 of the total area. The maximum light intensity is about half of the maximum light intensity 0.455 W/sr in Figure 6b. The reason is that part of the laser irradiated on the inner surface of the powersphere only passes through the first beam splitter. This condition can be avoided by adjusting the match relationship between the beam splitter and the diameter of the incident spot. In the range of 0°–60° in Figure 6b, except some areas exceeding 0.39 W/sr, most of the areas are below 0.39 W/sr, and the strongest area is located within 0°–10°, that is, it occupies 1/18 of the total area. This proves that light splitting can reduce the difference in light intensity and improve the uniformity of light in the powersphere. In the range of 60°–120° in Figure 6b, the light intensity values without splitting are the lowest area of the inner surface of the powersphere; the minimum light intensity is 0 W/sr. but the light intensity value with splitting is greater than the light intensity value without splitting; the area with zero light intensity no longer exists with splitting, indicating that the light intensity value of this area is improved. Compared with the ray-tracing diagram, it is found that the light density at this place with splitting is significantly higher than that without splitting. After 120° in Figure 6b, the light intensity gradually increases and increases from 0.065 W/sr to 0.20 W/sr without splitting, and the maximum light intensity reaches about 0.20 W/sr, which is located near 180°. In the range of 0°–165° in Figure 6a, the maximum light intensity is only 0.1 W/sr, which is less than 0.2 W/sr in the range of 10°–180° in Figure 6b. The green area in the figure further increases, whereas the blue area is further reduced. This means that the light intensity in the non-directly irradiated area is enhanced. In the range of 165°–180° in Figure 6a, the light intensity reaches the maximum value of 2.42 W/sr.

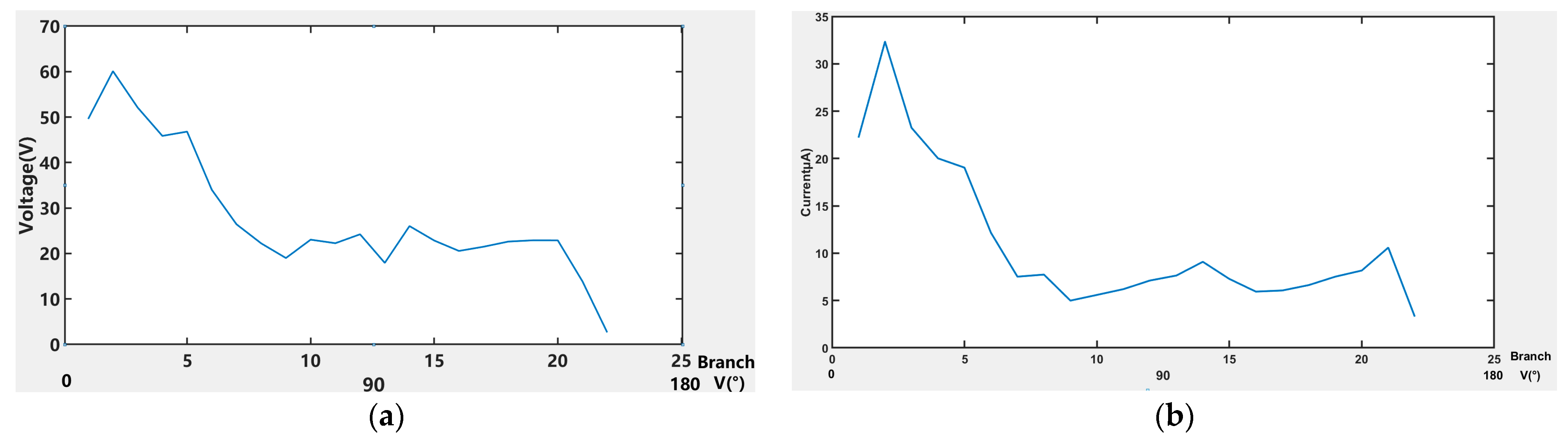
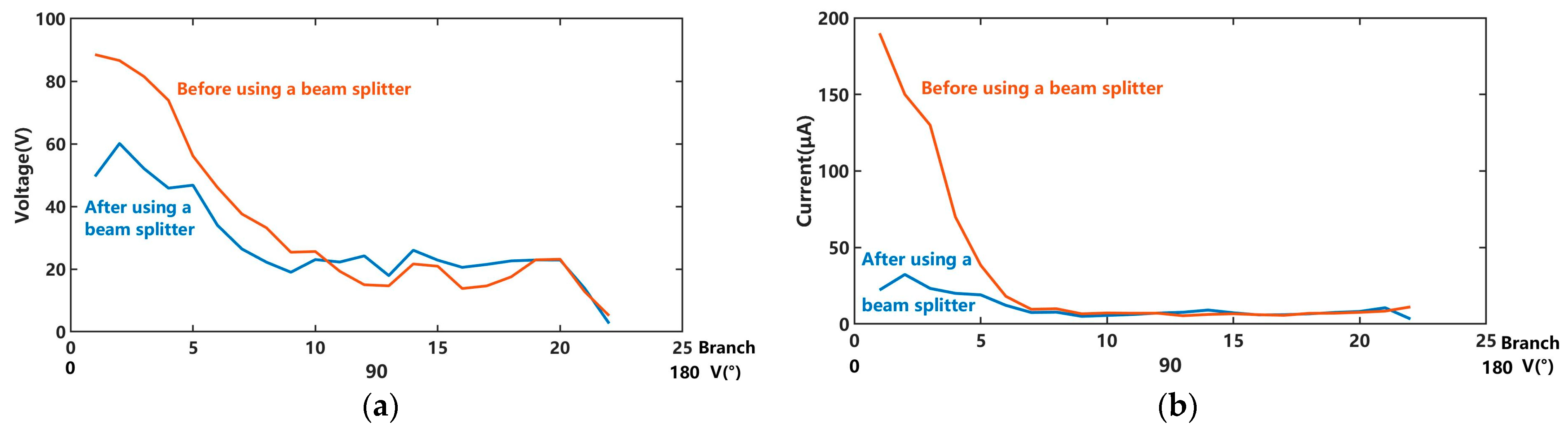
4. Testing Experiment and Analysis

The powersphere is a sphere composed of two hemispheres. The powersphere in the experiment consists of 6900 photovoltaic cells. Starting from the right side of the powersphere and following the physical connection sequence, every 100 photovoltaic cells are connected in series to form a group. Three of these groups are then connected in parallel to create one branch, resulting in a total of 22 branches. The branches are arranged in sequential order from the right side to the left side of the powersphere. The branch numbers are arranged in order from the right side to the left side of the powersphere. The hemisphere (branch 1–branch 11) whose inner surface can be directly irradiated by laser without beam splitting is called hemisphere 1, and the hemisphere (branch 12–branch 22) whose inner surface can only be irradiated by reflected light without beam splitting is called Hemisphere 2.

In order to verify the calculation, simulation, and design effects, three semi-transparent and semi-reflective mirrors with a diameter of 50 mm were combined to form a beam splitting system, as shown in Figure 7. The splitting ratio (R:T) of the beam splitting mirror was 50:50. The lens’s available wavelength was 650–900 nm, so it could be used for the 808 nm laser used in the experiment to split the light. The beam-splitting system was fixed near the center of the sphere, and the angle between the optical axis of the first beam splitter and the optical axis of the incident laser was kept as 45 degrees; the second and third beam splitter were perpendicular to the first beam splitter, respectively. In this way, beam could be divided into four beams, which are irradiated to the upper, lower, left, and right areas of the inner surface of the powersphere, respectively.

The beam-splitting system shown in Figure 7 was used together with the 808 nm semiconductor laser, beam expander, Fresnel lens, and powersphere receiver to build a beam-splitting experimental platform to verify the uniformity of the powersphere cavity with splitting. In the experiment, the voltage and current of 22 groups of circuits on the powersphere were measured, respectively, and the distribution curve was plotted using Matlab according to the measured data. Since the output voltage and current of the photovoltaic cell are proportional to the luminous flux, that is, the output voltage and current are proportional to the light intensity, the distribution of the laser on the inner surface of the powersphere can be understood by measuring the output voltage and current of the photovoltaic cells at various positions on the powersphere.

When the focal length of the Fresnel lens was 70 mm and the distance between the lens and the powersphere was 150 mm, the circuit distribution curve after adding three beam splitters is shown in Figure 8. Figure 8a represents the voltage distribution curve, while Figure 8b represents the current distribution curve. The horizontal axis in the figure is not only the serial number of the circuit, but also the V coordinate of the LV coordinate in the light intensity figure. It can be seen from Figure 8 that within the range of 0°–60° of the V coordinate, as the angle increases, the voltage and current gradually decrease. The main reason for this phenomenon is that this region corresponds to the area directly irradiated by the laser, which exhibits a higher light intensity compared to other regions. Additionally, as the angle decreases, the position of this region gets closer to the center of the beam spot, resulting in a higher light intensity. In the range of 60°–180° of the V coordinate, the distribution curve basically presents a linear distribution, that is, the light intensity is basically the same. There are several points in the figure where the voltage and current values deviate from the surrounding parameters, resulting in sharp drops in the curves. The main reason for this phenomenon is that there are problems with the photovoltaic cells in these places. In order not to affect the overall effect, these cells were removed before the experiment. They were disconnected from the total circuit so that no voltage and current were generated [32].

In order to gain a more detailed understanding of the beam splitting effects, the voltage and current distribution curves with beam splitting, as shown in Figure 8, were combined with the voltage and current distribution curves without beam splitting to create a consolidated graph presented as Figure 9. Figure 9a represents the voltage distribution curve, while Figure 9b represents the current distribution curve. It can be seen from the figure that the voltage and current distribution curves are smoother after the three beam splitter is added, that is, the difference between the maximum and minimum values of the curve is decreased.

After adding the beam splitter, the range of the higher voltage region decreased from 0°–75° in the V-coordinate to 0°–50°. Additionally, the maximum voltage decreased from about 90 V to approximately 60 V. This indicates an enlargement of the smoother region; moreover, the voltage values within this smoother region with beam splitting are slightly higher than the corresponding positions without beam splitting. This suggests a more uniform distribution of light intensity achieved through beam splitting.

Although the current value difference at different positions on the V coordinate in Figure 8b is still very large, compared with the curve without beam splitting, the current values on the different coordinates on the powersphere with beam splitting are nearly equal, as shown in Figure 9b. From Figure 9b, it can be seen that the current curve with beam splitting is close to a straight line, that is, the uniformity of the current value is significantly improved. The experimental results show that the addition of 3 beam splitters significantly improved the uniformity of the light intensity distribution on the inner wall of the powersphere.

In the experiment, all the branches on the hemisphere were connected in parallel to an output, and the output voltage and current were measured. The measurement data are shown in

Table 1. Voltage and current of the hemispheres with and without a beam-splitting system.

		With Beam Splitting	Without Beam Splitting
Hemisphere 1	Voltage (V)	11.29	40.42
	Current (mA)	0.30	0.54
Hemisphere 2	Voltage (V)	3.35	3.07
	Current (mA)	0.06	0.06
Total output	Voltage (V)	5.65	6.28
	Current (mA)	0.40	0.58

. It can be seen from Table 1 that the voltage of hemisphere 1 was 40.42 V, and the current of hemisphere 1 was 0.54 mA without beam splitting; the voltage of hemisphere 2 was 3.07 V, and the current of hemisphere 2 was 0.06 mA without beam splitting. Then, the two hemispheric output circuits were connected in parallel; the total output voltage was 6.28 V, and the total output current was 0.58 mA. The voltage of hemisphere 1 was 11.29 V, and the current of hemisphere 1 was 0.30 mA with beam splitting; the voltage of hemisphere 2 was 3.35 V, and the current of hemisphere 2 was 0.06 mA with beam splitting. The total output voltage after the parallel connection was 5.65 V, and the total output current after the parallel connection was 0.40 mA. It can be seen from Table 1 that the voltage and current of hemisphere 1 were reduced with beam splitting, the voltage of hemisphere 2 was increased, and the current remained unchanged. That is, the voltage difference and current difference between the two hemispheres became smaller, and the uniformity of the light intensity distribution was greatly improved. In particular, the voltage of hemisphere 2 with beam splitting was higher than the voltage without beam splitting, indicating that the light intensity of hemisphere 2 was increased with beam splitting, and the voltage difference between the two hemispheres was reduced. Thus, the loss caused by the unequal voltage and current in the circuit can be reduced, which is consistent with the conclusion obtained from the simulation.

In order to understand the uniformity more intuitively, divide the voltage of hemisphere 2 by the voltage of hemisphere 1 to obtain the uniformity of voltage, and calculate the uniformity of current and power in the same way, as shown in

Table 2. Uniformity with and without a beam-splitting system.

Parameter	With Beam Splitting	Without Beam Splitting
Voltage (V)	0.29	0.08
Current (mA)	0.20	0.11
Power (mW)	0.059	0.008

. From Table 2, it can be observed that the uniformity of voltage increases from 0.08 to 0.29, the uniformity of current increases from 0.11 to 0.20, and the uniformity of power increases from 0.008 to 0.059. This indicates a significant improvement in the uniformity of all three parameters, which is consistent with the conclusions obtained from the simulations.

However, the total conversion efficiency with splitting was slightly lower than the total output efficiency without splitting. The main reason is that the laser power density decreased with splitting, so the conversion efficiency of single photovoltaic cells became very low, which affected the experimental results.

In the experiment, the focused laser power was 0.54 W, and the power sum of each branch in the circuit was 0.0778 W without splitting and 0.0103 W with splitting, so the photoelectric conversion efficiency without and with splitting was 14.4% and 1.9%, respectively. Based on the linear relationship between the power density and the photoelectric conversion efficiency of photovoltaic cells, if the power density in the experiment is 1000 W/m², the photoelectric conversion efficiency of the photovoltaic cell is A. Then, the ratio of the two is the photoelectric conversion ratio between the laser power density in the experiment and the standard power density, that is, $\frac{A}{14.4\%}$ without splitting and $\frac{A}{1.9\%}$ with splitting. By multiplying the total voltage and total current of the powersphere in Table 1, the output power without splitting can be obtained as 0.00364 W, and with splitting, it is 0.00226 W, and the ratios to the focused laser power (0.54 W) are 0.67% and 0.42%, respectively. Multiplying the two values by the ratio of the photoelectric conversion ratio between the laser power density in the experiment and the standard power density gives the total efficiency of the experimental device at the standard power density:

$$\frac{0.42\%}{1.9\%}\times A=22\%A$$

(19)

$$\frac{0.67\%}{14.4\%}\times A=4.6\%A$$

(20)

Divide Equation (19) by Equation (20), and the ratio of the two is 4.78, that is, under the same power density, the total conversion efficiency with splitting will be 4.78 times that without splitting, indicating that beam splitting will significantly improve the conversion efficiency of the system. Meanwhile, in the future, when using a higher-power laser, more experimental measurements with different power densities will be carried out to obtain more accurate experimental validations.

5. Conclusions

The powersphere is a closed receiver for improving the uniformity of light at the receiving end of a laser wireless energy transmission system. However, due to the high absorption rate of photovoltaic cells, the powersphere is far from achieving the ideal effect in actual use. In order to solve this problem, the research team proposes to add a beam-splitting system composed of multiple beam splitters in the powersphere, divide one incident laser into multiple input lasers, increase the direct irradiation area, reduce the power density of the direct irradiation area, and, thus, increase the uniformity of light intensity distribution on the inner surface of the powersphere.

The ABCD matrix calculation, simulation, and experiment were used to study the uniformity of light in the cavity. The results of the above methods show that the technique of splitting light in the cavity can improve the uniformity of the light intensity distribution of the powersphere and reduce the energy loss of the powersphere. As the output power with splitting was smaller than that without splitting in the experiment, analyses and calculations were carried out to find out the reasons for the problem, and the conversion efficiency of the two at the standard power density was calculated. The calculation results show that at the same power density, the conversion efficiency with splitting will be about five times that without splitting, that is, the method of intracavity beam splitting greatly improves the conversion efficiency of the system.