Wavefront Reconstruction Using Two-Frame Random Interferometry Based on Swin-Unet
Abstract
1. Introduction
2. Methods
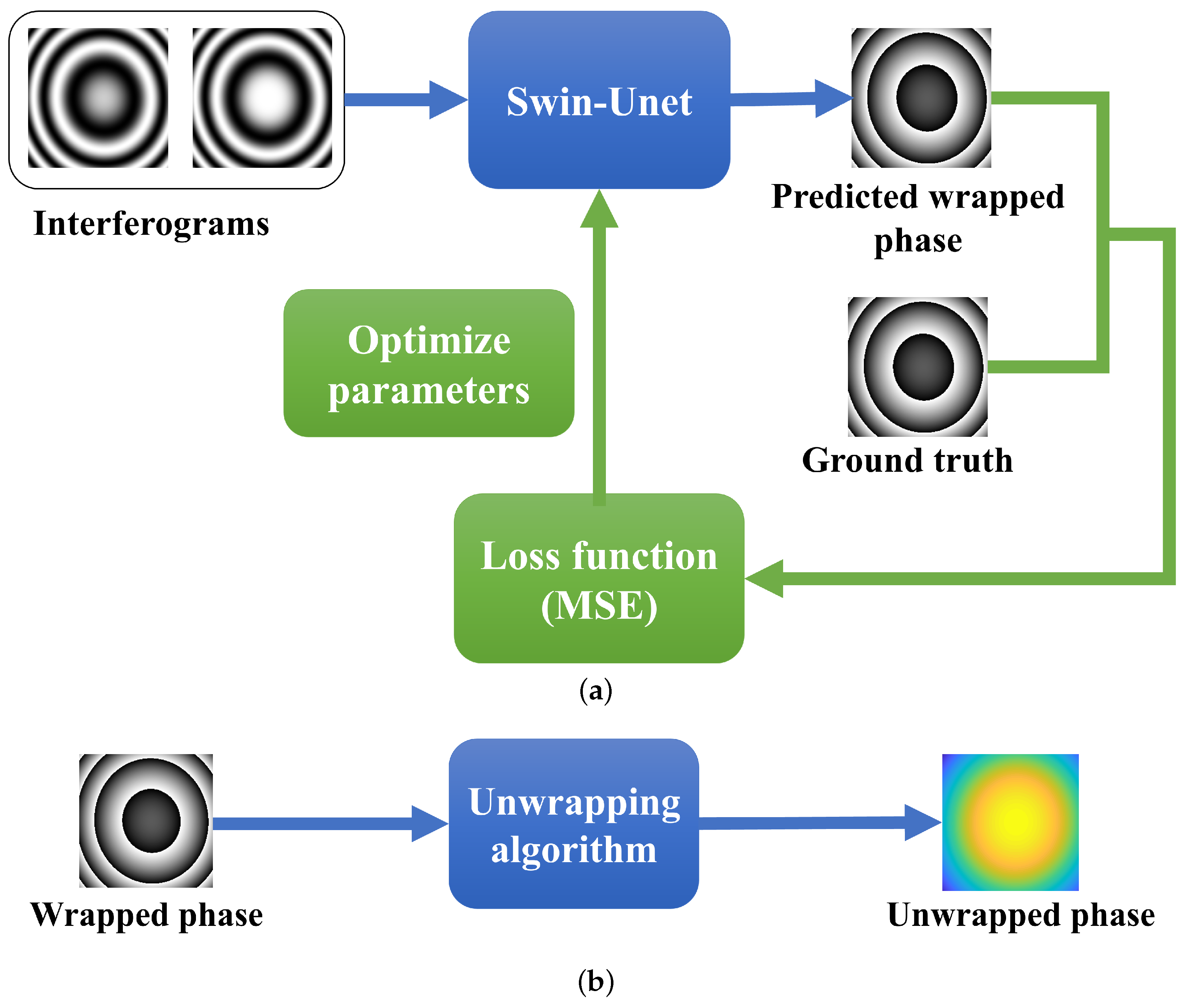
2.1. The Process of Proposed Method
2.2. Theoretical Background
2.3. The Architecture of Neural Networks
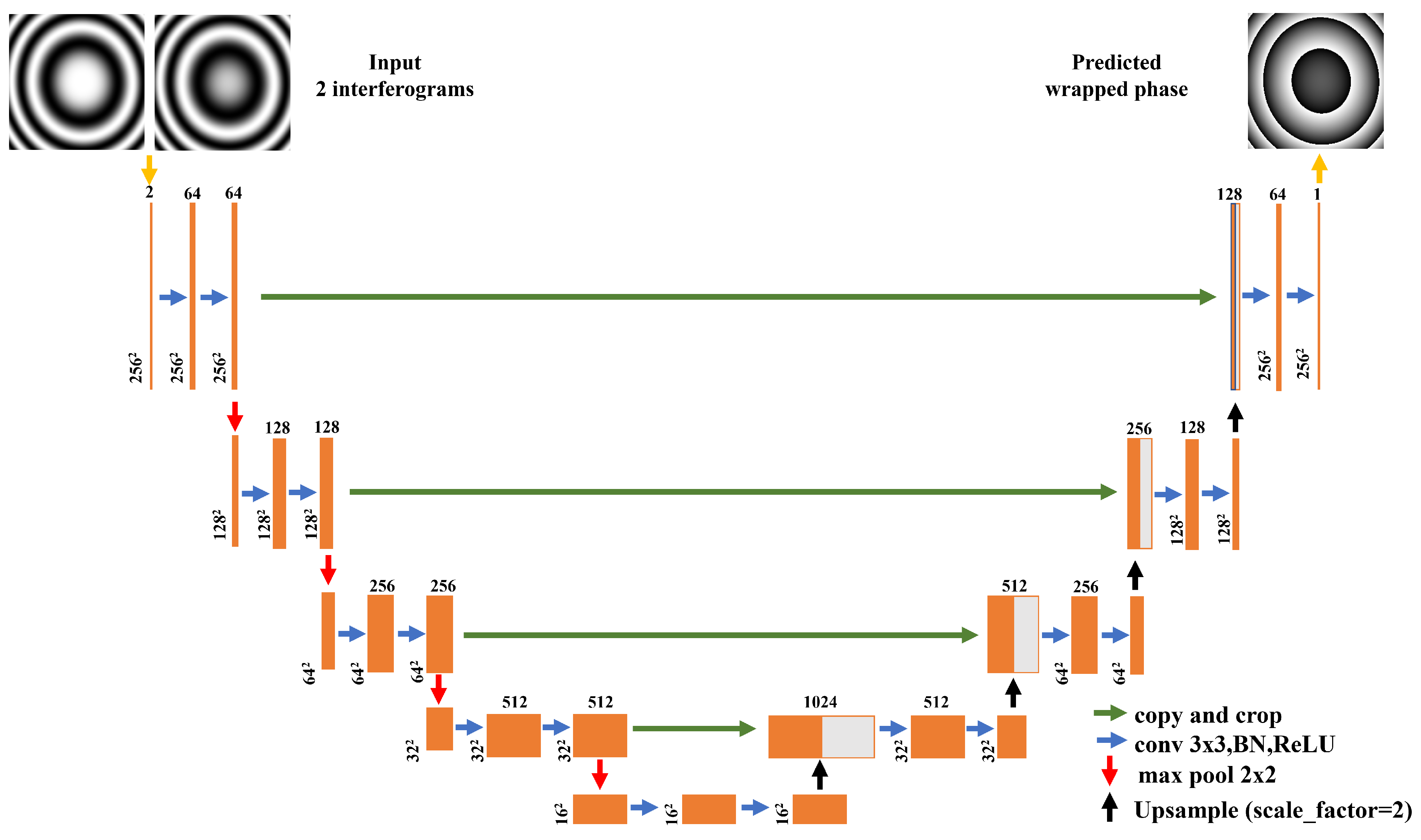
2.3.1. PUN+
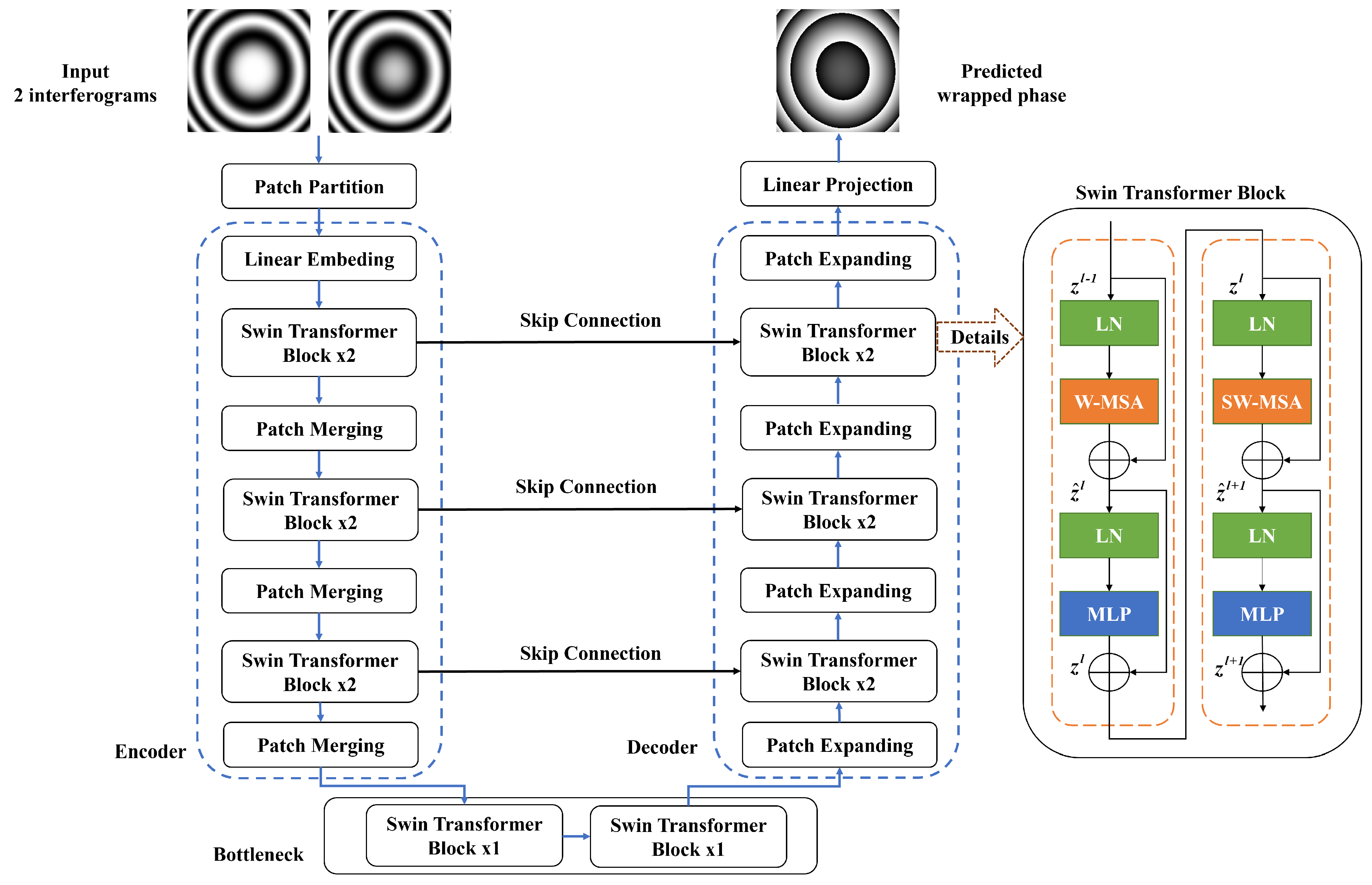
2.3.2. Swin-Unet
2.4. Network Training
3. Results and Analysis
3.1. Simulation Dataset
3.2. Accuracy Test
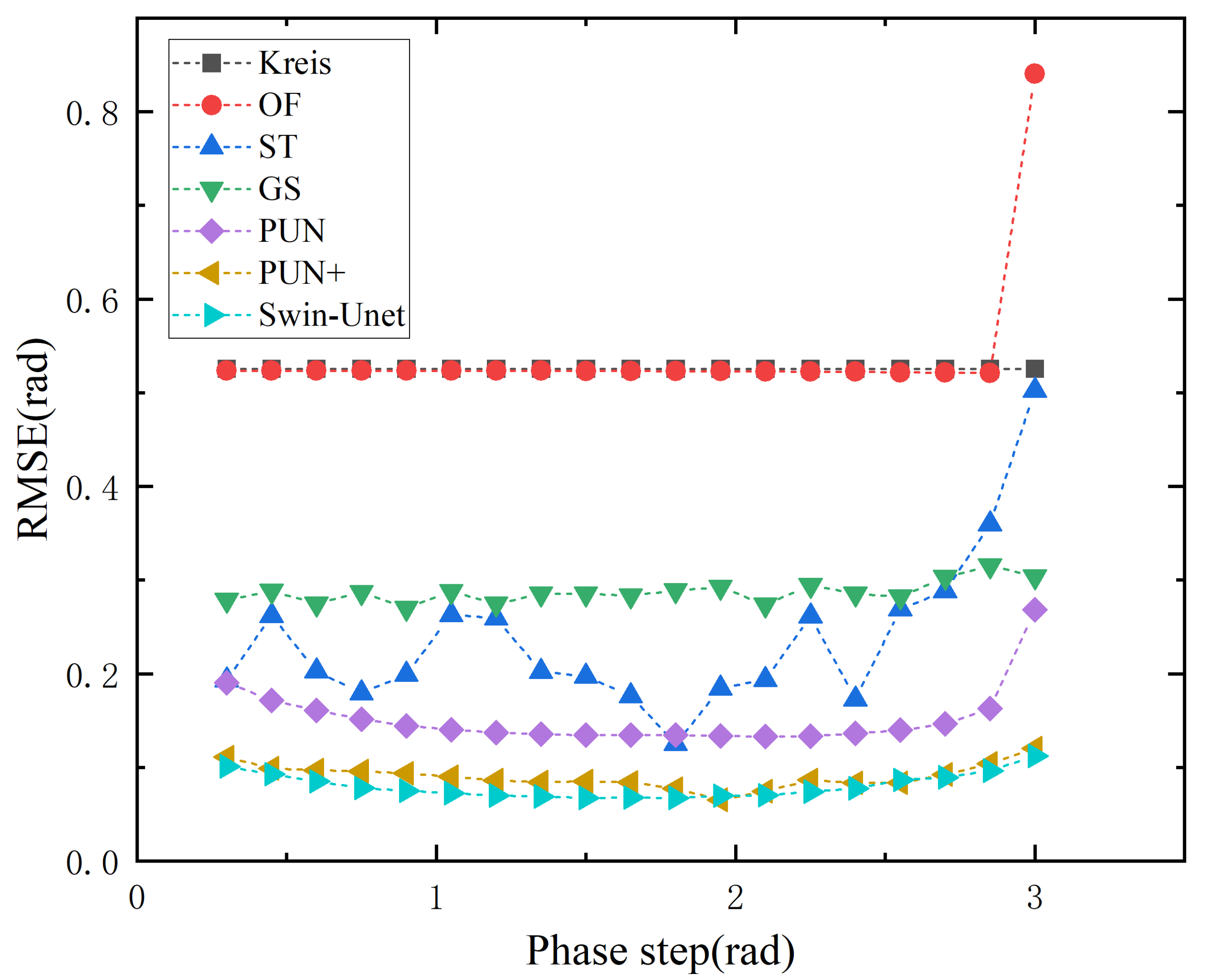
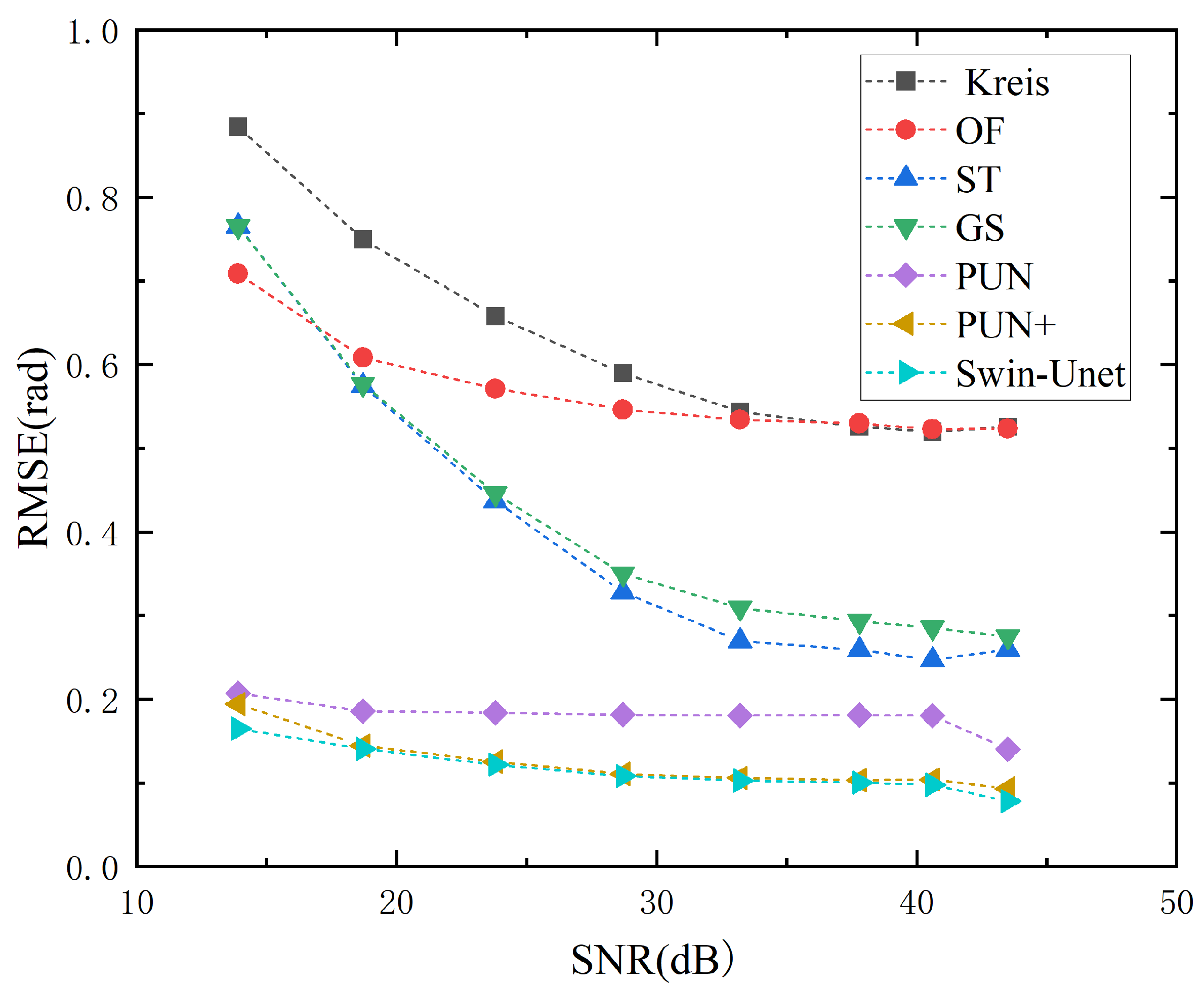
3.3. Anti-Noise Performance
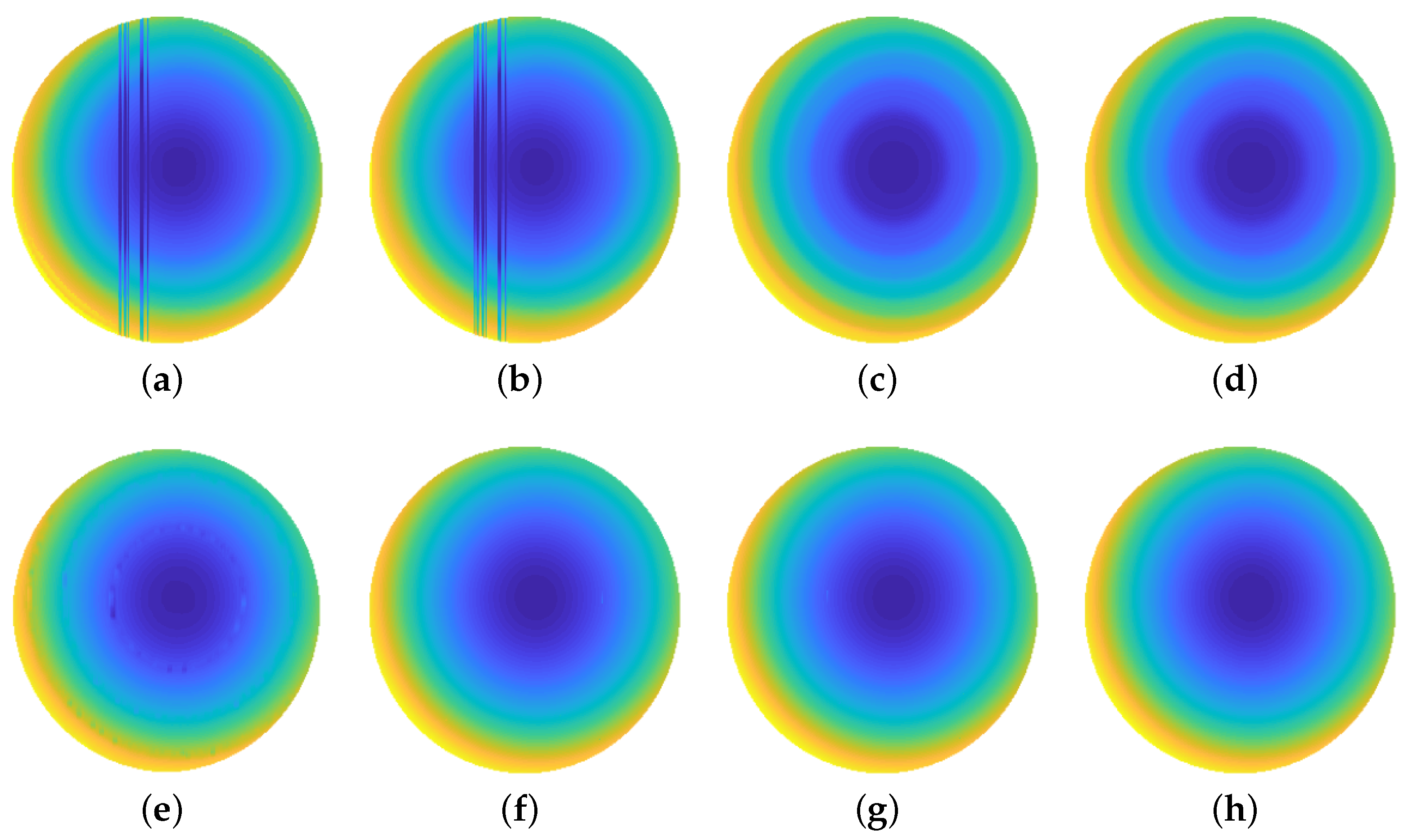
3.4. Low Modulation Test
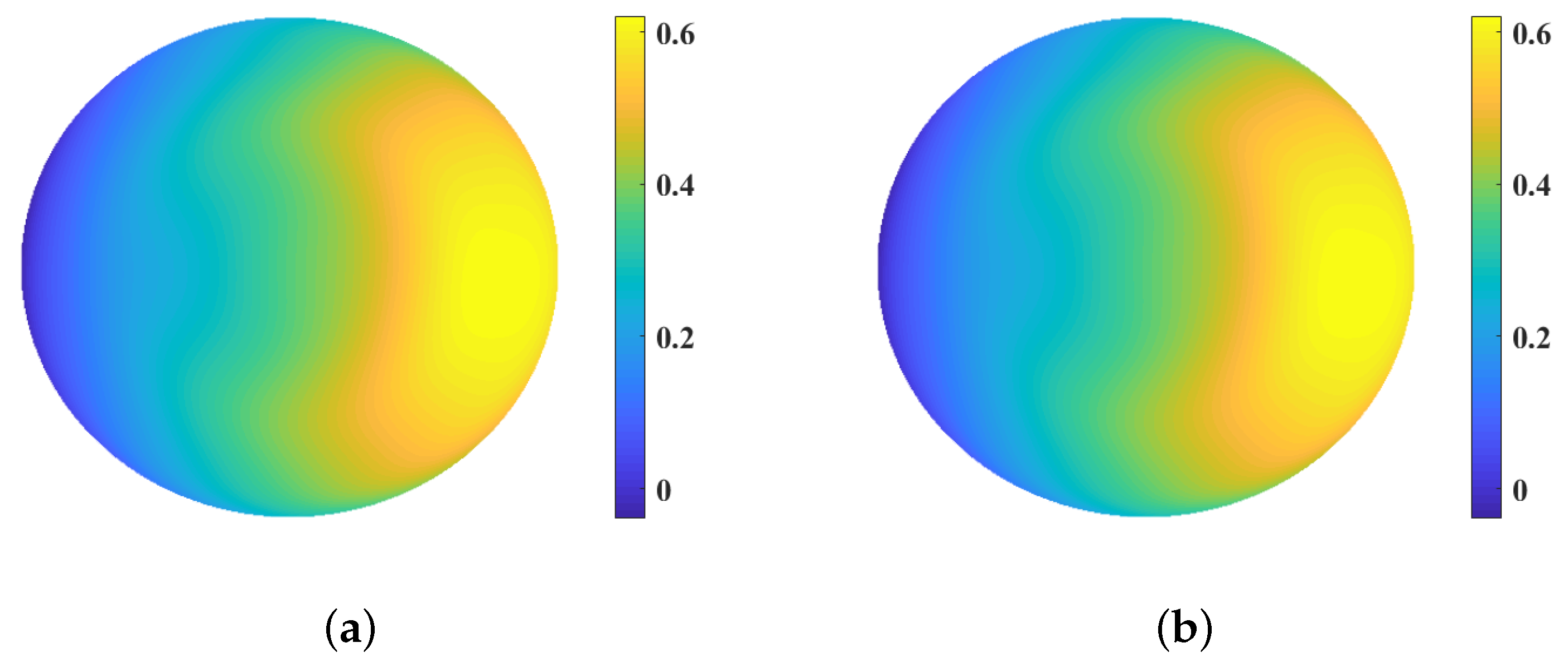
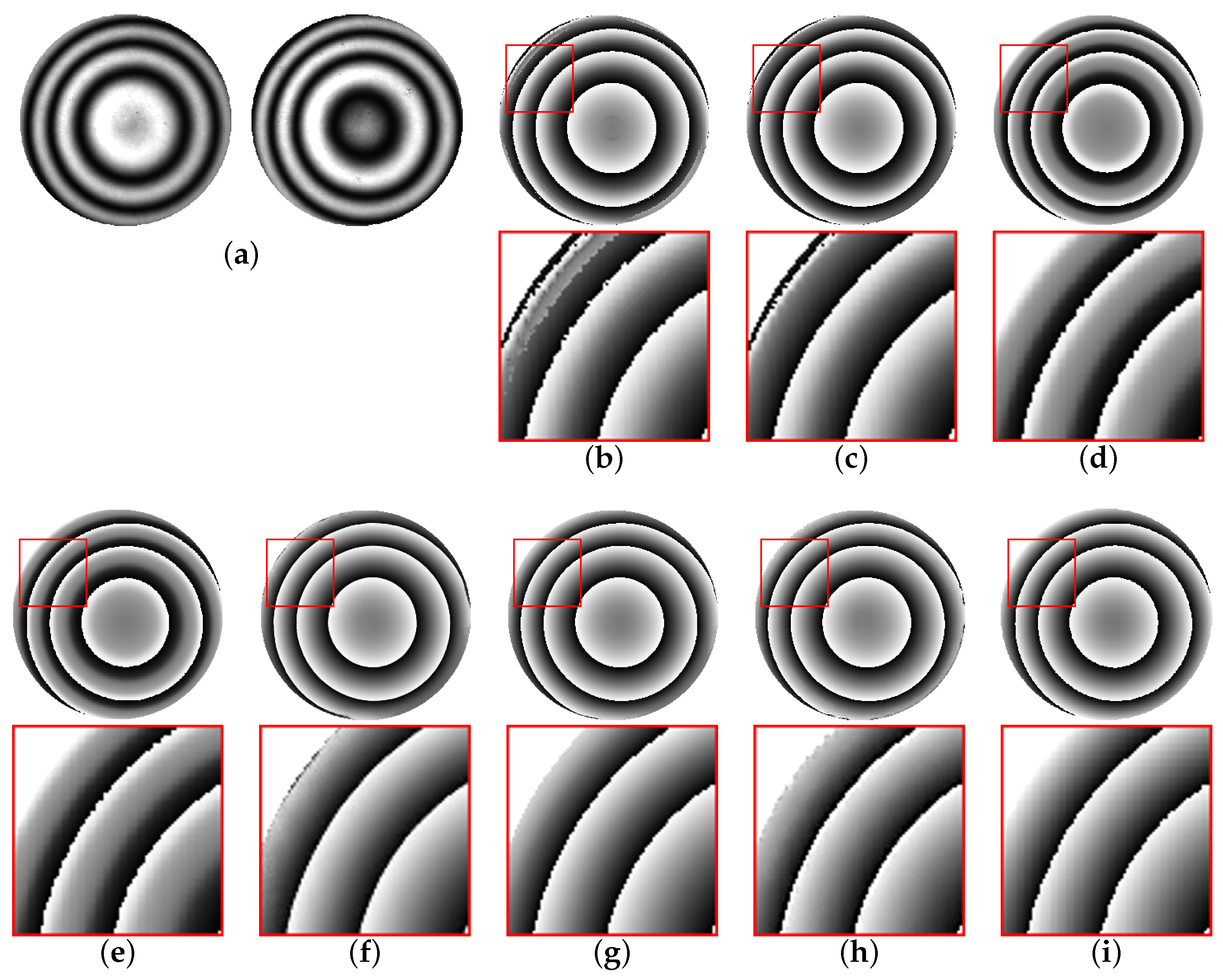
3.5. Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Malacara, D. Optical Shop Testing; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 59. [Google Scholar]
- Kinnstaetter, K.; Lohmann, A.W.; Schwider, J.; Streibl, N. Accuracy of phase shifting interferometry. Appl. Opt. 1988, 27, 5082–5089. [Google Scholar] [CrossRef] [PubMed]
- Abdelsalam, D.; Yao, B.; Gao, P.; Min, J.; Guo, R. Single-shot parallel four-step phase shifting using on-axis Fizeau interferometry. Appl. Opt. 2012, 51, 4891–4895. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Wang, K.; Wu, D.; Lv, X.; Li, C.; Hao, J.; Qin, J.; Chen, W. Advanced principal component analysis method for phase reconstruction. Opt. Express 2015, 23, 12222–12231. [Google Scholar] [CrossRef] [PubMed]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Ge, Z.; Kobayashi, F.; Matsuda, S.; Takeda, M. Coordinate-transform technique for closed-fringe analysis by the Fourier-transform method. Appl. Opt. 2001, 40, 1649–1657. [Google Scholar] [CrossRef] [PubMed]
- Kreis, T.M.; Jueptner, W.P. Fourier transform evaluation of interference patterns: Demodulation and sign ambiguity. In Proceedings of the Laser Interferometry IV: Computer-Aided Interferometry, San Diego, CA, USA, 1 January 1992; Volume 1553, pp. 263–273. [Google Scholar]
- Vargas, J.; Quiroga, J.A.; Sorzano, C.; Estrada, J.; Carazo, J. Two-step interferometry by a regularized optical flow algorithm. Opt. Lett. 2011, 36, 3485–3487. [Google Scholar] [CrossRef] [PubMed]
- Vargas, J.; Quiroga, J.A.; Belenguer, T.; Servín, M.; Estrada, J. Two-step self-tuning phase-shifting interferometry. Opt. Express 2011, 19, 638–648. [Google Scholar] [CrossRef]
- Vargas, J.; Quiroga, J.A.; Sorzano, C.; Estrada, J.; Carazo, J. Two-step demodulation based on the Gram–Schmidt orthonormalization method. Opt. Lett. 2012, 37, 443–445. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany; pp. 205–218. [Google Scholar]
- Shi, J.; Zhu, X.; Wang, H.; Song, L.; Guo, Q. Label enhanced and patch based deep learning for phase retrieval from single frame fringe pattern in fringe projection 3D measurement. Opt. Express 2019, 27, 28929–28943. [Google Scholar] [CrossRef]
- Yan, K.; Yu, Y.; Huang, C.; Sui, L.; Qian, K.; Asundi, A. Fringe pattern denoising based on deep learning. Opt. Commun. 2019, 437, 148–152. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3365–3387. [Google Scholar] [CrossRef]
- Hao, F.; Tang, C.; Xu, M.; Lei, Z. Batch denoising of ESPI fringe patterns based on convolutional neural network. Appl. Opt. 2019, 58, 3338–3346. [Google Scholar] [CrossRef]
- Wang, K.; Li, Y.; Kemao, Q.; Di, J.; Zhao, J. One-step robust deep learning phase unwrapping. Opt. Express 2019, 27, 15100–15115. [Google Scholar] [CrossRef] [PubMed]
- Spoorthi, G.; Gorthi, S.; Gorthi, R.K.S.S. PhaseNet: A deep convolutional neural network for two-dimensional phase unwrapping. IEEE Signal Process. Lett. 2018, 26, 54–58. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, X.; Shao, J.; Luo, H.; Liang, R. Phase unwrapping in optical metrology via denoised and convolutional segmentation networks. Opt. Express 2019, 27, 14903–14912. [Google Scholar] [CrossRef] [PubMed]
- Yin, W.; Chen, Q.; Feng, S.; Tao, T.; Huang, L.; Trusiak, M.; Asundi, A.; Zuo, C. Temporal phase unwrapping using deep learning. Sci. Rep. 2019, 9, 20175. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, X.; Liang, R. Random two-frame interferometry based on deep learning. Opt. Express 2020, 28, 24747–24760. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Liu, D. Fast and accurate wavefront reconstruction in two-frame phase-shifting interferometry with unknown phase step. Opt. Lett. 2018, 43, 3033–3036. [Google Scholar] [CrossRef] [PubMed]
- Zernike, F. Phase contrast. Z. Tech. Physik. 1935, 16, 454. [Google Scholar]
- Malacara, Z.; Servin, M. Interferogram Analysis for Optical Testing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wang, J.; Silva, D.E. Wave-front interpretation with Zernike polynomials. Appl. Opt. 1980, 19, 1510–1518. [Google Scholar] [CrossRef]
- Cubalchini, R. Modal wave-front estimation from phase derivative measurements. J. Opt. Soc. Am. 1979, 69, 972–977. [Google Scholar] [CrossRef]
- Ares, M.; Royo, S. Comparison of cubic B-spline and Zernike-fitting techniques in complex wavefront reconstruction. Appl. Opt. 2006, 45, 6954–6964. [Google Scholar] [CrossRef] [PubMed]
- Kometer, R.; Hofbauer, E. Fast and reliable in-situ measurements of large and complex surfaces using a novel deflectometric device. In Proceedings of the Fifth European Seminar on Precision Optics Manufacturing, Teisnach, Germany, 10–11 April 2018; Volume 10829, pp. 70–76. [Google Scholar]
- Van der Meer, F.D.; De Jong, S.M. Imaging Spectrometry: Basic Principles and Prospective Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 4. [Google Scholar]
- Géron, A. Hands-on machine learning with Scikit-Learn. In Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019; Volume 1. [Google Scholar]
- Zhu, X.; Wu, Y.Q.; Liu, F. Noise suppression performance of typical phase shifting algorithms. In Proceedings of the 8th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Optical Test, Measurement Technology, and Equipment, Suzhou, China, 26–29 April 2016; Volume 9684, pp. 1008–1013. [Google Scholar]









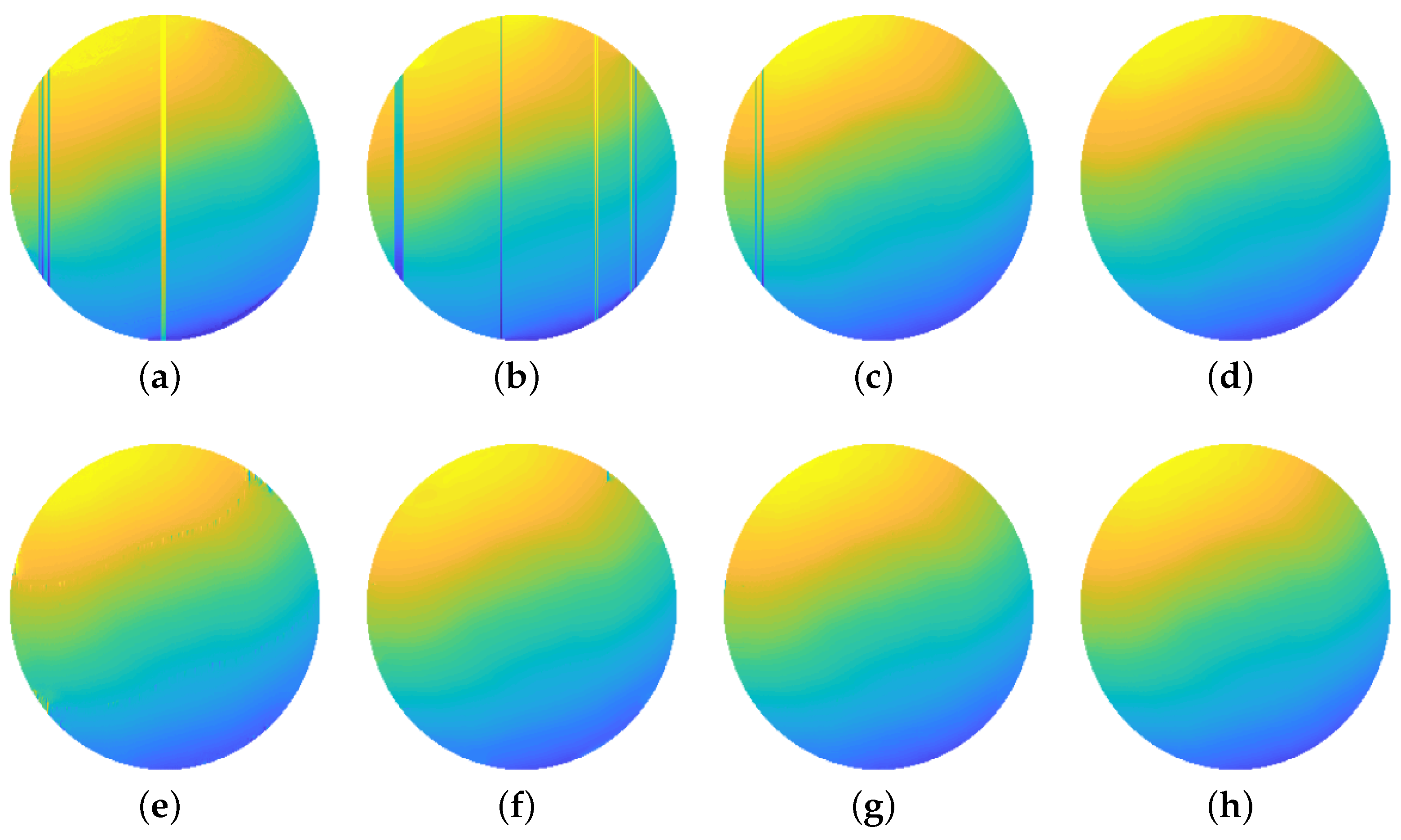
| Methods | Flops (G) | Parameters (M) | Time (s) | 13.9 dB | 28.7 dB | 43.5 dB |
|---|---|---|---|---|---|---|
| RMSE (rad) | RMSE (rad) | RMSE (rad) | ||||
| Kreis | — | — | 0.0463 | 0.8843 | 0.5894 | 0.5255 |
| OF | — | — | 0.1655 | 0.7085 | 0.5464 | 0.5234 |
| ST | — | — | 0.1094 | 0.7652 | 0.3282 | 0.2534 |
| GS | — | — | 0.0079 | 0.7651 | 0.3498 | 0.2792 |
| PUN | 18.02 | 58.61 | 0.0117 | 0.2068 | 0.1813 | 0.1418 |
| PUN+ | 40.15 | 17.26 | 0.0158 | 0.1840 | 0.1106 | 0.0921 |
| Swin-Unet | 7.72 | 27.14 | 0.0433 | 0.1647 | 0.1081 | 0.0719 |
| Methods | 29.7 dB | 30.6 dB | 31.3 dB | 33.0 dB |
|---|---|---|---|---|
| RMSE (rad) | RMSE (rad) | RMSE (rad) | RMSE (rad) | |
| Kreis | 0.6276 | 0.6077 | 0.6267 | 0.5847 |
| OF | 0.5668 | 0.5571 | 0.5706 | 0.5534 |
| ST | 0.5251 | 0.4141 | 0.4605 | 0.3310 |
| GS | 0.5010 | 0.4258 | 0.4396 | 0.3391 |
| PUN | 0.1636 | 0.1596 | 0.1567 | 0.1486 |
| PUN+ | 0.1329 | 0.1249 | 0.1133 | 0.1110 |
| Swin-Unet | 0.1166 | 0.1074 | 0.1013 | 0.0940 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, X.; Li, B.; Ma, Z. Wavefront Reconstruction Using Two-Frame Random Interferometry Based on Swin-Unet. Photonics 2024, 11, 122. https://doi.org/10.3390/photonics11020122
Shu X, Li B, Ma Z. Wavefront Reconstruction Using Two-Frame Random Interferometry Based on Swin-Unet. Photonics. 2024; 11(2):122. https://doi.org/10.3390/photonics11020122
Chicago/Turabian StyleShu, Xindong, Baopeng Li, and Zhen Ma. 2024. "Wavefront Reconstruction Using Two-Frame Random Interferometry Based on Swin-Unet" Photonics 11, no. 2: 122. https://doi.org/10.3390/photonics11020122
APA StyleShu, X., Li, B., & Ma, Z. (2024). Wavefront Reconstruction Using Two-Frame Random Interferometry Based on Swin-Unet. Photonics, 11(2), 122. https://doi.org/10.3390/photonics11020122





