A Chromatic Dispersion-Tolerant Frequency Offset Estimation Algorithm Based on Pilot Tone for Digital Subcarrier Multiplexing Systems

Abstract

A digital subcarrier multiplexing (DSCM) system has been proposed as a possible solution for large capacity and long-distance coherent optical transmissions due to its high tolerances for chromatic dispersion (CD), equalization-enhanced phase noise (EEPN) and fiber nonlinearity. In a DSCM receiver, for subcarrier-demultiplex to occur properly, frequency offset estimation (FOE) must be implemented before demultiplexing. It is beneficial to decrease complexity and EEPN by compensating CD on each subcarrier. Therefore, a high CD tolerance is indispensable for the FOE algorithm in a DSCM receiver. However, the mainstream blind FOE algorithms for single-carrier systems, such as the 4th power fast Fourier transform algorithm, could not work for DSCM systems. To deal with this challenge, a pilot tone-based FOE algorithm with high CD tolerance is proposed and verified using simulations and offline experiments. The final estimation accuracy of about 10 MHz of the proposed two-stage FOE is achieved at low computational complexity. Simulations and offline experiments show that DSCM systems with the proposed algorithm have a 0.5~1 dB Q-factor improvement over Nyquist single-carrier systems.

1. Introduction

A coherent optical transmission system with powerful digital signal processing (DSP) has become an indispensable solution for implementing large capacity and long-distance optical communications, especially when data consumers keep increasing tremendously. Enormous bandwidth pressure is presented on the current coherent optical transmission systems. Increasing the symbol rate and adopting high modulation formats are compelling for satisfying the capacity requirements. However, this kind of solution will suffer further severe influences from chromatic dispersion (CD), equalization-enhanced phase noise (EEPN), and fiber nonlinearity. Thus, the compensation and mitigation of CD, EEPN, and fiber nonlinearity have attracted worldwide attention. In this scenario, a digital subcarrier multiplexing (DSCM) system is studied by researchers extensively. By dividing a high symbol rate single carrier (SC) into multiple low symbol rate subcarriers and multiplexing these subcarriers in the frequency domain by DSP, the DSCM systems have high tolerances for CD [1,2], EEPN, and fiber nonlinearity [3,4,5,6,7]. These features are favored by large capacity and long-distance transmission. In addition, the DSCM systems could achieve a flexible configuration of transmission capacity and transmission distance by adjusting the subcarrier symbol rate and modulation format [8,9,10,11,12].

However, the DSP algorithms for DSCM systems, such as the frequency offset estimation (FOE) algorithm and CD compensation (CDC) algorithm, are quite different from those in SC systems when multiple low symbol rate subcarriers are multiplexed in the frequency domain to carry information. In DSCM systems, CDCs would be implemented on each subcarrier as the computational complexity of CDC scales quadratically with the symbol rate; CDCs on each subcarrier signal will reduce complexity compared with CDC on subcarrier multiplexed (SCM) signal. Additionally, CDCs on subcarriers are also beneficial to reducing EEPN because EEPN originates from local laser phase noise passing through the CDC in receiver DSP. The more dispersion the CDC compensates, the more severe EEPN would be [3]. In the meantime, FOE in a DSCM system should be implemented before subcarrier demultiplexing, as the subcarrier demultiplexing algorithm would fail with a large frequency offset (FO) presented. These lead to the FOE algorithms for DSCM systems should be tolerant to CD. However, the mainstream blind FOE algorithms designed for SC systems, such as fast Fourier transform (FFT)-based FOE and differential-based FOE, would fail to work when CD is not compensated [13]. A FOE algorithm that estimates FO by searching the SCM spectrum dip bottom between subcarriers is proposed to address this challenge. This algorithm estimates FO by comparing the dip bottom frequency of the original SCM spectrum with that of the received SCM spectrum [13]. However, it has been found that this algorithm cannot work with the DSCM systems using a small root-raised-cosine (RRC) roll-off factor. Another FOE algorithm based on measuring the location of the edge of the SCM signal spectrum is also reported [14]. This algorithm is feasible for DSCM systems using a small roll-off factor such as 0.05. In addition, a FOE algorithm based on the summed power of spectral components is carried out. It resorts to the total power change caused by FO within a specific bandwidth to evaluate FO [15]. But, this algorithm is only suitable for DSCM systems employing symmetrically distributed subcarriers.

In this paper, a pilot tone-based FOE algorithm is proposed for DSCM systems, which estimates FO by tracking the frequency offset of the pilot tone. The proposed algorithm features high spectrum efficiency since no guard band is needed with the pilot tone inserted at the SCM spectrum dip bottom. In addition, the proposed algorithm is testified to be insensitive to the roll-off factor. The remainder of this paper is organized as follows. The principle of the proposed algorithm is introduced in Section 2. In addition, the two-stage FOE structure for reducing computational complexity is described, and the interaction between the pilot tone-to-signal power ratio (PSR) and the Q-factor is discussed in this section. Then, the complexity of the proposed algorithm and two reported FOE algorithms from [13,15] are analyzed and compared under the assumption of the same estimation accuracy in Section 3. In Section 4 and Section 5, simulations and offline experiments verify that the proposed algorithm is tolerant to CD and feasible for DSCM systems. Finally, the work of this paper is summarized in Section 6.

2. Principle

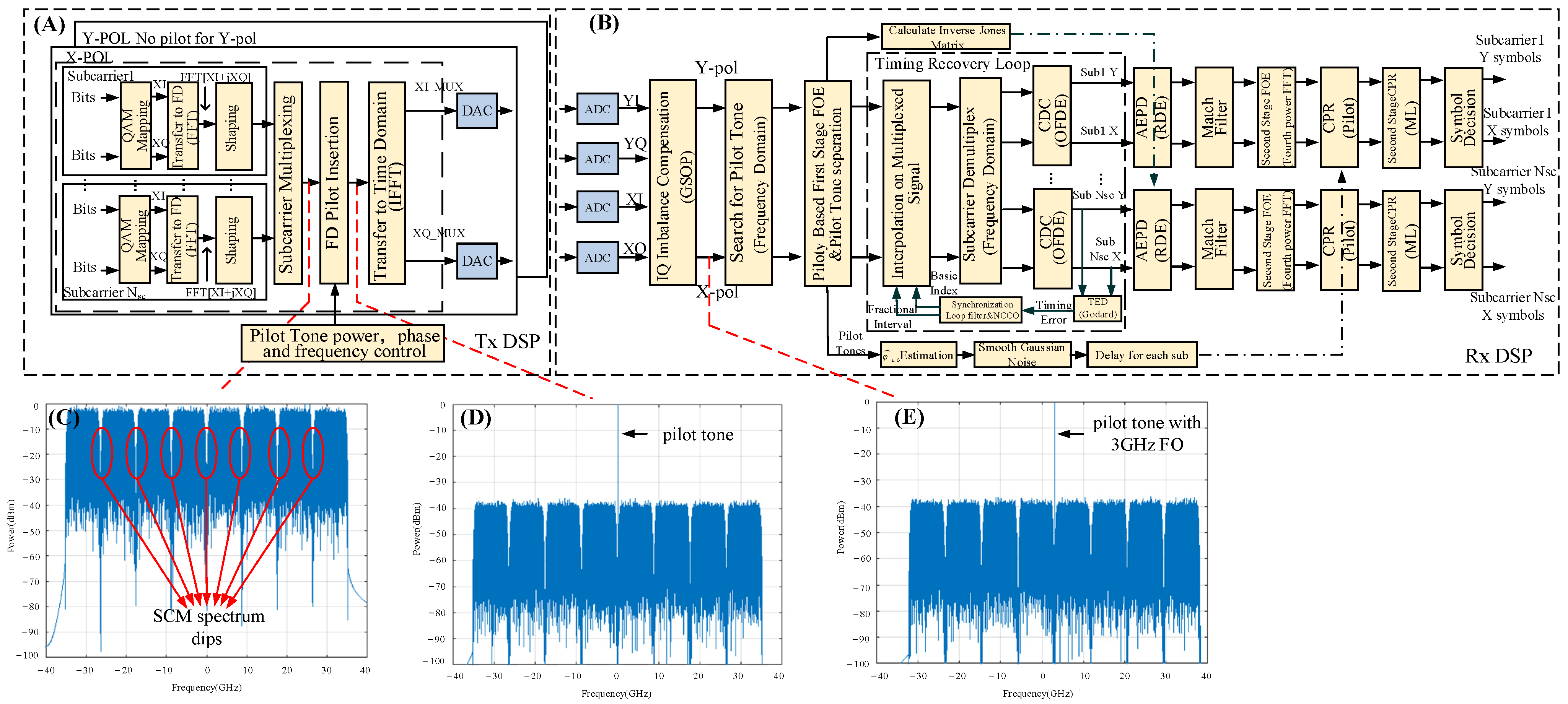
The pilot tone-based DSP scheme for DSCM systems with SCM signal spectrum is illustrated in Figure 1, with (A) and (B) representing transmitter (Tx) and receiver (Rx) DSP, respectively. Figure 1C,E are SCM signal spectrums at some concerned points of the signal processing flow path to help understand how the pilot tone-based algorithm works. In the Tx DSP, QAM mapping is first performed on each subcarrier. Then, the subcarrier signals are transformed into the frequency domain (FD) to obtain a Nyquist shape with a root-raised-cosine (RRC) filter and multiplexed to form the SCM signal. The SCM spectrum dips, highlighted by red circles in Figure 1C, are formed between two adjacent subcarriers. In order to minimize interference between the pilot tone and payload signal and the spectrum efficiency cost, the pilot tone is designed to be inserted at the bottom of an SCM spectrum dip without a guard band between the pilot tone and payload signal. When the subcarriers are distributed symmetrically at about frequency zero, as shown in Figure 1C, the pilot is inserted at frequency zero, as shown in Figure 1D. It is worth pointing out that when the subcarriers are not distributed symmetrically about frequency zero, the pilot tone may be inserted at the bottom of the dip at the lowest frequency, and the principle remains the same. Equation (1) shows the relationship among the real part of the pilot tone $R_{pilot}$, the imaginary tone $I_{pilot}$, the initial pilot tone phase ${\theta }_{ini}$, and pilot tone power $P_{pilot}$.

$$\begin{array}{l}{R}_{pilot}=\sqrt{\frac{P_{pilot}}{1+{\tan }^2{\theta }_{ini}}}\\ I_{pilot}=R_{pilot}\times \tan {\theta }_{ini}\end{array}$$

(1)

The pilot tone is inserted at only one polarization to realize pilot tone-based polarization demultiplexing (Pol-Demux). The pilot tone-based Pol-Demux calculates the Jones matrix using the pilot tone and its crosstalk in the other polarization, as described in [16]. After the pilot tone is inserted in the FD, the SCM signal with the pilot tone is transformed into the time domain to be sampled by digital-to-analog converters (DAC).

In the Rx DSP, the spectrum of the received SCM signal under 3 GHz FO is given in Figure 1E as an example. It could be observed that the pilot tone deviates from its original frequency in Tx due to the influence of FO. After coherent detection and 2-fold sampling by the analog-to-digital converters (ADC), the samples’ I/Q amplitude and phase imbalance are compensated by the Gram–Schmidt orthogonalization procedure (GSOP). Then, the frequency offset is estimated and compensated by FOE. FOE in this paper is divided into two stages to reduce total computational complexity. The first-stage FOE is based on pilot tone and performed on the SCM signal to compensate for the majority of FO. The second-stage FOE is carried out on subcarriers to compensate for the residual FO. The two-stage FOE scheme will be described in detail later in this section. After the first-stage FOE in the FD, the pilot tone and the payload signal are separated. The pilot tone is used to calculate the Jones matrix to initiate the filter taps of the adaptive equalization and polarization demultiplex (AEPD) algorithm to track the rotation of the state of polarization. Moreover, the pilot tone is adopted to estimate the carrier phase noise. The pilot tone-based AEPD and carrier phase estimation (CPE) could reduce computational complexity compared with blind ones [17,18,19,20]. The principle of those pilot tone-based algorithms will be introduced in our following papers. As for the payload signal, it is demultiplexed into subcarrier signals. The CD is compensated independently by the overlap frequency-domain equalization (OFDE) algorithm for each subcarrier to reduce total computational complexity. Timing synchronization is achieved by the scheme for DSCM systems proposed in our previous work [21]. Then, differential group delay (DGD) and residual CD on each subcarrier are compensated by the radius-directed equalization (RDE) algorithm with filter taps initialized by pilot tone. The subcarrier signals are matched with an RRC filter after RDE and the 4th power FFT algorithm is carried out to compensate for residual FO. The carrier phase noise on each subcarrier is compensated by pilot tone-based CPE. In the case of a relatively large laser linewidth symbol duration product $\Delta f_{line}·T_s$, where $\Delta f_{line}$ denotes laser linewidth and $T_s$ represents subcarrier symbol duration, a second-stage CPE is introduced to compensate for the residual phase noise. In this paper, the residual phase noise is compensated by the maximum likelihood (ML) algorithm because, with the majority of the phase noise canceled by the first-stage CPE, ML could improve linewidth tolerance with low complexity cost [17,18].

With the DSP scheme already introduced above, the principle of the two-stage FOE scheme will be described in detail. The first-stage FOE is based on the pilot tone. Since the power spectrum density of the pilot tone in the Tx is designed to be much higher than the payload signal, it is easy to identify the pilot tone by searching the peak of the received SCM spectrum. Then, FO could be estimated using Equation (2) with pilot tone frequency in the Tx/Rx denoted by $f_{Txpilot}$ and $f_{Rxpilot}$, respectively, as illustrated in Figure 2.

$$f_{offset}=f_{Txpilot}-f_{Rxpilot}$$

(2)

The pilot tone remains to be the peak of the SCM spectrum under the influence of CD, and the frequency of the pilot tone is not changed by CD. So, by identifying the peak of the SCM spectrum, the pilot tone could be located, and FO estimation could be made with the pilot tone frequency without CD compensated. In this way, the proposed FOE algorithm is tolerant to CD. Moreover, the pilot tone-based FOE is insensitive to the roll-off factor because the pilot tone also keeps being the peak of the SCM spectrum under different roll-off factors. Therefore, FO estimations by searching the peak of the SCM spectrum could work without being influenced by the roll-off factor changes.

A two-stage structure is employed to reduce the total complexity of the FOE algorithm. From the principle given above, the estimation accuracy is mainly determined by the frequency resolution, which is defined by $R_{sample}/N_{FFT}$, where $R_{sample}$ is the sampling rate of the SCM signal, and $N_{FFT}$ is the FFT length. Under a specific sampling rate, the longer the FFT length, the higher the frequency resolution, and the more accurate the estimation. However, the computational complexity also increases with frequency resolution. The proposed FOE algorithm employs a two-stage structure to reduce complexity. A low-frequency resolution is used in the first stage for the subcarriers to be demultiplexed properly. Then, the residual FO is compensated by the second-stage FOE on subcarriers with high-frequency resolution. The second-stage FOE could choose from mainstream blind FOE algorithms for SC systems because CDC is already compensated, and each subcarrier could be considered a single carrier; the 4th power FFT algorithm is selected as the second-stage FOE. The sampling rate for the subcarriers is only $1/2N_{SC}$ of the SCM signal, where $N_{SC}$ is the total subcarrier number, so the second-stage FOE could achieve an estimation accuracy $N_{SC}$ times higher than the first stage with half of the first-stage FFT length. Additionally, since all subcarriers share the same FO, the estimation from one subcarrier could be applied to all subcarriers. Therefore, the two-stage FOE scheme would reduce the total complexity under the final estimation accuracy of ~10 MHz level, which satisfies the residual FO tolerance of CPE algorithms. The specific parameters will be discussed in Section 4.

The FO estimation range of the pilot tone-based algorithm is decided by the receiver bandwidth since the FO estimation cannot be made when the receiver filters out the pilot tone. The FO estimation range will be verified by simulations in the following section.

The pilot tone-to-signal-power ratio also plays an important role in the pilot tone-based FOE. The PSR should be large enough to make sure that the noise does not severely mask the pilot tone. At the same time, it should also be small enough to ensure sufficient power is allocated to the payload signal to maintain the optical signal noise ratio (OSNR) of the payload signal [17,18,19]. The optimization of PSR shall be discussed in Section 4 and Section 5.

3. Complexity Analysis

In this section, the computational complexity of the proposed FOE scheme is analyzed. The complexity of two reported blind FOEs for DSCM systems from [13,15] are also referred to as comparisons.

The FFT length for searching the pilot tone is $N_{FFT}$, corresponding to $N_{FFT}/2$ symbols under 2-fold sampling. In this case, performing FFT needs $0.5N_{FFT}\log 2(N_{FFT})$ complex multiplications and $N_{FFT}\log 2(N_{FFT})$ complex additions. Then, locating the peak of the spectrum requires $N_{FFT}$ comparisons. Finally, the FO is calculated with Equation (2), which costs only one real addition. In the second-stage FOE, the sampling rate of each subcarrier is $1/2N_{SC}$ of the SCM signal and $N_{SC}$ is usually 8~16 in DSCM systems. Using half of the FFT length of the first-stage FOE, the frequency resolution of the second-stage FOE could be about ten times higher than the first-stage FOE, leading to a higher estimation accuracy and lower complexity cost. In addition, the FO estimated from one subcarrier could be applied to all subcarriers. These two factors determine that the complexity per symbol of the second-stage FOE takes less than 10% of the total complexity while the first-stage FOE takes more than 90%. In this case, the complexity of the first stage could be used to represent that of the whole FOE algorithm. Since multiplications are much more complex than real additions and comparisons, only real multiplications are counted in this paper. In this way, the computational complexity for the proposed FOE algorithm is $4\log 2(N_{FFT})$ real multiplications per symbol.

Then, two blind FOE algorithms reported for DSCM systems are referred to as comparisons; the FOE algorithm from [13] shall be referred to as blind-scheme1, and the FOE algorithm from [15] will be indicated as blind-scheme2 for convenience. These two algorithms also use a two-stage FOE structure. Only the first-stage complexity is counted here for comparison because the first-stage FOE takes most of the complexity, just as the proposed algorithm. The complexity of all algorithms is analyzed with 2-fold sampling. The complexity evaluated per symbol is shown in

Table 1. Computational complexity per symbol for three FOE algorithms.

DSCM FOE Algorithm	Real Multiplication
Pilot tone-based	$4\log 2(N_{FFT})$
blind-scheme1	$4\log 2(N_{FFT})$
blind-scheme2	$4\log 2(N_{FFT})+4$

.

The parameter $N_{FFT}$ is the FFT length for all the FOE algorithms analyzed. The complexity comparison is made under the same estimation accuracy for three FOE algorithms. To achieve this goal, the parameter $N_{FFT}$ is 1024 for all algorithms based on the principle introduced in [13,15] and our simulation for these algorithms. With the prerequisite stated above, the complexity of the pilot tone-based FOE is 40 real multiplications per symbol, just the same as that of blind-scheme1. The complexity of blind-scheme2 is 44 real multiplications per symbol. The complexity of the three FOE algorithms is almost the same because their performances are closely related to the frequency resolution of the DSCM spectrum, and the primary complexity source is from FFT. Under the same estimation accuracy, those three FOE algorithms have the same complexity.

4. Simulations

In this section, the proposed pilot tone-based FOE algorithm is simulated using an 8 × 8 G Baud PM-16QAM DSCM system. The simulation is based on VPI Transmission Maker V9.9 and software-coded DSP algorithms. External cavity lasers (ECL) with adjustable linewidth are used at the transmitter and the receiver. The Nyquist-shaped SCM signal is generated by the Tx DSP, as described in Figure 1A. After pilot tone insertion in X polarization, the SCM signal is converted to the analog domain by DACs and drives optical I/Q modulators for electrical-to-optical conversion. The launch power of the Tx laser in the simulation is 4.5 dBm. Then, the optical SCM signal is fed to the fiber link, which consists of 80 km standard single-mode fiber (SSMF) spans and an in-line erbium-doped fiber amplifier (EDFA) to compensate for the power loss after each span. The noise figure of the EDFA is 5 dB. The transmitted optical SCM signal is received by a coherent receiver headend and converted to the digital domain by ADCs with 2-fold sampling. Finally, the sampled signal is processed via Rx DSP, as described in Figure 1B, and the BER/Q-factor is calculated to evaluate system performance. In the simulation, the resolution of DAC and ADC is set to 7 bits. DSCM systems employing symmetrically distributed subcarriers are simulated as an example in this section. The conclusions of the simulation are also feasible for DSCM systems employing asymmetrically distributed subcarriers because the principle of the proposed FOE algorithm is the same for both kinds of DSCM systems.

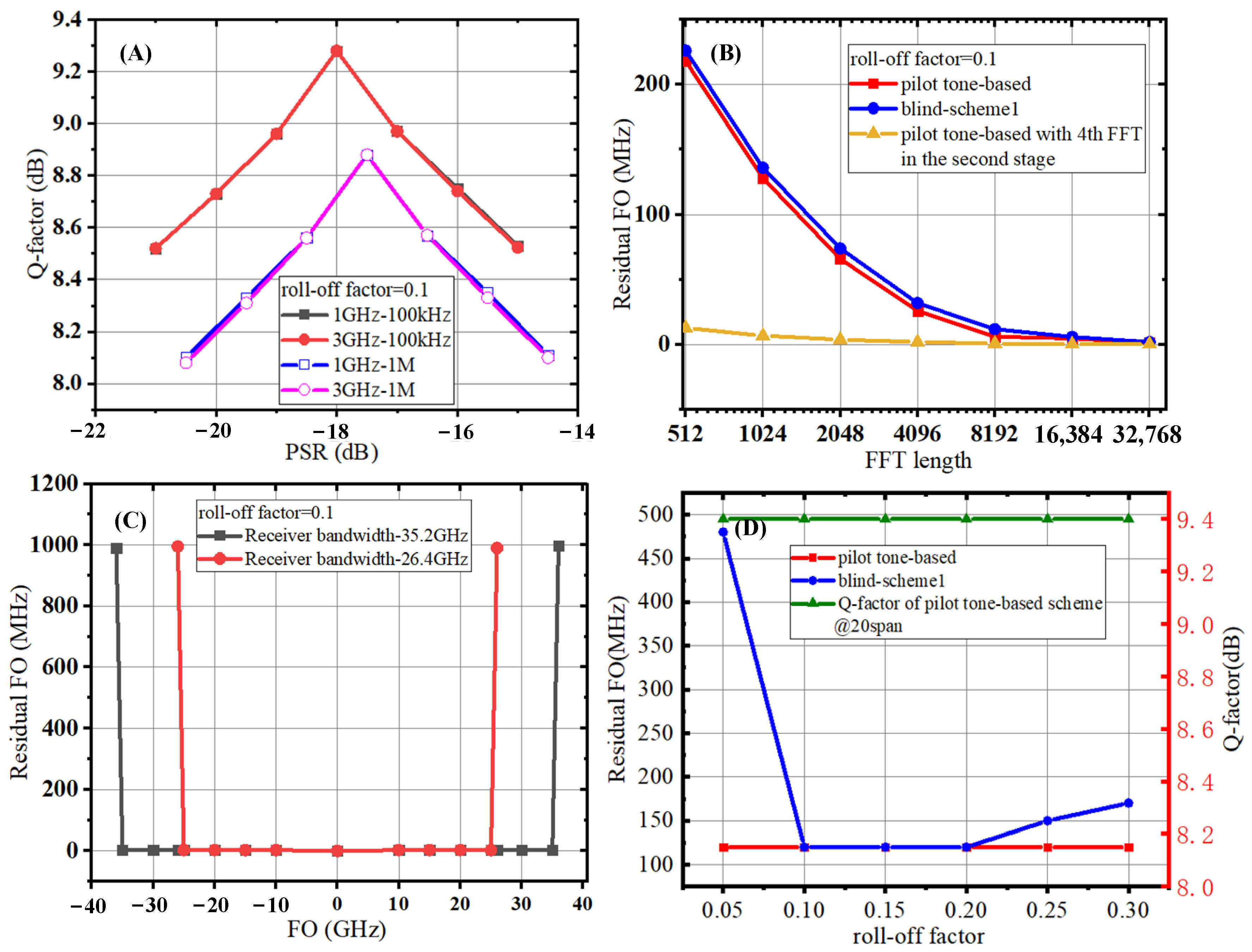
The PSR and frequency resolution must be optimized first to guarantee the best performance of the proposed algorithm. The PSR also plays an important role in pilot tone-based CPE, so it is examined with different FOs and laser linewidths. FO is configured to 1 GHz and 3 GHz; the laser linewidth is set to 100 kHz and 1 MHz. The simulation is carried out with 20 spans of transmission. In Figure 3A, Q-factors reach their maximum with PSR of −18 dB and −17.5 dB for linewidths of 100 kHz and 1 MHz, respectively, and drop down as the PSR increases or decreases. This phenomenon corresponds to the analysis made in the previous section. The quality of pilot’s tone is adversely impacted by noise with a low PSR. Performances of pilot tone-based FOE and CPE are degraded in this situation, and so are the Q-factors. As the power allocated to the pilot tone increases, pilot tone-based FOE and CPE performances improve, leading to increased Q-factors. However, as PSR keeps increasing, the power allocated to the payload signal is insufficient to maintain its OSNR, resulting in decreases in Q-factors. From the simulation, it could be observed that PSR is insensitive to FO; this is attributed to the fact that pilot tone frequency is not influenced by pilot tone power. It also should be noted that PSR is sensitive to laser linewidth because with larger laser linewidth, the pilot tone should be allocated more power so that it is less influenced by noise, and estimation accuracy is ensured [17,18]. The simulations below are executed with a PSR of −18 dB and typical 100 kHz laser linewidth.

In Figure 3B, the residual FOs versus FFT length via back-to-back (B2B) simulations are plotted for the pilot tone-based FOE and blind-scheme1. The residual FO of the proposed FOE algorithm is smaller than that of the blind-scheme1, and FO decreases as the FFT length or the frequency resolution increases. That is because both FOE algorithms depend on locating some positions of SCM spectrum features, either the pilot tone or the spectrum dip bottoms, to make estimations. With higher frequency resolution, it is easier for these algorithms to distinguish SCM spectrum features, leading to more accurate estimations and smaller residual FO. Compared with searching the SCM spectrum dip bottoms, the peak of the pilot tone is more robust to noise as the pilot tone power is much higher than noise, while the dip bottoms are more sensitive to noise, so the residual FO of the pilot tone-based FOE is smaller than that of blind-scheme1. The residual FO of the proposed algorithm reduces below 15 MHz when the FFT length reaches 8192 and becomes saturated afterward. That is because the estimation accuracy is mainly decided by frequency resolution when frequency resolution is below 30 MHz. As frequency resolution increases to 15 MHz, the influence of noise becomes the main factor that limits the estimation accuracy instead of frequency resolution. Increasing frequency resolution will not bring much improvement but pay extra computational complexity costs. To make a good tradeoff between the final estimation accuracy and total computational complexity for FOE, the FFT length for the first-stage FOE is set to 1024 with a residual FO of 120 MHz. The final estimation accuracy of 10 MHz is achieved via the second-stage FOE with an FFT length of 512. The simulation shows the estimation accuracy is decided by frequency resolution, which corroborates the analysis made in Section 2. Under the same estimation accuracy of 10 MHz, the complexity of a two-stage FOE with the FFT length stated above is about one-third of that of only using the first-stage FOE with an FFT length of 8192.

The FO estimation range is tested by B2B simulation under receiver bandwidths of 35.2 GHz and 26.4 GHz, corresponding to 100% and 75% of SCM signal bandwidth using the roll-off factor 0.1. The simulation results in Figure 3C show that the pilot tone-based FOE could make correct estimations in FO ranges of (−35.2 GHz, 35.2 GHz) and (−26.4 GHz, 26.4 GHz) under receiver bandwidth of 35.2 GHz and 26.4 GHz, respectively. The simulation result shows that the FO estimation range of the pilot tone-based algorithm is decided by the receiver bandwidth. That is because when the pilot tone is filtered out by the receiver, FO estimations cannot be made. For a commercial transceiver, FO is usually within [−3 GHz, 3 GHz]; the FO estimation range of the proposed algorithm could cover this FO range.

To compare with blind-scheme1, the impacts of the roll-off factor are examined by B2B simulation for the pilot tone-based FOE and blind-scheme1 under an FFT length of 1024; the result is plotted in Figure 3D. The residual FO of the pilot tone-based FOE is stable at 120 MHz under the roll-off factor span [0.05, 0.3]. That is because the pilot tone remains at the peak of the SCM spectrum despite the changes in the roll-off factor; FO estimation by identifying pilot tone frequency is not influenced. So, the pilot tone-based FOE is insensitive to the roll-off factor. On the contrary, blind-scheme1 is sensitive to the roll-off factor. The residual FO of blind-scheme1 increases by about 300 MHz when the roll-off factor decreases to 0.05 because it is challenging to identify the SCM spectrum dip bottom under a small roll-off factor. In addition, the residual FO of blind-scheme1 also slightly increases when a roll-off factor reaches 0.25. This is because the SCM spectrum dips generated by RRC shaping are not steep enough, leading to increased estimation errors. Then, the Q-factor of the pilot tone-based scheme is evaluated under different roll-off factors with 20 spans of transmission. As is shown in Figure 3D, the Q-factor is stable for the roll-off factor span [0.05, 0.3]. That is attributed to the fact that all DSP algorithms are insensitive to the roll-off factor in the proposed pilot tone-based scheme. The roll-off factor is set to 0.1 for the simulations and offline experiments as, in this case, both the proposed scheme and the blind-scheme1 could work, and spectrum efficiency is relatively high.

With PSR and frequency resolution optimized, a transmission simulation is carried out in an 8 × 8 G Baud PM-16QAM DSCM system to show the validity of the pilot tone-based FOE. Another 8 × 8 G Baud PM-16QAM DSCM system with different Rx DSP is simulated as a comparison. It is referred to as the so-called all-blind DSCM system for the following sections of this paper. The Tx DSP for the all-blind DSCM system uses the scheme illustrated in Figure 1A, except that no pilot tone is inserted. The Rx DSP for the all-blind DSCM system employs the scheme shown in Figure 1B with a few modifications: the pilot tone-based FOE algorithm is replaced with blind-scheme1, the pilot tone-based AEPD and CPE are changed by RDE and the blind phase searching (BPS), respectively. The 64 G Baud PM-16QAM Nyquist SC system simulation is also executed to compare with the DSCM systems. The Tx DSP for Nyquist SC systems consists of QAM mapping and Nyquist shaping. The Rx DSP includes I/Q orthonormalization, CD compensation, timing recovery, AEPD, RRC-matched filtering, and carrier recovery, as described in [22]. 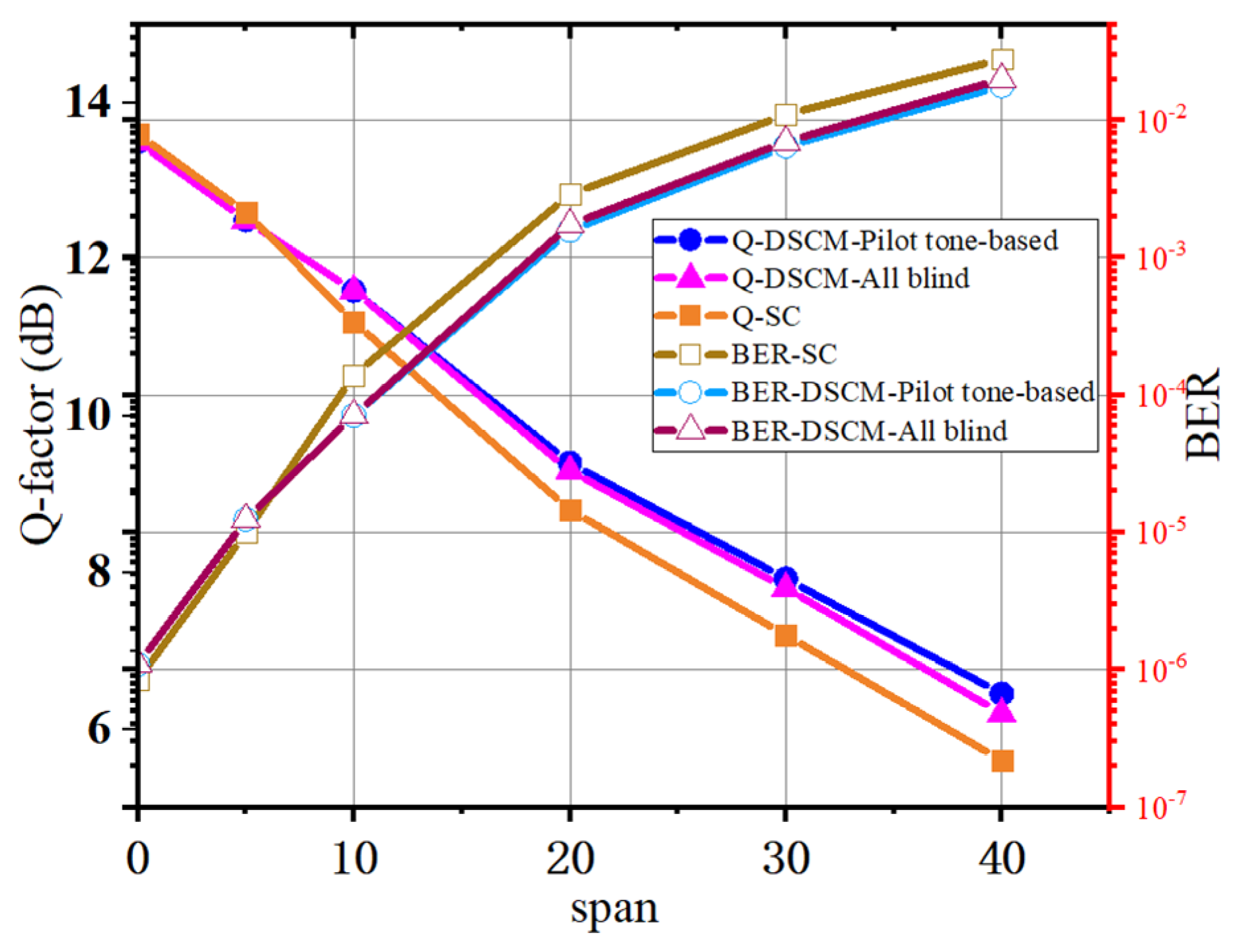The Q-factor/BER versus transmission spans are plotted in Figure 4.

The simulation results indicate that within five spans of transmission, the Nyquist SC system outperforms DSCM systems in Q-factor. It is attributed to the fact that with limited DAC/ADC resolution, quantization noise causes more severe performance penalties to DSCM systems than to Nyquist SC systems. In DSCM systems, multiplexed subcarriers lead to a larger amplitude range than the SC systems. As a result, quantifying SCM signal with limited DAC/ADC resolution induces more severe noise than SC signal when the fiber nonlinearity impact on the Q-factor is very small, such as within five spans of transmission. As the transmission distance increases to 10 spans, the Q-factors of DSCM systems are higher than Nyquist SC systems because the fiber nonlinearity tolerance of DSCM systems enables DSCM systems to perform better than Nyquist SC systems on long-distance transmission. Finally, the DSCM system employing pilot tone-based algorithms outperforms the Nyquist SC system and the all-blind DSCM system by 1 dB and 0.2 dB in Q-factor, respectively, at 40 spans transmission. The DSCM system with pilot tone performs slightly better than the all-blind DSCM system because the pilot tone-based AEPD and CPE perform better than RDE and BPS under long-distance transmission. The simulation results prove the pilot tone-based algorithm is tolerant to CD and insensitive to roll-off factor, supports a large enough FO estimation range for commercial transceivers, and secures the advantage of DSCM systems over Nyquist SC systems.

5. Offline Experiments

An offline experiment system is set up to verify the proposed algorithm further. The offline experiment system is illustrated in Figure 5A. The experiments are carried out with an 8 × 8 G Baud PM-16QAM DSCM system. The SCM signal with pilot tone is generated by Tx DSP under a roll-off factor of 0.1 and sent to the arbitrary waveform generator (AWG) with a 3 dB bandwidth of ~40 GHz and resolution of 8 bits to obtain converted into the analog domain. The converted SCM signal is sent to the dual-polarization I/Q modulator with the built-in ECL to be transformed into the optical domain. The ECL central frequency is set to 193.414 THz, and the measured linewidth of the ECL is ~50 kHz. The generated optical SCM signal is transmitted with the fiber loop. Its spectrum is illustrated in Figure 5B. The fiber loop mainly consists of a loop controller, 80 km SSMF, EDFAs, coupler, and optical bandpass filter (OBPF). EDFA1 controls the input power, and EDFA2 compensates for the power loss after each span. The noise figure of EDFAs is about 5 dB, and the input power to the SSMF is set to 1.5 dBm. After transmission, the SCM signal is received by the coherent receiver with an internal local oscillator (LO). The measured linewidth of LO is ~50 kHz, too, and the central frequency of LO is intentionally deviated from 193.414 THz to introduce FO. The spectrum of the received SCM signal under 3 GHz FO is given in Figure 5C as an example. The received SCM signal is sampled by a digital storage oscilloscope whose sampling rate is 80 G Sa/s, and whose resolution is 8 bits. The samples from the oscilloscope are processed by offline Rx DSP. In the experiments, the Tx DSP scheme is the same as that illustrated in Figure 1A. The Rx DSP up-samples the received signal to 2-fold sampling first and then employs the Rx DSP scheme depicted in Figure 1B. This offline experiment system also works for Nyquist SC systems when the Tx/Rx DSPs are replaced with those for the SC systems. It is important to point out that due to the limited frequency accuracy and stability of the laser, the frequencies of internal ECL and LO keep varying during the experiment, so the FO introduced by adjusting the central frequency of LO also keeps varying. In this situation, the estimated FO from the second-stage FOE is regarded as the residual FO of the pilot tone-based FOE. The frequency resolution of the second-stage FOE could be ten times smaller than the residual FO of pilot tone-based FOE, making it suitable to evaluate residual FO with the second-stage estimation.

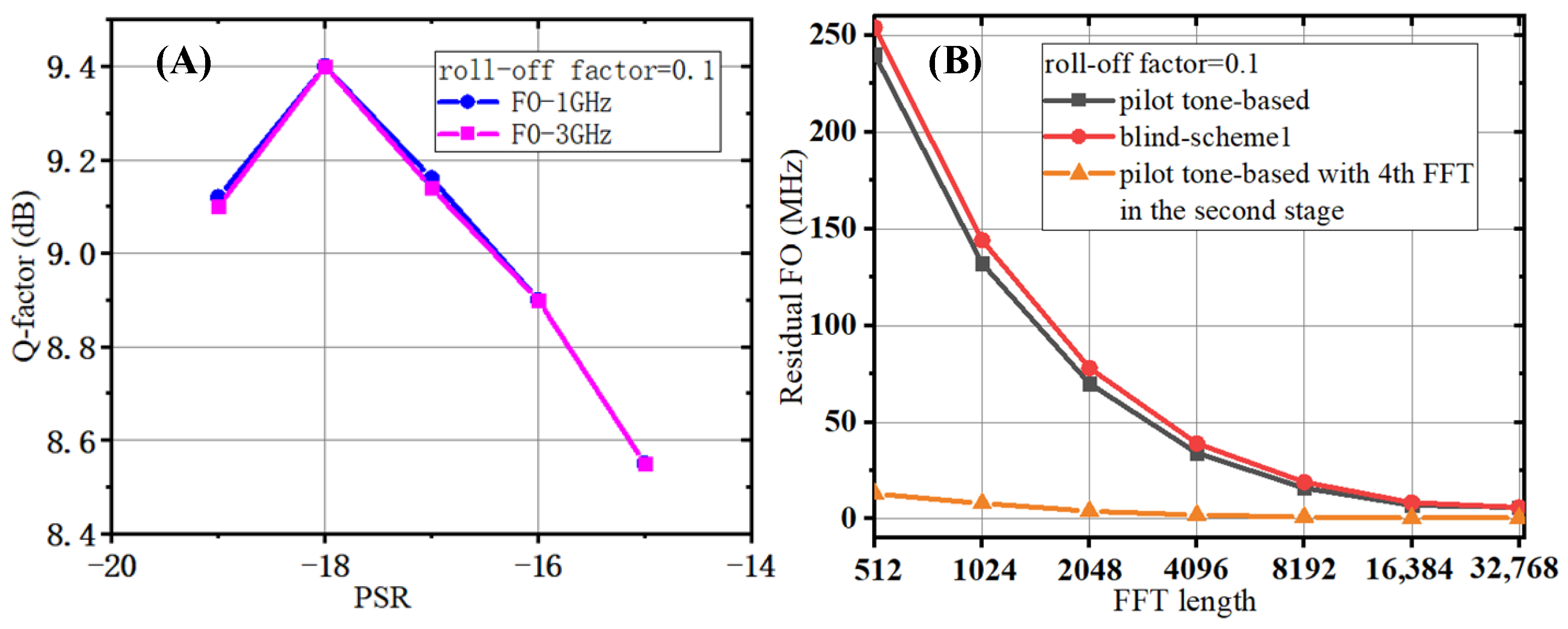
The PSR is to be optimized for offline experiments first. Since the highly integrated I/Q modulator and coherent receiver in the experiment do not support tunable laser linewidth, the impact of different laser linewidth on PSR is not tested. The PSR optimization is carried out with three span transmissions and different FOs; the result is given in Figure 6A. The Q-factors reach their maximum values when the PSR is −18 dB, and the PSR is insensitive to the FO. The experiment results, and simulation results corroborate. The rest of the offline experiments are executed with a PSR of −18 dB.

The residual FO vs. FFT length is then tested using B2B experiments. As illustrated in Figure 6B, the residual FO of the pilot tone-based FOE and blind-scheme1 decreases as FFT length increases, the residual FO is smaller than 15 MHz when FFT length reaches 8192 and then becomes saturated afterward, and the residual FO of the pilot tone-based FOE is smaller than that of blind-scheme1. These experiment results could be explained by the same reasons analyzed in Section 4. The first-stage FFT length is set to 1024 with a residual FO of 130 MHz for the experiments to achieve a good tradeoff between complexity and the final estimation accuracy. The final estimation accuracy of 10 MHz is achieved by the second-stage FOE with the FFT length of 512 as in the simulation. Compared with using the first-stage FOE only under FFT length of 8192, the two-stage FOE in the experiments achieves the same complexity reduction as that in Section 4.

Then, the DSCM system employing the proposed pilot tone-based algorithms and the DSCM system with the so-called all-blind DSP described above in Section 4 are testified with transmission experiments, a 64 G Baud PM-16QAM Nyquist SC system is also carried out as a comparison.

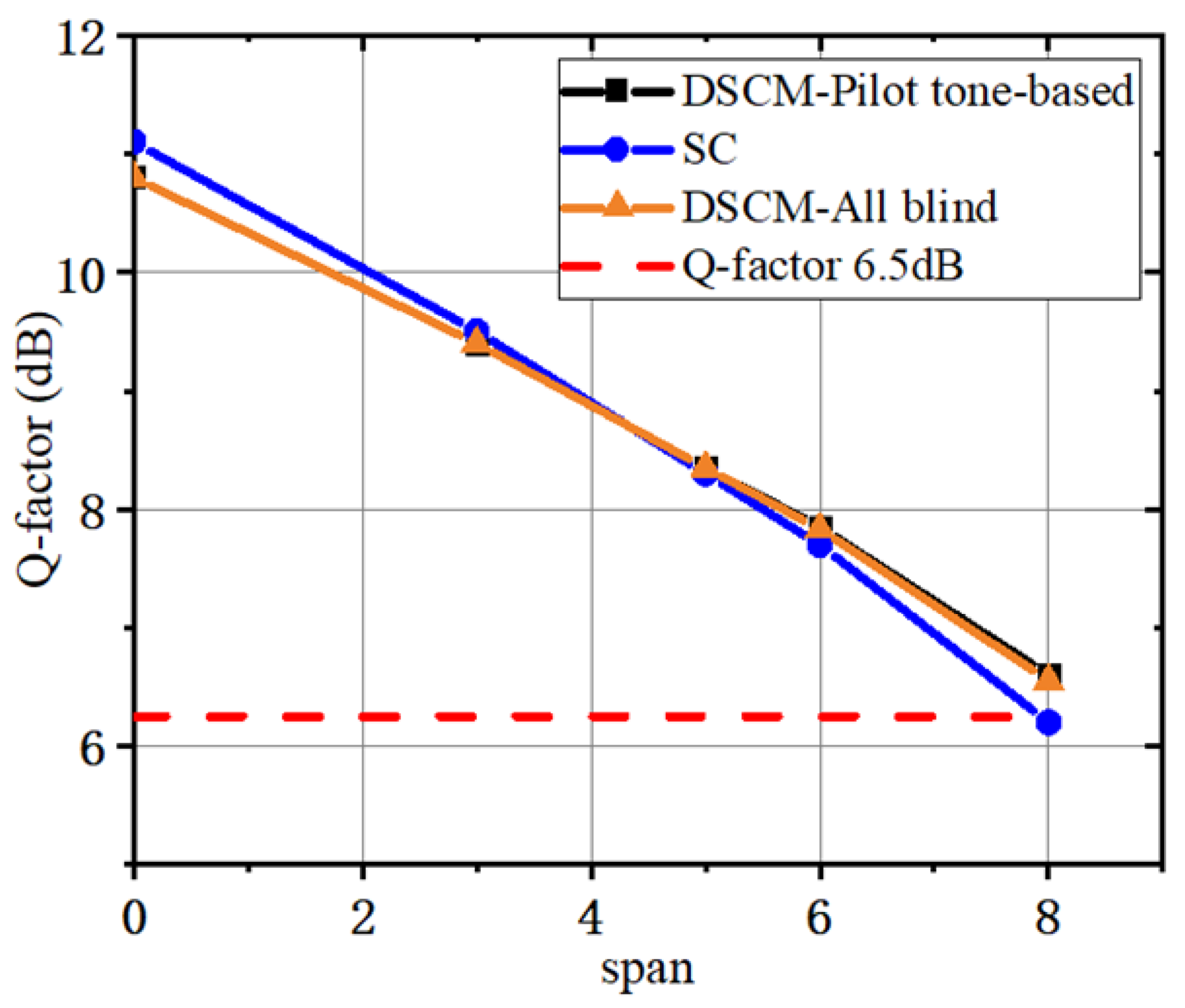
As depicted in Figure 7, the Q-factor of the DSCM system with pilot tone-based algorithms is lower than the Nyquist SC system within three spans transmission for the same reason as analyzed in Section 4. Then, the Q-factor of the DSCM system with pilot tone-based algorithms outperforms the Nyquist SC system as the transmission distance increases to five spans due to the greater fiber nonlinearity tolerance of DSCM systems. Finally, the Q-factors of the DSCM system are 0.5 dB higher than the Nyquist SC system under eight spans transmission. Additionally, the Q-factor of the DSCM system with pilot tone-based algorithms is about 0.1 dB higher than that of the DSCM system with all-blind DSP for the same reason stated in Section 4. The transmission experiment proves that the pilot tone-based FOE is tolerant to CD and secures the advantage of DSCM systems over SC systems on long-distance transmission.

6. Conclusions

The FOE algorithms in the DSCM systems should be tolerant of CD. However, the mainstream blind FOE algorithms for the SC systems are not feasible for the DSCM systems because of their poor CD tolerance. To address this challenge, a pilot tone-based FOE algorithm with a two-stage structure is proposed in this paper. The proposed FOE algorithm is tolerant to CD because the pilot tone keeps being the peak of the SCM spectrum under the influence of CD, and the FOE could be made by identifying the pilot tone. The interference between the payload signal and the pilot tone is minimized by inserting the pilot tone at the SCM spectrum dip bottom. Therefore, no guard band is needed for the proposed FOE algorithm, and high spectrum efficiency is ensured. The simulations show that the estimation accuracy of the pilot tone-based FOE is better than that of blind-shceme1 because the pilot tone is more robust to noise. The final estimation accuracy of 10 MHz is achieved by the two-stage FOE with one-third of the complexity of using first-stage FOE only. The FO estimation range decided by the receiver bandwidth could cover the FO range of a commercial transceiver. In addition, the proposed FOE algorithm is testified to be insensitive to the roll-off factor. Then, 3200 km transmission simulations indicate that the DSCM system employing the pilot tone-based algorithm outperforms the 64 G Baud PM-16QAM Nyquist SC system by 1 dB in Q-factor. The proposed FOE algorithm is also verified by offline experiments, and 10 MHz final estimation accuracy is achieved as in simulation. The transmission experiment shows that the 8 × 8 G Baud PM-16QAM DSCM system with the proposed algorithm outperforms the 64 G Baud PM-16QAM Nyquist SC system by 0.5 dB in Q-factor under 640 km transmission. Both simulations and offline experiments show that the DSCM system with pilot tone-based algorithms could bring 0.1~0.2 dB Q-factor improvement compared with the DSCM system using the so-called all-blind DSP.

In summary, compared to the reported FOE algorithms for DSCM systems, the proposed FOE algorithm achieves the same FO estimation accuracy and remains insensitive to the roll-off factor changes. In addition, the pilot tone-based AEPD and CPE are beneficial for tracking the rotation of the state of polarization and reducing complexity; these grant the proposed algorithm an advantage over the all-blind ones.