Designing and Tailoring Optical Properties: Theory and Simulation of Photonic Band Gaps in Photonic Materials

Abstract

Theoretical calculations and numerical simulations play a crucial role in analyzing material properties and devising effective research strategies. In this study, the photonic band gap (PBG) of polymethyl methacrylate (PMMA) and polystyrene (PS) photonic crystals was successfully predicted using theoretical calculations and numerical simulations. The agreement between the predicted results and the actual reflection peaks reached an impressive level of 99%. Utilizing SEM images, the prediction of reflection peaks in acrylamide (AM)—based photonic hydrogels was conducted using theoretical formulas and Rsoft 2019–Bandsolve software v2019.09. The relationship between the actual reflection peaks and compressive strains in AM-based photonic hydrogels featuring 251 nm PMMA PCs exhibited a remarkable similarity of over 96% with the theoretical and simulated results. In conclusion, an exploration was conducted into the relationship between reflection peaks and compressive strains for AM-based 270 nm PMMA photonic hydrogels, allowing the prediction of the actual reflection peaks under compression. The consistency observed between theoretical/simulated reflection peaks and actual reflection peaks validates the efficacy of this approach in evaluating the optical properties of photonic materials and predicting their responsive effects. This method offers a straightforward and expeditious solution for the design and fabrication of photonic materials.

1. Introduction

In nature, many organisms have gorgeous appearances, such as butterflies [1], opals [2] and insects [3]. Their vivid colors are the results of light scattering by natural periodic structures rather than pigments, which is the structural color. Organisms can camouflage or convey information by changing their structural color, such as chameleons and octopuses in disguise to hide from predators [4,5]. Photonic crystals (PCs) [6,7], proposed by natural periodic structures and semiconductor crystals, are artificial functional materials formed by materials with different refractive indexes. Similar to the semiconductor band [8,9,10], the photonic band gap (PBG) of PCs can tune incident light [11,12,13], and the incident light in the PBG is forbidden to propagate while others can transmit the PCs, which can change the transmission path of special electromagnetic waves and realize the dynamic control of the lights. The PBG center wavelength (λ_max) of the PCs satisfies Bragg’s diffraction law:

$${\lambda }_{\mathit{max}}=2d{\sqrt{n_{eff}^2-{\sin }^2\theta }}^{}$$

(1)

The λ_max is the center wavelength of the PBG, d is the lattice distance of the face-centered cubic structure (111), n_eff is the equivalent refractive index, and θ is the reflection angle. The equivalent refractive index (n_eff) satisfies the following equation:

$$n_{eff}^2=n_{sphere}^2{f}_{sphere}+n_{air}^2{\left(1-f_{sphere}\right)}^{}$$

(2)

n_air is the refractive index of air and is generally considered to be 1, n_sphere is the refractive index of microsphere, and the microsphere volume fraction of the PCs is f_sphere = 74%. The lattice distance of the face-centered cubic (111) satisfies Equation (3):

$$d_{111}=\frac{a}{\sqrt{1^2+1^2+1^2}}=\sqrt{\frac{2}{3}}{D}^{}$$

(3)

where a is the lattice constant of the face-centered cubic structure, and D is the diameter of microspheres.

External stimuli can change the structural parameters of PCs, especially the lattice distance and the effective refractive index, which will cause both tuning of the PBG and the shift of its structural color, and realize visual sensing and display of external stimuli. Based on their tunable optical properties and stimuli-responsive function, PCs are playing an increasingly essential role in environmental protection [14,15,16,17], biomimetic materials and sensors [18,19,20,21,22,23,24,25,26,27,28]. For example, we designed a non-closed-packed photonic crystal sensor for the visual monitoring of violent pressure fluctuations in aqueous fluids, and with a response time of 0.0001 s and a resolution of 0.21 mm⁵. However, the preparation of the PCs requires enough time and experimental cost, and it is difficult to judge the suitability of samples during an experiment, which is not conducive to the advancement of the research. Therefore, it is necessary to avoid meaningless experimental attempts and improve work efficiency. Theoretical calculations can accurately describe problems and grasp their essences; however, the limitations arising from research conditions make it more suitable for qualitative analysis. Numerical simulations can support and supplement the results of theoretical research, which can visualize the results in more ways and enhance the readability of the research results. Therefore, theoretical calculations, combined with numerical simulations that provide better visual data, can accurately describe the essential problem and provide a reliable basis for experimental research. At the same time, the latter tests the truth of the theoretical calculations and numerical simulations [29,30,31]. Theoretical calculations and numerical simulations can design target photonic crystals and study their optical properties [32,33,34], which can provide reliable theoretical support and guidance for experiments and greatly promote the research process. Rsoft is a numerical simulation software for designing and simulating the PBG of the PCs, which can calculate photonic crystals with various crystal forms using plane wave expansion (PWE), and the PBG can be visualized. The bandsolve module of the Rsoft software v2019.09 was used for calculating the PBG of photonic materials such as SiO₂ PCs, PMMA PCs, PS PCs and AM-based PMMA hydrogels, and the applied structural model of the numerical simulation was consistent with the FCC lattice in Bragg’s diffraction law, which guided the practical experimental studies.

In this paper, the combination of theoretical calculation and numerical simulation with Rsoft 2019 was used for predicting the PBG of the PMMA and PS PCs, the accuracy and feasibility was verified with experimental actual reflection peaks. The theoretical and simulated reflection peaks based on the SEM results were in agreement with the actual reflection peaks of the AM-based PMMA photonic hydrogels. Finally, the reflection peak–compressive strain relationship of the AM-based PMMA photonic hydrogels was calculated and simulated, which was consistent with the actual reflection peaks. Based on the consistency between the theoretical/simulated reflection peaks and the actual reflection peaks, the scheme can be used for evaluating the optical properties of photonic crystals and predicting their responsive effects, which provides a simple and fast solution for the design and fabrication of photonic materials.

2. Materials and Methods

2.1. Materials and Reagents

Methyl methacrylate (MMA, A.R.), styrene (Pt, A.R.) potassium persulfate (KPS, A.R.), Sodium dodecyl sulfonate (SDS, 99% A.R.), N, N′-methylenebis-acrylamide (BIS, 99% A.R.) and ammonium persulfate (APS, 98% A.R.) were purchased from J&K, Shanghai, China. Alumina (Al₂O₃, A.R.) and acrylamide (AM, 99% A.R.) were purchased from TCI.

ZEISS GeminiSEM (Oberkochen, Germany) was used to characterize the microstructure of photonic materials, an optical fiber spectrometer (Avaspec-2048TEC, LOKAMED Ltd., St. Petersburg, Russia) was used for optical performance testing, and a Leyue digital microscope (Z03-1, China) was used for physical image and video acquisition.

2.2. The Preparation of PMMA Microspheres

PMMA microspheres were prepared using soap-free emulsion polymerization [35]. DI water (360 mL) was added to a 500 mL four-mouth flask and heated to 75 °C with nitrogen blowing. MMA (15 mL) was added to the water, and the mixture was stirred at 300 rpm and heated to 80 °C within 15 min, then 10 mL KPS aqueous solution (0.02 g/mL) was added. The mixture was heated at 80 °C for 45 min followed by washing with DI water three times, and the PMMA suspensions were obtained. The PMMA microspheres with different distances were prepared by adjusting the amount of MMA.

2.3. The Preparation of PS Microspheres

PS microspheres were prepared by emulsion polymerization [36]. DI water (200 mL), 0.2 g KPS and 0.2 g SDS were added to a 500 mL four-mouth flask and heated to 75 °C with nitrogen blowing. St (15 mL) was added to the flask, and the mixture was stirred at 200 rpm and heated to 75 °C within 15 min. The mixture was heated at 75 °C for 12 h followed by washing with DI water three times, and the PS suspensions were obtained. The PS microspheres with different distances were prepared by adjusting the amount of SDS.

2.4. Preparation of 3D PMMA Photonic Crystals

The vertical self-assembly method was used to prepare three-dimensional (3D) photonic crystals, the PMMA/PS microspheres were self-assembled on glass slides, and we obtained a 3D photonic crystal array with face-centered cubic (FCC) stacking [37,38]. The specific preparation was as follows: the glass pieces were dewatered with a plasma cleaning instrument, then were clamped with dovetail clips and hung above the container. The 600 mL of PMMA suspension with a mass concentration of 0.15% was prepared and sonicated 30 min to disperse evenly, then the PMMA suspension was added into the container, and the container was placed in a box at constant temperature and humidity of 30 °C and 50% humidity for 72 h. The PMMA microspheres self-assembled on glass sheets to form PMMA photonic crystal arrays with the evaporating of the solvent (DI water).

2.5. Preparation of 3D PS Photonic Crystals

The preparation process of PS photonic crystals was the same as that of PMMA photonic crystals, and the specific preparation was as follows: the glass pieces were dewatered with a plasma cleaning instrument, then were clamped with dovetail clips and hung above the container. The 600 mL of PS suspension with a mass concentration of 0.10% was prepared and sonicated for 30 min to disperse evenly, and then the PS suspension was added into the container, and the container was placed in a box at a constant temperature and humidity of 30 °C and 50% humidity for 72 h. The PS microspheres self-assembled on glass sheets and the PS photonic crystal arrays were obtained with the evaporating of the solvent (DI water).

2.6. Preparation of the AM-Based Photonic Hydrogel

We added AM (5 g), APS (0.1 g) and BIS (0.1 g) to 15 mL H₂O and stirred magnetically until fully dissolved to obtain the prepolymer solution. Then, the prepolymer solution was injected into the PMMA photonic crystals to replace air and polymerized at 60 °C for 20 min to obtain the AM-based photonic hydrogel, and the hydrogel was swelled in H₂O for 48 h and the DI water was replaced every 12 h, which was conductive to removing the unreacted monomer and making the hydrogel fully swollen. Finally, the AM-based photonic hydrogel was obtained.

2.7. The Optical Simulation of the Photonic Materials

The necessary simulation parameters include the crystal form, the microsphere diameter, the refractive index of the dielectric and the size of the photonic crystal element, where the crystal form was the FCC lattice of the Rsoft–Bandsolve, the microsphere diameter was measured by SEM and the refractive index was determined by the dielectric type. The size of the photonic crystal element was √3/2 times the microsphere diameter.

3. Results

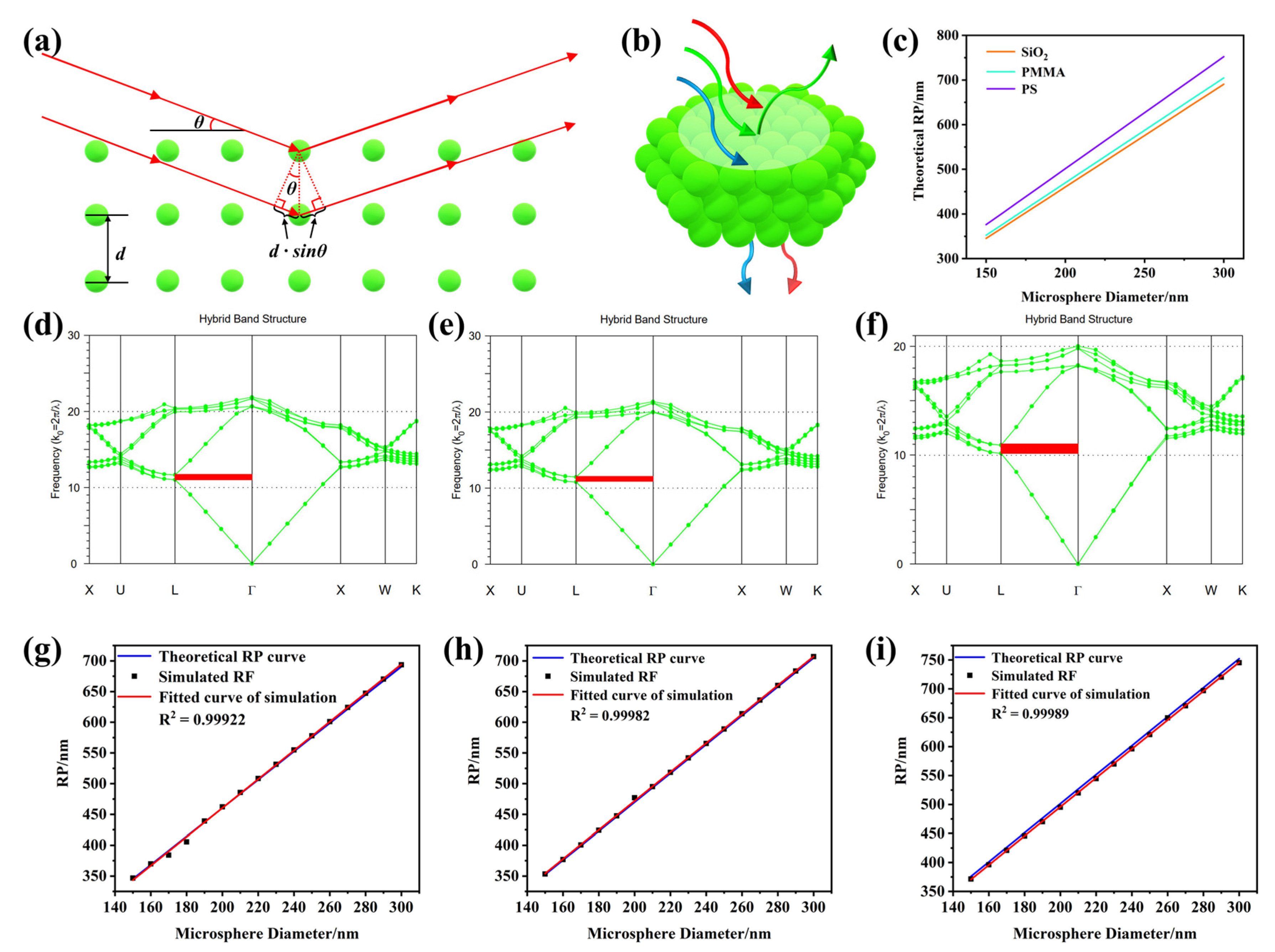
3.1. The Theory and Simulation of the Photonic Band Gap

The origin of the photonic band gap (PBG) in the photonic crystals (PCs) lies in their periodic structures. As light propagates through these structures with varying media in the form of electromagnetic waves, a periodic potential field, often referred to as the effective refractive index (n_eff), is generated. This field acts as a barrier for certain electromagnetic waves, which are in the photonic band gap (PBG), and preventing their propagation, while enabling the electromagnetic waves that are not in the PBG to pass through as shown in Figure 1a,b.

The diffraction of the PCs for incident electromagnetic waves satisfies the Bragg diffraction law (Equation (1)), and when the light is incident perpendicular, the angle between the incident light and the normal line of the photonic crystals interface is 0 (θ = 0):

$$\sin \theta =0^{}{}^{}$$

(4)

Equations (2)–(4) are substituted into Equation (1) to obtain the linear relationship between the theoretical reflectance peaks and diameters of SiO₂ PCs, PMMA PCs and PS PCs, which were λ_SiO2 = 2.3022 D (n_SiO2 = 1.46), λ_PMMA = 2.3495 D (n_PMMA = 1.49) and λ_PS = 2.5072 D (n_PS =1.59).

Figure 1c is the geometrical form of Equations (5)–(7), where the theoretical reflection peaks (RPs) of the PCs were proportional to their lattice distance and the greater effective refractive index resulted in a larger theoretical reflection peak of the PCs with the same diameter; at the same time, the slope of the geometric form was greater. Figure 1d–f show the simulated PBG with 240 nm silica PCs, PMMA PCs and PS PCs, and the k₀ were 11.017~11.635, 10.78~11.443 and 10.166~10.916, respectively. According to Equation (5):

$$k_0={\frac{2\pi }{{\lambda }_{\mathit{max}}}}^{}{}^{}$$

(5)

The photonic band gaps (PBGs) spanned from 540 nm to 570 nm, 549 nm to 583 nm and 575 nm to 619 nm, with corresponding intermediate values (λ_max) at 555 nm, 566 nm and 597 nm. These measurements closely aligned with the anticipated theoretical reflection peaks of 553 nm, 564 nm and 602 nm, exhibiting an impressive fit accuracy of 99%. Figure 1g–i show the linear relationship between the reflection peaks of Rsoft–Bandsolve simulation and microsphere diameter of 150~300 nm silica PCs, PMMA PCs and PS PCs, respectively (Figures S1–S3); the linear relationships between the simulated reflection peaks and microsphere diameter were y = 2.3398x − 7.5794, y = 2.3534x − 1.0882 and y = 2.5029x − 4.8814, and the R² values were 0.99922, 0.99982 and 0.99989, which were consistent with the theoretical linear relationship. The presented findings indicate that Rsoft–Bandsolve effectively simulates the photonic band gap (PBG) of photonic crystals (PCs). This simulation serves as a valuable and essential complement to both theoretical and experimental investigations in this field.

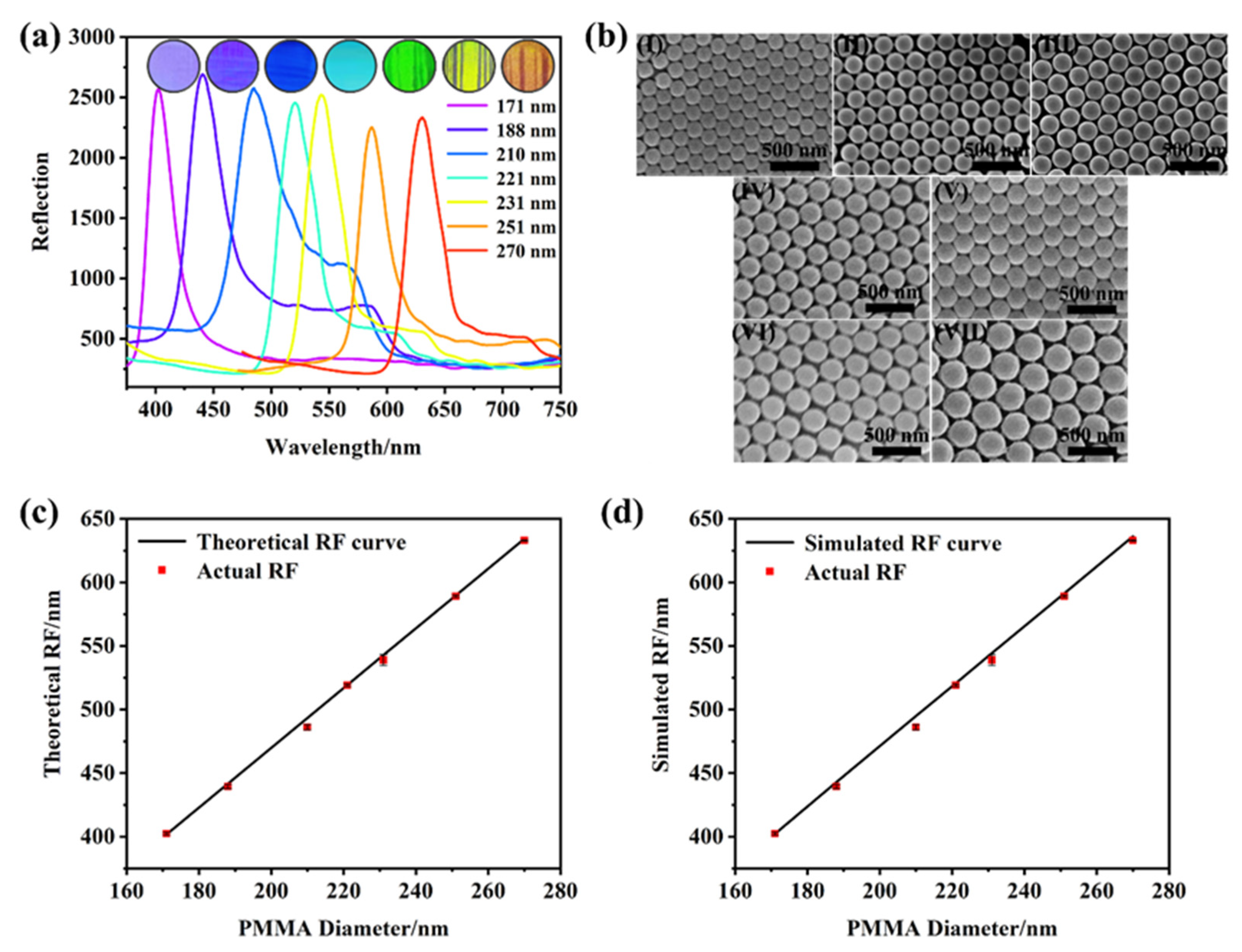
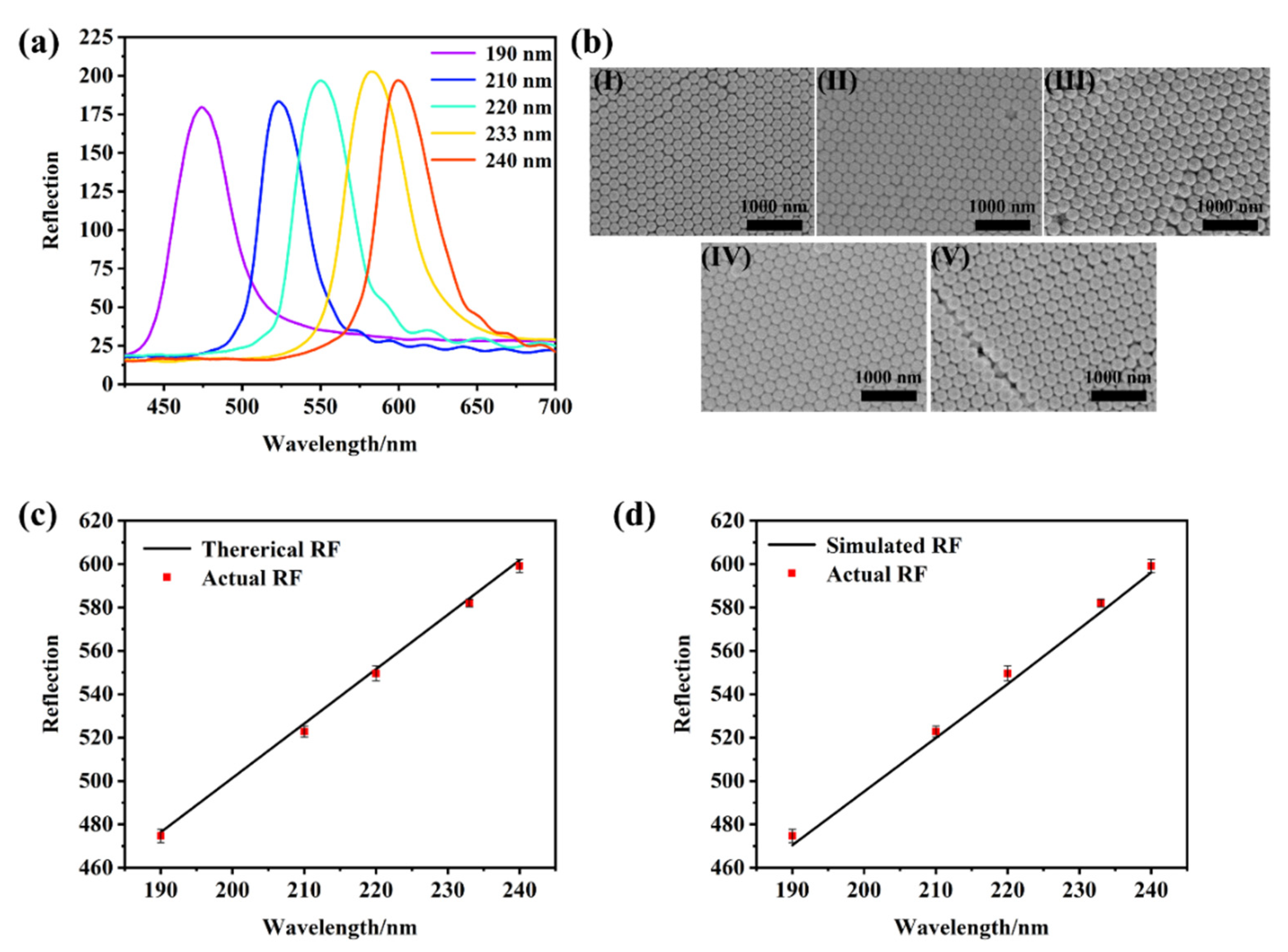
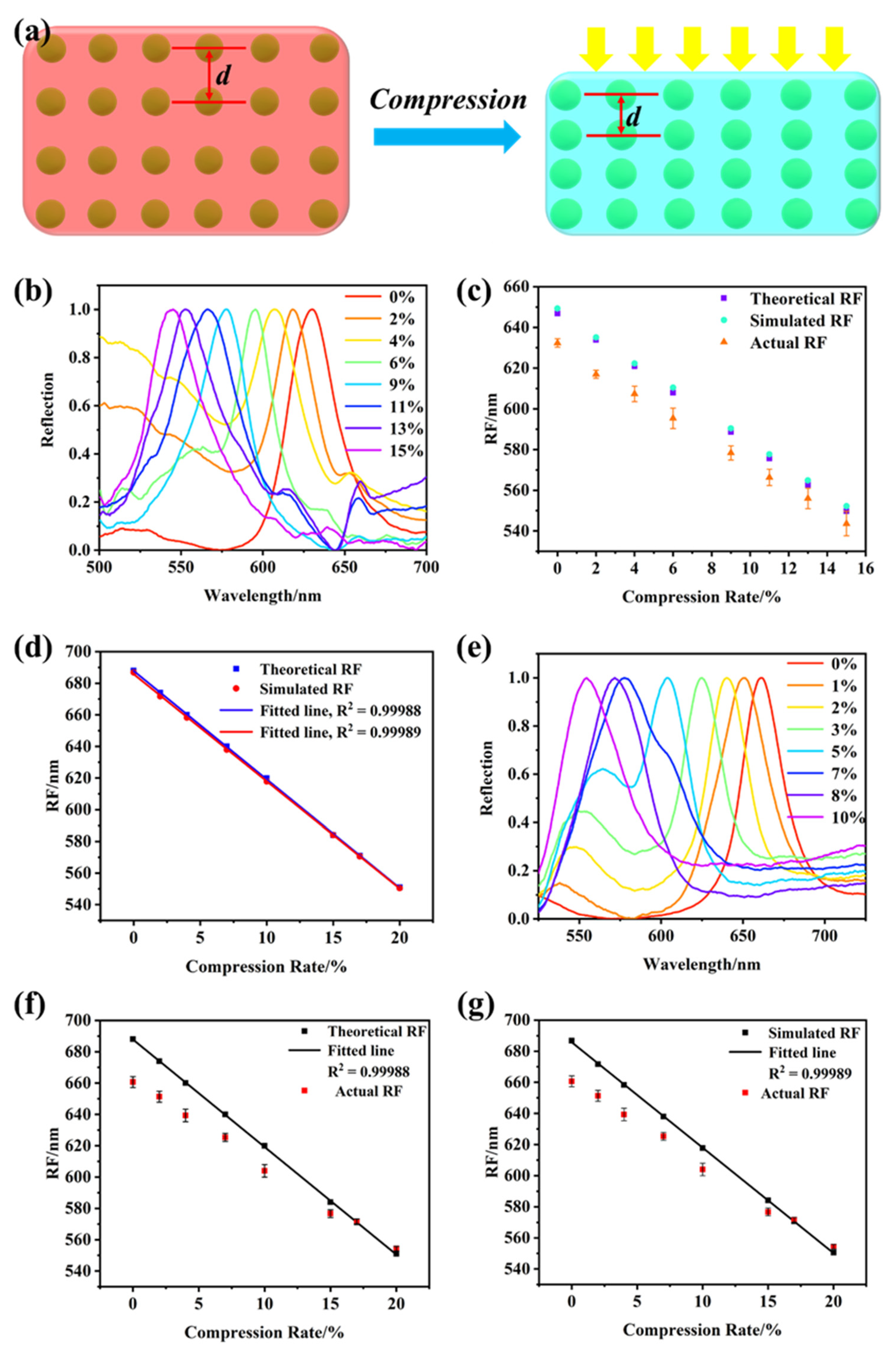
3.2. The Feasibility of the Theorical and Simulated Photonic Band Gap

The real reflection peaks of PMMA and PS photonic crystals with varying microsphere diameters were contrasted with the theoretical/simulated reflection peaks. This comparison serves to validate the instructive relevance of the theoretical and simulated reflection peaks for the experimental outcomes. In Figure 2a, the reflective spectrum and physical images of PMMA photonic crystals with diameters of 171 nm, 188 nm, 210 nm, 221 nm, 231 nm, 251 nm and 270 nm are presented. The observed reflection peaks for these crystals were measured at 402 nm, 438 nm, 489 nm, 519 nm, 538 nm, 589 nm and 634 nm, respectively. The associated structural colors corresponding to these peaks were visually identified as purple, blue–violet, blue, cyan, green, yellow and orange–red. The PMMA photonic crystals (PCs) exhibited an ordered periodic structure (see Figure 2b), leading to distinctive structural colors. The observed reflection peaks of the PMMA PCs closely matched those predicted by theoretical calculations (see Figure 2c) and simulations using Rsoft–Bandsolve (see Figure 2d and Figure S4). This alignment between actual and predicted reflection peaks suggests that theoretical analyses and Rsoft–Bandsolve simulations are reliable tools for tailoring the photonic band gap (PBG) of PCs in advance of experimental implementations.

At the same time, as illustrated in Figure 3a, the observed reflectance peaks for the 190 nm, 210 nm, 220 nm, 233 nm and 240 nm PS PCs were measured at 474 nm, 523 nm, 550 nm, 583 nm and 600 nm, respectively. Each of these crystals exhibited a well-defined ordered periodic structure, as depicted in Figure 3b. Analogous to the PMMA PCs presented in Figure 2, the actual reflection peaks of the PS PCs aligned closely with theoretical predictions and Rsoft–Bandsolve simulations. This alignment underscores the efficacy of theoretical analyses and Rsoft–Bandsolve simulations in steering the tailoring of PBGs in PCs involving diverse media. Such precision holds promise for advancing the exploration and utilization of novel materials within the field of the PCs.

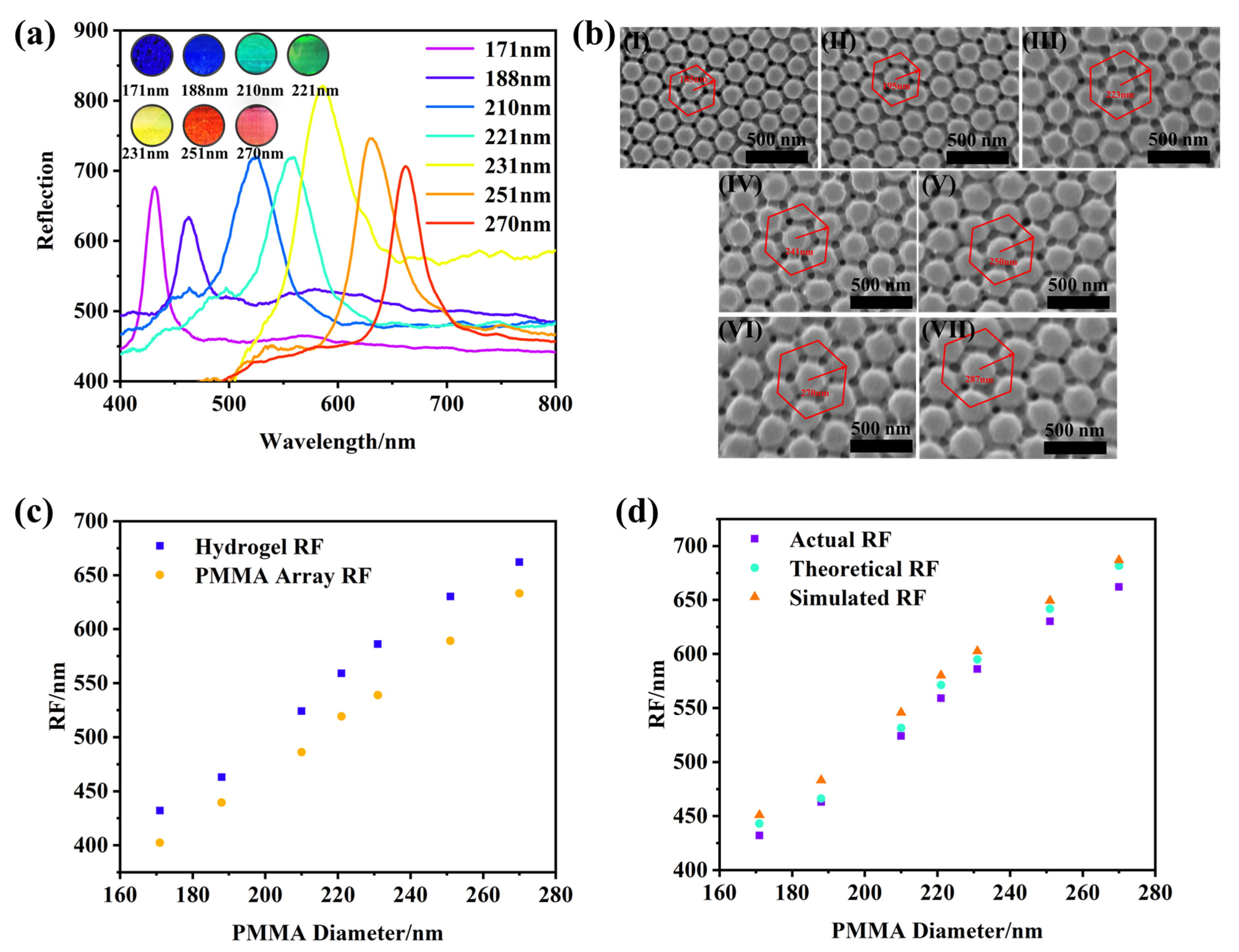
3.3. The Reflection Peaks of AM-Based Photonic Hydrogels

The incorporation of hydrogels with PCs induces modifications in the effective refractive index and expands their lattice distance. Consequently, this alteration leads to a redshift in the reflective spectrum compared to the pristine PCs. In Figure 4a, the reflective spectrum and accompanying physical images depict acrylamide (AM)—based photonic hydrogels integrated with PMMA PCs of varying sizes (171 nm, 188 nm, 210 nm, 221 nm, 231 nm, 251 nm and 270 nm). The corresponding reflection peaks for these configurations are observed at 432 nm, 463 nm, 524 nm, 559 nm, 586 nm, 630 nm and 662 nm, respectively, and the structural colors were blue–violet, blue, cyan, green, yellow, orange–red and red. Notably, these reflection peaks exhibited redshifts of 30 nm, 25 nm, 35 nm, 40 nm, 46 nm, 41 nm and 28 nm in comparison to the PMMA PCs alone (as shown in Figure 4c). The magnitudes of these redshifts were quantified as 6.94%, 5.40%, 6.68%, 7.16%, 7.85%, 6.51% and 4.23% of the respective reflection peaks. The SEM images of the photonic hydrogels in Figure 4b show their ordered periodic structures and the distance between microspheres was enlarged compared with that of the PMMA PCs array, which indicated that redshift of the reflection peaks was caused by both the effective refractive index and the lattice distance. Based on the PMMA microspheres’ distance derived from the SEM and the volume fraction of the microspheres in the photonic hydrogels (Equation (6)):

$$f_{sphere}=\frac{V_{sphere}}{V_{unit}}={\frac{\frac{4}{3}\pi {(\frac{D_{sphere}}{2})}^3}{D^3}}^{}{}^{}$$

(6)

and combined with Equations (1)–(3) to obtain Equation (7) and the n_hydrogel = 1.45:

$${\lambda }_{\mathit{max}}=2{\sqrt{n_{sphere}^2(\frac{\pi D_{{}_{sphere}}^3}{6D^3})+n_{hydrogel}^2(1-\frac{\pi D_{{}_{sphere}}^3}{6D^3})}}_{}·\sqrt{\frac{2}{3}}{D}^{}{}^{}$$

(7)

As per Equation (7), Figure 4d and Figure S6 display the theoretical, simulated and observed reflection peaks. The findings indicate that both the theoretical and simulated reflection peaks exceeded the actual reflection peaks due to nanosphere distant defects in the photonic hydrogels. Notably, the consistency among the theoretical, simulated and actual reflection peaks suggests that theoretical analysis and numerical simulation are reliable tools for guiding experimental research.

3.4. The Compressive Strain of the AM-Based Photonic Hydrogels

The mechanical compressive strain results in a decrease in the lattice distance between microspheres, and causes a blue shift in both reflection peaks and structural color (Figure 5a). The compressive strain reflective spectrum of the AM-based photonic hydrogel with 251 nm PMMA is shown in Figure 5b, and the reflection peaks were 633 nm, 619 nm, 609 nm, 596 nm, 578 nm, 567 nm, 556 nm and 543 nm when the compressive strain increased from 0% to 2%, 4%, 6%, 9%, 11%, 13% and 15%, respectively. In the same case, the actual reflection peak was lower than that of the theoretical and simulated results, which was the result of the uneven variation of the lattice distance between PMMA microspheres, and the actual reflection peaks were in agreement with the theoretical and simulated reflection peaks at more than 95% (Figure 5c). Figure 5d shows the relationships between the theorical/simulated reflection peaks and compressive strains, the theoretical reflection peaks were 688 nm, 674 nm, 660 nm, 640 nm, 620 nm, 584 nm, 571 nm and 551 nm, and the simulated reflection peaks were 687 nm, 672 nm, 658 nm, 638 nm, 618 nm, 584 nm, 571 nm and 551 nm, when the compressive strain increased from 0% to 2%, 4%, 7%, 10%, 15%, 17% and 20%, and the similarity between the theoretical and simulated reflection peaks was as high as 99%. The fitting formulas between reflection peak and compressive strain were y = −6.8641x + 687.85 (R² = 0.99988) and y = −6.7774x + 685.76 (R² = 0.99989), which can be used to predict the relationship between actual reflection peaks and compressive strains. As shown in Figure 5e, the observed reflection peaks were measured at 661 nm, 651 nm, 640 nm, 625 nm, 604 nm, 577 nm, 572 nm, 572 nm and 554 nm for hydrogel compression levels of 0%, 2%, 4%, 7%, 10%, 15%, 17% and 20%. The agreement between the actual reflection peaks and the corresponding theoretical/simulated reflection peaks exceeded 96%. These outcomes underscore the practical guidance provided by theoretical and simulation approaches in the design of photonic hydrogels under compressive strain.

4. Discussion

The theoretical calculations and numerical simulations for predicting the photonic band gap can be used to design and customize photonic materials with specific optical properties, which can effectively improve the efficiency of research work and reduce the experimental cost and time cost. The reflection peaks of photonic crystals with different medias and photonic materials were predicted with theoretical formulas and Rsoft–Bandsolve software v2019.09, and the prediction results were highly consistent with the experimental results, which indicated that both theoretical calculations and numerical simulations proved effective in predicting the optical properties of photonic crystals. Furthermore, the high consistency between the prediction results and experimental results of the reflection peak–compressive strain relationship, based on AM-based 270 nm PMMA photonic hydrogel, shows that the theoretical calculations and numerical simulations can effectively predict the optical properties of photonic materials and evaluate their response effects. Given their accuracy and reliability, both theoretical calculations and numerical simulations can also be applied for predicting the optical properties of photonic materials and evaluating their responsive effects to external stimuli, such as strain, temperature, pH and volatile organic gas (VOC) detection.

5. Conclusions

This study employed theoretical calculations and numerical simulations to predict the photonic band gap, facilitating the design and customization of specific photonic materials. Successful prediction of the reflection peaks for SiO₂ PCs, PMMA PCs, PS PCs and AM-based photonic hydrogels was achieved using theoretical formulas and Rsoft–Bandsolve software v2019.09. The relationship between actual reflection peaks and compressive strains in AM-based photonic hydrogels with 251 nm PMMA PCs demonstrated over 96% similarity with the theoretical and simulated results. Additionally, an exploration of the reflection peaks–compressive strains relationship for AM-based 270 nm PMMA photonic hydrogels was conducted to predict actual reflection peaks under compression. Given their accuracy and reliability, both theoretical calculations and numerical simulations prove effective in predicting the optical properties of photonic materials and evaluating their responsive effects. This approach offers a simple and rapid solution for the design and fabrication of photonic materials.