Thin and Large Depth-Of-Field Compound-Eye Imaging for Close-Up Photography
Abstract
1. Introduction
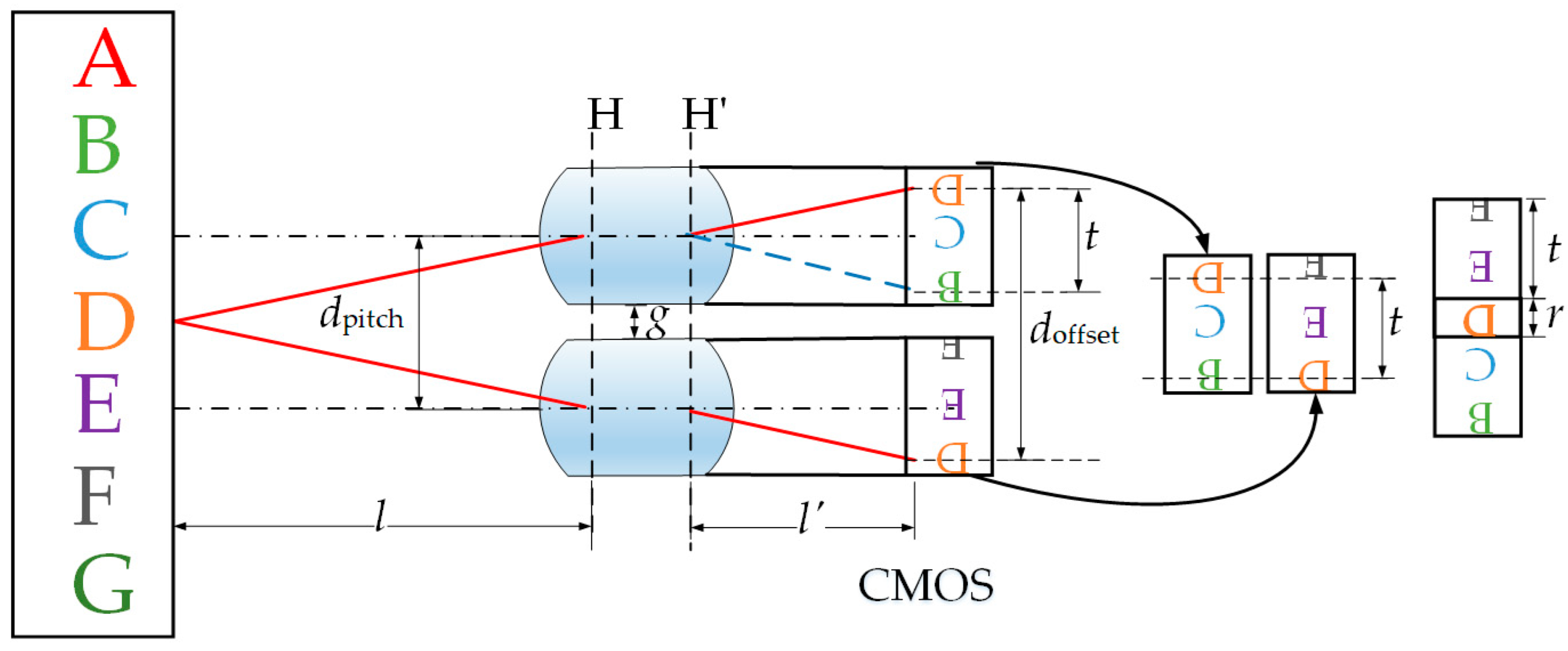
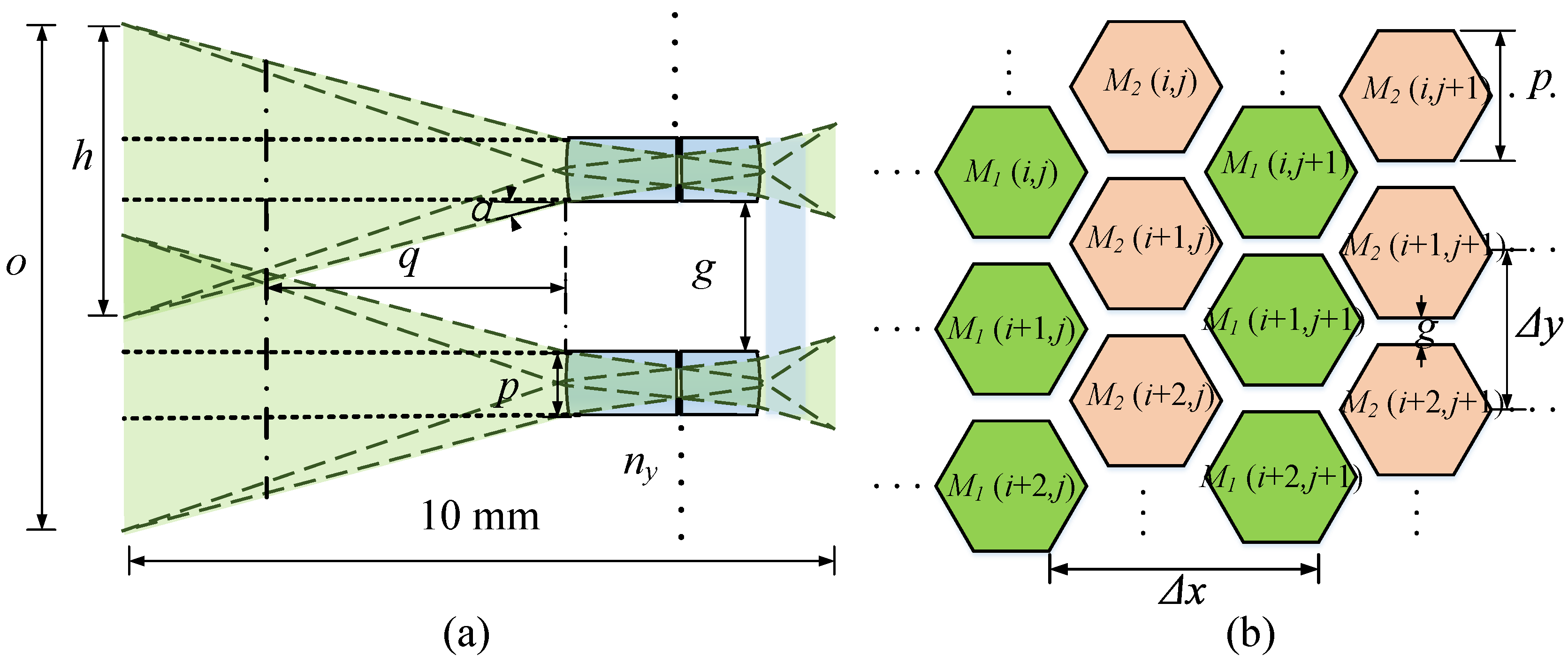
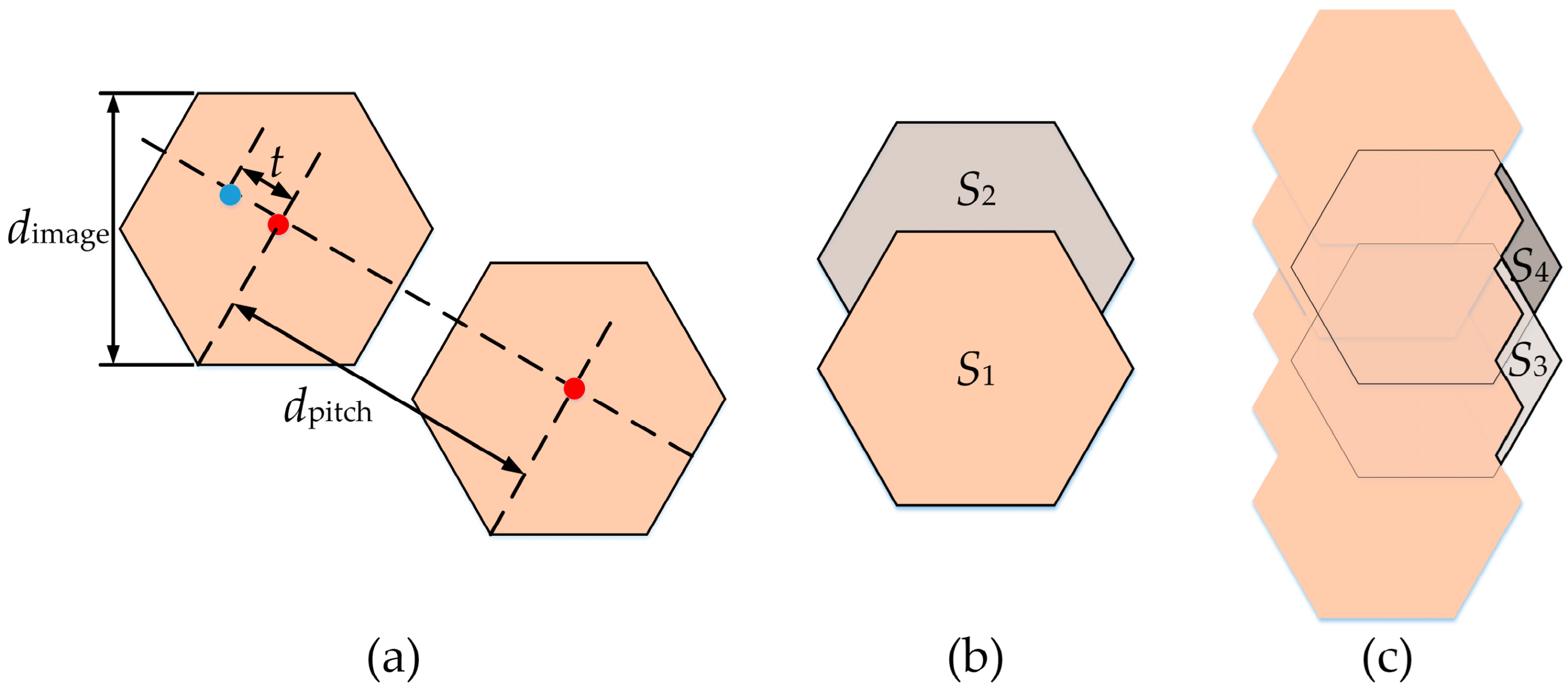
2. Principles of Micro Compound-Eye Optical Design
3. System Implementation
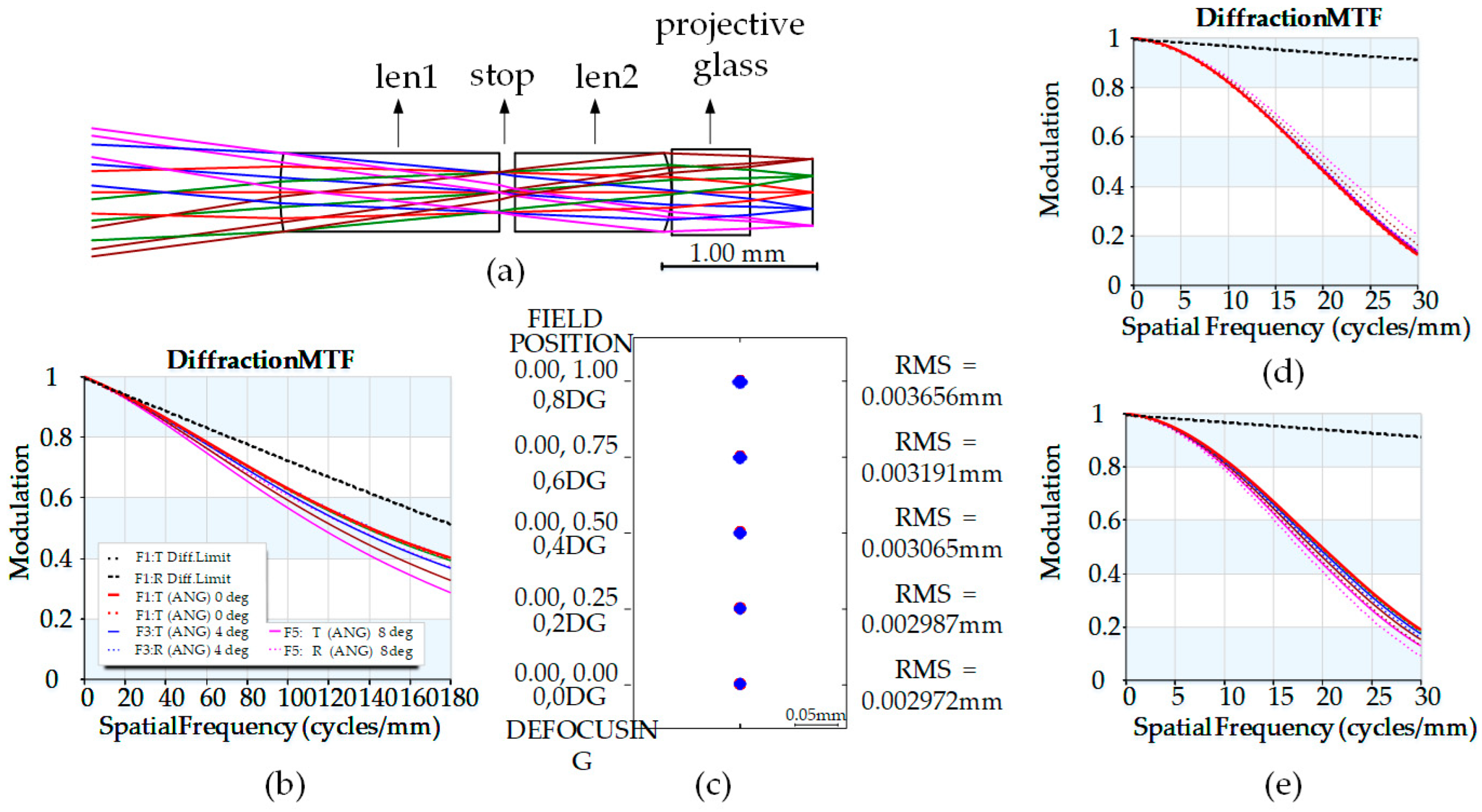
3.1. Optical Design
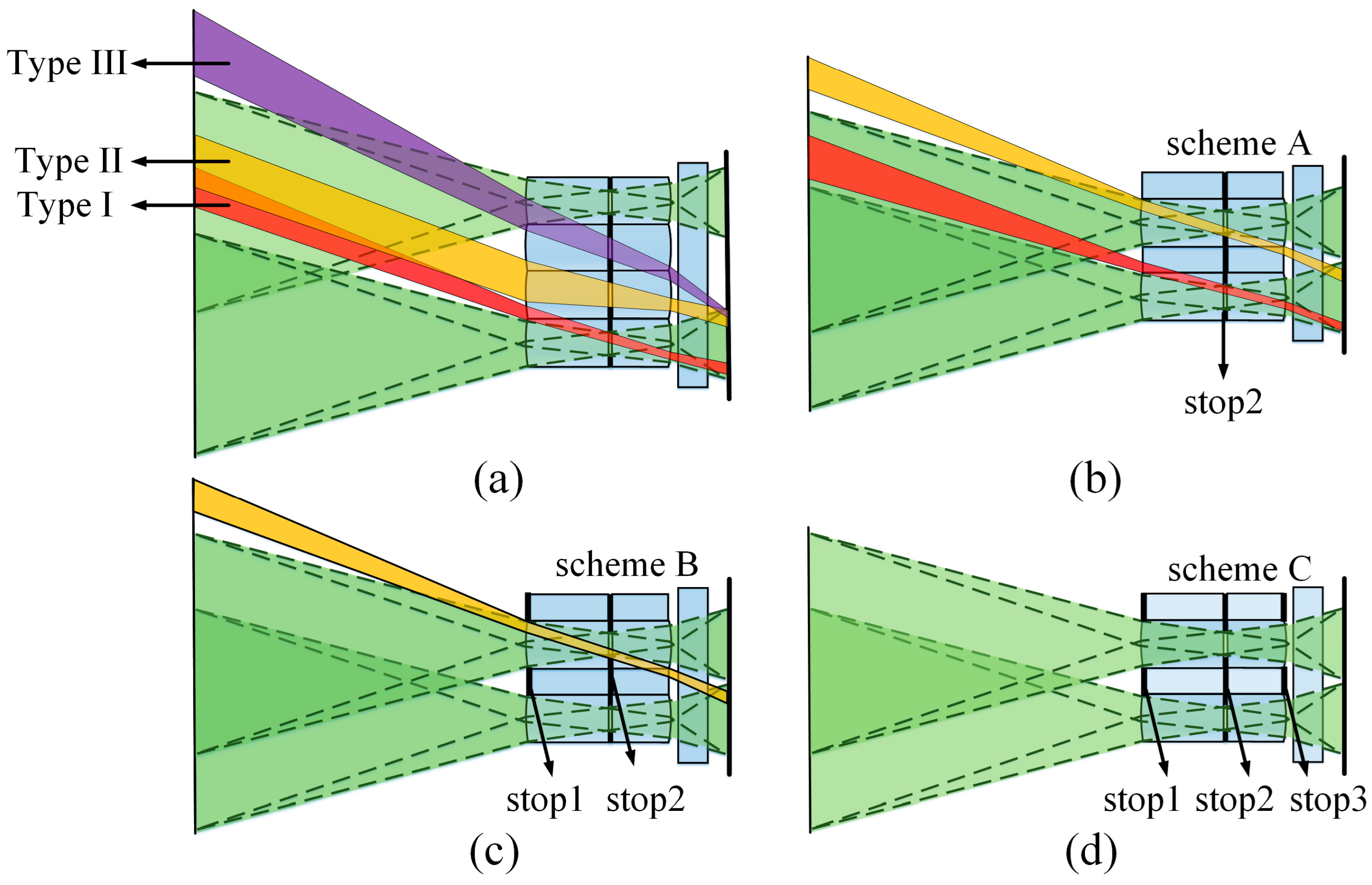
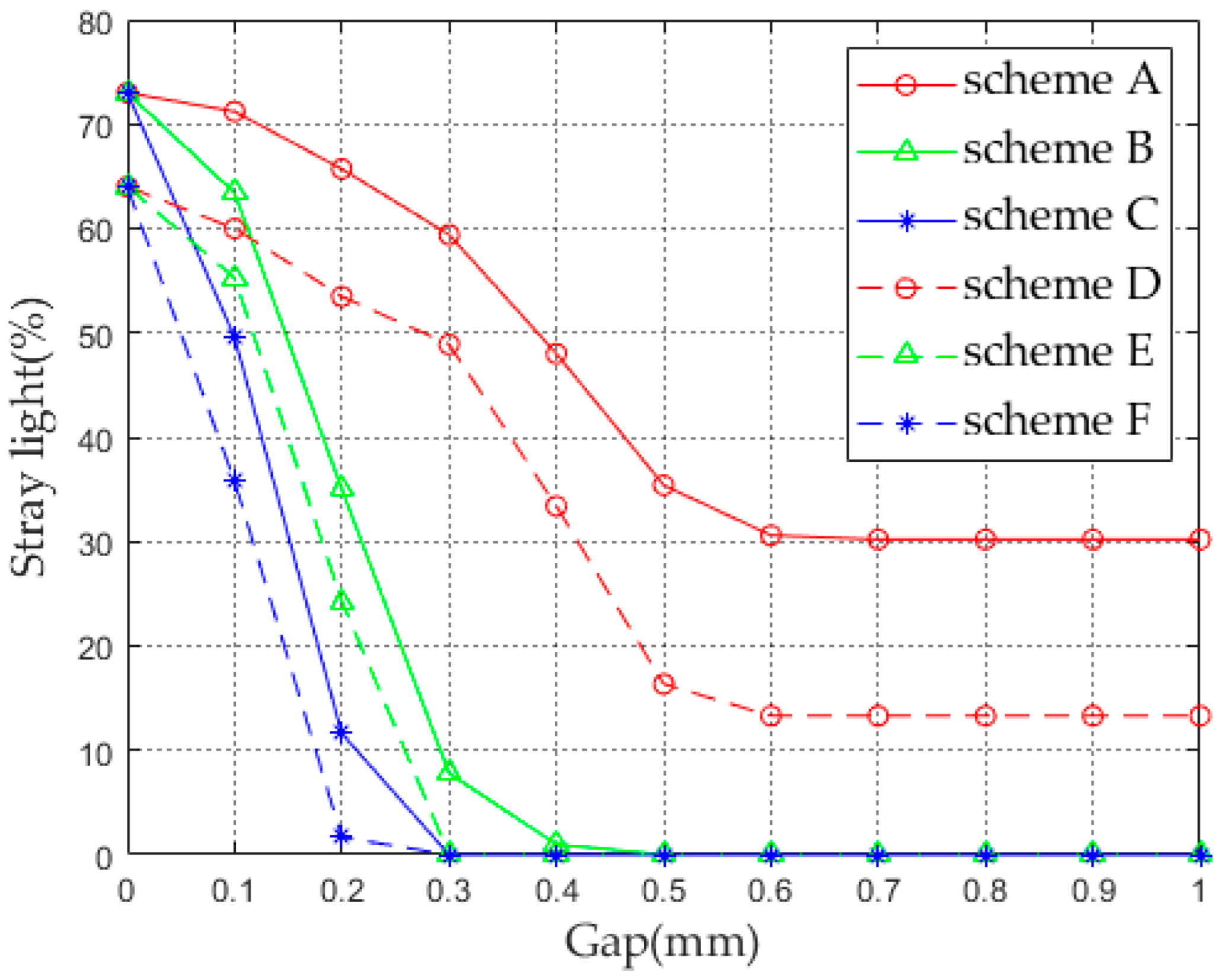
3.2. Stray Light Analysis and Elimination
3.3. Pixel Utilization
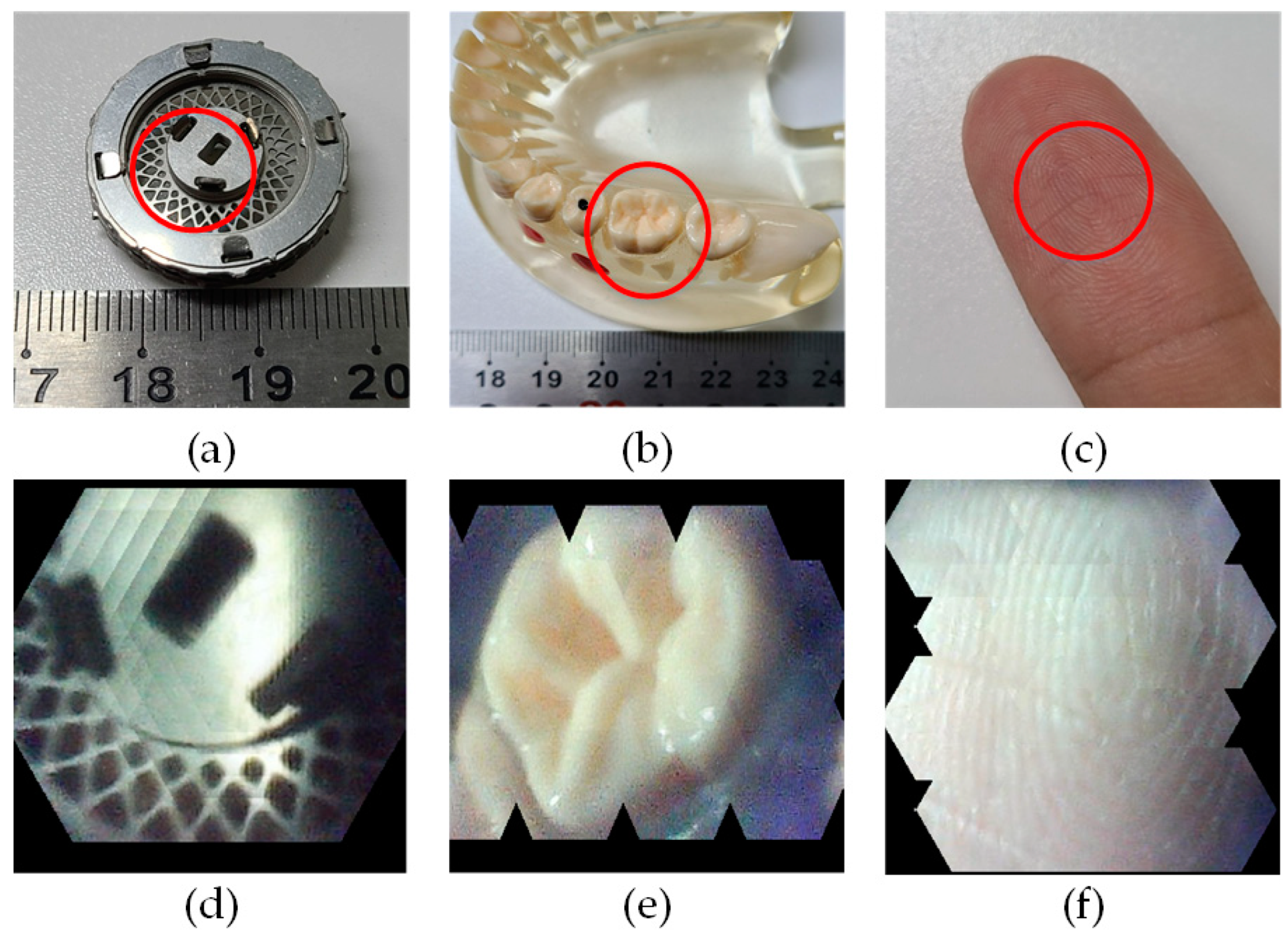
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Varela, F.G. The Vertebrate and the (Insect) Compound Eye in Evolutionary Perspective. Vis. Res. 1971, 11, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Borst, A.; Plett, J. Seeing the World through an Insect’s Eyes. Nature 2013, 497, 47–48. [Google Scholar] [CrossRef] [PubMed]
- Luo, T.; Yuan, J.; Chang, J.; Dai, Y.; Gong, H.; Luo, Q.; Yang, X. Resolution and Uniformity Improvement of Parallel Confocal Microscopy Based on Microlens Arrays and a Spatial Light Modulator. Opt. Express 2023, 31, 4537. [Google Scholar] [CrossRef]
- Horisaki, R.; Nakao, Y.; Toyoda, T.; Kagawa, K.; Masaki, Y.; Tanida, J. A Thin and Compact Compound-Eye Imaging System Incorporated with an Image Restoration Considering Color Shift, Brightness Variation, and Defocus. Opt. Rev. 2009, 16, 241–246. [Google Scholar] [CrossRef]
- Florian, C.; Piazza, S.; Diaspro, A.; Serra, P.; Duocastella, M. Direct Laser Printing of Tailored Polymeric Microlenses. ACS Appl. Mater. Interfaces 2016, 8, 17028–17032. [Google Scholar] [CrossRef] [PubMed]
- Surdo, S.; Carzino, R.; Diaspro, A.; Duocastella, M. Single-Shot Laser Additive Manufacturing of High Fill-Factor Microlens Arrays. Adv. Opt. Mater. 2018, 6, 1701190. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, F.; Luan, S.; Wan, H.; Song, Y.; Gui, C. 3D OPC Method for Controlling the Morphology of Micro Structures in Laser Direct Writing. Opt. Express 2023, 31, 3212. [Google Scholar] [CrossRef]
- Gissibl, T.; Thiele, S.; Herkommer, A.; Giessen, H. Two-Photon Direct Laser Writing of Ultracompact Multi-Lens Objectives. Nat. Photonics 2016, 10, 554–560. [Google Scholar] [CrossRef]
- Gong, J.; Zhou, J.; Sun, H.; Hu, S.; Wang, J.; Liu, J. Mask-Shifting-Based Projection Lithography for Microlens Array Fabrication. Photonics 2023, 10, 1135. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, N.; He, Y.; Liao, S.; Zhang, S.; Wang, Y. Control of Polymer Phase Separation by Roughness Transfer Printing for 2D Microlens Arrays. Small 2016, 12, 3788–3793. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, X.; Zhang, X.; Jiang, F.; Zhang, X.; Wang, Y. Supercritical Fluid-Driven Polymer Phase Separation for Microlens with Tunable Dimension and Curvature. ACS Appl. Mater. Interfaces 2016, 8, 8849–8858. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Xu, W.; Zhu, L.; Zhuang, Y.; Zhang, D. Superhydrophobic and Easy-to-Clean Full-Packing Nanopatterned Microlens Array with High-Quality Imaging. Opt. Express 2023, 31, 13601. [Google Scholar] [CrossRef] [PubMed]
- Ng, R.; Levoy, M.; Brédif, M.; Duval, G.; Horowitz, M.; Hanrahan, P. Light Field Photography with a Hand-Held Plenoptic Camera. Ph.D. Thesis, Stanford University, Stanford, CA, USA, February 2005. [Google Scholar]
- Li, H.; He, Y.; Yu, Y.; Wu, Y.; Zhang, S.; Zhang, Y. A Light Field Display Realization with a Nematic Liquid Crystal Microlens Array and a Polymer Dispersed Liquid Crystal Film. Photonics 2022, 9, 244. [Google Scholar] [CrossRef]
- Yao, C.; Cheng, D.; Yang, T.; Wang, Y. Design of an Optical See-through Light-Field near-Eye Display Using a Discrete Lenslet Array. Opt. Express 2018, 26, 18292. [Google Scholar] [CrossRef]
- Momonoi, Y.; Yamamoto, K.; Yokote, Y.; Sato, A.; Takaki, Y. Light Field Mirage Using Multiple Flat-Panel Light Field Displays. Opt. Express 2021, 29, 10406. [Google Scholar] [CrossRef] [PubMed]
- Holliman, N.S.; Dodgson, N.A.; Favalora, G.E.; Pockett, L. Three-Dimensional Displays: A Review and Applications Analysis. IEEE Trans. Broadcast. 2011, 57, 362–371. [Google Scholar] [CrossRef]
- Algorri, J.F.; Urruchi del Pozo, V.; Sanchez-Pena, J.M.; Oton, J.M. An Autostereoscopic Device for Mobile Applications Based on a Liquid Crystal Microlens Array and an OLED Display. J. Display Technol. 2014, 10, 713–720. [Google Scholar] [CrossRef]
- Kim, C.; Shin, D.; Koo, G.; Won, Y.H. Fabrication of an Electrowetting Liquid Microlens Array for a Focus Tunable Integral Imaging System. Opt. Lett. 2020, 45, 511. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, D.; Yang, T.; Chen, H.; Gu, L.; Ni, D.; Wang, Y. Ultra-Thin Multifocal Integral LED-Projector Based on Aspherical Microlens Arrays. Opt. Express 2022, 30, 825. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, D.; Yang, T.; Wang, Y. High Precision Integrated Projection Imaging Optical Design Based on Microlens Array. Opt. Express 2019, 27, 12264. [Google Scholar] [CrossRef]
- Kasztelanic, R.; Filipkowski, A.; Pysz, D.; Nguyen, H.T.; Stepien, R.; Liang, S.; Troles, J.; Karioja, P.; Buczynski, R. Development of Gradient Index Microlenses for the Broadband Infrared Range. Opt. Express 2022, 30, 2338. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Yang, J.; Wang, M.; Sun, C.; Song, N.; Cui, J.; Feng, S. Research on Spectral Reconstruction Algorithm for Snapshot Microlens Array Micro-Hyperspectral Imaging System. Opt. Express 2021, 29, 26713. [Google Scholar] [CrossRef]
- Yang, T.; Liu, Y.; Mu, Q.; Zhu, M.; Pu, D.; Chen, L.; Huang, W. Compact Compound-Eye Imaging Module Based on the Phase Diffractive Microlens Array for Biometric Fingerprint Capturing. Opt. Express 2019, 27, 7513. [Google Scholar] [CrossRef] [PubMed]
- Banerji, S.; Meem, M.; Majumder, A.; Sensale-Rodriguez, B.; Menon, R. Extreme-Depth-of-Focus Imaging with a Flat Lens. Optica 2020, 7, 214. [Google Scholar] [CrossRef]
- Phan, H.; Yi, J.; Bae, J.; Ko, H.; Lee, S.; Cho, D.; Seo, J.-M.; Koo, K. Artificial Compound Eye Systems and Their Application: A Review. Micromachines 2021, 12, 847. [Google Scholar] [CrossRef]
- Tanida, J.; Mima, H.; Kagawa, K.; Ogata, C.; Umeda, M. Application of a Compound Imaging System to Odontotherapy. Opt. Rev. 2015, 22, 322–328. [Google Scholar] [CrossRef]
- Berlich, R.; Brückner, A.; Leitel, R.; Oberdörster, A.; Wippermann, F.; Bräuer, A. Multi-Aperture Microoptical System for Close-Up Imaging; Johnson, R.B., Mahajan, V.N., Thibault, S., Eds.; SPIE: San Diego, CA, USA, 2014; p. 91920E. [Google Scholar]
- Hong, S.-H.; Jang, J.-S.; Javidi, B. Three-Dimensional Volumetric Object Reconstruction Using Computational Integral Imaging. Opt. Express 2004, 12, 483. [Google Scholar] [CrossRef]
- Hong, S.-H.; Javidi, B. Three-Dimensional Visualization of Partially Occluded Objects Using Integral Imaging. J. Display Technol. 2005, 1, 354–359. [Google Scholar] [CrossRef]
- Vaish, V.; Levoy, M.; Szeliski, R.; Zitnick, C.L.; Kang, S.B. Reconstructing Occluded Surfaces Using Synthetic Apertures: Stereo, Focus and Robust Measures. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition-Volume 2 (CVPR’06), New York, NY, USA, 17–22 June 2006; IEEE: New York, NY, USA, 2006; Volume 2, pp. 2331–2338. [Google Scholar]
- Liu, Y.; Cheng, D.; Hou, Q.; Chen, H.; Feng, Z.; Yang, T.; Wang, Y. Compact Integrator Design for Short-Distance Sharp and Unconventional Geometric Irradiance Tailoring. Appl. Opt. 2021, 60, 4165. [Google Scholar] [CrossRef]






| Parameter | Specification |
|---|---|
| Thickness | 1.4 mm (lens 1) + 1 mm (lens 2) |
| Material | P-CARBO |
| Refractive index | 1.585 |
| Diameter of sublens | 0.5 mm |
| FOV | 16° |
| MTF | >0.2@200 lp/mm |
| DOF | 10 mm |
| Focal distance | 1.387 mm |
| Distortion | <2% |
| Total thickness | 3.5 mm |
| Tolerance Type | Location | Value | Unit |
|---|---|---|---|
| DLT—delta thickness | S1–S4 | 20 | μm |
| DLN—delta refractive index | L1, L2 | 0.001 | - |
| DLV—delta V-number | L1, L2 | 0.004 | - |
| DLS—surface sag error | S1, S4 | 5 | μm |
| DLX—surface X-displacement | S1, S4 | 5 | μm |
| DLY—surface Y-displacement | S1, S4 | 20 | μm |
| DLA—surface alpha tilt | S1, S4 | 0.3 | mrad |
| DLB—surface beta tilt | S1, S4 | 0.3 | mrad |
| BTX—barrel alpha tilt | L1, L2 | 0.3 | mrad |
| BTY—barrel alpha tilt | L1, L2 | 0.3 | mrad |
| DSX—group X-decenter | L1, L2 | 20 | μm |
| DSY—group Y-decenter | L1, L2 | 20 | μm |
| Parameter | Specification |
|---|---|
| Size | 1″(16 mm) diagonally |
| Active display area | 13.13 mm × 8.76 mm |
| Resolution (CMOS) | 4096 × 2160 pixels |
| CMOS model | Sony IMX267 |
| Size of single pixel | 3.45 μm |
| Effective focal length | 1.39 mm |
| Sublens diameter | 0.5 mm |
| F/# | 3.467 |
| Overall dimensions of MLA | 13 × 10 × 3.5 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, D.; Wang, D.; Yao, C.; Liu, Y.; Dai, X.; Wang, Y. Thin and Large Depth-Of-Field Compound-Eye Imaging for Close-Up Photography. Photonics 2024, 11, 107. https://doi.org/10.3390/photonics11020107
Cheng D, Wang D, Yao C, Liu Y, Dai X, Wang Y. Thin and Large Depth-Of-Field Compound-Eye Imaging for Close-Up Photography. Photonics. 2024; 11(2):107. https://doi.org/10.3390/photonics11020107
Chicago/Turabian StyleCheng, Dewen, Da Wang, Cheng Yao, Yue Liu, Xilong Dai, and Yongtian Wang. 2024. "Thin and Large Depth-Of-Field Compound-Eye Imaging for Close-Up Photography" Photonics 11, no. 2: 107. https://doi.org/10.3390/photonics11020107
APA StyleCheng, D., Wang, D., Yao, C., Liu, Y., Dai, X., & Wang, Y. (2024). Thin and Large Depth-Of-Field Compound-Eye Imaging for Close-Up Photography. Photonics, 11(2), 107. https://doi.org/10.3390/photonics11020107





