Abstract
Integrated optical amplifiers are the building blocks of on-chip photonic systems, and they are often accompanied by a narrowband filter to limit noise. In this sense, a bandwidth-tunable optical amplifier with narrowband filtering function is crucial for on-chip optical circuits and radio frequency systems. The intrinsic loss and coupling coefficients between resonator and waveguide inherently limit the bandwidth. The parity-time symmetric coupled microresonators operating at exceptional points enable near zero bandwidth. In this study, we propose a parity-time symmetric coupled microresonators system operating near EPs to achieve a bandwidth of 46.4 MHz, significantly narrower than bandwidth of 600.0 MHz and 743.2 MHz achieved by two all-pass resonators with identical gain/loss coefficients. This system also functions as an optical bandwidth-tunable filter. The bandwidth tuning ranges from 175.7 MHz to 7.8 MHz as gain coefficient adjusts from 0.2 dB/cm to 0.4 dB/cm. Our scheme presents a unique method to obtain narrow bandwidth from two broadband resonators and serves as an optical bandwidth-tunable filter, thereby paving a new avenue for exploring non-Hermitian light manipulation in all-optical integrated devices.
1. Introduction
Parity-time (PT) symmetry in optical systems results from balance between gain and loss in the consisting subsystems [1,2,3]. This condition allows for real eigenvalues in non-Hermitian systems, contrasting with the traditional understanding that non-Hermitian systems typically exhibit complex eigenvalues [4]. Exceptional points (EPs) are non-Hermitian degeneracies where two or more eigenvalues and their eigenstates simultaneously coalesce [3,5]. Coupled waveguides and microresonators provide ideal platforms for the realization of EPs when material gain is introduced through optically pumping [6,7,8,9,10,11]. The exotic characteristics of PT symmetry and EPs have enabled microresonators to achieve stable single-longitudinal-mode lasing [6,9,10], unidirectional transmission [7,8], ultra-sensitive sensing [11,12,13,14,15,16,17], coherent perfect absorption [18], and bandwidth-tunable filters [19,20].
Optical tunable filters are essential devices in optical communication systems and integrated optics systems. In particular, narrow-bandwidth filters are critical for enabling high-performance microwave photonic devices [21,22,23]. Microring resonators, due to their compact size, flexible structure, and excellent filtering performance, are widely used to realize filters [24,25,26]. Shi et al. integrated a grating-assisted asymmetric coupler with a microring resonator to realize a bandwidth of 7.9 GHz [27]. Dai et al. designed a microring resonator filter with a curved asymmetric directional coupler to achieve a bandwidth of 100 GHz [28]. With controlled local heaters, it is possible to realize bandwidth tunable filter. Ong et al. proposed cascaded rings to realize an optical filter with a tuning range of 113 GHz, utilizing the synthetic spectra of multi-coupled resonant modes [29]. Passive PT-symmetric coupled microresonator structures have been demonstrated to realize optical bandpass filters [19,20]. With a relatively high coupling loss, the quality factor (Q-factor) of the filter is low and the bandwidth can be tuned range from 21 GHz to 49 GHz [19]. While thermal tuning schemes are experimentally feasible, the tuning range is limited to 2–10 times of the original bandwidth, with relatively slow tuning speed.
In this work, we propose an optical amplifier with narrowband filtering function based on PT symmetric coupled microresonators operating near the EPs, the bandwidth of which can be tuned over 20 times of the original bandwidth. On one hand, significantly narrowed bandwidth can be obtained in this system using accessible parameters. This feature is verified by comparing the differences of bandwidth between the coupled microresonators at the EPs and all-pass resonators with identical parameters, i.e., waveguide-resonator coupling and gain/loss coefficients. Results show that a bandwidth of 46.4 MHz is achieved in coupled resonators working near EPs, while the gain and loss resonators exhibit bandwidths of 600 MHz and 743.2 MHz. On the other hand, the bandwidth of the coupled resonators around the EP responses sensitively to the gain adjustment of a resonator, which can be practically implemented by tuning the pump power. When gain coefficient increases from 0.2 dB/cm to 0.4 dB/cm, the bandwidth tuning ranges from 175.7 MHz to 7.8 MHz. The bandwidth level is limited by the intrinsic gain/loss, coupling coefficients and radii.
2. Model and Principle
The schematic diagrams of coupled resonators and all-pass resonators are shown in Figure 1. In Figure 1a,b, the resonators with gain are plotted in red, and the resonators with loss are plotted in grey. Each of these resonators is coupled to a bus waveguide. Figure 1c,d show all-pass resonators with a single waveguide and a single resonator. Coupled mode theory in time is commonly employed to model the coupled micro-resonators and to determine the EP conditions, owning to its similarity to the Schrödinger equation. Before we employ transfer matrix method to investigate the coupled microresonators, we briefly review the PT symmetry and EP condition of coupled mode theory in time. As shown in Figure 1a, the time evolution of fields can be described as follows [30,31]
where Ein is the electric field at the input waveguide, Et is the output field of through port. aj is energy amplitude as introduced in Ref. [31]. ωj, and gj are the resonant angular frequency, and gain/loss rate in the ring with gain (j = 1, red colored) or the ring with loss (j = 2, blue colored), respectively. ω represents the signal frequency, with its detuning relative to the two resonators given by ω–ω1,2. g1,2 are related to the intrinsic gain/loss rates in the rings, γ1,2, and waveguide-ring coupling rates, γc1,c2, by g1,2 = γ1,2/2 + γc1,c2/2, and μ is the coupling strength between the rings. For simplicity, the two microrings are assumed to have the same radii (R1 = R2 = R), resonant frequencies (ω1 = ω2 = ω0) and the same waveguide-ring coupling rate (γc1 = γc2 = γc). In this regard, γ1,2 are related to the gain/loss coefficients in the waveguides consisting of the microrings, α1,2, by α1,22πR = γ1,2τR, where τR is the round-trip time of each ring. γc and μ are related to the ring-bus waveguide power coupling coefficient, κrb, and ring-ring power coupling coefficient, κrr, by γc = κrbvg/(2πR) and , respectively, where vg is the group velocity of the guided mode. The Equation (1) can also be written as
where A is [a1, a2]T, and the non-Hermitian Hamiltonian H is
The eigenfrequencies of the system are the eigenvalues of non-Hermitian Hamiltonian H, which can be written as
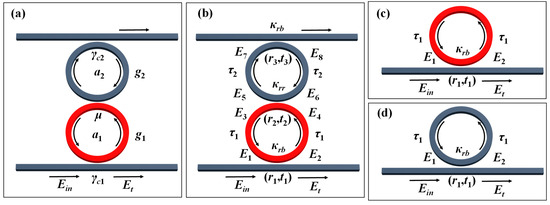
Figure 1.
The schematics of coupled microresonators and all-pass resonators. The red and grey represent structures with gain and loss, respectively. (a) Description of coupled mode theory in time for coupled microresonators. (b) Description of TMM for coupled microresonators. (c) Description of TMM for an all-pass microresonator with gain. (d) Description of TMM for an all-pass microresonator with loss.
The PT symmetry condition in optical systems is the spatial balance between gain and loss, i.e., g1 + g2 = 0. The EP condition is the coalescence of eigenfrequencies, i.e., μ2 = (g1 − g2)2/4. According to these two relations, the power coupling coefficients and the gain/loss coefficients should satisfy the relations as follows
where L = 2πR is the circumference of the resonators, α1,2 are gain/loss coefficients.
Although coupled mode theory in time provides an intuitive and convenient way to analyze coupled resonators near EPs, we employ the transfer matrix method (TMM) to investigate the differences and performance between coupled resonator systems near EPs and all-pass resonators, owning to its accuracy and fast computation [32,33]. The descriptions of TMM are shown in Figure 1b–d. According to the TMM, the transfer function is derived to be [32,33]
where , φ1,2 = πneffL/λ0 are phase shifts in half of the rings, λ0 is wavelength of pump light, are assumed to be 1, and neff is effective index of guided modes in the waveguides and resonators. τ1,2 = exp(−α1,2L1,2/2) are amplitude transmissions in half of the rings. r1,2,3 and t1,2,3 are the amplitude transmission and coupling coefficients at the coupling regions shown in Figure 1b, respectively, and r1,2,32 + t1,2,32 = 1. κrr = t22 and κrb = t1,32. For simplification, t1 is assumed to be the same as t3.
The PT symmetry and EP condition of the TMM have been derived, and the discrepancies between two approaches at EPs have been analyzed in [34]. We briefly review the PT symmetry and EP condition of the TMM as follows
Combine two equations of Equation (7), we can get relations between gain/loss and coupling coefficients under the conditions of PT symmetry and Eps
It is worth mentioning that the Equations (5) and (8) serve as guiding principles to design gain/loss coefficients, which are essential for configuring the coupled system to operate at EPs. In other words, a specific set of gain/loss coefficients could be calculated using Equation (8) or Equation (5), depending on the model applied.
One of the most important parameters of a resonator is its Q-factor and full-width-at-half-maximum (FWHM). Q-factor is commonly used to describe the loss of a resonator. Thus, we employ FWHM to describe the transmission characteristics in both resonators with gain and loss. The bandwidth of an all-pass resonator is expressed as follow [33]
where ∆f is FWHM in the frequency domain, ng is group index and c is the light velocity in the vacuum. Due to the possible mode splitting in coupled microresonators, it is difficult to derive the analytical expression of FWHM. Thus, the FWHM is obtained from transmission spectra.
When PT symmetry and EP condition are satisfied simultaneously, the bandwidth is zero and the energy in the resonators is infinite in theory. This condition is impractical to perfectly meet due to power-related effects such as gain saturation, Kerr nonlinearity. Thus, in this study, the coupled resonators satisfy the EP condition and slightly shift the gain/loss balance from the PT symmetry. In other words, the κrr is calculated by the EP condition. While, the κrb is slightly larger than the κrb0 calculated by the PT symmetry. The EP condition in coupled mode theory in time is μ2 = (g1 − g2)2/4. It can be converted into EP condition in coupled mode theory in space using the parameter relations. It is also the same as the second equation of Equation (8)
3. Results and Discussion
We propose PT-symmetric coupled microrings to realize a bandwidth-tunable optical amplifier with narrowband filtering function, as illustrated in Figure 1b. The parameters such as gain/loss coefficients and coupling coefficients of all-pass resonators in Figure 1c,d are the same in Figure 1b. Firstly, we quantitively compare the differences between coupled resonators operating at EPs near PT symmetry and all-pass resonators with identical parameters. We consider an example on SiN material platform. The radii are set to be 200 μm, the effective index is 1.9, the gain coefficient is 2 dB/cm and the loss coefficient is −0.2 dB/cm [35,36,37]. Although the SiN material is passive, optical gain can be introduced to the waveguide through Er3+ doping, with gain coefficient ranging from 0.75 dB/cm to 20 dB/cm [35,36,37,38]. According to Equation (8), the values of κrb0 and κrr0 are 0.026 and , respectively. κrb is set to be 0.029, slightly larger than κrb0 (0.026), so that the system operates below the lasing threshold. This results in the −i(g1 + g2)/2 < 0 and μ2 − (g1 − g2)2/4 = 0, indicating that the eigenfrequencies of coupled resonators acquire imaginary components, which correspond to dissipation. The resonant wavelength is set to be 1550 nm. At the EP, the power transmission at the through port (|Et|2/|Ein|2) of the resonant wavelength is , the FWHM is zero, as shown in Figure 2a. The phase spectra follow the expectations of Case Ⅰ in [39]. The transmission and phase spectra of the gain resonator are shown in Figure 2b. The transmission spectra in Figure 2b are characterized by a single peak with the maximum transmission of about 9.43 and the FWHM is 600 MHz. The phase spectra in Figure 2b are in over-coupled regime [33]. The transmission and phase spectra of loss resonator are shown in Figure 2c. The transmission spectra are characterized by a dip with the minimum transmission of about 0.45 and FWHM is 743.2 MHz. The phase spectrum exists in over-coupled regimes [33] and is similar to that in Figure 2a. The analysis implies that though the bandwidths of gain resonator and loss resonator are limited by gain/loss and coupling coefficients, the two all-pass resonators are supposed to possess narrower bandwidth if the coupling coefficient between two resonators is accurately manipulated to operate at EPs. In experiments, it is difficult to fabricate resonators with narrow FWHM. However, the coupled resonators operating near EPs provide an alternative approach to achieving narrowband resonators.
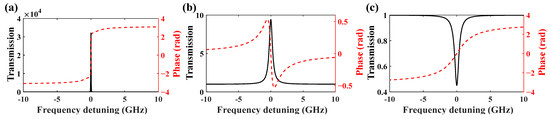
Figure 2.
Transmission and phase spectra of output field of through port. (a) Coupled resonator system operating at an EP with a shift to PT symmetry. (b) An all-pass microresonator with the same gain coefficient at the EP with a shift to PT symmetry. (c) An all-pass microresonator with the same loss coefficient at the EP with a shift to PT symmetry.
In order to investigate how narrow the bandwidth of an all-pass resonator can be with parameters from the EP, we scan gain and loss coefficients to plot FWHM, as shown in Figure 3a. The PT symmetry is considered, and the κrb is set to be the same as κrb0. Only the regimes where gain coefficients are larger than loss coefficients are depicted in Figure 3. This is due to the necessity for the gain of resonator to compensate the loss of resonator in order to maintain practical and positive coupling coefficients. For better understanding, the loss coefficients have been converted to positive values, although they were treated as negative during our computations. Whenever the gain and loss coefficients are varied, the bandwidths of PT symmetric coupled resonators at EPs are always zero. Thus, the bandwidths varying gain and loss of PT symmetric coupled resonators at EPs are not plotted in this article. From Figure 3a, we can infer that when gain and loss coefficients are small, the FWHM are narrow. When gain and loss coefficients are large enough, the FWHM can even be as broad as 106 GHz. It is feasible for the two broadband all-pass resonators to achieve narrow bandwidth through EP operation by adjusting the coupling coefficient κrr. The corresponding coupling coefficients κrr and κrb at EPs are plotted in Figure 3b,c, respectively. It can be observed that when gain and loss coefficients are small, the corresponding κrr and κrb are also small. It implied that, in experiments, the broadband resonators with gain and loss can achieve narrow bandwidth through accurately manipulating the coupling coefficients κrr and κrb to work near the EPs.
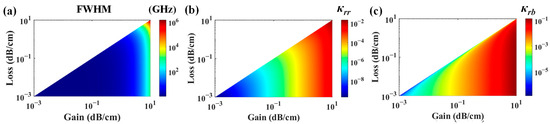
Figure 3.
Combinations of gain and loss coefficients range from 0.001 dB/cm to 10 dB/cm are scanned to get coupling coefficients meeting the EP condition. Every point represents a parameter set of an EP. Then the parameter sets are put into all-pass resonators to get the Q-factor. (a) Q-factors varying gain and loss. (b) κrr varying gain and loss. (c) κrb varying gain and loss.
Subsequently, we realize a bandwidth-tunable optical amplifier based the coupled microresonators working near the EP with a shift of PT symmetry, as shown in Figure 1b. The radii are set to be 800 μm, the effective index is 1.9, the gain coefficient is 0.2 dB/cm, which is easier to achieve in experiments, and the loss coefficient is −0.2 dB/cm. The bandwidth tuning is realized by the adjustment of gain coefficient, which is possible in experiment by controlling the power of the pump light. The κrr is set to be to satisfy the EP condition. The κrb is selected to be , which is slightly larger than the κrb0, 0, calculated by the PT symmetry. Under this condition, the coupled resonators system operates below the lasing threshold. The FWHM and group delay at the resonant wavelength as a function of gain coefficient are shown in Figure 4a. The four blue dashed lines represent the gain coefficients of 0.11 dB/cm, 0.2 dB/cm, 0.4 dB/cm and 0.6 dB/cm. The corresponding transmission spectra and group delay spectra are shown in Figure 4b, Figure 4c, Figure 4e and Figure 4f, respectively. The region where gain coefficient is smaller than 0.2 dB/cm represents transmission spectra with mode splitting. As shown in Figure 4b, the transmission spectra possess large bandwidth and the real parts of eigenfrequencies of two modes are split. When gain coefficient is 0.2 dB/cm, as shown in Figure 4c, the coupled microresonators work at the EP, resulting in coalesced eigenfrequencies as shown in Figure 4d. However, the bandwidth, 175.7 MHz, is not minimum at the EP. As the gain coefficient increases above 0.2 dB/cm and becomes smaller than 0.42 dB/cm, the FWHM decreases while the group delay displays a minor change. When gain coefficient is 0.4 dB/cm, as shown in Figure 4e, the FWHM is 7.8 MHz. When gain coefficient is 0.42 dB/cm, one of the eigenfrequencies possess zero imaginary part, denoted by the blue dashed line shown in Figure 4d. Conversely, when the gain coefficient exceeds 0.42 dB/cm and moves further from 0.42 dB/cm, the FWHM is becoming larger. The group delay at resonant frequency is becoming close to zero from negative values. When gain coefficient is 0.5 dB/cm, a single peak with limited FWHM is observed. The group delay is negative whenever gain coefficient is larger than 0.42 dB/cm. In practical, we take advantage of the region where gain coefficient is larger than 0.2 dB/cm to realize the optical amplifier. Due to the difficulty of precisely controlling the spatial balance between gain and loss to work at EPs, we select the gain coefficient tuning range from 0.2 dB/cm to 0.4 dB/cm, which is easier to achieve in experiments in contrast to 2 dB/cm. The FWHM ranges from 175.7 MHz to 7.8 MHz, and the group delay at the resonant wavelength is always positive. Thus, the coupled resonators working at the regimes where the gain coefficient is larger than the 0.2 dB/cm are practical to realize a bandwidth-tunable optical amplifier with narrowband filtering function.
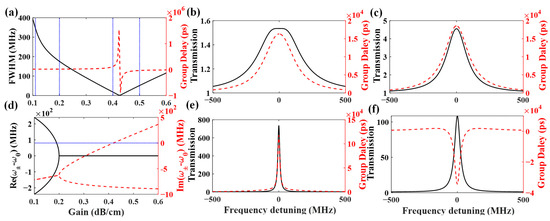
Figure 4.
The bandwidth-tunable optical amplifier based on coupled microresonators. (a) FWHM and group delay varying gain coefficient near the EP. (b) Transmission and group delay spectra when gain coefficient is 0.11 dB/cm. (c) Transmission and group delay spectra when gain coefficient is 0.2 dB/cm. (d) FWHM and group delay when gain coefficient ranges from 0.1 dB/cm to 0.6 dB/cm. (e) Transmission and group delay spectra when gain coefficient is 0.4 dB/cm; (f) Transmission and group delay spectra when gain coefficient is 0.5 dB/cm.
To investigate the group delay spectra, we plot the phase spectra shown in Figure 5. The spectral shape of the delay profile would be influential in determining the signal quality of a real data channel in optical communications [40]. When the gain coefficient is smaller than 0.42 dB/cm, as shown in Figure 5a–c the phase spectra are in over-coupled regimes, resulting the positive single-peak group delay spectra. As the gain coefficient increase from 0.2 dB/cm to 0.42 dB/cm, the group delay at resonant frequency gradually increases. When the gain coefficient is near the two sides of 0.42 dB/cm, the sign of group delay is abruptly change. Thus, the regime near the 0.42 dB/cm should be avoided in practical applications due to fluctuation of noise, gain, etc. When gain coefficient is larger than 0.42 dB/cm, as shown in Figure 5d, the phase spectra is in under-coupled regime, resulting the negative group delay at resonant frequency.
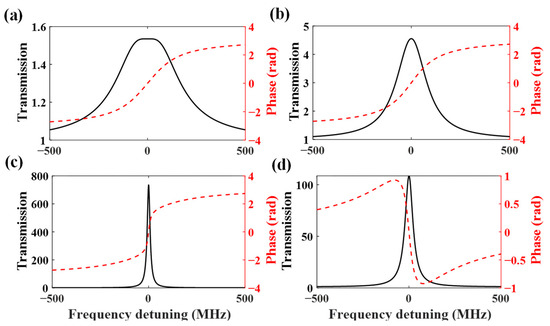
Figure 5.
Transmission and phase spectra of coupled microresonators at different gain coefficients. (a) Gain coefficient is 0.11 dB/cm. (b) Gain coefficient is 0.2 dB/cm. (c) Gain coefficient is 0.4 dB/cm. (d) Gain coefficient is 0.5 dB/cm.
4. Conclusions
In conclusion, we propose a bandwidth-tunable optical amplifier with narrowband filtering function based on PT symmetric coupled microresonators operating near the EP. The bandwidth tuning is realized by adjusting the gain coefficient, which can be realized by manipulating the pump power. The bandwidth tuning ranges from 7.8 MHz to 175.7 MHz, a 22.5 times tuning range of the minimum bandwidth. We also leverage the PT symmetric coupled resonator working at EPs to operate near the EP, thereby narrowing the bandwidth from 743.2 MHz to 46.4 MHz in comparison to an all-pass resonator. Our scheme presents an approach to realize a bandwidth-tunable optical filter as well as to transform from broadband resonators to narrowband coupled resonators by satisfying the PT symmetry condition and operating near EPs. Our results pave a promising way of utilizing non-Hermitian optics to realize multi-functional devices.
Author Contributions
Conceptualization, L.Z. and X.Z.; validation, K.Z.; formal analysis, K.Z.; investigation, K.Z. and X.Z.; resources, Y.Z. and Z.H.; data curation, K.Z.; writing—original draft preparation, K.Z.; writing—review and editing, L.Z. and X.Z.; supervision, L.Z.; project administration, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
National Key R&D Program of China (2021YFB2800400).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
We acknowledge support by the Advanced Integrated Optoelectronics Facility at Tianjin University.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having P T Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Özdemir, Ş.K.; Rotter, S.; Nori, F.; Yang, L. Parity–Time Symmetry and Exceptional Points in Photonics. Nat. Mater. 2019, 18, 783–798. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; El-Ganainy, R.; Ge, L. Non-Hermitian Photonics Based on Parity–Time Symmetry. Nat. Photonics 2017, 11, 752–762. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-0-521-88972-8. [Google Scholar]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian Physics and PT Symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
- Hodaei, H.; Miri, M.-A.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-Time–Symmetric Microring Lasers. Science 2014, 346, 975–978. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity–Time-Symmetric Whispering-Gallery Microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Chang, L.; Jiang, X.; Hua, S.; Yang, C.; Wen, J.; Jiang, L.; Li, G.; Wang, G.; Xiao, M. Parity–Time Symmetry and Variable Optical Isolation in Active–Passive-Coupled Microresonators. Nat. Photonics 2014, 8, 524–529. [Google Scholar] [CrossRef]
- Feng, L.; Wong, Z.J.; Ma, R.-M.; Wang, Y.; Zhang, X. Single-Mode Laser by Parity-Time Symmetry Breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef]
- Hodaei, H.; Miri, M.; Hassan, A.U.; Hayenga, W.E.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Single Mode Lasing in Transversely Multi-moded PT-symmetric Microring Resonators. Laser Photonics Rev. 2016, 10, 494–499. [Google Scholar] [CrossRef]
- Hodaei, H.; Hassan, A.U.; Wittek, S.; Garcia-Gracia, H.; El-Ganainy, R.; Christodoulides, D.N.; Khajavikhan, M. Enhanced Sensitivity at Higher-Order Exceptional Points. Nature 2017, 548, 187–191. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Hodaei, H.; Harari, G.; Hassan, A.U.; Chow, W.; Soltani, M.; Christodoulides, D.; Khajavikhan, M. Ultrasensitive Micro-Scale Parity-Time-Symmetric Ring Laser Gyroscope. Opt. Lett. 2017, 42, 1556–1559. [Google Scholar] [CrossRef]
- Lai, Y.-H.; Lu, Y.-K.; Suh, M.-G.; Yuan, Z.; Vahala, K. Observation of the Exceptional-Point-Enhanced Sagnac Effect. Nature 2019, 576, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Hokmabadi, M.P.; Schumer, A.; Christodoulides, D.N.; Khajavikhan, M. Non-Hermitian Ring Laser Gyroscopes with Enhanced Sagnac Sensitivity. Nature 2019, 576, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Kaya Özdemir, Ş.; Zhao, G.; Wiersig, J.; Yang, L. Exceptional Points Enhance Sensing in an Optical Microcavity. Nature 2017, 548, 192–196. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.; Zhang, Q.; Chen, Y.; Wang, Y.; Yu, Y.; Yang, Y.; Wang, T. Dominated Mode Switching and Nanoparticle Detection at Exceptional Points. J. Opt. Soc. Am. B 2023, 40, 108. [Google Scholar] [CrossRef]
- Li, J.; Tang, M.; Duan, J.; Xu, X.; Xu, K.; Ma, L.; Wang, J. Exceptional Points in a Spiral Ring Cavity for Enhanced Biosensing. J. Light. Technol. 2023, 41, 2870–2878. [Google Scholar] [CrossRef]
- Wang, C.; Sweeney, W.R.; Stone, A.D.; Yang, L. Coherent Perfect Absorption at an Exceptional Point. Science 2021, 373, 1261–1265. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Chen, N.; Lu, X.; Hu, Y.; Yang, Z.; Zhang, X.; Xu, J. Bandwidth Tunable Optical Bandpass Filter Based on Parity-Time Symmetry. Micromachines 2022, 13, 89. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Chen, N.; Zhang, B.; Yang, H.; Chen, Y.; Zhang, X.; Xu, J. Parity-Time Symmetry Enabled Band-Pass Filter Featuring High Bandwidth-Tunable Contrast Ratio. Photonics 2022, 9, 380. [Google Scholar] [CrossRef]
- Vahala, K. Optical Microcavities; Advanced Series in Applied Physics; World Scientific: Hackensack, NJ, USA; Singapore, 2007; ISBN 978-981-238-775-2. [Google Scholar]
- Yu, B.; Chen, Y.; Pan, J.; Zhang, B.; Li, F.; Wan, L.; Guo, X.; Li, J.; Li, Z. Silica-Microsphere-Cavity-Based Microwave Photonic Notch Filter with Ultra-Narrow Bandwidth and High Peak Rejection. Opt. Lett. 2019, 44, 1411. [Google Scholar] [CrossRef]
- Liu, L.; Liao, S. Si3 N4-Based Narrowband and High Peak Rejection Microwave Photonic Filter with Adjustable Bandwidth. J. Light. Technol. 2024, 42, 1580–1585. [Google Scholar] [CrossRef]
- Little, B.E.; Chu, S.T.; Absil, P.P.; Hryniewicz, J.V.; Johnson, F.G.; Seiferth, F.; Gill, D.; Van, V.; King, O.; Trakalo, M. Very High-Order Microring Resonator Filters for WDM Applications. IEEE Photon. Technol. Lett. 2004, 16, 2263–2265. [Google Scholar] [CrossRef]
- Popovíc, M.A.; Barwicz, T.; Watts, M.R.; Rakich, P.T.; Socci, L.; Ippen, E.P.; Kärtner, F.X.; Smith, H.I. Multistage High-Order Microring-Resonator Add-Drop Filters. Opt. Lett. 2006, 31, 2571. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Xu, H.; Tan, Y.; Shi, Y.; Dai, D. Silicon Photonic Filters. Micro Opt. Tech. Lett. 2021, 63, 2252–2268. [Google Scholar] [CrossRef]
- Shi, W.; Wang, X.; Zhang, W.; Yun, H.; Lin, C.; Chrostowski, L.; Jaeger, N.A.F. Grating-Coupled Silicon Microring Resonators. Appl. Phys. Lett. 2012, 100, 121118. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, C.; Liang, D.; Dai, D. Submicron-Resonator-Based Add-Drop Optical Filter with an Ultra-Large Free Spectral Range. Opt. Express 2019, 27, 416. [Google Scholar] [CrossRef] [PubMed]
- Ong, J.R.; Kumar, R.; Mookherjea, S. Ultra-High-Contrast and Tunable-Bandwidth Filter Using Cascaded High-Order Silicon Microring Filters. IEEE Photon. Technol. Lett. 2013, 25, 1543–1546. [Google Scholar] [CrossRef]
- Haus, H.A. Waves and Fields in Optoelectronics; Prentice-Hall Series in Solid State Physical Electronics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984; ISBN 978-0-13-946053-1. [Google Scholar]
- Little, B.E.; Chu, S.T.; Haus, H.A.; Foresi, J.; Laine, J.-P. Microring Resonator Channel Dropping Filters. J. Light. Technol. 1997, 15, 998–1005. [Google Scholar] [CrossRef]
- Yariv, A. Universal Relations for Coupling of Optical Power between Microresonators and Dielectric Waveguides. Electron. Lett. 2000, 36, 321–322. [Google Scholar] [CrossRef]
- Van, V. Optical Microring Resonators: Theory, Techniques, and Applications; CRC Press: Boca Raton, FL, USA, 2016; ISBN 978-1-315-30351-2. [Google Scholar]
- Zhu, K.; Zhou, X.; Zhang, Y.; Huang, Z.; Zhang, L. A New Exceptional Point Condition for Coupled Microresonators with Coupled Mode Theory in Space. arXiv 2024, arXiv:2410.17955. [Google Scholar]
- Vázquez-Córdova, S.A.; Dijkstra, M.; Bernhardi, E.H.; Ay, F.; Wörhoff, K.; Herek, J.L.; García-Blanco, S.M.; Pollnau, M. Erbium-Doped Spiral Amplifiers with 20 dB of Net Gain on Silicon. Opt. Express 2014, 22, 25993. [Google Scholar] [CrossRef] [PubMed]
- Rönn, J.; Zhang, W.; Autere, A.; Leroux, X.; Pakarinen, L.; Alonso-Ramos, C.; Säynätjoki, A.; Lipsanen, H.; Vivien, L.; Cassan, E.; et al. Ultra-High on-Chip Optical Gain in Erbium-Based Hybrid Slot Waveguides. Nat. Commun. 2019, 10, 432. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Qiu, Z.; Ji, X.; Lukashchuk, A.; He, J.; Riemensberger, J.; Hafermann, M.; Wang, R.N.; Liu, J.; Ronning, C.; et al. A Photonic Integrated Circuit–Based Erbium-Doped Amplifier. Science 2022, 376, 1309–1313. [Google Scholar] [CrossRef] [PubMed]
- Frankis, H.C.; Mbonde, H.M.; Bonneville, D.B.; Zhang, C.; Mateman, R.; Leinse, A.; Bradley, J.D.B. Erbium-Doped TeO2-Coated Si3 N4 Waveguide Amplifiers with 5 dB Net Gain. Photon. Res. 2020, 8, 127. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, X.; Zhang, L. Phase Regimes of Parity-Time-Symmetric Coupled-Ring Systems at Exceptional Points. Photon. Res. 2022, 10, 2374. [Google Scholar] [CrossRef]
- Yu, C.; Luo, T.; Zhang, L.; Willner, A.E. Data Pulse Distortion Induced by a Slow-Light Tunable Delay Line in Optical Fiber. Opt. Lett. 2007, 32, 20. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).