An Analysis and Optimization of Distortion Effect Caused by Pupil Decentering in Optical Gun Scope
Abstract
1. Introduction
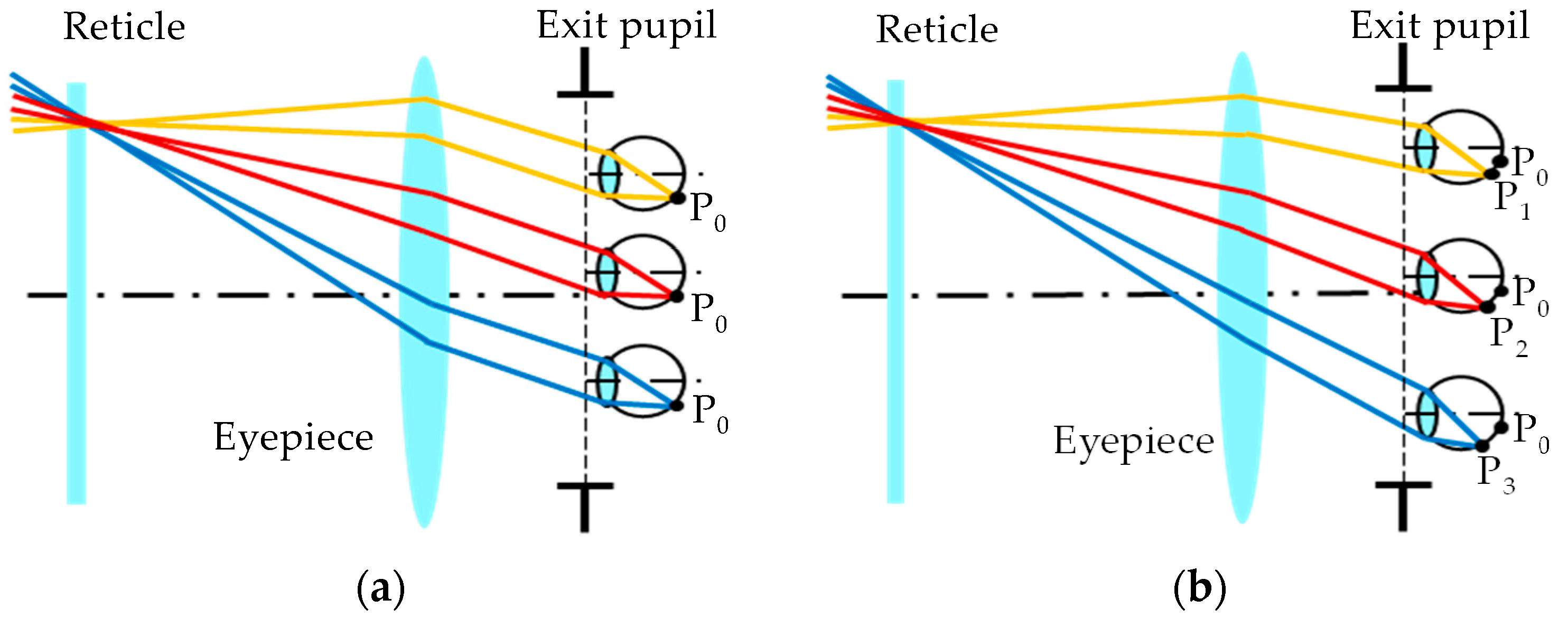
2. Analysis of Pupil-Decentering-Induced Distortion
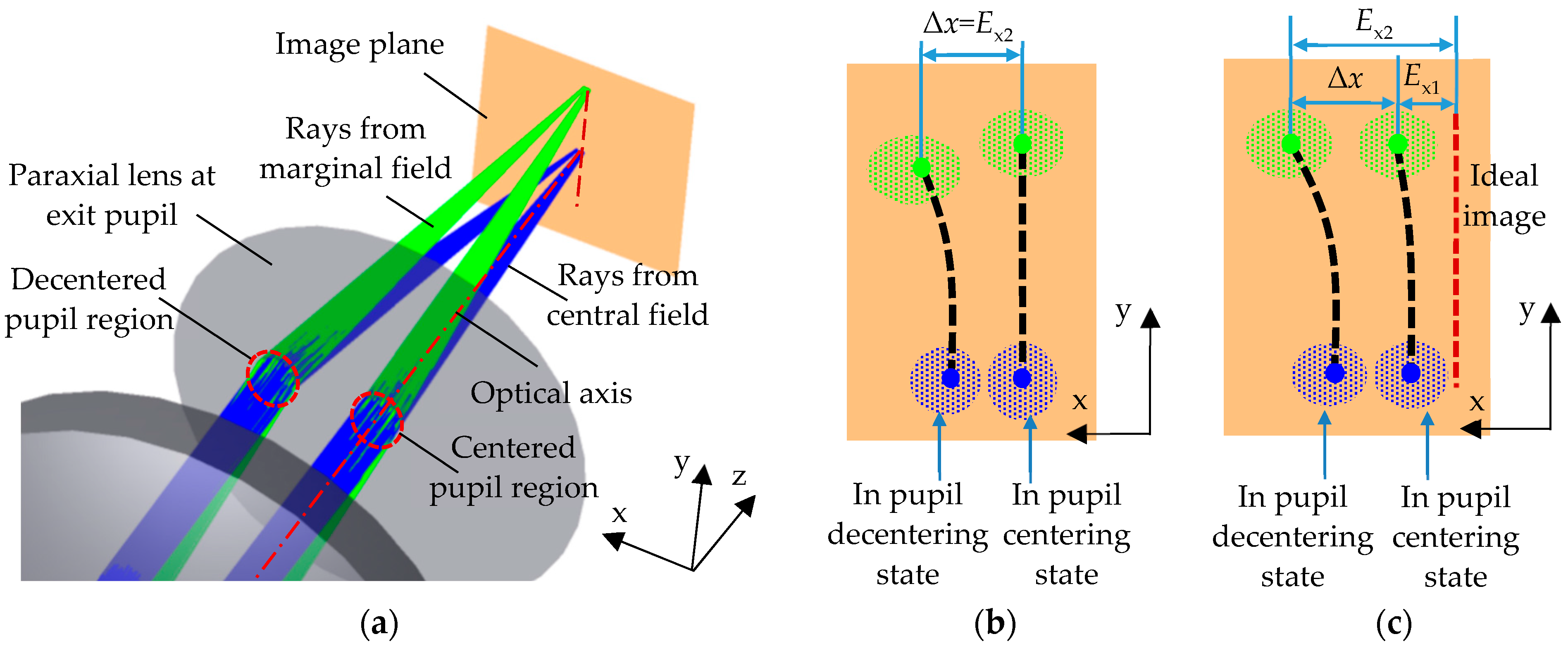
2.1. Mechanism Analysis
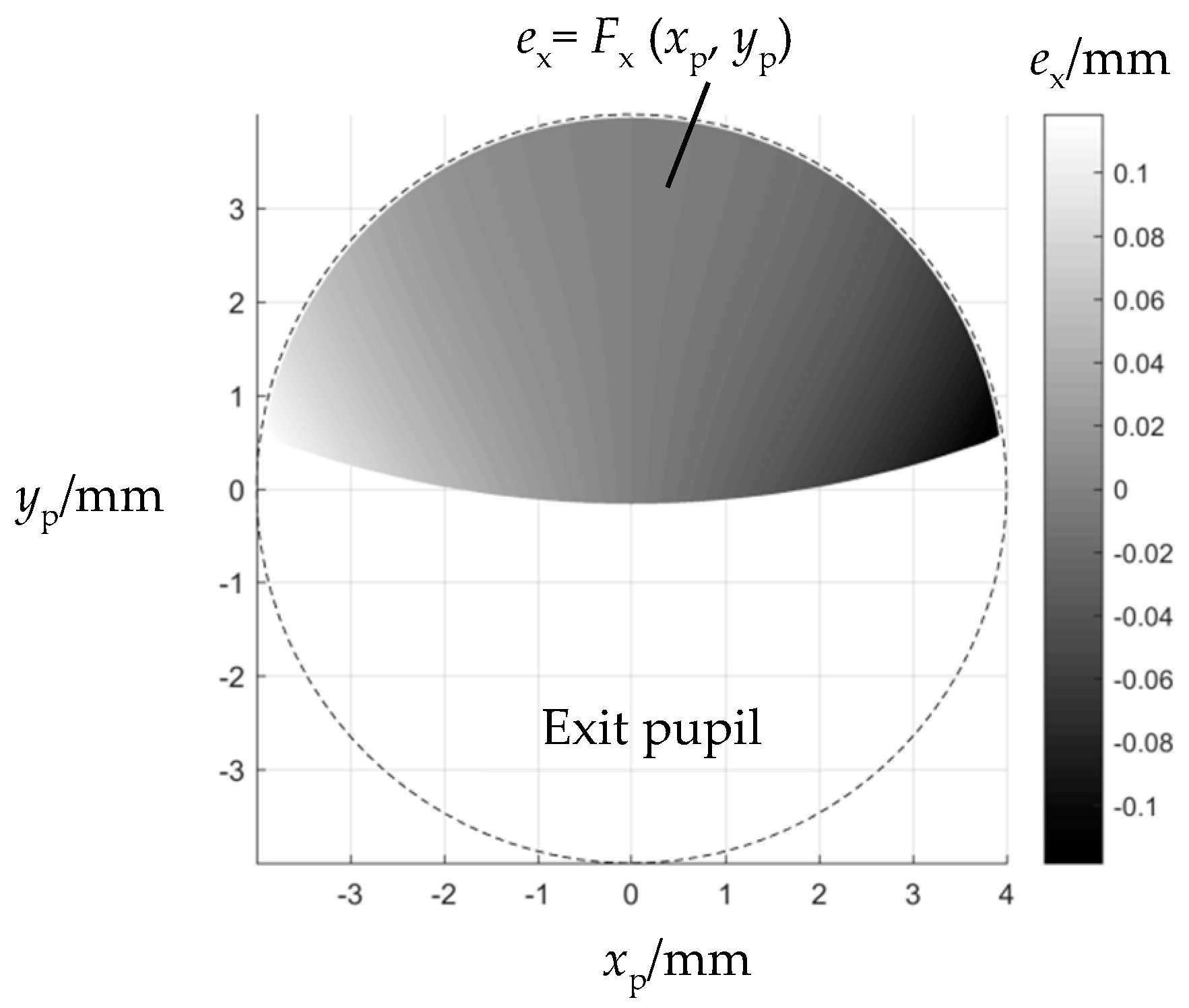
2.2. Distortion Evaluation
3. Distortion Reduction
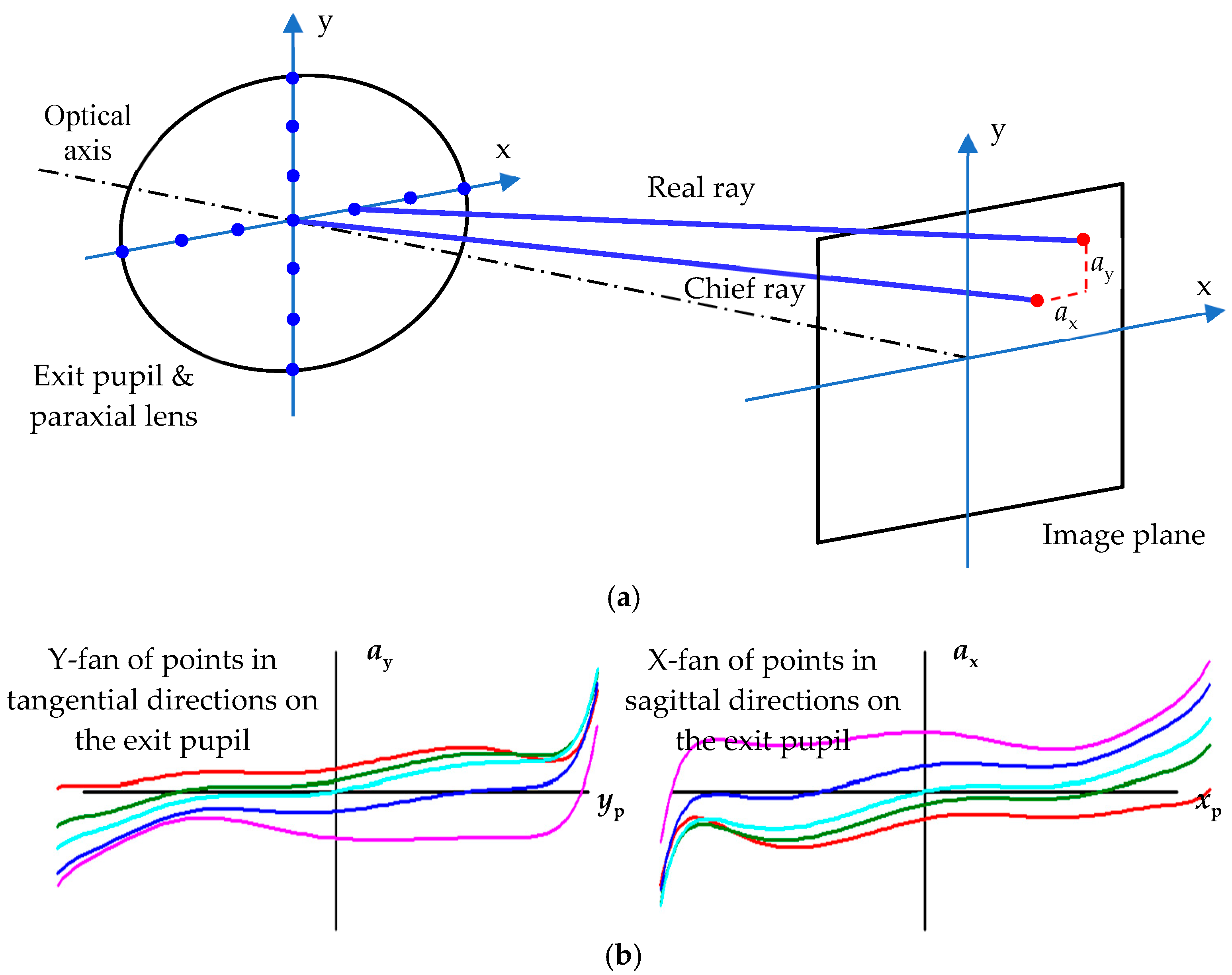
3.1. Optimization of Ray Aberration
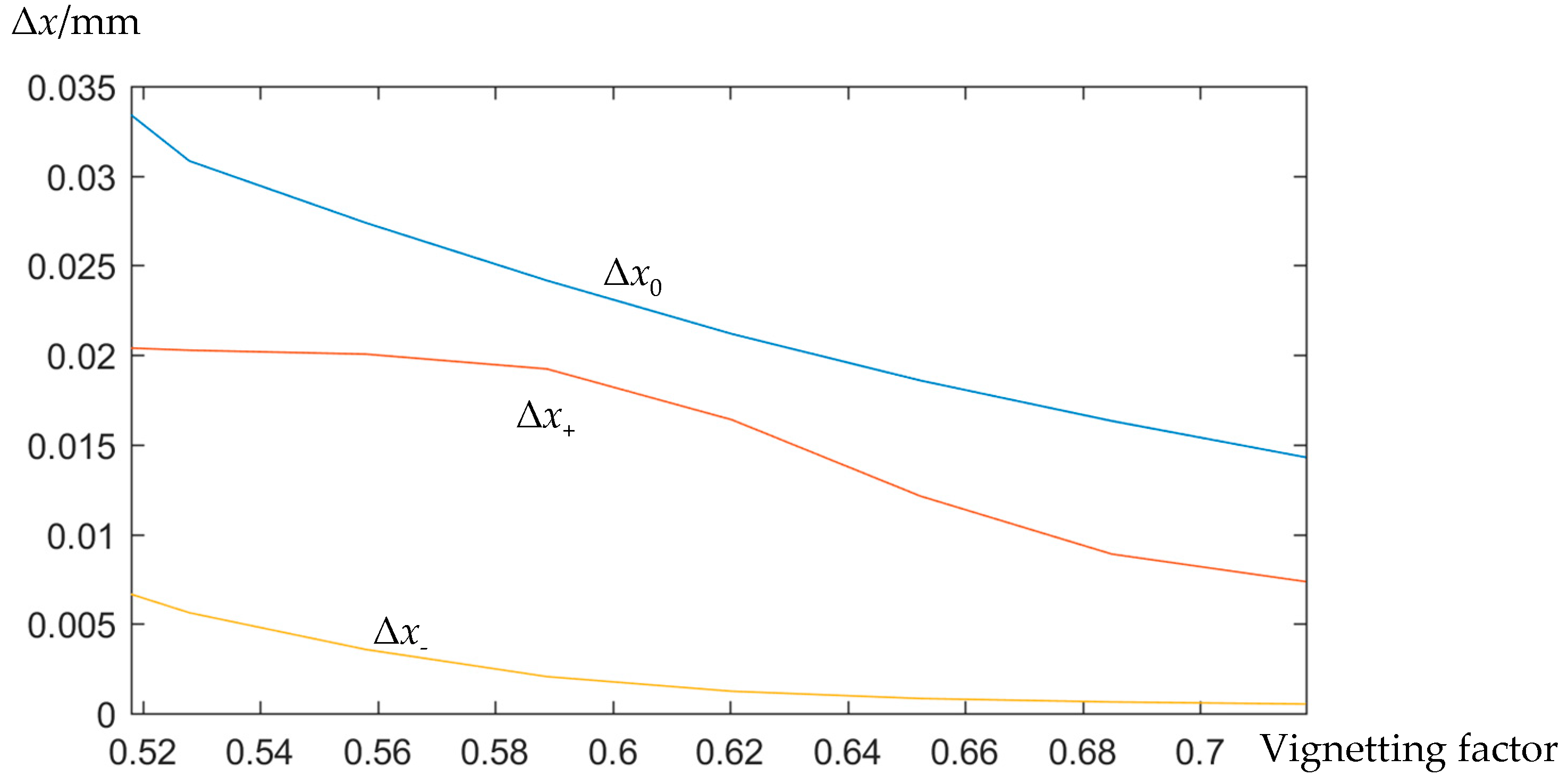
3.2. Optimization of the Value of Δx
3.3. Utilization of Vignetting
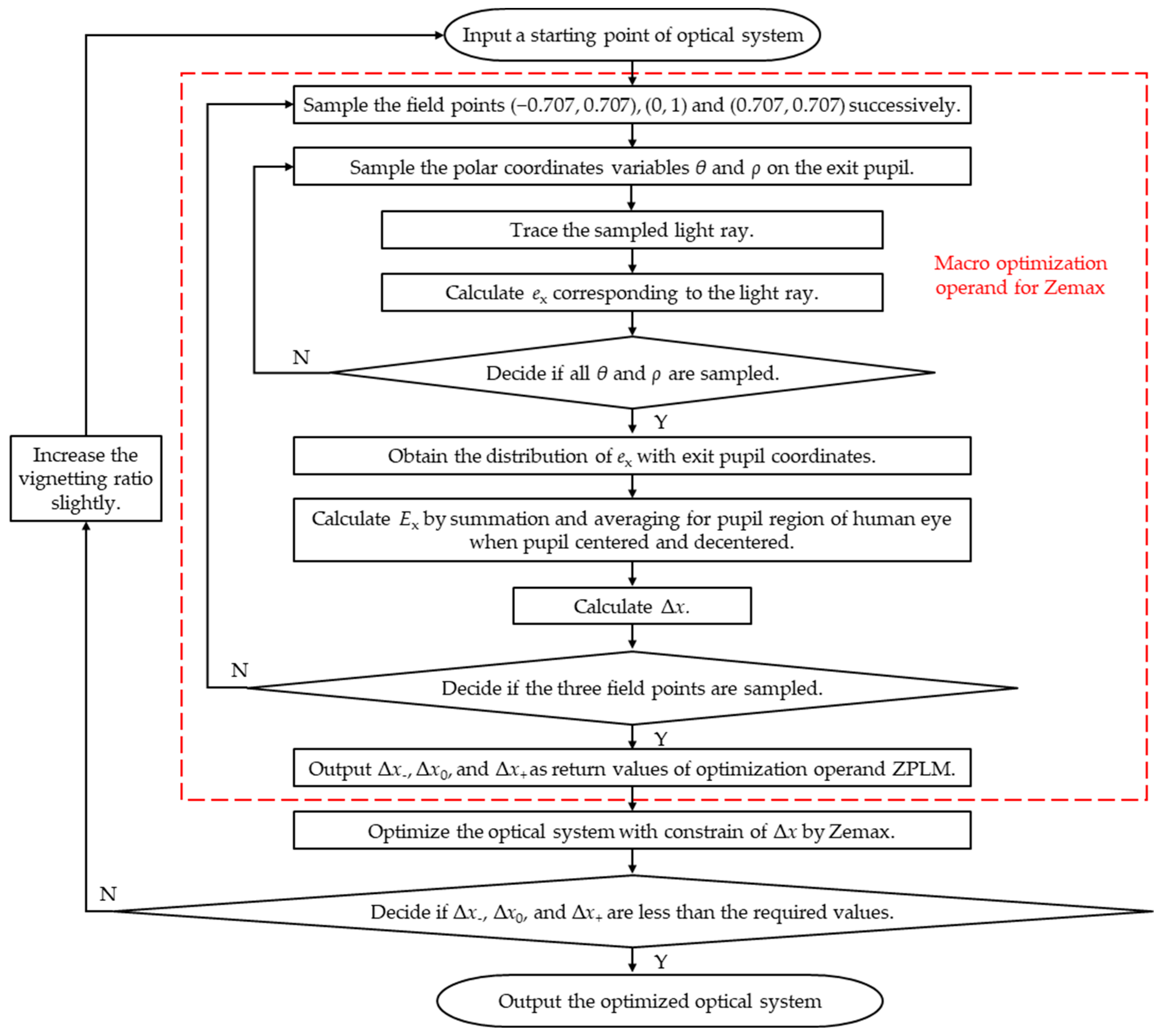
3.4. Basic Process for Optimizing the Distortion
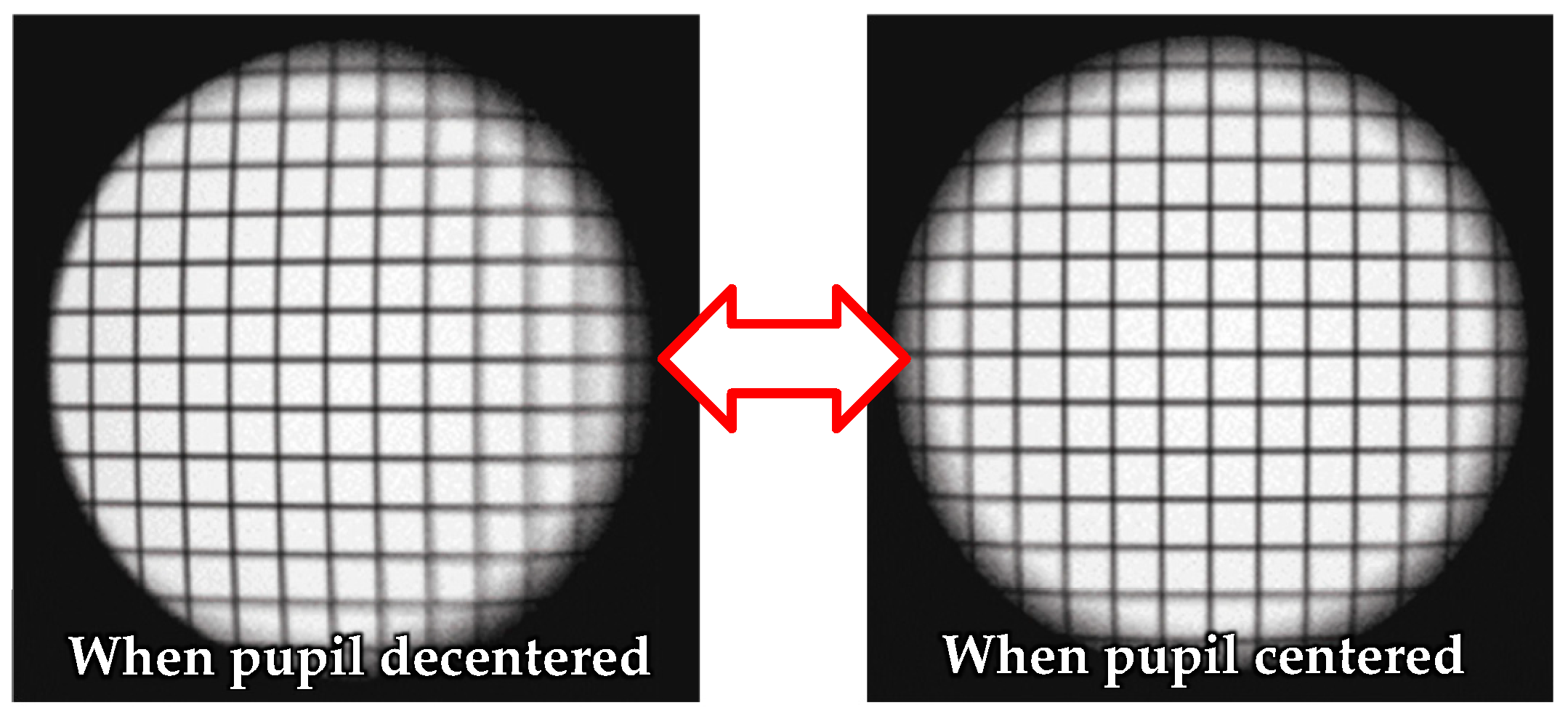
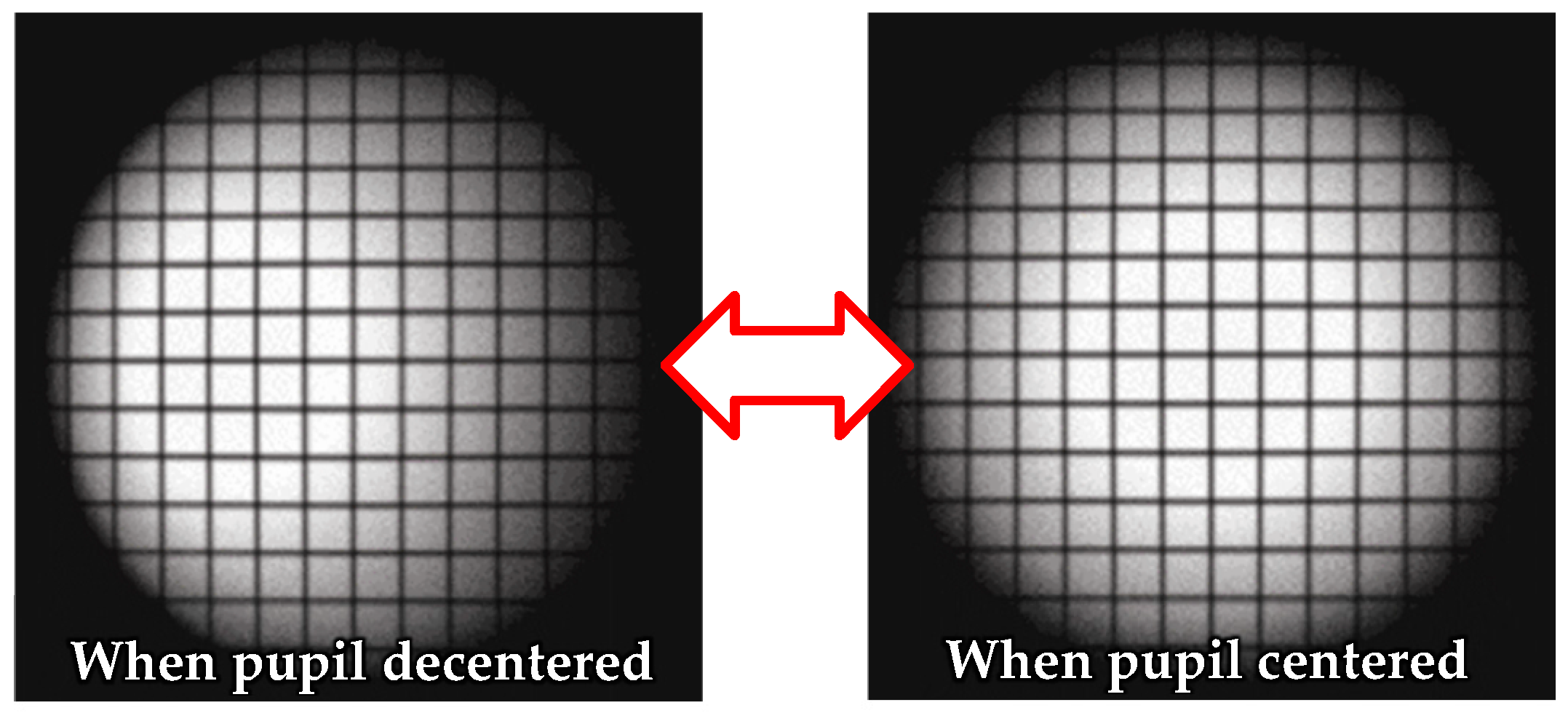
4. Practical Application of Optimization Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| f′ | Combined focal length of the gun scope and the human eye |
| xi | X-coordinate of the image spot |
| θx | Field angle of the object point |
| ax | X-directional transverse aberration with respect to the chief ray |
| ay | Y-directional transverse aberration with respect to the chief ray |
| ex | X-directional deviation between a real image spot and the ideal image point |
| xp | Ray’s x-coordinate on the exit pupil plane |
| yp | Ray’s y-coordinate on the exit pupil plane |
| Fx(xp, yp) | Function expression for the distribution of ex with xp and yp |
| D | Effective integration region of the human eye’s pupil for Fx (xp, yp) |
| Ex | X-directional deviation of the centroid of image spots |
| Ex1 | Ex in pupil centering state |
| Ex2 | Ex in pupil decentering state |
| Δx | Shift in the x-coordinate of the centroid of the image spots after and before pupil decentering |
| Δx− | Δx corresponding to an objebt point with normalized field coordinate of (−0.707, 0.707) |
| Δx0 | Δx corresponding to an objebt point with normalized field coordinate of (0, 1) |
| Δx+ | Δx corresponding to an objebt point with normalized field coordinate of (0.707, 0.707) |
| θ | Local angular coordinate of the sampled point on the exit pupil |
| ρ | Local radial coordinate of the sampled point on the exit pupil |
| M | Number of samples for θ |
| N | Number of samples for ρ |
| Me | Effective number of samples for θ |
| Ne | Effective number of samples forρ |
| m | Sampling sequence number of θ |
| n | Sampling sequence number of ρ |
| θm | The m’th θ |
| ρn | The n’th ρ |
| Δθ | Sampling intervals for θ |
| Δρ | Sampling intervals for ρ |
References
- Miks, A.; Novák, J. Method of paraxial design of rifle scope with four-element image-erecting zoom system and high zoom factor. Appl. Opt. 2019, 58, 4787–4796. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.; Chan, T.T.; Lian, T.; Rio, K. Local pupil swim in Virtual- and Augmented-Reality: Root cause and perception model. J. Soc. Inf. Disp. 2023, 31, 1021–1040. [Google Scholar] [CrossRef]
- Chi, J.; Liu, J.; Wang, F.; Chi, Y.; Hou, Z. 3-D Gaze-Estimation Method Using a Multi-Camera-Multi-Light-Source System. IEEE Trans. Instrum. Meas. 2020, 69, 9695–9708. [Google Scholar] [CrossRef]
- Kaufeld, M.; Mundt, M.; Forst, S.; Hecht, H. Optical see-through augmented reality can induce severe motion sickness. Displays 2022, 74, 102283. [Google Scholar] [CrossRef]
- Fischler, M.; Campbell, D.; Atac, R.; Melzer, J. Application of large head-box aircraft transparency distortion measurement and compensation for improved cueing in helmet-mounted displays. Opt. Eng. 2017, 56, 051403. [Google Scholar] [CrossRef]
- Jiang, W.; Li, G.; Ren, G.; Li, D. Influence of vibration on stabilization performance of vehicle-mounted sighting telescope. Appl. Mech. Mater. 2014, 687–691, 3836–3839. [Google Scholar] [CrossRef]
- Allain, G.; Thibault, S. Lens design distortion management using orthogonal polynomial functions. Opt. Eng. 2023, 62, 035108. [Google Scholar] [CrossRef]
- Siew, R. Relative illumination and image distortion. Opt. Eng. 2017, 56, 049701. [Google Scholar] [CrossRef]
- Thibault, S.; Parent, J.; Zhang, H.; Larivière-Bastien, M.; Poulin-Girard, A.; Arfaoui, A.; Desaulniers, P. Developments in modern panoramic lenses: Lens design, controlled distortion, and characterization. In Proceedings of the International Conference on Optical Instruments and Technology (OIT2011), Beijing, China, 6–9 November 2011. [Google Scholar]
- Flynn, R.A.; Beadie, G. Using GRIN to save 50% lens weight for an 8x rifle scope design. In Proceedings of the Advanced Optics for Defense Applications: UV through LWIR II, 101810A, Anaheim, CA, USA, 9–13 April 2017. [Google Scholar]
- Siew, R. Concept, design, and manufacture of a 3X rifle gun sight. Proc. SPIE 2004, 5249, 281–287. [Google Scholar]
- Vrbik, J. Geometrical optics from the ground up. Appl. Math. 2020, 11, 1021–1040. [Google Scholar] [CrossRef]
- Zhao, Y.; Fang, F. Dynamic opto-mechanical eye model with peripheral refractions. Opt. Express 2023, 31, 12097–12113. [Google Scholar] [CrossRef] [PubMed]
- Petelczyc, K.; Bara, S.; Lopez, A.; Jaroszewicz, Z.; Kakarenko, K.; Kolodziejczyk, A.; Sypek, M. Imaging properties of the light sword optical element used as a contact lens in a presbyopic eye model. Opt. Express 2011, 19, 25602–25616. [Google Scholar] [CrossRef] [PubMed]
- Bakaraju, R.; Ehrmann, K.; Falk, D.; Ho, A.; Papas, E. Physical human model eye and methods of its use to analyse optical performance of soft contact lenses. Opt. Express 2010, 18, 16868–16882. [Google Scholar] [CrossRef] [PubMed]
- Strojnik, M.; Bravo-Medina, B.; Martin, R.; Wang, Y. Ensquared energy and optical centroid efficiency in optical sensors: Part 1, Theory. Photonics 2023, 10, 254. [Google Scholar] [CrossRef]
- Synopsys. CODE V Optimization Reference Manual; Synopsys: Pasadena, CA, USA, 2017. [Google Scholar]
- Ansys Company. User Manual of Ansys Zemax OpticStudio; Ansys Company: Canonsburg, PA, USA, 2022. [Google Scholar]
- Forbes, G.; Ruoff, J. Rapid evaluation of vignetting-free high-performance systems. Opt. Eng. 2018, 57, 101709. [Google Scholar] [CrossRef]
- Duplov, R. Angle-dependent vignetting stop. Opt. Eng. 2022, 61, 065106. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, Q.; Chen, T. Vignetting correction for a single star-sky observation image. Appl. Opt. 2019, 58, 4337–4344. [Google Scholar] [CrossRef] [PubMed]
- Rosete-Aguilar, M.; Rayces, J. Eye rotation and vignetting in visual instruments. Appl. Opt. 2002, 41, 6593–6602. [Google Scholar] [CrossRef] [PubMed]





| Normalized Field | Ex2 (When Pupil Decentered) | Ex1 (When Pupil Centered) | Δx |
|---|---|---|---|
| (−0.707, 0.707) | 0.08006 | 0.10045 | Δx− = −0.02039 |
| (0, 1) | −0.03342 | 0.00000 | Δx0 = −0.03342 |
| (0.707, 0.707) | −0.10711 | −0.10045 | Δx+ = −0.00666 |
| Normalized Field | Ex2 (When Pupil Decentered) | Ex1 (When Pupil Centered) | Δx |
|---|---|---|---|
| (−0.707, 0.707) | 0.05279 | 0.04613 | Δx− = 0.00666 |
| (0, 1) | −0.00917 | 0.00000 | Δx0 = −0.00917 |
| (0.707, 0.707) | −0.03687 | −0.04613 | Δx+ = 0.00926 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Jin, N.; Yang, D.; Xu, M.; Dong, S. An Analysis and Optimization of Distortion Effect Caused by Pupil Decentering in Optical Gun Scope. Photonics 2024, 11, 995. https://doi.org/10.3390/photonics11110995
Yang K, Jin N, Yang D, Xu M, Dong S. An Analysis and Optimization of Distortion Effect Caused by Pupil Decentering in Optical Gun Scope. Photonics. 2024; 11(11):995. https://doi.org/10.3390/photonics11110995
Chicago/Turabian StyleYang, Kaiyu, Ning Jin, Dan Yang, Man Xu, and Shulin Dong. 2024. "An Analysis and Optimization of Distortion Effect Caused by Pupil Decentering in Optical Gun Scope" Photonics 11, no. 11: 995. https://doi.org/10.3390/photonics11110995
APA StyleYang, K., Jin, N., Yang, D., Xu, M., & Dong, S. (2024). An Analysis and Optimization of Distortion Effect Caused by Pupil Decentering in Optical Gun Scope. Photonics, 11(11), 995. https://doi.org/10.3390/photonics11110995





