Optical System Design of a Self-Calibrating Real Entrance Pupil Imaging Spectrometer
Abstract
1. Introduction
2. Principles
2.1. Working Principle of the Instrument
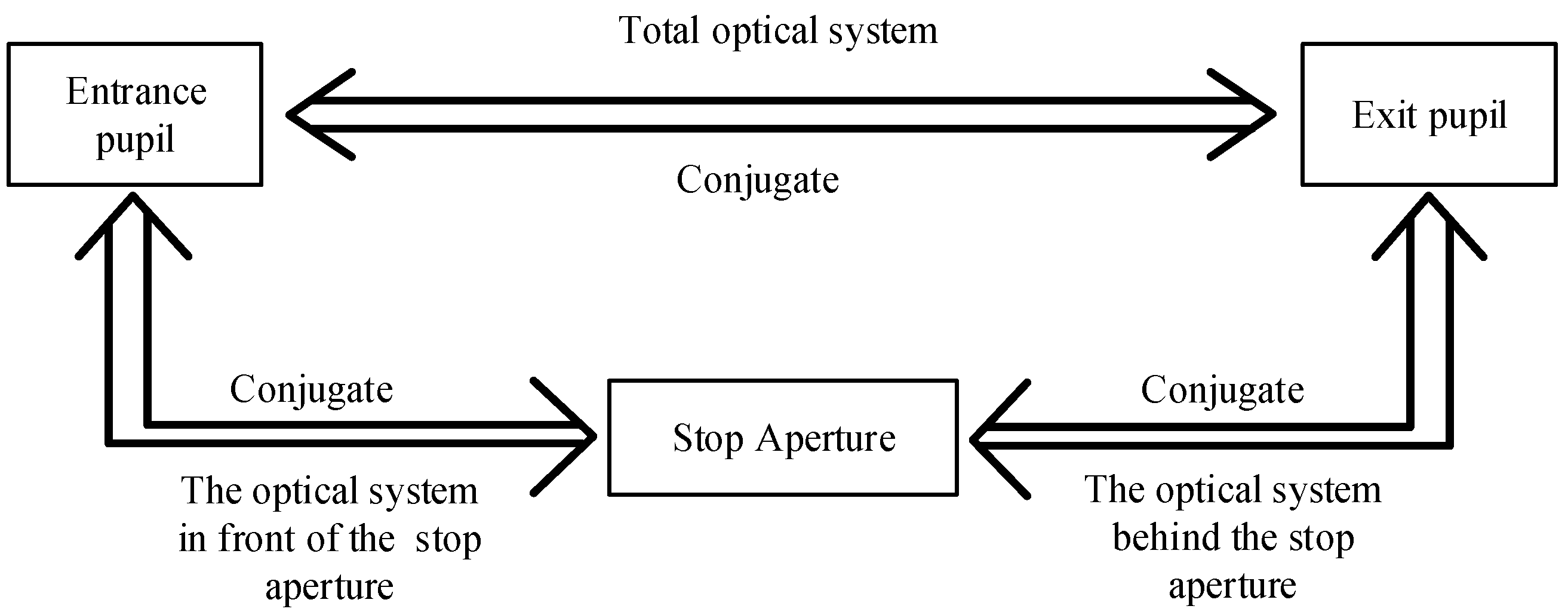
2.2. Principles of the Optical System Design
3. Optical System Design
3.1. Technical Indicators of the Instrument
3.2. Initial Structure Derivation
3.3. Front-End Optical System Design
4. Overall Design of the Optical Instrument
4.1. Posterior Optical System Design
4.2. Joint Optical Design
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.P.; Hu, X.Q.; Wang, H.R.; Ye, X.; Fang, W. Standard transfer chain for radiometric calibration of optical sensing instruments with traceability in solar reflective bands. Opt. Precis. Eng. 2015, 23, 1807–1812. [Google Scholar] [CrossRef]
- Lu, N.M.; Ding, L.; Zheng, X.B.; Ye, X.; Li, C.R.; Lu, D.R.; Zhang, P.; Hu, X.Q.; Zhou, C.H.; You, Z.; et al. Introduction of the radiometric benchmark satellite being developed in China for remote sensing. J. Remote Sens. 2020, 24, 672–680. (In Chinese) [Google Scholar] [CrossRef]
- Available online: https://sunclimate.gsfc.nasa.gov/mission/sorce (accessed on 12 April 2024).
- Xiong, X.; Angal, A.; Twedt, K.A.; Chen, H.; Link, D.; Geng, X.; Aldoretta, E.; Mu, Q. MODIS reflective solar bands on-orbit calibration and performance. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6355–6371. [Google Scholar] [CrossRef]
- Xiong, X.; Xie, X.; Angal, A.; Choi, J.; Sun, J.; Barnes, W.L. Characterization of MODIS solar diffuser on-orbit degradation. In Proceedings of the Optical Engineering + Applications, San Diego, CA, USA, 26–30 August 2007; Volume 6677, p. 66770O. [Google Scholar]
- Cui, Z.; Ma, C.; Zhang, H.; Hu, Y.; Yan, L.; Dou, C.; Li, X.-M. Vicarious Radiometric Calibration of the Multispectral Imager Onboard SDGSAT-1 over the Dunhuang Calibration Site, China. Remote Sens. 2023, 15, 2578. [Google Scholar] [CrossRef]
- Gross, G.; Helder, D.; Begeman, C.; Leigh, L.; Kaewmanee, M.; Shah, R. Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underfly Event. Remote Sens. 2022, 14, 2418. [Google Scholar] [CrossRef]
- Barnes, R.A. SeaWiFS Data: Actual and Simulated; World Wide Web Page; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1994. Available online: https://science.nasa.gov/mission/seawifs (accessed on 12 April 2024).
- Xu, W.; Zheng, X.; Yi, W. Cross-calibration method based on hyperspectral imager hyperion. Acta Opt. Sin. 2013, 33, 0528002. [Google Scholar]
- Raut, B.; Kaewmanee, M.; Angal, A.; Xiong, X.; Helder, D. Empirical absolute calibration model for multiple pseudo-invariant calibration sites. Remote Sens. 2019, 11, 1105. [Google Scholar] [CrossRef]
- Read, P.D.; Hardie, A.L.; Magraw, J.E.; Taylor, H.S.; Jelley, J.V. A calibration system, using an opal diffuser, for the visual channels of the Along Track Scanning Radiometer, ATSR-2. In Proceedings of the 10th IOP Symposium, London, UK, 2–6 September 1991; IOP Conference Series. Volume 121, pp. 207–213. [Google Scholar]
- Ahern, J.; Goodenough, D.G.; Jain, S.C.; Rao, U.P. Use of clear lakes as standard reflectors for Atmospheric measurements. In Proceedings of the Eleventh International Symposium, on Remote Sensing of Environment, Ann Arbor, MI, USA, 25–29 April 1977; Volume 11, pp. 731–755. [Google Scholar]
- Li, Y.; Rong, Z.; Zheng, Z. Post launch site calibration of the visible and near-infrared channels of FY-3A visible and infrared radiometer. Opt. Precis. Eng. 2009, 17, 2966–2974. (In Chinese) [Google Scholar]
- Pilewskie, P.; Viereck, R.; Kopp, G.; Harder, J.; Woods, T. NPOESS TSIS: Measuring Solar Irradiance; PolarMax: Southern Pines, NC, USA, 2005. [Google Scholar]
- Thompson, P.L.; Hill, P.C. Conceptual optical design and system engineering of the clarreo/rs (reflected solar) instrument suite. In Imaging Spectrometry XVII; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; Volume 8515, p. 85150N. [Google Scholar]
- Available online: https://clarreo-pathfinder.larc.nasa.gov/ (accessed on 5 May 2024).
- Thome, K.; McCorkel, J.; Hair, J.; McAndrew, B.; Daw, A.; Jennings, D.; Rabin, D. Test plan for a calibration demonstration system for the reflected solar instrument for the climate absolute radiance and refractivity observatory. In Remote Sensing System Engineering IV; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; Volume 8516, p. 851602. [Google Scholar]
- Ge, M.F. Hyperspectrcal Imagery Remote Sensing Technology Based on Lightweight Unmanned Aerial Vehicle. Ph.D. Thesis, Shanghai Institute of Technical Physics, Chinese Academy of Science, Shanghai, China, 2015. (In Chinese). [Google Scholar]
- Yuan, L.; He, Z.; Lv, G.; Wang, Y.; Li, C.; Xie, J.; Wang, L. Optical design, laboratory test, and calibration of airborne long wave infrared imaging spectrometer. Opt. Express 2017, 25, 22440–22454. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Zhao, Z.; Liu, Q.; Chen, X.; Li, H.; Tang, S.; Shen, W. Geostationary Full-Spectrum Wide-Swath High-Fidelity Imaging Spectrometer: Optical Design and Prototype Development. Remote Sens. 2023, 15, 396. [Google Scholar] [CrossRef]
- Pan, Q.; Chen, X.; Zhou, J.; Liu, Q.; Zhao, Z.; Shen, W. Manufacture of the Compact Conical Diffraction Offner Hyperspectral Imaging Spectrometer. Appl. Opt. 2019, 58, 7298–7304. [Google Scholar] [CrossRef] [PubMed]
- Fowler, J.B.; Saunders, R.D.; Parr, A.C. Summary of the high-accuracy aperture-area measurement capabilities at the NIST. Metrologia 2000, 37, 621–623. [Google Scholar] [CrossRef]
- Chrisp, M.P.; Lockwood, R.B.; Smith, M.A.; Balonek, G.; Holtsberg, C.; Thome, K.J.; Murray, K.E.; Ghuman, P. Development of a Compact Imaging Spectrometer Form for the Solar Reflective Spectral Region. Appl. Opt. 2020, 59, 10007. [Google Scholar] [CrossRef] [PubMed]
- Cook, L.G.; Silny, J.F. Imaging spectrometer trade studies: A detailed comparison of the Offner-Chrisp and reflective triplet optical design forms. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 1–5 August 2010; Volume 7813, p. 78130F. [Google Scholar]
- Liu, Y.N.; Sun, D.X.; Hu, X.N.; Ye, X.; Li, Y.D.; Liu, S.F.; Cao, K.Q.; Chai, M.Y.; Zhou, W.Y.N.; Zhang, J.; et al. The Advanced Hyperspectral Imager: Aboard China’s GaoFen-5 Satellite. IEEE Geosci. Remote Sens. Mag. 2019, 7, 23–32. [Google Scholar] [CrossRef]
- Committee on Earth Science and Applications from Space: A Community Assessment and Strategy for the Future. In Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond; National Research Council: Rockville, MD, USA, 2007; ISBN 0-309-66714-3.
- Mouroulis, P.; Sellar, R.G.; Wilson, D.W.; Shea, J.J.; Green, R.O. Optical design of a compact imaging spectrometer for planetary mineralogy. Opt. Eng. 2007, 46, 063001. [Google Scholar] [CrossRef]
- Espejo, J.; Drake, G.; Heuerman, K.; Kopp, G.; Lieber, A.; Smith, P.; Vermeer, B. A hyperspectral imager for high radiometric accuracy Earth climate studies. In Imaging Spectrometry XVI; SPIE: Bellingham, WA, USA, 2011; Volume 8158, p. 81580B. [Google Scholar] [CrossRef]
- Li, H.; Xiang, Y. Design of 10°FOV telecentric off-Axis three-mirror anastigmatic telescope. Acta Photonica Sin. 2009, 38, 2256–2259. [Google Scholar]
- Liu, X.; Xiang, Y. Research and Design of Telecentric Off-Axis Three-Mirror System with Real Entrance pupil. Acta Opt. Sin. 2011, 31, 261–264. [Google Scholar]
- Cook, L.G. Compact All-Reflective Imaging Spectrometer. U.S. Patent 5,260,767, 9 November 1993. [Google Scholar]
- Cook, L.G. High-Resolution, All-Reflective Imaging Spectrometer. U.S. Patent 7,080,912, 25 July 2006. [Google Scholar]
- Cook, L.G. Reflective Optical Triplet Having a Real Entrance Pupil. U.S. Patent 4,733,955, 29 March 1988. [Google Scholar]
- Xie, Y.; Liu, C.; Liu, S.; Xu, M.; Fan, X.; Rao, Q. Optical design of a cooled mid-wave infrared off-axis three-mirror system with a low F-number and wide field of view. Appl. Opt. 2022, 61, 1652–1659. [Google Scholar] [CrossRef] [PubMed]
- Cao, D.; Bridges, F.; Kowach, G.R.; Ramirez, A.P. Correlated Atomic Motions in the Negative Thermal Expansion Material ZrW2O8: A Local Structure Study. Phys. Rev. B 2003, 68, 014303. [Google Scholar] [CrossRef]
- Smartt, R.N.; Strong, J. Point-diffraction interferometer. Opt. Soc. Am. 1974, 62, 737–742. [Google Scholar]











| Parameters | ||||||
|---|---|---|---|---|---|---|
| Radius | Diameter | Distance | Conic | Tilt About X | Y Decenter | |
| Primary mirror | −106.736 mm | 26.6 mm | −25.912 mm | −2.394 | −18.505° | −12.379 mm |
| Secondary mirror | −37.050 mm | 9 mm | 19.124 mm | −1.733 | −11.580° | −23.593 mm |
| Tertiary mirror | −69.432 mm | 15.7 mm | −47.663 mm | −1.294 | −4.952° | −29.242 mm |
| The Name of the Parameter | Object Space | Image Space |
|---|---|---|
| Focal Length | −92.918735 | 92.918735 |
| Focal Planes | 50.337575 | −386.768950 |
| Name | Parameters | ||
|---|---|---|---|
| Radius | Diameter | Tilt About X | |
| Convex grating | −50 mm | 15 mm | 0.36° |
| Concave mirrors | −99.14 mm | 78 mm | 2.36° |
| Position of the Aperture Stop | Pupil Type | Field of View | F-Number | Focal Length | Pupil Diameter |
|---|---|---|---|---|---|
| On the secondary mirror | Virtual pupil | 7° | 3.7 | 92.3 mm | 25 mm |
| In front of the primary mirror | Real entry pupil | 7° | 3.7 | 92.9 mm | 25 mm |
| Variable Diaphragm Diameter | Aperture Stop in Front of the Primary Mirror | Aperture Stop on the Secondary Mirror | ||||||
|---|---|---|---|---|---|---|---|---|
| 0° | ±1.5° | ±2.5° | ±3.5° | 0° | ±1.5° | ±2.5° | ±3.5° | |
| 25 mm | 25 W | 25 W | 25 W | 25 W | 25 W | 25 W | 23 W | 20 W |
| 20 mm | 16 W | 16 W | 16 W | 16 W | 16 W | 16 W | 16 W | 15 W |
| 10 mm | 4 W | 4 W | 4 W | 4 W | 4 W | 4 W | 4 W | 4 W |
| 5 mm | 1 W | 1 W | 1 W | 1 W | 1 W | 1 W | 1 W | 1 W |
| 1 mm | 0.04 W | 0.04 W | 0.04 W | 0.04 W | 0.04 W | 0.04 W | 0.04 W | 0.04 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, X.; Zhang, Q.; Shi, Y.; Wei, W.; Liu, E. Optical System Design of a Self-Calibrating Real Entrance Pupil Imaging Spectrometer. Photonics 2024, 11, 1072. https://doi.org/10.3390/photonics11111072
Wang X, Li X, Zhang Q, Shi Y, Wei W, Liu E. Optical System Design of a Self-Calibrating Real Entrance Pupil Imaging Spectrometer. Photonics. 2024; 11(11):1072. https://doi.org/10.3390/photonics11111072
Chicago/Turabian StyleWang, Xinrui, Xin Li, Quan Zhang, Yuanjian Shi, Wei Wei, and Enchao Liu. 2024. "Optical System Design of a Self-Calibrating Real Entrance Pupil Imaging Spectrometer" Photonics 11, no. 11: 1072. https://doi.org/10.3390/photonics11111072
APA StyleWang, X., Li, X., Zhang, Q., Shi, Y., Wei, W., & Liu, E. (2024). Optical System Design of a Self-Calibrating Real Entrance Pupil Imaging Spectrometer. Photonics, 11(11), 1072. https://doi.org/10.3390/photonics11111072





