Single-Shot, Monochrome, Spatial Pixel-Encoded, Structured Light System for Determining Surface Orientations
Abstract
1. Introduction
2. Materials and Methods
2.1. Designing of a Pattern
2.1.1. Defining Symbols
2.1.2. Robust Pseudo-Random Sequences or M-Arrays
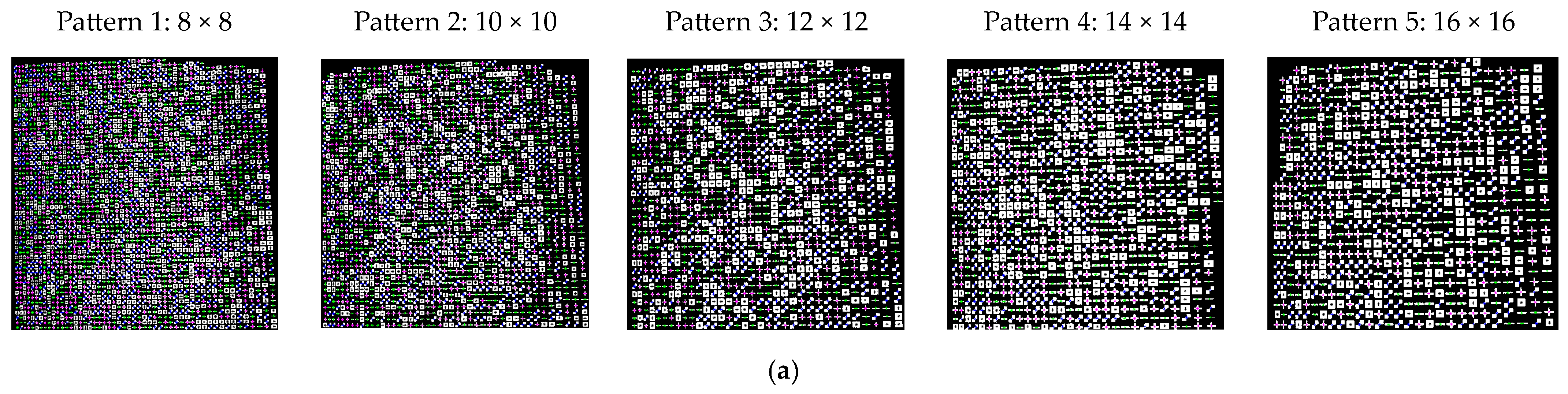
2.1.3. Formation of a Projection Pattern
2.2. Computation of Surface Normals
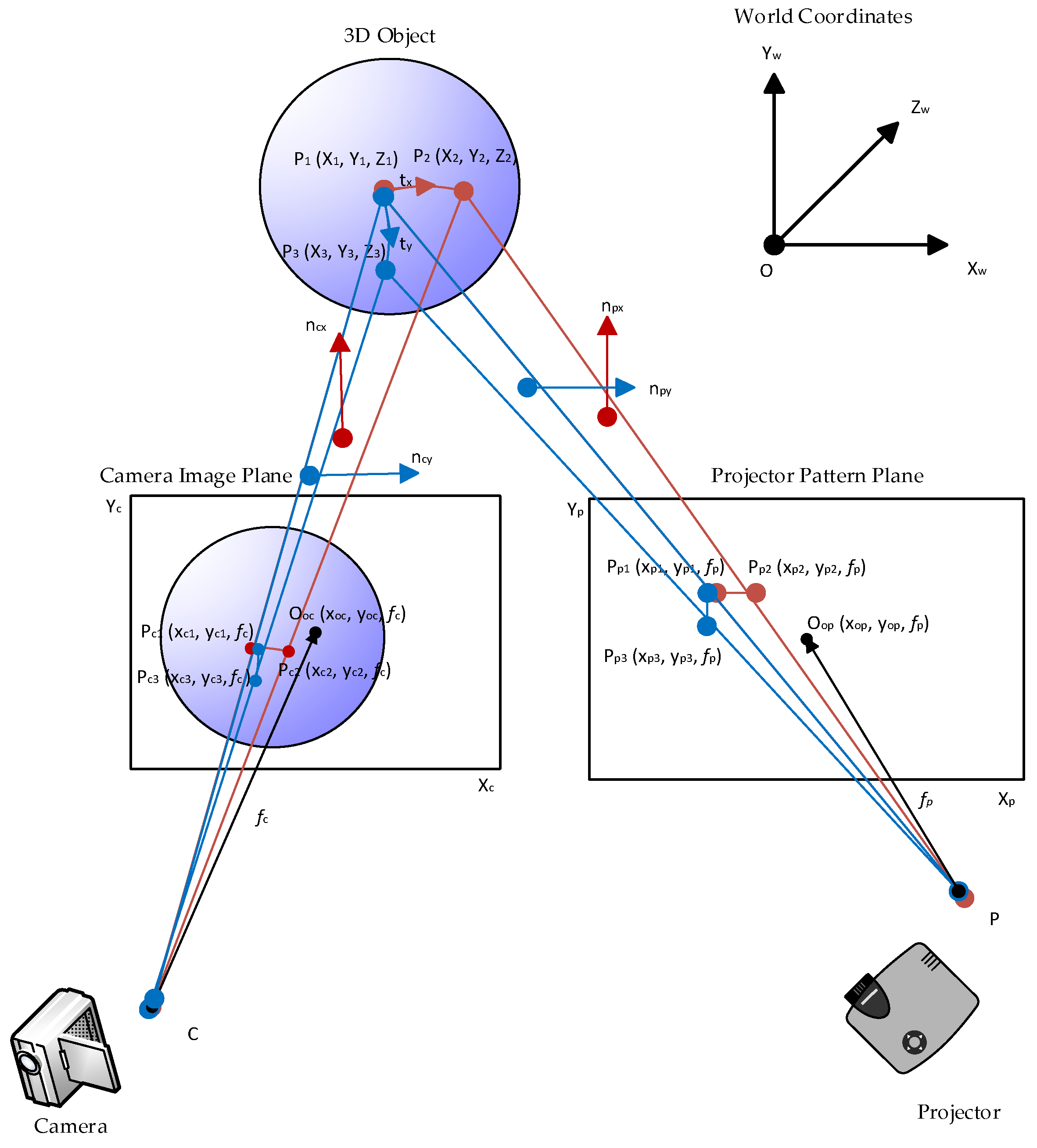
2.2.1. Defining of Points Geometry
2.2.2. Defining Device Parameters, Projection, and Image Planes
2.2.3. Defining Light Planes and Their Normals
2.2.4. Underlying Principle
Computation of Light Planes Normals to the Projector Side
Computation of Light Plane Normals to the Camera Side
Computation of Surface Tangents
2.3. Computation of 3D World Coordinates [43,44,45,46]
2.4. Decoding of Patterns
2.4.1. Preprocessing, Segmentation, and Labeling
2.4.2. Decoding, Classification, and Computation of Parameters
2.4.3. Calibration
2.5. Experiment and Devices
2.5.1. Camera and Projector Devices
2.5.2. Target Surfaces
2.5.3. Experiment Setup
Pattern Employed in the Experiment
3. Results
3.1. Comparison of Measured Resolution
3.2. Classification or Decoding of Symbols or Feature Points in a Pattern
3.3. Point Clouds and Surface Normals of the Measured Objects
3.4. Time Durations of the Different Processes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A State of the Art in Structured Light Patterns for Surface Profilometry. Pattern Recognit. 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Zhang, S. High-Speed 3D Shape Measurement with Structured Light Methods: A Review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Webster, J.G.; Bell, T.; Li, B.; Zhang, S. Structured Light Techniques and Applications; Wiley: Hoboken, NJ, USA, 2016; pp. 1–24. [Google Scholar]
- Geng, J. Structured-Light 3D Surface Imaging: A Tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Salvi, J.; Pagès, J.; Batlle, J. Pattern Codification Strategies in Structured Light Systems. Pattern Recognit. 2004, 37, 827–849. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Hall-Holt, O.; Levoy, M. Real-Time 3D Model Acquisition. ACM Trans. Graph. 2002, 21, 438–446. [Google Scholar] [CrossRef]
- Nguyen, H.; Wang, Y.; Wang, Z. Single-Shot 3D Shape Reconstruction Using Structured Light and Deep Convolutional Neural Networks. Sensors 2020, 20, 3718. [Google Scholar] [CrossRef]
- Ahsan, E.; QiDan, Z.; Jun, L.; Yong, L.; Muhammad, B. Grid-Indexed Based Three-Dimensional Profilometry. In Coded Optical Imaging; Liang, D.J., Ed.; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Wang, Z. A Tutorial on Single-Shot 3D Surface Imaging Techniques. IEEE Signal Process. Magzine 2024, 41, 71–92. [Google Scholar] [CrossRef]
- Pagès, J.; Salvi, J.; Collewet, C.; Forest, J. Optimised de Bruijn Patterns for One-Shot Shape Acquisition. Image Vis. Comput. 2005, 23, 707–720. [Google Scholar] [CrossRef]
- Petriu, E.M.; Sakr, Z.; Spoelder, H.J.W.; Moica, A. Object Recognition Using Pseudo-Random Color Encoded Structured Light. In Proceedings of the 17th IEEE Instrumentation and Measurement Technology Conference, Baltimore, MD, USA, 1–4 May 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 1237–1241. [Google Scholar]
- Albitar, C.; Graebling, P.; Doignon, C. Robust Structured Light Coding for 3D Reconstruction. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio De Janeiro, Brazil, 14–21 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–6. [Google Scholar]
- Morano, R.A.; Ozturk, C.; Conn, R.; Dubin, S.; Zietz, S.; Nissanov, J. Structured Light Using Pseudorandom Codes. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 322–327. [Google Scholar] [CrossRef]
- Elahi, A.; Lu, J.; Zhu, Q.D.; Yong, L. A Single-Shot, Pixel Encoded 3D Measurement Technique for Structure Light. IEEE Access 2020, 8, 127254–127271. [Google Scholar] [CrossRef]
- Lu, J.; Han, J.; Ahsan, E.; Xia, G.; Xu, Q. A Structured Light Vision Measurement with Large Size M-Array for Dynamic Scenes. In Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3834–3839. [Google Scholar]
- Zhou, X.; Zhou, C.; Kang, Y.; Zhang, T.; Mou, X. Pattern Encoding of Robust M-Array Driven by Texture Constraints. IEEE Trans. Instrum. Meas. 2023, 72, 5014816. [Google Scholar] [CrossRef]
- Maruyama, M.; Abe, S. Range Sensing by Projecting Multiple Slits with Random Cuts. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 647–651. [Google Scholar] [CrossRef]
- Ito, M.; Ishii, A. A Three-Level Checkerboard Pattern (TCP) Projection Method for Curved Surface Measurement. Pattern Recognit. 1995, 28, 27–40. [Google Scholar] [CrossRef]
- Yin, W.; Hu, Y.; Feng, S.; Huang, L.; Kemao, Q.; Chen, Q.; Zuo, C. Single-Shot 3D Shape Measurement Using an End-to-End Stereo Matching Network for Speckle Projection Profilometry. Opt. Express 2021, 29, 13388. [Google Scholar] [CrossRef]
- Woodham, R.J. Photometric Method For Determining Surface Orientation From Multiple Images. Opt. Eng. 1980, 19, 139–144. [Google Scholar] [CrossRef]
- Knill, D.C. Surface Orientation from Texture: Ideal Observers, Generic Observers and the Information Content of Texture Cues. Vision Res. 1998, 38, 1655–1682. [Google Scholar] [CrossRef]
- Garding, J. Direct Estimation of Shape from Texture. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 1202–1208. [Google Scholar] [CrossRef]
- Zhang, R.; Tsai, P.-S.; Cryer, J.E.; Shah, M. Shape-from-Shading: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 690–706. [Google Scholar] [CrossRef]
- Adato, Y.; Vasilyev, Y.; Zickler, T.; Ben-Shahar, O. Shape from Specular Flow. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2054–2070. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, F.; Gui, L.; Wu, L.; Lang, L. Polarization-Based Method for Object Surface Orientation Information in Passive Millimeter-Wave Imaging. IEEE Photonics J. 2016, 8, 5500112. [Google Scholar] [CrossRef]
- Lu, J.; Guo, C.; Fang, Y.; Xia, G.; Wang, W.; Elahi, A. Fast Point Cloud Registration Algorithm Using Multiscale Angle Features. J. Electron. Imaging 2017, 26, 033019. [Google Scholar] [CrossRef]
- Nehab, D.; Rusinkiewicz, S.; Davis, J.; Ramamoorthi, R. Efficiently Combining Positions and Normals for Precise 3D Geometry. ACM Trans. Graph. 2005, 24, 536–543. [Google Scholar] [CrossRef]
- Fan, R.; Wang, H.; Cai, P.; Liu, M. SNE-RoadSeg: Incorporating Surface Normal Information into Semantic Segmentation for Accurate Freespace Detection. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Vedaldi, A., Bischof, H., Brox, T., Frahm, J., Eds.; Springer: Cham, Switzerland, 2020; Volume 12375 LNCS, pp. 340–356. ISBN 9783030585761. [Google Scholar]
- Grilli, E.; Menna, F.; Remondino, F. A Review of Point Clouds Segmentation and Classification Algorithms. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 339–344. [Google Scholar] [CrossRef]
- Campbell, R.J.; Flynn, P.J. A Survey of Free-Form Object Representation and Recognition Techniques. Comput. Vis. Image Underst. 2001, 81, 166–210. [Google Scholar] [CrossRef]
- Pomerleau, F.; Colas, F.; Siegwart, R. A Review of Point Cloud Registration Algorithms for Mobile Robotics. Found. Trends® Robot. 2015, 4, 1–104. [Google Scholar] [CrossRef]
- Badino, H.; Huber, D.; Park, Y.; Kanade, T. Fast and Accurate Computation of Surface Normals from Range Images. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3084–3091. [Google Scholar]
- Wang, Y.F.; Mitiche, A.; Aggarwal, J.K. Computation of Surface Orientation and Structure of Objects Using Grid Coding. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-9, 129–137. [Google Scholar] [CrossRef]
- Hu, G.; Stockman, G. 3-D Surface Solution Using Structured Light and Constraint Propagation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 390–402. [Google Scholar] [CrossRef]
- Shrikhande, N.; Stockman, G. Surface Orientation from a Projected Grid. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 650–655. [Google Scholar] [CrossRef]
- Asada, M.; Ichikawa, H.; Tsuji, S. Determining Surface Orientation by Projecting a Stripe Pattern. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 2–7. [Google Scholar] [CrossRef]
- Davies, C.J.; Nixon, M.S. A Hough Transform for Detecting the Location and Orientation of Three-Dimensional Surfaces Via Color Encoded Spots. IEEE Trans. Syst. man Cybern. B Cybern. 1998, 28, 90–95. [Google Scholar] [CrossRef]
- Winkelbach, S.; Wahl, F.M. Shape from 2D Edge Gradients. In Lecture Notes in Computer Science, Proceedings of the 23rd DAGM Symposium, Munich, Germany, 12–14 September 2001; Radig, B., Florczyk, S., Eds.; Springer: Berlin, Germany, 2001; pp. 377–384. [Google Scholar]
- Winkelbach, S.; Wahl, F.M. Shape from Single Stripe Pattern Illumination. In Lecture Notes in Computer Science, Proceedings of the 24th DAGM Symposium, Zurich, Switzerland, 16–18 September 2002; Goo, L., Van, L., Eds.; Springer: Berlin, Germany, 2002; pp. 240–247. [Google Scholar]
- Song, Z.; Chung, R. Determining Both Surface Position and Orientation in Structured-Light-Based Sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1770–1780. [Google Scholar] [CrossRef] [PubMed]
- Shi, G.; Li, R.; Li, F.; Niu, Y.; Yang, L. Depth Sensing with Coding-Free Pattern Based on Topological Constraint. J. Vis. Commun. Image Represent. 2018, 55, 229–242. [Google Scholar] [CrossRef]
- Elahi, A.; Zhu, Q.; Lu, J.; Hammad, Z.; Bilal, M.; Li, Y. Single-Shot, Pixel-Encoded Strip Patterns for High-Resolution 3D Measurement. Photonics 2023, 10, 1212. [Google Scholar] [CrossRef]
- Savarese, S. Lecture 2: Camera Models; Stanford University: Stanford, CA, USA, 2015; p. 18. [Google Scholar]
- Hata, K.; Savarese, S. CS231A Course Notes 1 Camera Models; Stanford University: Stanford, CA, USA, 2015; p. 16. [Google Scholar]
- Collins, R. CSE486, Penn State Lecture 12: Camera Projection; Penn State University: University Park, PA, USA, 2007. [Google Scholar]
- Collins, R. CSE486, Penn State Lecture 13: Camera Projection II; Penn State University: University Park, PA, USA, 2020. [Google Scholar]
- Meza, J.; Vargas, R.; Romero, L.A.; Zhang, S.; Marrugo, A.G. What Is the Best Triangulation Approach for a Structured Light System? In Proceedings of the SPIE, Volume 11397: Dimensional Optical Metrology and Inspection for Practical Applications IX 113970D, Bellingham, WA, USA, 18 May 2020; SPIE: Bellingham, WA, USA, 2020; p. 113970D. [Google Scholar]
- Sezgin, M.; Sankur, B. Survey over Image Thresholding Techniques and Quantitative Performance Evaluation. J. Electron. Imaging 2004, 13, 146–165. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shapiro, L.G. Computer and Robot Vision; Addison-Wesley Publishing Company: San Francisco, CA, USA, 1992; Volume 1, ISBN 9780201569438. [Google Scholar]
- Xie, Z.; Wang, X.; Chi, S. Simultaneous Calibration of the Intrinsic and Extrinsic Parameters of Structured-Light Sensors. Opt. Lasers Eng. 2014, 58, 9–18. [Google Scholar] [CrossRef]
- Nie, L.; Ye, Y.; Song, Z. Method for Calibration Accuracy Improvement of Projector-Camera-Based Structured Light System. Opt. Eng. 2017, 56, 074101. [Google Scholar] [CrossRef]
- Huang, B.; Ozdemir, S.; Tang, Y.; Liao, C.; Ling, H. A Single-Shot-Per-Pose Camera-Projector Calibration System for Imperfect Planar Targets. In Proceedings of the IEEE International Symposium on Mixed and Augmented Reality Adjunct (ISMAR-Adjunct), LMU Munich, Munich, Germany, 16–20 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 15–20. [Google Scholar]
- Moreno, D.; Taubin, G. Simple, Accurate, and Robust Projector-Camera Calibration. In Proceedings of the 2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 464–471. [Google Scholar]
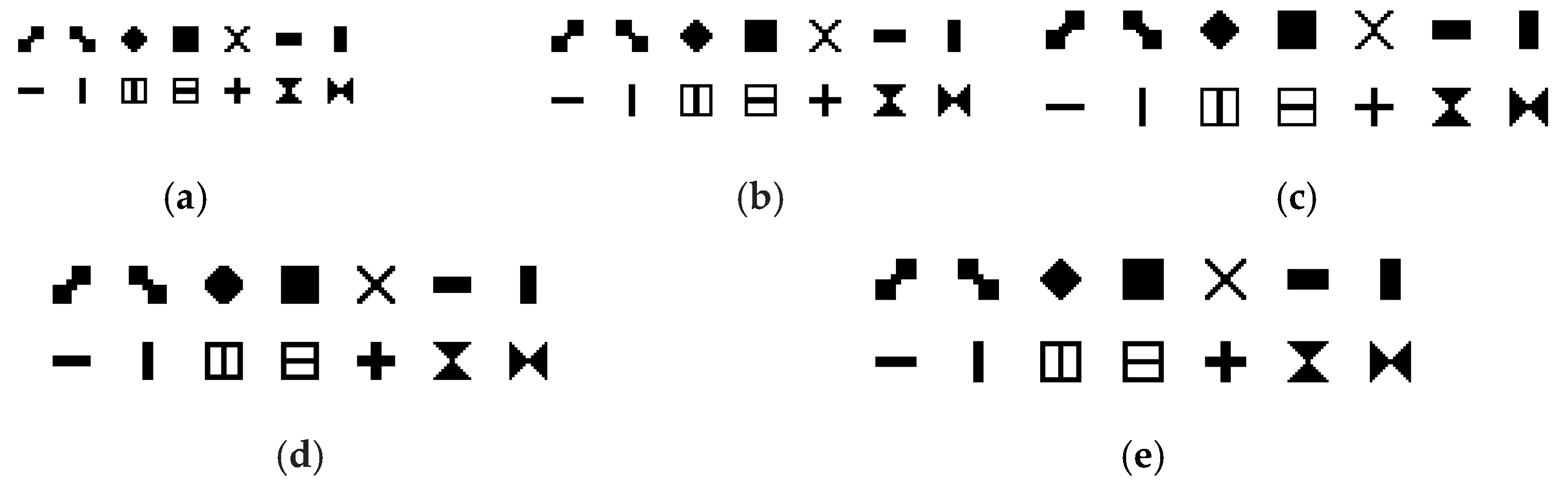



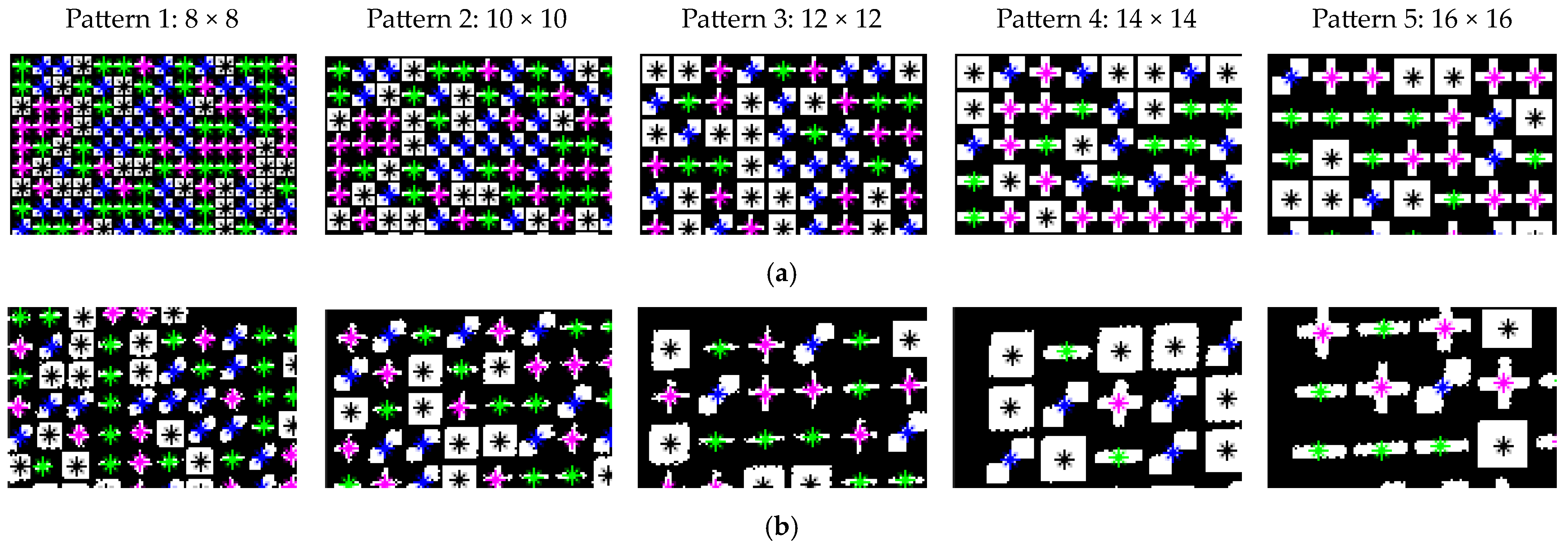




| Symbol Size | Spacing Between Consecutive Symbols | No. of Symbols Used in M-Array | M-Array Dimensions (m × n) | Average Hamming Distance | Robust Codewords (%) | No. of Feature Points in the Projected Pattern |
|---|---|---|---|---|---|---|
| 8 × 8 | 1 | 4 | 90 × 144 | 6.7517 | 99.8683 | 12,496 |
| 10 × 10 | 1 | 4 | 75 × 117 | 6.7524 | 99.8667 | 8352 |
| 12 × 12 | 2 | 4 | 60 × 93 | 6.7503 | 99.8713 | 5187 |
| 14 × 14 | 2 | 4 | 51 × 81 | 6.7489 | 99.8734 | 4000 |
| 16 × 16 | 2 | 4 | 45 × 72 | 6.7495 | 99.8452 | 3124 |
| Pattern Resolution | Depth (z) cm | Area (cm2) | Proposed Method | Zhou (2023) [16] | Yin (2021) [19] | Nguyen (2020) [7] | Song (2010) [40] | Winkelbach (2001, 2002) [38,39] | Davies (1998) [37] |
|---|---|---|---|---|---|---|---|---|---|
| Position and Orientation | Position Based Methods | Position and Orientation | Orientation | Position and Orientation | |||||
| Resolution (mm) | Resolution (mm) | Resolution (mm) | Resolution (mm) | Resolution (mm) | Resolution (mm) | Resolution (mm) | |||
| 8 × 8 | 250 | 103.8 × 166 | 11.7 | 26.7 | 25.9 | 41.4 | 25.7 | 87.4 | 57.6 (Area reduced to 63.0 × 166) |
| 10 × 10 | 14.3 | ||||||||
| 12 × 12 | 18.3 | ||||||||
| 14 × 14 | 20.9 | ||||||||
| 16 × 16 | 23.5 | ||||||||
| 8 × 8 | 200 | 83 × 132.8 | 9.4 | 21.3 | 20.7 | 33.1 | 20.6 | 69.9 | 46.1 (Area reduced to 50.4 × 132.8) |
| 10 × 10 | 11.5 | ||||||||
| 12 × 12 | 14.6 | ||||||||
| 14 × 14 | 16.7 | ||||||||
| 16 × 16 | 18.8 | ||||||||
| 8 × 8 | 150 | 62.3 × 99.6 | 7.0 | 16.1 | 15.6 | 24.9 | 15.4 | 52.4 | 34.5 (Area reduced to 37.8 × 99.6) |
| 10 × 10 | 8.6 | ||||||||
| 12 × 12 | 11.0 | ||||||||
| 14 × 14 | 12.5 | ||||||||
| 16 × 16 | 14.1 | ||||||||
| 8 × 8 | 120 | 49.8 × 79.7 | 5.6 | 12.7 | 12.3 | 19.7 | 12.3 | 41.9 | 27.6 (Area reduced to 30.2 × 79.7) |
| 10 × 10 | 6.9 | ||||||||
| 12 × 12 | 8.8 | ||||||||
| 14 × 14 | 10.0 | ||||||||
| 16 × 16 | 11.3 | ||||||||
| 8 × 8 | 110 | 45.7 × 73.0 | 5.2 | 11.8 | 11.3 | 18.2 | 11.3 | 38.5 | 25.3 (Area reduced to 27.7 × 73.0) |
| 10 × 10 | 6.3 | ||||||||
| 12 × 12 | 8 | ||||||||
| 14 × 14 | 9.2 | ||||||||
| 16 × 16 | 10.3 | ||||||||
| 8 × 8 | 100 | 41.5 × 66.4 | 4.7 | 10.7 | 10.3 | 16.5 | 10.3 | 35.0 | 23.0 (Area reduced to 25.2 × 66.4) |
| 10 × 10 | 5.7 | ||||||||
| 12 × 12 | 7.3 | ||||||||
| 14 × 14 | 8.3 | ||||||||
| 16 × 16 | 9.4 | ||||||||
| 8 × 8 | 80 | 33.2 × 53.1 | 3.8 | 8.5 | 8.2 | 13.2 | 8.2 | 28.0 | 18.4 (Area reduced to 20.1 × 53.1) |
| 10 × 10 | 4.6 | ||||||||
| 12 × 12 | 5.8 | ||||||||
| 14 × 14 | 6.7 | ||||||||
| 16 × 16 | 7.5 | ||||||||
| 8 × 8 | 60 | 24.9 × 39.8 | 2.8 | 6.4 | 6.2 | 10.0 | 6.2 | 21.0 | 13.8 (Area reduced to 15.1 × 39.8) |
| 10 × 10 | 3.4 | ||||||||
| 12 × 12 | 4.4 | ||||||||
| 14 × 14 | 5.0 | ||||||||
| 16 × 16 | 5.6 | ||||||||
| 8 × 8 | 40 | 16.6 × 26.6 | 1.9 | 4.2 | 4.1 | 7.5 | 4.1 | 14.0 | 9.2 (Area reduced to 10.1 × 26.6) |
| 10 × 10 | 2.3 | ||||||||
| 12 × 12 | 2.9 | ||||||||
| 14 × 14 | 3.3 | ||||||||
| 16 × 16 | 3.8 | ||||||||
| Pattern Type & Depth | Surface Types | ||||
|---|---|---|---|---|---|
| Primitives | Original Pattern | Plane | Cylinder | Sculpture | |
| Pattern 1 (8 × 8 resolution) Depth 110 cm | Detected | 12,496 | 4205 | 2739 | 2127 |
| Decoded | 12,496 | 4205 | 2724 | 2103 | |
| % | 100 | 100 | 99.5 | 98.9 | |
| Pattern 2 (10 × 10 resolution) Depth 110 cm | Detected | 8352 | 2810 | 1967 | 1449 |
| Decoded | 8352 | 2810 | 1954 | 1426 | |
| % | 100 | 100 | 99.3 | 98.4 | |
| Pattern 3 (12 × 12 resolution) Depth 110 cm | Detected | 5187 | 1717 | 1159 | 901 |
| Decoded | 5187 | 1717 | 1148 | 879 | |
| % | 100 | 100 | 99.0 | 97.6 | |
| Pattern 4 (14 × 14 resolution) Depth 110 cm | Detected | 4000 | 1281 | 951 | 723 |
| Decoded | 4000 | 1281 | 939 | 702 | |
| % | 100 | 100 | 98.7 | 97.1 | |
| Pattern 5 (16 × 16 resolution) Depth 110 cm | Detected | 3124 | 1031 | 749 | 558 |
| Decoded | 3124 | 1031 | 737 | 537 | |
| % | 100 | 100 | 98.4 | 96.2 | |
| Ahsan (2020) [14] (16 × 16 resolution) Depth 200 cm | Detected | 3124 | 1650 | 1161 | 689 |
| Decoded | 3124 | 1617 | 1128 | 585 | |
| % | 100 | 98.0 | 97.1 | 84.9 | |
| Pattern Type & Depth | Surface Types | ||||
|---|---|---|---|---|---|
| Primitives | Original Pattern | Plane | Cylinder | Sculpture | |
| Pattern 1 (8 × 8 resolution) Depth 110 cm | Correspondence | 12,040 | 3937 | 2517 | 1654 |
| Decoded | 12,496 | 4205 | 2724 | 2103 | |
| % | 96.4 | 93.6 | 92.4 | 78.7 | |
| Pattern 2 (10 × 10 resolution) Depth 110 cm | Correspondence | 7980 | 2596 | 1780 | 1076 |
| Decoded | 8352 | 2810 | 1954 | 1426 | |
| % | 95.6 | 92.4 | 91.1 | 75.5 | |
| Pattern 3 (12 × 12 resolution) Depth 110 cm | Correspondence | 4895 | 1550 | 1014 | 662 |
| Decoded | 5187 | 1717 | 1148 | 879 | |
| % | 94.4 | 90.3 | 88.3 | 75.3 | |
| Pattern 4 (14 × 14 resolution) Depth 110 cm | Correspondence | 3744 | 1139 | 819 | 521 |
| Decoded | 4000 | 1281 | 939 | 702 | |
| % | 93.6 | 88.9 | 87.2 | 74.2 | |
| Pattern 5 (16 × 16 resolution) Depth 110 cm | Correspondence | 2898 | 903 | 631 | 400 |
| Decoded | 3124 | 1031 | 737 | 537 | |
| % | 92.8 | 87.6 | 85.6 | 74.5 | |
| Ahsan (2020) [14] (16 × 16 resolution) Depth 200 cm | Correspondence | 2898 | 1329 | 859 | 397 |
| Decoded | 3124 | 1617 | 1128 | 585 | |
| % | 92.8 | 82.2 | 76.1 | 67.9 | |
| Surface Type | Method | Resolution | Preprocessing (Filtering + Thresholding) | Labeling | Parameter Calculation | Classification | Correspondence | Rate of Correspondence | Computation of Surface Normals | Computation of 3D Point Cloud |
|---|---|---|---|---|---|---|---|---|---|---|
| Original Pattern | Ahsan [14] (2020) depth: 200 cm | 16 × 16 | 566 | 42 | 587 | 3.3 | 485 | 0.19 | - | - |
| Proposed Method depth: 110 cm | 16 × 16 | 307.6 | 18.9 | 1105.4 | 1.2 | 836.9 | 0.27 | - | - | |
| 14 × 14 | 322.3 | 21.9 | 1366.4 | 1.4 | 1278.1 | 0.32 | - | - | ||
| 12 × 12 | 342.4 | 26.3 | 1644.6 | 1.6 | 1969.6 | 0.38 | - | - | ||
| 10 × 10 | 352.6 | 34.4 | 2651.8 | 2.6 | 4604.0 | 0.55 | - | - | ||
| 8 × 8 | 363.7 | 59.2 | 4011.4 | 4.4 | 8437.8 | 0.68 | - | - | ||
| Plane Surface | Ahsan (2020) [14] depth: 200 cm | 16 × 16 | 611 | 53 | 365.6 | 2.2 | 480 | 0.3 | - | 24.7 |
| Proposed Method depth: 110 cm | 16 × 16 | 380.9 | 17.7 | 472.6 | 0.52 | 265.3 | 0.26 | 18.5 | 22.4 | |
| 14 × 14 | 390.4 | 24.0 | 594.1 | 0.63 | 388.9 | 0.30 | 19.3 | 25.6 | ||
| 12 × 12 | 401.3 | 25.3 | 739.9 | 0.75 | 587.0 | 0.34 | 28.5 | 38.2 | ||
| 10 × 10 | 412.3 | 33.2 | 1048.1 | 0.92 | 1403.1 | 0.50 | 69.3 | 89.6 | ||
| 8 × 8 | 422.6 | 36.5 | 1492.5 | 1.4 | 2301.1 | 0.55 | 174.1 | 207.7 | ||
| Cylinder | Ahsan (2020) [14] depth: 200 cm | 16 × 16 | 649 | 41.5 | 361 | 2.7 | 331.1 | 0.29 | - | 24.3 |
| Proposed Method depth: 110 cm | 16 × 16 | 360.8 | 17.8 | 326.1 | 0.25 | 178.7 | 0.25 | 10.6 | 14.4 | |
| 14 × 14 | 371.0 | 19.1 | 415.8 | 0.31 | 292.5 | 0.31 | 15.0 | 21.2 | ||
| 12 × 12 | 379.6 | 20.8 | 463.4 | 0.38 | 372.5 | 0.33 | 16.4 | 21.8 | ||
| 10 × 10 | 386.7 | 23.2 | 746.8 | 0.62 | 904.9 | 0.46 | 29.3 | 39.4 | ||
| 8 × 8 | 397.3 | 26.9 | 977.6 | 0.92 | 1505.2 | 0.55 | 68.9 | 89.4 | ||
| Sculpture | Ahsan (2020) [14] depth: 200 cm | 16 × 16 | 644 | 38 | 271 | 2.7 | 318 | 0.5 | - | 15.4 |
| Proposed Method depth: 110 cm | 16 × 16 | 372.0 | 12.2 | 260.1 | 0.18 | 196.2 | 0.37 | 7.0 | 10.4 | |
| 14 × 14 | 384.5 | 16.2 | 307.2 | 0.25 | 321.1 | 0.46 | 7.4 | 11.4 | ||
| 12 × 12 | 393.6 | 17.5 | 326.7 | 0.29 | 474.1 | 0.54 | 11.4 | 16.2 | ||
| 10 × 10 | 401.0 | 18.6 | 524.1 | 0.46 | 934.5 | 0.66 | 19.3 | 26.2 | ||
| 8 × 8 | 411.9 | 20.4 | 764.6 | 0.68 | 2097.8 | 1.00 | 29.4 | 42.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elahi, A.; Zhu, Q.; Lu, J.; Farooq, U.; Farid, G.; Bilal, M.; Li, Y. Single-Shot, Monochrome, Spatial Pixel-Encoded, Structured Light System for Determining Surface Orientations. Photonics 2024, 11, 1046. https://doi.org/10.3390/photonics11111046
Elahi A, Zhu Q, Lu J, Farooq U, Farid G, Bilal M, Li Y. Single-Shot, Monochrome, Spatial Pixel-Encoded, Structured Light System for Determining Surface Orientations. Photonics. 2024; 11(11):1046. https://doi.org/10.3390/photonics11111046
Chicago/Turabian StyleElahi, Ahsan, Qidan Zhu, Jun Lu, Umer Farooq, Ghulam Farid, Muhammad Bilal, and Yong Li. 2024. "Single-Shot, Monochrome, Spatial Pixel-Encoded, Structured Light System for Determining Surface Orientations" Photonics 11, no. 11: 1046. https://doi.org/10.3390/photonics11111046
APA StyleElahi, A., Zhu, Q., Lu, J., Farooq, U., Farid, G., Bilal, M., & Li, Y. (2024). Single-Shot, Monochrome, Spatial Pixel-Encoded, Structured Light System for Determining Surface Orientations. Photonics, 11(11), 1046. https://doi.org/10.3390/photonics11111046





