All-Dielectric Dual-Band Anisotropic Zero-Index Materials
Abstract
1. Introduction
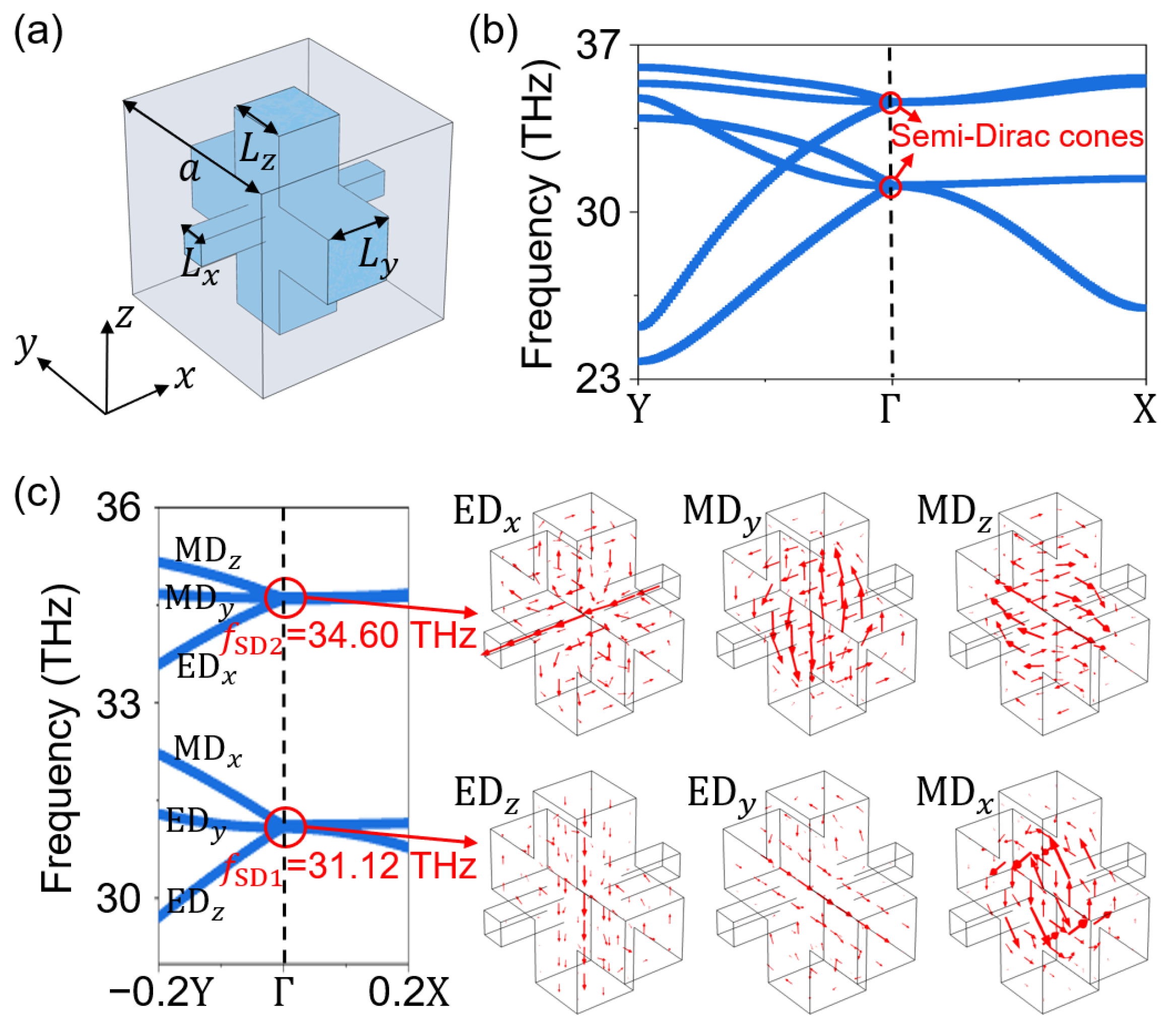
2. Silicon PhC with Dual Semi-Dirac Cones
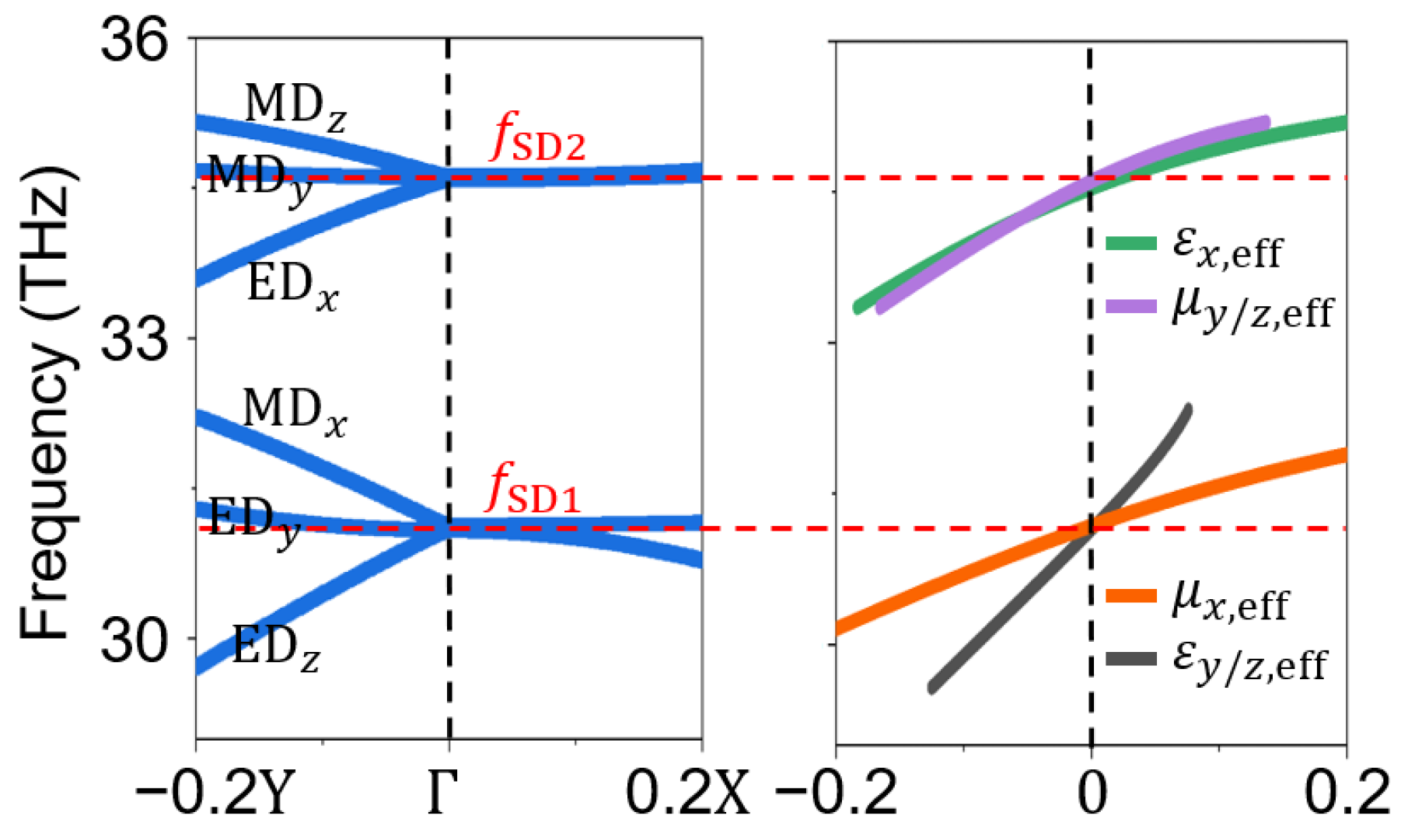
3. PhC-Based Effective AZIM
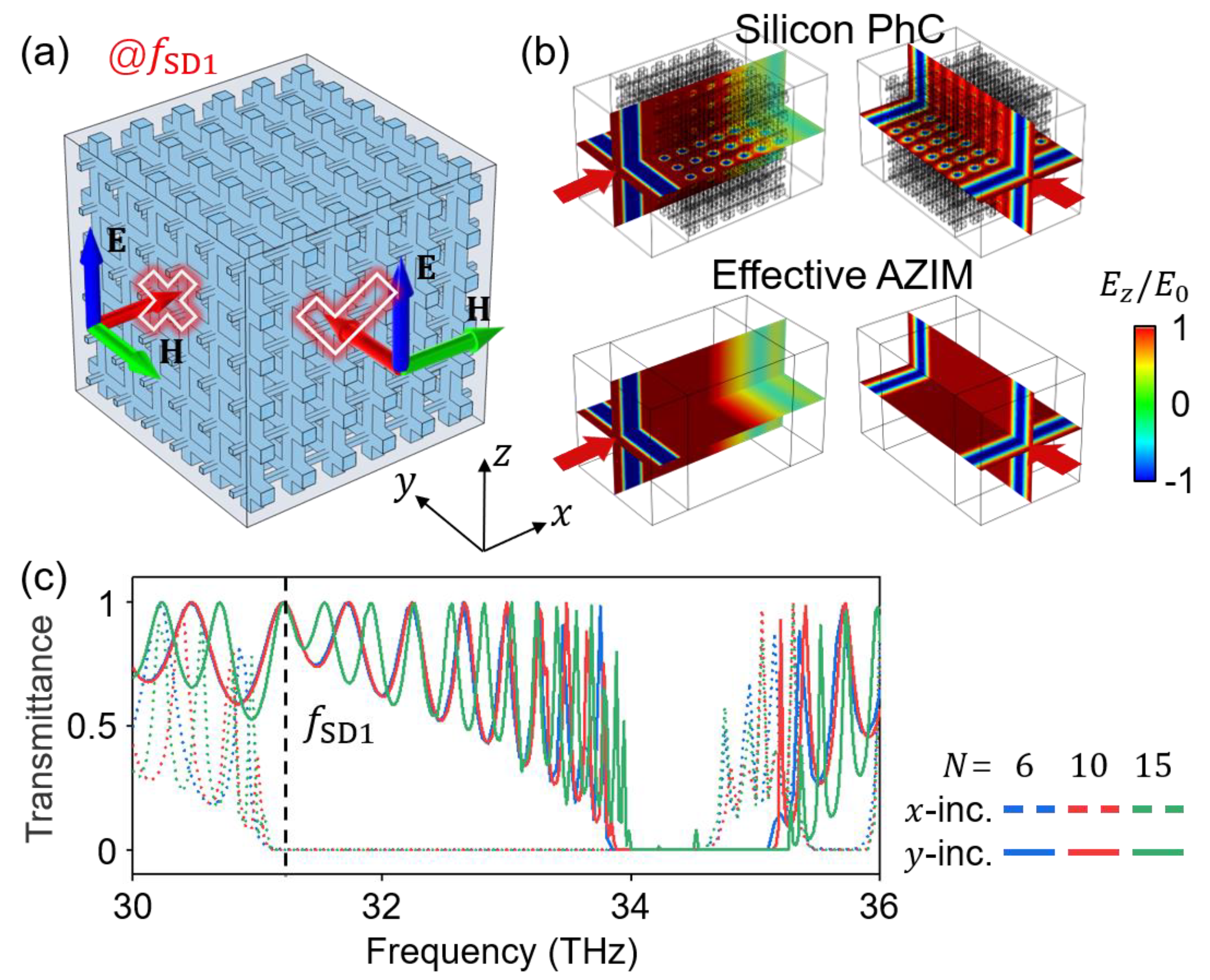
4. Highly Anisotropic Wave Transport Property
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liberal, I.; Engheta, N. Near-zero refractive index photonics. Nat. Photonics 2017, 11, 149–158. [Google Scholar] [CrossRef]
- Niu, X.; Hu, X.; Chu, S.; Gong, Q. Epsilon-near-zero photonics: A new platform for integrated devices. Adv. Opt. Mater. 2018, 2018, 1701292. [Google Scholar] [CrossRef]
- Kinsey, N.; DeVault, C.; Boltasseva, A.; Shalaev, V.M. Near-zero-index materials for photonics. Nat. Rev. Mater. 2019, 4, 742–760. [Google Scholar] [CrossRef]
- Vertchenko, L.; Nikitin, M.; Lavrinenko, A. Near-zero-index platform in photonics: Tutorial. J. Opt. Soc. Am. B 2023, 40, 1467. [Google Scholar] [CrossRef]
- Silveirinha, M.; Engheta, N. Tunneling of electromagnetic energy through subwavelength channels and bends using ϵ-near-zero materials. Phys. Rev. Lett. 2006, 97, 157403. [Google Scholar] [CrossRef]
- Edwards, B.; Alù, A.; Young, M.; Silveirinha, M.; Engheta, N. Experimental verification of epsilon-near-zero metamaterial coupling and energy squeezing using a microwave waveguide. Phys. Rev. Lett. 2008, 100, 33903. [Google Scholar] [CrossRef]
- Liu, R.; Cheng, Q.; Hand, T.; Mock, J.; Cui, T.; Cummer, S.; Smith, D. Experimental demonstration of electromagnetic tunneling through an epsilon-near-zero metamaterial at microwave frequencies. Phys. Rev. Lett. 2008, 100, 23903. [Google Scholar] [CrossRef]
- Yan, W.; Zhou, Z.; Li, H.; Li, Y. Transmission-type photonic doping for high-efficiency epsilon-near-zero supercoupling. Nat. Commun. 2023, 14, 6154. [Google Scholar] [CrossRef]
- Ma, H.F.; Shi, J.H.; Jiang, W.X.; Cui, T.J. Experimental realization of bending waveguide using anisotropic zero-index materials. Appl. Phys. Lett. 2012, 101, 253513. [Google Scholar] [CrossRef]
- Enoch, S.; Tayeb, G.; Sabouroux, P.; Guérin, N.; Vincent, P. A metamaterial for directive emission. Phys. Rev. Lett. 2002, 89, 213902. [Google Scholar] [CrossRef]
- Cheng, Q.; Jiang, W.X.; Cui, T.J. Spatial power combination for omnidirectional radiation via anisotropic metamaterials. Phys. Rev. Lett. 2012, 108, 213903. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Lu, W.; Hang, Z.; Chen, H.; Hou, B.; Lai, Y.; Chan, C.T. Arbitrary control of electromagnetic flux in inhomogeneous anisotropic media with near-zero index. Phys. Rev. Lett. 2014, 112, 73903. [Google Scholar] [CrossRef]
- Ji, W.; Luo, J.; Lai, Y. Extremely anisotropic epsilon-near-zero media in waveguide metamaterials. Opt. Express 2019, 27, 19463–19473. [Google Scholar] [CrossRef] [PubMed]
- Mei, R.; Xu, Y.; Gao, L.; Xu, H.X.; Lai, Y.; Luo, J. Skin effect of electromagnetic flux in anisotropic zero-index metamaterials. Adv. Opt. Mater. 2024, 2024, 2401569. [Google Scholar] [CrossRef]
- Liberal, I.; Mahmoud, A.M.; Li, Y.; Edwards, B.; Engheta, N. Photonic doping of epsilon-near-zero media. Science 2017, 355, 1058–1062. [Google Scholar] [CrossRef] [PubMed]
- Liberal, I.; Li, Y.; Engheta, N. Reconfigurable epsilon-near-zero metasurfaces via photonic doping. Nanophotonics 2018, 7, 1117–1127. [Google Scholar] [CrossRef]
- Luo, J.; Li, J.; Lai, Y. Electromagnetic impurity-immunity induced by parity-time symmetry. Phys. Rev. X 2018, 8, 31035. [Google Scholar] [CrossRef]
- Luo, J.; Liu, B.; Hang, Z.H.; Lai, Y. Coherent perfect absorption via photonic doping of zero-index media. Laser Photonics Rev. 2018, 2018, 1800001. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Y.; Li, H.; Sun, W.; Liberal, I.; Engheta, N. Substrate-integrated photonic doping for near-zero-index devices. Nat. Commun. 2019, 10, 4132. [Google Scholar] [CrossRef]
- Coppolaro, M.; Moccia, M.; Castaldi, G.; Engheta, N.; Galdi, V. Non-Hermitian doping of epsilon-near-zero media. Proc. Natl. Acad. Sci. USA 2020, 117, 13921–13928. [Google Scholar] [CrossRef]
- Zhou, Q.; Fu, Y.; Huang, L.; Wu, Q.; Miroshnichenko, A.; Gao, L.; Xu, Y. Geometry symmetry-free and higher-order optical bound states in the continuum. Nat. Commun. 2021, 12, 4390. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Fu, P.; Zhou, Z.; Sun, W.; Li, Y.; Wu, J.; Dai, Q. Performing calculus with epsilon-near-zero metamaterials. Sci. Adv. 2022, 8, eabq6198. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Chu, H.; Luo, J.; Hang, Z.H.; Wu, Y.; Lai, Y. Three-dimensional electromagnetic void space. Phys. Rev. Lett. 2021, 127, 123902. [Google Scholar] [CrossRef] [PubMed]
- Yan, D.; Mei, R.; Li, M.; Ma, Z.; Hang, Z.H.; Luo, J. Controlling coherent perfect absorption via long-range connectivity of defects in three-dimensional zero-index media. Nanophotonics 2023, 12, 4205–4214. [Google Scholar] [CrossRef]
- Liu, C.; Yan, D.; Sun, B.; Xu, Y.; Fang, C.; Gao, L.; Luo, J. Low-gain generalized pt symmetry for electromagnetic impurity-immunity via non-Hermitian doped zero-index materials. Photonics Res. 2024, 12, 2424–2434. [Google Scholar] [CrossRef]
- Alam, M.Z.; De Leon, I.; Boyd, R.W. Large optical nonlinearity of indium tin oxide in its epsilon-near-zero region. Science 2016, 352, 795–797. [Google Scholar] [CrossRef]
- Alam, M.Z.; Schulz, S.A.; Upham, J.; De Leon, I.; Boyd, R.W. Large optical nonlinearity of nanoantennas coupled to an epsilon-near-zero material. Nat. Photonics 2018, 12, 79–83. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, J.; Manjavacas, A.; Luk, T.S.; Liu, H.; Kelley, K.; Maria, J.; Runnerstrom, E.L.; Sinclair, M.B.; Ghimire, S.; et al. High-harmonic generation from an epsilon-near-zero material. Nat. Phys. 2019, 15, 1022–1026. [Google Scholar] [CrossRef]
- Caspani, L.; Kaipurath, R.P.M.; Clerici, M.; Ferrera, M.; Roger, T.; Kim, J.; Kinsey, N.; Pietrzyk, M.; Di Falco, A.; Shalaev, V.M.; et al. Enhanced nonlinear refractive index in ε-near-zero materials. Phys. Rev. Lett. 2016, 116, 233901. [Google Scholar] [CrossRef]
- Jia, W.; Liu, M.; Lu, Y.; Feng, X.; Wang, Q.; Zhang, X.; Ni, Y.; Hu, F.; Gong, M.; Xu, X.; et al. Broadband terahertz wave generation from an epsilon-near-zero material. Light-Sci. Appl. 2021, 10, 11. [Google Scholar] [CrossRef]
- Reshef, O.; De Leon, I.; Alam, M.Z.; Boyd, R.W. Nonlinear optical effects in epsilon-near-zero media. Nat. Rev. Mater. 2019, 4, 535–551. [Google Scholar] [CrossRef]
- Vertchenko, L.; Lavrinenko, A. Implications of Low-Refractive Mode Index on Nonlinear Optical Interactions. Laser Photonics Rev. 2023, 17, 2200741. [Google Scholar] [CrossRef]
- Wang, C.; Shi, R.; Gao, L.; Shalin, A.S.; Luo, J. Quenching of second-harmonic generation by epsilon-near-zero media. Photonics Res. 2023, 11, 1437. [Google Scholar] [CrossRef]
- Lobet, M.; Liberal, I.; Vertchenko, L.; Lavrinenko, A.V.; Engheta, N.; Mazur, E. Momentum considerations inside near-zero index materials. Light-Sci. Appl. 2022, 11, 110. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.C.; Inampudi, S.; Ribaudo, T.; Slocum, D.; Vangala, S.; Kuhta, N.A.; Goodhue, W.D.; Podolskiy, V.A.; Wasserman, D. Funneling light through a subwavelength aperture with epsilon-near-zero materials. Phys. Rev. Lett. 2011, 107, 133901. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Dutta, A.; Naik, G.V.; Giles, A.J.; Bezares, F.J.; Ellis, C.T.; Tischler, J.G.; Mahmoud, A.M.; Caglayan, H.; Glembocki, O.J. Role of epsilon-near-zero substrates in the optical response of plasmonic antennas. Optica 2016, 3, 339–346. [Google Scholar] [CrossRef]
- Xu, J.; Mandal, J.; Raman, A.P. Broadband directional control of thermal emission. Science 2021, 372, 393–397. [Google Scholar] [CrossRef]
- Wu, J.; Clementi, M.; Huang, C.; Ye, F.; Fu, H.; Lu, L.; Zhang, S.; Li, Q.; Bres, C.S. Thermo-optic epsilon-near-zero effects. Nat. Commun. 2024, 15, 794. [Google Scholar] [CrossRef]
- Anopchenko, A.; Gurung, S.; Tao, L.; Arndt, C.; Lee, H.W.H. Atomic layer deposition of ultra-thin and smooth Al-doped ZnO for zero-index photonics. Mater. Res. Express 2018, 5, 14012. [Google Scholar] [CrossRef]
- Tao, L.; Anopchenko, A.; Gurung, S.; Zhang, J.; Lee, H.W.H. Gate-tunable plasmon-induced transparency modulator based on stub-resonator waveguide with epsilon-near-zero materials. Sci. Rep. 2019, 9, 2789. [Google Scholar] [CrossRef]
- Lee, H.W.; Papadakis, G.; Burgos, S.P.; Chander, K.; Kriesch, A.; Pala, R.; Peschel, U.; Atwater, H.A. Nanoscale conducting oxide plasMOStor. Nano Lett. 2014, 14, 6463–6468. [Google Scholar] [CrossRef]
- Anopchenko, A.; Gurung, S.; Bej, S.; Lee, H.W.H. Field enhancement of epsilon-near-zero modes in realistic ultrathin absorbing films. Nanophotonics 2023, 12, 2913–2920. [Google Scholar] [CrossRef]
- Zhang, L.; Love, S.; Anopchenko, A.; Lee, H.W.H. Hollow core optical fiber enabled by epsilon-near-zero material. Nanophotonics 2024, 13, 1025–1031. [Google Scholar] [CrossRef]
- Maas, R.; Parsons, J.; Engheta, N.; Polman, A. Experimental realization of an epsilon-near-zero metamaterial at visible wavelengths. Nat. Photonics 2013, 7, 907–912. [Google Scholar] [CrossRef]
- Dai, J.; Jiang, H.; Guo, Z.; Qiu, J. Tunable epsilon-and-mu-near-zero metacomposites. Adv. Funct. Mater. 2023, 34, 2308338. [Google Scholar] [CrossRef]
- Luo, J.; Lai, Y. Epsilon-near-zero or mu-near-zero materials composed of dielectric photonic crystals. Sci. China Inf. Sci. 2013, 56, 1–10. [Google Scholar] [CrossRef]
- Qin, X.; Sun, W.; Zhou, Z.; Fu, P.; Li, H.; Li, Y. Waveguide effective plasmonics with structure dispersion. Nanophotonics 2022, 11, 1659–1676. [Google Scholar] [CrossRef]
- Ji, W.; Luo, J.; Chu, H.; Zhou, X.; Meng, X.; Peng, R.; Wang, M.; Lai, Y. Crosstalk prohibition at the deep-subwavelength scale by epsilon-near-zero claddings. Nanophotonics 2023, 12, 2007–2017. [Google Scholar] [CrossRef]
- Vulis, D.I.; Reshef, O.; Camayd-Muñoz, P.; Mazur, E. Manipulating the flow of light using Dirac-cone zero-index metamaterials. Rep. Prog. Phys. 2019, 82, 12001. [Google Scholar] [CrossRef]
- Li, Y.; Chan, C.T.; Mazur, E. Dirac-like cone-based electromagnetic zero-index metamaterials. Light-Sci. Appl. 2021, 10, 203. [Google Scholar] [CrossRef]
- Luo, J.; Lai, Y. Hermitian and non-Hermitian Dirac-like cones in photonic and phononic structures. Front. Phys. 2022, 10, 845624. [Google Scholar] [CrossRef]
- Huang, X.; Lai, Y.; Hang, Z.H.; Zheng, H.; Chan, C.T. Dirac cones induced by accidental degeneracy in photonic crystals and zero-refractive-index materials. Nat. Mater. 2011, 10, 582–586. [Google Scholar] [CrossRef]
- Moitra, P.; Yang, Y.; Anderson, Z.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Realization of an all-dielectric zero-index optical metamaterial. Nat. Photonics 2013, 7, 791–795. [Google Scholar] [CrossRef]
- Li, Y.; Kita, S.; Muñoz, P.; Reshef, O.; Vulis, D.I.; Yin, M.; Lončar, M.; Mazur, E. On-chip zero-index metamaterials. Nat. Photonics 2015, 9, 738–742. [Google Scholar] [CrossRef]
- Dong, T.; Dai, T.; Chen, Y.; Liu, Y.; Liu, H.; Wang, Y.; Ma, A.; Hu, H.; Xu, L.; Zhao, L.; et al. Low-loss nanoscale zero-index metawaveguides and metadevices. Optica 2024, 11, 799. [Google Scholar] [CrossRef]
- Tang, H.; DeVault, C.; Camayd-Muñoz, S.A.; Liu, Y.; Jia, D.; Du, F.; Mello, O.; Vulis, D.I.; Li, Y.; Mazur, E. Low-loss zero-index materials. Nano Lett. 2021, 21, 914–920. [Google Scholar] [CrossRef]
- Dong, T.; Liang, J.; Camayd-Muñoz, S.; Liu, Y.; Tang, H.; Kita, S.; Chen, P.; Wu, X.; Chu, W.; Mazur, E.; et al. Ultra-low-loss on-chip zero-index materials. Light-Sci. Appl. 2021, 10, 10. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, T.; Qin, X.; Luo, W.; Leng, N.; He, Y.; Yuan, Y.; Bai, M.; Sun, J.; Zhou, J.; et al. High-permittivity ceramics enabled highly homogeneous zero-index metamaterials for high-directivity antennas and beyond. Elight 2024, 4, 4. [Google Scholar] [CrossRef]
- Li, Y.; Mei, J. Double Dirac cones in two-dimensional dielectric photonic crystals. Opt. Express 2015, 23, 12089. [Google Scholar] [CrossRef]
- Wu, Y. A semi-Dirac point and an electromagnetic topological transition in a dielectric photonic crystal. Opt. Express 2014, 22, 1906–1917. [Google Scholar] [CrossRef]
- Yasa, U.G.; Turduev, M.; Giden, I.H.; Kurt, H. Full utilization of semi-Dirac cones in photonics. Phys. Rev. B 2018, 97, 195131. [Google Scholar] [CrossRef]
- Bor, E.; Turduev, M.; Yasa, U.G.; Kurt, H.; Staliunas, K. Asymmetric light transmission effect based on an evolutionary optimized semi-Dirac cone dispersion photonic structure. Phys. Rev. B 2018, 98, 245112. [Google Scholar] [CrossRef]
- Bor, E.; Gorkem Yasa, U.; Kurt, H.; Turduev, M. Demonstration of carpet cloaking by an anisotropic zero refractive index medium. Opt. Lett. 2020, 45, 2423. [Google Scholar] [CrossRef]
- Vertchenko, L.; DeVault, C.; Malureanu, R.; Mazur, E.; Lavrinenko, A. Near-zero index photonic crystals with directive bound states in the continuum. Laser Photonics Rev. 2021, 15, 2000559. [Google Scholar] [CrossRef]
- Yang, D.; Feng, F.; Sun, L.; Wang, N.; Wang, G.P. Realization of magneto-optical near-zero-index metamaterial by using an array of spinning cylinders. Phys. Rev. A 2022, 105, 43517. [Google Scholar] [CrossRef]
- Li, M.; Mei, R.; Yan, D.; Ma, Z.; Cao, F.; Xu, Y.; Xu, C.; Luo, J. Dual semi-Dirac cones in three-dimensional photonic crystals. Phys. Rev. B 2024, 109, 125432. [Google Scholar] [CrossRef]
- Shkondin, E.; Takayama, O.; Panah, M.E.A.; Liu, P.; Larsen, P.V.; Mar, M.D.; Jensen, F.; Lavrinenko, A.V. Large-scale high aspect ratio Al-doped ZnO nanopillars arrays as anisotropic metamaterials. Opt. Mater. Express 2017, 7, 1606. [Google Scholar] [CrossRef]
- van de Haar, M.A.; van de Groep, J.; Brenny, B.J.M.; Polman, A. Controlling magnetic and electric dipole modes in hollow silicon nanocylinders. Opt. Express 2016, 24, 2047–2064. [Google Scholar] [CrossRef]
- Luo, J.; Yang, Y.; Yao, Z.; Lu, W.; Hou, B.; Hang, Z.H.; Chan, C.T.; Lai, Y. Ultratransparent media and transformation optics with shifted spatial dispersions. Phys. Rev. Lett. 2016, 117, 223901. [Google Scholar] [CrossRef]
- Luo, H.; Luo, J.; Zhang, Z.; Wu, C.; Li, Q.; Liu, W.; Peng, R.; Wang, M.; Li, H.; Lai, Y. Dielectric metamaterials with effective self-duality and full-polarization omnidirectional brewster effect. Light-Sci. Appl. 2024, 13, 262. [Google Scholar] [CrossRef]
- Śmigaj, W.; Gralak, B. Validity of the effective-medium approximation of photonic crystals. Phys. Rev. B 2008, 77, 235445. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Mei, R.; Li, M.; Xu, Y.; Luo, J.; Liu, Y. All-Dielectric Dual-Band Anisotropic Zero-Index Materials. Photonics 2024, 11, 1018. https://doi.org/10.3390/photonics11111018
Sun B, Mei R, Li M, Xu Y, Luo J, Liu Y. All-Dielectric Dual-Band Anisotropic Zero-Index Materials. Photonics. 2024; 11(11):1018. https://doi.org/10.3390/photonics11111018
Chicago/Turabian StyleSun, Baoyin, Ran Mei, Mingyan Li, Yadong Xu, Jie Luo, and Youwen Liu. 2024. "All-Dielectric Dual-Band Anisotropic Zero-Index Materials" Photonics 11, no. 11: 1018. https://doi.org/10.3390/photonics11111018
APA StyleSun, B., Mei, R., Li, M., Xu, Y., Luo, J., & Liu, Y. (2024). All-Dielectric Dual-Band Anisotropic Zero-Index Materials. Photonics, 11(11), 1018. https://doi.org/10.3390/photonics11111018





