Online Optical Axis Parallelism Measurement Method for Continuous Zoom Camera Based on High-Precision Spot Center Positioning Algorithm
Abstract
1. Introduction
- This paper presents a morphology-based method for extracting the spot center. A novel structuring element is designed to dilate the spot, followed by implementing an edge tracing algorithm to extract the contour of the binary spot. This method achieves sub-pixel accuracy in spot center extraction and exhibits excellent repeatability.
- The measurement software is capable of calculating and outputting the optical axis parallelism across the entire focal range. This software continuously acquires target images during zooming, extracts the coordinate of the target center, and automatically retrieves focal length data via serial communication.
- An experimental platform was established to conduct tests that validate the accuracy of the proposed algorithm and assess the feasibility of the optical axis parallelism measurement system.
2. Algorithm Research
2.1. Traditional Center Positioning Algorithm
2.1.1. Hough Transform Method
2.1.2. Grayscale Centroid Method
2.1.3. Least Squares Circle Fitting Method
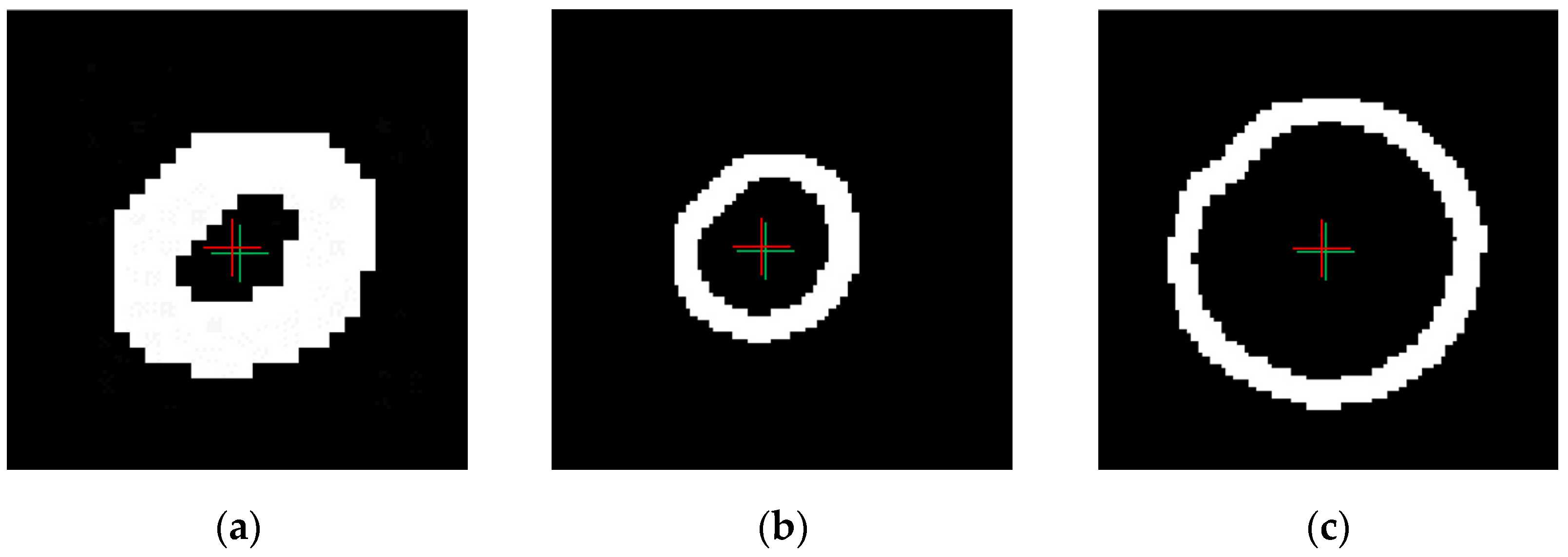
2.2. Proposed Algorithm
2.2.1. Preprocessing
2.2.2. Processing
2.2.3. Detection
3. System Design
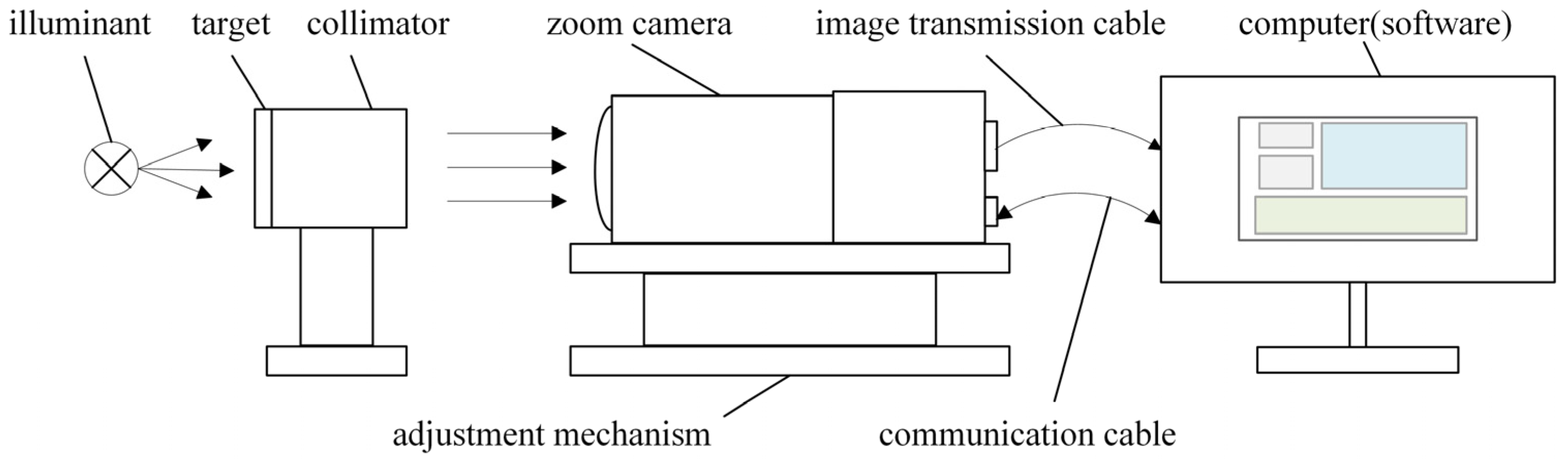
3.1. Measuring Principle
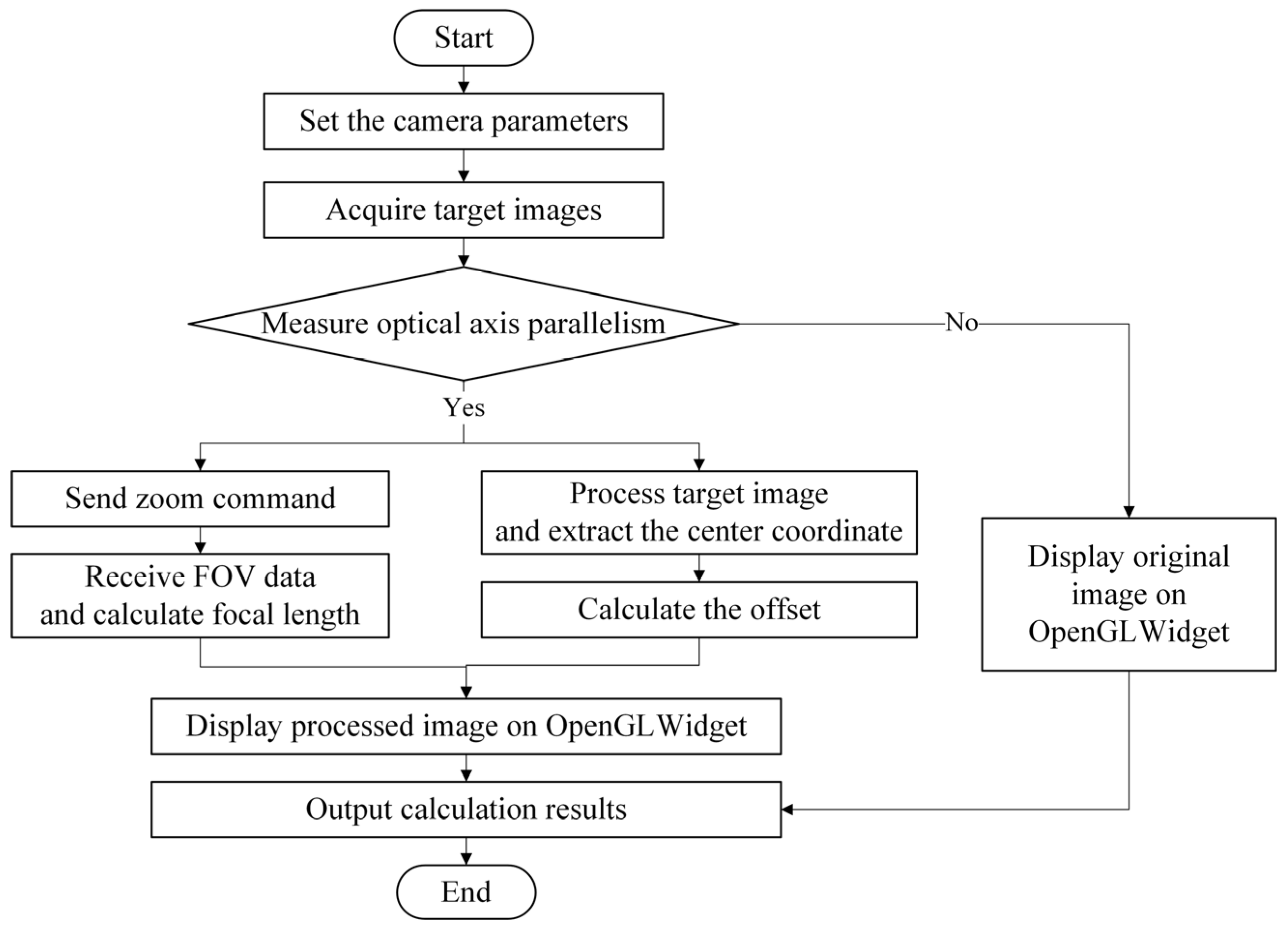
3.2. Measurement Software Design
4. Experiment and Result Analysis
4.1. Measurement System
4.2. Results Analysis
4.2.1. Evaluation of Algorithm Accuracy
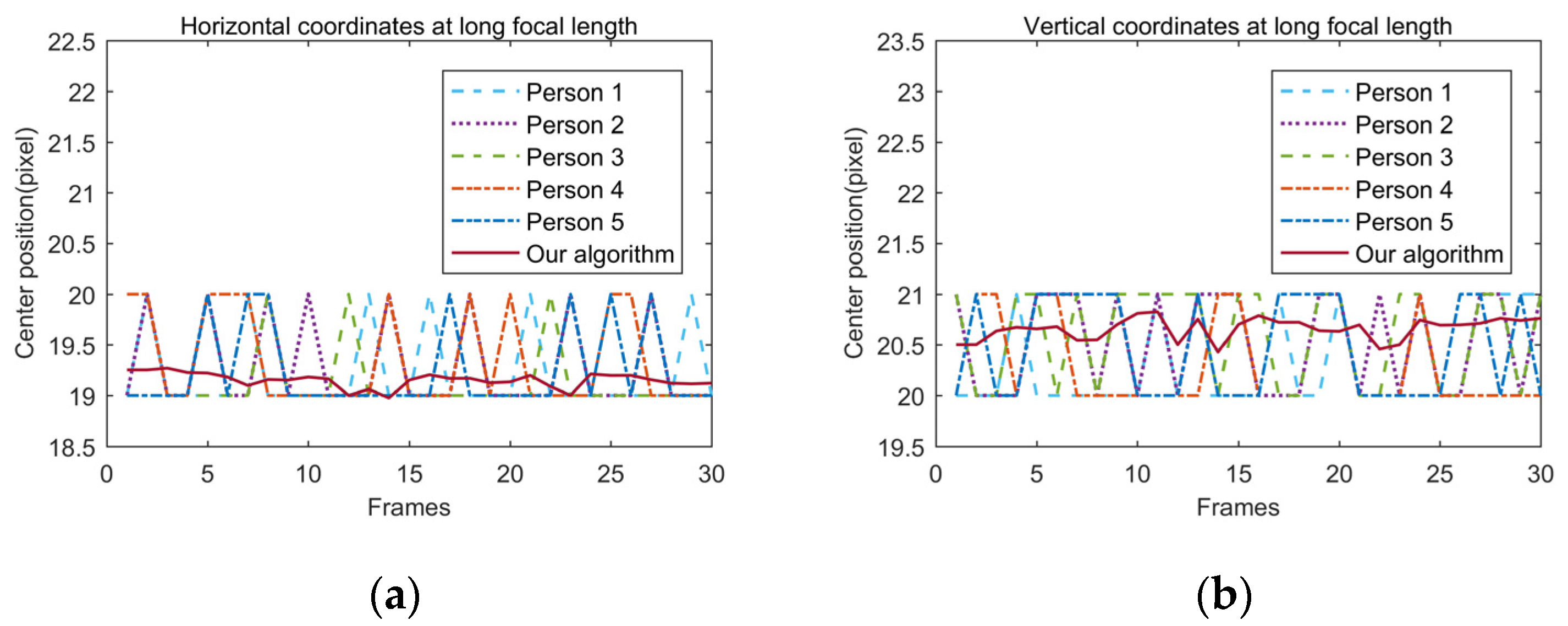
4.2.2. Verification of System Function
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Neil, I.A. Evolution of Zoom Lens Optical Design Technology and Manufacture. Opt. Eng. 2021, 60, 051211. [Google Scholar] [CrossRef]
- Liu, E.; Zheng, Y.; Lin, C.; Zhang, J.; Niu, Y.; Song, L. Research on Distortion Control in Off-Axis Three-Mirror Astronomical Telescope Systems. Photonics 2024, 11, 686. [Google Scholar] [CrossRef]
- Gorshkov, V.A.; Churilin, V.A. Multispectral Apparatus Based on an Off-Axis Mirror Collimator for Monitoring the Quality of Optical Systems. J. Opt. Technol. 2015, 82, 646–648. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, S. Multi-Optical Axis Parallelism Calibration of Space Photoelectric Tracking and Aiming System. Chin. Opt. 2021, 14, 625–633. [Google Scholar] [CrossRef]
- Chen, Z.; Xiao, W.; Ma, D. A Method for Large Distance Multi-Optical Axis Parallelism Online Detection. Acta Opt. Sin. 2017, 37, 112006. [Google Scholar] [CrossRef]
- Jin, W.; Wang, X.; Zhang, Q.; Jiang, Y.; Li, Y.; Fan, F.; Fan, J.; Wang, N. Technical Progress and Its Analysis in Detecting of Multi-Axes Parallelism System. Infrared Laser Eng. 2010, 39, 526–531. [Google Scholar]
- Zhang, L.; Zhao, X. Method for Detecting Coherence of Multiple Optical Axes. In Proceedings of the Fourth Seminar on Novel Optoelectronic Detection Technology and Application, Nanjing, China, 24–26 October 2017. [Google Scholar]
- Luo, M.; Li, S.; Gao, M.; Zhang, Y. Optical Axis Collimation of Biaxial Laser Ceilometer based on CCD. Laser Infrared 2017, 47, 1002–1005. [Google Scholar]
- Zou, H.; Wu, H.; Zhou, L. A Testing Method of Optical Axes Parallelism of Shipboard Photoelectrical Theodolite. In Proceedings of the 8th International Symposium on Advanced Optical Manufacturing and Testing Technology (AOMATT), Suzhou, China, 26–29 April 2016. [Google Scholar]
- Xie, G.; Li, C.; Cai, J. The Test Method of Laser Range Finder Multi-Axis Parallelism. Electron. Test. 2020, 19, 48–51. [Google Scholar]
- Xu, D.; Tang, X.; Fang, G. Method for Calibration of Optical Axis Parallelism Based on Interference Fringes. Acta Opt. Sin. 2020, 40, 129–136. [Google Scholar]
- Kong, F.; Wang, H.; Fang, Y.; Kang, C.; Zhou, F. Measurement Method of Optical Axis Parallelism of Continuous Zoom Camera Based on Skeleton Thinning Algorithm. In Proceedings of the Optical Sensing, Imaging, and Display Technology and Applications, and Biomedical Optics (AOPC), Beijing, China, 25–27 July 2023. [Google Scholar]
- Yao, Z.; Yi, W. Curvature Aided Hough Transform for Circle Detection. Expert Syst. Appl. 2016, 51, 26–33. [Google Scholar] [CrossRef]
- Li, Z.; Liao, L. Bright Field Droplet Image Recognition Based on Fast Hough Circle Detection Algorithm. In Proceedings of the 2022 14th International Conference on Computer Research and Development (ICCRD), Shenzhen, China, 7–9 January 2022. [Google Scholar]
- Yao, R.; Wang, B.; Hu, M.; Hua, D.; Wu, L.; Lu, H.; Liu, X. A Method for Extracting a Laser Center Line Based on an Improved Grayscale Center of Gravity Method: Application on the 3D Reconstruction of Battery Film Defects. Appl. Sci. 2023, 13, 9831. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Jiao, X.; Ding, Y. Research on the Center Extraction Algorithm of Structured Light Fringe Based on an Improved Gray Gravity Center Method. J. Intell. Syst. 2023, 32, 20220195. [Google Scholar] [CrossRef]
- Chernov, N.; Lesort, C. Least Squares Fitting of Circles. J. Math. Imaging Vis. 2005, 23, 239–252. [Google Scholar] [CrossRef]
- Yatabe, K.; Ishikawa, K.; Oikawa, Y. Simple, Flexible, and Accurate Phase Retrieval Method for Generalized Phase-Shifting Interferometry. J. Opt. Soc. Am. A 2016, 34, 87–96. [Google Scholar] [CrossRef]
- Klančar, G.; Zdešar, A.; Krishnan, M. Robot Navigation Based on Potential Field and Gradient Obtained by Bilinear Interpolation and a Grid-Based Search. Sensors 2022, 22, 3295. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Xu, S.; Jin, L.; Song, E. Characteristic Analysis of Otsu Threshold and Its Applications. Pattern Recognit. Lett. 2011, 32, 956–961. [Google Scholar] [CrossRef]
- Said, K.A.M.; Jambek, A.B.; Sulaiman, N. A Study of Image Processing Using Morphological Opening and Closing Processes. Int. J. Control Theory Appl. 2016, 9, 15–21. [Google Scholar]
- Sekehravani, E.A.; Babulak, E.; Masoodi, M. Implementing Canny Edge Detection Algorithm for Noisy Image. Bull. Electr. Eng. Inform. 2020, 9, 1404–1410. [Google Scholar] [CrossRef]
- Suzuki, S. Topological Structural Analysis of Digitized Binary Images by Border Following. Comput. Vis. Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- Hu, F.; Yan, Y.; Huang, Y. Research on Simulation Monitoring System of 828D Machining Center Based on QT. Sci. J. Intell. Syst. Res. Vol. 2021, 3, 3. [Google Scholar]
- Ma, J.; Ren, X.; Tsviatkou, V.Y.; Kanapelka, V.K. A Novel Fully Parallel Skeletonization Algorithm. Pattern Anal. Appl. 2022, 25, 169–188. [Google Scholar] [CrossRef]










| Resolution | Bit Depth (bit) | Pixel Size (μm) | Focal Length (mm) | Image Interface | Communication Interface |
|---|---|---|---|---|---|
| 1280 × 1024 | 8 | 3.45 | 10–130 | Camera Link | RS-422 |
| Image Type | Metric | Hough Transform | Grayscale Centroid | Circle Fitting | Single Dilation (Ours) | Our Algorithm |
|---|---|---|---|---|---|---|
| Short focal length | average error (pixel) | / | 0.71 | 0.07 | 0.36 | 0.10 |
| maximum error (pixel) | / | 0.71 | 0.56 | 0.52 | 0.19 | |
| Long focal length | average error (pixel) | 1.49 | 0.71 | 2.18 | 0.39 | 0.13 |
| maximum error (pixel) | 2.92 | 0.71 | 7.49 | 0.61 | 0.24 |
| Image Type | Person 1 | Person 2 | Person 3 | Person 4 | Person 5 | Average | Our Algorithm | |
|---|---|---|---|---|---|---|---|---|
| Short focal length | horizontal | 17 | 17 | 17 | 17 | 17 | 17 | 17.24 |
| vertical | 18 | 18 | 18 | 18 | 18 | 18 | 18.44 | |
| Long focal length | horizontal | 19.20 | 19.27 | 19.10 | 19.33 | 19.23 | 19.23 | 19.15 |
| vertical | 20.30 | 20.53 | 20.60 | 20.37 | 20.47 | 20.45 | 20.66 | |
| Image Type | Metric | Hough Transform | Grayscale Centroid | Circle Fitting | Single Dilation (Ours) | Our Algorithm |
|---|---|---|---|---|---|---|
| Short focal length | average error (pixel) | / | 0.50 | 0.49 | 0.26 | 0.10 |
| maximum error (pixel) | / | 0.50 | 1.20 | 0.30 | 0.31 | |
| time (ms) | / | 15.89 | 29.28 | 14.43 | 16.88 | |
| Long focal length | average error (pixel) | 1.71 | 0.48 | 0.39 | 0.35 | 0.11 |
| maximum error (pixel) | 6.75 | 0.68 | 0.50 | 0.50 | 0.29 | |
| time (ms) | 35.53 | 15.24 | 32.78 | 16.48 | 18.14 |
| Image Type | Gaussian Noise (Standard Deviation) | Salt-and-Pepper Noise (Probability) | ||||
|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 0.01 | 0.03 | 0.05 | |
| Short focal length | 0.08 | 0.11 | 0.21 | \ | \ | \ |
| Long focal length | 0.10 | 0.13 | 0.14 | 0.19 | 0.34 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, C.; Fang, Y.; Wang, H.; Zhou, F.; Ren, Z.; Han, F. Online Optical Axis Parallelism Measurement Method for Continuous Zoom Camera Based on High-Precision Spot Center Positioning Algorithm. Photonics 2024, 11, 1017. https://doi.org/10.3390/photonics11111017
Kang C, Fang Y, Wang H, Zhou F, Ren Z, Han F. Online Optical Axis Parallelism Measurement Method for Continuous Zoom Camera Based on High-Precision Spot Center Positioning Algorithm. Photonics. 2024; 11(11):1017. https://doi.org/10.3390/photonics11111017
Chicago/Turabian StyleKang, Chanchan, Yao Fang, Huawei Wang, Feng Zhou, Zeyue Ren, and Feixiang Han. 2024. "Online Optical Axis Parallelism Measurement Method for Continuous Zoom Camera Based on High-Precision Spot Center Positioning Algorithm" Photonics 11, no. 11: 1017. https://doi.org/10.3390/photonics11111017
APA StyleKang, C., Fang, Y., Wang, H., Zhou, F., Ren, Z., & Han, F. (2024). Online Optical Axis Parallelism Measurement Method for Continuous Zoom Camera Based on High-Precision Spot Center Positioning Algorithm. Photonics, 11(11), 1017. https://doi.org/10.3390/photonics11111017





