Absorber-Free Mode-Locking of a Hybrid Integrated Diode Laser at Sub-GHz Repetition Rate †
Abstract
1. Introduction
2. Experimental Results
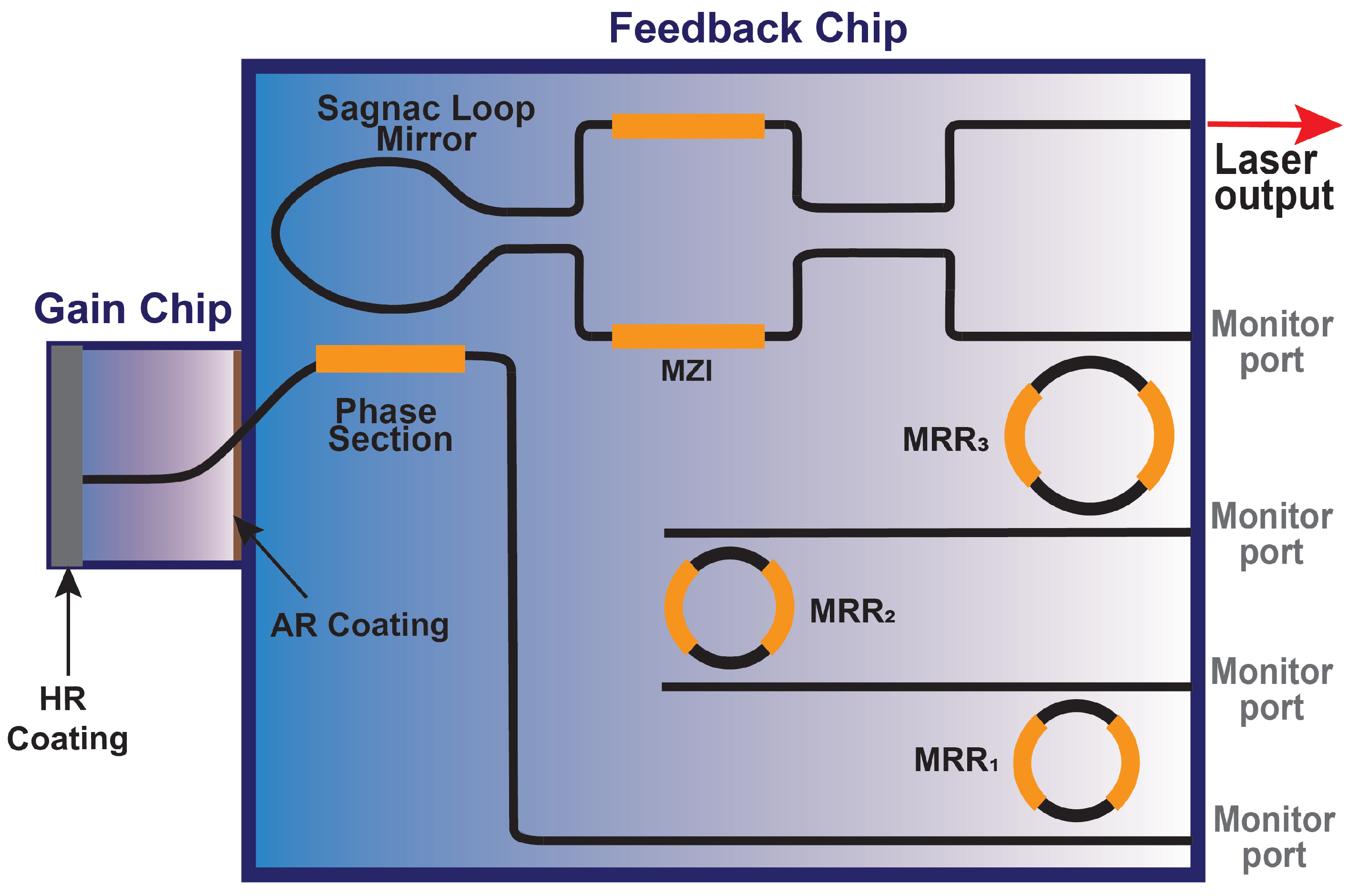
2.1. Hybrid Integrated Laser
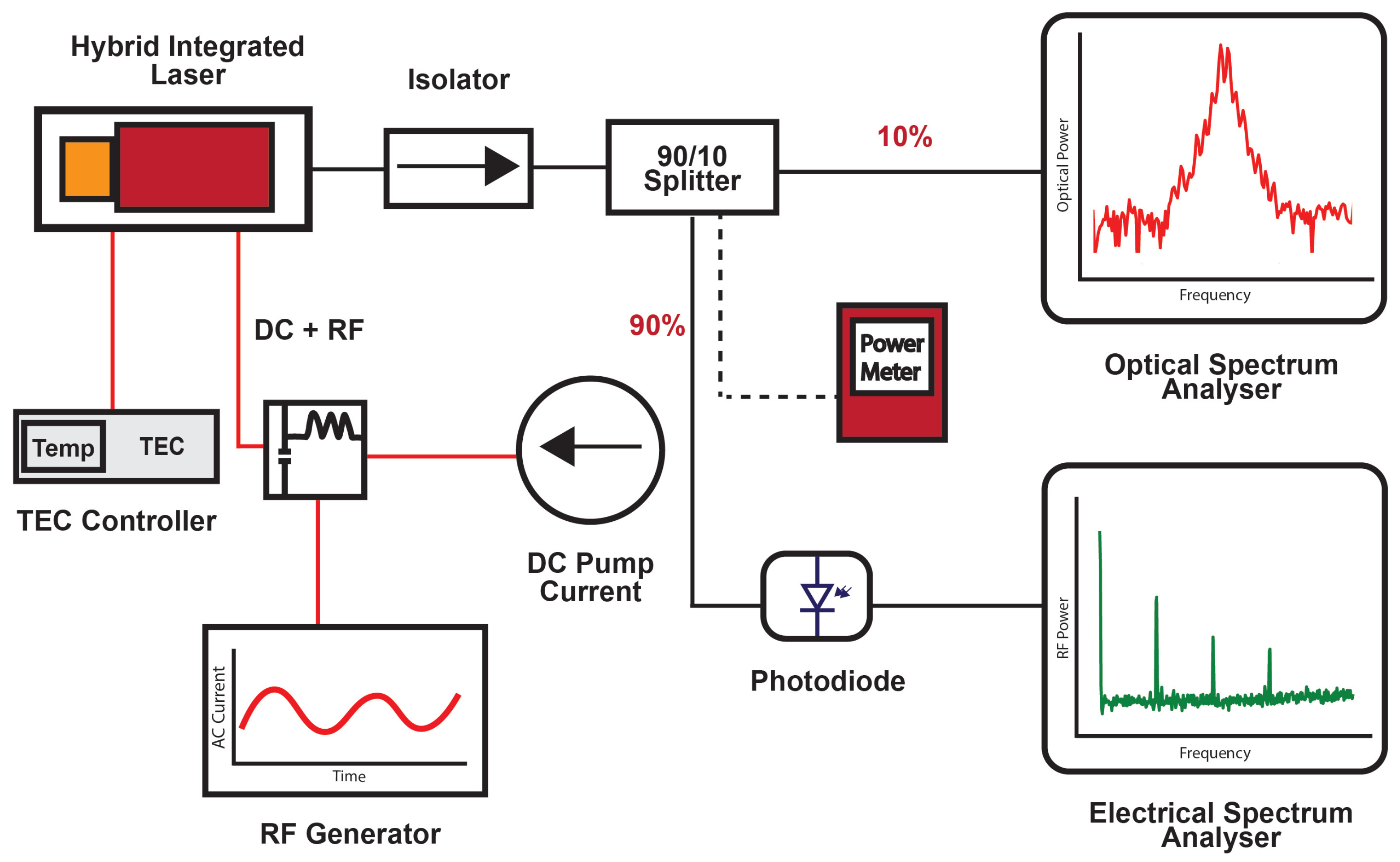
2.2. Experimental Setup
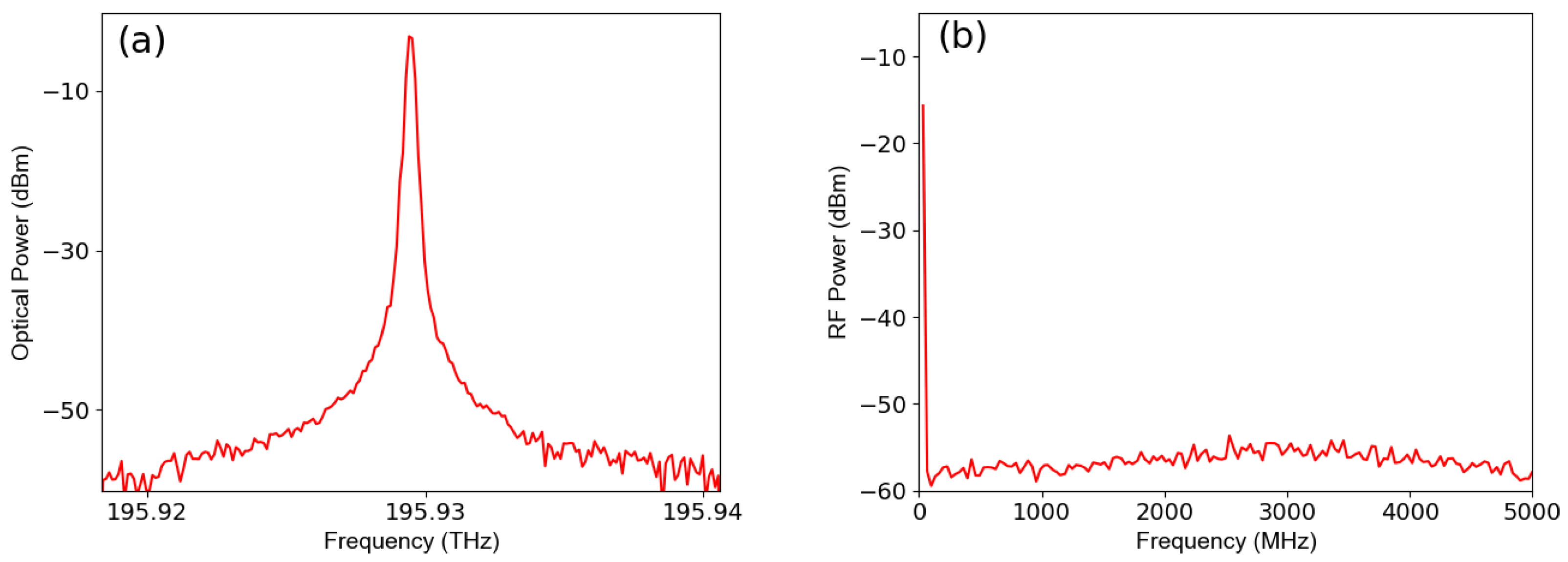
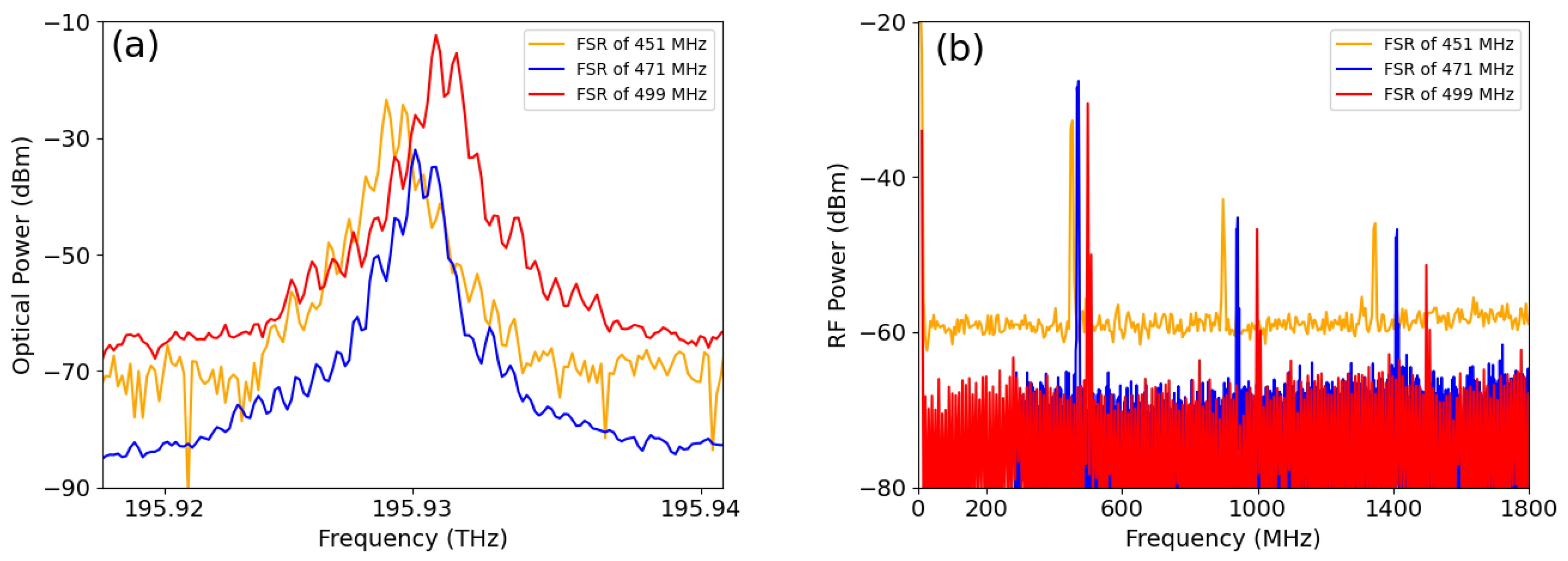
2.3. Passive Mode-Locking
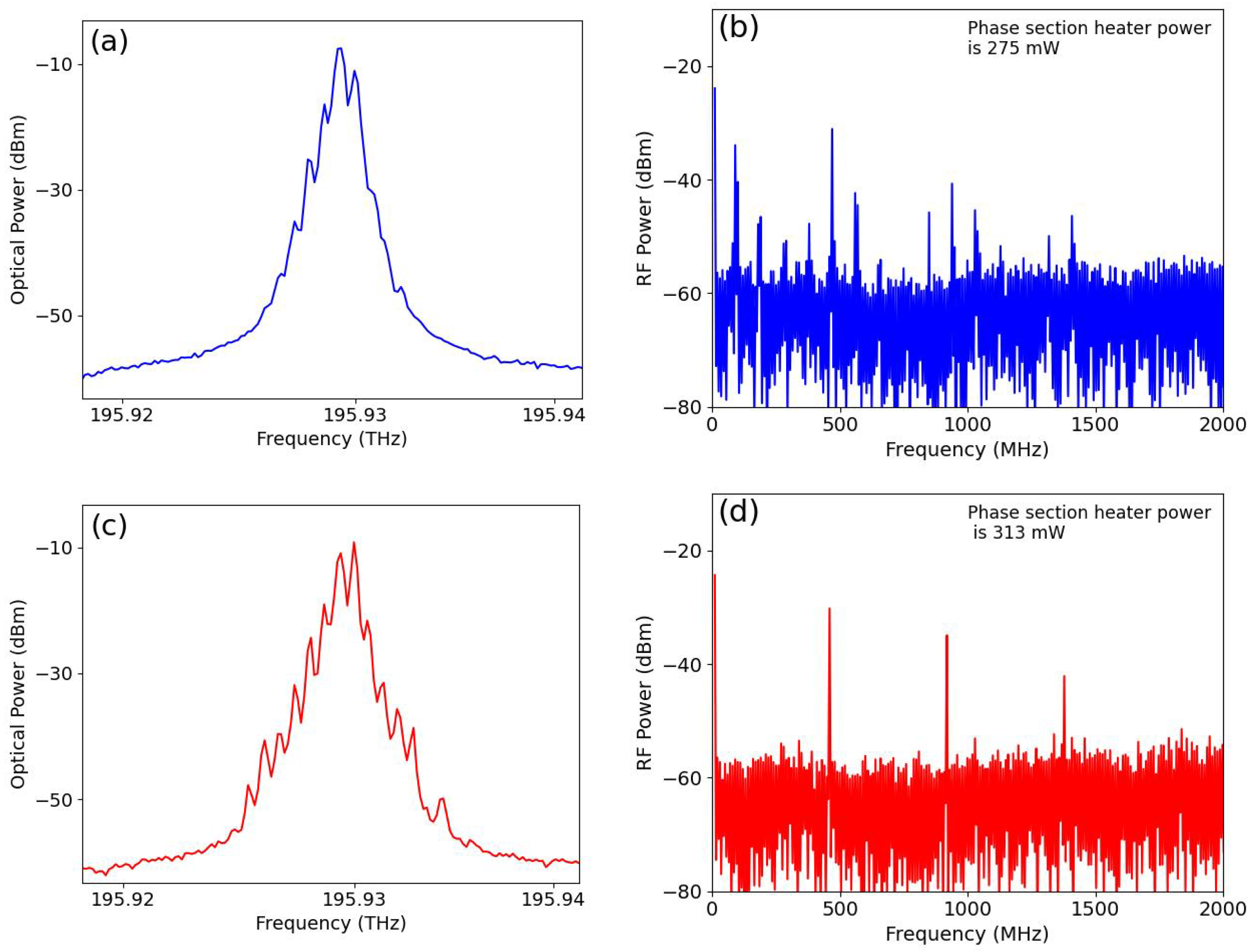
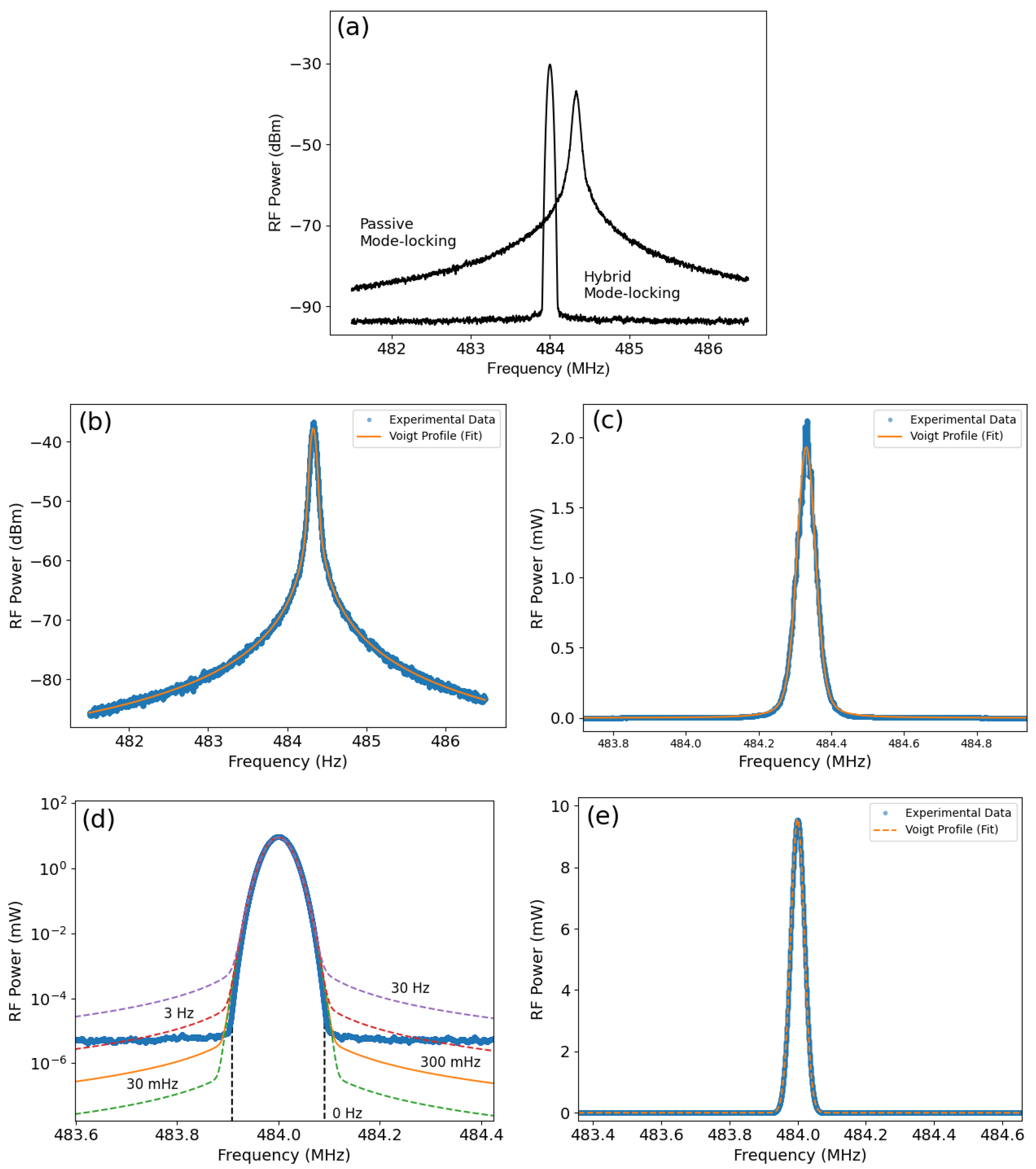
2.4. Hybrid Mode-Locking
2.5. Locking Range
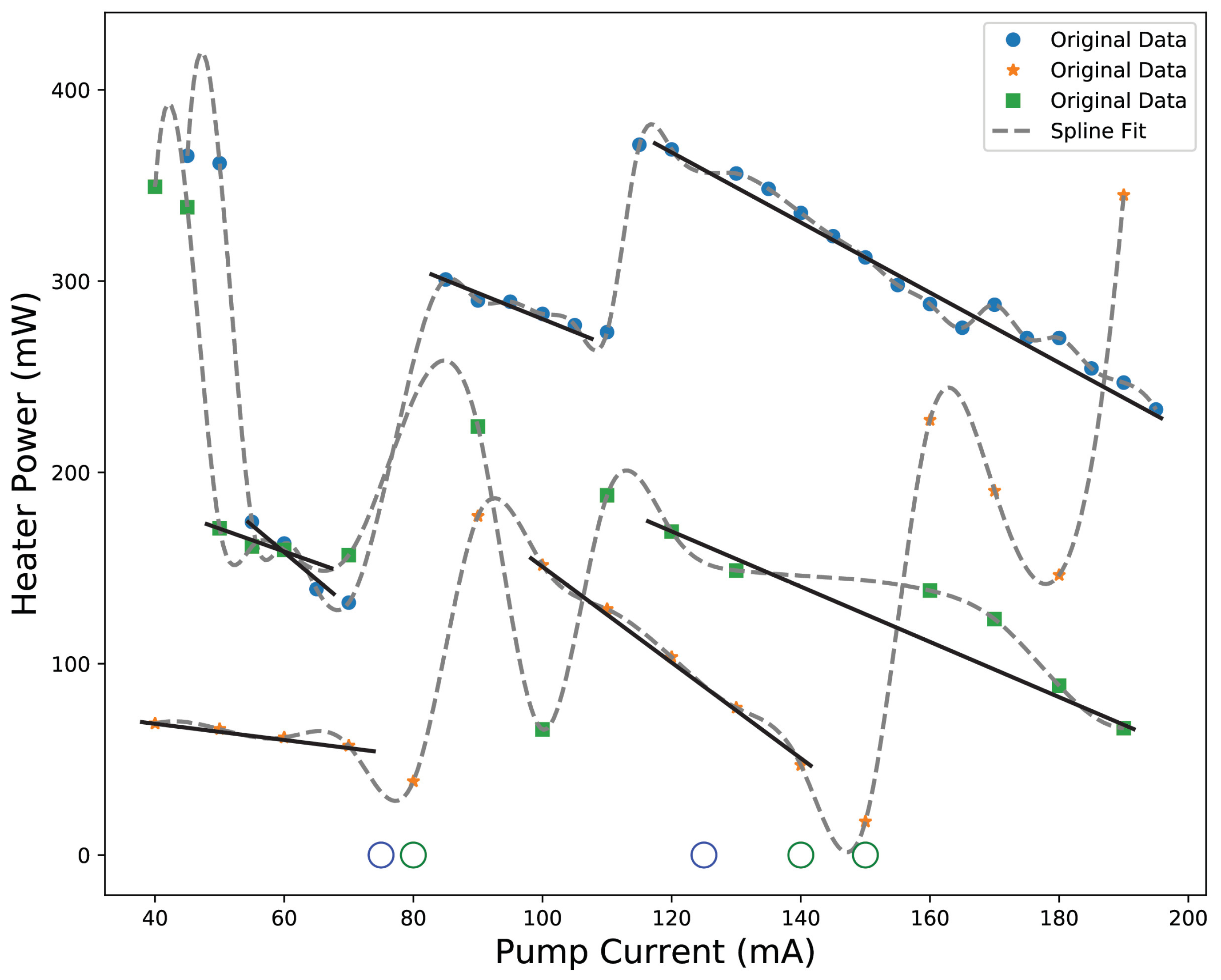
2.6. Relation Between Pump Current and Heater Settings
3. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cuyvers, S.; Haq, B.; Op de Beeck, C.; Poelman, S.; Hermans, A.; Wang, Z.; Gocalinska, A.; Pelucchi, E.; Corbett, B.; Roelkens, G.; et al. Low Noise Heterogeneous III-V-on-Silicon-Nitride Mode-Locked Comb Laser. Laser Photonics Rev. 2021, 15, 2000485. [Google Scholar] [CrossRef]
- Uvin, S.; Keyvaninia, S.; Lelarge, F.; Duan, G.H.; Kuyken, B.; Roelkens, G. Narrow line width frequency comb source based on an injection-locked III-V-on-silicon mode-locked laser. Opt. Express 2016, 24, 5277. [Google Scholar] [CrossRef]
- Diddams, S.; Vahala, K.-J.; Udem, T. Optical frequency combs: Coherently uniting the electromagnetic spectrum. Science 2020, 369, eaay3676. [Google Scholar] [CrossRef]
- Kranendonk, L.A.; An, X.; Caswell, A.W.; Herold, R.E.; Sanders, S.T.; Huber, R.; Fujimoto, J.G.; Okura, Y.; Urata, Y. High speed engine gas thermometry by Fourier-domain mode-locked laser absorption spectroscopy. Opt. Express 2007, 15, 15115. [Google Scholar] [CrossRef]
- Trocha, P.; Kemal, J.N.; Gaimard, Q.; Guy, A.; François, L.; Abderrahim, R.; Wolfgang, F.; Sebastian, R.; Christian, K. Ultra-fast optical ranging using quantum-dash mode-locked laser diodes. Sci. Rep. 2022, 12, 1076. [Google Scholar] [CrossRef] [PubMed]
- Coburn, S.; Alden, C.B.; Wright, R.; Cossel, K.; Baumann, E.; Truong, G.-W.; Giorgetta, F.; Sweeney, C.; Newbury, N.R.; Prasad, K.; et al. Regional trace-gas source attribution using a field-deployed dual frequency comb spectrometer. Optica 2018, 5, 320. [Google Scholar] [CrossRef]
- Swann, W.C.; Gilbert, S.L. Pressure-induced shift and broadening of 1510–1540-nm acetylene wavelength calibration lines. J. Opt. Soc. Am. B 2000, 17, 1263. [Google Scholar] [CrossRef]
- Lei, L.; Zhang, J.; Zhou, J.; Gao, G.; Xue, M.; Zhang, X. Study on all-optical cross-band frequency conversion for communication satellite. In Proceedings of the 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017; Volume 5, p. 1079. [Google Scholar]
- Reimer, C.; Caspani, L.; Clerici, M.; Ferrera, M.; Kues, M.; Peccianti, M.; Pasquazi, A.; Razzari, L.; Little, B.E.; Chu, S.T.; et al. Integrated frequency comb source of heralded single photons. Opt. Express 2014, 22, 6535. [Google Scholar] [CrossRef]
- Nicholas, H.; Bunandar, D.; Pant, M.; Steinbrecher, G.; Mower, J.; Mihika, P.; Baehr-Jones, T.; Hochberg, M.; Englund, D. Large-scale quantum photonic circuits in silicon. Nanophotonics 2016, 5, 456. [Google Scholar]
- Taballione, C.; Anguita, M.; Goede, M.; Venderbosch, P.; Kassenberg, B.; Snijders, H.; Kannan, N.; Vleeshouwers, W.; Smith, D.; Epping, J.; et al. Large-scale quantum photonic circuits in silicon. Quantum 2023, 7, 1071. [Google Scholar] [CrossRef]
- Mahmudlu, H.; Robert, J.; Rees, A.; Kashi, A.H.; Epping, J.; Haldar, R.; Boller, K.-J.; Kues, M. Fully on-chip photonic turnkey quantum source for entangled qubit/qudit state generation. Nat. Photonics 2023, 17, 518. [Google Scholar] [CrossRef]
- Swann, W.; Newbury, N.R. Frequency-resolved coherent lidar using a femtosecond fiber laser. Opt. Lett. 2006, 31, 826. [Google Scholar] [CrossRef] [PubMed]
- Pascal, D.; Schliesser, A.; Arcizet, O.; Wilken, T.; Holzwarth, R.; Kippenberg, T. Optical Frequency Comb Generation from a Monolithic Microresonator. Nature 2008, 450, 1214. [Google Scholar]
- Stern, B.; Ji, X.; Okawachi, Y.; Gaeta, A.L.; Lipson, M. Battery-operated integrated frequency comb generator. Nature 2018, 562, 401. [Google Scholar] [CrossRef]
- Wang, P.-H.; Jaramillo-Villegas, J.A.; Xuan, X.; Xue, X.; Bao, C.; Leaird, D.E.; Qi, M.; Weiner, A.M. Intracavity characterization of micro-comb generation in the single-soliton regime. Opt. Express 2016, 24, 10890. [Google Scholar] [CrossRef]
- Hou, L.; Haji, M.; Marsh, J.H. Monolithic Mode-Locked Laser with an Integrated Optical Amplifier for Low-Noise and High-Power Operation. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1100808. [Google Scholar] [CrossRef]
- Pozzi, F.; De La Rue, R.; Sorel, M. Dual-Wavelength InAlGaAs–InP Laterally Coupled Distributed Feedback Laser. IEEE Photonics Technol. Lett. 2007, 18, 2563. [Google Scholar] [CrossRef]
- Guzmán, R.; Gordon, C.; Orbe, L.; Carpintero, G. 1 GHz InP on-chip monolithic extended cavity colliding-pulse mode-locked laser. Opt. Lett. 2017, 42, 2318. [Google Scholar] [CrossRef]
- Bastiaens, H.M.J.; Neijts, G.; Memon, A.; Fan, Y.; Mak, J.; Geskus, D.; Hoekman, M.; Moskalenko, V.; Bente, E.A.J.M.; Boller, K.-J. First demonstration of a hybrid integrated InP-Si3N4 diode laser for broadband optical frequency comb generation. Proc. SPIE 2021, 11705, 1170508. [Google Scholar]
- Yoon, T.H.; Jang, G.H. Period-doubling and total mode-locking, and chaotic pulsations in a GaAs ridge wave-guide external-cavity diode laser. Opt. Express 2007, 15, 14704. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Turaev, D. Model for passive mode locking in semiconductor lasers. Phys. Rev. A 2005, 72, 33808. [Google Scholar] [CrossRef]
- Zhang, Q.; Jasim, K.; Nurmikko, A.V.; Mooradian, A.; Carey, G.; Ha, W.; Ippen, E. Operation of a passively mode-locked extended-cavity surface-emitting diode laser in multi-GHz regime. IEEE Photonics Technol. Lett. 2004, 16, 885. [Google Scholar] [CrossRef]
- Paschotta, R. Field Guide to Laser Pulse Generation; SPIE: Bellingham, WA, USA, 2008; Volume FG14, ISBN 9780819478276. [Google Scholar]
- Liao, R.; Chao, M.; Youjian, S.; Demircan, A.; Steinmeyer, G. Spontaneous emission noise in mode-locked lasers and frequency combs. Phys. Rev. A 2020, 102, 013506. [Google Scholar] [CrossRef]
- Huber, R.; Wojtkowski, M.; Fujimoto, J.G. Fourier Domain Mode Locking (FDML): A new laser operating regime and applications for optical coherence tomography. Opt. Express 2006, 14, 3225. [Google Scholar] [CrossRef] [PubMed]
- Heck, M.; Bowers, J.E. Integrated Fourier-Domain Mode-Locked Lasers: Analysis of a Novel Coherent Comb Laser. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 201. [Google Scholar] [CrossRef]
- Dong, B.; Dumont, M.; Terra, O.; Wang, H.; Netherton, A.; Bowers, J.E. Broadband quantum-dot frequency-modulated comb laser. Light Sci. Appl. 2023, 12, 182. [Google Scholar] [CrossRef]
- Nagar, R.; Abraham, D.; Tessler, N.; Fraenkel, A.; Eisenstein, G.; Ippen, E.P.; Koren, U.; Raybon, G. Broadband quantum-dot frequency-modulated comb laser. Opt. Lett. 1991, 16, 1750. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Binh, L.N. Generation of high order multi-bound solitons and propagation in optical fibers. Opt. Commun. 2009, 282, 2394. [Google Scholar] [CrossRef]
- Ibrahimi, Y.; Boust, S.; Wilmart, Q.; Paret, J.-F.; Garreau, A.; Mekhazni, K.; Fortin, C.; Duport, F.; Dijk, F.; Sciancalepore, C.; et al. Low FSR mode-locked laser based on InP-Si3N4 hybrid integration. J. Light. Technol. 2021, 39, 7573. [Google Scholar] [CrossRef]
- Yuan, M.; Wang, W.; Wang, X.; Wang, Y.; Yang, Q.; Cheng, D.; Liu, Y.; Huang, L.; Zhang, M.; Liang, B.; et al. Demonstration of an external cavity semiconductor mode-locked laser. Opt. Lett. 2021, 46, 4855. [Google Scholar] [CrossRef] [PubMed]
- Rimoldi, C.; Columbo, L.L.; Bovington, J.; Romero-García, S.; Gioannini, M. CW Emission and Self-Pulsing in a III-V/SiN Hybrid Laser with Narrow Band Mirror. IEEE Photonics J. 2022, 14, 1540707. [Google Scholar] [CrossRef]
- Vahala, K.; Yariv, A. Detuned loading in coupled cavity semiconductor lasers—Effect on quantum noise and dynamics. Appl. Phys. Lett. 1984, 45, 501. [Google Scholar] [CrossRef]
- Mak, J.; van Rees, A.; Fan, Y.; Klein, E.J.; Geskus, D.; van der Slot, P.J.M.; Boller, K.-J. Linewidth narrowing via low-loss dielectric waveguide feedback circuits in hybrid integrated frequency comb lasers. Opt. Express 2019, 27, 13307. [Google Scholar] [CrossRef]
- Klaver, Y.; Epping, J.P.; Roeloffzen, C.G.H.; Marpaung, D.A.I. Self-mode-locking in a high-power hybrid silicon nitride integrated laser. Opt. Lett. 2022, 47, 198. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; van Rees, A.; van der Slot, P.J.M.; Mak, J.; Oldenbeuving, R.M.; Hoekman, M.; Geskus, D.; Roeloffzen, C.G.H.; Boller, K.-J. Hybrid integrated InP-Si3N4 diode laser with a 40-Hz intrinsic linewidth. Opt. Express 2020, 28, 21713. [Google Scholar] [CrossRef]
- Roeloffzen, C.G.H.; Hoekman, M.; Klein, E.J.; Wevers, L.S.; Timens, R.B.; Marchenko, D.; Geskus, D.; Dekker, R.; Alippi, A.; Grootjans, R.; et al. Low-Loss Si3N4 TriPleX Optical Waveguides: Technology and Applications Overview. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 4400321. [Google Scholar] [CrossRef]
- Tran, M.A.; Huang, D.; Guo, J.; Komljenovic, T.; Morton, P.A.; Bowers, J.E. Ring-Resonator Based Widely-Tunable Narrow-Linewidth Si/InP Integrated Lasers. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1500514. [Google Scholar] [CrossRef]
- van Rees, A.; Fan, Y.; Geskus, D.; Klein, E.J.; Oldenbeuving, R.M.; van der Slot, P.J.M.; Boller, K.-J. Ring resonator enhanced mode-hop-free wavelength tuning of an integrated extended-cavity laser. Opt. Express 2020, 28, 5669. [Google Scholar] [CrossRef]
- Liu, B.; Shakouri, A.; Bowers, J.E. Wide tunable double ring resonator coupled lasers. IEEE Photonics Technol. Lett. 2002, 14, 600. [Google Scholar]
- Rimoldi, C.; Columbo, L.L.; Bovington, J.; Romero-García, S.; Gioannini, M. Damping of relaxation oscillations, photon-photon resonance, and tolerance to external optical feedback of III-V/SiN hybrid lasers with a dispersive narrow band mirror. Opt. Express 2022, 30, 11090. [Google Scholar] [CrossRef] [PubMed]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Coherent Multiheterodyne Spectroscopy Using Stabilized Optical Frequency Combs. Phys. Rev. Lett. 2008, 100, 013902. [Google Scholar] [CrossRef]
- Arkhipov, R.; Pimenov, A.; Radziunas, M.; Rachinskii, D.; Vladimirov, A.G.; Arsenijević, D.; Schmeckebier, H.; Bimberg, D. Hybrid Mode Locking in Semiconductor Lasers: Simulations, Analysis, and Experiments. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1100208. [Google Scholar] [CrossRef]
- Vladimirov, A.G.; Wolfrum, M.; Fiol, G.; Arsenijevic, D.; Bimberg, D.; Viktorov, E.; Mandel, P.; Rachinskii, D. Locking characteristics of a 40-GHz hybrid mode-locked monolithic quantum dot laser. Proc. SPIE 2010, 7720, 77200Y. [Google Scholar]
- Chen, M.; Meng, Z.; Wang, J.; Chen, W. Ultra-narrow linewidth measurement based on Voigt profile fitting. Opt. Express. 2015, 23, 6803. [Google Scholar] [CrossRef]
- Han, J.-H.; Park, S.W. Effect of temperature and injection current on characteristics of TO–CAN packaged Fabry–Perot laser diode. Curr. Appl. Phys. 2007, 7, 6. [Google Scholar] [CrossRef]
- Alemany, R.; Muñoz, P.; Pastor, D.; Domínguez, C. Thermo-Optic Phase Tuners Analysis and Design for Process Modules on a Silicon Nitride Platform. Photonics 2007, 8, 496. [Google Scholar] [CrossRef]
- Della Corte, F.G.; Cocorullo, G.; Iodice, M.; Rendina, I. Temperature dependence of the thermo-optic coefficient of InP, GaAs, and SiC from room temperature to 600 K at the wavelength of 1.5 μm. Appl. Phys. Lett. 2000, 77, 1614. [Google Scholar] [CrossRef]
- Arbabi, A.; Goddard, L.L. Measurements of the refractive indices and thermo-optic coefficients of Si3N4 and SiOx using microring resonances. Opt. Lett. 2013, 38, 3878. [Google Scholar] [CrossRef]
- Wang, Z.; Van Gasse, K.; Moskalenko, V.; Latkowski, S.; Bente, E.; Kuyken, B.; Roelkens, G.A. III-V-on-Si Ultra-dense comb laser. Light Sci. Appl. 2017, 6, e16260. [Google Scholar] [CrossRef]
- Mak, J. Extending Hybrid Integrated Diode Lasers to Multi-Frequency Oscillation. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2023. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memon, A.; van Rees, A.; Mak, J.; Fan, Y.; van der Slot, P.J.M.; Bastiaens, H.M.J.; Boller, K.-J. Absorber-Free Mode-Locking of a Hybrid Integrated Diode Laser at Sub-GHz Repetition Rate. Photonics 2024, 11, 1002. https://doi.org/10.3390/photonics11111002
Memon A, van Rees A, Mak J, Fan Y, van der Slot PJM, Bastiaens HMJ, Boller K-J. Absorber-Free Mode-Locking of a Hybrid Integrated Diode Laser at Sub-GHz Repetition Rate. Photonics. 2024; 11(11):1002. https://doi.org/10.3390/photonics11111002
Chicago/Turabian StyleMemon, Anzal, Albert van Rees, Jesse Mak, Youwen Fan, Peter J. M. van der Slot, Hubertus M. J. Bastiaens, and Klaus-Jochen Boller. 2024. "Absorber-Free Mode-Locking of a Hybrid Integrated Diode Laser at Sub-GHz Repetition Rate" Photonics 11, no. 11: 1002. https://doi.org/10.3390/photonics11111002
APA StyleMemon, A., van Rees, A., Mak, J., Fan, Y., van der Slot, P. J. M., Bastiaens, H. M. J., & Boller, K.-J. (2024). Absorber-Free Mode-Locking of a Hybrid Integrated Diode Laser at Sub-GHz Repetition Rate. Photonics, 11(11), 1002. https://doi.org/10.3390/photonics11111002





