NOMA Visible Light Communications with Distinct Optical Beam Configurations
Abstract
1. Introduction
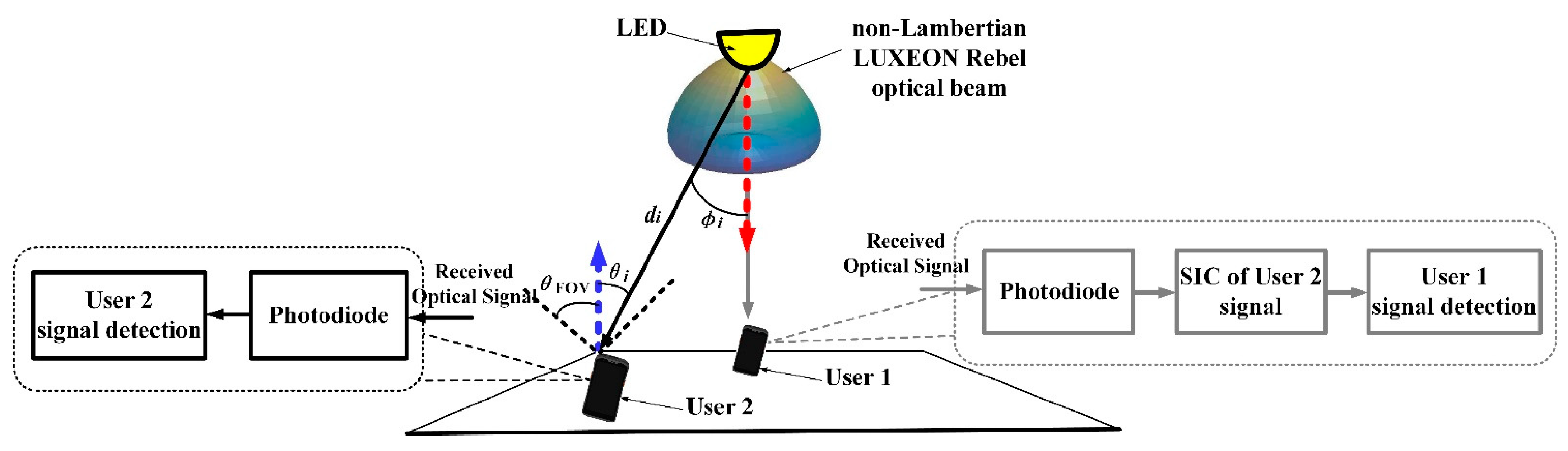
2. NOMA Visible Light Communications with Distinct Optical Beam Configurations
2.1. NOMA Visible Light Communications with Baseline Lambertian Optical Beam Configuration
2.2. NOMA Visible Light Communications with Distinct Non-Lambertian Optical Beam Configuration
3. Numerical Evaluation
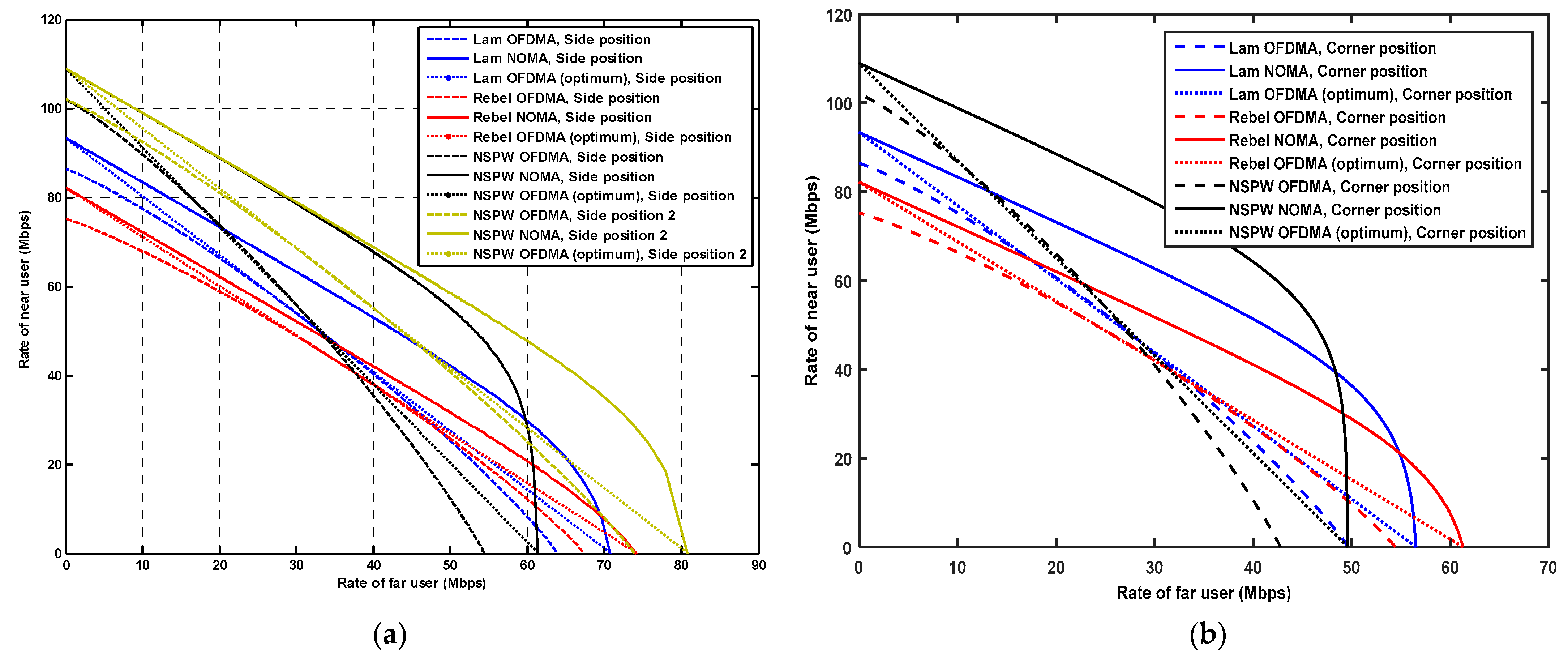
3.1. Comparison of Capacity Region Performance
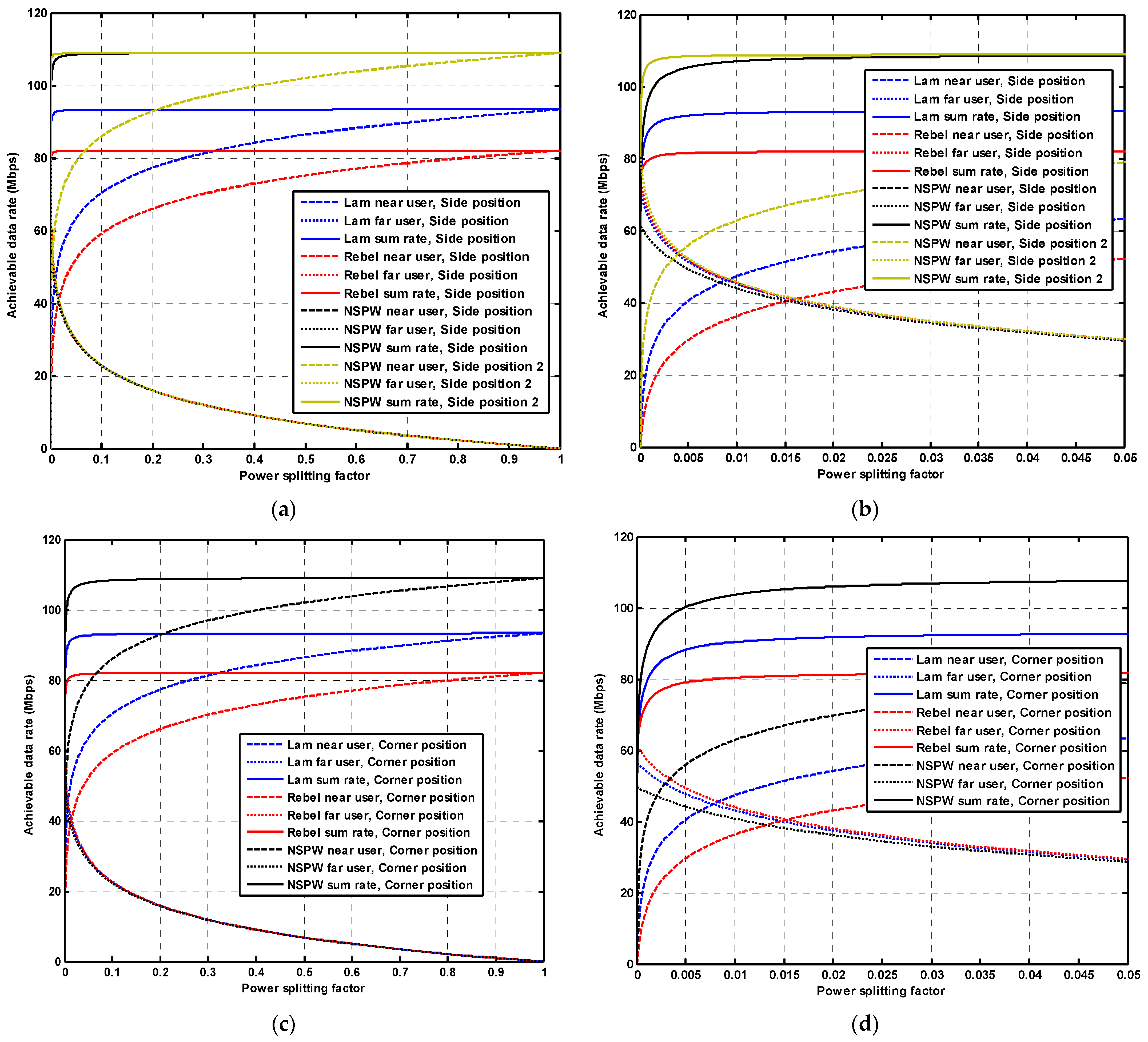
3.2. Effect of Power Splitting Factor
3.3. Effect of Total Available Signal Power
4. Discussion of Contributions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Zhang, H.; Cosmas, J.; Jawad, N.; Ali, K.; Meunier, B.; Zarakovitis, C.C. Internet of radio and light: 5G building network radio and edge architecture. Intell. Converg. Netw. 2020, 1, 37–57. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Hossan, M.T.; Islam, A.; Jang, Y.M. A comparative survey of optical wireless technologies: Architectures and applications. IEEE Access 2018, 6, 9819–9840. [Google Scholar] [CrossRef]
- Sun, S.; Yang, F.; Song, J. Sum rate maximization for intelligent reflecting surface-aided visible light communications. IEEE Commun. Lett. 2021, 25, 3619–3623. [Google Scholar] [CrossRef]
- Sun, S.; Wang, T.; Yang, F.; Song, J.; Han, Z. Intelligent reflecting surface-aided visible light communications: Potentials and challenges. IEEE Veh. Technol. Mag. 2022, 17, 47–56. [Google Scholar] [CrossRef]
- Wang, T.; Yang, F.; Song, J.; Han, Z. Dimming Techniques of Visible Light Communications for Human-Centric Illumination Networks: State-of-the-Art, Challenges, and Trends. IEEE Wirel. Commun. 2020, 27, 88–95. [Google Scholar] [CrossRef]
- Ding, J.; I, C.-L.; Wang, J.; Song, J. Coverage Performance of Non-Lambertian Underwater Wireless Optical Communications for 6G Internet of Things. Inventions 2024, 9, 49. [Google Scholar] [CrossRef]
- Hamza, A.S.; Deogun, J.S.; Alexander, D.R. Classification framework for free space optical communication links and systems. IEEE Commun. Surv. Tuts. 2019, 21, 1346–1382. [Google Scholar] [CrossRef]
- Higuchi, K.; Benjebbour, A. Non-orthogonal Multiple Access (NOMA) with Successive Interference Cancellation for Future Radio Access. IEICE Trans. Commun. 2015, 3, 403–414. [Google Scholar] [CrossRef]
- Bawazir, S.; Sofotasios, P.; Muhaidat, S.; Al-Hammadi, Y.; Karagiannidis, G. Multiple Access for Visible Light Communications: Research Challenges and Future Trends. IEEE Access 2018, 6, 26167–26174. [Google Scholar] [CrossRef]
- Kizilirmak, R.; Rowell, C.; Uysal, M. Non-orthogonal multiple access (NOMA) for indoor visible light communications. In Proceedings of the 2015 4th International Workshop on Optical Wireless Communications (IWOW), Istanbul, Turkey, 7–8 September 2015; IEEE: New York, NY, USA, 2015. [Google Scholar]
- Rajput, V.; Ashok, D.; Chockalingam, A. Joint NOMA Transmission in Indoor Multi-cell VLC Networks. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Raj, R.; Dixit, A. An Energy-Efficient Power Allocation Scheme for NOMA-Based IoT Sensor Networks in 6G. IEEE Sens. J. 2022, 22, 7371–7384. [Google Scholar] [CrossRef]
- Alhammadi, A.; Bariah, L.; Muhaidat, S.; Alqutayri, M.; Sofotasios, P.C.; Debbah, M. Deep Q-Learning-based Resource Allocation in NOMA Visible Light Communications. IEEE Open J. Commun. Soc. 2022, 3, 2284–2297. [Google Scholar] [CrossRef]
- Raj, R.; Jindal, K.; Dixit, A. Fairness Enhancement of Non-Orthogonal Multiple Access in VLC-Based IoT Networks for Intravehicular Applications. IEEE Trans. Veh. Technol. 2022, 71, 7414–7427. [Google Scholar] [CrossRef]
- Tennakoon, P.; Rajkumar, S.; Jayakody, D. Game Theory Based Delta-OMA Scheme for VLC Network. IEEE Access 2023, 50, 10777–10791. [Google Scholar] [CrossRef]
- Uday, T.; Kumar, A.; Natarajan, L. Joint NOMA for Improved ser of Cell-Edge Users in Multi-Cell Indoor VLC. IEEE Wirel. Commun. Lett. 2022, 11, 13–17. [Google Scholar] [CrossRef]
- Chen, C.; Zhong, W.; Yang, H.; Du, P. On the Performance of MIMO-NOMA Based Visible Light Communication Systems. IEEE Photonics Technol. Lett. 2018, 11, 307–310. [Google Scholar] [CrossRef]
- Cang, Y.; Chen, M.; Zhao, J.; Yang, Z.; Huang, C.; Gong, T.; Zhang, Z. Optimal Resource Management for NOMA-Based Visible Light Communication Systems with Shot Noise. IEEE Trans. Green Commun. Netw. 2022, 6, 2015–2031. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, Y.; Liu, X.; Ma, S.; Zhang, X.; Fu, Y. Performance Analysis for DF Relay-aided Visible Light Communication System with NOMA. IEEE Photonics J. 2022, 6, 7350809. [Google Scholar] [CrossRef]
- Tran, M.; Vu, T.; Kim, S. Performance Analysis of Optical Backhauled Cooperative NOMA Visible Light Communication. IEEE Trans. Veh. Technol. 2021, 70, 12932–12945. [Google Scholar] [CrossRef]
- Tran, G.; Kim, S. Performance Analysis of Short Packets in NOMA VLC Systems. IEEE Access 2022, 10, 6505–6517. [Google Scholar] [CrossRef]
- Li, G.; Wang, P.; Yang, T.; Che, H. Secrecy Sum-Rate Enhancement for NOMA-VLC System with Pseudo User. IEEE Commun. Lett. 2023, 27, 243–247. [Google Scholar] [CrossRef]
- Shi, G.; Aboagye, S.; Ngatched, T.; Dobre, O.; Li, Y.; Cheng, W. Secure Transmission in NOMA-Aided Multiuser Visible Light Communication Broadcasting Network with Cooperative Precoding Design. IEEE Trans. Inf. Forensics Secur. 2022, 17, 3123–3138. [Google Scholar] [CrossRef]
- Komine, T.; Nakagawa, M. Fundamental analysis for visible-light communication system using LED lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Moreno, I.; Sun, C.-C. Modeling the radiation pattern of LEDs. Opt. Exp. 2008, 16, 1808–1819. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Chih-Lin, I.; Xu, Z. Indoor optical wireless channel characteristics with distinct source radiation patterns. IEEE Photonics J. 2016, 8, 7900115. [Google Scholar] [CrossRef]
- Ding, J.; I, C.-L.; Wang, J.; Song, J. Performance Evaluation of Non-Lambertian SLIPT for 6G Visible Light Communication Systems. Photonics 2024, 11, 856. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Room size (W × L × H) | 5 × 5 × 3 m3 |
| Total available signal power of transmitter | 1 W |
| Number of transmitters | 1 |
| Location of transmitter | (2.5, 2.5, 3) m |
| LED Lambertian semi-angle | 60° |
| Receiver field of view | 90° |
| Height of receiving plane | 0.7 m |
| Physical area of PD | 1.0 cm2 |
| Responsivity of PD | 0.25 A/W |
| Concentrator refractive index | 1.54 |
| Optical filter gain | 1 |
| LED modulation bandwidth | 20 MHz |
| VLC noise power density | −180 dBm/Hz |
| Location of near user | (2.5, 2.5, 0.7) m |
| Location 1 of far user | (2.5, 0.5, 0.7) m |
| Location 2 of far user | (0.5, 0.5, 0.7) m |
| Location 3 of far user | (0.5, 2.5, 0.7) m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, J.; I, C.-L.; Wang, J.; Yang, H. NOMA Visible Light Communications with Distinct Optical Beam Configurations. Photonics 2024, 11, 944. https://doi.org/10.3390/photonics11100944
Ding J, I C-L, Wang J, Yang H. NOMA Visible Light Communications with Distinct Optical Beam Configurations. Photonics. 2024; 11(10):944. https://doi.org/10.3390/photonics11100944
Chicago/Turabian StyleDing, Jupeng, Chih-Lin I, Jintao Wang, and Hui Yang. 2024. "NOMA Visible Light Communications with Distinct Optical Beam Configurations" Photonics 11, no. 10: 944. https://doi.org/10.3390/photonics11100944
APA StyleDing, J., I, C.-L., Wang, J., & Yang, H. (2024). NOMA Visible Light Communications with Distinct Optical Beam Configurations. Photonics, 11(10), 944. https://doi.org/10.3390/photonics11100944






