Erbium-Doped Tunable Fiber Laser Based on a Vernier Effect Filter

Abstract

A novel vernier effect filter is designed utilizing two cascaded Mach–Zehnder interferometers (MZIs). Integrating the filter into an erbium-doped fiber laser (EDFL), the tunability of laser wavelength is achieved. Each MZI comprises two sequentially interconnected 3 dB optical couplers (OCs), where the incoming light is initially split into two arms at the first OC and subsequently recombined at the second OC. Interference occurs due to the optical path difference between these two beams. Notably, the two MZIs exhibit closely matched free spectral ranges (FSRs), leading to the formation of a broadened envelope in the superimposed spectrum. By delicately adjusting the optical path difference between the two arms of one MZI, a little drift of the interference spectrum is induced. This small amount of drift, in turn, triggers a significant movement of the envelope, giving rise to the so-called vernier effect. Integrating the vernier effect filter into an EDFL, the wavelength of the fiber laser can be tuned from 1542.56 nm to 1556.62 nm, with a tuning range of 14.06 nm. Furthermore, by employing a high-precision stepper motor, a remarkable tuning accuracy of 0.01 nm is attainable. The side mode suppression ratio of all wavelengths is above 55 dB. In comparison to reported tunable fiber lasers utilizing MZI filters, the proposed fiber laser in this study offers enhanced precision and a more user-friendly tuning process.

1. Introduction

Tunable wavelength lasers hold immense promise for a diverse array of applications, spanning optical communications, spectroscopy, biomedical imaging, and industrial processing [1,2,3,4,5]. Depending on the gain medium employed, these lasers operate across different wavelength bands. Notably, erbium-doped fiber lasers (EDFLs) utilize erbium-ion-doped fibers as their gain medium, leveraging the unique energy level structure of erbium ions to generate light around the 1.5 μm band. These lasers offer several advantages, including high output power, low thresholds, excellent beam quality, and natural compatibility with conventional optical fibers, making them indispensable components in optical communication and fiber sensing systems. Furthermore, their robust temperature stability enhances their reliability and performance [6,7,8,9,10].

To suppress gain competition in EDFLs and achieve stable, tunable wavelength output, wavelength-selective devices play a pivotal role [11,12,13]. Various technologies have been employed in EDFLs to achieve stable tunable outputs, including fiber Bragg gratings, Lyot filters, and optical fiber interference filters based on diverse interferometer designs [14,15,16,17,18]. Among these, optical fiber interference filters have attracted widespread attention due to their ease of fabrication, simple structure, and seamless integration with other fiber-optic devices.

Optical fiber interference filters typically leverage various interferometer designs to split light transmitted in the fiber into different arms or excite it into different modes. These lights converge and interfere with each other after passing through different optical paths. Light with different wavelengths that meet specific interference conditions is enhanced or suppressed, thereby achieving wavelength separation and selection [19,20,21,22,23]. In order to achieve wavelength tunability, the interference conditions are typically manipulated by altering physical parameters, such as applying tension, bending, or modifying the refractive index [24,25,26,27]. Recently, Ma et al. proposed a tunable fiber laser based on a Fabry–Perot interference (FPI) filter, achieving a tuning range of 7.47 nm from 1559.75 nm to 1567.04 nm [28]. Similarly, L. Li et al. introduced a tunable fiber laser based on a long-period fiber grating filter, enabling tuning of the wavelength from 1552 nm to 1567 nm, with a tuning range of 15 nm [29]. This wavelength-tuning device is essentially a sensor that combines sensing and wavelength selection functions. Therefore, employing sensors with higher sensitivity can facilitate more convenient and precise wavelength tuning.

The vernier effect is a method that significantly enhances the precision of measurement instruments. It has found extensive applications in the field of fiber sensing in recent years. Fiber sensors based on the vernier effect usually consist of two interferometers with comparable FSRs. The superposition of their individual spectra results in a periodic envelope in the superimposed spectrum. By detecting the response of this envelope, the sensitivity of the fiber sensor can be effectively improved. For instance, cascading two strongly coupled seven-core fiber interferometers, the bending sensitivity of a sensor is enhanced from −2.20 nm/m⁻¹ to 42.32 nm/m⁻¹ [30]. Additionally, X. Pan et al. employed two pairs of chirped fiber Bragg gratings (CFBGs), forming two independent CFBG-FPIs, to achieve the vernier effect. The strain sensitivity achieved a remarkable 91-fold increase compared to that of a single CFBG-FPI [31].

In this paper, we present a novel approach where two Mach–Zehnder interferometers (MZIs, denoted as MZI1 and MZI2) are fabricated using 3 dB couplers and connected in series to form a vernier effect sensor. Employing the filter effect of this sensor, we obtain a stable single-wavelength laser output in an EDFL. By stretching one arm of MZI2, the laser wavelength can be tuned within the range of 1542.1 nm to 1558.6 nm. With the stepper motor step size set to 8 nm, a tuning accuracy of 0.01 nm is achievable, while maintaining a side mode suppression ratio (SMSR) exceeding 55 dB across all wavelengths. The proposed fiber laser boasts a simple structure, higher wavelength tuning accuracy, and easier tuning, making it an ideal candidate for various applications.

2. Structure and Operation Principle of the Vernier Effect Filter

The proposed filter is comprised of four 3 dB OCs arranged in a cascaded configuration, as depicted in Figure 1. The incident light first passes through OC1, where it is divided into two separate arms. These arms expose the light to different optical path lengths before converging back into one single-mode fiber at the second OC (OC2). Lights in these two arms interfere with each other due to the optical path difference between them, generating a modulated interference spectrum. OC1 and OC2 collectively form the first MZI (MZI1), while OC3 and OC4 constitute the second MZI (MZI2). Within this setup, MZI2 serves as the sensing interferometer, tasked with detecting changes in the environment, while MZI1 functions as the reference interferometer, providing a stable reference point. When the FSRs of the two MZIs are closely matched but not identical, the transmission spectrum that emerges from their superposition takes the form of an envelope. Intriguingly, even minor variations in the optical path difference within the sensing interferometer (MZI2) lead to pronounced shifts in this envelope. This phenomenon, known as the vernier effect, significantly enhances the sensitivity of the sensor, allowing for more precise and convenient wavelength tuning in the fiber laser.

The transmittance of one single MZI filter can be expressed as:

$$T={\displaystyle \frac{1}{2}}\left(1-cos{\displaystyle \frac{2\pi n_{eff}·\Delta L}{\lambda }}\right) .$$

(1)

In Equation (1), $n_{eff}$ is the effective refractive index, $\lambda$ is the working wavelength, and $\Delta L$ is the length difference between the two arms of the MZI.

The transmission spectrum is periodic, and the peak wavelengths satisfy the

$${ n}_{eff}·\Delta L=m\lambda ,m=\mathrm{1,2},\cdots .$$

(2)

The FSR of a single MZI filter can be expressed as:

$$\Delta \lambda ={\displaystyle \frac{{\lambda }^2}{n_{eff}·∆L}}$$

(3)

The pigtails of the two arms are the same single-mode fibers, so the effective refractive index $n_{eff}$ is the same. From Equation (3), the FSR of the oscillation curve is inversely proportional to $\Delta L$.

When two MZIs with close FSRs are cascaded in series, the superimposed transmission spectrum shows a large envelope. The FSR of the vernier effect envelope can be expressed by Equation (4) as:

$${ FSR}_v={\displaystyle \frac{{FSR}_1{·FSR}_2}{\left|{FSR}_1-{FSR}_2\right|}} ,$$

(4)

where ${FSR}_1$ and ${FSR}_2$ are the FSRs of MZI1 and MZI2, respectively, and ${FSR}_v$ is the FSR of the vernier effect envelope of the superimposed transmission spectrum. When we change the optical range difference by stretching one arm of MZI2, the transmission curve of MZI2 shifts. A small drift in the transmission curve of MZI2 will cause a significant shift in the envelope. The amplification of the vernier effect sensor is expressed as:

$$M={\displaystyle \frac{{FSR}_v}{{FSR}_2}}={\displaystyle \frac{{FSR}_1}{\left|{FSR}_1-{FSR}_2\right|}} .$$

(5)

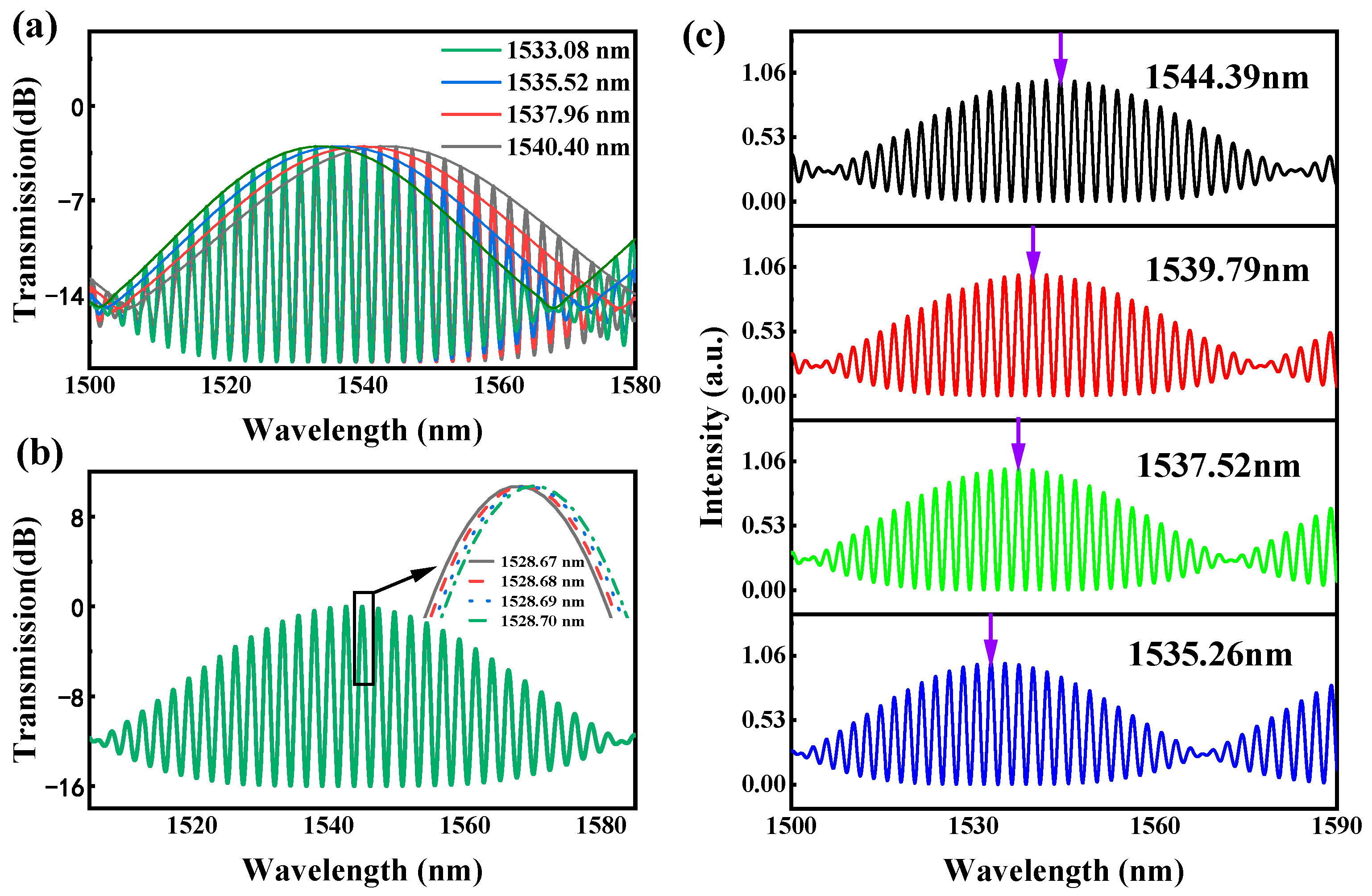
We have conducted numerical simulations to analyze the characteristics of the vernier effect filter. Figure 2a illustrates the transmission curves of these two MZIs as well as their superimposed transmission. Specifically, MZI1 exhibits an FSR of 2.42 nm, while MZI2 has an FSR of 2.34 nm. The superimposed spectrum clearly exhibits an envelope. During the simulation, we varied the optical path difference of MZI2 to evaluate the corresponding shift in the envelope of the superimposed spectrum. As shown in Figure 2(a2,a3), when the optical path difference of MZI2 was adjusted by 128 nm, the transmission curve of MZI2 shifted by 0.11 nm. Consequently, the peak wavelength of the envelope in the superimposed spectrum shifted from 1549.12 nm to 1551.53 nm, covering a range of 2.41 nm. According to Equation (5), the amplification is 21.9. As mentioned above, the FSRs of MZI1 and MZI2 are 2.42 nm and 2.34 nm. The calculated magnification is 30.2. For comparison, Figure 2b presents the superimposed spectra when there is a significant difference between FSR1 and FSR2. Specifically, when FSR1 is 80.23 nm and FSR2 is 11.06 nm, the FSR of the resulting envelope aligns with the FSR of MZI1. In this scenario, the drift of the peak transmittance spectrum of the envelope is also achieved by altering the optical path difference of MZI2. However, when the peak wavelength of the transmission spectrum shifts from 1549.12 nm to 1551.53 nm, the required change in the optical path difference of MZI2 is 4.7 μm, which is substantially larger than the case of a vernier effect of 128 nm.

Figure 3a depicts the variation in the peak wavelength of the envelope as the optical path difference of MZI2 is adjusted in increments of 128 nm. The center wavelength can be tuned within a range from 1533.08 nm to 1540.40 nm. It is worth noting that the wavelength changes shown in Figure 3a are not continuous. If the optical path difference between the two arms of MZI2 is altered by a small step, the peak wavelength of the envelope shifts continuously within a small range. Figure 3b illustrates the wavelength changes when the optical path difference is varied in increments of 8 nm. Here, the wavelength shifts within a narrow range of 1528.67 nm to 1528.70 nm, achieving a wavelength tuning accuracy of 0.01 nm. From the above, by adjusting the optical path difference of MZI2, the laser wavelength can be tuned accordingly.

The FSR of MZI1 and MZI2 are 2.42 nm and 2.34 nm, respectively, with a difference of 0.08 nm. According to Equation (4), the FSR of the vernier effect envelope $FS{R}_v$ is inversely proportional to $\Delta FSR$; the smaller $\Delta FSR$ is, the larger the $FS{R}_v$. During the simulation process, reducing the FSR of MZI2 increases $\Delta FSR$, thereby decreasing the $FS{R}_v$, as shown in Figure 3a. Similarly, the FSR of MZI1 can also be altered to increase or decrease, correspondingly decreasing or increasing the $FS{R}_v$. In fact, whether this $FS{R}_v$ is increased or decreased, it can cause a shift in the envelope, thereby achieving wavelength tuning of the fiber laser. Figure 3c shows variation in the peak wavelength of the envelope when the optical path difference of MZI1 is adjusted in increments of 128 nm. The peak wavelength of the envelope shifts from 1544.39 nm to 1535.26 nm.

3. Experimental Results and Discussion

During the experiment, each MZI is fabricated using two 3 dB couplers. The most important thing is to control the physical length difference ∆L between the two arms of the MZI. The ∆L is calculated based on the desired FSR. Then, the pigtails of OC1 are trimmed to an identical length, while the pigtails of OC2 are trimmed to create the difference ∆L. The two couplers are then fused together to form an MZI. MZI2 is prepared using similar steps. These two MZIs were then cascaded to create a vernier effect sensor, which served as a filter in an EDFL to facilitate tuning of the operating wavelength.

Figure 4a–c present the transmission curves for both MZIs, as well as their superimposed spectrum. The FSRs of MZI1 and MZI2 are 2.42 nm and 2.32 nm, respectively. The difference between the FSR of the actual production of MZI and the simulated FSR may mainly be due to measurement errors during the fiber fusion process. The superimposed spectrum shows a distinct vernier effect. By stretching one arm of MZI2, the optical path difference between its two arms was altered. Consequently, the transmission curve of MZI2 drifts, and so does the superimposed spectrum. Figure 4d shows the shift in the superimposed spectrum when one arm of MZI2 is stretched.

The designed filter has been incorporated into an EDFL, and the experimental setup is depicted in Figure 5. The gain medium is a two-meter-long erbium-doped fiber (EDF) for the C-band (EDF7/6125-23). This fiber boasts an absorption peak wavelength at 1532 nm and a typical absorption value of 7 dB/m. A 1480 nm pump laser serves as the pump source and is coupled into the gain fiber via a 1480/1550 nm wavelength division multiplexer (WDM). An optical isolator (ISO) is employed to guarantee unidirectional light transmission and enhance the laser’s stability. A polarization controller (PC) is utilized to adjust the polarization state of the light. A 20/80 coupler (OC) is used to direct 20% of the light out of the cavity. An optical spectrum analyzer (OSA) with a resolution of 0.05 nm is used to measure the laser spectrum. During the experiment, to mitigate the impact of environmental factors such as vibrations and air currents, protective measures were taken for the laser. The experimental setup was placed on an air-floating platform to prevent vibrations. Additionally, an acrylic box was used to shield the stepper motor, and a plastic protective cover was placed over the entire laser system.

Figure 6a illustrates the laser spectra as the pump power is increased. As the pump power increases from 26.1 mW to 99.1 mW, the SMSR of the laser increases from 42.40 dB to 55.77 dB. Continuing to increase the pump power, the SMSR remains almost unchanged. Figure 6b depicts the gain spectrum of the erbium-doped fiber, providing insights into its optical properties and performance characteristics. As shown in Figure 6, the spectrum drifts with the increase in pump power. In an erbium-doped fiber laser, the gain characteristics of the erbium-doped fiber change with pump power. As the pump power increases, more pump light is converted into signal light, which leads to an increase in gain. This increase in gain affects the laser’s output spectrum, causing it to shift towards a more stable wavelength. Consequently, higher gain efficiency and a more stable laser output are achieved.

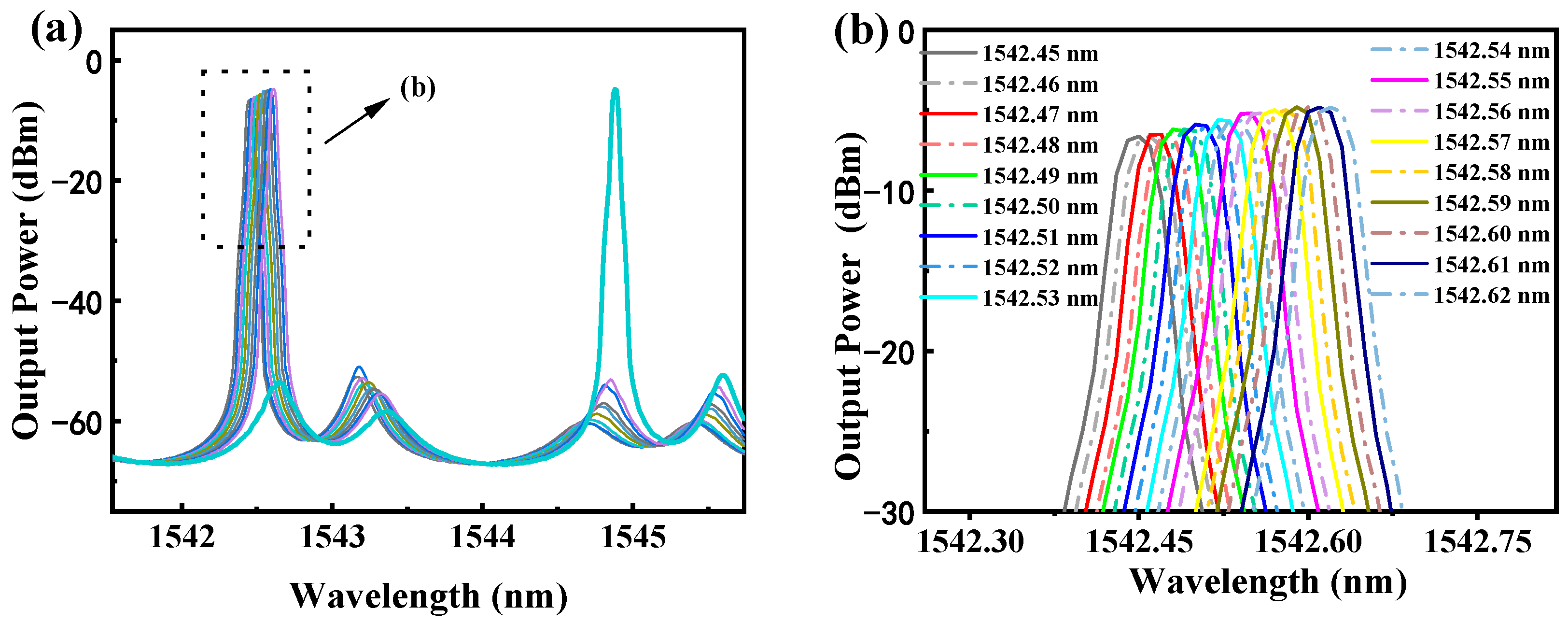
Figure 7a shows the variation in the laser spectrum with the stretching of one arm of MZI2 when the pump power is set to 99.1 mW. MZI2 is stretched with a step size of 128 nm, and the spectra are repeatedly scanned until they remain unchanged. As shown in Figure 7b, as the stretching amount is gradually increased from 0 nm to 768 nm, the peak wavelength of the laser shifts from 1542.56 nm to 1556.62 nm, achieving a tuning range of 14.06 nm. The narrowest 3 dB bandwidth is 0.058 nm, with a wavelength of 1556.62 nm. The widest 3 dB bandwidth is 0.071 nm, and the corresponding wavelength is 1542.56 nm. During the tuning process, the SMSR for each wavelength exceeds 55 dB. Notably, when the stretching step size is 128 nm, the wavelength change step size is about 2.40 nm.

Consistent with the numerical simulation results, the wavelength tuning in Figure 7a is discontinuous. When the stepper motor is moved at intervals of 8 nm, the spectrum is tuned with high precision but within small ranges around 1542 nm, 1545 nm, 1554 nm, and 1556 nm. Figure 8b illustrates the tuning results near the wavelength of 1542 nm, where the wavelength shifts from 1542.45 nm to 1542.62 nm, encompassing a tuning range of 0.18 nm with a tuning accuracy of 0.01 nm. Continuing to stretch MZI2, the operating wavelength of the laser jumps from 1542.45 nm to 1544.87 nm. Continuing to move the stepper motor at 8 nm intervals, the spectrum can be tuned with high precision around 1544.87 nm until it jumps to 1547.23 nm. During the tuning process, the SMSR ranges between 55.14 dB and 55.18 dB, demonstrating a high SMSR across all tunable ranges. The high-precision stepper motor and the high sensitivity of the cursor vernier filter ensure the high tuning accuracy of the laser.

During the stretching experiments, a dual-wavelength state is also observed. As depicted in Figure 9a, the central wavelengths of the two distinct peaks are 1542.63 nm and 1544.85 nm, respectively, separated by a gap of 2.22 nm. Figure 9b illustrates an alternative dual-wavelength state, with the peaks occurring at 1554.39 nm and 1556.65 nm, respectively, and an interval of 2.26 nm between them.

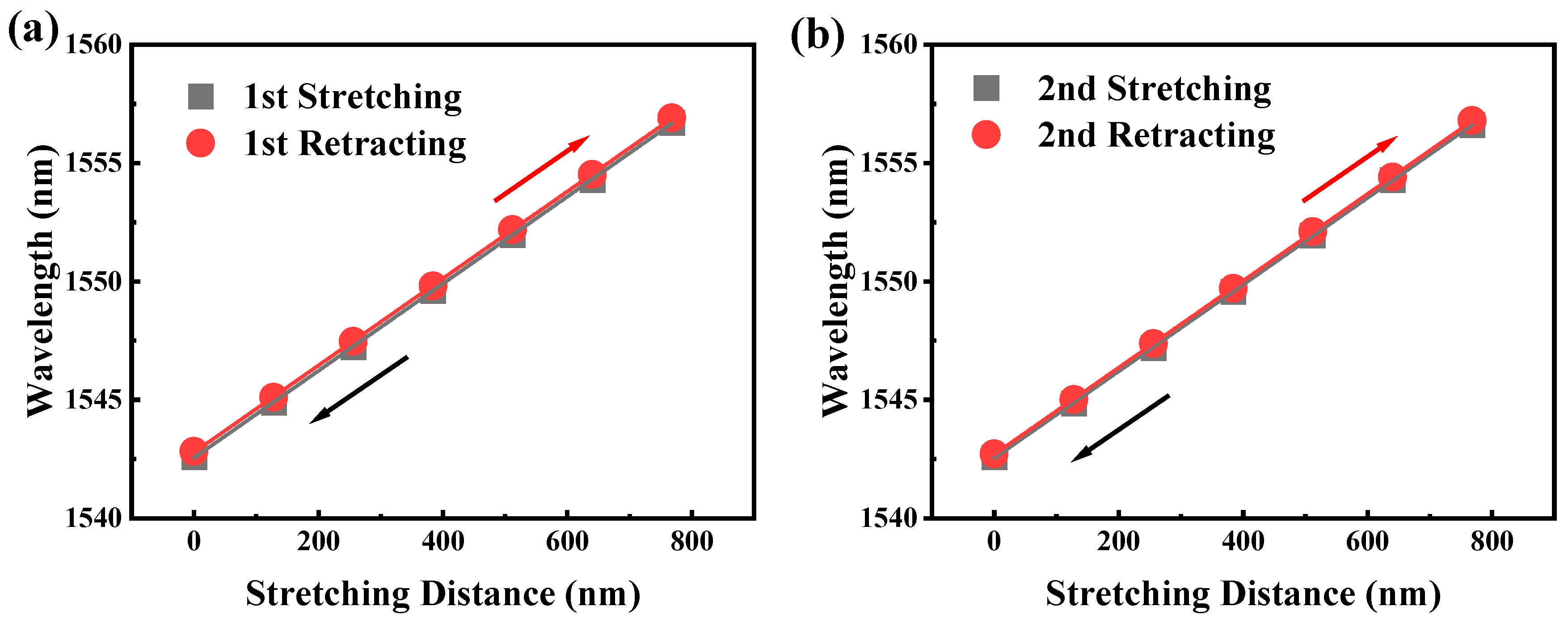
We further evaluated the repeatability of the wavelength-tuning process in the experiment. MZI2 is stretched to 768 nm with a step length of 128 nm, and then restored to its original length with the same step length. Figure 10a,b show the results of repeating twice. The wavelength drift ranges in Figure 10a,b are 0.1 nm and 0.03 nm, respectively, indicating that the tuning process of the laser has good repeatability. During the experiment, the spacing between the MZI2 clamping parts was 10 cm, and the stretching step size was 128 nm. According to the formula, $\Delta \epsilon ={\displaystyle \frac{\Delta L}{L_0}}$, the corresponding strain is 1.28 με. The elasticity of the fiber coating layer, combined with the minimal tensile stress applied, contributes to the high reproducibility of the wavelength-tuning process. The ability of the laser to achieve wavelength tuning with minimal strain is attributed to the high sensitivity of the vernier effect.

We measured the stability of the laser when MZI2 was in its unstretched state and when the stretching amount was 128 nm. During the measurement, the spectrum was scanned every 5 min for a total duration of 1 h. The results are depicted in Figure 11. When MZI2 was in its unstretched state, the laser wavelength varied within a range of 0.03 nm, between 1544.58 nm and 1544.61 nm. The output of power fluctuates by a maximum of 0.23 dBm during this period. When the stretching amount was 128 nm, the laser wavelength varied between 1546.93 nm and 1546.96 nm, representing a variation of 0.03 nm. The maximum fluctuation in output power is observed to be 0.13 dB. As mentioned above, to mitigate the impact of the environment, the experimental setup was placed on an air-floating platform, and a plastic protective cover was placed over the entire laser system. Despite these stability measures, the fiber laser shows a power fluctuation of 0.23 dB. There may be two reasons for power fluctuations. One is the power fluctuation of the pump source, and the other is the unavoidable environmental factors.

Compared to traditional fiber interferometers, vernier effect sensors exhibit higher sensitivity, enabling wavelength tuning with only minor alterations in physical parameters. We have compared the stretching amount and tuning range of the vernier effect filter proposed in this paper with the results reported with various interference filters, as summarized in

Table 1. Comparison of this work with the literature data.

Ref.	Method	Strain Distance	Tuning Range	SMSR	Wavelength Shift	Power Fluctuation
Current Work	Vernier Effect MZI	0.768 μm	14.06 nm	Higher than 55 dB	Less than 0.03 nm	Less than 0.23 dB
[19]	TCPCF and MMF	629 μm	19.7 nm	Higher than 50 dB	Less than 0.06 nm	Less than 0.96 dB
[20]	TCF	2975 μm	4.42 nm	Higher than 45 dB	Less than 0.05 nm	Less than 0.5 dB
[21]	FBG	3000 μm	2.04 nm	Higher than 36.53 dB	Less than 0.03 nm	Less than 0.015 dB
[22]	IMZI	60 μm	6.19 nm	Not available	Not available	Not available
[23]	TCPCF	126 μm	14.6 nm	Higher than 52 dB	Not available	Not available
[28]	F-P	3000 μm	7.47 nm	Higher than 40 dB	Not available	Less than 0.712 dB
[29]	LPFG	240 μm	15 nm	Higher than 36 dB	Less than 0.21 nm	Less than 2.69 dB

. As shown in Table 1, the fiber laser proposed here can be tuned with a range of 14.06 nm, with a small strain amount of 0.768 μm. A tunable erbium-doped fiber laser is reported in Ref. [19] by inserting an in-line MZI. The in-line MZI is composed of a segment of triple-core photonic crystal fiber and a segment of multi-mode fiber between SMFs. When the strain changes from 0 to 9113.9 με, the peak wavelength of the filter shifts towards the shorter wavelength direction by about 19.7 nm. The wavelength tuning range is relatively wide, but the corresponding stretching amount is 629 μm. A wavelength-tunable fiber laser based on a twin-core fiber (TCF) comb filter is proposed and demonstrated in Ref. [20], where the TCF filter is fabricated by splicing a 0.85 m long TCF between two segments of SMFs. The wavelength of the fiber laser can be tuned from 1553.62 nm to 1558.04 nm when the axial strain is increased from o to 3500 με. The tuning range is 4.42 nm. Considering the length of the TCF of 0.85 m, the corresponding strain distance is 2975 μm. Integrating a tapered in-line MZI into an erbium-doped fiber laser as an intracavity filter, a tunable fiber laser is proposed in Ref. [22]. When the strain amount is 60 μm, the wavelength can be tuned from 1552.94 nm to 1559.13 nm, with a tuning range of only 6.19 nm. It is evident from Table 1 that the stretching amount requirement for the vernier effect filter presented in this study is significantly reduced by an order of magnitude compared to the tunable fiber lasers utilizing interference filters previously reported.

4. Conclusions

In this study, we designed a vernier effect filter utilizing cascaded MZIs and integrated it into an EDFL to achieve precise tuning of the laser’s wavelength. The filter comprises two MZIs connected in series, and by adjusting the optical path difference between the two arms of one of the MZIs, the wavelength can be tuned from 1542.56 nm to 1556.62 nm, encompassing a total tuning range of 14.06 nm. By employing a high-precision stepping motor, a tuning accuracy of 0.01 nm has been achieved. The SMSR of the laser exceeded 55 dB across all wavelengths, demonstrating its superior performance. Compared to the reported tunable fiber lasers that utilized MZI filters, the proposed laser offers better tuning accuracy and easier operability. This laser holds promise for a wide range of applications in precision measurement, fiber sensing, and optical communication.