Picometer-Sensitivity Surface Profile Measurement Using Swept-Source Phase Microscopy

Abstract

In recent years, the Swept-Source Phase Microscope (SS-PM) has gained more attention due to its greater robustness to sample motion and lower signal decay with depth. However, the mechanical wavelength tuning of the swept source creates small variations in the wavenumber sampling of spectra that introduce serious phase noise. We present a software post-processing method to eliminate phase noise in SS-PM. This method does not require high-quality swept light sources or high-precision synchronization devices and achieves ~72 pm displacement sensitivity using a conventional SS-PM system. We compare the performance of this method with traditional software-based methods by measuring phase fluctuations. The phase fluctuations in the traditional software-based method are five times those of the proposed method, which means the proposed method has better sensitivity. Using this method, we reconstructed phase images of air wedges and resolution plates to demonstrate the SS-PM’s potential for high-sensitivity surface profiling measurement. Finally, we discuss the advantages of SS-PM over traditional Spectral-Domain PM techniques.

1. Introduction

Surface profile measurement is essential for evaluating product characteristics and qualities such as roughness, friction, wear, and manufacturing tolerances. In recent years, various optical and non-optical methods have been applied to surface profile measurement. However, achieving picometer-level sensitivity remains challenging for these methods [1].

Frequency Domain-Optical Coherence Tomography (FD-OCT) was proposed for biological imaging. A Fourier transform was performed on the interference spectrum to obtain cross-sectional images of samples in vivo. In recent years, FD-OCT has been widely used in surface profile measurement due to its advantages of non-contact, high speed, and good linearity [2]. There are two general implementations of FD-OCT depending on the type of light source and detector: Spectral-Domain OCT (SD-OCT) and Swept-Source OCT (SS-OCT). In SD-OCT, a broadband light source is used, and the interference spectrum is detected with a spectrometer [3]. For SS-OCT, the components with different wavelengths are decomposed by the swept source in the time domain, and the spectrum is converted by a photodetector and recorded by a digitizer [4]. The axial resolution of FD-OCT, around a few microns, is determined by the spectral bandwidth. Low axial resolution makes it difficult to meet the requirements of high-precision surface profile measurement.

Phase Microscopy (PM) is a technique that provides high axial sensitivity. PM combines spectral interference and common-path structure, retrieving OPD through phase information [5]. Since PM uses the same optical system as FD-OCT, it also has two general implementations: Spectral-Domain PM (SD-PM) and Swept-Source PM (SS-PM). The stability of the broadband light source and spectrometer in SD-PM makes it better in terms of optical alignment stability and the exact reproduction of wavenumber sampling. Therefore, PM’s most common optical configuration is SD-PM [6,7]. In recent years, SS-PM has gained more attention due to its greater robustness to sample motion and lower signal decay with depth [8]. However, the mechanical wavelength tuning of the swept source creates small variations in wavelength sweeps, trigger timing, and sampling, which adversely affects the reproducibility of interference spectra and introduces serious phase noise [9]. To suppress the phase noise introduced by the swept source and data acquisition system, some hardware-based or software-based methods are proposed: Hardware-based methods mainly involve employing buffered Fourier domain mode-locked lasers [10] or utilizing synchronous sampling techniques [11]. Software-based methods are proposed to avoid the need for high-quality swept light sources or high-precision synchronization devices [12]. For example, Braaf et al. proposed a correction method based on the inverse Fourier transform [13]; however, this method can only correct the spectral shift in a small range due to phase wrapping. Shangguan et al. used cross-correlation operations to align interference spectra, but this method can only achieve alignment at the pixel level and cannot correct deviations at the sub-pixel level [14].

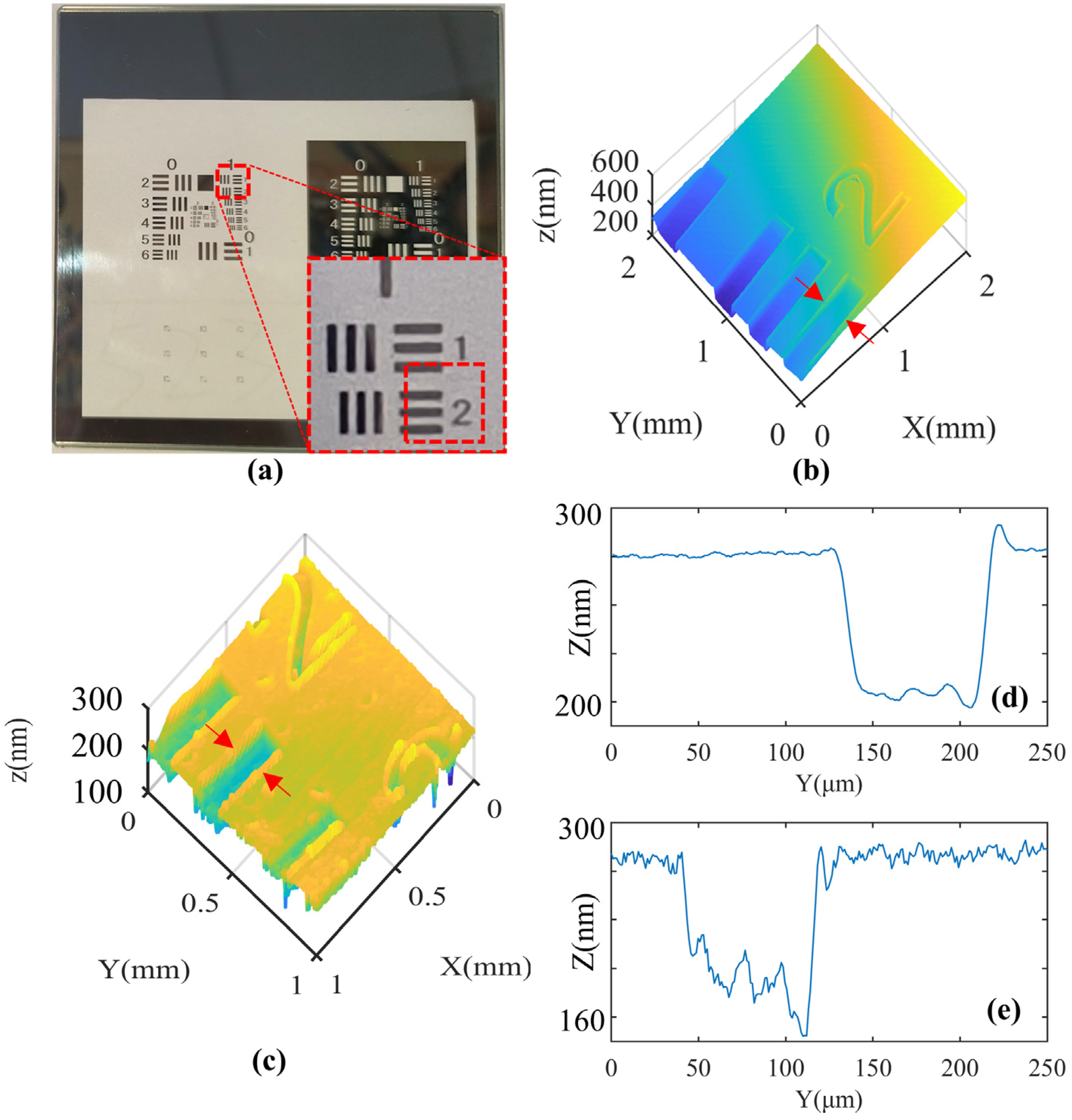
In this paper, we propose a software post-processing method to eliminate phase noise in SS-PM. This method does not require additional optical elements or reference spectra to provide phase calibration signals. This algorithm eliminates phase noise in the spectrum through specific folding operations and achieves a displacement sensitivity of 72 pm in the air. The feasibility of this method has been demonstrated by measuring the surface profile of an air wedge and a resolution target. This initial demonstration indicates that SS-PM has the potential to achieve picometer-sensitivity surface profile measurements.

2. Methods

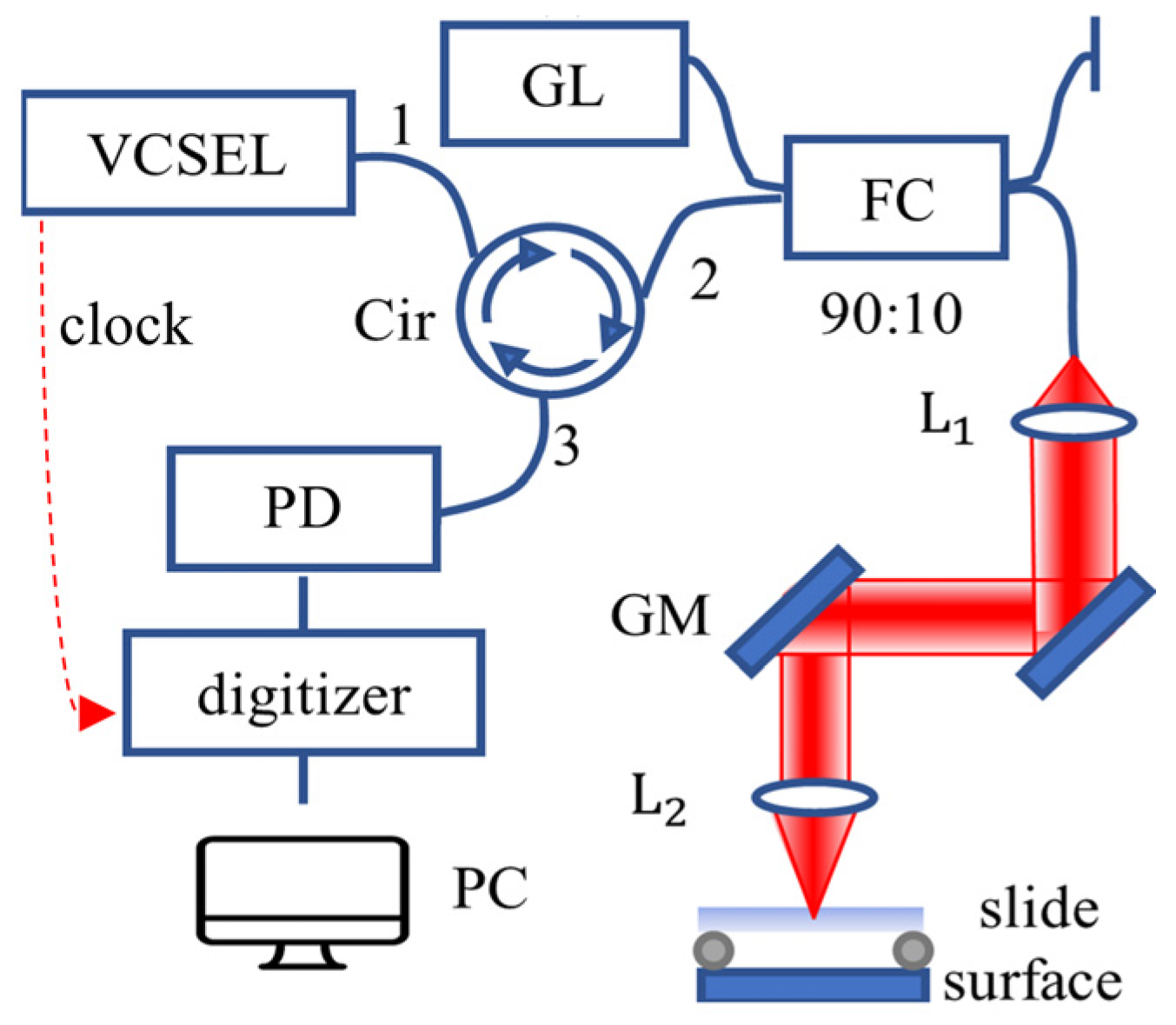
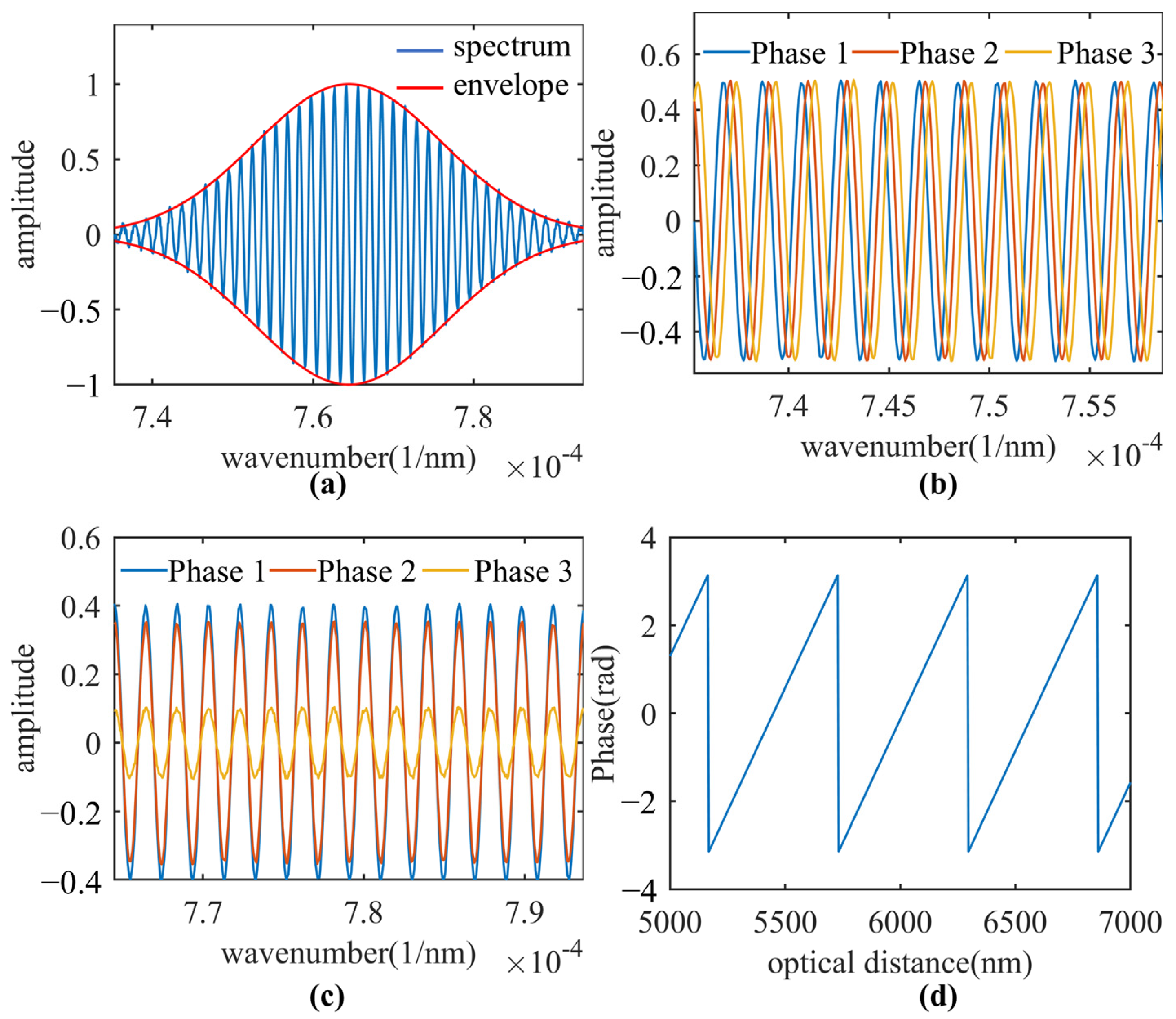
In surface profile measurement, the reflection from the sample surface serves as the sample arm signal. Consequently, the detector signal contains a single-frequency interferometric component whose frequency is linearly encoded with the optical path difference (OPD). The instability of the swept source and data collection system leads to a random shift of the A-line in k-space. Figure 1a shows two spectra with different initial phases and the same OPD. In the case of a single sample reflector and an unstable interferometric system, this interferometric component $i\left(k\right)$ is given by:

$$i\left(k\right)=\left({\displaystyle \frac{\rho }{e}}\right)S\left(k\right)\sqrt{R_r{R}_s}\mathit{cos}\left[2nk\left(\delta d+M\Delta d\right)+N_{rand}\right]$$

(1)

where $k$ is the wave number; $S\left(k\right)$ is the source power spectral density; $R_r$ is the reference arm reflectivity; $R_s$ is the reflectivity of the sample surface; $\rho$ is the detector responsivity; $e$ is the electric charge; $n$ is the refractive index; $N_{rand}$ is the phase noise introduced by the swept source; $\delta d+M\Delta d$ is the free distance between sample surface and reference reflector; $\Delta d$ is the resolution of the FFT; $\Delta d=2\pi /\Delta k,\Delta k$ is the spectral bandwidth in k-space [2];$M$ is a positive integer, $M\Delta d$ is an integer multiple of the discrete sampling interval in the A-Scan; $\delta d$ is the sub-resolution deviation position of the sample surface away from $M\Delta d$; the change of $\delta d$ is mainly reflected in the phase. The Fourier transform $I\left(d\right)$ of the spectrum is A-Scan that has a peak value at $\pm 2nM\Delta d$:

$$I\left(\pm 2nM\Delta d\right)=\left({\displaystyle \frac{\rho }{2e}}\right)\sqrt{R_r{R}_s}E\left(2n\delta d\right)exp\left(\pm j2n{k}_0\delta d+N_{rand}\right)$$

(2)

where $k_0$ is the source center wave number; $j$ is the imaginary unit; $E$ is the unity-amplitude coherence envelope function; the phase term $\phi \left(\pm 2nM\Delta d\right)$ of $I\left(\pm 2nM\Delta d\right)$ is $\pm j2n{k}_0\delta d+N_{rand}$. When $N_{rand}=0$, the phase term $\phi \left(\pm 2nM\Delta d\right)$ is a linear function of the sub-resolution deviation $\delta d$. The variation of the sub-resolution deviation $\delta d$ can be accurately calculated by measuring the phase variation. Figure 1b shows the linear function between the sub-resolution deviation $\delta d$ and the phase $\phi \left(\pm 2nM\Delta d\right)$ in the range of [−pi, pi]. Unfortunately, the linear function between $\delta d$ and $\phi \left(\pm 2nM\Delta d\right)$ is destroyed by the phase noise $N_{rand}$. Therefore, SS-PM cannot directly measure the phase $\phi \left(\pm 2nM\Delta d\right)$ to calculate $\delta d$. Figure 1c shows the relationship between $\phi \left(\pm 2nM\Delta d\right)$ and $\delta d$ under the influence of phase noise.

Firstly, we need to extract the cosine term $\mathit{cos}\left[2nk\left(\delta d+M\Delta d\right)+N_{rand}\right]$ from the original spectrum $i\left(k\right)$; this involves removing the envelope of spectrum in Equation (1). A method based on spline interpolating is used for the envelope estimation [15]. First, in order to eliminate erroneous maxima and minima caused by shot noise, the interference spectrum is smoothed by convolution with a Hanning window. Then, we calculate the upper envelope $E_u\left(k\right)$ and lower envelope $E_d\left(k\right)$ by spline interpolating the maxima and minima of the smoothed spectrum, respectively. Using these two envelopes, we extract the cosine term from Equation (1):

$$i_n\left(k\right)=2\ast {\displaystyle \frac{i\left(k\right)-E_d\left(k\right)}{E_u\left(k\right)-E_d\left(k\right)}}-1=\mathit{cos}\left[2nk\left(\delta d+M\Delta d\right)+N_{rand}\right]$$

(3)

Here, $i_n\left(k\right)$ is the cosine term without an envelope; Figure 2a shows the envelopes calculated by spline interpolation.

To eliminate the phase noise $N_{rand}$, a folding operation is introduced:

$$\begin{array}{c}{i}_{pz}\left(\overline{k}\right)=i_n\left(k_0\right)\left[i_n\left(k_0-\overline{k}\right)+i_n\left(k_0+\overline{k}\right)\right] \\ =i_n\left(k_0\right)\left\{\mathit{cos}\left[2n\left(k_0-\overline{k}\right)\left(\delta d+M\Delta d\right)+N_{rand}\right]+\mathit{cos}\left[2n\left(k_0+\overline{k}\right)\left(\delta d+M\Delta d\right)+N_{rand}\right]\right\} \\ =2i_n^2\left(k_0\right)\mathit{cos}\left[2n\left(\delta d+M\ast \Delta d\right)\overline{k}\right]\end{array}$$

(4)

where $i_n\left(k_0\right)$ is the midpoint of the cosine term $i_n\left(k\right)$; $i_n\left(k_0+\overline{k}\right)$ is the latter half of $i_n\left(k\right)$; $i_n\left(k_0-\overline{k}\right)$ is the reversed first half of $i_n\left(k\right)$; $\overline{k}$ is the distance between the symmetry points ($i_n\left(k_0+\overline{k}\right)$ and $i_n\left(k_0-\overline{k}\right)$) and the midpoint, and its domain is [0, $\Delta k$/2]; the folding operation is a summation of symmetric points in the cosine term $i_n$. Each pair of points symmetric about a middle point are added together. The folding operation eliminates phase noise in the spectrum and produces a cosine signal $i_{pz}\left(\overline{k}\right)$ with an amplitude of $2i_n^2\left(k_0\right)$, an initial phase of zero, and a length of $\Delta k$/2 + 1. Figure 2b shows three spectra with the same OPD under phase noise. The phase noise in these spectra is eliminated by a folding operation, as shown in Figure 2c. The time complexity of the folding operation is O(N/2), where N is the length of the spectrum. This means that the folding operation has very little impact on real-time performance. SS-PM applies the Fourier transform to the zero-filled cosine term $i_{pz}\left(\overline{k}\right)$ to obtain A-Scan as follows:

$$I_{pz}\left(2nd\right)=i_n^2\left(k_0\right)\mathcal{F}\left[u\left(\mathrm{k}\right)\right]\otimes \mathsf{\delta }\left[2n{k}_0\left(d-\mathsf{\delta }\mathrm{d}-M\Delta d\right)\left]\exp \right[-j2n{k}_0\left(d-\delta d-M\Delta d\right)\right]$$

(5)

Here, the coherent ghost image is disregarded for simplicity; $\mathcal{F}\left[u\left(\mathrm{k}\right)\right]$ denotes the Fourier transformation of the rectangular window; $d$ represents distance; $\mathsf{\delta }\left[2n{k}_0\left(d-\mathsf{\delta }\mathrm{d}-\mathrm{M}\mathsf{\Delta }\mathrm{d}\right)\right]$ is the unit impulse function with a peak value at $\delta d+M\Delta d$; $\otimes$ represents convolution; $i_n^2\left(k_0\right)\mathcal{F}\left[u\left(k\right)\right]\otimes \left\{\delta \left[2n{k}_0\left(d-\delta d-M\Delta d\right)\right]\right\}$ is the amplitude spectrum of the Fourier transformation; $exp\left[-j2n{k}_0\left(d-\delta d-M\Delta d\right)\right]$ is the phase spectrum, which is used to calculate the sub-resolution position $\delta d$. In actual calculations, the FFT samples the amplitude spectrum at intervals of $\Delta d$. The nearest sampling point at the peaked value $d=M\Delta d$ is given by:

$$I_{pz}\left(2nM\Delta d\right)=i_n^2\left(k_0\right)\mathcal{F}\left[u\left(\mathrm{k}\right)\right]\otimes \mathsf{\delta }\left(-2n{k}_0\mathsf{\delta }\mathrm{d}\right)\exp \left(j2n{k}_0\delta d\right)$$

(6)

The folding operation eliminates the phase noise in the $\exp \left(j2n{k}_0\delta d\right)$ compared to Equation (2). This method restores the linear function between the sub-resolution position and the phase term. The sub-resolution position change of the surface profile can be measured with the phase difference between two adjacent A-lines:

$$\mathsf{\delta }\mathrm{d}={\displaystyle \frac{1}{4n\pi k_0}}\left[\angle I_{pz1}\left(M\Delta d\right)-\angle I_{pz2}\left(M\Delta d\right)\right]$$

(7)

Here, $\angle$ denotes the phase operator.

Figure 2d shows the phase variation with a sub-resolution position, which proves that the folding operation can effectively eliminate the phase noise introduced by the swept light source. The folding operation eliminates the phase noise introduced by the swept source. Therefore, OPD can be obtained using phase information, indicating that the presented algorithm can effectively improve axial sensitivity. By using linear regression of the phase in the Hilbert domain [16] or the least squares method in the spectral domain [5] to remove phase wrapping in SS-PM, the measurement depth range of SS-PM can reach a few centimeters.

3. Setup and Experiment

3.1. Setup

Figure 3 illustrates the schematic diagram of the SS-PM system. The light source is a vertical-cavity surface-emitting laser (VCSEL) (OCS1310V1, Thorlabs, Newton, NJ, USA) with a central wavelength of 1310 nm, a bandwidth of 100 nm, and a swept speed of 200 kHz. Through the circulator and fiber coupler, the light is projected onto the sample surface, which is set in a common-path configuration. The lower surface of the slide acts as a reference arm and the sample surface serves as a sample arm. The interference spectrum is converted by a photodetector with a bandwidth of 1.6 GHz (PDB465C, Thorlabs, Newton, NJ, USA) and recorded by a 10-bit digitizer (PXIe-5162, National Instruments, Austin, TX, USA). The Mach–Zehnder interferometer inside the swept source produces a clock signal for spectrum resampling in k-space.

3.2. Evaluation of Sensitivity in Different Phase Noise Suppression Methods

The minimum detectable change in the sub-resolution position is assessed by the phase fluctuations of the SS-PM system. At the same OPD, smaller phase fluctuations mean higher sensitivity. To compare the proposed method with the inverse Fourier transform method [13] and the cross-correlation method [14], we collected 1000 interference spectra between the upper and lower surfaces of the slide, under the condition that the galvanometric mirror is turned off. Since all phase noise is common-mode between the reference and sample optical fields, the OPD of the interference spectrum depends only on the thickness of the slide at the sampling point. Figure 4a shows the phase fluctuations of the original spectrum. The noise introduced by the swept source results in the phase uniformly distributing in the range of [−pi, pi], which proves that the original spectrum cannot be used for sub-resolution position measurement. The proposed method eliminates phase noise through a folding operation and achieves a standard deviation of ~0.69 mrad, corresponding to a sensitivity of 71.93 pm in the air (Figure 4b). The histogram from the same experimental data corrected with the inverse Fourier transform method is shown in Figure 4c, with a standard deviation of ~17.2 mrad. Due to phase wrapping in the inverse Fourier transform method, this approach can only correct small phase fluctuations. Figure 4d shows the phase histogram of the cross-correlation method, which has a standard deviation of ~4.62 mrad. The cross-correlation method can only achieve alignment at the pixel level and cannot correct deviations at the sub-pixel level. Therefore, the method proposed in this paper is more effective than both the cross-correlation method and the inverse Fourier transform method in phase noise suppression.

To demonstrate the feasibility of sub-nanometer displacement measurement, we measured the thermal expansion coefficient of a 213 µm thick borosilicate coverslip using the SS-PM system. With the galvanometric mirror turned off, we continually acquired 40,000 spectra between the upper and lower surfaces of the borosilicate coverslip in 60 s. The change in the coverslip thickness was recorded as the water bath was cooled by 1.2 °C, from 37.1 °C to 35.9 °C. Figure 5 demonstrates the thickness changes over the 1.2 °C temperature range. The coverslip contracted by 1.5 nm, yielding a thermal expansion coefficient of 59 × 10⁻⁷/°C. This is consistent with previous reports [17]. The discontinuity point (red box in Figure 5) in the curve is caused by the write delay from RAM to ROM.

3.3. Experiment on Phase Noise Suppression

In order to verify the ability of the proposed method to suppress phase noise, we measured the height variation of an air wedge using SS-PM. The air wedge consists of two smooth slides; the configuration of the sample is shown in Figure 6a, where two optical fibers with diameters of 500 µm and 700 µm are placed at each end of the slide. The interference spectrum between the lower surface of slide 1 and the upper surface of slide 2 is collected for the sub-resolution position calculation. The scanning range of the galvanometer mirror in the X direction is 15 µm. Theoretically, the difference in height of the air wedge is 120 nm over this 15 µm range. Figure 6b shows the phase obtained from the original spectrum, which appears as random noise. Figure 6c demonstrates the sub-resolution position changes obtained from spectra corrected using the proposed method. The results show that the height of the air wedge increases by 100 nm. The difference between the actual height (100 nm) and the theoretical height (120 nm) may be introduced by the small step size of the galvanometer mirror. This experiment demonstrates that the proposed method can effectively suppress phase noise.

3.4. Surface Profile Measurement of Resolution Target

We further measured the surface profile of a resolution target (1951 USAF), which is a glass plate approximately 1.7 mm thick, coated with an approximately 80 nm thick Ag film. We employed two pencil leads (approximately 0.5 mm in diameter) as supports between the resolution target and a 1 mm glass slide to establish a common-path structure. We measured 500 × 500 points on the resolution target within a range of 2 mm × 2 mm (the red dashed box in the lower right corner of Figure 7a). The method proposed in this paper eliminates phase noise in the interference spectra, and the sub-resolution position is estimated by calculating the phase. Figure 7b shows the surface profile obtained by SS-PM; it clearly shows the details of the resolution target. The surface profiler based on white-light interferometry (WLI) is a common instrument for quantitative surface profile measurement. A WLI with a bandwidth of 50 nm is used for profile measurement. Figure 7c shows the surface profile obtained by WLI. Figure 7d,e are cross-section curves of SS-PM and WLI, respectively, corresponding to the red arrows in Figure 7b,c. As expected, the noise intensity of WLI is higher than that of SS-PM, since the moving reference arm in WLI typically introduces a significant level of phase noise [16]. Additionally, due to the large reflection coefficient of the Ag film and the small measurement range of the line scan camera [18], the spectrum of the Ag film is saturated. This saturation introduces location-dependent low-frequency noise in the range [50 µm, 100 µm] in Figure 7e.

4. Discussion

In SS-PM, the spectrum $i\left(k\right)$ contains the phase noise $N_{rand}$ introduced by unstable interference systems and the shot noise introduced by the photodetector. The influence of phase noise $N_{rand}$ is more significant than shot noise for sub-resolution position measurement. The swept source with mechanical wavelength tuning generates tiny variations in wave number sweeps, trigger timing, and sampling, which manifest as random shifts of the spectrum in k-space. 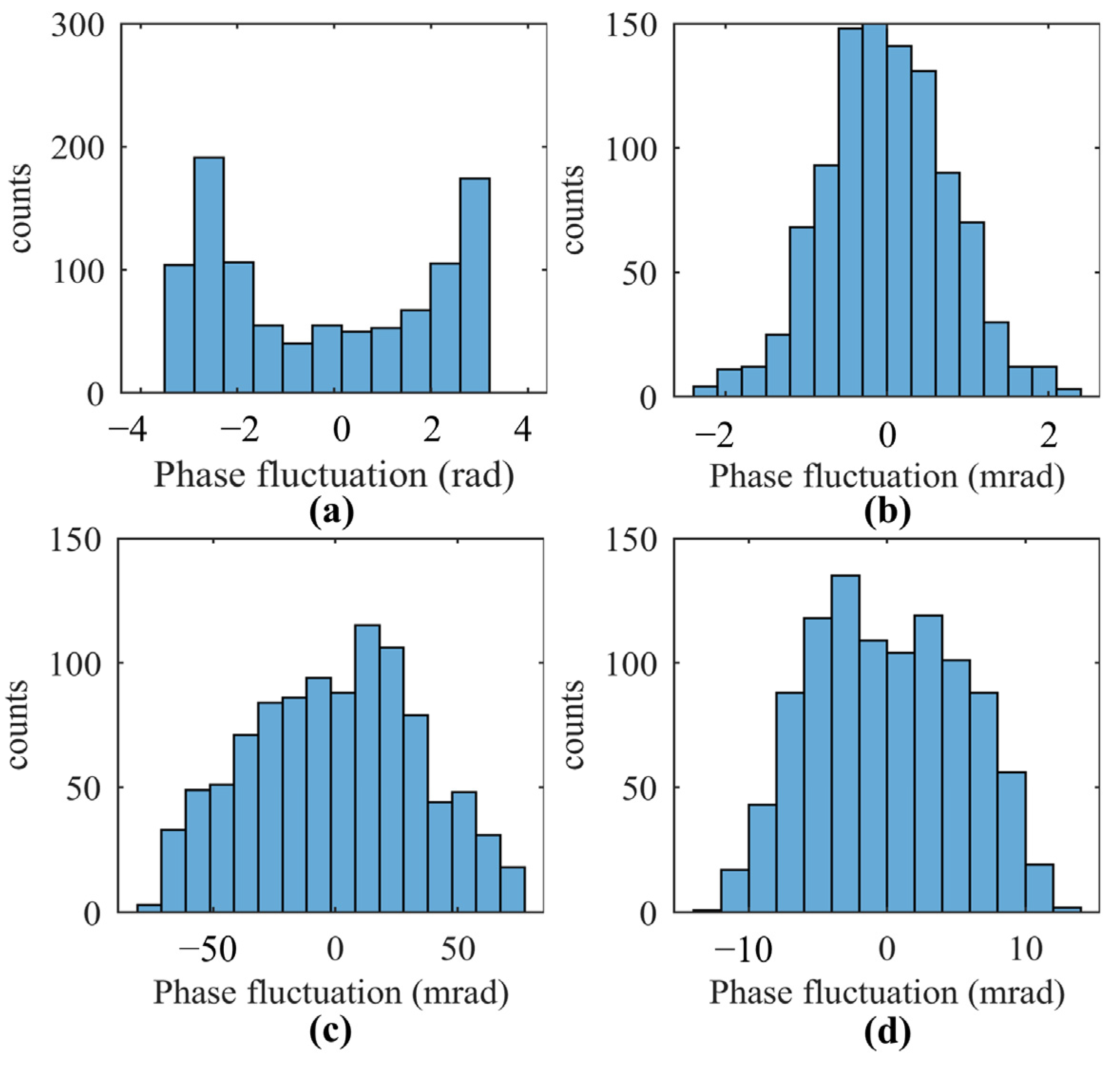Figure 8a shows the influence of phase noise in the complex plane of the FT. $I_{signal}$ is a signal vector corresponding to the FT of the spectrum. The angle between $I_{signal}$ and the positive real axis is used to calculate the sub-resolution position. The gray circular region in Figure 8a represents the fluctuation range of the phase noise, which corresponds to the histogram in Figure 4a. The phase noise acts as a twiddle factor in the complex plane of the FT, rotating the result of the Fourier transform $I_{signal}$ by a random angle around the origin of the coordinates. The large fluctuation range of the phase noise conceals the real angle of $I_{signal}$, making it difficult to use uncorrected spectra for sub-resolution position measurement.

After the phase noise is eliminated by the folding operation, the fundamental lower limit of the sub-resolution position change (position sensitivity) is determined by the shot noise. Shot noise can be approximated as additive, independent Gaussian white noise [1]. At $d=M\Delta d$, the Fourier transform of the shot noise is:

$$I_{shot noise}\left(M\Delta d\right)=\sqrt{{\displaystyle \frac{\rho S{R}_r\Delta t}{e}}}\mathit{exp}\left(j{\varphi }_{shot noise}\right)$$

(8)

Here, $S$ is the total source power; ${\varphi }_{shot noise}$ is the random phase of the shot noise; $\Delta \mathrm{t}$ is the integration time. Figure 8b shows the influence of shot noise in the complex plane of the FT. The vector of the practical spectrum is obtained by the vectorial addition of the signal vector $I_{signal}$ and the shot-noise vector ${\mathrm{I}}_{\mathrm{shot}\mathrm{noise}}$ in the complex plane. The angular orientation ${\mathsf{\phi }}_{\mathrm{sn}}$ between the signal vector and the noise vector is random. Since the signal vector has a certain amplitude and angle, the shot-noise vector can be decomposed into a vertical component (${\mathrm{I}}_{\mathrm{shot}\mathrm{noise}}\sin \left({\mathsf{\phi }}_{\mathrm{sn}}\right)$) and a parallel component (${\mathrm{I}}_{\mathrm{shot}\mathrm{noise}}\cos \left({\mathsf{\phi }}_{\mathrm{sn}}\right)$). Under the premise that the intensity of ${\mathrm{I}}_{\mathrm{shot}\mathrm{noise}}$ is much less than the intensity of ${\mathrm{I}}_{\mathrm{signal}}$, the influence of the parallel component can be neglected. The vertical component changes the angle of the actual spectrum by $\mathsf{\delta }\mathrm{d}$. The smallest observable change in the phase of the signal vector is determined by the shot noise. In other words, an observable change in the signal phase must be larger than $\mathsf{\delta }\mathsf{\varphi }$. The fundamental lower limit of the sub-resolution position change is:

$${\mathsf{\delta }\mathrm{d}}_{sens}={\displaystyle \frac{{\mathsf{\lambda }}_0}{4n\pi }}arctan\left[{\displaystyle \frac{1}{\sqrt{SNR}}}\right]\approx {\displaystyle \frac{{\mathsf{\lambda }}_0}{4n\pi }}{\displaystyle \frac{1}{\sqrt{SNR}}}$$

(9)

The swept source decomposes the components with different wavelengths in the time domain, and the integration time $\Delta t$ of a single pixel in SS-PM is much shorter than that in conventional SD-PM. Equation (8) shows that the intensity of the shot noise is proportional to the integration time, which means that SS-PM can achieve a lower shot noise and a better fundamental lower limit of the sub-resolution position change than traditional SD-PM. To quantitatively evaluate the performance differences between SS-PM and SD-PM, we continuously acquired 1000 interference spectra between the beams reflected from the top and bottom surfaces of a stationary glass slide using the SD-PM system. The histogram of the OPD is shown in Figure 9. The standard deviation of the calculated phases is 0.89 mrad, while the standard deviation of SS-PM using the presented method is 0.69 mrad. Therefore, it is observed that the sensitivity of SS-PM is superior to that of SD-PM due to the reduced shot noise.

5. Conclusions

In conclusion, we have demonstrated that the phase noise in SS-PM can be eliminated by a new post-processing algorithm. This algorithm achieves phase stability with a standard deviation of 0.69 mrad by a special folding operation. It is demonstrated that the phase stability of the presented method is better than that of the cross-correlation method and the inverse Fourier transform method. The utilization potential of this technology was demonstrated by measuring the surface profile of an air wedge and a resolution target. This first demonstration shows that SS-PM has the potential to achieve highly sensitive surface profile measurements.