Abstract
In this paper, a dual-wavelength narrow-linewidth fiber laser based on parity-time (PT) symmetry theory is proposed and experimentally demonstrated. The PT-symmetric filter system consists of two optical couplers (OCs), four polarization controllers (PCs), a polarization beam splitter (PBS), and cascaded fiber Bragg gratings (FBGs), enabling stable switchable dual-wavelength output and single longitudinal-mode (SLM) operation. The realization of single-frequency oscillation requires precise tuning of the PCs to match gain, loss, and coupling coefficients to ensure that the PT-broken phase occurs. During single-wavelength operation at 1548.71 nm (λ1) over a 60-min period, power and wavelength fluctuations were observed to be 0.94 dB and 0.01 nm, respectively, while for the other wavelength at 1550.91 nm (λ2), fluctuations were measured at 0.76 dB and 0.01 nm. The linewidths of each wavelength were 1.01 kHz and 0.89 kHz, with a relative intensity noise (RIN) lower than −117 dB/Hz. Under dual-wavelength operation, the maximum wavelength fluctuations for λ1 and λ2 were 0.03 nm and 0.01 nm, respectively, with maximum power fluctuations of 3.23 dB and 2.38 dB. The SLM laser source is suitable for applications in long-distance fiber-optic sensing and coherent LiDAR detection.
1. Introduction
Switchable multi-wavelength narrow-linewidth erbium-doped fiber lasers (EDFLs) have become a key area of research within laser technology, owing to their simple structure, efficient thermal dissipation, high energy conversion efficiency, and superior beam quality [1]. Single-frequency narrow-linewidth fiber lasers, in particular, have been the focus of significant attention due to their broad applicability in optical communications [2], sensing technology [3], precision measurement [4], radar telemetry [5], and military systems [6]. The versatility of these lasers remains a critical research focus. Additionally, lasers capable of multi-wavelength operation play an essential role in dense wavelength division multiplexing and phased array antenna systems [7].
Various methods are available for achieving switchable single- and multi-wavelength outputs, including magneto-optical switches and acousto-optic modulators (AOM) [8], Mach–Zehnder interferometers (MZIs) [9], Lyot filters [10], and FBGs [11]. Among these, FBGs are regarded as a more straightforward and convenient approach. Given the wide spectral bandwidth of erbium ion gain [12], the wavelength-switchable output is achieved by cascading multiple appropriately tuned FBGs, often in conjunction with polarization [13] or birefringence filtering [14]. Achieving single-frequency oscillation with narrow-linewidth output within the broad spectral gain profile of erbium ions necessitates effective longitudinal mode selection techniques, such as the linear short-cavity method [15] and the composite ring cavity method [16]. The free spectral range (FSR) is increased by reducing the cavity length with the linear short cavity method, thus facilitating SLM operation. However, this method is limited by the finite length of the gain medium and the efficiency of pump light utilization. Additionally, performing spatial hole burning by standing waves can be challenging [17]. Alternatively, the Vernier effect [18] is utilized in the composite ring cavity method, leading to significant enhancement of the stability of SLM output. Nonetheless, the practicality of this method is reduced by its structural complexity and susceptibility to environmental factors [19]. Mode selection utilizing polarization-maintaining chirped fiber Bragg gratings (PM-CFBG) [13] has also been demonstrated. This method involves complex processes such as the fabrication of non-periodic phase masks [15], which increases the difficulty of manufacturing. In recent years, the application of PT symmetry theory to optical systems has been introduced to SLM selection as a novel approach [20,21]. By carefully distributing gain and loss within the laser cavity, higher-order modes are effectively suppressed through the inherent symmetry-breaking mechanism of PT-symmetric lasers, eliminating the need for external filters [22]. This mechanism not only enhances efficiency and power stability but also significantly improves beam quality, resulting in optimized laser output performance [23].
The PT-symmetric laser design facilitates precise control over laser emissions through the balanced application of gain and loss within the cavity. This approach effectively suppresses higher-order transverse modes, supporting single-longitudinal mode operation and enhancing beam quality. The design’s ability to maintain stable single-mode performance across various pump conditions has been demonstrated both theoretically and experimentally [20,21]. Furthermore, the integration potential of PT-symmetric lasers is notable. These lasers are compatible with standard photonic integrated circuit (PIC) fabrication processes, allowing for straightforward integration with other PIC components. Recent demonstrations of high-power, single-mode operation from edge-emitting PT-symmetric lasers at room temperature have been achieved, with output powers exceeding 400 mW and a beam quality characterized by an M2 value close to unity [24]. These results indicate that PT-symmetric lasers are viable candidates for high-power photonic integration applications. The dynamic characteristics of PT-symmetric lasers, including the spontaneous PT-symmetry breaking observed in lasing dynamics [25,26], suggest their suitability for tunable and reconfigurable photonic systems. As the photonics field advances, PT-symmetric lasers may contribute significantly to the development of next-generation integrated photonic platforms.
This paper proposes a narrow-linewidth, switchable dual-wavelength SLM fiber laser based on a PT-symmetric system, utilizing cascaded FBGs for wavelength selection. Through integration with the PT-symmetric system, stable SLM operation can be achieved. The coupling loop in this design employs two OCs and a PBS to control the path length difference. Additionally, two sets of PCs are incorporated within the coupling loop to precisely regulate the polarization state entering the PBS and to adjust the gain and loss coefficients within the PT-symmetric system. This configuration enhances system stability and beam quality, enabling SLM output in the PT-broken phase. Furthermore, the birefringence filtering effect is introduced, allowing for stable operation in both single- and dual-wavelength states by tuning the PCs. The experimental results demonstrate that the SLM output exhibits excellent stability in single-wavelength operation, with linewidths of 1.01 kHz at 1548.71 nm (λ1) and 0.89 kHz at 1550.91 nm (λ2). During dual-wavelength operation, maximum wavelength fluctuations for λ1 and λ2 are measured at 0.03 nm and 0.01 nm, respectively, with maximum power fluctuations of 3.23 dB and 2.38 dB.
2. Working Structure and Experimental Principle
2.1. PT Symmetry
The PT symmetry theory first originated in the field of quantum mechanics. The expression of the Schrödinger equation is:
where represents the wave function of the particle, is its energy eigenvalue, and is the Hamiltonian operator, which can be expressed as , where and are the momentum and position operators, respectively, and denotes the particle’s mass. The ubiquitous parity operator and the time-reversal operator are defined as follows [21]:
According to C.M. Bender, the operators and are considered PT-symmetric if they share the same set of eigenvectors, meaning they are reciprocal. Based on the requirements of PT symmetry, the following expression is obtained by applying the parity operator and the time reversal operator to the Hamiltonian operator :
Solving the equation gives:
The above equation indicates that PT symmetry requires the real part of the potential energy function to be an even function of the position x, while the imaginary part must be an odd function of x. C.M. Bender further proposed that a threshold value exists for the imaginary component of the potential energy function in the Hamiltonian quantity that satisfies PT symmetry. When the imaginary part is below this threshold, the energy eigenvalue remains real, and the system is in the PT-unbroken phase. However, when the imaginary part exceeds this threshold, the energy eigenvalue becomes imaginary, placing the system in the PT-broken phase.
PT symmetry theory can also be applied to photonics [27]. R. El-Ganainy et al. drew an analogy between Schrödinger’s equation and the optical fiber propagation equation for electric field envelope fluctuation along the transverse axis [28]. The time-dependent Schrödinger equation is expressed as:
where is the potential energy function, which determines the behavior of the wave function solution. When the potential function depends only on spatial coordinates, the Schrödinger equation can be written as:
It is important to note that this quantum system is still time-dependent, but the potential function is stationary, meaning that the wave function takes the form . In this case, the Schrödinger equation resembles the paraxial optical diffraction equation, which is expressed as:
Here, represents the electric field envelope, is the wave vector, is the transverse coordinate, is the propagation distance, is the complex refractive index distribution, where represents the real refractive index profile of the fiber and describes the gain or loss distribution of the structure. By comparing Equations (8) and (9), we can establish correspondence, which satisfies the earlier assumption that the potential function is stationary:
This analogy suggests that by spatially modulating the refractive index, it is possible to appropriately balance gain and loss [28], leading to complex PT symmetry potential in optical systems under specific conditions. The ability to control gain–loss contrasts in PT symmetry theory offers unique advantages in longitudinal mode selection.
2.2. Laser Structure
The SLM fiber laser, structured as a PT-symmetric system and a cascaded FBG, is depicted in Figure 1. A 980 nm laser diode is utilized as the pump source, with 300 mW of power injected into the main ring cavity through a 980/1550 nm wavelength division multiplexer (WDM). The gain medium is a 2-meter erbium-doped fiber (EDF; YOFC-ED1016), providing amplification within the cavity. Light enters the circulator (Cir) at port 1 and reflects off the cascaded FBG, subsequently emerging from port 3 of the Cir. The cascaded FBG is composed of two single-wavelength FBGs, with reflection rates of 99.97% and 99.93%, and central wavelengths of 1548.72 nm and 1550.92 nm, respectively. The distance between the two gratings is 2 cm. The corresponding reflection spectrum is shown in Inset 1 of Figure 1. One end of the cascaded FBG is connected to the PC5, while the other end serves as the output port, facilitating preliminary mode selection and wavelength switching.
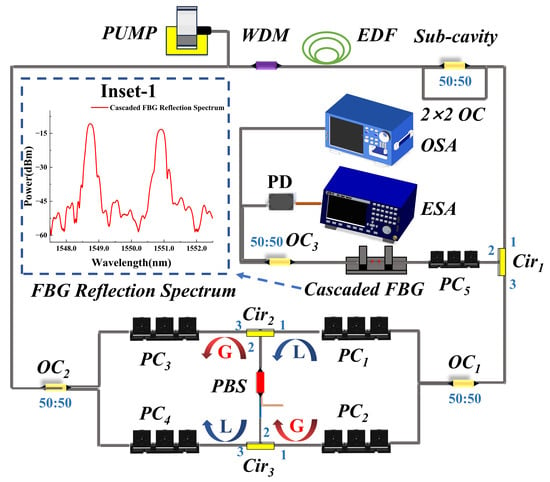
Figure 1.
Experimental structure of the proposed PT-symmetric fiber laser.
The PT-symmetric filter incorporates a dual-ring configuration, comprising two Cirs, four PCs, and a PBS. These components are coupled by a 2 × 2 OC with a 50:50 coupling ratio, which effectively reduces the number of longitudinal modes and ensures stable SLM laser output. To effectively filter out excess longitudinal modes, the sub-cavity, comprising 2 × 2 OCs, is configured with a length of 20 cm, resulting in an FSR of 1013 MHz. The oscillating laser is transmitted directly through the cascaded FBG, providing stable output.
Spectral data are continuously recorded and analyzed using an optical spectrum analyzer (OSA, YOKOGAWA/AQ6370D) with a resolution of 0.02 nm and a precision of 0.01 nm. While the instrument estimates values to three decimal places (0.001 nm), actual fluctuations are smaller than 0.01 nm, which the instrument cannot detect. To better reflect the true accuracy of the measurements, we reported the wavelength data to two decimal places. Additionally, spectral characteristics are monitored via an electrical spectrum analyzer (ESA, Agilent N9020A), following the conversion of the optical signal into an electrical signal by a photodetector (PD, Thorlabs PDB480C-AC, with a bandwidth of 1.6 GHz). The self-heterodyne system is employed to verify the single-frequency laser output and to measure the laser linewidth with accuracy.
2.3. Longitudinal Mode Selection Based on Dual-Physics Ring PT-Symmetric Structure
The PT-symmetric structure of the dual-physics loop system is shown in an enlarged view in Figure 2, where the PT-symmetric configuration with nonreciprocal transmission is depicted. This PT-symmetric system consists of gain and loss dual loops. The loss loop is formed by PC1 and PC4, while the gain loop is constructed using PC2 and PC3. After passing through the 50:50 OC1, the signal light is split into two beams. One beam is injected into the PBS in a counterclockwise (CCW) direction through PC1 and Cir2, where it attains a linearly polarized state before continuing through Cir3, PC4, and OC2, forming the loss loop. The second beam is injected from the opposite end of the PBS in a clockwise (CW) direction via PC2 and Cir3, then it passes through Cir2, PC3, and OC2, forming the gain loop. The gain and loss loops are coupled via OC1 and OC2, each with a 50:50 coupling ratio. To prevent interference between the signals entering the PBS from both directions, independent polarization direction rotations and phase delays are introduced into the incident light using PC1 and PC2.
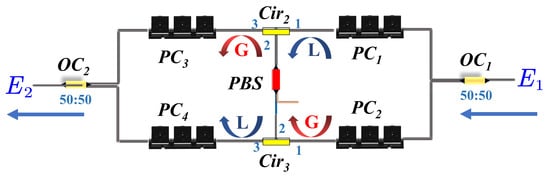
Figure 2.
Schematic diagram of non-reciprocal light transmission in a dual-physical ring PT-symmetric structure.
In the application of PT symmetry theory in optics, the system typically consists of two counter-propagating and mutually coupled light waves forming loops. When PT symmetry theory is combined with Brillouin gain to achieve ultra-narrow-linewidth SLM lasers [29], the loop experiencing Brillouin gain is referred to as the gain loop, while the loop containing only losses is referred to as the loss loop. In configurations where both loops occupy the same physical space [30], the loop with less attenuation is designated as the gain loop, and the one with higher attenuation as the loss loop. In most studies, the two coupled loops are of equal length and contain identical optical components, maintaining spatial symmetry [31]. In such cases, for simplicity, one loop is labeled as the gain loop and the other as the loss loop. The necessary asymmetry is typically introduced by adjusting the PCs to alter the orientation and intensity of the birefringent fast axis. In our experiment, the loop injected into the PBS in the CCW direction is defined as the loss loop, while the loop injected into the PBS in the CW direction is defined as the gain loop.
A three-paddle PC consists of two quarter-wave plates and one half-wave plate. Its transmission matrix can be expressed as follows [32]:
where and represent the phase delays introduced by the two quarter-wave plates along two orthogonal polarization directions, and is the polarization rotation angle introduced by the half-wave plate.
The beams injected into the PBS in the CW and CCW directions have orthogonal polarization states and pass through PC3 and PC4. Although the optical path lengths from the PBS output to the polarization loop entering OC2 are the same, residual birefringence effects caused by fiber bending and polarization mode dispersion from optical components may perturb the eigenfrequencies of the polarization loops, leading to mismatched eigenmodes. To satisfy PT symmetry, the angles of the two quarter-wave plates in PC3 and PC4, denoted as , are adjusted so that the phase delays of the two polarization loops are matched, ensuring that the real parts of the eigenfrequencies are equal.
Assuming that the polarization direction of light exiting the PBS remains unchanged after passing through the cavity and returning to the PBS, and that the rotation angles of the half-wave plates in PC1 and PC2 are set to zero, the following expression can be derived [23]:
where and represent the round-trip gain when PC3 and PC4 do not change the polarization direction; and are the polarization rotation angles of the corresponding loops in the PCs. By adjusting the half-wave plates in PC3 and PC4, the condition is achieved, ensuring that the gain and loss coefficients are matched in the PT system.
Next, along the optical path from the PBS output to the round trip then re-injected into the PBS, the rotation angles of the quarter-wave plates in PC1 and PC2 are adjusted to compensate for the polarization mode dispersion contributed by all optical components.
Finally, the two loops are coupled in OC2. The coupling coefficient can be expressed as in Ref. [33]:
where is the coupling length, is the loop length, and is the coupling ratio of OC2 corresponding to the intensity ratio of light waves transmitted in the CW and CCW directions.
Assuming identical delays, i.e., the same eigenfrequency in both coupled loops, denoted as , the modes of the two loops can be described using the following mode-coupling equation from Ref. [34]:
where and represent the amplitudes of the two coupled modes, and is the eigenfrequency of the nth mode in the resonant cavity.
Solving Equations (10) and (11), the eigenfrequencies of several pairs of Hamiltonian quantities of the laser under coupling conditions can be expressed as follows:
By adjusting the PC so that the value of the gain and loss coefficients of the corresponding loops are equal (note , ), i.e., the equation simplifies to:
When the coupling coefficient κ exceeds , the eigenfrequencies split into two distinct real frequencies, representing the PT-symmetric phase. Conversely, when the coupling coefficient κ is smaller than , the eigenfrequencies become a pair of complex conjugates due to the negative square root, described as . In this case, one mode, , leads to optical energy amplification and oscillation, while the other mode, , results in optical energy attenuation.
Another important characteristic of PT-symmetry is the substantial increase in gain contrast. In conventional laser systems, gain contrast is defined as the ratio of the gain of the central mode to that of the adjacent mode :
In the PT-symmetric system, the gain-contrast is expressed as in Ref. [35]:
The introduction of the square root term results in a significant improvement in gain contrast, quantified by the enhancement factor :
Since , is always greater than 1. As shown in Figure 3, the gain contrast increases significantly when approaches 1, and becomes especially pronounced when exceeds a threshold value.
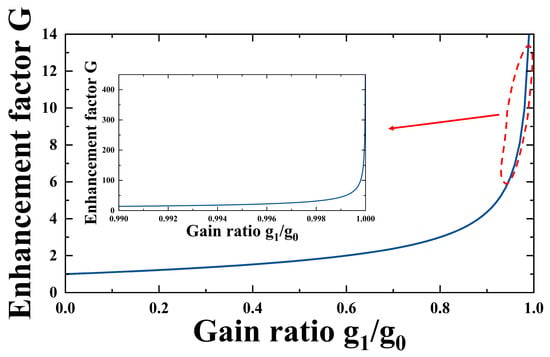
Figure 3.
Trend of the enhancement factor G with gain ratio variation.
In conclusion, by ensuring that the gain coefficient matches the loss coefficient and exceeds the coupling coefficient through precise adjustment of the PCs, the system enters the PT-broken phase. In the PT-broken phase, the eigenfrequencies split, and the gain contrast is enhanced. The primary mode is more likely to reach the PT-broken threshold due to a higher degree of confinement and a lower coupling coefficient. The primary mode is amplified by the increased gain contrast, while the side modes are suppressed before reaching the oscillation threshold, resulting in stable single-frequency laser output.
Specifically, when the incident light first passes through the initial PC, any polarization phase delay induced by the fiber bending or by other factors within the optical loop is eliminated by adjusting the quarter-wave plate. This ensures that the eigenfrequencies in the resonant cavity align with the real part of the PT-symmetric phase. As the light passes through the PBS, it is converted into a single polarization state, facilitating more precise gain control. The output from the PBS is directed through another PC, with the gain coefficient modulated by fine adjustments to the half-wave plate. This process enables the regulation of the PT-symmetric system and allows for switchable single- and dual-wavelength operation in SLM lasers.
2.4. Switchable Wavelength Output Based on Birefringence Filtering and PC Adjustment
The birefringence effect of SMF and the interaction with cascaded FBGs can generate a comb-like spectrum, which is a periodic transmission spectrum. By rotating the PC5, the total phase shift in the optical path is altered, leading to changes in the transmission coefficient of the comb-like spectrum and a corresponding wavelength shift of the entire transmission curve [36]. Since the cascaded FBG in the experiment is composed of two FBGs with single central wavelengths, the reflection curve exhibits two non-overlapping bandwidths with peaks. When the transmission peak of the comb-like spectrum falls within one of the reflection bandwidths of the cascaded FBG, single-wavelength laser oscillation output is generated at the wavelength corresponding to that transmission peak. When the transmission curve of the comb-like spectrum is symmetrical within the two reflection bandwidths of the cascaded FBG, the fiber laser may achieve dual-wavelength laser oscillation output at the two central wavelengths of the cascaded FBG [37].
3. Experimental Results and Discussion
3.1. Laser Spectral Characterization and Stability Studies
The experiment was conducted on a clean optical platform maintained at a constant temperature of 20 °C, with the components securely fixed to the platform using nuts or 3M tape. When the pump power was set to 300 mW, adjustments to the PCs enabled the switchable output to change between dual- and single-wavelength modes, as well as to toggle between two distinct single-wavelength outputs. In dual-wavelength mode, the output spectrum was captured and analyzed. As shown in Figure 4a, the two central wavelengths, defined by the cascaded FBG, were recorded at 1548.72 nm and 1550.91 nm. The optical signal-to-noise ratio (OSNR) exceeded 38.3 dB, and the wavelength separation between the two peaks was 2.19 nm. The stability of the wavelengths and power levels was measured at 6-minute intervals over a duration of 60 min, with the results depicted in Figure 4b–d. The maximum wavelength fluctuations for the left and right wavelengths (λ1 and λ2) were 0.03 nm and 0.01 nm, respectively, while the maximum power variations were 3.23 dB and 2.38 dB, respectively. These fluctuations are attributed to external environmental disturbances, as well as to internal gain competition and thermal effects within the pump source.
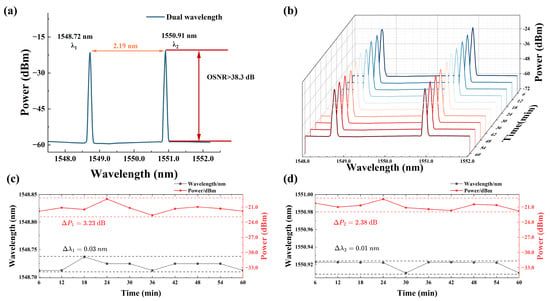
Figure 4.
(a) Dual wavelength spectrum of laser output. (b) The output spectra of the laser’s dual wavelength at 6-minute intervals over 60 min; (c,d) the wavelength and power stability of λ1 and λ2.
The performance of the output laser is influenced by gain competition in dual-wavelength operation and external environmental factors. To assess the laser’s performance after switching to single-wavelength mode, careful adjustment of the PCs mitigates the strong gain competition at different wavelengths, resulting in stable single-wavelength output. Based on the principle of birefringence filtering, the PC5 was meticulously adjusted to accomplish the transition from dual-wavelength to single-wavelength operation. The central wavelengths of the two single-wavelength lasers were recorded at 1548.71 nm and 1550.91 nm, with a wavelength separation of approximately 2.20 nm, as shown in Figure 5a,b. The stability of the output spectrum was monitored over a 60-min period, with measurements taken every 6 min, as depicted in Figure 5c,d. As shown in Figure 5e,f, the wavelength and power fluctuations for λ1 and λ2 were both 0.01 nm, 0.94 dB, and 0.76 dB, respectively. These fluctuations are primarily attributed to slight changes in the polarization state due to external environmental disturbances. The implementation of a vibration isolation system is expected to significantly enhance the overall stability of the system.
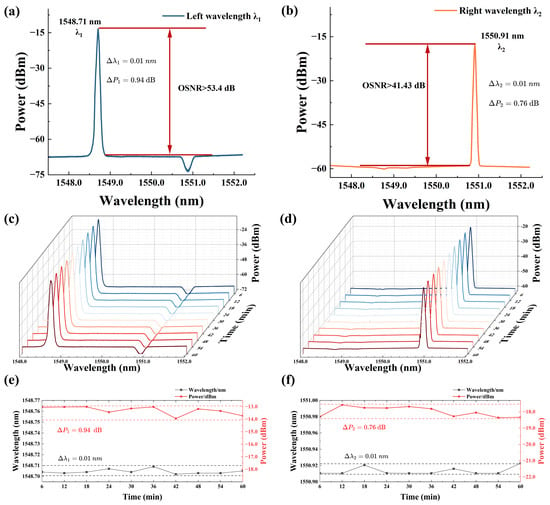
Figure 5.
Output laser spectra. (a,b) Output laser spectra; (c,d) spectral fluctuations within 60 min. (e,f) wavelength and power fluctuations for λ1 and λ2.
The relationship between the output power and pumping power of the laser in both dual-wavelength and single-wavelength states is presented in Figure 6. The pumping thresholds of the laser are 15 mW for λ1, 25 mW for λ2, and 15 mW for the dual-wavelength operation. Once the threshold is exceeded, the output power increases linearly with the pump power, as expressed by the following linear equations: y = 1.3033x − 18.5842, y = 0.6791x − 7.7306, and y = 0.9088x − 13.11857. A direct proportionality between the pump power and the laser output is demonstrated by these efficiencies. The overall output power of the laser is affected by optical transmission losses within the cavity, including losses from splitting and splicing due to multiple cutting and welding.
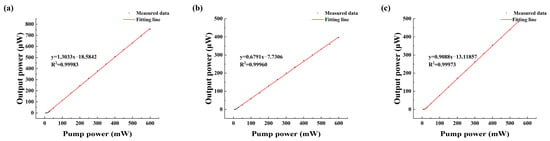
Figure 6.
Corresponding relationship between pump power and laser output of (a) λ1, (b) λ2, and (c) a dual-wavelength test.
3.2. Laser Longitudinal Modeling and Stability Study
To investigate the spectral characteristics of the laser, the self-homodyne method was employed. The output laser was connected to a 200 MHz photodetector (PD), which converted the optical signal into an electrical signal. This electrical signal was then routed to an ESA via a radio frequency (RF) line to monitor the beat frequency signal. The ESA had a scanning range of 0–200 MHz, with a resolution bandwidth (RBW) set to 0.5 Hz at 100 kHz. Figure 7 presents the beat frequency spectral characteristics under various conditions. Figure 7a–d depicts the spectra obtained when either the PT-symmetric system or the sub-cavity is used individually. Figure 7e,f shows that the laser operates in multiple longitudinal modes when the PT symmetry is unbroken. However, by finely adjusting PC2, the system transitions to the PT-broken phase, resulting in single-frequency laser output. Figure 7g,h demonstrates that stable SLM lasers were achieved for the different center wavelengths, λ1 and λ2. These results indicate that single-frequency oscillations were not achieved with either method alone or in the PT-unbroken phase, although mode selectivity was observed with both methods.
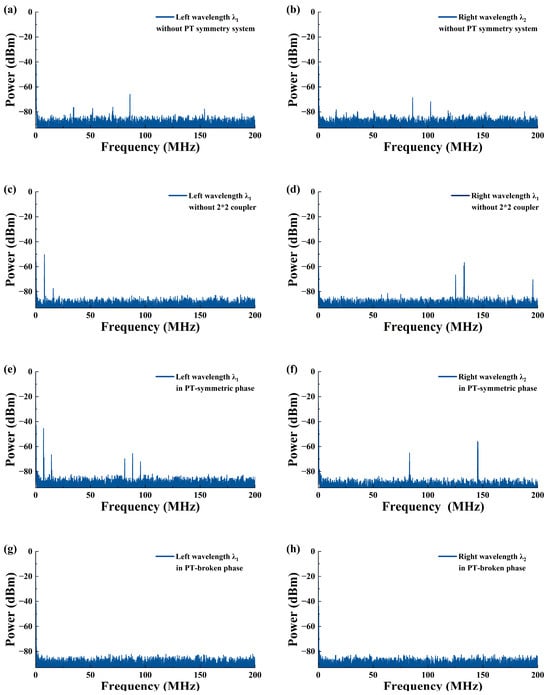
Figure 7.
Spectra of laser output under different conditions. (a,b) Output spectra without the PT-symmetric system; (c,d) output spectra without the 2 × 2 coupled sub-cavity; (e,f) spectra when PT symmetry was unbroken; (g,h) spectra when λ1 and λ2 were in the PT-broken phase.
Additionally, the single-frequency stability of the laser under single-wavelength output conditions was assessed over a 60-min period using a delayed self-heterodyne frequency measurement system. This system comprised an AOM with a 100 MHz frequency shift and a 50 km SMF delay line. The test results confirm that the system maintained stable single-frequency laser output throughout the 60-min duration in the PT-broken phase, as illustrated in Figure 8, where Figure 8a and 8b depict the frequency spectra stability of stable SLM operation at λ1 and λ2, respectively.
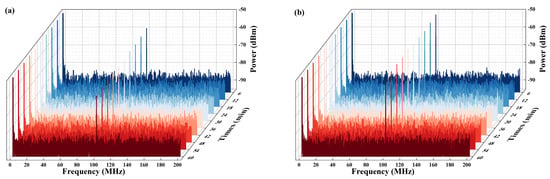
Figure 8.
Frequency spectra stability of stable SLM operation at λ1 and λ2.
3.3. The Measured Linewidth Characteristics Based on the Self-Heterodyne Method
The linewidth of each wavelength in the dual-wavelength erbium-doped fiber laser (DW-EDFL) was measured using the delayed self-heterodyne interferometer (DSHI) method [38]. Compared to traditional spectrometer measurements, greater accuracy in the phase information of optical signals and higher detection precision is provided by the DSHI method. In the experiment, the linewidth of the output laser was extensively measured using the delayed autocorrelation technique. Additionally, the detection errors were further minimized through fitting to the Lorentzian function. The beat frequency center was positioned at 100 MHz, with the ESA range set to 200 kHz and a resolution of 56 Hz. Lorentzian curve fitting enhances the linewidth measurement accuracy. As shown in Figure 9a,b, the 20 dB linewidths for λ1 and λ2 were 20.2 kHz and 17.8 kHz, respectively, corresponding to 3 dB linewidths of 1.01 kHz and 0.89 kHz.
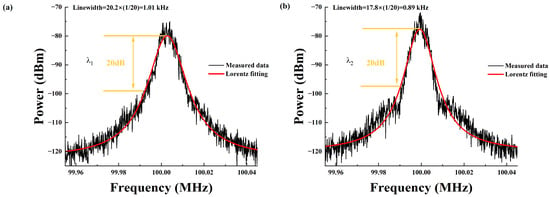
Figure 9.
Measurement of the DW-EDFL linewidth: measurement results for (a) λ1 and (b) λ2.
3.4. RIN Measurement Based on the Direct Detection Method
The direct detection method [39] was employed in the experiment to evaluate the proposed PT-symmetry-based laser system and the noise characteristics of the detector system. The frequency spectral density of RIN is depicted in Figure 10. Figure 10a illustrates the detector’s noise floor in the absence of input light, which primarily results from the electronic noise of the PD and the ESA, as well as interference from the external environment. For the seed laser, a relaxation oscillation frequency peak was observed at 0.3 MHz, with an intensity of −90 dB/Hz [40]. Figure 10b–d shows the RIN of the output laser for single-wavelength and dual-wavelength operating states, respectively. The RIN of the proposed DW-EDFL decreased as frequency increased, stabilizing around −117 dB/Hz for frequencies exceeding 1 kHz. Relaxation oscillation peaks were present near 58 kHz, 66 kHz, and 62 kHz. Beyond 1 kHz, these peaks were no longer observed in the DW-EDFL, indicating that the PT dual-loop filter effectively provides mode selectivity and ensures stable SLM output.
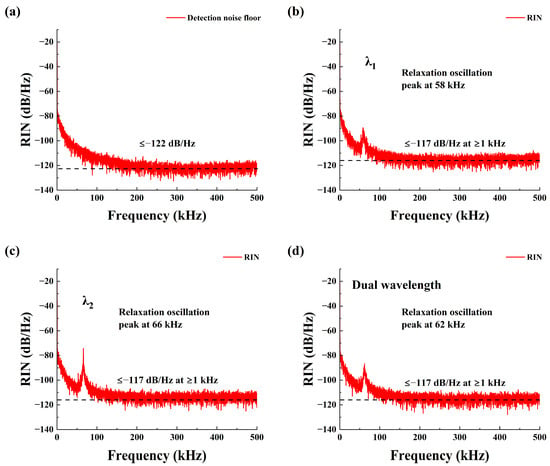
Figure 10.
Laser intensity noise. (a) Detector baseline noise; (b–d) intensity noise of λ1, λ2, and dual-wavelength operation.
3.5. Phase Noise Measurements Based on the Unbalanced Interferometer Method
The phase noise of the output laser was experimentally measured using an unbalanced interferometer with a 3 × 3 coupler [41]. The power spectral density of the phase fluctuations is presented in Figure 11. The results indicate that in the low-frequency range, the higher power spectral density is primarily influenced by 1/f noise [42]. In contrast, in the high-frequency range, the phase noise of the PT-symmetric laser remains stable at a lower intensity, showing no significant spikes. The phase noise was measured at 10−5 rad2/Hz@10 kHz.
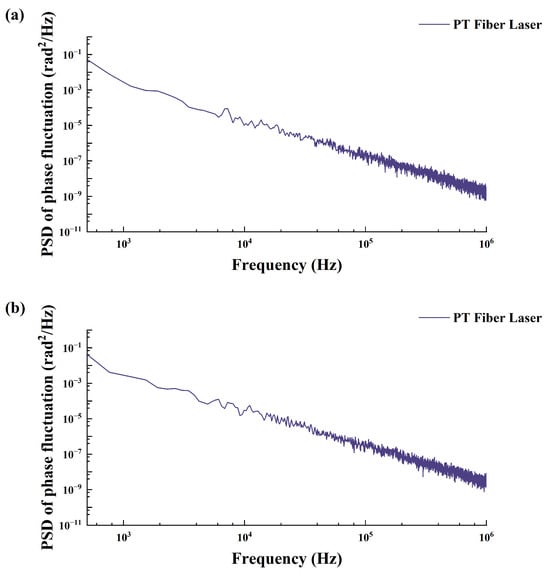
Figure 11.
Phase noise of output laser (a) λ1 and (b) λ2.
4. Conclusions
In this paper, a stable, switchable dual-wavelength SLM fiber laser based on the PT-symmetry system and cascaded FBGs is proposed and experimentally demonstrated. The PT-symmetric filter system comprises PCs, PBS, and OCs. Precise adjustment of the PCs enables stable SLM output upon reaching the PT-broken phase. FBGs with center wavelengths suited to the erbium ion gain bandwidth were selected for cascading. Combined with PC adjustments, this setup achieves both single-wavelength and dual-wavelength switchable outputs. Under dual-wavelength operation, the wavelength and power fluctuations were measured to be less than 0.03 nm and 3.23 dB for one wavelength, and 0.01 nm and 2.38 dB for the other. During single-wavelength operation, the OSNRs exceeded 40 dB over a 60-min period, with power and wavelength fluctuations of 0.01 nm and 0.94 dB, and 0.01 nm and 0.76 dB, respectively. The RIN was measured to be below −117 dB/Hz, and the phase noise was 10−5 rad2/Hz at 10 kHz. To verify the SLM characteristics, beat frequency signals of the laser output are experimentally measured under different cascade conditions, confirming the essential roles of the PT filter, cascaded FBGs, and sub-cavity in mode selection. The linewidths of each wavelength reached 1.01 kHz and 0.89 kHz. This high-performance SLM narrow-linewidth fiber laser shows significant potential for applications in coherent LiDAR detection and long-distance fiber-optic sensing.
Author Contributions
Conceptualization, K.W.; data curation, K.W.; formal analysis, F.Y. and Z.Z.; funding acquisition, B.Y.; investigation, K.W. and Q.W.; methodology, K.W.; project administration, B.Y.; resources, B.Y.; software, Q.W. and S.W. (Shiyang Wang); supervision, Z.L. and S.W. (Songhua Wu); validation, K.W., Y.L., Q.W. and F.Y.; visualization, Y.W. and H.L.; writing—original draft, K.W.; writing—review and editing, B.Y., C.L. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (U2006217, 61901429, 62075007), the Natural Science Foundation of Shandong Province (ZR2023MF071), and the Youth Innovation Team Project of High Schools in Shandong Province (2022KJ044).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shi, W.; Schulzgen, A.; Amezcua, R.; Zhu, X.S.; Alam, S.U. Fiber lasers and their applications: Introduction. J. Opt. Soc. Am. B-Opt. Phys. 2017, 34, FLA1. [Google Scholar] [CrossRef]
- Al-Mashhadani, M.K.S.; Al-Mashhadani, T.F.; Goktas, H.H. Broadly tunable 40 GHz Brillouin frequency spacing multiwavelength Brillouin-Erbium fiber laser for DWDM. Opt. Commun. 2019, 451, 116–123. [Google Scholar] [CrossRef]
- Liu, D.; Ngo, N.Q.; Tjin, S.C.; Dong, X. A dual-wavelength fiber laser sensor system for measurement of temperature and strain. IEEE Photonics Technol. Lett. 2007, 19, 1148–1150. [Google Scholar] [CrossRef]
- Fotiadi, A.A.; Korobko, D.A.; Zolotovskii, I.O. Brillouin Lasers and Sensors: Trends and Possibilities. Optoelectron. Instrum. Data Process. 2023, 59, 66–76. [Google Scholar] [CrossRef]
- Jingguo, Z.; Ye, Y.; Chenghao, J.; Yu, L.; Zhengwei, Z. Research progress of on-chip integrated FMCW LiDAR (cover paper· invited). Infrared Laser Eng. 2024, 53, 20240239-1–20240239-17. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Applications of Lasers for Tactical Military Operations. IEEE Access 2017, 5, 20736–20753. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, X.; Xu, S.; Zhang, H. Recent progress in multi-wavelength fiber lasers: Principles, status, and challenges. Chin. Opt. Lett. 2020, 18, 36–62. [Google Scholar] [CrossRef]
- Wang, L.; Sun, S.; Yan, W.; Qu, J.; Wang, Y. L-band switchable dual-wavelength, high-energy pulsed fiber laser. Infrared Laser Eng. 2021, 50, 20200370. [Google Scholar]
- Bianchetti, M.; Sierra-Hernandez, J.M.; Mata-Chavez, R.I.; Gallegos-Arellano, E.; Estudillo-Ayala, J.M.; Jauregui-Vazquez, D.; Fernandez-Jaramillo, A.A.; Salceda-Delgado, G.; Rojas-Laguna, R. Switchable multi-wavelength laser based on a core-offset Mach-Zehnder interferometer with non-zero dispersion-shifted fiber. Opt. Laser Technol. 2018, 104, 49–55. [Google Scholar] [CrossRef]
- Sun, Z.; Ding, X.; Yin, B.; Lv, Y.; Lv, C.; Wang, M.; Wu, S. Tunable and switchable dual-wavelength SLM narrow-linewidth fiber laser with Lyot filter cascaded by double-ring cavity. Infrared Phys. Technol. 2024, 140, 105397. [Google Scholar] [CrossRef]
- Feng, X.H.; Sun, L.; Xiong, L.Y.; Liu, Y.G.; Yuan, S.H.; Kai, G.Y.; Dong, X.Y. Switchable and tunable dual-wavelength erbium-doped fiber laser based on one fiber Bragg grating. Opt. Fiber Technol. 2004, 10, 275–282. [Google Scholar] [CrossRef]
- Wang, D.N.; Tong, F.W.; Fang, X.H.; Jin, W.; Wai, P.K.A.; Gong, J.M. Multiwavelength erbium-doped fiber ring laser source with a hybrid gain medium. Opt. Commun. 2003, 228, 295–301. [Google Scholar] [CrossRef]
- Yin, B.; Feng, S.; Bai, Y.; Liu, Z.; Liang, L.; Liu, S.; Jian, S. Switchable Single-Polarization Dual-Wavelength Ring Laser Based on Structured PM-CFBG. IEEE Photonics Technol. Lett. 2014, 26, 1227–1230. [Google Scholar] [CrossRef]
- Zhang, J.; Qiao, X.; Liu, F.; Weng, Y.; Wang, R.; Ma, Y.; Rong, Q.; Hu, M.; Feng, Z. A tunable erbium-doped fiber laser based on an MZ interferometer and a birefringence fiber filter. J. Opt. 2012, 14, 015402. [Google Scholar] [CrossRef]
- Wang, S.; Wan, J.; Lei, H.; Zhao, L.; Luo, H.; Li, J. High reflectivity, ultraflat-spectrum chirped fiber Bragg grating written using low energy UV femtosecond pulses. Opt. Laser Technol. 2024, 176, 111035. [Google Scholar] [CrossRef]
- Lu, B.-L.; Kang, J.; Qi, X.-Y.; Feng, X.-Q.; Hou, L.; Jiang, M.; Chen, H.-W.; Wang, Y.; Wang, K.-L.; Bai, J.-T. High-Stability Broadband Wavelength-Tunable Single-Frequency Ytterbium-Doped All-Fiber Compound Ring Cavity. IEEE Photonics J. 2017, 9, 1501708. [Google Scholar] [CrossRef]
- Zayhowski, J.J. Limits imposed by spatial hole burning on the single-mode operation of standing-wave laser cavities. Opt. Lett. 1990, 15, 431–433. [Google Scholar] [CrossRef]
- Lu, J.; Chen, S.; Bai, Y. Study on single-mode compound-ring fiber laser. Opt. Technol. 2005, 31, 212–213. [Google Scholar]
- Gao, M.; Yin, B.; Lv, Y.; Sang, G.; Hou, B.; Li, H.; Wang, M.; Wu, S. Tunable and Switchable Dual-Wavelength SLM Narrow-Linewidth Fiber Laser with a PMFBG-FP Filter Cascaded by Multi-Ring Cavity. Photonics 2022, 9, 756. [Google Scholar] [CrossRef]
- Feng, L.; Wong, Z.J.; Ma, R.-M.; Wang, Y.; Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef]
- Hodaei, H.; Miri, M.-A.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-time-symmetric microring lasers. Science 2014, 346, 975–978. [Google Scholar] [CrossRef] [PubMed]
- Fu, T.; Wang, Y.; Wang, X.; Chen, J.; Zhou, X.; Zheng, W. Microstructure Lasers Based on Parity-Time Symmetry and Supersymmetry. Chin. J. Lasers 2021, 48, 1201005. [Google Scholar] [CrossRef]
- Li, L.; Cao, Y.; Zhi, Y.; Zhang, J.; Zou, Y.; Feng, X.; Guan, B.-O.; Yao, J. Polarimetric parity-time symmetry in a photonic system. Light Sci. Appl. 2020, 9, 169. [Google Scholar] [CrossRef] [PubMed]
- Seker, E.; Olyaeefar, B.; Dadashi, K.; Sengul, S.; Teimourpour, M.H.; El-Ganainy, R.; Demir, A. Single-mode quasi PT-symmetric laser with high power emission. Light-Sci. Appl. 2023, 12, 149. [Google Scholar] [CrossRef]
- Ramezani, H.; Kottos, T.; El-Ganainy, R.; Christodoulides, D.N. Unidirectional nonlinear PT-symmetric optical structures. Phys. Rev. A 2010, 82, 043803. [Google Scholar] [CrossRef]
- Kang, M.; Liu, F.; Li, J. Effective spontaneous PT-symmetry breaking in hybridized metamaterials. Phys. Rev. A 2013, 87, 053824. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Complex extension of quantum mechanics. Phys. Rev. Lett. 2002, 89, 270401. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of coupled optical PT-symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef]
- Lv, Y.; Yin, B.; Chen, X.; Sang, G.; Liu, S.; Li, G.; Xiao, S.; Wang, M.; Wu, S. Tunable single frequency Hz-magnitude narrow linewidth Brillouin fiber laser based on parity-time symmetry. Opt. Express 2024, 32, 4974–4986. [Google Scholar] [CrossRef]
- Lv, Y.; Yin, B.; Wang, M.; Li, H.; Gao, M.; Sang, G.; Wang, Q.; Wu, S. Switchable and tunable orthogonal single-polarization dual wavelength SLM fiber laser based on parity-time symmetric system and PM-FBG. Opt. Laser Technol. 2023, 166, 109695. [Google Scholar] [CrossRef]
- Lv, Y.; Yin, B.; Gao, M.; Liu, S.; Li, H.; Wang, M.; Wu, S. Polarimetric parity-time symmetry fiber laser with switchable and tunable orthogonal single-polarization narrow-linewidth output. Results Phys. 2023, 51, 106637. [Google Scholar] [CrossRef]
- Liu, W.; Wang, M.; Yao, J. Tunable Microwave and Sub-Terahertz Generation Based on Frequency Quadrupling Using a Single Polarization Modulator. J. Light. Technol. 2013, 31, 1636–1644. [Google Scholar] [CrossRef]
- Dai, Z.; Fan, Z.; Li, P.; Yao, J. Widely Wavelength-Tunable Parity-Time Symmetric Single-Longitudinal-Mode Fiber Ring Laser With a Single Physical Loop. J. Light. Technol. 2021, 39, 2151–2157. [Google Scholar] [CrossRef]
- Krasnok, A.; Nefedkin, N.; Alu, A. Parity-Time Symmetry and Exceptional Points. IEEE Antennas Propag. Mag. 2021, 63, 110–121. [Google Scholar] [CrossRef]
- Haus, H.A.; Huang, W.P. Coupled-Mode Theory. Proc. IEEE 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Zhao, X.-l.; Luo, F.; Zhang, Y.-m.; Meng, F.-y.; Dong, M.-l. A switchable dual-wavelength fiber laser based on phase-shifted fiber Bragg grating combined with Sagnac loop. Optoelectron. Lett. 2019, 15, 122–126. [Google Scholar] [CrossRef]
- Meng, X.; Wen, H.; Chen, H.; Sun, B.; Lu, B.; Bai, J. Wavelength switchable and tunable single-frequency narrow linewidth ytterbium doped fiber laser (Invited). Infrared Laser Eng. 2022, 51, 20220325. [Google Scholar]
- Xiao, H.; Wang, X.; Ma, Y.; Zhang, J. Linewidth Measurement of Narrow Fiber Laser Based on the DSHI. Opto-Electron. Eng. 2010, 37, 57–61. [Google Scholar]
- Hu, G.; Guo, Y.; Li, X.; Wang, Y. Noise measuring methods of semiconductor lasers. Semicond. Technol. 2001, 1, 53–56. [Google Scholar]
- Collin, R.; Chartier, T.; Besnard, P. Numerical investigation of relative intensity noise in frequency-doubled multimode fiber lasers. Opt. Commun. 2021, 485, 126724. [Google Scholar] [CrossRef]
- Bai, Y.; Yan, F.; Han, W.; Zhang, L.; Cheng, D.; Bai, Z.; Wen, X. High-stability laser phase demodulation system based on 3*3 polarization maintaining fiber coupler. Opt. Precis. Eng. 2019, 27, 739–746. [Google Scholar]
- Kikuchi, K. Effect of 1/f-type FM noise on semiconductor-laser linewidth residual in high-power limit. IEEE J. Quantum Electron. 1989, 25, 684–688. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).