Ultrahigh-Reflectivity Circularly Polarized Mirrors Based on the High-Contrast Subwavelength Chiral Metasurface
Abstract
1. Introduction
2. Materials and Methods
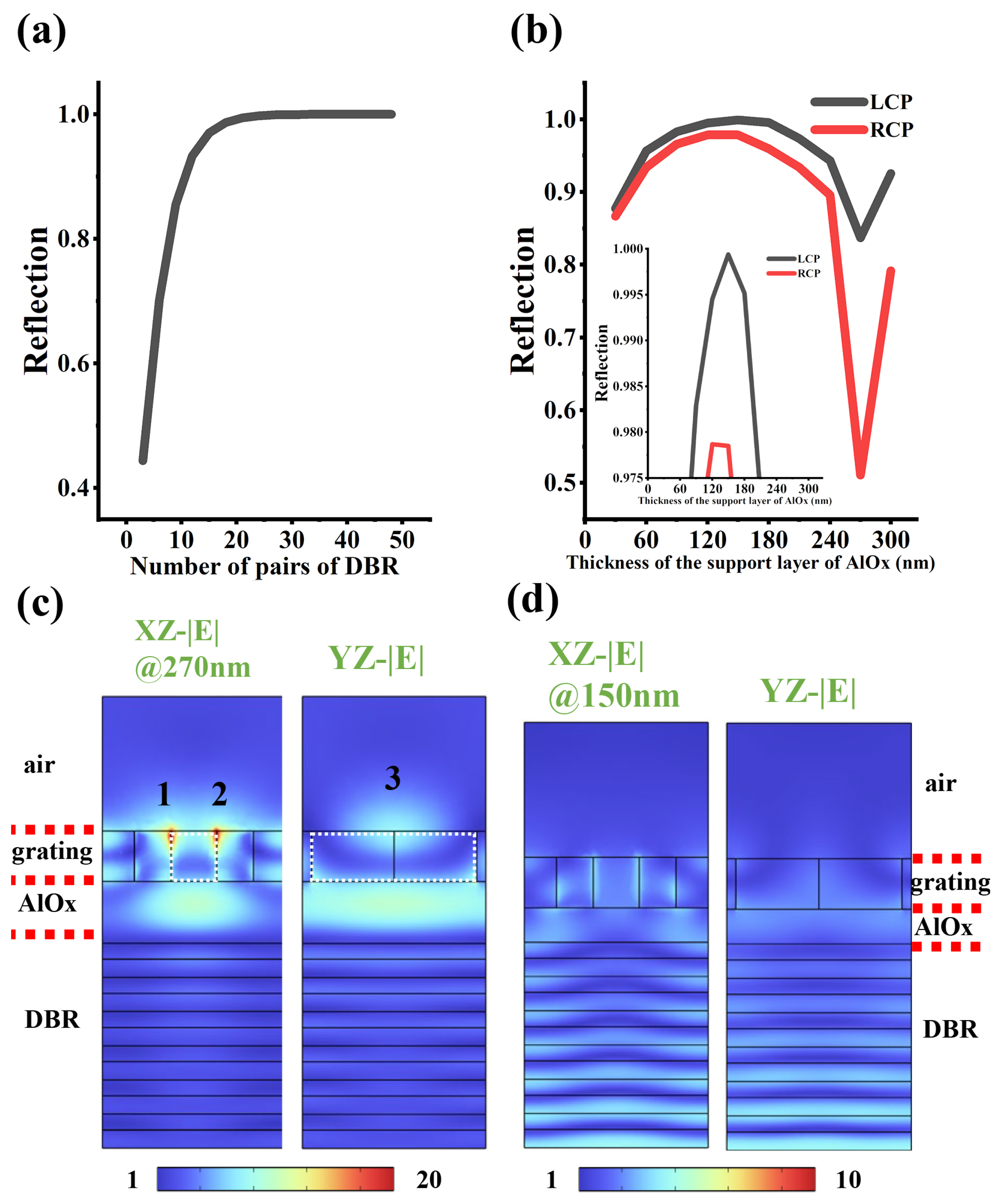
2.1. Structure and Optimization
2.2. Optical Mode and Chiral Analysis
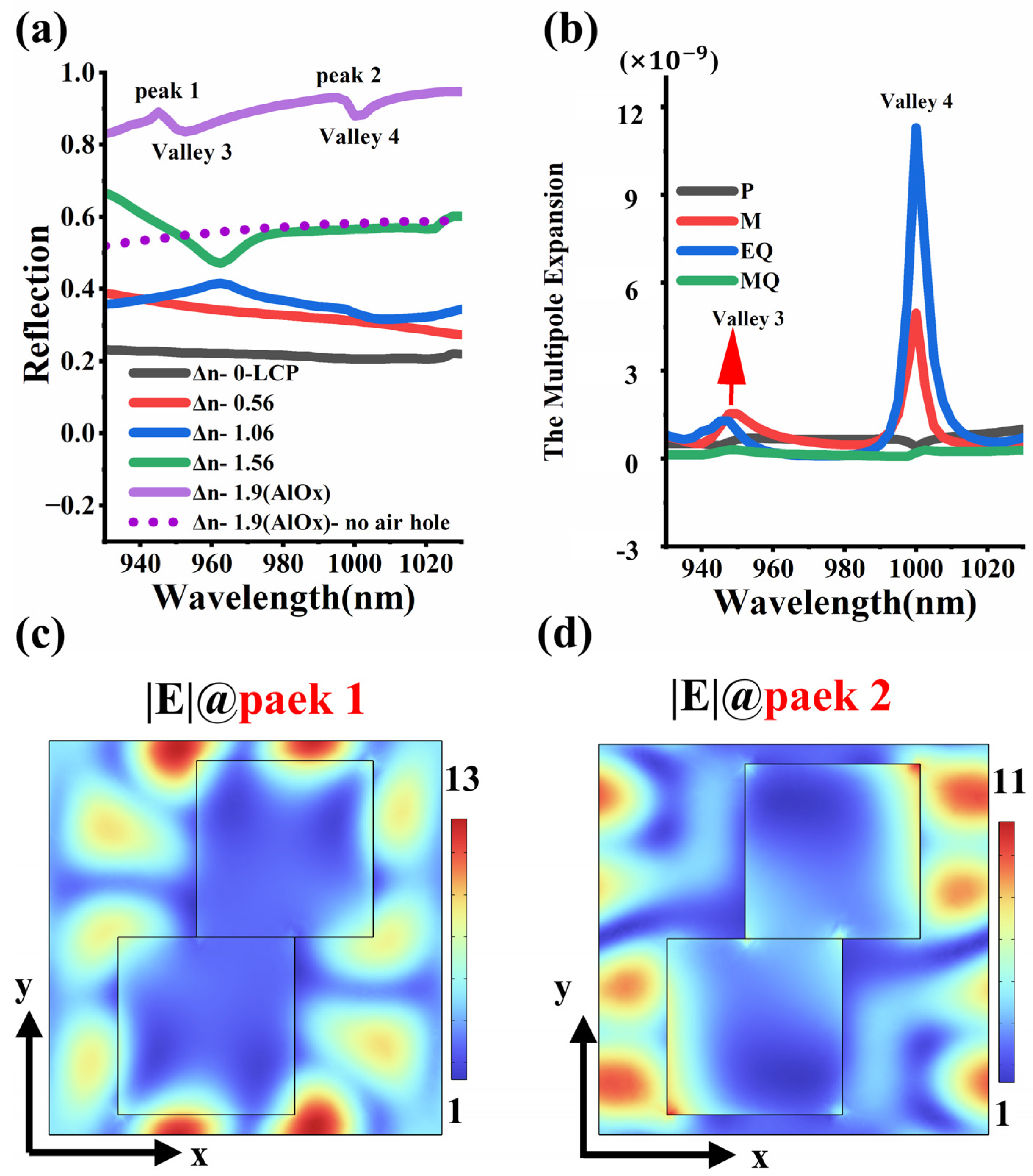
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stanciu, C.D.; Hansteen, F.; Kimel, A.V.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-Optical Magnetic Recording with Circularly Polarized Light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.-W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef] [PubMed]
- Spandana, K.U.; Mahato, K.K.; Mazumder, N. Polarization-resolved Stokes-Mueller imaging: A review of technology and applications. Lasers Med. Sci. 2019, 34, 1283–1293. [Google Scholar] [CrossRef]
- He, H.; Liao, R.; Zeng, N.; Li, P.; Chen, Z.; Liu, X.; Ma, H. Mueller Matrix Polarimetry—An Emerging New Tool for Characterizing the Microstructural Feature of Complex Biological Specimen. J. Light. Technol. 2019, 37, 2534–2548. [Google Scholar] [CrossRef]
- Soda, H.; Iga, K.-i.; Kitahara, C.; Suematsu, Y. GaInAsP/InP Surface Emitting Injection Lasers. Jpn. J. Appl. Phys. 1979, 18, 2329. [Google Scholar] [CrossRef]
- Ra, Y.H.; Rashid, R.T.; Liu, X.; Sadaf, S.M.; Mashooq, K.; Mi, Z. An electrically pumped surface-emitting semiconductor green laser. Sci. Adv. 2020, 6, eaav7523. [Google Scholar] [CrossRef]
- McPolin, C.P.T.; Bouillard, J.-S.; Vilain, S.; Krasavin, A.V.; Dickson, W.; O’Connor, D.; Wurtz, G.A.; Justice, J.; Corbett, B.; Zayats, A.V. Integrated plasmonic circuitry on a vertical-cavity surface-emitting semiconductor laser platform. Nat. Commun. 2016, 7, 12409. [Google Scholar] [CrossRef]
- Han, Y.; Li, Z.; Wu, L.; Mai, S.; Xing, X.; Fu, H.Y. High-Speed Two-Dimensional Spectral-Scanning Coherent LiDAR System Based on Tunable VCSEL. J. Light. Technol. 2023, 41, 412–419. [Google Scholar] [CrossRef]
- Kwon, O.; Moon, S.; Yun, Y.; Nam, Y.-h.; Kim, N.-h.; Kim, D.; Choi, W.; Park, S.; Lee, J. Highly efficient thin-film 930 nm VCSEL on PDMS for biomedical applications. Sci. Rep. 2023, 13, 571. [Google Scholar] [CrossRef]
- Pieczarka, M.; Gębski, M.; Piasecka, A.N.; Lott, J.A.; Pelster, A.; Wasiak, M.; Czyszanowski, T. Bose–Einstein condensation of photons in a vertical-cavity surface-emitting laser. Nat. Photonics 2024. [Google Scholar] [CrossRef]
- Lee, S.; Forman, C.A.; Kearns, J.; Leonard, J.T.; Cohen, D.A.; Nakamura, S.; DenBaars, S.P. Demonstration of GaN-based vertical-cavity surface-emitting lasers with buried tunnel junction contacts. Opt. Express 2019, 27, 31621–31628. [Google Scholar] [CrossRef] [PubMed]
- Ando, H.; Sogawa, T.; Gotoh, H. Photon-spin controlled lasing oscillation in surface-emitting lasers. Appl. Phys. Lett. 1998, 73, 566–568. [Google Scholar] [CrossRef]
- Iba, S.; Koh, S.; Ikeda, K.; Kawaguchi, H. Room temperature circularly polarized lasing in an optically spin injected vertical-cavity surface-emitting laser with (110) GaAs quantum wells. Appl. Phys. Lett. 2011, 98, 081113. [Google Scholar] [CrossRef]
- Lindemann, M.; Xu, G.; Pusch, T.; Michalzik, R.; Hofmann, M.R.; Žutić, I.; Gerhardt, N.C. Ultrafast spin-lasers. Nature 2019, 568, 212–215. [Google Scholar] [CrossRef]
- Holub, M.; Bhattacharya, P. Spin-polarized light-emitting diodes and lasers. J. Phys. D Appl. Phys. 2007, 40, R179. [Google Scholar] [CrossRef]
- Hodgkinson, I.J.; Wu, Q.h.; Arnold, M.D.; McCall, M.W.; Lakhtakia, A. Chiral mirror and optical resonator designs for circularly polarized light: Suppression of cross-polarized reflectances and transmittances. Opt. Commun. 2002, 210, 201–211. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, Y.; Wu, S.T. Enhancing cholesteric liquid crystal laser performance using a cholesteric reflector. Opt. Express 2006, 14, 3906–3916. [Google Scholar] [CrossRef]
- Kopp, V.I.; Fan, B.; Vithana, H.K.; Genack, A.Z. Low-threshold lasing at the edge of a photonic stop band in cholesteric liquid crystals. Opt. Lett. 1998, 23, 1707–1709. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, F.; Liu, J.; Zhang, J.D.; Lakhtakia, A.; Xu, J. Stable Circularly Polarized Emission from a Vertical-Cavity Surface-Emitting Laser with a Chiral Reflector. Appl. Phys. Express 2012, 5, 032102. [Google Scholar] [CrossRef]
- Magnusson, R.; Shokooh-Saremi, M. Physical basis for wideband resonant reflectors. Opt. Express 2008, 16, 3456–3462. [Google Scholar] [CrossRef]
- Magnusson, R. Wideband reflectors with zero-contrast gratings. Opt. Lett. 2014, 39, 4337–4340. [Google Scholar] [CrossRef]
- Zou, Y.; Jin, H.; Zhu, R.; Zhang, T. Metasurface Holography with Multiplexing and Reconfigurability. Nanomaterials 2023, 14, 66. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Lin, X. A review of metasurface polarization devices. Opt. Mater. 2023, 146, 114567. [Google Scholar] [CrossRef]
- Hu, J.; Bandyopadhyay, S.; Liu, Y.; Shao, L. A Review on Metasurface: From Principle to Smart Metadevices. Front. Phys. 2021, 8, 586087. [Google Scholar] [CrossRef]
- Zhao, R.; Huang, L.; Wang, Y. Recent advances in multi-dimensional metasurfaces holographic technologies. PhotoniX 2020, 1, 20. [Google Scholar] [CrossRef]
- Wang, T.; Cai, H.; Li, S.; Ren, Y.; Shi, J.; Zhou, J.; Li, D.; Ding, S.; Hua, Y.; Qu, G. Research Progress of Novel Metasurface Spectral Imaging Chips. Laser Optoelectron. Prog. 2023, 60, 1106014. [Google Scholar]
- Wang, Z.; Xiao, Y.; Liao, K.; Li, T.; Song, H.; Chen, H.; Uddin, S.M.Z.; Mao, D.; Wang, F.; Zhou, Z.; et al. Metasurface on integrated photonic platform: From mode converters to machine learning. Nanophotonics 2022, 11, 3531–3546. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar photonics with metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef]
- Achouri, K.; Caloz, C. Design, concepts, and applications of electromagnetic metasurfaces. Nanophotonics 2018, 7, 1095–1116. [Google Scholar] [CrossRef]
- Maksimov, A.A.; Tartakovskii, I.I.; Filatov, E.V.; Lobanov, S.V.; Gippius, N.A.; Tikhodeev, S.G.; Schneider, C.; Kamp, M.; Maier, S.; Höfling, S.; et al. Circularly polarized light emission from chiral spatially-structured planar semiconductor microcavities. Phys. Rev. B 2014, 89, 045316. [Google Scholar] [CrossRef]
- Demenev, A.A.; Kulakovskii, V.D.; Schneider, C.; Brodbeck, S.; Kamp, M.; Höfling, S.; Lobanov, S.V.; Weiss, T.; Gippius, N.A.; Tikhodeev, S.G. Circularly polarized lasing in chiral modulated semiconductor microcavity with GaAs quantum wells. Appl. Phys. Lett. 2016, 109, 171106. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Han, J.; Kivshar, Y.; Song, Q. Chiral emission from resonant metasurfaces. Science 2022, 377, 1215–1218. [Google Scholar] [CrossRef]
- Jia, X.; Kapraun, J.; Wang, J.; Qi, J.; Ji, Y.; Chang-Hasnain, C.J. Metasurface reflector enables room-temperature circularly polarized emission from VCSEL. Optica 2023, 10, 1093–1099. [Google Scholar] [CrossRef]
- Bai, J.; Wang, C.; Chen, X.; Basiri, A.; Wang, C.; Yao, Y. Chip-integrated plasmonic flat optics for mid-infrared full-Stokes polarization detection. Photon. Res. 2019, 7, 1051–1060. [Google Scholar] [CrossRef]
- Basiri, A.; Chen, X.; Bai, J.; Amrollahi, P.; Carpenter, J.; Holman, Z.; Wang, C.; Yao, Y. Nature-inspired chiral metasurfaces for circular polarization detection and full-Stokes polarimetric measurements. Light Sci. Appl. 2019, 8, 78. [Google Scholar] [CrossRef]
- Cheng, B.; Song, G. Full-Stokes polarization photodetector based on the hexagonal lattice chiral metasurface. Opt. Express 2023, 31, 30993–31004. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, X.; Lin, Y.; Zhu, A.; Zhu, X.; Guo, P.; Cao, B.; Wang, C. All-dielectric metasurface circular dichroism waveplate. Sci. Rep. 2017, 7, 41893. [Google Scholar] [CrossRef]
- Pao, Y.H.; Onstott, J.R. Reflection circular dichroism of naturally optically active substances. Int. J. Quantum Chem. 2015, 3, 119–128. [Google Scholar] [CrossRef]
- Yang, B.; Liu, W.; Li, Z.; Cheng, H.; Choi, D.Y.; Chen, S.; Tian, J. Ultrahighly Saturated Structural Colors Enhanced by Multipolar-Modulated Metasurfaces. Nano Lett. 2019, 19, 4221–4228. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, B.; Jiang, B.; Zou, Y.; Song, G. Ultrahigh-Reflectivity Circularly Polarized Mirrors Based on the High-Contrast Subwavelength Chiral Metasurface. Photonics 2024, 11, 923. https://doi.org/10.3390/photonics11100923
Cheng B, Jiang B, Zou Y, Song G. Ultrahigh-Reflectivity Circularly Polarized Mirrors Based on the High-Contrast Subwavelength Chiral Metasurface. Photonics. 2024; 11(10):923. https://doi.org/10.3390/photonics11100923
Chicago/Turabian StyleCheng, Bo, Botao Jiang, Yuxiao Zou, and Guofeng Song. 2024. "Ultrahigh-Reflectivity Circularly Polarized Mirrors Based on the High-Contrast Subwavelength Chiral Metasurface" Photonics 11, no. 10: 923. https://doi.org/10.3390/photonics11100923
APA StyleCheng, B., Jiang, B., Zou, Y., & Song, G. (2024). Ultrahigh-Reflectivity Circularly Polarized Mirrors Based on the High-Contrast Subwavelength Chiral Metasurface. Photonics, 11(10), 923. https://doi.org/10.3390/photonics11100923





