Enhanced Thermoacoustic Imaging System with Parallel Ultrasonic Velocity Measurement for Distinguishing Types of Microwave-Absorbing Anomalies
Abstract
1. Introduction
2. Model and Methods
2.1. Model
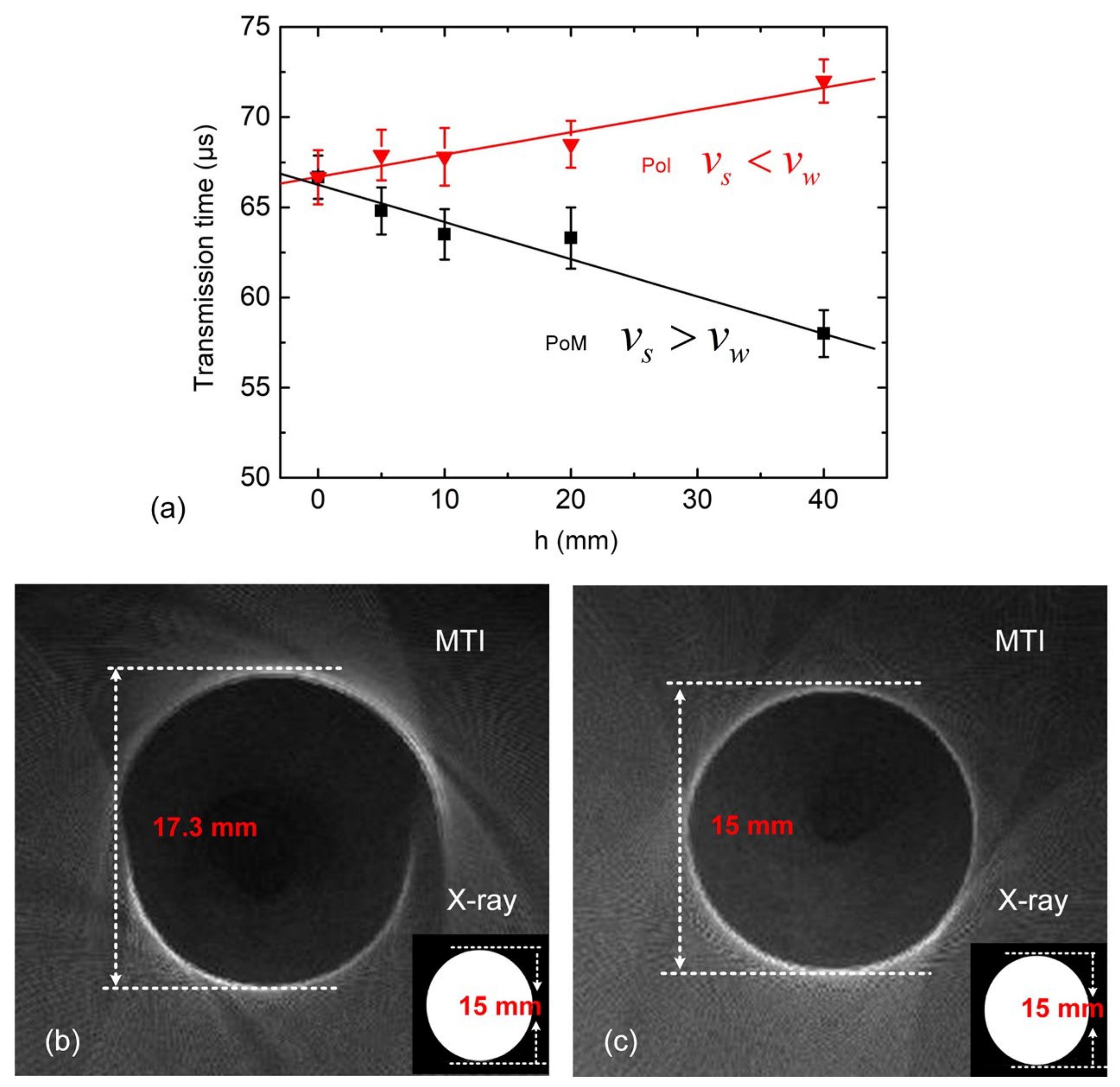
2.2. Apparent Thickness and Actual Thickness
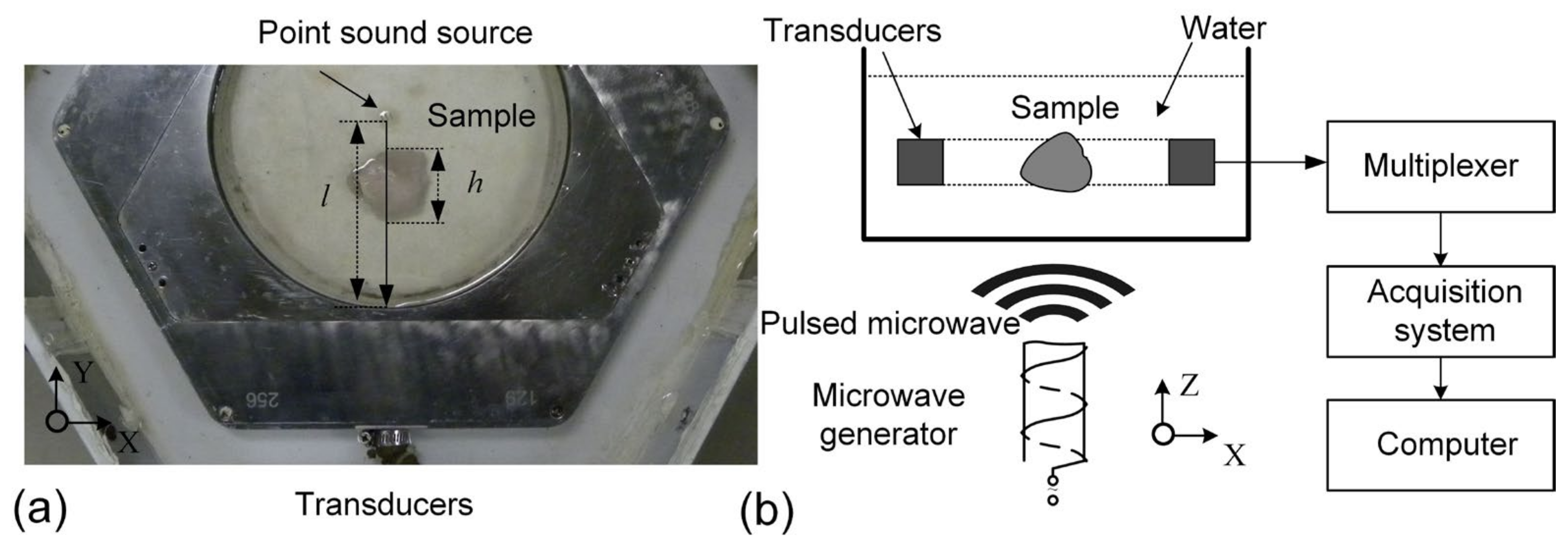
2.3. Experimental Setup
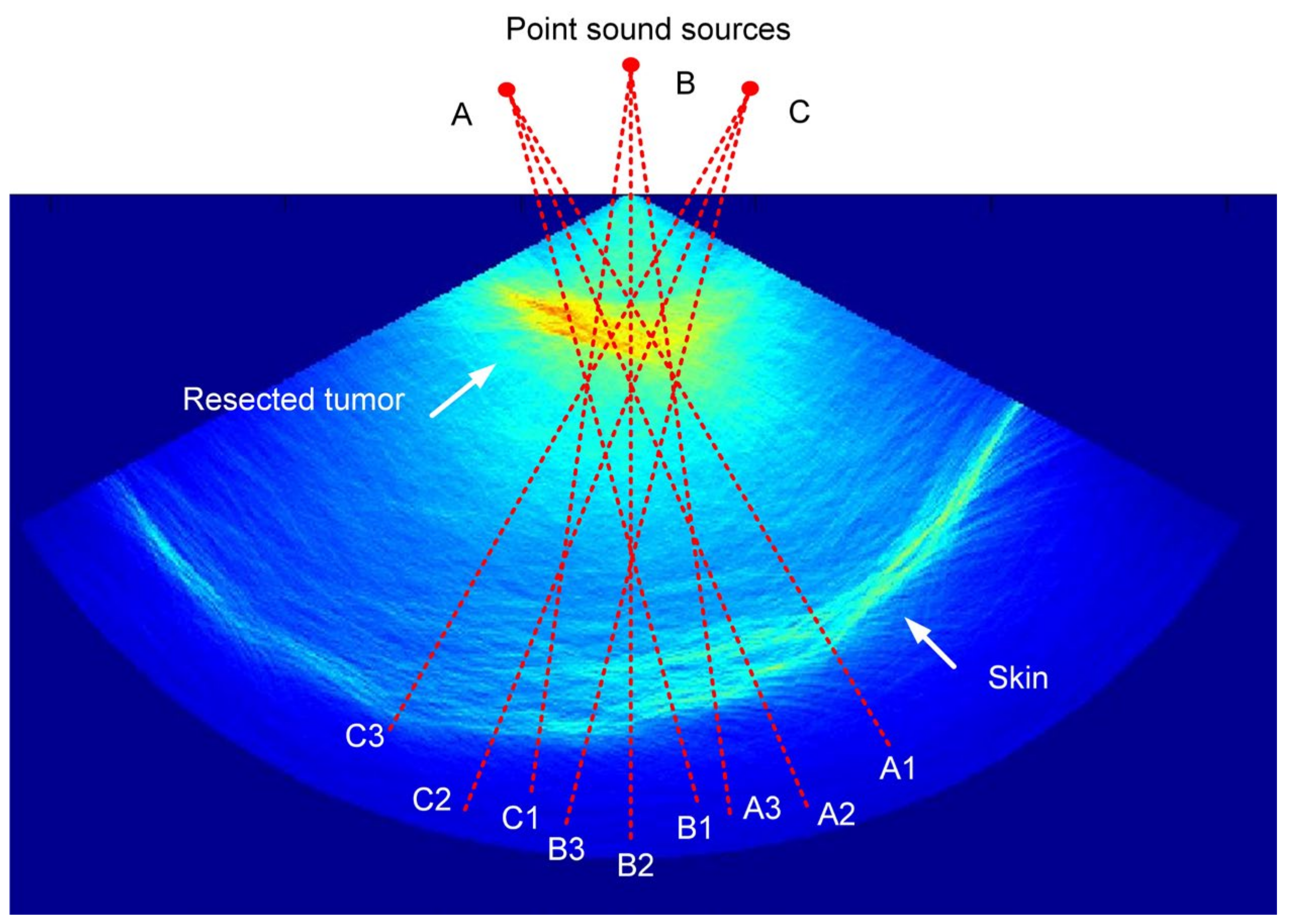
3. Results
3.1. Influence of Non-Uniform Ultrasonic Velocity
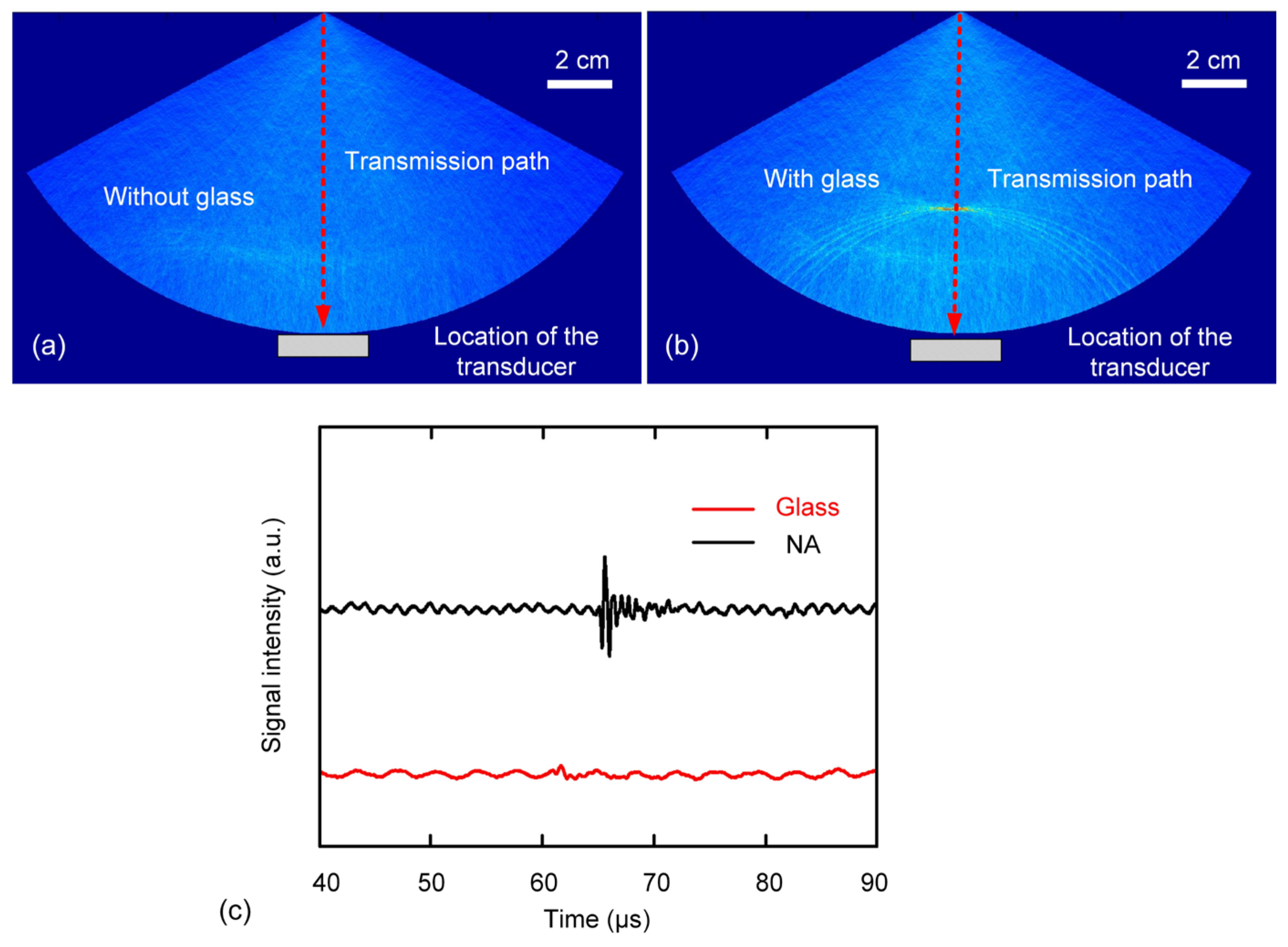
3.2. Two-Layer Situations
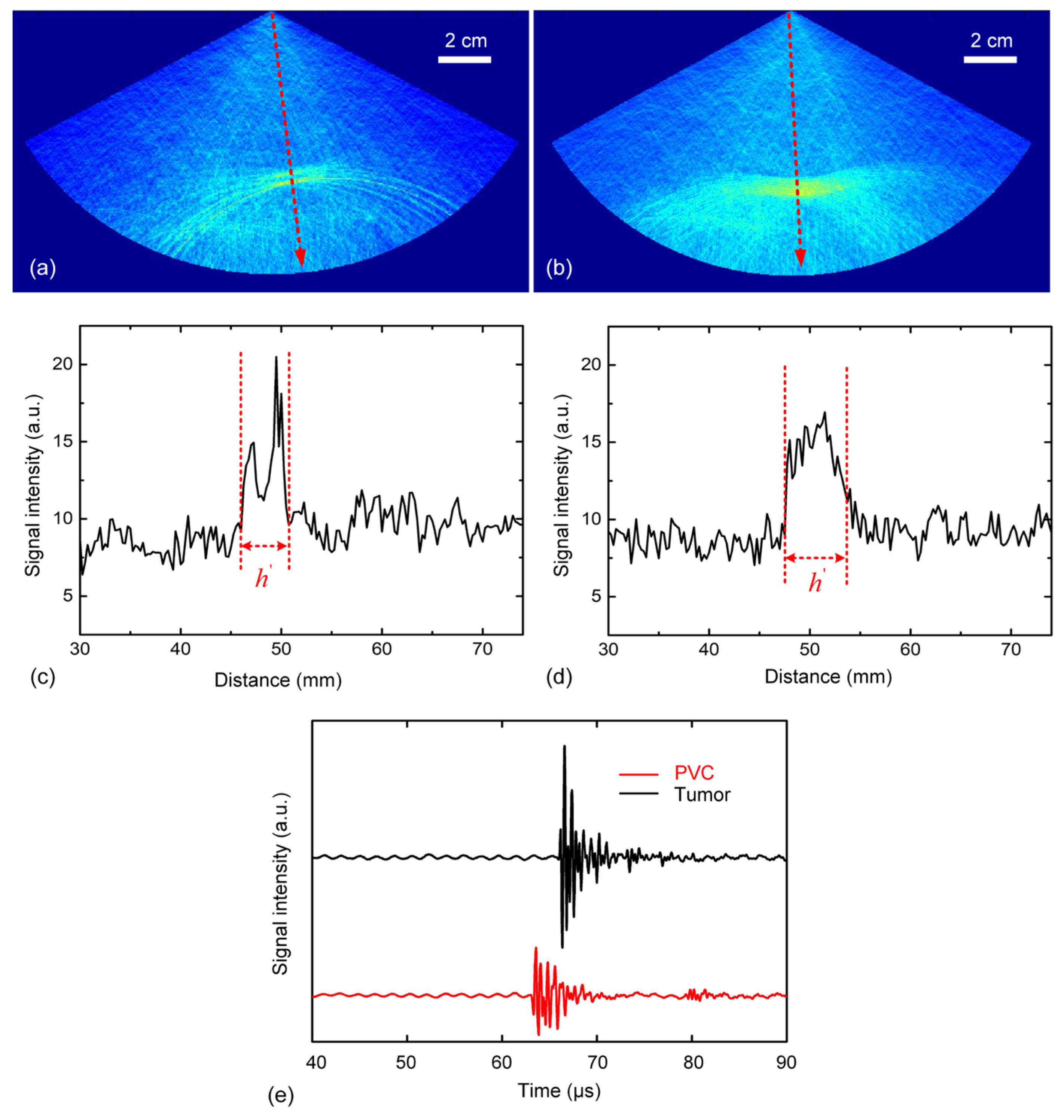
3.3. Three-Layer Situations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Q.; Liang, X.; Qi, W.; Gong, Y.; Jiang, H.; Xi, L. Biomedical microwave-induced thermoacoustic imaging. J. Innov. Opt. Health Sci. 2022, 15, 2230007. [Google Scholar] [CrossRef]
- Wang, B.; Sun, Y.; Wang, Z.; Wang, X. Three-Dimensional Microwave-Induced Thermoacoustic Imaging Based on Compressive Sensing Using an Analytically Constructed Dictionary. IEEE Trans. Microw. Theory Tech. 2020, 68, 377–386. [Google Scholar] [CrossRef]
- Wu, L.; Cheng, Z.; Ma, Y.; Li, Y.; Ren, M.; Xing, D.; Qin, H. A Handheld Microwave Thermoacoustic Imaging System with an Impedance Matching Microwave-Sono Probe for Breast Tumor Screening. IEEE Trans. Med. Imaging 2022, 41, 1080–1086. [Google Scholar] [CrossRef] [PubMed]
- Chi, Z.; Huang, L.; Wu, D.; Long, X.; Xu, X.; Jiang, H. First assessment of thermoacoustic tomography for in vivo detection of rheumatoid arthritis in the finger joints. Med. Phys. 2022, 49, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Singhvi, A.; Boyle, K.C.; Fallahpour, M.; Khuri-Yakub, B.T.; Arbabian, A. A Microwave-Induced Thermoacoustic Imaging System with Non-Contact Ultrasound Detection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1587–1599. [Google Scholar] [CrossRef]
- Tamimi, E.A.; Xin, H.; Witte, R.S. Real-time 3D thermoacoustic imaging and thermometry using a self-calibration technique. Appl. Opt. 2020, 59, G255. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhang, X.; Su, N.; Shi, X.; Chen, J.; Wu, H.; Liu, G.; Li, L.; Bai, C.; Xiu, J.; et al. Mechanical characterization of osteoporosis based on x-ray induced acoustic computed tomography. Appl. Phys. Lett. 2023, 123, 063701. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Yang, S. Real-time interleaved photoacoustic and ultrasound imaging for guiding interventional procedures. Appl. Acoust. 2019, 156, 1–6. [Google Scholar] [CrossRef]
- Huang, L.; Zheng, Z.; Chi, Z.; Jiang, H. Technical Note: Compact thermoacoustic imaging system based on a low-cost and miniaturized microwave generator for in vivo biomedical imaging. Med. Phys. 2021, 48, 4242–4248. [Google Scholar] [CrossRef]
- Kruger, R.A.; Miller, K.D.; Reynolds, H.E.; Kiser, W.L.; Reinecke, D.R.; Kruger, G.A. Breast Cancer in Vivo: Contrast Enhancement with Thermoacoustic CT at 434 MHz—Feasibility Study. Radiology 2000, 216, 279–283. [Google Scholar] [CrossRef]
- Ji, Z.; Lou, C.; Yang, S.; Xing, D. Three-dimensional thermoacoustic imaging for early breast cancer detection. Med. Phys. 2012, 39, 6738–6744. [Google Scholar] [CrossRef] [PubMed]
- Ji, Z.; Ding, W.; Ye, F.; Lou, C. Handheld Thermoacoustic Scanning System Based on a Linear-array Transducer. Ultrason. Imaging 2016, 38, 276–284. [Google Scholar] [CrossRef] [PubMed]
- Nie, L.; Xing, D.; Yang, D.; Zeng, L.; Zhou, Q. Detection of foreign body using fast thermoacoustic tomography with a multielement linear transducer array. Appl. Phys. Lett. 2007, 90, 174109. [Google Scholar] [CrossRef] [PubMed]
- Nie, L.; Xing, D.; Yang, S. In vivo detection and imaging of low-density foreign body with microwave-induced thermoacoustic tomography: In vivo foreign body detection with thermoacoustic tomography. Med. Phys. 2009, 36, 3429–3437. [Google Scholar] [CrossRef] [PubMed]
- Lou, C.; Yang, S.; Ji, Z.; Chen, Q.; Xing, D. Ultrashort Microwave-Induced Thermoacoustic Imaging: A Breakthrough in Excitation Efficiency and Spatial Resolution. Phys. Rev. Lett. 2012, 109, 218101. [Google Scholar] [CrossRef]
- Ye, F.; Ji, Z.; Ding, W.; Lou, C.; Yang, S.; Xing, D. Ultrashort Microwave-Pumped Real-Time Thermoacoustic Breast Tumor Imaging System. IEEE Trans. Med. Imaging 2016, 35, 839–844. [Google Scholar] [CrossRef]
- Kellnberger, S.; Hajiaboli, A.; Razansky, D.; Ntziachristos, V. Near-field thermoacoustic tomography of small animals. Phys. Med. Biol. 2011, 56, 3433–3444. [Google Scholar] [CrossRef]
- Wu, X.; Luo, Z.; Wang, S.; Zhang, H. The researches on convolutional beamforming for linear-array photoacoustic tomography. Appl. Acoust. 2022, 186, 108441. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y. A reconstruction algorithm for thermoacoustic tomography with compensation for acoustic speed heterogeneity. Phys. Med. Biol. 2008, 53, 4971–4982. [Google Scholar] [CrossRef]
- Stefanov, P.; Uhlmann, G. Thermoacoustic tomography with variable sound speed. Inverse Probl. 2009, 25, 075011. [Google Scholar] [CrossRef]
- Agranovsky, M.; Kuchment, P. Uniqueness of reconstruction and an inversion procedure for thermoacoustic and photoacoustic tomography with variable sound speed. Inverse Probl. 2007, 23, 2089–2102. [Google Scholar] [CrossRef]
- Jin, X.; Wang, L.V. Thermoacoustic tomography with correction for acoustic speed variations. Phys. Med. Biol. 2006, 51, 6437–6448. [Google Scholar] [CrossRef]
- Li, C.; Duric, N.; Littrup, P.; Huang, L. In vivo Breast Sound-Speed Imaging with Ultrasound Tomography. Ultrasound Med. Biol. 2009, 35, 1615–1628. [Google Scholar] [CrossRef] [PubMed]
- Mast, T.D. Empirical relationships between acoustic parameters in human soft tissues. Acoust. Res. Lett. Online 2000, 1, 37–42. [Google Scholar] [CrossRef]
- Ophir, J.; Lin, T. A calibration-free method for measurement of sound speed in biological tissue samples. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1988, 35, 573–577. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.E.; Trahey, G.E. The direct estimation of sound speed using pulse–echo ultrasound. J. Acoust. Soc. Am. 1998, 104, 3099–3106. [Google Scholar] [CrossRef] [PubMed]
- Nebeker, J.; Nelson, T.R. Imaging of Sound Speed Using Reflection Ultrasound Tomography. J. Ultrasound Med. 2012, 31, 1389–1404. [Google Scholar] [CrossRef]
- Ma, D.; Shen, H. Acoustic Manual; Science Press: Beijing, China, 2004; pp. 123–135. [Google Scholar]
- Tserevelakis, G.J.; Zacharakis, G. High precision photoacoustic interferometer for the determination of the speed of sound in liquid media. Opt. Express 2022, 30, 28559–28568. [Google Scholar] [CrossRef]
- Tserevelakis George, J.; Charalampos, A.; Giannis, Z. Optoacoustic interferometric characterization system (OPTICS) for the evaluation of fuel quality through speed of sound measurements. Ultrasonics 2024, 139, 107291. [Google Scholar] [CrossRef]
- Kolkman, R.G.M.; Steenbergen, W.; van Leeuwen, T.G. Reflection mode photoacoustic measurement of speed of sound. Opt. Express 2007, 15, 3291–3300. [Google Scholar] [CrossRef]
- C95.1 2005; IEEE Standard for Safety Levels with Respect to Human Exposure to Radio Frequency Electromagnetic Fields 3 kHz to 300 GHz. IEEE: New York, NY, USA, 2005.

| Materials (26 °C) | Velocity of Ultrasound (SD) (m/s) | |
|---|---|---|
| Used in the Literature | Calculated by This Work | |
| Softwood | 523~590 | 545 (7) |
| Rubber | 1152~1272 | 1182 (9) |
| Polyfoam | 1285~1388 | 1328 (6) |
| Mineral oil | 1322~1467 | 1337 (13) |
| Polyvinyl chloride | 2329~2520 | 2388 (9) |
| Water | 1511 | 1502 (5) |
| Fat | 1468~1487 | 1469 (6) |
| Muscle | 1568~1600 | 1586 (9) |
| Breast tumor | 1470~1513 | 1510 (9) |
| A1 | A2 | A3 | B1 | B2 | B3 | B1 | B2 | B3 | |
|---|---|---|---|---|---|---|---|---|---|
| (mm) Setted | 150 | 150 | 150 | 150 | 150 | 150 | 150 | 150 | 150 |
| (mm) Measured | 98 | 92 | 114 | 100 | 89 | 94 | 102 | 89 | 117 |
| (mm) Measured | 8 | 12 | 9 | 10 | 15 | 13 | 14 | 10 | 12 |
| (μs) Measured | 100.6 | 98.1 | 99.7 | 99.2 | 96.2 | 97.5 | 96.7 | 99.5 | 97.7 |
| (m/s) Calculated | 1521 | 1511 | 1507 | 1522 | 1531 | 1551 | 1514 | 1523 | 1524 |
| (m/s) Calculated | 1522 (13) | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.; Zhang, Y. Enhanced Thermoacoustic Imaging System with Parallel Ultrasonic Velocity Measurement for Distinguishing Types of Microwave-Absorbing Anomalies. Photonics 2024, 11, 916. https://doi.org/10.3390/photonics11100916
Ding W, Zhang Y. Enhanced Thermoacoustic Imaging System with Parallel Ultrasonic Velocity Measurement for Distinguishing Types of Microwave-Absorbing Anomalies. Photonics. 2024; 11(10):916. https://doi.org/10.3390/photonics11100916
Chicago/Turabian StyleDing, Wenzheng, and Yao Zhang. 2024. "Enhanced Thermoacoustic Imaging System with Parallel Ultrasonic Velocity Measurement for Distinguishing Types of Microwave-Absorbing Anomalies" Photonics 11, no. 10: 916. https://doi.org/10.3390/photonics11100916
APA StyleDing, W., & Zhang, Y. (2024). Enhanced Thermoacoustic Imaging System with Parallel Ultrasonic Velocity Measurement for Distinguishing Types of Microwave-Absorbing Anomalies. Photonics, 11(10), 916. https://doi.org/10.3390/photonics11100916





