Analysis of High-Order Surface Gratings Based on Micron Lasers on Silicon
Abstract
1. Introduction
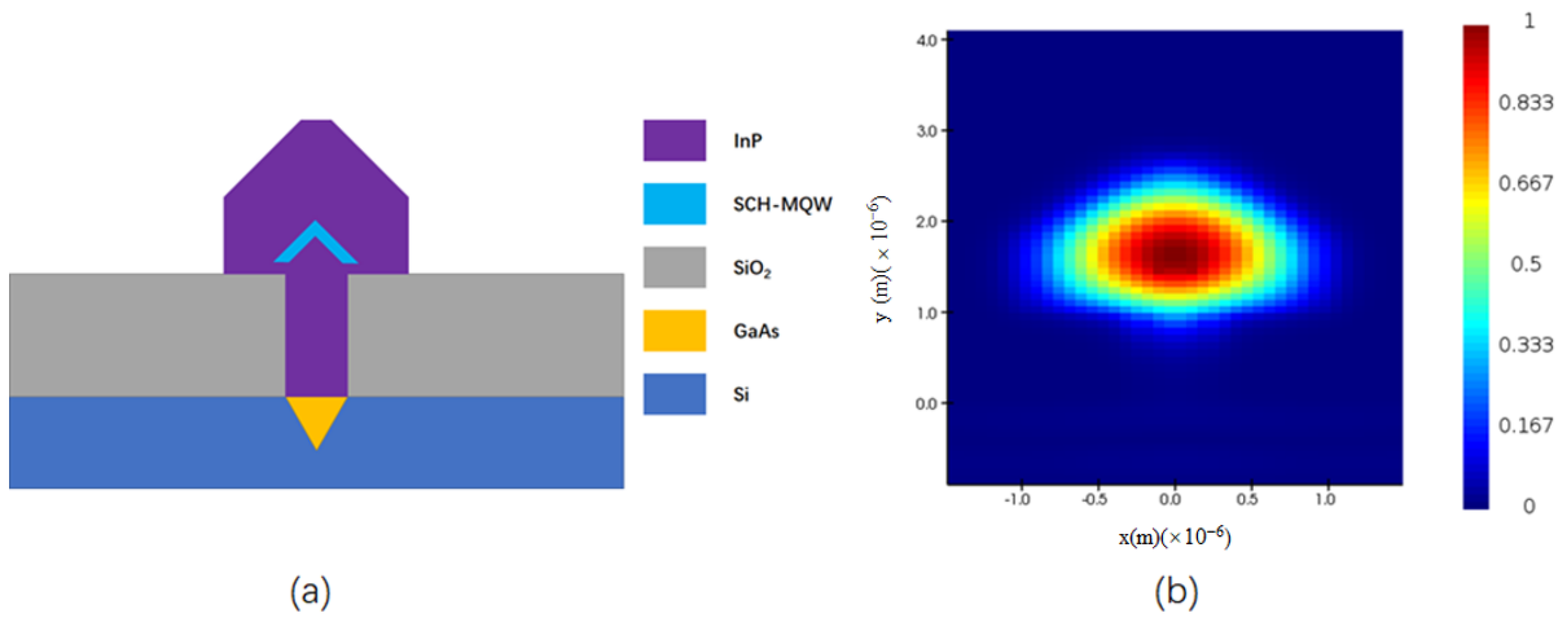
2. Laser Structure and Simulation Model
3. Simulations
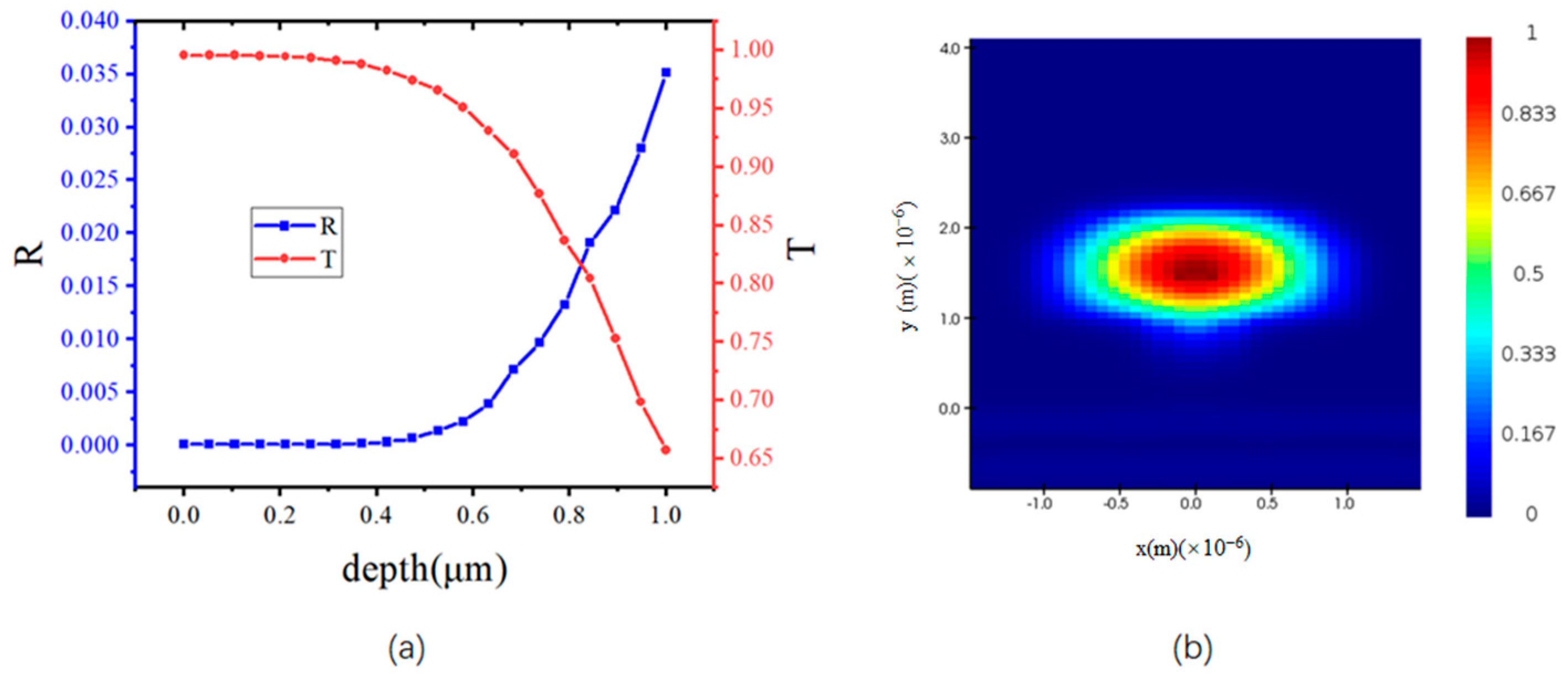
3.1. Single Slot Structure Simulated with 3D FDTD
3.2. Single Slot Structure Simulated with the EME Method
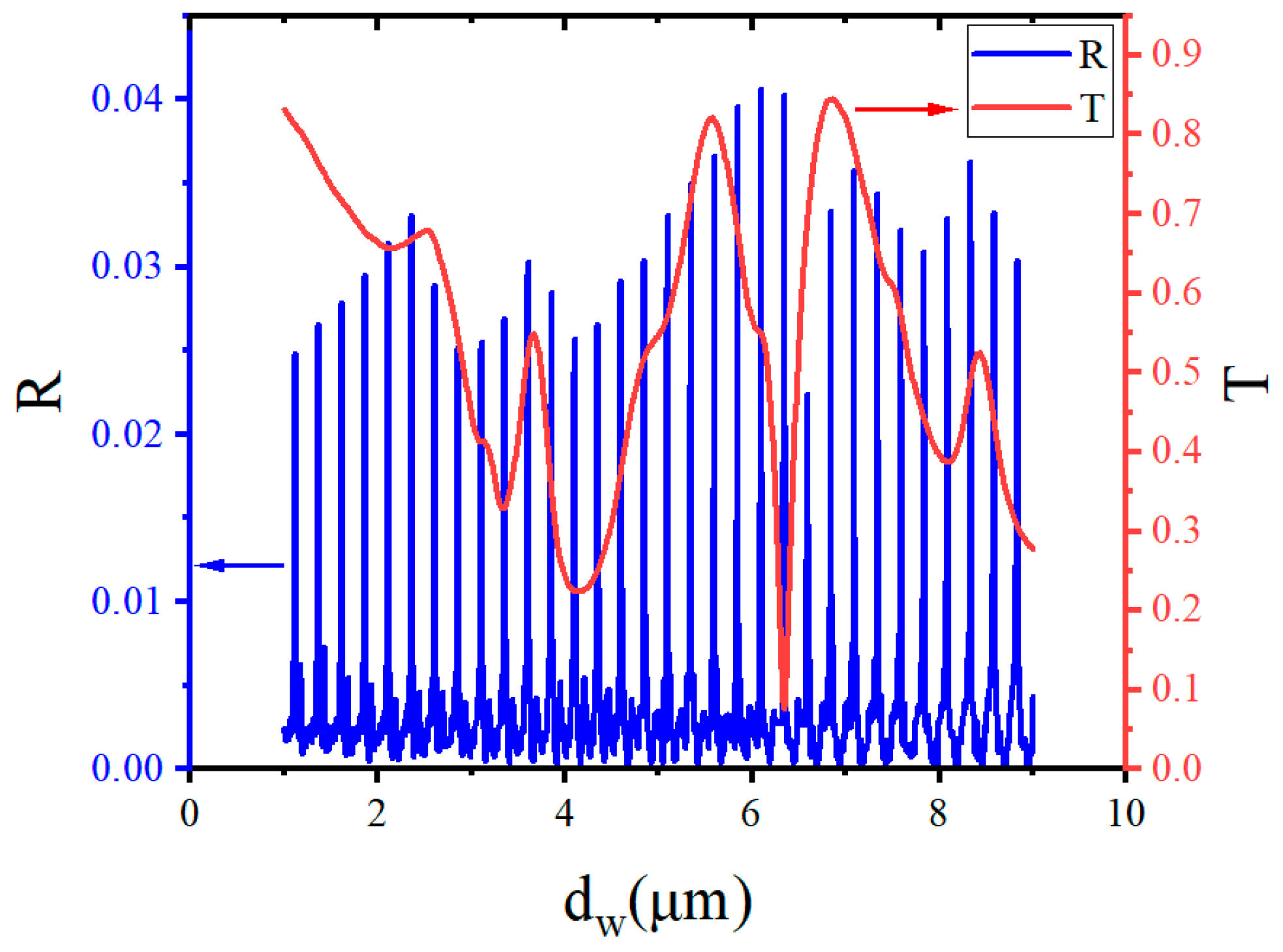
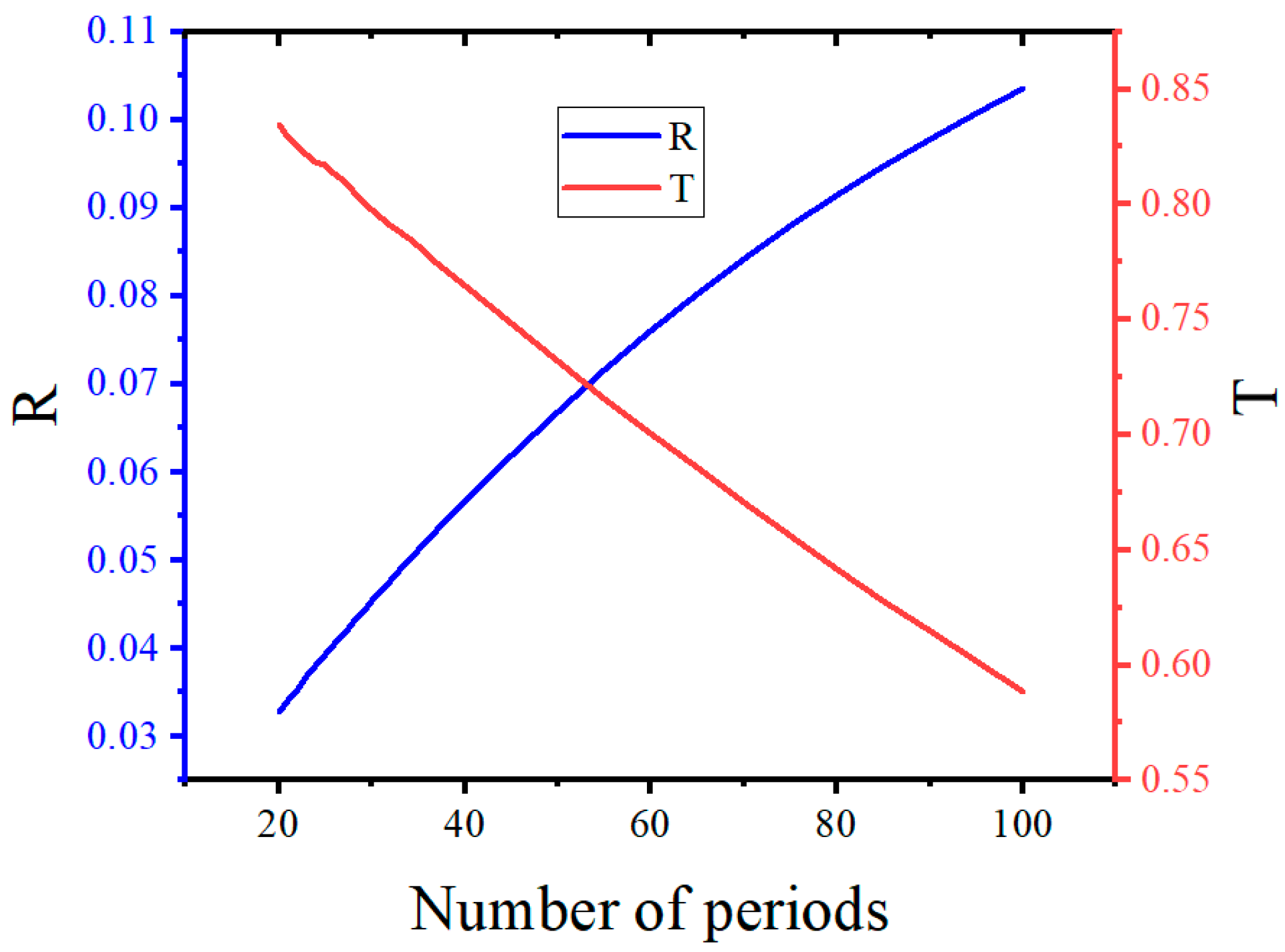
3.3. Multi-Slot Structure Simulated with the EME Method
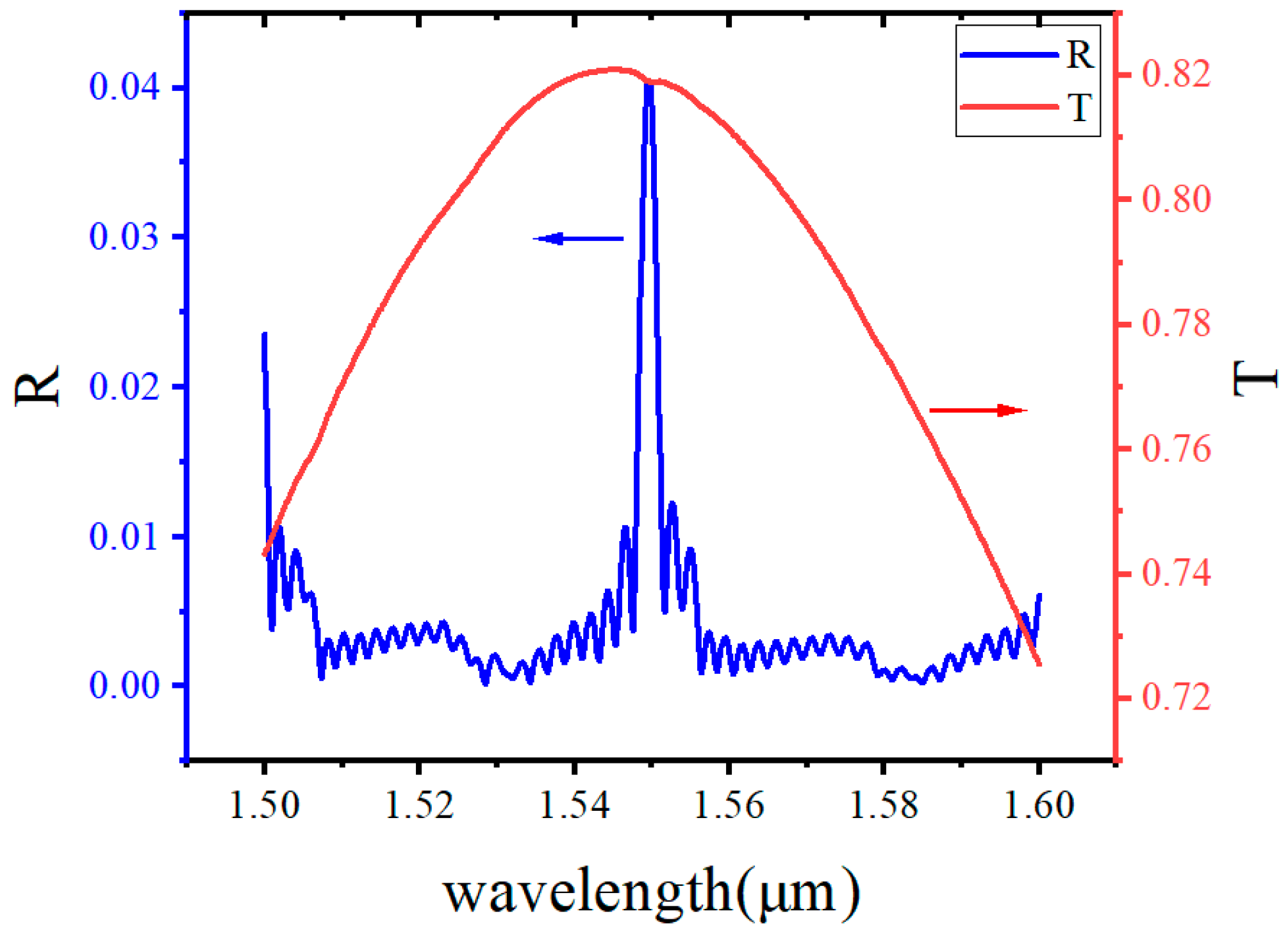
3.4. Final Verification of High-Order Surface Gratings by FDTD
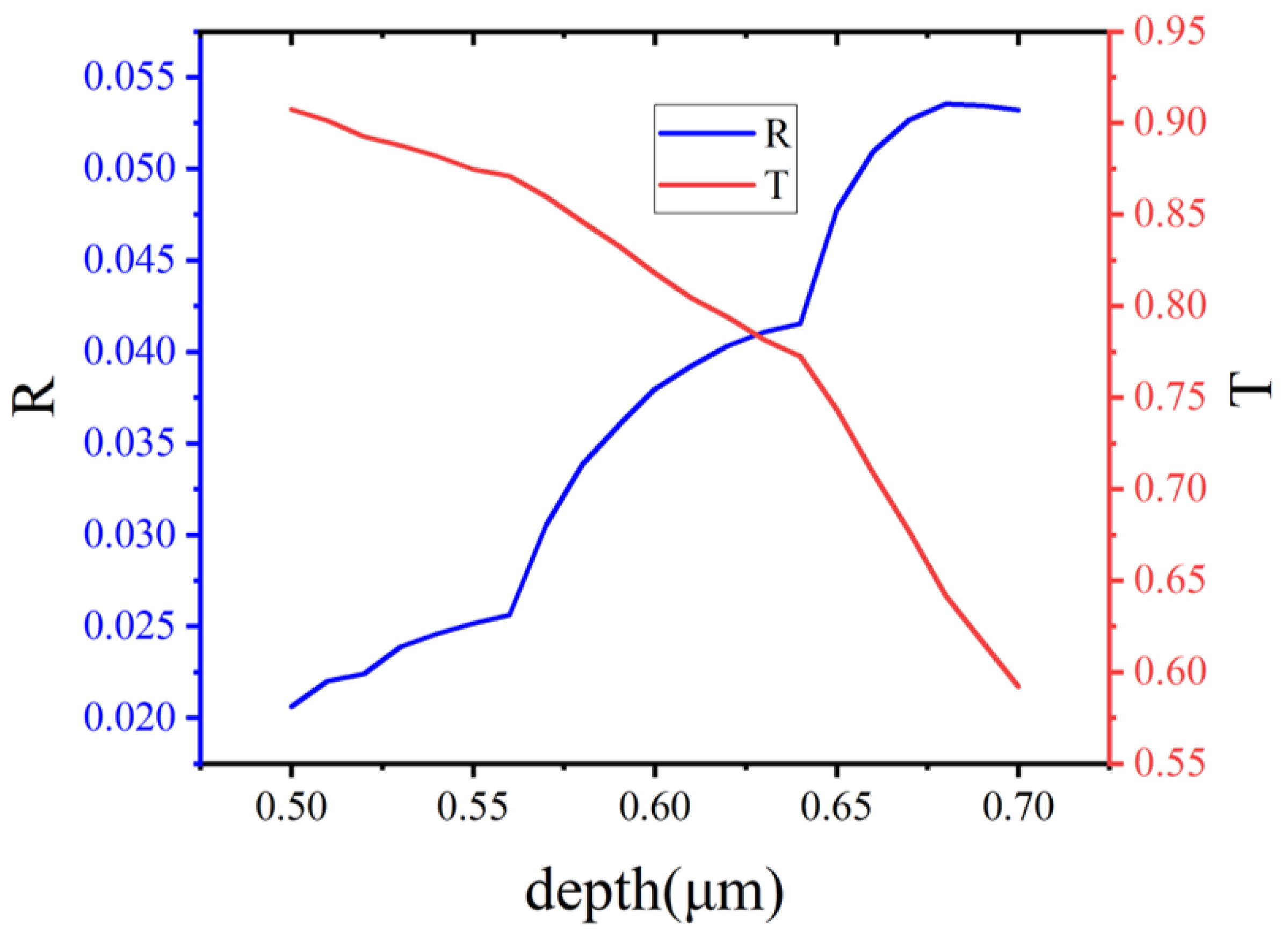
3.5. Fabrication Tolerance Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Wang, M.; Fang, X.; Li, Y.; Zhou, X.; Yu, H.; Wang, P.; Wang, W.; Pan, J. Monolithic integration of InGaAs/InP multiple quantum wells on SOI substrates for photonic devices. J. Appl. Phys. 2018, 123, 053102. [Google Scholar] [CrossRef]
- Liang, D.; Bowers, J.E. Recent progress in lasers on silicon. Nat. Photonics 2010, 4, 511–517. [Google Scholar] [CrossRef]
- Li, N.; Chen, G.; Ng, D.K.T.; Lim, L.W.; Xue, J.; Ho, C.P.; Fu, Y.H.; Lee, L.Y.T. Integrated Lasers on Silicon at Communication Wavelength: A Progress Review. Adv. Opt. Mater. 2022, 10, 2201008. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.; Wu, J.; Jiang, Q.; Tang, M.; Shutts, S.; Elliott, S.N.; Sobiesierski, A.; Seeds, A.J.; Ross, I.; et al. Electrically pumped continuous-wave III–V quantum dot lasers on silicon. Nat. Photonics 2016, 10, 307–311. [Google Scholar] [CrossRef]
- Wan, Y.; Norman, J.C.; Tong, Y.; Kennedy, M.J.; He, W.; Selvidge, J.; Shang, C.; Dumont, M.; Malik, A.; Tsang, H.K.; et al. 1.3 µm quantum dot-distributed feedback lasers directly grown on (001) Si. Laser Photonics Rev. 2020, 14, 2000037. [Google Scholar] [CrossRef]
- Wei, W.-Q.; He, A.; Yang, B.; Wang, Z.-H.; Huang, J.-Z.; Han, D.; Ming, M.; Guo, X.; Su, Y.; Zhang, J.-J.; et al. Monolithic integration of embedded III–V lasers on SOI. Light. Sci. Appl. 2023, 12, 84. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Fang, A.W.; Kodama, S.; Bowers, J.E. Hybrid silicon evanescent laser fabricated with a silicon waveguide and III–V offset quantum wells. Opt. Express 2005, 13, 9460–9464. [Google Scholar] [CrossRef] [PubMed]
- Fang, A.W.; Park, H.; Cohen, O.; Jones, R.; Paniccia, M.J.; Bowers, J.E. Electrically pumped hybrid AlGaInAs-silicon evanescent laser. Opt. Express 2006, 14, 9203–9210. [Google Scholar] [PubMed]
- Lin, Q.; Huang, J.; Lin, L.; Luo, W.; Gu, W.; Lau, K.M. 980 nm electrically pumped continuous lasing of QW lasers grown on silicon. Opt. Express 2023, 31, 15326–15333. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhou, X.; Li, M.; Kong, X.; Mi, J.; Wang, M.; Wang, W.; Pan, J. Ridge InGaAs/InP multi-quantum-well selective growth in nanoscale trenches on Si (001) substrate. Appl. Phys. Lett. 2016, 108, 021902. [Google Scholar] [CrossRef]
- Langdo, T.A.; Leitz, C.W.; Currie, M.T.; Fitzgerald, E.A.; Lochtefeld, A.; Antoniadis, D.A. High quality Ge on Si by epitaxial necking. Appl. Phys. Lett. 2000, 76, 3700–3702. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, X.; Yang, W.; Wang, M.; Yu, H.; Zhang, Y.; Pan, J. III–V Microwires with Reversed Ridge Waveguides Selectively Grown on Pre-Patterned Si Substrates. Crystals 2022, 12, 1561. [Google Scholar] [CrossRef]
- Lu, Q.; Abdullaev, A.; Nawrocka, M.; Guo, W.-H.; O’Callaghan, J.; Donegan, J.F. Slotted Single Mode Lasers Integrated with a Semiconductor Optical Amplifier. IEEE Photon.-Technol. Lett. 2013, 25, 564–567. [Google Scholar] [CrossRef]
- Wang, M.; Wang, H.; Ma, P.; Dong, F.; Liu, A.; Zheng, W. Eight-channel laser array with 100 GHz channel spacing based on surface-slotted structures fabricated by standard lithography. Opt. Lett. 2018, 43, 4867–4870. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wang, H.; Meng, R.; Qi, A.; Zheng, W. 1550 nm AlGaInAs MQWs 10-channel laser array for optical interconnects. In CLEO: Applications and Technology; Optica Publishing Group: Washington, DC, USA, 2018. [Google Scholar]
- Ma, P.; Liu, A.; Dong, F.; Wang, M.; Zheng, W. Single-mode semiconductor lasers fabricated by standard photolithography for direct modulation. Opt. Express 2019, 27, 5502–5511. [Google Scholar] [CrossRef] [PubMed]
- Fricke, J.; Wenzel, H.; Bugge, F.; Brox, O.P.; Ginolas, A.; John, W.; Ressel, P.; Weixelbaum, L.; Erbert, G. High-Power Distributed Feedback Lasers With Surface Gratings. IEEE Photon.-Technol. Lett. 2012, 24, 1443–1445. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Y.; Zhou, X.; Pan, J. Design of electrically pumped sub-micron lasers on patterned SOI substrates. In Proceedings of the International Conference on Optoelectronic and Microelectronic Technology and Application, Nanjing, China, 20–22 October 2020. [Google Scholar]
- Wenzel, H.; Fricke, J.; Decker, J.; Crump, P.; Erbert, G. High-Power Distributed Feedback Lasers with Surface Gratings: Theory and Experiment. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 352–358. [Google Scholar] [CrossRef]
- Decker, J.; Crump, P.; Fricke, J.; Maassdorf, A.; Erbert, G.; Trankle, G. Narrow Stripe Broad Area Lasers with High Order Distributed Feedback Surface Gratings. IEEE Photon.-Technol. Lett. 2014, 26, 829–832. [Google Scholar] [CrossRef]





| Methods | Bonding | Quantum Dots | Aspect Ratio Trapping |
|---|---|---|---|
| Commercialization | Already Commercialized | Under Research | Under Research |
| Coupling | Needs to be Aligned | Hard | Easy |
| Electronically Pumped At C-band | Already Realized | Already Realized | Not Realized |
| Buffer Layer | No Buffer Layer | Thick | Thin |
| Parameters | Simulations by FDTD | Simulations by EME |
|---|---|---|
| Time | 3000 fs | 3000 fs |
| Source Type | Mode Source | Mode |
| Mesh Size | 5 μm × 5 μm × 180 μm | 4 μm × 3 μm × (ds + dw) × number of periods |
| Mesh Step | 2.5 × 10−4 μm | 1 × 10−6 μm |
| Simulation Temperature | 300 K | 300 K |
| Boundary Conditions | PML | PML |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Chen, L.; Zhou, X.; Yu, H.; Zhang, Y.; Pan, J. Analysis of High-Order Surface Gratings Based on Micron Lasers on Silicon. Photonics 2024, 11, 92. https://doi.org/10.3390/photonics11010092
Tian J, Chen L, Zhou X, Yu H, Zhang Y, Pan J. Analysis of High-Order Surface Gratings Based on Micron Lasers on Silicon. Photonics. 2024; 11(1):92. https://doi.org/10.3390/photonics11010092
Chicago/Turabian StyleTian, Jiachen, Licheng Chen, Xuliang Zhou, Hongyan Yu, Yejin Zhang, and Jiaoqing Pan. 2024. "Analysis of High-Order Surface Gratings Based on Micron Lasers on Silicon" Photonics 11, no. 1: 92. https://doi.org/10.3390/photonics11010092
APA StyleTian, J., Chen, L., Zhou, X., Yu, H., Zhang, Y., & Pan, J. (2024). Analysis of High-Order Surface Gratings Based on Micron Lasers on Silicon. Photonics, 11(1), 92. https://doi.org/10.3390/photonics11010092





