The Propagation Characteristics of Circular Airy Beams with Propagational Fractional-Order Optical Vortices
Abstract
1. Introduction
2. Theory and Model
3. Results and Discussion
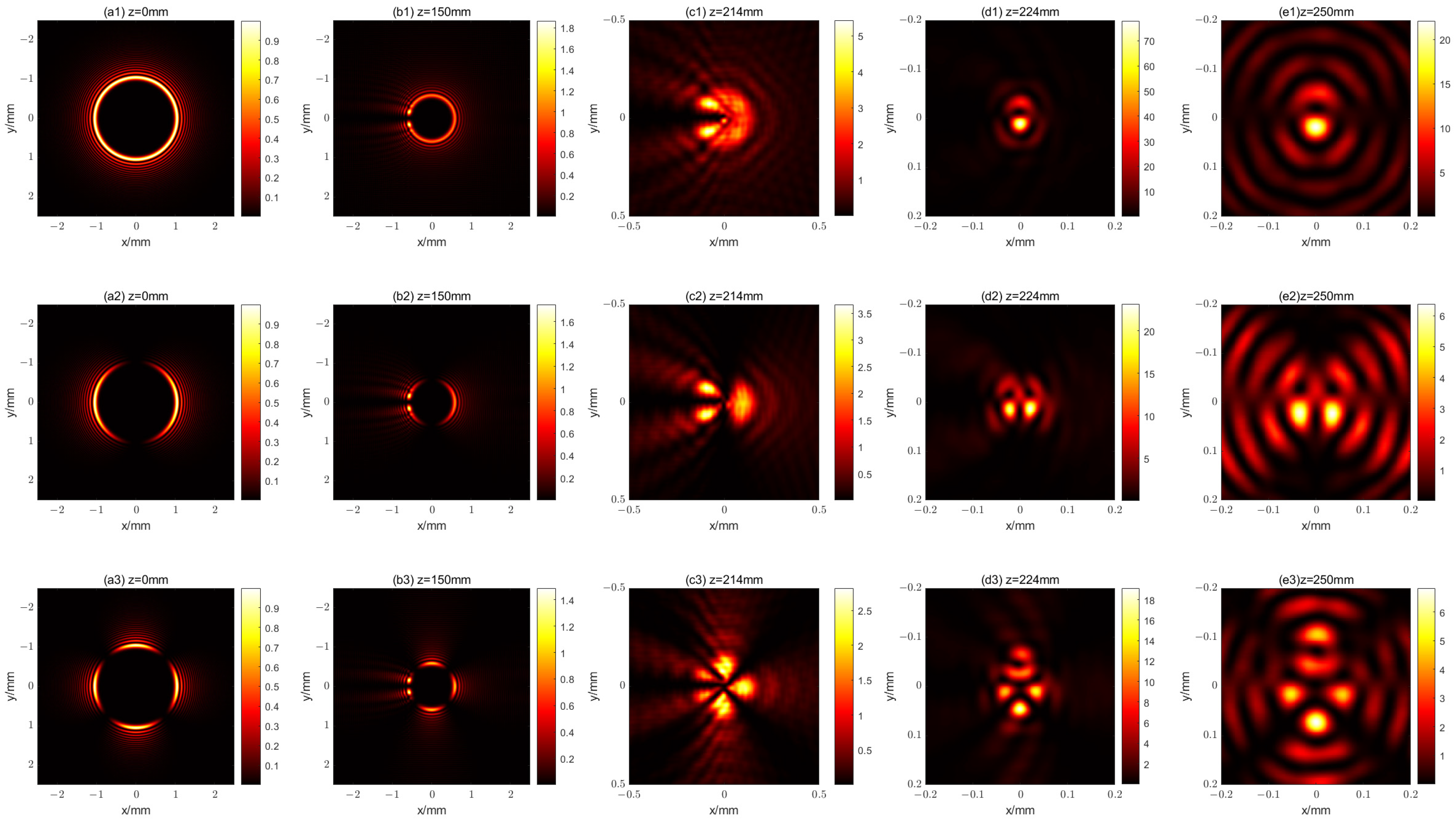
3.1. The First Kind of Propagational Fractional Vortex CAB
3.2. The Second Kind of Propagational Fractional Vortex CAB
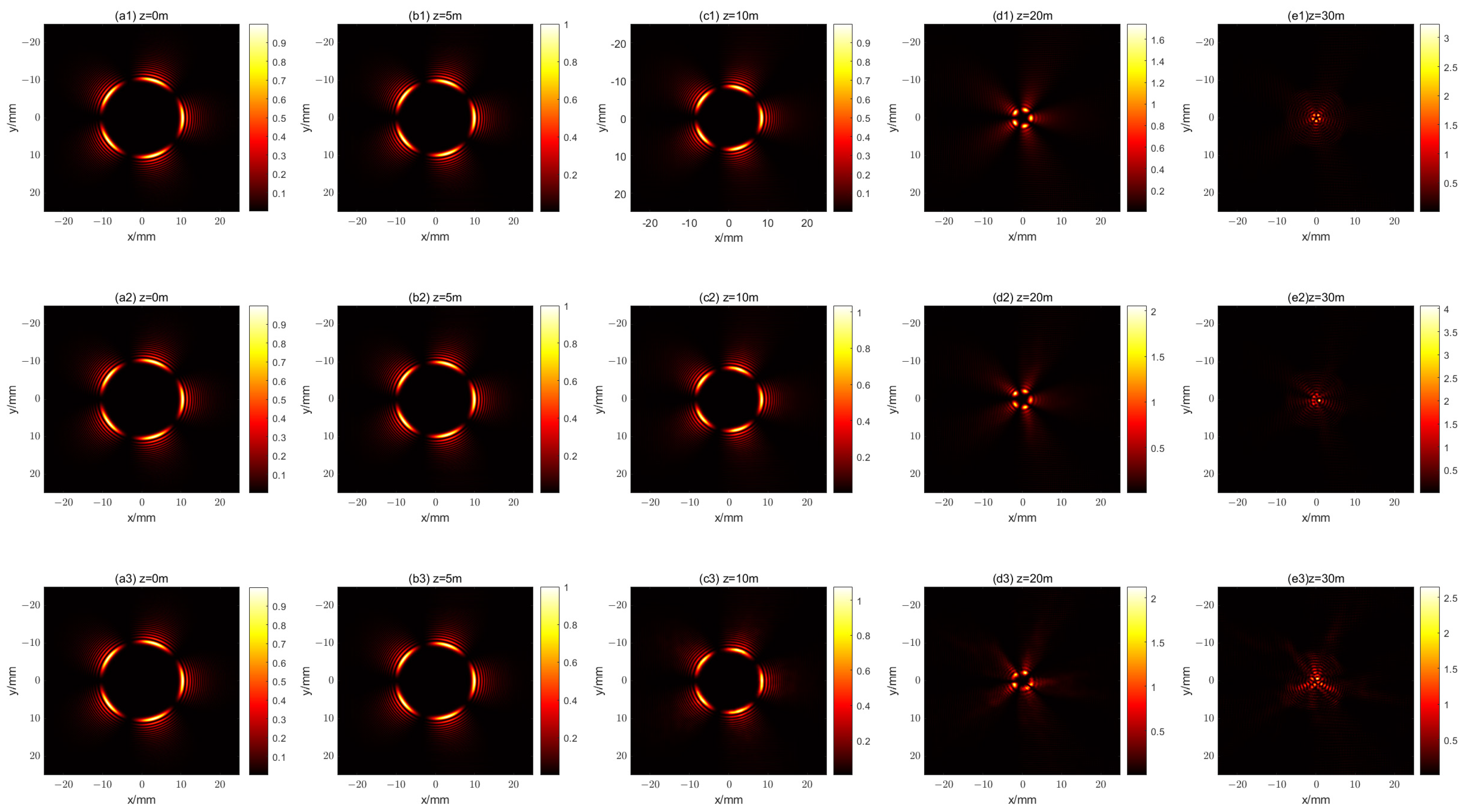
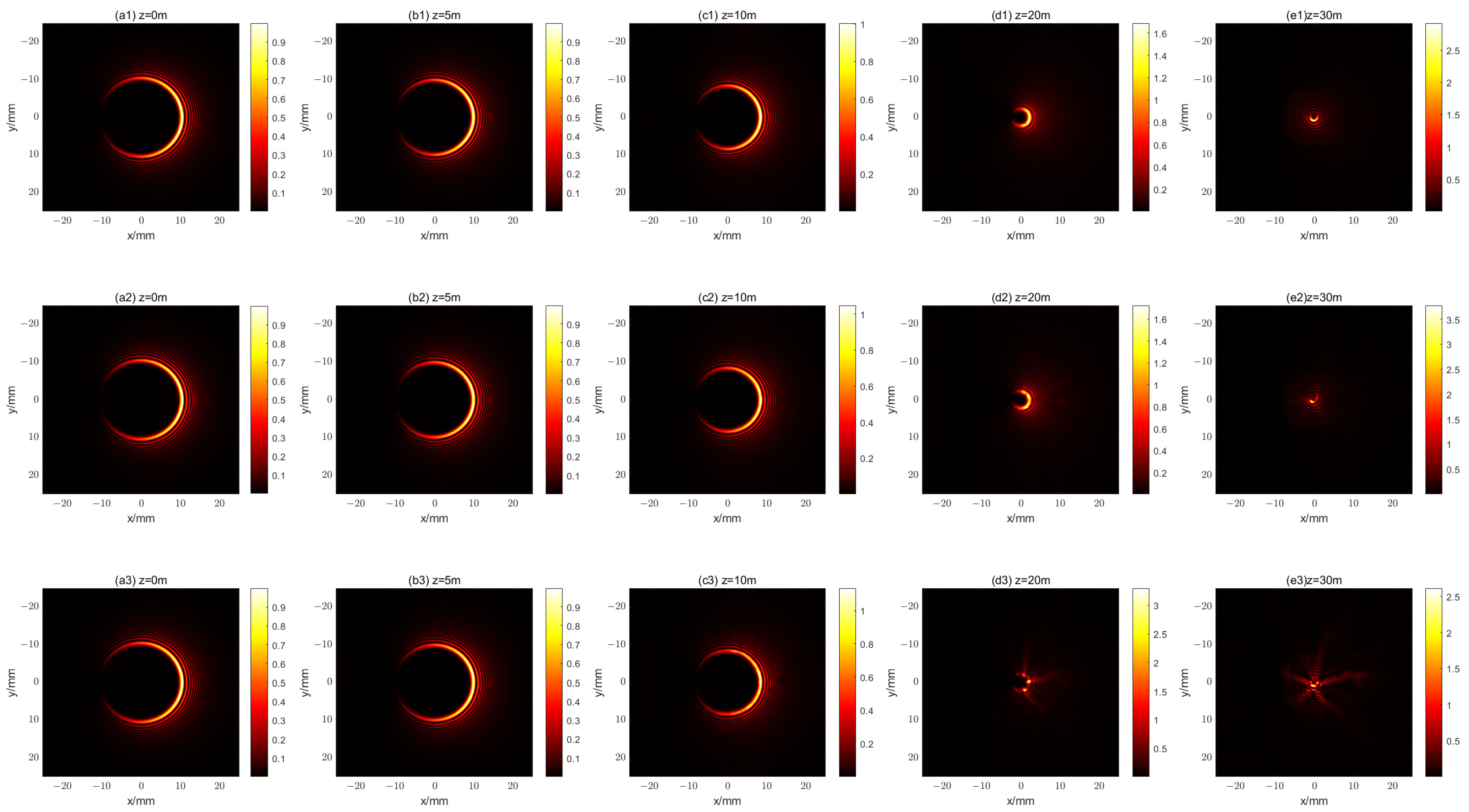
4. Fractional Vortex CAB Propagation in Turbulent Atmospheres
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coullet, P.; Gil, L.; Rocca, F. Optical vortices. Opt. Commun. 1989, 73, 403–408. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary spin-to–orbital angular momentum conversion of light. Science 2017, 358, 896–901. [Google Scholar] [CrossRef] [PubMed]
- Stav, T.; Faerman, A.; Maguid, E.; Oren, D.; Kleiner, V.; Hasman, E.; Segev, M. Quantum entanglement of the spin and orbital angular momentum of photons using metamaterials. Science 2018, 361, 1101–1104. [Google Scholar] [CrossRef] [PubMed]
- Courtial, J.; Robertson, D.A.; Dholakia, K.; Allen, L.; Padgett, M.J. Rotational Frequency Shift of a Light Beam. Phys. Rev. Lett. 1998, 81, 4828–4830. [Google Scholar] [CrossRef]
- Li, G.; Zentgraf, T.; Zhang, S. Rotational Doppler effect in nonlinear optics. Nat. Phys. 2016, 12, 736–740. [Google Scholar] [CrossRef]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a Spinning Object Using Light’s Orbital Angular Momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- He, H.; Friese, M.E.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Direct Observation of Transfer of Angular Momentum to Absorptive Particles from a Laser Beam with a Phase Singularity. Phys. Rev. Lett. 1995, 75, 826–829. [Google Scholar] [CrossRef]
- Simpson, N.B.; Dholakia, K.; Allen, L.; Padgett, M.J. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh Criterion Limit with Optical Vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Prunsche, B.; Zhou, L.; Nienhaus, K.; Nienhaus, G.U. Background suppression in fluorescence nanoscopy with stimulated emission double depletion. Nat. Photonics 2017, 11, 163–169. [Google Scholar] [CrossRef]
- Gibson, G.; Courtial, J.; Padgett, M.J.; Vasnetsov, M.; Pas’ko, V.; Barnett, S.M.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-Scale Orbital Angular Momentum Mode Division Multiplexing in Fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Wang, X.-L.; Cai, X.-D.; Su, Z.-E.; Chen, M.-C.; Wu, D.; Li, L.; Liu, N.-L.; Lu, C.-Y.; Pan, J.-W. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, J.; Lu, X.; Wang, Z.; Zhao, C.; Cai, Y. Review on fractional vortex beam. Nanophotonics 2022, 11, 241–273. [Google Scholar] [CrossRef]
- Tao, S.H.; Yuan, X.C.; Lin, J.; Peng, X.; Niu, H.B. Fractional optical vortex beam induced rotation of particles. Opt. Express 2005, 13, 7726–7731. [Google Scholar] [CrossRef]
- Zhu, G.; Bai, Z.; Chen, J.; Huang, C.; Wu, L.; Fu, C.; Wang, Y. Ultra-dense perfect optical orbital angular momentum multiplexed holography. Opt. Express 2021, 29, 28452–28460. [Google Scholar] [CrossRef]
- Situ, G.; Pedrini, G.; Osten, W. Spiral phase filtering and orientation-selective edge detection/enhancement. J. Opt. Soc. Am. A 2009, 26, 1788–1797. [Google Scholar] [CrossRef]
- Oemrawsingh, S.S.R.; Ma, X.; Voigt, D.; Aiello, A.; Eliel, E.R.; ’t Hooft, G.W.; Woerdman, J.P. Experimental Demonstration of Fractional Orbital Angular Momentum Entanglement of Two Photons. Phys. Rev. Lett. 2005, 95, 240501. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259. [Google Scholar] [CrossRef]
- Gbur, G. Fractional vortex Hilbert’s Hotel. Optica 2016, 3, 222–225. [Google Scholar] [CrossRef]
- Leach, J.; Yao, E.; Padgett, M.J. Observation of the vortex structure of a non-integer vortex beam. New J. Phys. 2004, 6, 71. [Google Scholar] [CrossRef]
- Weng, X.; Miao, Y.; Wang, G.; Zhan, Q.; Dong, X.; Qu, J.; Gao, X.; Zhuang, S. Propagable Optical Vortices with Natural Noninteger Orbital Angular Momentum in Free Space. Adv. Photonics Res. 2023, 4, 2200094. [Google Scholar] [CrossRef]
- Weng, X.; Miao, Y.; Chen, Y.; Song, Q.; Liu, L.; He, J.; Liao, C.; Wang, Y.; Gao, X.; Qu, J.; et al. Physical Essence of Propagable Fractional-Strength Optical Vortices in Free Space. Adv. Photonics Res. 2023, 4, 2300152. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Christodoulides, D.N. Abruptly autofocusing waves. Opt. Lett. 2010, 35, 4045–4047. [Google Scholar] [CrossRef]
- Papazoglou, D.G.; Efremidis, N.K.; Christodoulides, D.N.; Tzortzakis, S. Observation of abruptly autofocusing waves. Opt. Lett. 2011, 36, 1842–1844. [Google Scholar] [CrossRef]
- Liu, S.; Wang, M.; Li, P.; Zhang, P.; Zhao, J. Abrupt polarization transition of vector autofocusing Airy beams. Opt. Lett. 2013, 38, 2416–2418. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, K.; Lu, X. Propagation dynamics of abruptly autofocusing Airy beams with optical vortices. Opt. Express 2012, 20, 18579–18584. [Google Scholar] [CrossRef]
- Chremmos, I.; Zhang, P.; Prakash, J.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z. Fourier-space generation of abruptly autofocusing beams and optical bottle beams. Opt. Lett. 2011, 36, 3675–3677. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; Cottrell, D.M.; Sand, D. Abruptly autofocusing vortex beams. Opt. Express 2012, 20, 13302–13310. [Google Scholar] [CrossRef] [PubMed]
- Panagiotopoulos, P.; Papazoglou, D.G.; Couairon, A.; Tzortzakis, S. Sharply autofocused ring-Airy beams transforming into non-linear intense light bullets. Nat. Commun. 2013, 4, 2622. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, R.; Ahlawat, S.; Verma, R.S.; Gupta, P.K. Optical orientation and rotation of trapped red blood cells with Laguerre-Gaussian mode. Opt. Express 2011, 19, 7680–7688. [Google Scholar] [CrossRef] [PubMed]
- Rozas, D.; Law, C.T.; Swartzlander, G.A. Propagation dynamics of optical vortices. J. Opt. Soc. Am. B 1997, 14, 3054–3065. [Google Scholar] [CrossRef]
- Chen, B.; Chen, C.; Peng, X.; Peng, Y.; Zhou, M.; Deng, D. Propagation of sharply autofocused ring Airy Gaussian vortex beams. Opt. Express 2015, 23, 19288–19298. [Google Scholar] [CrossRef]
- Chen, G.; Huang, X.; Xu, C.; Huang, L.; Xie, J.; Deng, D. Propagation properties of autofocusing off-axis hollow vortex Gaussian beams in free space. Opt. Express 2019, 27, 6357–6369. [Google Scholar] [CrossRef]
- Zheng, G.; Wu, Q.; He, T.; Zhang, X. Propagation Characteristics of Circular Airy Vortex Beams in a Uniaxial Crystal along the Optical Axis. Micromachines 2022, 13, 1006. [Google Scholar] [CrossRef]
- Milione, G.; Lavery, M.P.J.; Huang, H.; Ren, Y.; Xie, G.; Nguyen, T.A.; Karimi, E.; Marrucci, L.; Nolan, D.A.; Alfano, R.R.; et al. 4 × 20 Gbit/s mode division multiplexing over free space using vector modes and a q-plate mode (de)multiplexer. Opt. Lett. 2015, 40, 1980–1983. [Google Scholar] [CrossRef]
- Miao, Y.; Weng, X.; Wang, Y.; Wang, L.; Wang, G.; Gao, X.; Zhuang, S. Parallel creation of propagable integer- and fractional-order vector vortex beams using mode extraction principle. Opt. Lett. 2022, 47, 3319–3322. [Google Scholar] [CrossRef]
- McGlamery, B.L. Restoration of Turbulence-Degraded Images. J. Opt. Soc. Am. 1967, 57, 293–297. [Google Scholar] [CrossRef]
- He, W.; Wu, J.; Yang, C.; Han, Y.; Xu, G. Numerical Simulation of Beam Propagation through Atmospheric Turbulence for Laser Radar; SPIE: Bellingham, WA, USA, 2008; Volume 6832. [Google Scholar]
- Roddier, N. Atmospheric wavefront simulation using Zernike polynomials. Opt. Eng. 1990, 29, 1174–1180. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, G.; Wan, L.; He, T.; Wu, Q.; Zhang, X. The Propagation Characteristics of Circular Airy Beams with Propagational Fractional-Order Optical Vortices. Photonics 2024, 11, 64. https://doi.org/10.3390/photonics11010064
Zheng G, Wan L, He T, Wu Q, Zhang X. The Propagation Characteristics of Circular Airy Beams with Propagational Fractional-Order Optical Vortices. Photonics. 2024; 11(1):64. https://doi.org/10.3390/photonics11010064
Chicago/Turabian StyleZheng, Guoliang, Lili Wan, Tiefeng He, Qingyang Wu, and Xuhui Zhang. 2024. "The Propagation Characteristics of Circular Airy Beams with Propagational Fractional-Order Optical Vortices" Photonics 11, no. 1: 64. https://doi.org/10.3390/photonics11010064
APA StyleZheng, G., Wan, L., He, T., Wu, Q., & Zhang, X. (2024). The Propagation Characteristics of Circular Airy Beams with Propagational Fractional-Order Optical Vortices. Photonics, 11(1), 64. https://doi.org/10.3390/photonics11010064




