Cooperative Terrestrial–Underwater FSO System: Design and Performance Analysis

Abstract

In this paper, we propose, design, and evaluate a new hybrid terrestrial–underwater optical communication link for providing high-speed connectivity between land and underwater systems. A device based on an amplify-and-forward strategy is considered and used for the hybrid optical link. A performance analysis of the proposed hybrid system is then carried out, taking into account both the atmospheric and underwater channels and their respective degradation sources. Different networking scenarios and conditions are evaluated. To this end, the channel model of the terrestrial free-space optical (FSO) link is modeled using the Gamma–Gamma distribution, while the underwater optical link is modeled using the Weibull distribution. The former takes into account atmospheric and turbulence attenuation, geometric spread and pointing errors, while the latter takes into account underwater and turbulence attenuation and geometric spread. Accordingly, a new analytical closed-form expression for the bit error rate (BER), which depends on the cumulative distribution function of the holistic hybrid system, is derived. Analytical results show that pointing errors as well as atmospheric and oceanic turbulence seriously degrade the performance of the hybrid system. In addition, ocean turbulence leads to the occurrence of a BER floor in some scenarios. This is the first time that such a network is proposed and modeled under the assumption of critical channel impairments.

1. Introduction

Over the last few years, there has been a constant and growing interest in free-space optical (FSO) technologies mainly due to the straightforward creation of point-to-point high-capacity transmissions in terrestrial and space networks [1,2,3,4]. This is in addition to the fact that FSO technologies offer broadband and high-speed transmissions far beyond those offered by radio frequency systems [5]. The inherent security of FSO technologies makes it difficult to intercept the transmitted optical signal, which has further contributed to the popularity of this technology, not only in traditional networking scenarios but also in mobile networks [6]. On the other hand, given the enormous interest aroused by all aspects of the marine environment and the need to develop wireless communication systems for underwater environments that can support emerging applications such as offshore installation monitoring, underwater robotics, and port security, to name a few, a rational objective has emerged to extend telecommunication networks into the underwater domain. Underwater wireless optical communications (UWOC) can offer high security, low delay and much higher data rates than acoustic communications. As a result, the research community has recently focused its efforts on the research and development of optical wireless communication systems in the underwater environment [7,8,9,10,11,12,13].

Despite the many advantages of wireless optical links, they are also subject to certain limitations due to the adverse nature of the optical channel. The main phenomena that degrade the quality of terrestrial FSO links are atmospheric loss, caused by the absorption and scattering of molecules and particles suspended in the atmosphere; pointing errors, caused by the random misalignment caused by wind gusts or vibrations at the ends of the link; and, finally, atmospheric turbulence, which is due to the small variations in pressure and temperature that occur in the medium and result in random variations of the atmospheric refractive index [14,15] causing fluctuation of the received optical signal in both phase and intensity. These fluctuations, also known as atmospheric scintillation, are considered to be the most relevant degradation factor in terrestrial links. Extensive research has been carried out by the scientific community to model the random fading of atmospheric channels under variable turbulence conditions. Accordingly, several mathematical models for the probability density function (PDF) of the received irradiance have been proposed to date [16,17,18,19,20,21]. The Gamma–Gamma distribution, which is valid for any turbulence regime, stands out to characterize the scintillation originating from terrestrial links.

In the case of UWOC links, the limiting factors are similar to those described above, but now taking into account the underwater environment. The transmitted optical beam suffers from absorption and scattering through propagation in seawater. Absorption is caused by the molecules and other particles that form the water and which, when interacting with the photons of the optical beam, cause a loss of energy. Scattering is due to the presence in the water of organic material, mineral salts and other dissolved particles that cause changes in the direction of propagation of the photons of the optical beam. Both phenomena (absorption and scattering) cause path loss and, in the case of scattering, also spatial and temporal dispersion of the transmitted signal. To minimize path loss, UWOC links use the blue/green region of the visible light spectrum for data transmission, since this region of light suffers the least attenuation in natural water [22]. Furthermore, in the underwater environment, the ocean currents that describe the movement of seawater induce differences in temperature and pressure which, together with other characteristics such as turbidity or salinity of the water, lead to changes in its refractive index and thus to fluctuations in the received power. These fluctuations give rise to ocean turbulence which is one of the main factors affecting the quality of UWOC links. Among several distributions, the Weibull distribution provides excellent accuracy for the scintillation generated in underwater links [9,23].

This work presents a novel communication system that extends optical wireless networks from terrestrial to underwater environments, considering different channel degradation factors that reflect a practical scenario. In particular, this paper proposes and evaluates the design of a cooperative terrestrial–underwater FSO (FSO-TU) system. The FSO-TU system is a combination of terrestrial and underwater FSO links that form a hybrid network. In this work, a new closed-form expression for calculating the average bit error rate (BER) in FSO-TU systems is derived. This new expression carefully considers various network degradation factors for a realistic evaluation of hybrid networks not previously considered in other works such as [24]. Therefore, in order to include these new degradation factors, a novel channel model for the end-to-end FSO-TU system is developed. In particular, our new model considers atmospheric attenuation, geometric spread, pointing errors and atmospheric turbulence for the terrestrial link and oceanic attenuation, geometric spread and oceanic turbulence for the undersea link. In this respect, Gamma–Gamma distribution is used to model the effect of atmospheric turbulence while the Weibull distribution is chosen to model ocean turbulence. Finally, performance evaluation of the proposed cooperative FSO-TU system is carried out and discussed under various conditions and real scenarios.

The rest of the paper is organised as follows. Section 2 presents a model of the proposed system. The main channel degradation phenomena for the terrestrial and underwater link are discussed in Section 3. Then, in Section 4, the closed-form expression for the average BER is derived. The analysis of different realistic scenarios is performed in Section 5. Finally, the most relevant conclusions are summarized in Section 6.

2. System Model and Definitions

This section describes the new hybrid communication system. As shown in Figure 1, the hybrid FSO-TU system has two different hops or links, both of which are considered point-to-point optical links: the terrestrial link and the underwater link. Both links operate with an intensity modulation with a direct detection (IM/DD) system. Therefore, intensity modulation (IM) varies the amplitude of the optical signal transmitted on both links to carry the information, so that a certain optical power is emitted to transmit a “1” and no power is emitted to transmit a “0”. This traditional modulation scheme is known as on–off keying (OOK) and is chosen here because of its low cost and simplicity of implementation [25]. At the receiver, the optical signal is then directly detected (DD) in a photodetector, which converts it into an electrical signal proportional to the received power. We note that, as seen below, in such harsh environments, high levels of attenuation and signal degradation are expected.

As shown in Figure 1, the terrestrial link consists of an optical transmitter located on land and a receiver located at sea level on a structure that is assumed to be sufficiently stable to be unaffected by the characteristic maritime movements that could greatly degrade the performance of the link. The signal current induced in the terrestrial receiver can be described as follows:

$$i_1=x{R}_1{h}_1+i_{n1},$$

(1)

where $R_1$ represents the detector responsivity measured in A/W, with x denoting the transmitted intensity measured in W, and with $h_1$ being the channel attenuation factor. Furthermore, it is assumed that the detector current noise signal, $i_{n1}$, is modelled as a zero-mean additive white Gaussian noise (AWGN) with variance ${\sigma }_1^2$. The transmitted signal is taken as symbols drawn equiprobably from an OOK constellation such that $x\in \{0,2P_1\}$, and $P_1$ is the average transmitted optical power. The signal-to-noise ratio (SNR) corresponding to the terrestrial link is defined as

$${\gamma }_1=\frac{P_1{R}_1{h}_1}{{\sigma }_1},$$

(2)

and can also be expressed in a simpler way as ${\gamma }_1={\gamma }_a{h}_1$ assuming that ${\gamma }_a=\left(P_1{R}_1\right)/{\sigma }_1$.

The scheme of Figure 1 depicts the terrestrial receiver working as a relay node in an amplify and forward (AF) scheme, amplifying the signal that is later transmitted underwater. This amplification can compensate for part of the losses that occur when the optical signal propagates through the atmospheric medium. Once the signal is amplified at the relay node, it is transmitted under the seawater, resulting in an underwater link. This second link is assumed to be short range with a depth of up to several tens of meters. After covering this distance, the optical signal is picked up by a receiver in a submerged station, in an autonomous underwater vehicle (AUV) or in a submarine as illustrated in Figure 1. There, the signal current induced in the underwater detector can then be expressed as

$$i_2=g{i}_1{R}_2{h}_2+i_{n2},$$

(3)

where g is the relay gain, and $h_2$ is the attenuation factor of the underwater channel. In addition, $R_2$ and $i_{n2}$ are defined in the same way as $R_1$ and $i_{n1}$, described in Equation (1), but in this case corresponding to the underwater channel. For the sake of simplicity, the ambient ocean noise, $i_{n2}$, is assumed to follow an AWGN model with variance ${\sigma }_n^2$. However, this assumption can be improved by adding an impulsive noise [26,27,28] since the AWGN model ignores the impulsive occurrence of electromagnetic interference, ocean noise or noise caused by humans using other machines, especially for shallow water scenarios. Additional noise sources, such as water bubbles caused by ship propellers inside ports and harbors, will be further investigated and published elsewhere.

Furthermore, in this paper, optical scattering [10,22,29] is incorporated into our model in a simple and straightforward manner as in [24]. As explained above, scattering, which depends on the amount of impurities and the turbidity of the water [30], leads to a temporal broadening of the transmitted pulses and, consequently, may produce inter-symbol interference (ISI). The amount of ISI depends, however, on both the bit rate and the propagation environment. In this sense, the effect of ISI is usually greater in shallow water environments, where reflections from the sea surface and seabed are added to reflections from particles in the water. In contrast, in deep oceans, these reflections do not occur and the ISI effect is smaller. Therefore, ISI degradation is more harmful in coastal areas than in the open ocean. Since ISI may limit the performance of any underwater optical communication system, we incorporate its effect in our model by adding to Equation (3) an additional term due to ISI, $i_{\mathrm{ISI}}$, which is also affected by $h_2$. Therefore, the equation is as follows:

$$i_2=g{i}_1{R}_2{h}_2+i_{\mathrm{ISI}}{h}_2+i_{n2}.$$

(4)

For the sake of simplicity, the ISI interference is modeled here by its variance ${\sigma }_s^2$. Taking into account the modification of Equation (4), the signal-to-noise ratio of the underwater link is now defined as follows:

$${\gamma }_2=\frac{P_2{R}_2{h}_2}{{\sigma }_2},$$

(5)

where $P_2$ is the average optical power emitted by the transmitter of the underwater link, and ${\sigma }_2^2={\sigma }_n^2+{\sigma }_s^2$. We note that ${\sigma }_s^2$ depends on $h_2$. However, averaging the noise and the inter-symbol interference over oceanic turbulence in the way proposed in [24], ${\gamma }_2$ can be approximated as follows:

$${\gamma }_2\simeq \frac{P_2{R}_2{h}_2}{\sqrt{<{\sigma }_n^2>+<{\sigma }_s^2>}},$$

(6)

where $<·>$ denotes the average over turbulence. Here, as in the first link, Equation (6) can be expressed as ${\gamma }_2={\gamma }_u{h}_2$, assuming that ${\gamma }_u=P_2{R}_2/\sqrt{<{\sigma }_n^2>+<{\sigma }_s^2>}$.

3. Channel Model

The following sections present the modeling of attenuation factor $h_1$ and $h_2$ corresponding to terrestrial and underwater links as well as the joint FSO-TU channel modeling.

3.1. Terrestrial Link

The three main atmospheric phenomena that affect optical wave propagation and give rise to attenuation factor $h_1$ described in the previous section are (i) path loss $h_l$, (ii) geometric spread and pointing errors $h_p$, and (iii) atmospheric turbulence $h_a$. Therefore, the total channel attenuation is modeled as the product of these channel factors as

$$h_1=h_l{h}_p{h}_a,$$

(7)

where $h_l$ is deterministic and $h_p$ and $h_a$ are random variables (RVs) whose modeling is described in the following sections.

Path loss $h_l$ occurs due to atmospheric absorption and scattering caused by the molecules that form the air and by solid and liquid particles suspended in the atmosphere. This path loss can be computed by the exponential law of Beers–Lambert [31] as

$$h_l=\exp (-aL),$$

(8)

where L is the propagation distance and a is the attenuation coefficient which depends on the size and distribution of the scattering particles and the wavelength utilized. Since atmospheric conditions change very slowly over time (especially compared to the transmitted symbol period), they can be considered constant over long periods. Thus, in our analysis, it is assumed that atmospheric path loss $h_l$ has a deterministic nature.

In line-of-sight links, pointing errors are due to the dynamic misalignment between the transmitter and the receiver as a result of meteorological phenomena such as strong gusts of wind or other phenomena of different origin that cause equipment vibration. For example, in our link, as the repeater node is located on the surface of the sea, it can be affected by wave motion causing pointing errors. However, as indicated in the previous section, this particular effect is not taken into account in our analysis. Pointing errors are particularly critical in narrow beam links as they cause deep fading of the received signal. Even without pointing errors, there is always a geometric loss due to the broadening of the beam as it propagates through the atmosphere. As depicted in Figure 1, at distance L, the beamwidth defined by its waist ${\omega }_l$ can be obtained as ${\omega }_l\simeq {\theta }_{T}L$, where ${\theta }_T$ is the divergence angle of the laser and L is the path length of the propagation path. Since the beamwidth is generally larger than the size of the receiver aperture, this leads to overflow loss. Therefore, geometric loss depends mainly on the ratio at the receiver between the beam waist, ${\omega }_l$, and the receiver aperture radius, r, ${\omega }_l/r$. To consider both phenomena, here, we follow the general model proposed in [32]. Thus, assuming a Gaussian beam profile with a beam waist, ${\omega }_l$, and a circular aperture receiver of radius, r, the attenuation due to the geometric spread and pointing errors can be approximated as the Gaussian form

$$h_p\approx A_0\exp \left(-\frac{2{\rho }^2}{{\omega }_{leq}^2}\right),$$

(9)

where, as shown in Figure 1, $\rho$ is the radial pointing error, $A_0$ is the fraction of collected power without pointing error, i.e., only due to geometric spread, and ${\omega }_{leq}^2$ is the equivalent beam width. Here, $A_0$ and ${\omega }_{leq}^2$ are given by $A_0=\mathrm{erf}{\left(v\right)}^2$ and ${\omega }_{leq}^2={\omega }_l^2\sqrt{\pi }\mathrm{erf}\left(v\right)/$$\left[2v\exp (-v^2)\right]$, respectively; $\mathrm{erf}(·)$ is the error function; and $v=\sqrt{\pi }r/\left(\sqrt{2}{\omega }_l\right)$. Moreover, considering independent identical Gaussian distribution for horizontal x and vertical y displacements in the receiver plane, radial error $\rho =\sqrt{x^2+y^2}$ is modeled as a Rayleigh distribution with a jitter variance at the receiver, ${\sigma }_{\rho }^2$. Under these assumptions, the channel coefficient, $h_p$, can be seen as a function of the radial displacement, $\rho$, which is an RV. Hence, the PDF of $h_p$ can be seen as a random variable transformation problem, which leads to the following expression [32]:

$$f_{h_p}\left(h_p\right)=\frac{{\xi }_{\rho }^2}{A_0^{{\xi }_{\rho }^2}}{h}_p^{{\xi }_{\rho }^2-1},$$

(10)

where ${\xi }_{\rho }={\omega }_{leq}/\left(2{\sigma }_{\rho }\right)$ denotes the ratio between the equivalent beam radius at the receiver and the pointing error displacement standard deviation.

In order to model intensity fluctuations caused by atmospheric turbulence, the statistical Gamma–Gamma distribution is assumed here because of its mathematical tractability and accuracy in characterizing a wide range of scenarios from weak to strong turbulence. Thus, and following [17], the probability density function (PDF) of $h_a$ is written as

$$f_{h_a}\left(h_a\right)=\frac{2{\left(\alpha \beta \right)}^{(\alpha +\beta )/2}}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{h}_a^{(\alpha +\beta )/2-1}{K}_{\alpha -\beta }\left(2{\left(\alpha \beta h_a\right)}^{1/2}\right),$$

(11)

where $K_p\left(x\right)$ is the modified Bessel function of the second kind, and $\Gamma \left(x\right)$ is the Gamma function, with $\alpha$ representing the effective number of large-scale cells of the scattering process, and with $\beta$ denoting the effective number of small-scale cells. These parameters provide information on the level of intensity of the atmospheric turbulence and, since the atmospheric link is modeled by Gamma–Gamma distribution, the irradiance variance, ${\sigma }_a^2$, depends on these parameters as follows: ${\sigma }_a^2={\alpha }^{-1}+{\beta }^{-1}+{\left(\alpha \beta \right)}^{-1}$. We note that large $\alpha$ and $\beta$ values are associated with weak turbulence regimes, while small values are related to a strong turbulence level. This is equivalent to saying that a regime of weak fluctuations is associated with ${\sigma }_a^2<1$, moderate fluctuations with ${\sigma }_a^2\approx 1$, whereas strong fluctuations are characterized by ${\sigma }_a^2>1$. Such parameters, $\alpha$ and $\beta$, can be obtained as follows [16]:

$$\alpha ={\left[\exp \left(0.49{\sigma }_R^2{(1+1.11{\sigma }_R^{12/5})}^{-7/6}\right)-1\right]}^{-1}$$

(12)

$$\beta ={\left[\exp \left(0.51{\sigma }_R^2{(1+0.69{\sigma }_R^{12/5})}^{-5/6}\right)-1\right]}^{-1},$$

(13)

where ${\sigma }_R^2$ is the Rytov variance which, in turn, can be obtained for downlinks as follows [16]:

$${\sigma }_R^2=2.25k^{\frac{7}{6}}{\sec }^{\frac{11}{6}}\left(\theta \right){\int }_0^Z{C}_n^2\left(z\right)z^{\frac{5}{6}}dz,$$

(14)

assuming that the receiver is at sea level. In this expression, $C_n^2\left(z\right)$ is the index of refraction structure parameter at altitude z, $k=2\pi /\lambda$ is the optical wave number, Z is the transmitter height and $\theta$ is the zenith angle, respectively. We note that $C_n^2$ is a characteristic parameter of atmospheric turbulence that gives a measure of the strength of the turbulence. Due to its dependence on height, this parameter is usually considered constant for scenarios where the signal propagates horizontally. However, for vertical or inclined links, the value of $C_n^2\left(z\right)$ must be obtained from models [16].

Once the three factors included in Equation (7) are individually discussed, the statistical characterization of composite channel $h_1$ can be achieved. Thus, from [32], the PDF of $h_1$ is given by

$$f_{h_1}\left(h_1\right)=\frac{2{\xi }_{\rho }^2{\left(\alpha \beta \right)}^{\frac{\alpha +\beta }{2}}}{{\left(A_o{h}_l\right)}^{{\xi }_{\rho }^2}\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{h}_1^{{\xi }_{\rho }^2-1}{\int }_{\frac{h_1}{A_0{h}_l}}^{\infty }{h}_a^{\frac{\alpha +\beta }{2}-1-{\xi }_{\rho }^2}{K}_{\alpha -\beta }\left(2\sqrt{\alpha \beta h_a}\right)d{h}_a,$$

(15)

where $\alpha$ and $\beta$ parameters include the information on the strength of the turbulence, $\xi$ contains the severity of the pointing error, $A_0$ denotes the geometric spread attenuation and $h_l$ is the path loss. We note that such a joint PDF is used later in Section 3.3 to derive the probability of error, taking into account both atmospheric and underwater links, by calculating the cumulative distribution function (CDF).

3.2. Underwater Link

The propagation of an optical beam underwater is very challenging due to the different characteristics and properties of the water bodies, ranging from shallow to deep water, which give rise to phenomena such as absorption and scattering. These effects collectively affect the underwater optical beam and are more or less relevant depending on the underwater environment through which it propagates. In addition, underwater wireless optical communications are affected not only by absorption and scattering but also by ocean turbulence, which is the main cause of fading in wireless optical communications. Thus, the total attenuation of the underwater link is modeled as the product of two factors as

$$h_2=h_{lg}{h}_u,$$

(16)

where the first factor, $h_{lg}$, includes path loss and geometric loss and it is assumed to be deterministic, and the second factor, $h_u$, is irradiance fluctuation due to ocean turbulence which is a random variable. This turbulence together with scattering and movements of the transmitter and receiver can cause severe pointing errors in the underwater links. However, in the case of scattering, because it causes the beam broadening to be increased, it provides a natural mechanism to mitigate potential angular pointing errors due to jitter at the expense of a higher attenuation due to geometric spread [33]. We did not consider the effect of pointing errors in $h_2$. The $h_{lg}$ factor can be obtained as follows:

$$h_{lg}\simeq \exp (-F{c}_{T}z)\times k_1\mathrm{erf}{\left(\frac{\sqrt{\pi }r}{\sqrt{2}{\omega }_z}\right)}^2,$$

(17)

where the first term represents the path loss and the second term represents the geometric loss. The path loss is given by the exponential Beers–Lambert law, where z represents the depth of the underwater link, $c_T$ is the extinction coefficient and F is a coefficient that takes into account the increase in received power due to scattering. In this work, we assume $F=1$ while the values of $c_T$ are taken from [33]. Furthermore, in the second term corresponding to geometric loss, r is the detector radius, ${\omega }_z\simeq k_2{\theta }_{T}z$ is the beam waist at depth z, ${\theta }_T$ is the divergence angle of the transmitted beam, and $k_1$ and $k_2$ are two coefficients that model the increase in beam spreading due to scattering [33].

On the other hand, ocean turbulence or ocean scintillation occurs as a result of random variations in the refractive index of the propagation medium caused by currents, turbulent eddies, temperature and salinity changes, among other factors. In this paper, this phenomenon, given random factor $h_u$, is characterized by the Weibull model [9,23], recently proposed to characterize salinity- or temperature-induced fading in submarine optical channels. Taking into account the Weibull model for $h_u$ and the losses, $h_{lg}$, defined in Equation (17), the behavior of the joint underwater channel, $h_2$, can be modeled by the following PDF:

$$f_{h_2}\left(h_2\right)=\frac{K}{\Lambda }{\left(\frac{h_2}{h_{lg}\Lambda }\right)}^{K-1}\exp \left[-{\left(\frac{h_2}{h_{lg}\Lambda }\right)}^K\right],$$

(18)

where $K>0$ corresponds to the shape parameter relative to the scintillation index of irradiance fluctuations, and $\Lambda >0$ is the scaling parameter relative to the mean value of the irradiance [34]. Here, assuming $E\left[h_u\right]=1$ and according to [35] $\Lambda =\frac{1}{\Gamma (1+1/K)}$, whereas the scintillation index is provided by

$${\sigma }_u^2=\frac{\Gamma (1+2/K)}{\Gamma {(1+1/K)}^2}-1\approx K^{-11/6}.$$

(19)

Thus, from this equation, the value of K is computed as $K\simeq {\left({\sigma }_u^2\right)}^{-6/11}$ where the scintillation index can be obtained using a simple analytic approximation proposed in Appendix A in [33], which is given by the following equation:

$${\sigma }_u^2={\Lambda }_1{z}^2+{\Lambda }_{2}z+{\Lambda }_3,$$

(20)

where z is the link distance (depth) for $z<100$ m, and parameters ${\Lambda }_1$, ${\Lambda }_2$ and ${\Lambda }_3$ can be obtained after a curve-fitting approach for different values of the relative strength of temperature and salinity fluctuations.

We note that from the integration of (18) we can obtain the CDF of the underwater channel, which is key to the derivation of the expression for the error probability in Section 3.3, from obtaining the joint CDF of the FSO-TU system.

3.3. Composite FSO-TU Channel

This section describes how the CDF of the FSO-TU system is obtained to address the performance evaluation of the end-to-end hybrid network. Accordingly, once the statistical PDFs of the terrestrial and underwater channels are obtained, this information can now be used to develop the expressions for the CDF of the hybrid AF-based FSO-TU system. Thus, we have

$$F_{\gamma }\left(\gamma \right)\approx \mathrm{Pr}[{\gamma }_1<\gamma \bigcup {\gamma }_2<\gamma ]=F_{{\gamma }_1}\left(\gamma \right)+F_{{\gamma }_2}\left(\gamma \right)-F_{{\gamma }_1}\left(\gamma \right)F_{{\gamma }_2}\left(\gamma \right),$$

(21)

where ${\gamma }_1$, and ${\gamma }_2$ are the signal-to-noise ratios of the terrestrial and the underwater links, which are defined in Section 2, and $F_{{\gamma }_1}\left({\gamma }_1\right)$ and $F_{{\gamma }_2}\left({\gamma }_2\right)$ are their corresponding CDFs. These two functions are directly obtained by integrating their PDFs which can be calculated from the Equations (15) and (18), taking into account that $f_{{\gamma }_1}\left({\gamma }_1\right)=f_{h_1}({\gamma }_1/{\gamma }_a)$ and $f_{{\gamma }_2}\left({\gamma }_2\right)=f_{h_2}({\gamma }_2/{\gamma }_u)$, respectively. Thus,

$$F_{{\gamma }_1}\left({\gamma }_1\right)=\frac{{\xi }_{\rho }^2}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{G}_{2,4}^{3,1}\left(\frac{\alpha \beta {\gamma }_1}{A_0{h}_l{\gamma }_a}|\begin{array}{c}1,1+{\xi }_{\rho }^2\\ {\xi }_{\rho }^2,\alpha ,\beta ,0\end{array}\right),$$

(22)

$$F_{{\gamma }_2}\left({\gamma }_2\right)=1-\exp \left[-{\left(\frac{{\gamma }_2}{\Lambda {\gamma }_u{h}_{lg}}\right)}^K\right],$$

(23)

where the cumulative probability function in Equation (22) is obtained by using Equations (07.34.21.0085.01) and (07.34.21.0084.01) [36]. In a similar fashion, Equation (07.34.16.0001.01) [36] is used in order to develop the equation one step further, allowing simplification of the result by adding $(\alpha +\beta )/2$ to the obtained $a_i$ and $b_i$. Hence, by inserting Equations (22) and (23) into (21), the resulting overall CDF is obtained as

$$F_{\gamma }\left(\gamma \right)=1-\exp \left[-{\left(\frac{\gamma }{\Lambda {\gamma }_u{h}_{lg}}\right)}^K\right]\times \left\{1-\frac{{\xi }_{\rho }^2}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{G}_{2,4}^{3,1}\left(\frac{\alpha \beta \gamma }{A_0{h}_l{\gamma }_a}|\begin{array}{c}1,1+{\xi }_{\rho }^2\\ {\xi }_{\rho }^2,\alpha ,\beta ,0\end{array}\right)\right\}.$$

(24)

4. Performance Analysis

In this section, the closed analytical expression of the average BER (ABER) for the FSO-TU cooperative system is developed. To this end, we first obtain the conditional BER (CBER) expression associated with an ideal scenario in absence of channel fluctuations, considering the OOK modulation scheme with IM/DD and AWGN. In this scenario, from [16], and under the assumption that channel state information (CSI) is available at the receiver, the CBER is given by

$$Pb(e/h)=\frac{1}{2}\mathrm{erfc}\left(\frac{i_{s}h}{2\sqrt{2({\sigma }_n^2+{\sigma }_s^2)}}\right),$$

(25)

where $i_s$ is the ideal signal current without considering channel degradation effects, which in this case is obtained as $i_s=P_1{R}_1{R}_{2}g$, where $P_1$ represents the average of transmitted optical power, $R_1$ and $R_2$ are the responsiveness corresponding to the detectors of both links, g is the repeater gain, $h=h_1{h}_2$ represents the random irradiance fluctuation and ${\sigma }_n^2$ and ${\sigma }_s^2$ are the noise and ISI variances. In practical terms, irradiance fluctuation can be estimated using training sequences or pilot symbols [37]. Thereafter, pilot-based channel estimation methods, namely least squares and minimum mean-square error, can be employed.

Following [38,39], we assume in (25) that the ISI interference is Gaussian distributed. Now, we define the signal-to-interference-plus-noise ratio (SINR) without considering the effects of optical channel degradation as follows:

$${\gamma }_0=\frac{i_s}{\sqrt{{\sigma }_n^2+{\sigma }_s^2}}.$$

(26)

In order to solve the integral involving ABER, calculated by averaging $Pb\left(e\right|h)$ over the PDF of the irradiance, $f_h\left(h\right)$, the SINR can be approximated by averaging the noises and the inter-symbol interference over oceanic turbulence in the way proposed in [24,38].

$${\gamma }_0\simeq \frac{i_s}{\sqrt{<{\sigma }_n^2>+<{\sigma }_s^2>}}.$$

(27)

Now, to be consistent with the notation used in (24), we can identify $\gamma ={\gamma }_{0}h$. In this way, the probability of error $P_b\left(e\right)$ is calculated, following the development presented in [24], from the average of $P_b\left(e\right|h)$ and the probability density function of the irradiance, $f_h\left(h\right)$. Hence, the BER is derived as follows:

$$P_b={\int }_0^{\infty }\frac{1}{2}\mathrm{erfc}\left(\frac{{\gamma }_{0}h}{2\sqrt{2}}\right)f_h\left(h\right)\mathrm{d}h.$$

(28)

Applying integration by parts to Equation (28), we can obtain the $P_b$ from the CDF given in (24), using the following formula:

$$P_b={\left.\left(P_b\left(e\right|h)F_h\left(h\right)\right)\right|}_0^{\infty }-{\int }_0^{\infty }\frac{\mathrm{d}}{\mathrm{d}h}\left[P_b\left(e\right|h)\right]F_h\left(h\right)\mathrm{d}h.$$

(29)

Since $P_b\left(e\right|\infty )=0$ and $F_h\left(0\right)=0$ (note that negative values are not allowed for the optical irradiance), then the above expression can be reduced to the following expression:

$$\begin{array}{cc}\hfill P_b=& -{\int }_0^{\infty }\frac{\mathrm{d}}{\mathrm{d}h}\left[P_b\left(e\right|h)\right]F_h\left(h\right)\mathrm{d}h=-{\int }_0^{\infty }\frac{\mathrm{d}}{\mathrm{d}h}\left[\frac{1}{2}\mathrm{erfc}\left(\frac{{\gamma }_{0}h}{2\sqrt{2}}\right)\right]F_h\left(h\right)\mathrm{d}h,\hfill \end{array}$$

(30)

where $F_h\left(h\right)$ is obtained directly from (24). Next, we apply Equation (06.27.13.0005.01) [36] to derive an expression for the derivative of $P_b\left(e\right|h)$ with respect to h:

$$\frac{\mathrm{d}}{\mathrm{d}h}\left[P_b\left(e\right|h)\right]=-\frac{{\gamma }_0}{2\sqrt{2\pi }}\exp \left[-{\left(\frac{{\gamma }_{0}h}{2\sqrt{2}}\right)}^2\right].$$

(31)

Next, (31) is introduced in (30) to solve the resulting integral. To this end, a generalized Gauss–Laguerre quadrature is proposed, (31), and defined as

$${\int }_0^{\infty }{x}^{\upsilon }{e}^{-x}f\left(x\right)\mathrm{d}x=\sum _{i=1}^n{H}_{i}f\left(x_i\right)+E_n,$$

(32)

where v is a constant, $x_i$ represents the ith zero of the Laguerre polynomial, $L_n^{\upsilon }\left(x\right)$, $H_i$ is the corresponding weight coefficients associated with the Gauss–Laguerre quadrature and $E_n$ denotes the truncation error. If the normalization of the Laguerre polynomials is chosen such that the following is the case,

$$L_n^{\upsilon }=\sum _{m=0}^n\left(\genfrac{}{}{0pt}{}{n+\upsilon }{n-m}\right)\frac{{(-x)}^m}{m!},$$

(33)

then, according to [40], the weight coefficients can be provided as follows:

$$H_i=\frac{\Gamma \left(n+\upsilon +1\right)x_i}{n!{(n+1)}^2{\left[L_{n+1}^{\upsilon }\left(x_i\right)\right]}^2},(i=1,2,\dots ,n).$$

(34)

If at this point we make the following change in variable,

$$x={\left(\frac{{\gamma }_0}{2\sqrt{2}}\right)}^2{h}^2;\mathrm{d}x=2{\left(\frac{{\gamma }_0}{2\sqrt{2}}\right)}^{2}h\mathrm{d}h;,$$

(35)

then we can apply (32) to solve (30). In this way, we identify $v=-1/2$, and therefore we obtain the following:

$$P_b=\frac{1}{2\sqrt{\pi }}\sum _{i=1}^n{H}_i{F}_{\gamma }\left({\gamma }_i\right){|}_{{\gamma }_i=\left(2\sqrt{2}{x}_i^{1/2}\right)},$$

(36)

where, again, $F_{\gamma }\left({\gamma }_i\right)$ is the cumulative distribution function, which corresponds to Equation (24), and ${\gamma }_i={\gamma }_0·h$ y ${\gamma }_0\approx {i_S}_0/\sqrt{<{\sigma }_n^2>+<{\sigma }_s^2>}$.

5. Results

In this section, the closed-form mathematical expression for the average BER derived in the previous section is used to evaluate the performance of the proposed cooperative FSO-TU system. The aim of this analysis is to better understand the BER performance of the hybrid FSO-TU system under realistic scenario conditions, as well as to draw some ideas and conclusions that may lead to a better future design of cooperative FSO-TU systems based on the scheme investigated here.

Table 1. System parameters.

Terrestrial Optical Link
Parameter	Symbol	Value
Wavelength	${\lambda }_1$	1550 nm
Responsivity	$R_1$	$0.5$ A/W
Distance	L	1 km
Transmitter divergence	${\theta }_T$	1 mrad
Transmitted beamwidth at 1 km	${\omega }_l$	1 m
Receiver radius	r	10 cm
Jitter standard deviation	${\sigma }_{\rho }$	10/30/60 cm
Atmospheric turbulence (weak)		0.37
Atmospheric turbulence (moderate)	${\sigma }_a^2$	0.5
Atmospheric turbulence (strong)		1.17
Attenuation coefficient (very clear air)		0.0647 dB/km
Attenuation coefficient (clear air)	a	0.2208 dB/km
Attenuation coefficient (haze)		0.7360 dB/km
Underwater optical link
Parameter	Symbol	Value
Wavelength	${\lambda }_2$	532 nm
Responsivity	$R_2$	$0.5$ A/W
Depth	z	$20/30/40$ m
Transmitter divergence	${\theta }_T$	10 mrad
Transmitted beamwidth at z	${\omega }_z$	30.8/46.2/61.6 cm
Receiver radius	r	10 cm
Underwater turbulence (moderate-weak)		$0.2453$
Underwater turbulence (moderate-strong)	${\sigma }_u^2$	$0.7885$
Underwater turbulence (strong)		$1.0652$
Extinction coefficient (clear ocean water)	c${}_T$	0.151 m${}^{-1}$
Extinction coefficient (coastal water)		0.398 m${}^{-1}$

summarizes the realistic parameters considered in our analysis for the terrestrial an underwater links. On the one hand, as far as the terrestrial link is concerned, this first link operates at ${\lambda }_1=1550$ nm over a distance $L=1$ km, as shown in Figure 1. Here, the transmitter laser emits an average optical power $P_1$ with a divergence angle of ${\theta }_T=10$ mrad, resulting at the receiver end in a beam footprint with a waist of ${\omega }_l=1$ m. With this optical beam broadening, only a fraction of the transmitted power is collected for the detector of $r=10$ cm radius and responsiveness $R_1=0.5$ A/W. Thus, this terrestrial link operates with a ratio of $({\omega }_l/r)$ = 10.

Moreover, with regard to the limiting factors of the networking environment, three atmospheric turbulence conditions are considered for the terrestrial channel: strong, moderate, and weak. As discussed in Section 3, the intensity of atmospheric turbulence, ${\sigma }_a^2$, depends on the wavelength, ${\lambda }_1$, the link distance, L, the link inclination angle, $\theta$, and the refractive index structure parameter $C_n^2$. In turn, parameter $C_n^2$ changes with height, as shown by different models such as the Hufnagle–Valley and the SLC models [16]. In our analysis, we use different values of $\theta$ and $C_n^2$ according to the aforementioned models in order to obtain, by means of Equations (12) and (13), the values of $\alpha$ and $\beta$ required by the Gamma–Gamma model to emulate the mentioned turbulent conditions. In particular, the values of $\alpha$ and $\beta$ considered in our calculations are 6.76 and 5.22, 5.383 and 3.753, and 4.345 and 1.307, which correspond to weak (${\sigma }_a^2=$ 0.37), moderate (${\sigma }_a^2=$ 0.5), and strong (${\sigma }_a^2=$ 1.17) turbulence conditions, respectively. In addition, three climatic conditions such as very clear air, clear air, and haze are also considered. The values of the attenuation coefficient, a, for these three climatic conditions are taken from [31]. Finally, concerning the misalignment effect, three values of jitters are used with standard deviations of ${\sigma }_{\rho }=$10, 30, and 60 cm, which corresponds to ratios $({\sigma }_{\rho }/{\omega }_l)=$ 0.1, 0.3, and 0.6, respectively.

On the other hand, as far as the underwater link is concerned, this second link operates at a ${\lambda }_2=532$ nm for three different depths of $z=20$, 30 and 40 m. We note that the distances in this second link are much smaller than in the terrestrial link due to the huge degradation of the underwater channel. Here, the transmitter emits average optical power $P_2$ with a divergence angle of ${\theta }_T=10$ mrad which results, for a detector size of 10 cm radius, in $({\omega }_z/r)$ ratios of two, three and four for each of the above-mentioned depths. The value of $P_2$ can be obtained from the terrestrial link parameters and the gain of the relay node as $P_2=g{R}_1{P}_1{A}_0{h}_l{\gamma }_{\rho }^2/(1+{\gamma }_{\rho }^2)$. Moreover, to calculate coefficient $h_{lg}$ that takes into account the path loss and geometric losses, we use the values of extinction coefficient $c_T$ and of coefficients $k_1$ and $k_2$ published in [33], according to the type of water and depth considered in each case. In this respect, to illustrate the large degradation of the underwater channel, Figure 2 shows the received signal level, expressed in $A^2$, for different water types and transmitted powers as a function of link depth, assuming only geometrical and path loss.

Regarding ocean turbulence, three intensities are considered (strong, moderate-to-strong, weak-to-moderate). The scintillation index of the ocean turbulence, ${\sigma }_u^2$, depends on parameters such as wavelength, underwater link length, and salinity and temperature variations of the medium. In our analysis, values of ${\sigma }_u^2$ = 0.2453, 0.7885 and 1.0652 are considered for weak-to-moderate, moderate-to-strong and strong turbulence, respectively [24,41]. Finally, for the repeater, a gain of $g=1/A_0$ is assumed.

In order to properly analyze the behavior of the FSO-TU system, different realistic scenarios were considered in which the impact of the main degradation phenomena for the terrestrial link and the underwater link on the BER performance were analyzed separately.

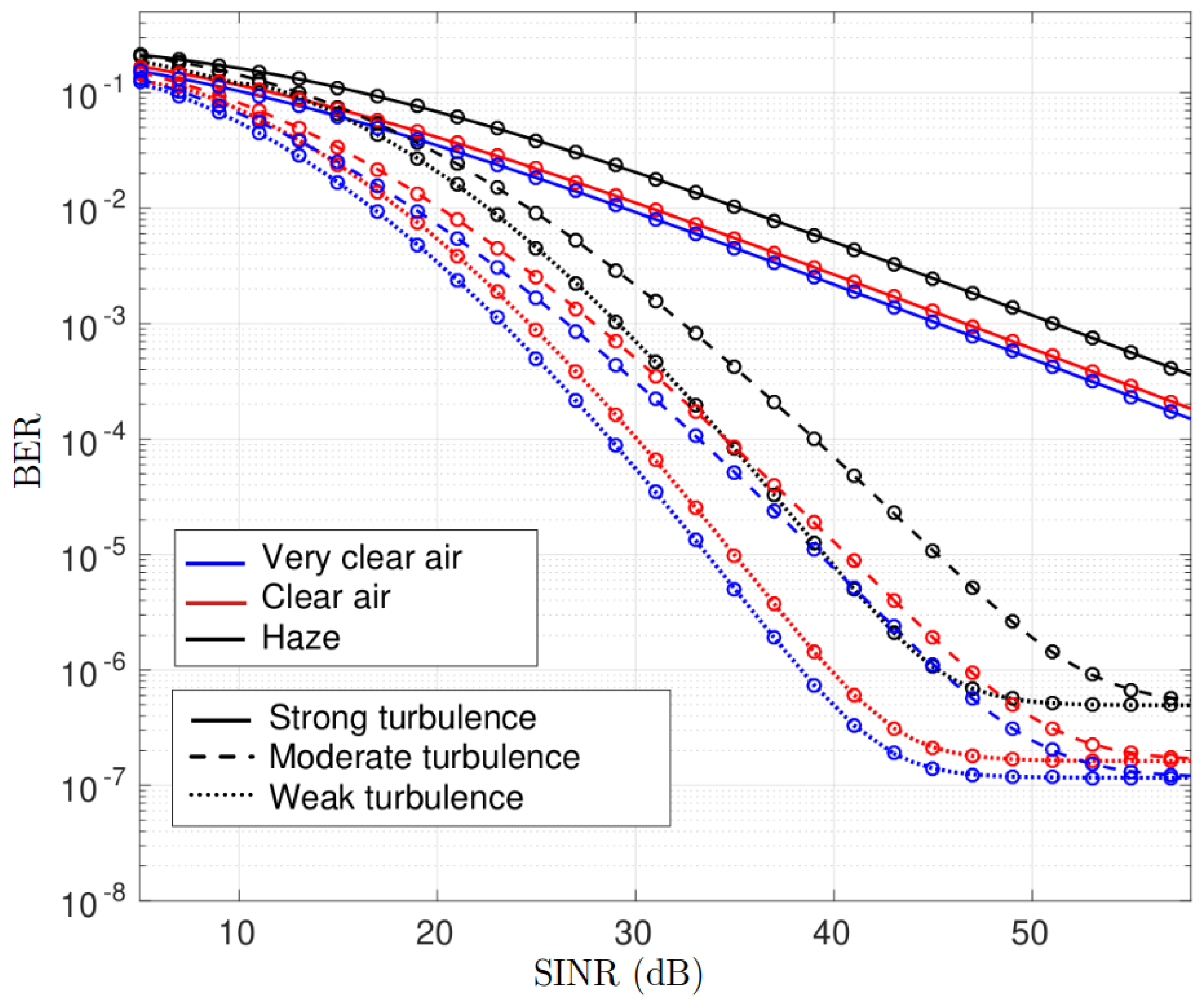
First, Figure 3 presents the results of the impact of terrestrial link degradation factors on the BER of the FSO-TU system. Therefore, in this figure, the underwater channel conditions are not modified, assuming the most favorable conditions, i.e., moderate-weak ocean turbulence, clean ocean water and a depth of 20 m. In particular, Figure 3 shows the BER obtained with Equation (36) as a function of the SINR for three different atmospheric turbulence conditions and three different weather conditions. We note that the SINR depicted in the figure is the maximum achievable SINR and therefore includes the minimum losses of both links, i.e., the geometric losses and the underwater channel path loss for $z=20$ m. Values of ${\sigma }_1={10}^{-7}$ A and ${\sigma }_2={10}^{-6}$ A are assumed in our analysis. We note that both values are consistent with the noise variance measured in [42]. Here, solid, dashed and dotted curves correspond to scenarios with strong, moderate and weak turbulence, respectively, while black, red and blue curves correspond to haze, clear air and very clear air conditions, respectively. A fixed jitter with ${\sigma }_{\rho }=10$ cm is assumed in all cases due to pointing error. We note that along with the analytical results provided by the closed expression for the BER mentioned above, numerical results obtained by Monte Carlo simulations are also plotted in the figure. These numerical results are plotted with circular markers. It is important to note that, in all cases, a perfect match is shown between the simulated results and those obtained from the derived expression.

As can be seen from Figure 3, the FSO-TU system has a different behavior under strong, moderate and weak turbulence. For weak and moderate turbulence, the BER decreases rapidly as the SINR increases; however, under strong turbulence, the decay of the BER curves is much slower. We notice that under weak and moderate turbulence, the BER curves change behavior for SINR values above 40 dB. From this SINR level onwards, a BER floor occurs. The appearance of this BER floor for high SNR ratios is an expected phenomenon in a turbulent environment as shown by the analysis published in [43]. This floor imposes a limit on the BER performance achievable by the system. In particular, for the most favorable scenario in Figure 3, the BER cannot be less than ${10}^{-7}$ in any case. Furthermore, the detailed analysis of the figure shows that the BER floor of the curves corresponding to weak turbulence and moderate turbulence tend to coincide as the SINR increases. In fact, it would also coincide with the BER floor of the curves with strong turbulence whenever sufficiently high SINR values are drawn. This behavior leads to the important conclusion that the BER floor of the FSO-TU system is independent of the intensity of atmospheric turbulence and, therefore, is imposed by the intensity of the underwater turbulence of the second link. Lastly, as far as weather conditions are concerned, Figure 3 shows that their effect on BER degradation is less pronounced than that of turbulence, which is understandable for short links of up to 1 km. However, a higher degradation is seen in the case of haze.

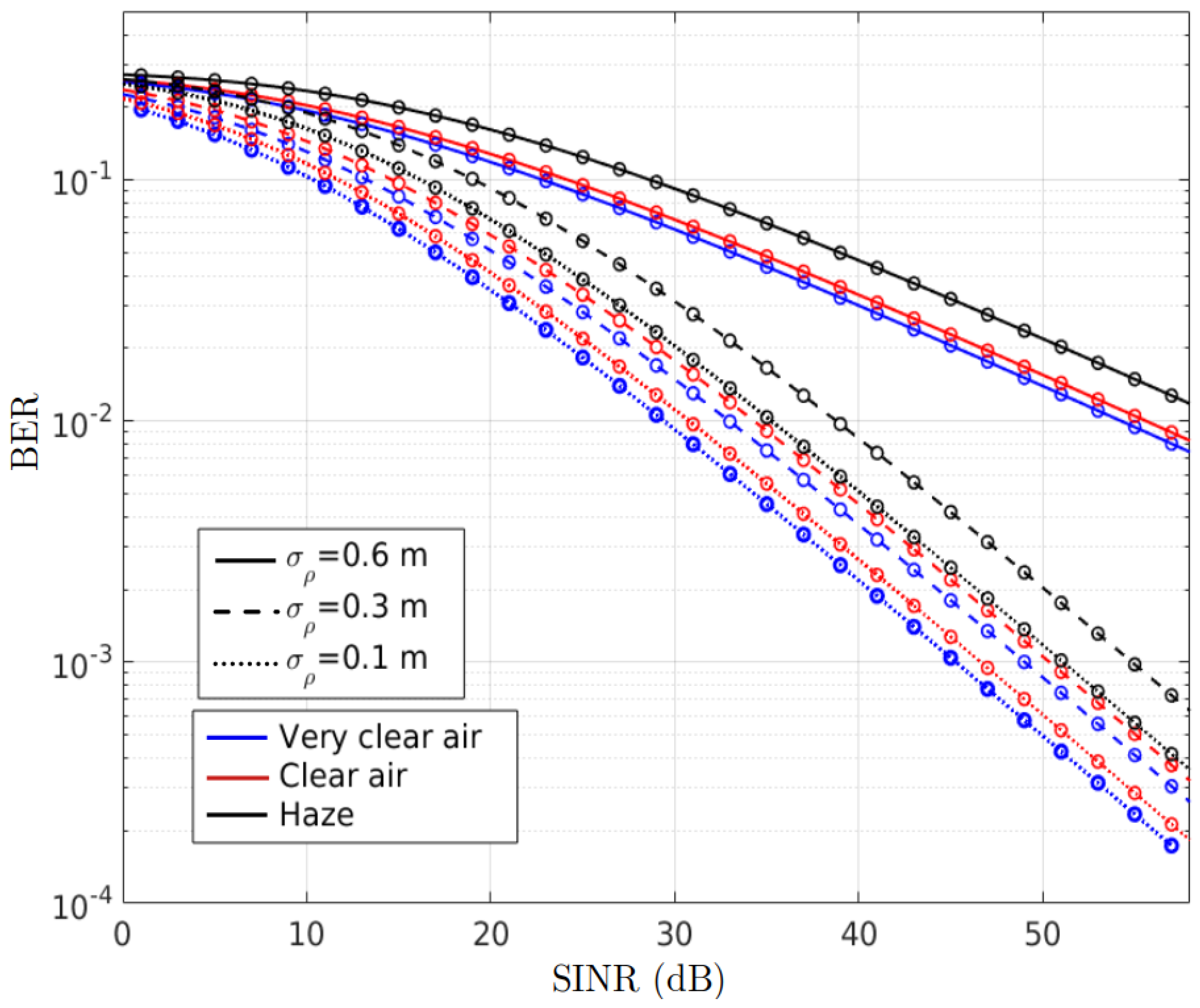
Next, the impact of pointing errors occurring in the terrestrial link on BER performance is analyzed separately in Figure 4. As in the previous figure, in order to reduce the influence of the underwater link, the most favorable conditions are assumed for this link, i.e., moderate–weak ocean turbulence, clean ocean water and a depth of 20 m. In addition, the strong atmospheric turbulence condition is assumed for the terrestrial link in all cases.

This figure shows the average BER obtained analytically (depicted with lines) from Equation (36) and numerically (repesented with circular markers) by Monte Carlo simulations for three levels of pointing errors and three atmospheric transparency conditions. We note that, as expected, the analytical and numerical results coincide again. The three jitter levels chosen in the figure, ${\sigma }_{\rho }=0.1$, 0.3 and 0.6 m, model real situations with pointing errors of different severity. The severity of the pointing error depends on the $({\sigma }_{\rho }/{\omega }_l)$ ratio, so that the higher the $({\sigma }_{\rho }/{\omega }_l)$, the higher the severity. In the figure, the dotted line curves shows the BER corresponding to a low-severity pointing error, while the dashed and solid line curves show the BER for low–moderate and high-severity errors, respectively. As expected, the impact of pointing errors at ${\sigma }_{\rho }=0.1$ m and ${\sigma }_{\rho }=0.3$ m causes a moderate increase in BER; however, at ${\sigma }_{\rho }=0.6$ m there is a sharp increase in BER that seriously compromises the performance of the FSO-TU system. Higher ${\sigma }_{\rho }$ values with $({\sigma }_{\rho }/{\omega }_l)\sim 1$ result in link failure. Again, we can see how the effect on BER degradation is less pronounced with very clear air than with haze, although the difference is small due to the short distance of the link.

Following the approach described at the beginning of the section, the results of the impact of the underwater link degradation factors on BER performance are drawn in Figure 5. Again, the most favourable conditions are assumed for the terrestrial channel, i.e., weak atmospheric turbulence, a jitter due to the pointing error of 0.1 m and a path loss, optical-wireless networks $h_l=1$. Specifically, Figure 5 shows the average BER of the cooperative FSO-TU system as a function of SINR obtained analytically, using Equation (36), and numerically, using Monte Carlo simulations, for three different underwater turbulence conditions and three different depths under clear ocean water conditions. As in Figure 3, the solid, dashed and dotted line curves represent the BER analytical results for oceanic conditions with strong, moderate and weak turbulence, while the blue, red and black colors indicate depths of 20, 30 and 40 m, respectively. Numerical results are represented with circular markers. It is worth noting that, again, a perfect match is shown between the simulated results and those obtained from the closed-form expression derived in this work.

Figure 5 shows much more clearly than Figure 3 the appearance of the BER floor explained above. We note that as the SINR increases, all curves tend to a constant BER value that no longer decreases. The specific BER floor value depends on the level of ocean turbulence and the depth of the link, although both factors are, in turn, related. In addition, the results shown in Figure 5 indicate that ocean turbulence has a determining influence on the BER floor. Thus, even for a link as shallow as 20 m, an increase in ocean turbulence conditions from weak-to-moderate to moderate-to-strong causes a strong increase in the BER floor from ${10}^{-7}$ to ${10}^{-4}$. Likewise, for the most favourable turbulence conditions, an increase in the link from 20 to 30 m causes an increase in the BER floor from ${10}^{-7}$ to ${10}^{-5}$, and a further increase in the depth from 30 to 40 m increases the BER floor to ${10}^{-3}$. It is clear from the results in Figure 5 that the underwater link has a huge impact on system performance, as even over short distances there is high degradation. Therefore, the underwater link requires the most attention in the design of the cooperative FSO-TU system.

6. Concluding Remarks

In this work, a new cooperative system that extends optical–wireless networks from terrestrial to underwater environments is proposed and analyzed. The proposed FSO-TU system consists of two links, a terrestrial link and an underwater link, both joined through a relay node operating in an amplify and forward scheme. In order to analyze the performance of the proposed system, a new closed-form expression for the average BER is derived. This novel expression includes the effect of the main phenomena that degrade the signal quality on both links, some of which have not previously been considered. In particular, the derived expression considers, for the terrestrial link, the effect of path loss, pointing errors and atmospheric turbulence and, for the underwater link, the effect of path loss and oceanic turbulence. The Gamma–Gamma and Weibull statistical distributions are used to model atmospheric and oceanic turbulence, respectively. The analysis of BER performance under different channel conditions and different practical scenarios shows that pointing errors such as atmospheric and oceanic turbulence can seriously degrade the performance of the hybrid system. In addition, ocean turbulence causes the occurrence of a BER floor that limits system performance in some scenarios. It should be noted that the analytical expression of the BER proposed here provides a simple and efficient procedure to estimate the behavior of the system under main channel degradation factors in real scenarios, thus constituting a valuable tool for the design of these systems.