Abstract
In fields such as polarization navigation and imaging, there is a demand for polarizers to simultaneously possess a high transmittance and extinction ratio. However, most studies focus solely on a single metric for polarizer design. To address this issue, this paper proposed a metasurface polarizer with a transition layer and its efficient design method, aiming to enhance the polarizers’ transmittance and extinction ratio performance simultaneously. An all-dielectric metasurface polarizer with a TiO2 transition layer was designed, and a tandem neural network was constructed by combining forward prediction and inverse design networks. The network is successfully trained by utilizing structural parameters and spectral response Tx and Ty datasets collected through simulation software. A high-performance metasurface polarizer was designed under the desired metrics with a transmittance of 90% and an extinction ratio of 40 dB. The proposed method in this paper made progress in the comprehensive optimization of polarizer performance. It is more accurate and efficient compared to other design methods and is better suited for practical applications.
1. Introduction
Polarizers are important optical components in systems such as optical information processing [1], optical imaging detection [2], and optical communication [3]. Traditional polarizers often use natural crystals or multilayer film structures, resulting in large volumes that hinder miniaturization and integration. To meet the requirements of device portability and integration, there is a need to reduce the volume of polarizing elements while ensuring the quality of the optical field. Due to their unique optical modulation mechanism, metasurfaces have emerged as a solution for miniaturizing and lightweighting polarizers. Metasurfaces are artificially designed micro-nanostructures composed of subwavelength periodic structural units. These units, arranged in a specific manner, can precisely control incident light, enabling various operations on light [4]. The design and fabrication of metasurfaces involve selecting appropriate materials and designing rational structural units. Through thoughtful design, the anisotropy and isotropy of metasurface structures can be flexibly adjusted, allowing for the creation of nanoscale polarizers [5,6].
Metasurfaces have found widespread applications in various optical devices due to their compact size, powerful functionality, and ease of integration. Devices such as metalenses [7], holographic imaging [8], and beam deflectors [9] leverage the characteristics of metasurfaces to enhance their performance and efficiency. Therefore, research and applications of metasurfaces hold significant prospects. However, traditional methods for metasurface structure design are complex and inefficient, requiring the establishment of numerous simulation models, parameter scans, and optimizations for each model. This consumes considerable computational resources and time and is limited by the designer’s experience and intuition. Rapidly designing metasurface structural parameters and finding solutions that best meet performance criteria are crucial challenges in metasurface structure research.
In recent years, neural networks have been employed to assist optical design with notable success [10,11]. Neural networks, as machine learning models, can learn patterns and features from data. By using simulation datasets as inputs for training, neural networks can rapidly and accurately learn the relationship between metasurface structural parameters and corresponding spectral responses [12,13]. This reduces the computational and human costs of traditional metasurface design, eliminating the need for complex simulation and parameter scan studies, thus achieving rapid and intelligent metasurface design. Chen et al. [14] proposed the use of deep neural networks to predict the spectral response of metasurfaces, optimizing the parameters of the DNN model. After 50,000 training iterations, the mean squared error (MSE) of the loss function reached 2.665 × 10−3. However, their study did not involve the inverse design of metasurface structures. Tanriover et al. [15] demonstrated the inverse design of a VO2 tunable absorber using a neural network, achieving an overall MSE of 6 × 10−4 after training the inverse network. Deng et al. [16] used an LSTM network to predict extinction ratio and inverse design of nanofin metasurfaces. After 40,000 training iterations, the minimum MSE of the loss function reached 0.06. However, this study only used the extinction ratio as an input, had fewer performance indicators, and had a longer training time. Currently, deep learning-based metasurface spectral prediction and design methods mainly focus on metrics such as the spectrum [17], S-parameters [18], and far-field responses [19].
Nevertheless, for polarizers, the transmittance and extinction ratios [20] are more critical performance indicators, reflecting the polarization efficiency and quality of polarizers. Transmittance refers to the proportion of linearly polarized or unpolarized light in the polarization axis direction that passes through the polarizer. The extinction ratio refers to the ratio of the minimum to maximum transmittance of the polarizer. A higher extinction ratio indicates a stronger ability of the polarizer to suppress unwanted polarized light, indicating better polarization quality. However, most previous studies have focused only on transmittance or extinction ratio as a single criterion for polarizer design due to the inverse relationship between transmittance and extinction ratios that makes it difficult for polarizers to simultaneously meet high-performance requirements, leading to poor performance and difficulty in meeting the demand for high transmittance and high extinction ratio in practical applications.
To address these issues, this article proposes an efficient metasurface polarizer design method that can optimize the transmittance and extinction ratios of the polarizer at the same time. By decomposing the extinction ratio into transmission spectra Tx and Ty, simultaneously utilizing them as network inputs to design the parameters of the metasurface structure. Moreover, a TiO2 transition layer is introduced to suppress the undesired polarization Ty while ensuring the transmission of the required polarization Tx, which successfully achieved the purpose of balancing the transmittance and extinction ratios. In the second section, we introduced the structure of the polarizer. To achieve a high-performance metasurface polarizer, the third section describes the tandem inverse design network and the construction of its dataset. Following the design of the metasurface polarizer and neural network structure, various activation functions and gradient descent algorithms were experimented with for network optimization. Experimental validation demonstrated that by inputting desired performance metrics, the network can rapidly design metasurface structures that meet expectations. This provided a solution for enhancing polarizer performance metrics and facilitating the efficient design of metasurface polarizers.
2. Design of the Metasurface Polarizer
Figure 1 depicts the metasurface polarizer designed in this paper, which is based on a silica substrate covered with a TiO2 transition layer and Si nano-pillars for manipulating the optical field. We chose silicon as the material for rectangular nano-pillars due to its higher real part of the refractive index. When light enters silicon from the air, significant refraction occurs, leading to a substantial accumulated phase shift during the propagation of light waves. This cumulative phase shift has a crucial impact on the transmission and modulation of light. Additionally, silicon provides a large contrast in orthogonal axis refractive indices, which is crucial for polarization manipulation as it determines the material’s response to light of different polarization states, offering favorable conditions for polarization manipulation of light in silicon.
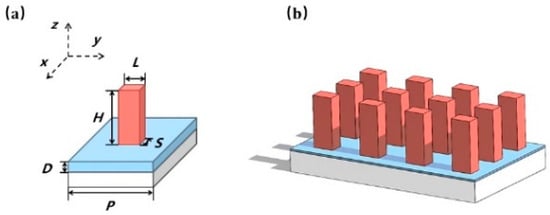
Figure 1.
The polarizer structure design discussed in this paper. (a) Metasurface structural unit; (b) metasurface polarizer.
Furthermore, the rectangular nano-pillar structure designed in this paper exhibits anisotropic characteristics, meaning its electromagnetic response to incident light in two polarization directions is different. Thus, it demonstrates sensitivity to the polarization of light, showing distinct responses to light with different polarization directions. By carefully designing the geometric parameters of the rectangular nano-pillars, namely, the period P of the unit cell, the height D of the TiO2 layer, the height H of the Si nano-pillars, the length L of the Si nano-pillars, and the width S of the Si nano-pillars, the transmittance Tx and Ty of incident light can be controlled in the x and y polarization directions, respectively. This enables the calculation of the extinction ratio with the following equation:
In summary, the rectangular nano-pillar metasurface designed in this paper can achieve the functionality of a nano-polarizer, allowing for the control of light polarization properties at the nanoscale.
In order to enhance the extinction ratio of the metasurface polarizer, we introduced a TiO2 transition layer situated between the substrate and the nano-pillars. TiO2 exhibits excellent optical properties in the visible spectrum, with a high refractive index and large dielectric constant. Additionally, it possesses stable mechanical and chemical properties [21], making it widely used as a transition layer in optical elements. In this study, TiO2 was investigated as the material for the transition layer, and the impact of the TiO2 layer thickness on the performance of the metasurface polarizer was studied in simulated experiments. While keeping other structural parameters constant, only the thickness of the TiO2 transition layer was varied, and the change in extinction ratio was observed. Figure 2a illustrates the variation curves of polarizer transmission spectra for TiO2 layer thicknesses of 0 and 20 nm, respectively. Before introducing the TiO2 transition layer, the transmittance reached a maximum of 96%. When the TiO2 layer thickness was increased to 20 nm, the maximum transmittance decreased to 90%, representing a 6% reduction. Notably, near the 429 nm wavelength, the polarizer Tx was 61.4%, and Ty was 0.3% without the added TiO2 layer. With the introduction of a 20 nm TiO2 transition layer, Tx decreased to 28.5%, and Ty decreased to 0.014%. The relative reduction of Ty was observed to be much higher than that of Tx. Figure 2b points out that also near the 429 nm wavelength, the maximum extinction ratio increased from 22 dB to 33 dB with the addition of the TiO2 layer, indicating an 11 dB improvement and a significant impact on enhanced extinction ratio performance. In general, we have succeeded in achieving more suppression of the unwanted y-polarized light compared to the desired x-polarized light by introducing an appropriate thickness of the TiO2 transition layer in the metasurface structure. As can be seen from Equation (1), this design can significantly improve the extinction ratio while ensuring that the transmittance meets the practical requirements and enabling precise control of light by the polarizer.
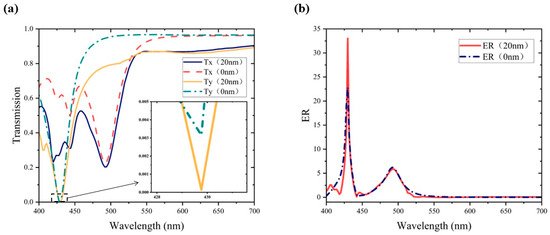
Figure 2.
Comparison of the performance of the metasurface polarizers with TiO2 layers of 0 nm and 20 nm, respectively: (a) comparison of transmission spectra; (b) comparison of extinction ratios.
3. Design Methodology Based on a Tandem Network
3.1. The Structural Framework of Neural Networks
The ResNet network is a deep residual network based on residual modules and residual connections [22]. It finds extensive applications in various domains, such as image classification [23], object detection [24], and semantic segmentation [25], among others. We observe that the deep architecture of ResNet effectively models the complex relationships between input and output, thereby improving the modeling accuracy of electromagnetic transmission characteristics. Additionally, the residual learning framework of ResNet contributes to feature learning and extraction, enabling the network to capture key features in the electromagnetic field accurately. This is crucial for metasurface design, as precise understanding and utilization of important electromagnetic features can significantly enhance the performance of the design. The adaptive nature of the ResNet structure allows it to adapt to different input sizes and complexities, providing greater flexibility for metasurface design. Therefore, this paper introduces ResNet into metasurface design.
To address the issue of multiple metasurface structural parameters corresponding to a single spectral response, this study adopts a serial network structure, connecting the forward prediction network with the inverse design network, as illustrated in Figure 3. The first half of the network represents a conventional inverse design network, while the latter half is dedicated to the metasurface spectral prediction network. The entire serial network takes the expected spectral response as input, with the intermediate layer representing the designed metasurface structural parameters and the output reflecting the spectral response of the metasurface designed by the network. The final design result does not need to precisely match the actual design results in the dataset. The loss function will be low when the spectral response generated by the designed metasurface parameters is similar to the expected spectral response.
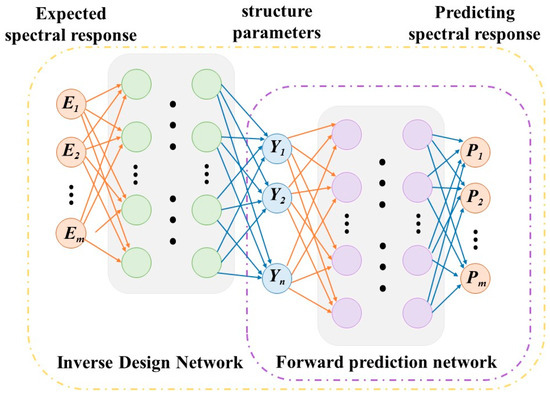
Figure 3.
Tandem inverse design network model.
This paper achieved the inverse design of metasurface structural parameters by constructing a tandem network using ResNet. Due to the difference between metasurface structural datasets and image data, convolutional operations cannot be employed for feature extraction. Therefore, fully connected layers replace the original convolutional layers. Mean Squared Error (MSE) is adopted as the loss function for this task. The equation for calculating MSE is as follows:
where n is the number of samples, Ei represents the actual values, and Pi denotes the predicted values.
Additionally, the paper computes the correlation coefficient r between the predicted and simulated results as an evaluation metric for the prediction method. The closer the absolute value of the correlation coefficient is to 1, the higher the precision of the network prediction. The calculation equation for the correlation coefficient is as follows:
where Xi and Yi are the values of the actual and predicted results, respectively.
3.2. Construction of the Data Sets
To obtain the data required for training the predictive neural network, simulations of the metasurface structure were conducted using the Lumerical software and the finite-difference time-domain(FDTD) method [25]. The wavelength range of the incident light was set to 400–700 nm, with periodic boundary conditions applied along the x and y axes and a perfect matching layer implemented in the z-axis direction. Monitors were incorporated to capture the transmission spectra. The five structural parameters of the metasurface were varied within the ranges P ∈ [200, 300] nm, D ∈ [0, 50] nm, H ∈ [200, 300] nm, L ∈ [70, 200] nm, and S ∈ [10, 90] nm, with a step size of 10 nm. Random combinations of these parameters were generated, resulting in a total of 31,571 data points. Each set of parameters was simulated using the Lumerical software, obtaining corresponding transmission spectra Tx and Ty, from which 100 data points were sampled to construct the dataset. The extinction ratio was calculated using Equation (1), allowing for the simultaneous prediction of the transmittance and extinction ratios while designing the structural parameters of the metasurface.
4. Experimentation and Analysis
4.1. Forward Prediction
To achieve optimal performance in the forward prediction network, we conducted experiments with different activation functions and gradient descent algorithms to identify the most suitable design approach for this network. The first step involved building a forward prediction network for metasurfaces, where the network’s input consists of the structural parameters of the metasurface, and the output corresponds to its spectral response. Through this network, the relationship between the structural parameters and spectral response of the metasurface can be rapidly established. This enables the quick determination of the metasurface polarizer’s transmittance and extinction ratio and, more importantly, facilitates the rapid and accurate design of metasurfaces.
Activation functions play a crucial role in nonlinear transformations of data within neural networks, simulating the processing of neurons and enhancing the network’s ability to fit more complex functions, thereby improving model expressiveness and generalization capabilities. In this study, we compared three commonly used activation functions—Tanh, Sigmoid, and ReLU—and analyzed their impact on model performance. While keeping other model parameters constant, such as the number of parameters, training epochs, batch sizes, etc., we varied only the type of activation function and observed the effects on model prediction and loss function.
The Tanh function compresses input values to the range of (−1, 1), imparting stronger nonlinear characteristics to the output. However, it involves relatively high computational costs due to the need for exponential calculations. The utilization of the Tanh activation function was first explored. The predicted results, as shown in Figure 4a, indicate that the model struggled to accurately predict the spectral curve of the metasurface. The predictions were highly disordered and inaccurate, possibly indicating the occurrence of the vanishing gradient problem, where the network struggled to learn effective weight updates.
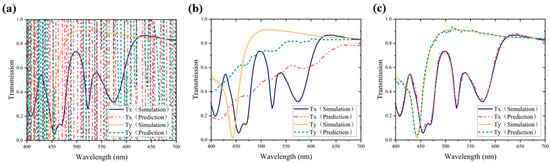
Figure 4.
Predicted results of three activation functions: (a) Tanh; (b) Sigmoid; (c) Relu.
Sigmoid compresses input values to the range of (0, 1), but it also involves higher computational costs and is prone to issues such as gradient vanishing and output saturation. When used as the activation function for the forward prediction network, the results shown in Figure 4b display two upward-trending curves that do not align well with the simulation data. At this point, the neural network still faced challenges in predicting the spectral curve. This situation may also be attributed to the vanishing gradient problem, preventing the network from learning the complex relationships within the data.
The ReLU sets negative input values to zero, leaving positive input values unchanged. It is computationally efficient, involves only threshold judgment, converges rapidly, and is not susceptible to the vanishing gradient problem. The prediction results, as shown in Figure 4c, exhibit a favorable alignment with the test outcomes. This alignment holds true even in regions characterized by significant data fluctuations, owing to the inherent advantages of the ReLU function. Consequently, we chose the ReLU function as the activation function for our metasurface spectral prediction network.
After determining the activation function, we conducted a systematic exploration incorporating four popular gradient descent algorithms with the aim of enhancing the predictive accuracy of our network model. The gradient descent algorithm is a pivotal means for determining the minimum value of the loss function. This algorithm aids in adjusting parameters within the neural network, thereby minimizing discrepancies between the network output and actual values to the greatest extent possible. Widely used gradient descent algorithms include the RMSprop optimization algorithm, the adaptive moment estimation algorithm (Adam), the stochastic gradient descent algorithm (SGD), and the adaptive learning rate optimization algorithm (Adagrad).
RMSprop, characterized by its adaptive learning rate adjustment for individual parameters, was employed to enhance optimization efficiency, with its prediction results shown in Figure 5a. Observing the prediction results reveals an extremely chaotic trend, lacking any obvious pattern. This indicates that the network fails to effectively learn the relationship between metasurface structural parameters and transmission spectra, possibly due to gradient explosions during network training, hindering RMSprop’s ability to adjust the learning rate effectively and resulting in extremely poor predictions. While Stochastic Gradient Descent (SGD) is well-suited for large-scale datasets, its convergence is characterized by a slow pace, and susceptibility to noise and outliers is pronounced. The predictions generated by SGD are depicted in Figure 5b. Although the prediction results exhibit a similar trend to the test data, the accuracy is compromised. This indicates that the network is more sensitive to capturing the general trend of data changes but struggles to predict actual values accurately. The use of the SGD gradient descent algorithm hinders capturing all patterns and relationships in the data, leading to less accurate predictions. Adagrad possesses the property of adaptively adjusting the learning rate for different types and sizes of data. Its prediction results, as shown in Figure 5c, are more accurate than the previous two methods in overall prediction, capturing the general contour of the spectral curve effectively. However, significant noise is present, and predictions are poor in the part of the curve where bending occurs. This phenomenon may be attributed to Adagrad’s sensitivity to certain parameters during the training process, resulting in noisy and unsmooth predictions in later stages when the learning rate of these parameters becomes smaller and is difficult to adapt to new data patterns. Since Adam utilizes both the first-order and the second-order moments of the gradient to adjust the learning rate for each parameter, overcoming, to some degree, some limitations of Adagrad is able to provide a more accurate prediction of the spectral curve. As shown in Figure 5d, the network’s prediction performance at this point is highly fitted and almost completely overlaps with the curve of the actual transmittance. At the peaks and troughs of the curves, the predictions also fit perfectly with the actual data. Therefore, we choose Adam as the gradient descent algorithm for the network.
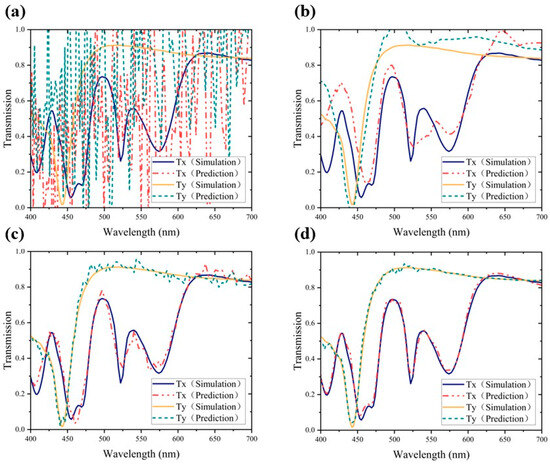
Figure 5.
Comparison of the prediction results of four gradient descent algorithms: (a) RMSprop; (b) SGD; (c) Adagrad; (d) Adam.
After determining the network’s activation function and optimization algorithm, the network undergoes 1000 rounds of training. The MSE iteration graph is shown in Figure 6. As training progressed, the MSE exhibited a robust decreasing trend, ultimately reaching a commendable performance level with a minimum value of 1.4 × 10−8.
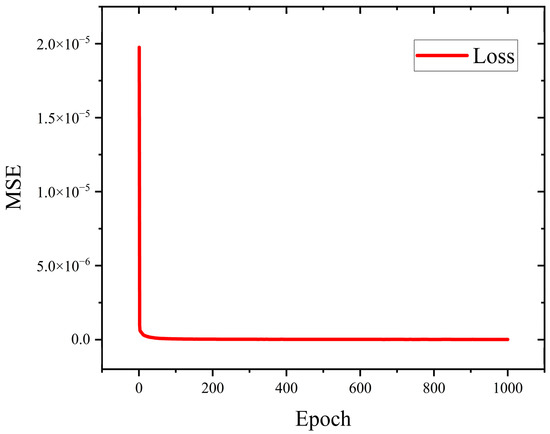
Figure 6.
MSE values.
The extinction ratio is calculated using Equation (1) and compared with simulated values, as depicted in Figure 7. The high level of fit between the predicted and simulated extinction ratios showed that the network has a precise understanding of the intricate relationships in the data. Guided by the gradually diminishing MSE values, the predictive network constructed in this study successfully captured and simulated the intricate relationship between metasurface structural parameters and spectral response data. This demonstrated its outstanding learning capability. Upon calculation, the correlation coefficient (r) between the predicted values of the ResNet network and the simulated values reached 0.996. It is evident that a strong positive correlation exists between the actual values and the predicted values, indicating a high level of accuracy in the forward network predictions. The trained network can predict the corresponding spectral response within 0.8 s. In contrast, utilizing Lumerical FDTD requires an average simulation time of 2 min and 36 s. The efficiency improvement of the network in predicting metasurface performance can be calculated through Equation (4) as 99.48%.
TFDTD stands for the simulation time using Lumerical FDTD, while TNetwork represents the time expended on spectral prediction using the forward network. The efficiency enhancement of the network is denoted by η.
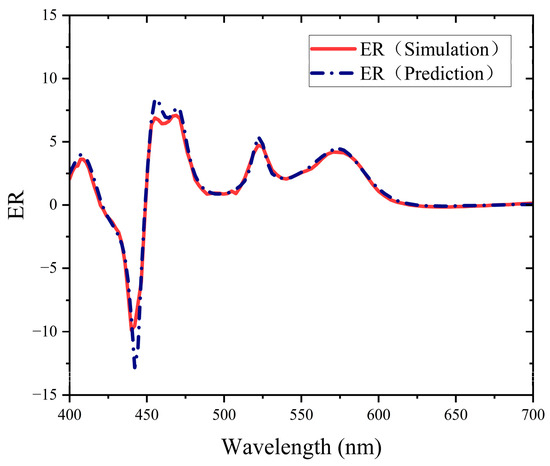
Figure 7.
Comparison of extinction ratio prediction.
Deep neural networks are commonly employed for the prediction and design of metasurfaces. A deep neural network (DNN) is constructed and compared with ResNet, with the same number of hidden layers and nodes. The conditions for training and testing, including the dataset, activation function, and optimization function, are also the same. Figure 8a,b show the DNN prediction of the transmission spectrum and extinction ratio compared with the simulation results, respectively. The DNN network shows an overall upward trend in predicting the transmittance spectrum, but its predicted values significantly differ from the simulated data. Significant differences are also observed by calculating the extinction ratio predicted by the DNN and comparing it with the simulation results, indicating that the network has not learned the relationship between the data. These results indicate that, under similar conditions, the predictive performance of the DNN in our study lags far behind that of ResNet. This is because DNN tends to encounter the issue of vanishing gradients in deep networks, making it challenging for the network to learn. In contrast, ResNet introduces residual blocks that partially alleviate the problem of vanishing gradients through cross-layer connections. This makes the network more adept at capturing complex features in the data, resulting in improved performance in predictive tasks.
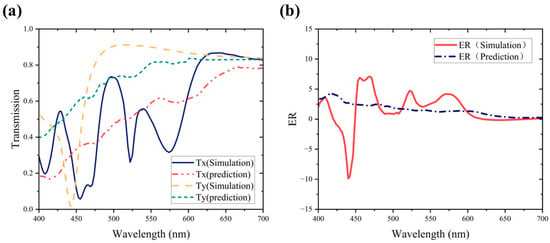
Figure 8.
Forward prediction results of DNN with similar structures: (a) transmittance spectrum; (b) extinction ratio.
4.2. Inverse Design
After successfully establishing the forward prediction network, its weights were fixed, and a complete metasurface inverse design network was constructed. Subsequently, the entire concatenated network was trained using the same activation function and optimization algorithm as the forward prediction network. After 1000 rounds of training, the loss function was only 1.18 × 10−5, and the correlation coefficient between the training data and the network’s predicted results reached 0.9999. A comparison between the metasurface structural parameters designed by the network and the validation set is shown in Figure 9a. The predicted structural parameters by the network exhibit minimal differences compared to the actual values, ranging from a minimum of 0.32 nm to a maximum of 2.56 nm. The impact on the spectral response is almost negligible. It can be seen that the inverse design network we constructed performs well in the design of metasurface structural parameters.
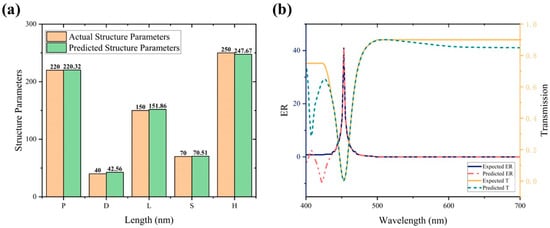
Figure 9.
Inverse Prediction Network Results: (a) Comparison of the actual structure parameters and the predicted structure parameters from the trained inverse networks; (b) comparison between expected and predicted spectral responses.
Finally, we input the desired spectral response data into the inverse design network, which outputs the corresponding metasurface structure parameters: a period of 290 nm, nanorod length of 70 nm, width of 50 nm, height of 260 nm, and TiO2 layer thickness of 10 nm. The metasurface structure designed through the network is simulated using Lumerical FDTD software to obtain its spectral response, and the extinction ratio is calculated for comparison with our specified target. As illustrated in Figure 9b, the solid lines represent our expected transmittance and extinction ratio, while the dashed lines represent the transmittance and extinction ratio of the metasurface structure designed by the network. The final designed metasurface polarizer achieves a maximum transmittance of 90%, and the extinction ratio reaches up to 40 dB. This closely aligns with our specified targets, meeting our expectations.
5. Conclusions
To address the challenge of simultaneously achieving high transmittance and extinction ratios in existing design methods, this paper introduced a more targeted metasurface polarizer structure and its design method by adding a TiO2 transition layer to the metasurface structure and splitting the transmittance and extinction ratios into transmission spectra Tx and Ty. With the desired metrics inputted into the tandem network, we successfully designed a metasurface polarizer with a maximum transmittance of 90% and an extinction ratio of 40 dB, thus verifying the validity of our effectiveness of the proposed method. Compared to traditional simulation methods, our design method improved the efficiency of predicting metasurface performance metrics by 99.48%, which enables even researchers with little experience in optical device design to quickly design a metasurface polarizer that meets their expectations and helps to drive the rapid development of the metasurface.
Author Contributions
Conceptualization, S.W. and Y.H.; methodology, S.W.; software, S.W.; validation, S.W.; data curation, H.Z. and H.W.; writing—original draft preparation, S.W.; writing—review and editing, Y.H.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China, grant number 2020YFA0711200.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Z.G.; Dong, F.L.; Cheng, T.; Qian, K.M.; Qiu, K.; Zhang, Q.C.; Chu, W.G.; Wu, X.P. Electron Beam Lithographic Pixelated Micropolarizer Array for Real-Time Phase Measurement. Chin. Phys. Lett. 2014, 31, 114208. [Google Scholar] [CrossRef]
- Gao, S.K.; Mondal, S.B.; Zhu, N.; Liang, R.G.; Achilefu, S.; Gruev, V. Image overlay solution based on threshold detection for a compact near infrared fluorescence goggle system. J. Biomed. Opt. 2015, 20, 016018. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, M.; Gruev, V. Integrated spectral-polarization imaging sensor with aluminum nanowire polarization filters. Opt. Express 2012, 20, 22997–23012. [Google Scholar] [CrossRef] [PubMed]
- Giordano, M.C.; Longhi, S.; Barelli, M.; Mazzanti, A.; Mongeot, F.B.; Valle, G.D. Plasmon hybridization engineering in self-organized anisotropic metasurfaces. Nano Res. 2018, 11, 3943–3956. [Google Scholar] [CrossRef]
- Gao, S.; Zhou, C.Y.; Yue, W.J.; Li, Y.; Zhang, C.W.; Kan, H.; Li, C.; Lee, S.S.; Choi, D.Y. Efficient All-Dielectric Diatomic Metasurface for Linear Polarization Generation and 1-Bit Phase Control. ACS Appl. Mater. Interfaces 2021, 13, 14497–14506. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Chang, B.D.; Wei, Q.S.; Huang, L.L.; Guan, X.W.; Bozhevolnyi, S.I. Versatile Polarization Generation and Manipulation Using Dielectric Metasurfaces. Laser Photonics Rev. 2020, 14, 2000116. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef]
- Wan, W.Q.; Wen, Q.; Pu, D.L.; Li, R.B.; Wang, C.H.; Hu, Y.Q.; Duan, H.G.; Guo, L.J.; Chen, L.S. Holographic Sampling Display Based on Metagratings. iScience 2020, 23, 100773. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, M.Z.; Liao, T.D.; Cui, X.D. Design of beam deflector, splitters, wave plates and metalens using photonic elements with dielectric metasurface. Opt. Commun. 2018, 411, 93–100. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Arbouet, A.; Girard, C.; Muskens, O.L. Deep learning in nano-photonics: Inverse design and beyond. Photonics Res. 2021, 9, B182–B200. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, M.K.; Fan, J.A. Deep neural networks for the evaluation and design of photonic devices. Nat. Rev. Mater. 2021, 6, 679–700. [Google Scholar] [CrossRef]
- Qiu, T.S.; Shi, X.; Wang, J.; Li, Y.; Qu, S.; Cheng, Q.; Cui, T.; Sui, S. Deep Learning: A Rapid and Efficient Route to Automatic Metasurface Design. Adv. Sci. 2019, 6, 1900128. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.C.; Wang, D.S.; Qin, J.; Li, J.; Ye, H.; Zhang, Z.G.; Chen, X.; Zhang, M.; Boucouvalas, A.C. Physical Information-Embedded Deep Learning for Forward Prediction and Inverse Design of Nanophotonic Devices. J. Light. Technol. 2021, 39, 6498–6508. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, Z.X.; Wang, J.K.; Zhou, J.; Zhang, M. Prediction of metasurface spectral response based on a deep neural network. Opt. Lett. 2022, 47, 5092–5095. [Google Scholar] [CrossRef] [PubMed]
- Tanriover, I.; Hadibrata, W.; Scheuer, J.; Aydin, K. Neural networks enabled forward and inverse design of reconfigurable metasurfaces. Opt. Express 2021, 29, 27219–27227. [Google Scholar] [CrossRef]
- Deng, W.Q.; Xu, Z.J.; Wang, J.H.; Lv, J.W. Long short-term memory neural network for directly inverse design of nanofin metasurface. Opt. Lett. 2022, 47, 3239–3242. [Google Scholar] [CrossRef]
- Liu, D.J.; Tan, Y.X.; Khoram, E.; Yu, Z.F. Training Deep Neural Networks for the Inverse Design of Nanophotonic Structures. ACS Photonics 2018, 5, 1365–1369. [Google Scholar] [CrossRef]
- Liu, K.Z.; Sun, C.S. Metasurface design with a complex residual neural network. Appl. Opt. 2023, 62, 1200–1205. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Muskens, O.L. Deep Learning Meets Nanophotonics: A Generalized Accurate Predictor for Near Fields and Far Fields of Arbitrary 3D Nanostructures. Nano Lett. 2020, 20, 329–338. [Google Scholar] [CrossRef]
- Xu, Z.J.; Dong, Y.; Tseng, C.K.; Hu, T.; Tong, J.C.; Zhong, Q.Z.; Li, N.X.; Sim, L.; Lai, K.H.; Lin, Y.; et al. CMOS-compatible all-Si metasurface polarizing bandpass filters on 12-inch wafers. Opt. Express 2019, 27, 26060–26069. [Google Scholar] [CrossRef]
- Sezgin, A.; Čtvrtlík, R.; Václavek, L.; Tomáštík, J.; Nožka, L.; Menşur, E.; Türküz, S. Optical, structural and mechanical properties of TiO2 and TiO2-ZrO2 thin films deposited on glass using magnetron sputtering. Mater. Today Commun. 2023, 35, 106334. [Google Scholar] [CrossRef]
- Shafiq, M.; Gu, Z. Deep Residual Learning for Image Recognition: A Survey. Appl. Sci. 2022, 12, 8972. [Google Scholar] [CrossRef]
- Lu, Y.; Qin, X.J.; Fan, H.Y.; Lai, T.T.; Li, Z.Y. WBC-Net: A white blood cell segmentation network based on UNet++ and ResNet. Appl. Soft. Comput. 2021, 101, 107006. [Google Scholar] [CrossRef]
- Ou, X.F.; Yan, P.C.; Zhang, Y.M.; Tu, B.; Zhang, G.Y.; Wu, J.H.; Li, W.J. Moving Object Detection Method via ResNet-18 With Encoder–Decoder Structure in Complex Scenes. IEEE Access 2019, 7, 108152–108160. [Google Scholar] [CrossRef]
- Ding, L.; Zheng, K.; Lin, D.; Chen, Y.X.; Liu, B.; Li, J.S.; Bruzzone, L. MP-ResNet: Multipath Residual Network for the Semantic Segmentation of High-Resolution PolSAR Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).