Enhanced Bolometric Detection of THz Signals by a Resonant Structure for Inclined Radiation Incidence
Abstract
:1. Introduction
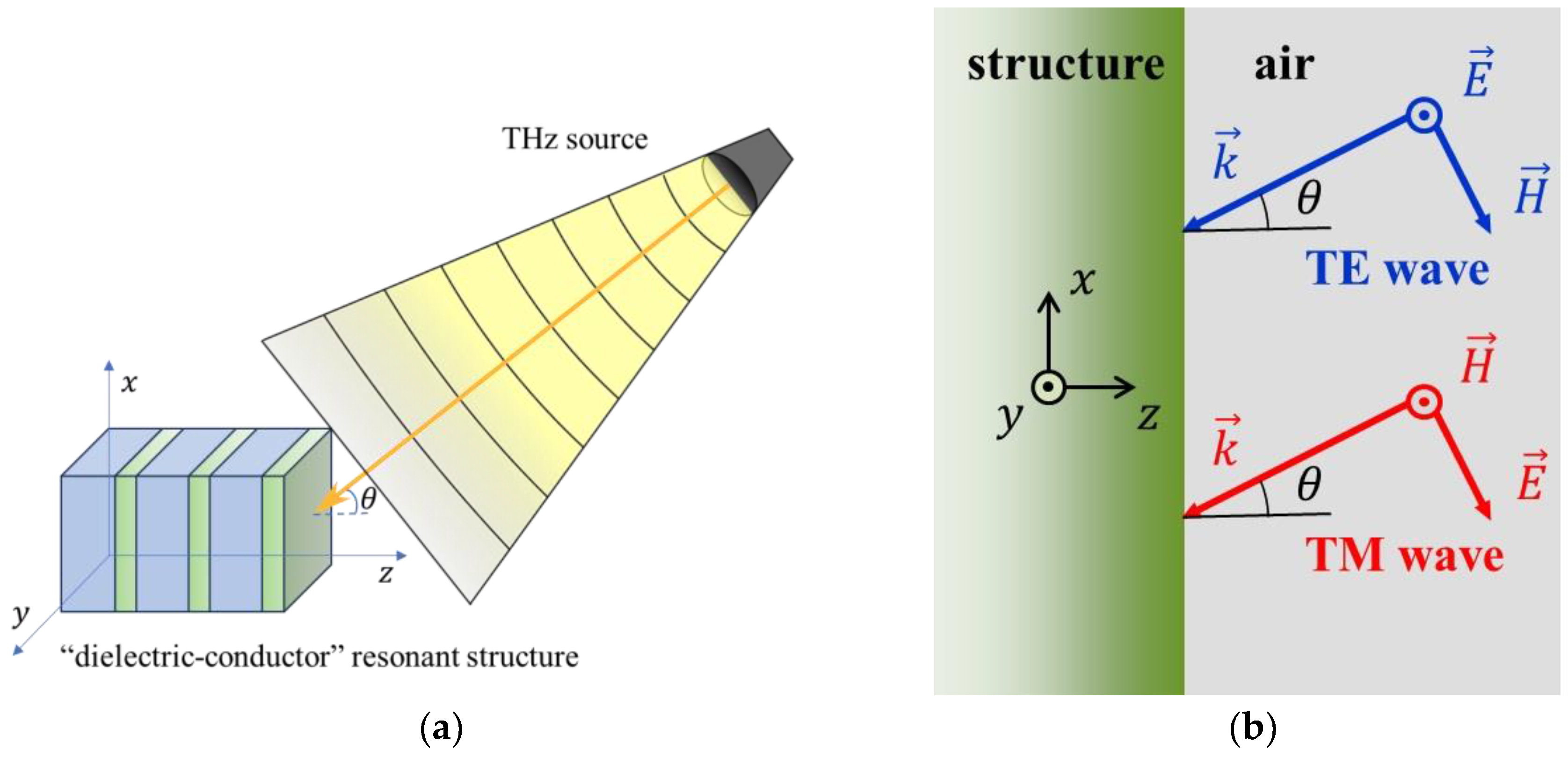
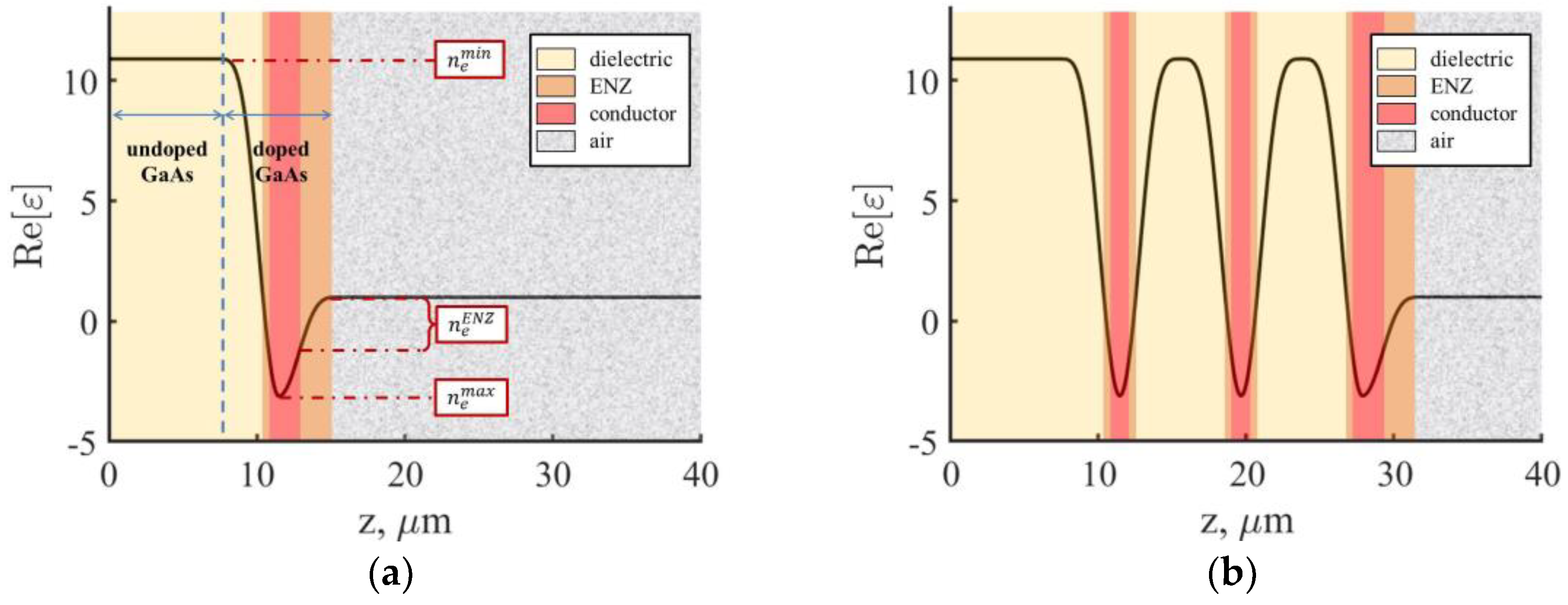
2. Modeling
3. Results and Discussion
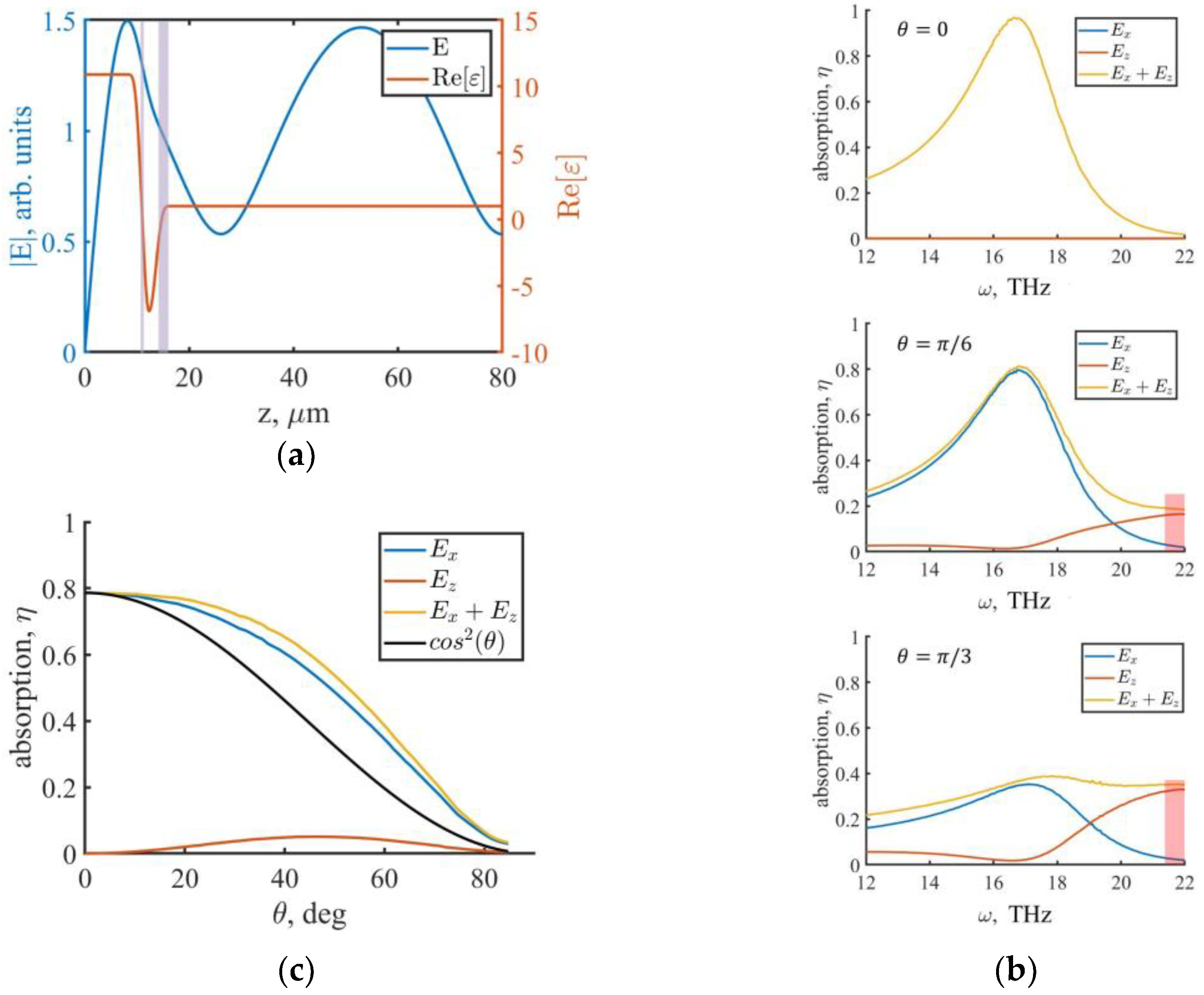
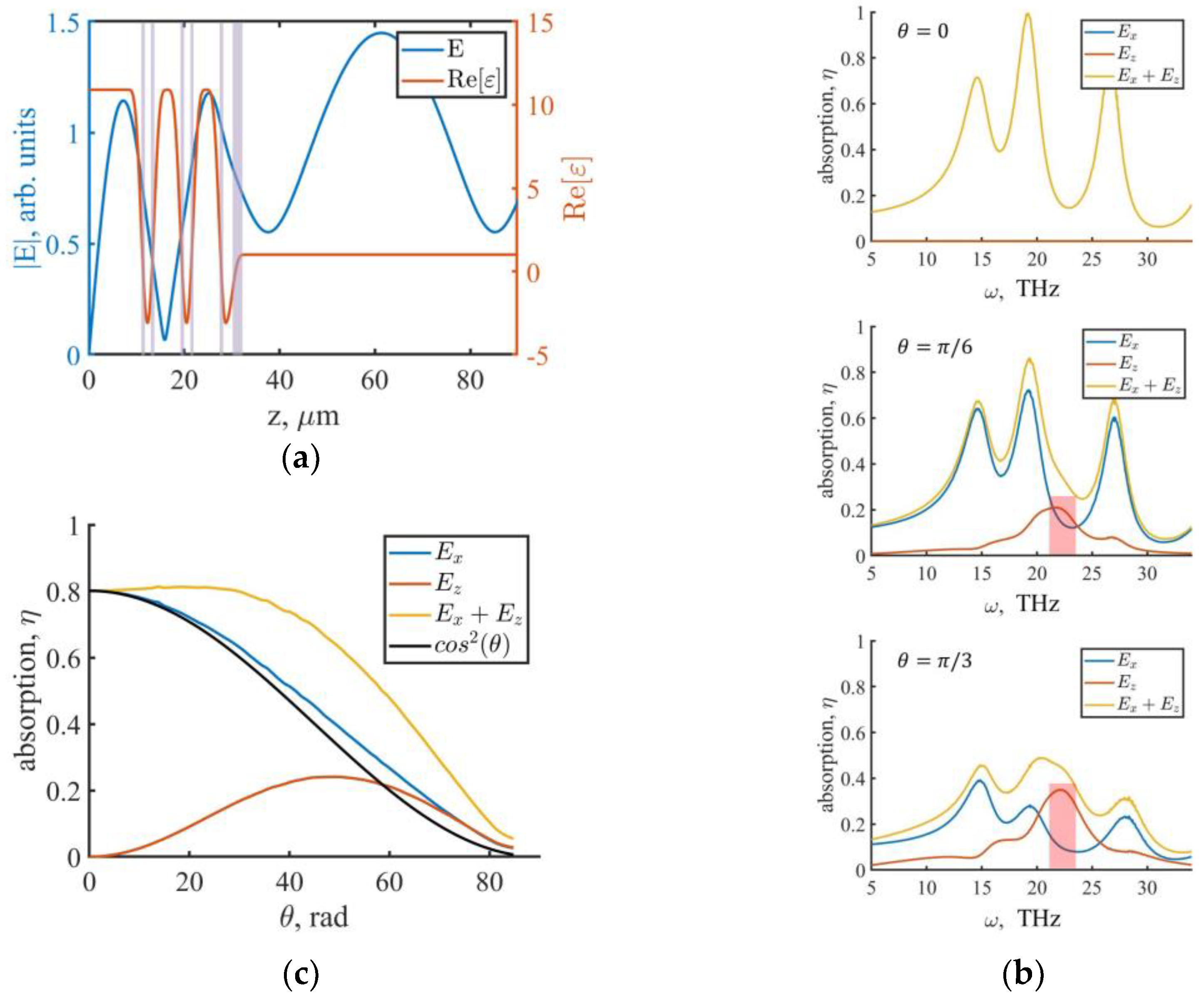
3.1. Absorption Results for the Case with One Dielectric Layer
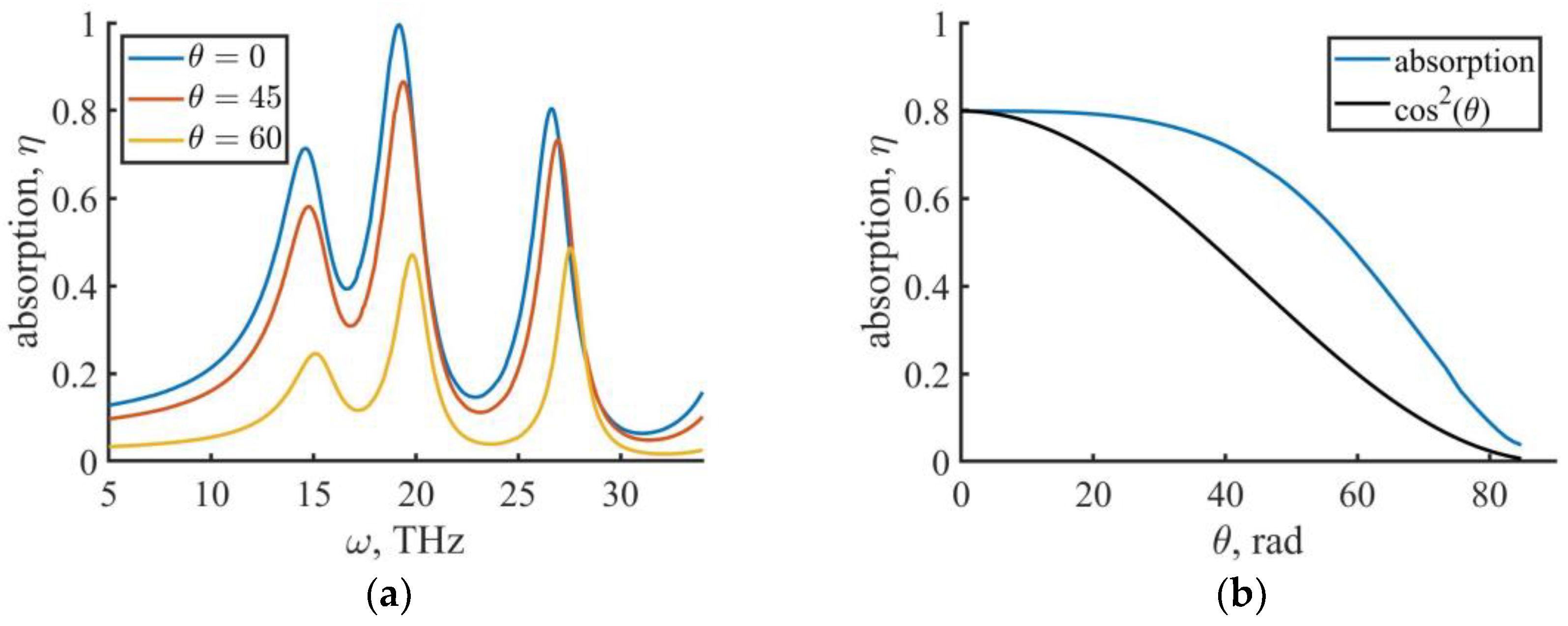
3.2. Absorption Results for the Case with Three Dielectric Layers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Ma, X.; Zhang, B.; Niu, Z.; Kuang, N.; Chen, W.; Li, L.; Li, S. A survey on terahertz communications. China Commun. 2019, 16, 1–35. [Google Scholar] [CrossRef]
- Sarieddeen, H.; Alouini, M.-S.; Al-Naffouri, T.Y. An Overview of Signal Processing Techniques for Terahertz Communications. Proc. IEEE 2021, 109, 1628–1665. [Google Scholar] [CrossRef]
- Tao, Y.H.; Fitzgerald, A.J.; Wallace, V.P. Non-Contact, Non-Destructive Testing in Various Industrial Sectors with Terahertz Technology. Sensors 2020, 20, 712. [Google Scholar] [CrossRef] [PubMed]
- Liebermeister, L.; Nellen, S.; Kohlhaas, R.; Breuer, S.; Schell, M.; Globisch, B. Ultra-fast, High-Bandwidth Coherent cw THz Spectrometer for Non-destructive Testing. J. Infrared Millim. Terahz. Waves 2019, 40, 288–296. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, C.; Xu, W.; Xie, L. Biological applications of terahertz technology based on nanomaterials and nanostructures. Nanoscale 2019, 11, 3445–3457. [Google Scholar] [CrossRef] [PubMed]
- Gong, A.; Qiu, Y.; Chen, X.; Zhao, Z.; Xia, L.; Shao, Y. Biomedical applications of terahertz technology. Appl. Spectrosc. Rev. 2020, 55, 418–438. [Google Scholar] [CrossRef]
- Ren, A.; Zahid, A.; Fan, D.; Yang, X.; Imran, M.A.; Alomainy, A.; Abbasi, Q.H. State-of-the-art in terahertz sensing for food and water security—A comprehensive review. Trends Food Sci. Technol. 2019, 85, 241–251. [Google Scholar] [CrossRef]
- Tzydynzhapov, G.; Gusikhin, P.; Muravev, V.; Dremin, A.; Nefyodov, Y.; Kukushkin, I. New Real-Time Sub-Terahertz Security Body Scanner. J. Infrared Millim. Terahz. Waves 2020, 41, 632–641. [Google Scholar] [CrossRef]
- Stantchev, R.I.; Yu, X.; Blu, T.; Pickwell-MacPherson, E. Real-time terahertz imaging with a single-pixel detector. Nat. Commun. 2020, 11, 2535. [Google Scholar] [CrossRef]
- Valušis, G.; Lisauskas, A.; Yuan, H.; Knap, W.; Roskos, H.G. Roadmap of Terahertz Imaging 2021. Sensors 2021, 21, 4092. [Google Scholar] [CrossRef]
- Zhang, Y.; Hosono, S.; Nagai, N.; Song, S.H.; Hirakawa, K. Fast and sensitive bolometric terahertz detection at room temperature through thermomechanical transduction. J. Appl. Phys. 2019, 125, 151602. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, Z.; Tang, W.; Xu, X. Design and fabrication of low-deformation micro-bolometers for THz detectors. Infrared Phys. Technol. 2020, 105, 103241. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, D.; Lee, S.H.; Seo, M.; Jung, H.-J.; Kang, B.; Lee, S.-M.; Lee, H.-J. Single-layer metamaterial bolometer for sensitive detection of low-power terahertz waves at room temperature. Opt. Express 2020, 28, 17143–17152. [Google Scholar] [CrossRef] [PubMed]
- Ryger, I.; Lobotka, P.; Steiger, A.; Chromik, S.; Lalinsky, T.; Raida, Z.; Pítra, K.; Zehetner, J.; Spankova, M.; Gazi, S.; et al. Uncooled Antenna-Coupled Microbolometer for Detection of Terahertz Radiation. J. Infrared Millim. Terahz. Waves 2021, 42, 462–478. [Google Scholar] [CrossRef]
- Jin, M.; Wang, Y.; Chai, M.; Chen, C.; Zhao, Z.; He, T. Terahertz detectors based on carbon nanomaterials. Adv. Funct. Mater. 2022, 32, 2107499. [Google Scholar] [CrossRef]
- Perenzoni, M.; Paul, D.J. (Eds.) Physics and Applications of Terahertz Radiation; Springer: New York, NY, USA, 2014; Volume 173, p. 36. [Google Scholar] [CrossRef]
- Bogatskaya, A.V.; Klenov, N.V.; Popov, A.M.; Tereshonok, M.V. Resonance Tunneling of Electromagnetic Waves for Enhancing the Efficiency of Bolometric Photodetectors. Tech. Phys. Lett. 2018, 44, 667–670. [Google Scholar] [CrossRef]
- Schegolev, A.E.; Popov, A.M.; Bogatskaya, A.V.; Nikiforova, P.M.; Tereshonok, M.V.; Klenov, N.V. Detection of Terahertz, Mid- and Near Infrared Radiation by a Multilayer Metal—Insulator Heterostructure. JETP Lett. 2020, 111, 371–375. [Google Scholar] [CrossRef]
- Bogatskaya, A.V.; Klenov, N.V.; Nikiforova, P.M.; Popov, A.M.; Schegolev, A.E. Resonant Bolometric Detection of Broadband Terahertz Signals. Tech. Phys. Lett. 2021, 47, 838–842. [Google Scholar] [CrossRef]
- Bogatskaya, A.V.; Klenov, N.V.; Nikiforova, P.M.; Popov, A.M.; Schegolev, A.E. Features of propagation and absorption of electromagnetic signals in periodic structures of conducting and dielectric layers. Opt. Spectrosc. 2022, 130, 385. [Google Scholar] [CrossRef]
- Luk, T.S.; Campione, S.; Kim, I.; Feng, S.; Jun, Y.C.; Liu, S.; Wright, J.B.; Brener, I.; Catrysse, P.B.; Fan, S.; et al. Directional perfect absorption using deep subwavelength low-permittivity films. Phys. Rev. B 2014, 90, 085411. [Google Scholar] [CrossRef]
- Anopchenko, A.; Tao, L.; Arndt, C.; Lee, H.W.H. Field-effect tunable and broadband epsilon-near-zero perfect absorbers with deep subwavelength thickness. ACS Photonics 2018, 5, 2631–2637. [Google Scholar] [CrossRef]
- Wu, J.; Xie, Z.T.; Sha, Y.; Fu, H.Y.; Li, Q. Epsilon-near-zero photonics: Infinite potentials. Photonics Res. 2021, 9, 1616–1644. [Google Scholar] [CrossRef]
- Reshef, O.; De Leon, I.; Alam, M.Z.; Boyd, R.W. Nonlinear optical effects in epsilon-near-zero media. Nat. Rev. Mater. 2019, 4, 535–551. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media, 2nd ed.; Pergamon Press: Oxford, UK, 1985; pp. 304–305. [Google Scholar]
- GaAs—Gallium Arsenide. Available online: https://www.ioffe.ru/SVA/NSM/Semicond/GaAs/bandstr.html (accessed on 29 September 2023).
- Maremyanin, K.V.; Parshin, V.V.; Serov, E.A.; Rumyantsev, V.V.; Kudryavtsev, K.E.; Dubinov, A.A.; Fokin, A.P.; Morosov, S.S.; Aleshkin, V.Y.; Glyavin, M.Y.; et al. Investigation into Microwave Absorption in Semiconductors for Frequency-Multiplication Devices and Radiation-Output Control of Continuous and Pulsed Gyrotrons. Semiconductors 2020, 54, 1069–1074. [Google Scholar] [CrossRef]
- Bogatskaya, A.V.; Schegolev, A.E.; Klenov, N.V.; Lobov, E.M.; Tereshonok, M.V.; Popov, A.M. Issues with Modeling a Tunnel Communication Channel through a Plasma Sheath. Sensors 2022, 22, 398. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikiforova, P.; Bogatskaya, A.; Popov, A. Enhanced Bolometric Detection of THz Signals by a Resonant Structure for Inclined Radiation Incidence. Photonics 2024, 11, 42. https://doi.org/10.3390/photonics11010042
Nikiforova P, Bogatskaya A, Popov A. Enhanced Bolometric Detection of THz Signals by a Resonant Structure for Inclined Radiation Incidence. Photonics. 2024; 11(1):42. https://doi.org/10.3390/photonics11010042
Chicago/Turabian StyleNikiforova, Polina, Anna Bogatskaya, and Alexander Popov. 2024. "Enhanced Bolometric Detection of THz Signals by a Resonant Structure for Inclined Radiation Incidence" Photonics 11, no. 1: 42. https://doi.org/10.3390/photonics11010042
APA StyleNikiforova, P., Bogatskaya, A., & Popov, A. (2024). Enhanced Bolometric Detection of THz Signals by a Resonant Structure for Inclined Radiation Incidence. Photonics, 11(1), 42. https://doi.org/10.3390/photonics11010042




