Improvement in Signal Phase Detection Using Deep Learning with Parallel Fully Connected Layers
Abstract
:1. Introduction
2. Methods
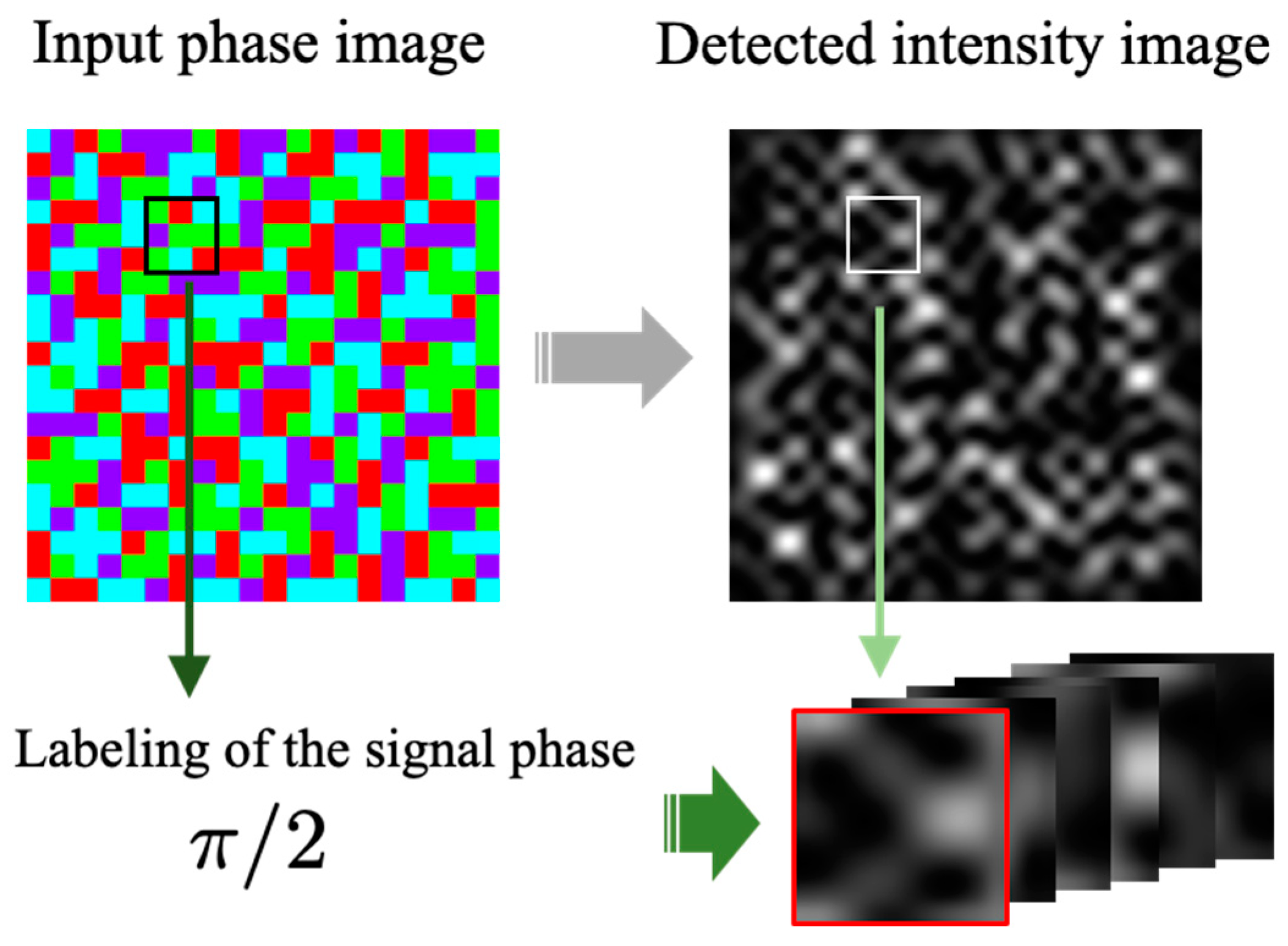
2.1. Principle of Phase Detection Using Interpixel Crosstalk
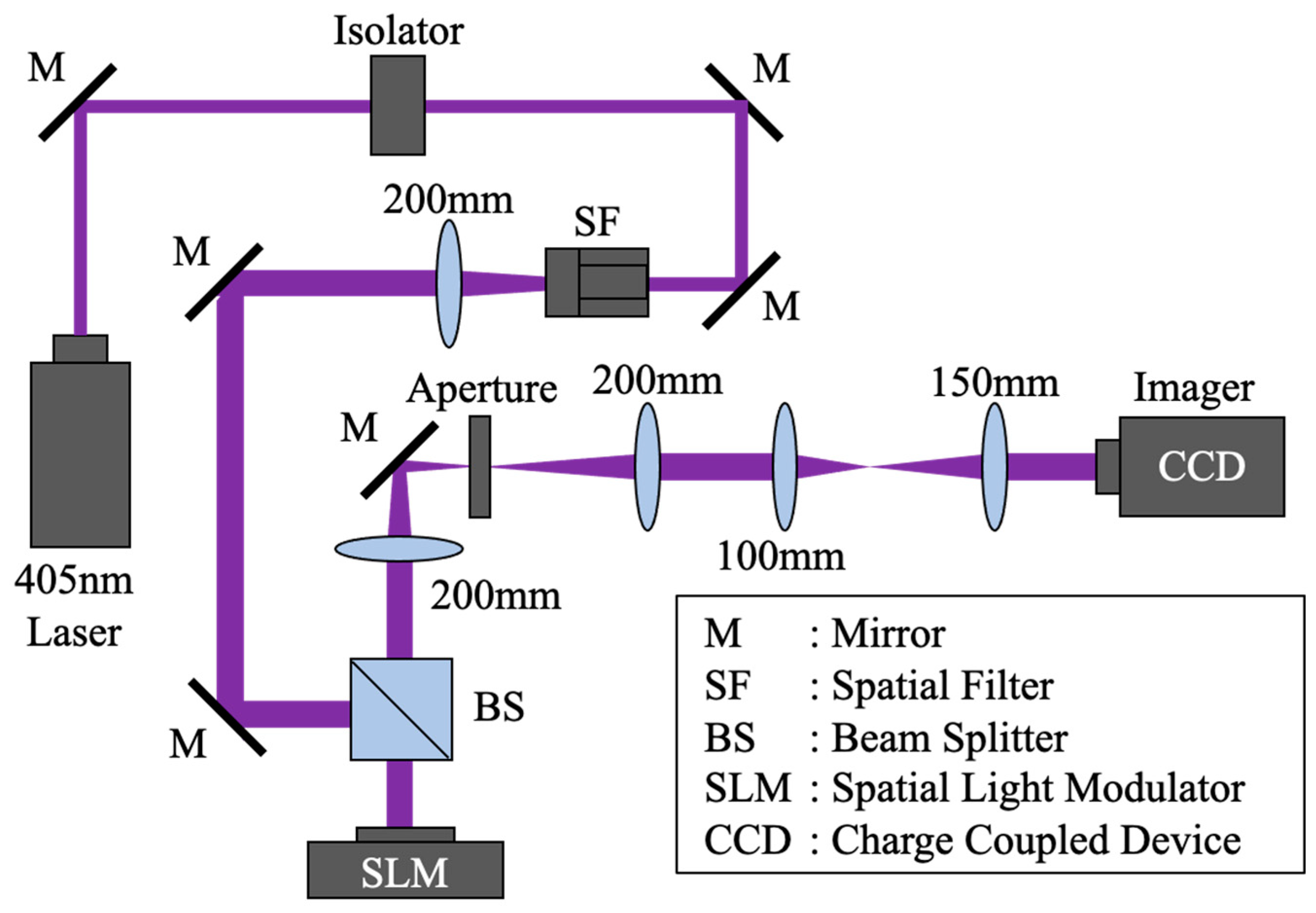
2.2. Acquisition of Experimental Training Data
2.3. Structure of the Neural Network
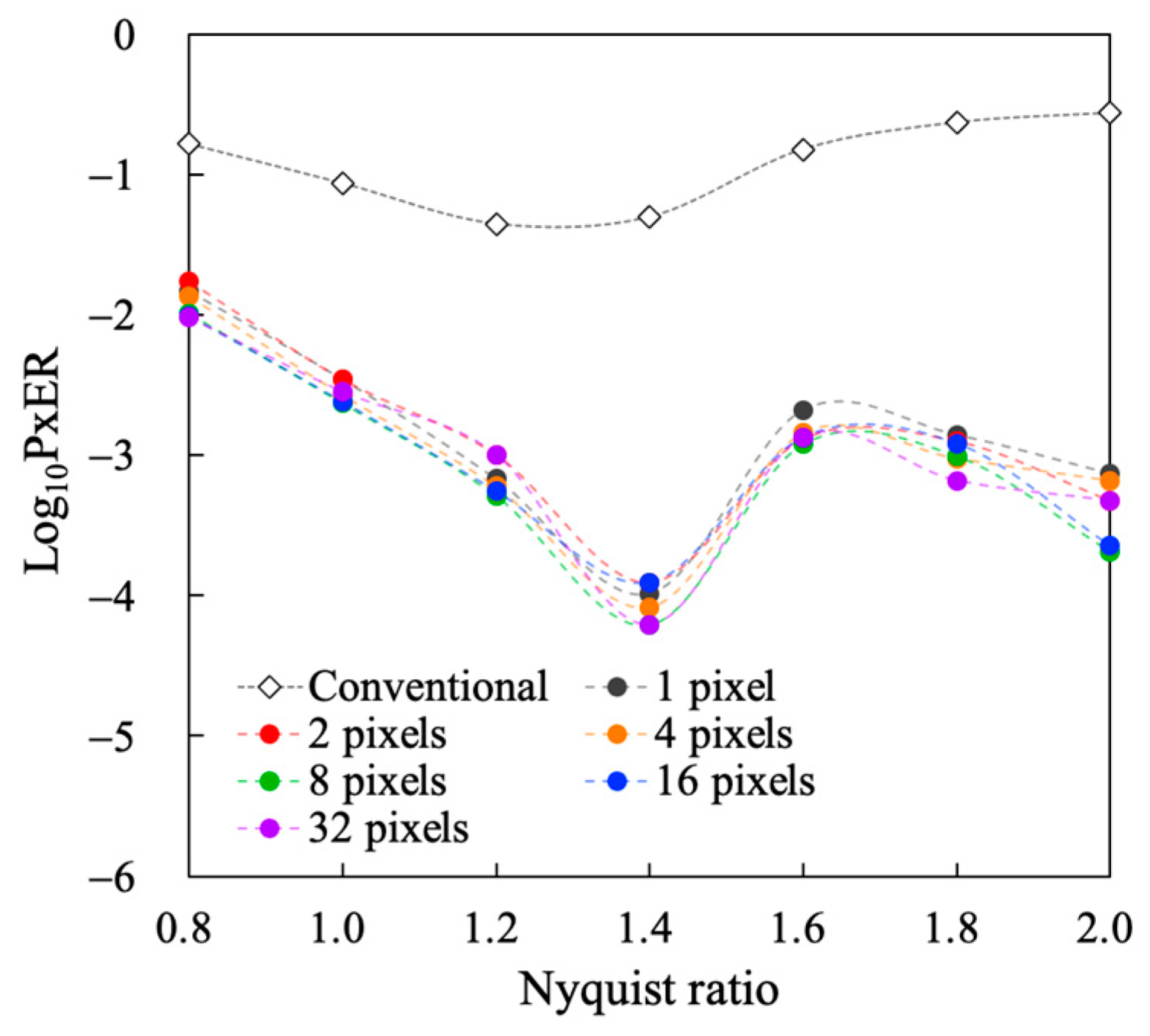
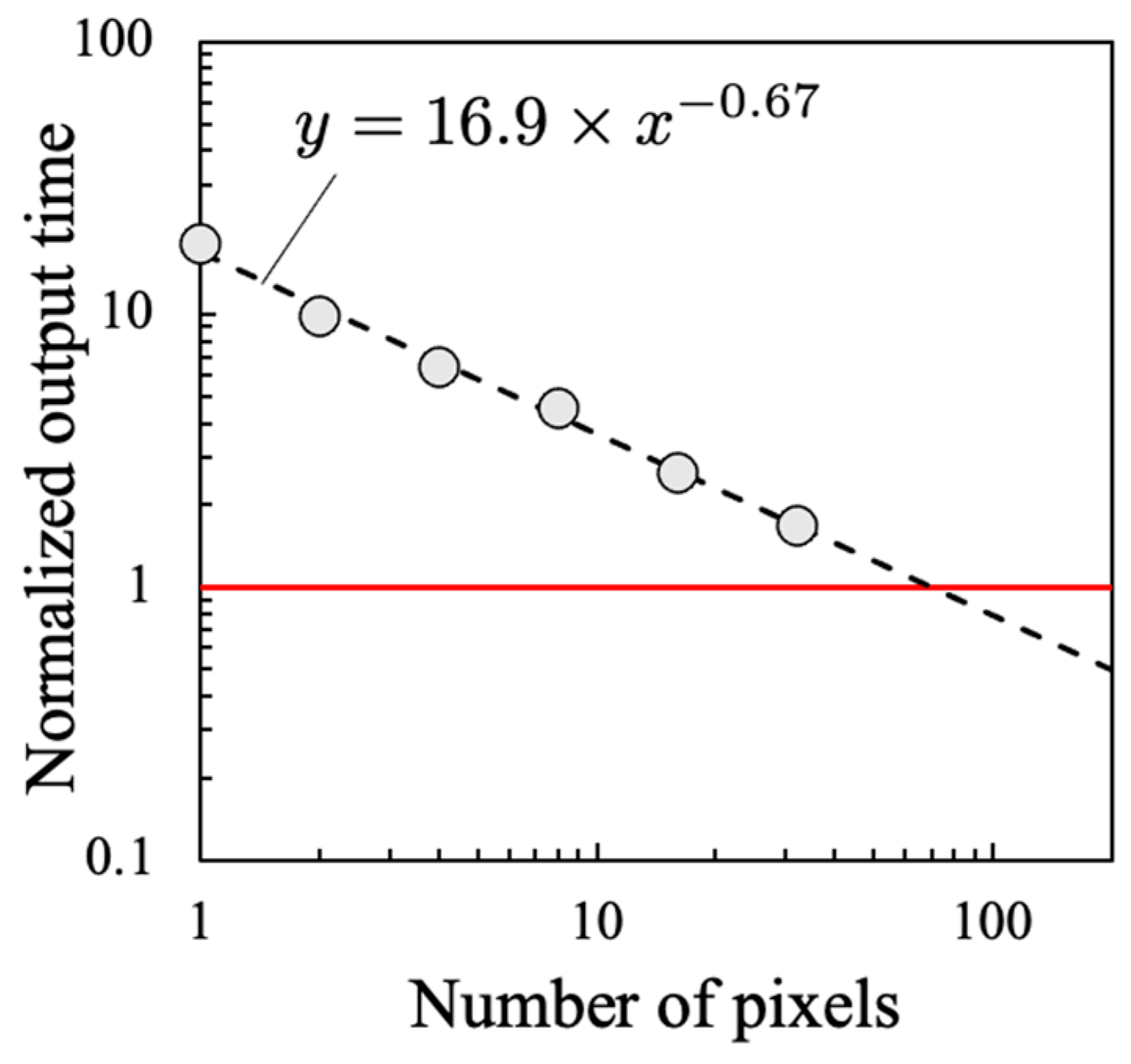
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- van Heerden, P.J. Theory of optical information storage in solids. Appl. Opt. 1963, 2, 393–400. [Google Scholar] [CrossRef]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777. [Google Scholar] [CrossRef]
- Orlov, S.S.; Phillips, W.; Bjornson, E.; Takashima, Y.; Sundaram, P.; Hesselink, L.; Okas, R.; Kwan, D.; Snyder, R. High-transfer-rate high-capacity holographic disk data-storage system. Appl. Opt. 2004, 43, 4902–4914. [Google Scholar] [CrossRef]
- Denz, C.; Pauliat, G.; Roosen, G.; Tschudi, T. Volume hologram multiplexing using a deterministic phase encoding method. Opt. Commun. 1991, 85, 171–176. [Google Scholar] [CrossRef]
- Rakuljic, G.A.; Leyva, V.; Yariv, A. Optical data storage using orthogonal wavelength multiplexed volume holograms. Opt. Lett. 1992, 17, 1471. [Google Scholar] [CrossRef]
- Mok, F.H. Angle-multiplexed storage of 5000 holograms in lithium niobate. Opt. Lett. 1993, 18, 915. [Google Scholar] [CrossRef]
- Curtis, K.; Pu, A.; Psaltis, D. Method for holographic storage using peristrophic multiplexing. Opt. Lett. 1994, 19, 993–994. [Google Scholar] [CrossRef]
- Psaltis, D.; Levene, M.; Pu, A.; Barbastathis, G.; Curtis, K. Holographic storage using shift multiplexing. Opt. Lett. 1995, 20, 782–784. [Google Scholar] [CrossRef]
- Barbastathis, G.; Levene, M.; Psaltis, D. Shift multiplexing with spherical reference waves. Appl. Opt. 1996, 35, 2403–2417. [Google Scholar] [CrossRef]
- Barbastathis, G.; Psaltis, D. Shift-multiplexed holographic memory using the two-lambda method. Opt. Lett. 1996, 21, 432–434. [Google Scholar] [CrossRef]
- Chuang, E.; Psaltis, D. Storage of 1000 holograms with use of a dual-wavelength method. Appl. Opt. 1997, 36, 8445–8454. [Google Scholar] [CrossRef] [PubMed]
- Anderson, K.; Curtis, K. Polytopic multiplexing. Opt. Lett. 2004, 29, 1402–1404. [Google Scholar] [CrossRef] [PubMed]
- Hoshizawa, T.; Shimada, K.; Fujita, K.; Tada, Y. Practical angular-multiplexing holographic data storage system with 2 terabyte capacity and 1 gigabit transfer rate. Jpn. J. Appl. Phys. 2016, 55, 09SA06. [Google Scholar] [CrossRef]
- John, R.; Joseph, J.; Singh, K. Holographic digital data storage using phase-modulated pixels. Opt. Lasers Eng. 2005, 43, 183–194. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, S.; Kam, P.Y.; Chen, J. Bit-error rate performance of coherent optical M-ary PSK/QAM using decision-aided maximum likelihood phase estimation. Opt. Express 2010, 18, 12088–12103. [Google Scholar] [CrossRef]
- Takabayashi, M.; Okamoto, A.; Tomita, A.; Bunsen, M. Symbol error characteristics of hybrid-modulated holographic data storage by intensity and multi phase modulation. Jpn. J. Appl. Phys. 2011, 50, 09ME05. [Google Scholar] [CrossRef]
- Nakamura, Y.; Fujimura, R. Wavelength diversity detection for phase-modulation holographic data storage system. Jpn. J. Appl. Phys. 2020, 59, 012004. [Google Scholar] [CrossRef]
- Schwider, J.; Burow, R.; Elssner, K.E.; Grzanna, J.; Spolaczyk, R.; Merkel, K. Digital wave-front measuring interferometry: Some systematic error sources. Appl. Opt. 1983, 22, 3421. [Google Scholar] [CrossRef]
- Tokoro, M.; Fujimura, R. Single-shot detection of four-level phase modulated signals using inter-pixel crosstalk for holographic data storage. Jpn. J. Appl. Phys. 2021, 60, 022004. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep convolutional neural networks for image classification: A comprehensive review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef] [PubMed]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems 2, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; pp. 3104–3112. [Google Scholar]
- Chen, H.; Engkvist, O.; Wang, Y.; Olivecrona, M.; Blaschke, T. The rise of deep learning in drug discovery. Drug Discov. Today 2018, 23, 1241–1250. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Lin, X.; Lin, Y.; Chen, M.; Chen, R.; Situ, G.; Horimai, H.; Tan, X. Lensless complex amplitude demodulation based on deep learning in holographic data storage. OEA 2023, 6, 220157. [Google Scholar] [CrossRef]
- Hao, J.; Lin, X.; Chen, R.; Lin, Y.; Liu, H.; Song, H.; Lin, D.; Tan, X. Phase retrieval combined with the deep learning denoising method in holographic data storage. Opt. Contin. 2022, 1, 51. [Google Scholar] [CrossRef]
- Shimobaba, T.; Kuwata, N.; Homma, M.; Takahashi, T.; Nagahama, Y.; Sano, M.; Hasegawa, S.; Hirayama, R.; Kakue, T.; Shiraki, A.; et al. Convolutional neural network-based data page classification for holographic memory. Appl. Opt. 2017, 56, 7327–7330. [Google Scholar] [CrossRef]
- Katano, Y.; Muroi, T.; Kinoshita, N.; Ishii, N.; Hayashi, N. Data demodulation using convolutional neural networks for holographic data storage. Jpn. J. Appl. Phys. 2018, 57, 09SC01. [Google Scholar] [CrossRef]
- Hao, J.; Lin, X.; Lin, Y.; Song, H.; Chen, R.; Chen, M.; Wang, K.; Tan, X. Lensless phase retrieval based on deep learning used in holographic data storage. Opt. Lett. 2021, 46, 4168–4171. [Google Scholar] [CrossRef]
- Lee, S.H.; Lim, S.Y.; Kim, N.; Park, N.C.; Yang, H.; Park, K.S.; Park, Y.P. Increasing the storage density of a page-based holographic data storage system by image upscaling using the PSF of the Nyquist aperture. Opt. Express 2011, 19, 12053–12065. [Google Scholar] [CrossRef]
- Lin, X.; Hao, J.; Wang, K.; Zhang, Y.; Li, H.; Tan, X. Frequency expanded non-interferometric phase retrieval for holographic data storage. Opt. Express 2020, 28, 511–518. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, L.J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]


| Number of Fully Connected Layers | Input Image Size |
|---|---|
| 1 | 3 × 3 data pixels |
| 2 | 4 × 4 data pixels |
| 4 | 4 × 6 data pixels |
| 8 | 6 × 6 data pixels |
| 16 | 6 × 10 data pixels |
| 32 | 10 × 10 data pixels |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tokoro, M.; Fujimura, R. Improvement in Signal Phase Detection Using Deep Learning with Parallel Fully Connected Layers. Photonics 2023, 10, 1006. https://doi.org/10.3390/photonics10091006
Tokoro M, Fujimura R. Improvement in Signal Phase Detection Using Deep Learning with Parallel Fully Connected Layers. Photonics. 2023; 10(9):1006. https://doi.org/10.3390/photonics10091006
Chicago/Turabian StyleTokoro, Michito, and Ryushi Fujimura. 2023. "Improvement in Signal Phase Detection Using Deep Learning with Parallel Fully Connected Layers" Photonics 10, no. 9: 1006. https://doi.org/10.3390/photonics10091006
APA StyleTokoro, M., & Fujimura, R. (2023). Improvement in Signal Phase Detection Using Deep Learning with Parallel Fully Connected Layers. Photonics, 10(9), 1006. https://doi.org/10.3390/photonics10091006





