Performance of HQAM/XQAM Laser Communication System in Anisotropic Non-Kolmogorov Ground–HAP–Satellite Uplink

Abstract

Satellite laser communication can achieve high-speed, high-precision, and high-security broadband communication without being constrained by the electromagnetic spectrum, which has attracted attention. So, this paper proposes the use of a high-altitude platform (HAP) under anisotropic non-Kolmogorov turbulence to improve the communication performance of the system. Cross quadrature amplitude modulation (XQAM) and hexagon quadrature amplitude modulation (HQAM) are applied to the ground–HAP–satellite (G-H-S) laser communication system. Considering the combined effects of uplink light intensity scintillation, beam wander, and the angle of arrival fluctuation, the G-H-S system’s bit error rate (BER) closure expression is derived under the EW distribution. Simultaneously, the relationship between the G-H-S system’s signal-to-noise ratio (SNR) and BER under different anisotropic factor u values is simulated and compared with the traditional ground–satellite (G-S) system. The results show that the communication performance of the G-H-S system with HQAM modulation is better. In addition, the effects of the zenith angle, receiving aperture, transmitter beam radius, and beam divergence angle on the BER performance of the system are also studied. Finally, the correctness of the analysis results is verified via Monte Carlo simulation. This research will benefit the design and optimization of satellite laser communication systems.

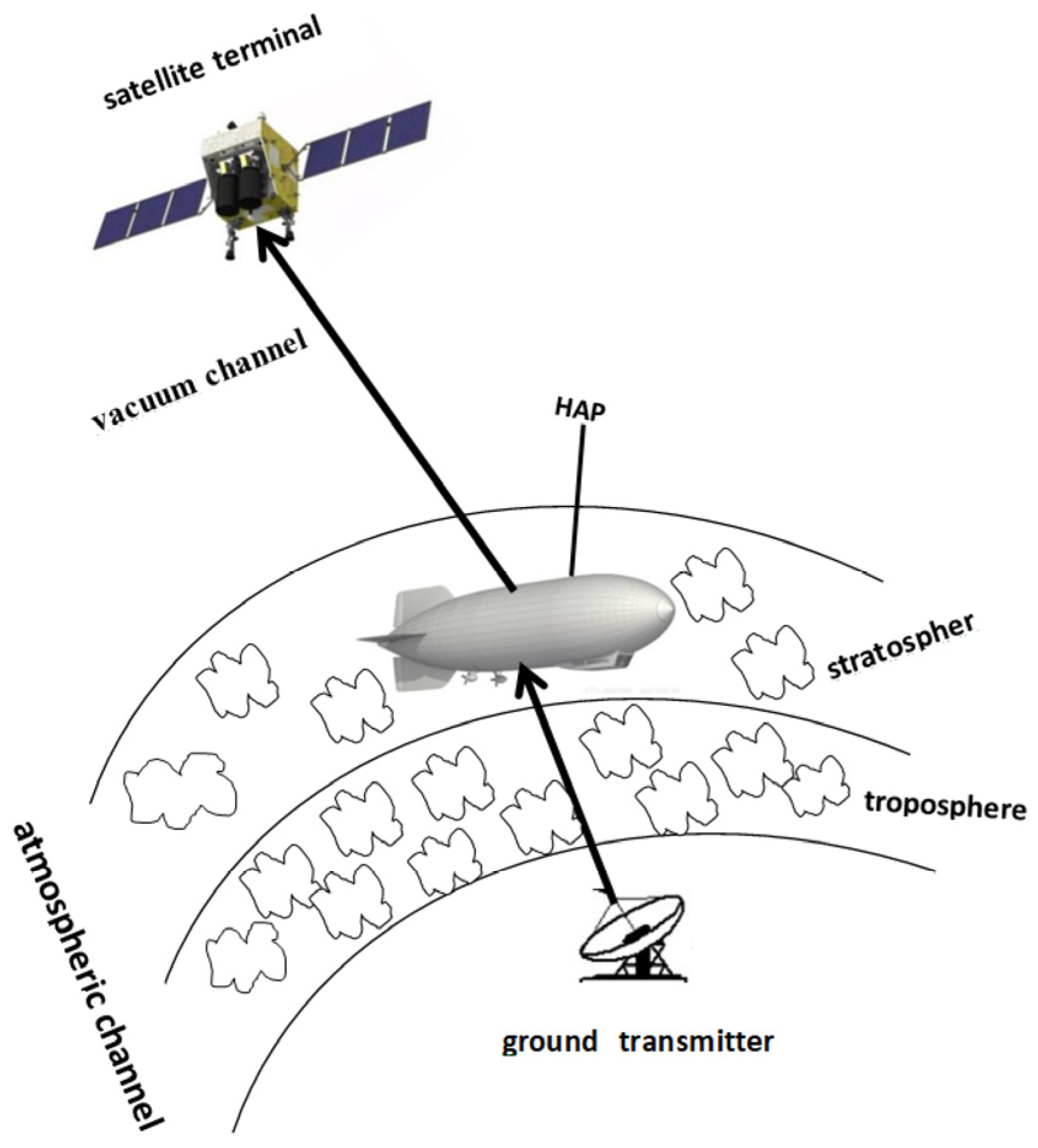
1. Introduction

Free-space optical (FSO) communication technology can realize efficient wireless broadband communication by using a laser beam as a data carrier, which has obvious advantages with respect to data rate, confidentiality, terminal size, weight, power consumption, and anti-interference, so it is widely used in the satellite communication field [1]. The satellite laser link has the advantages of large capacity, comprehensive coverage, low power consumption, and low cost, meaning that it has garnered significant attention from the academic community [2,3]. Satellite laser communication is divided into inter-satellite and satellite–ground laser communication, and satellite–ground laser communication links can be divided into uplink and downlink [4]. The optical effects generated by atmospheric turbulence are different for uplink and downlink. In addition to the influence of light intensity scintillation and the angle of arrival fluctuation, the uplink also has the phenomenon of beam wander, which will directly affect the communication performance of the system. When the downlink transmission beam reaches the atmosphere, its beam diameter is much larger than the vortex scale of the atmosphere. So, the influence of beam wander on the system can be ignored [5,6]. Therefore, the effect of atmospheric turbulence on the uplink is more complicated.

In the direct backhaul transmission between the ground and the satellite, the laser beam is susceptible to jitter and divergence due to atmospheric turbulence and cloud obstruction, which will reduce the communication performance of the system and even interrupt the communication link. A high-altitude platform (HAP) can be regarded as an effective solution to the above problems [7]. A HAP is a quasi-stationary aircraft with flexibility and maneuverability. It can adjust the spatial position and adaptive height to alleviate cloud interference and optimize the transmission quality of the laser beam [8,9]. Concomitantly, a HAP has advantages such as low cost, low propagation delay, faster deployment, easy maintenance of ground communication, and high capacity and high-quality satellite communication. It can be used as a relay node to assist ground–satellite and satellite–ground backhaul laser communication [10,11]. HAPs have mainly focused on researching backhaul communication between the ground and HAP in recent years. However, there are few studies on HAPs in backhaul laser communication between the ground and satellite. For example, Markus Knapek et al. originally proposed the use of a HAP in addition to satellite–ground downlink and HAP and GEO satellites as relay stations to improve the efficiency of LEO satellite-to-ground data transmission [12]. Minh Q. Vu et al. proposed the use of all-optical HAP-based relay technology to enhance the performance of free-space optical communication (FSO) systems from low Earth orbit (LEO) satellites to ground stations [11]. Minh Quang Vu et al. studied the design of a HAP as a relay-assisted satellite free-space optical (FSO) quantum key distribution (QKD) system for secure vehicle networks. They analyzed security performance in terms of quantum bit error and traversal key rates [13]. Suyash Shah et al. proposed a satellite communication system with adaptive FSO and RF switching schemes and analyzed outage performance and average symbol error rate (SER) [14]. Yaln Ata et al. analyzed the outage probability of FSO communication links of ground–HAP–satellite, HAP–HAP, and satellite–HAP–ground under different atmospheric turbulence channel models [15]. Moreover, we propose the use of a HAP and reconfigurable intelligent surface (RIS) to improve the system performance in the downlink of satellite–ground laser communication and derive the closed BER expression of a satellite–quasi-stationary aircraft–RIS–ground laser communication system. Simultaneously, increasing the number of RIS components allows the system to obtain a lower bit error rate [16]. The isotropic Kolmogorov turbulence model is used in the above publications on ground–satellite and satellite–ground backhaul communication. However, HAP is located at a height of 17 to 32 km in the stratosphere. Suppose the isotropic Kolmogorov turbulence model in the troposphere is used. In this case, it cannot better describe the influence of eddy currents on light wave transmission in turbulent random media. There is an error compared with the actual situation. Primarily, when the beam propagates in the vertical or non-horizontal direction, the non-Kolmogorov effect of atmospheric turbulence is more apparent [1,17]. It has not been reported that the HAP in the stratosphere adopts an anisotropic non-Kolmogorov turbulence model in the backhaul optical communication between ground and satellite.

Additionally, the modulation technologies used in satellite laser communication include differential phase shift keying (DPSK), minimum frequency shift keying (MSK), Gaussian minimum frequency shift keying (GMSK), etc. For example, Prabu Krishna et al. used binary shift keying subcarrier intensity modulation and differential phase shift keying subcarrier intensity modulation (DPSK-SIM) to evaluate the bit error rate (BER) performance of free-space optical satellite downlink [18]. We studied the application of minimum frequency shift keying (MSK) modulation with coherent detection and Gaussian minimum frequency shift keying (GMSK) in satellite laser communication systems [19,20]. So far, quadrature amplitude modulation (QAM) has attracted attention due to its advantages of achieving a high communication data rate without increasing system bandwidth. Compared with traditional quadrature amplitude modulation (QAM), rectangular quadrature amplitude modulation (RQAM) improves power efficiency and data transmission rate [21]. Chao Zhai studied the BER performance of the FSO communication system using a rectangular quadrature amplitude modulation (RQAM) scheme in ground-to-satellite uplink under weak turbulence [1]. Then, based on rectangular quadrature amplitude modulation (RQAM), two new modulation techniques emerged, namely cross quadrature amplitude modulation (XQAM) and hexagonal quadrature amplitude modulation (HQAM). The peak-to-average power ratio (PAPR) of cross quadrature amplitude modulation (XQAM) with higher flexibility and hexagonal quadrature amplitude modulation (HQAM) with the densest two-dimensional (2D) encapsulated hexagonal lattice structure is lower than that of rectangular quadrature amplitude modulation (RQAM), which can improve spectral efficiency and energy efficiency [22,23].

The rest of this paper is organized as follows: In Section 2, the system and channel model are presented. In Section 3, the bit error rate of the system is analyzed. In Section 4, the effects of hexagonal quadrature amplitude modulation (HQAM) and cross quadrature amplitude modulation (XQAM) on the bit error rate (BER) performance of the system are simulated and analyzed and compared with the ground–satellite (G-S) laser communication system using modulation technology and without a HAP in the satellite–ground laser system. The paper is concluded in Section 5.

2. System and Channel Model

2.1. Model of Satellite Laser Communication System

Figure 1 is a schematic diagram of a ground–satellite laser communication system, including the ground transmitter, HAP, and satellite terminal. The ground station is equipped with a single-antenna transmitter. The HAP is fitted with a multi-aperture receiver. It adopts the decode-and-forward relay protocol (DF), and the satellite station has a laser receiver. The laser beam is emitted from the ground transmitting end in the uplink. When transmitted upward through HAP, it is affected by atmospheric turbulence such as light intensity scintillation, beam drift, and the angle of arrival fluctuation. Finally, after transmission through the vacuum channel, it is received by the satellite terminal through the receiving antenna.

2.2. Channel Model

In satellite–ground laser communication, EW distribution can be applied to all turbulence conditions and give the experimental data an excellent fitting effect when the aperture smoothing effect occurs. Therefore, the EW probability distribution model is established in the ground–satellite uplink, and its probability density function (PDF) is as follows [24]:

$$f_I\left(I\right)=\frac{\alpha \beta }{\eta }{\left(\frac{I}{\eta }\right)}^{\beta -1}exp\left[-{\left(\frac{I}{\eta }\right)}^{\beta }\right]\times {\left\{1-exp\left[-{\left(\frac{I}{\eta }\right)}^{\beta }\right]\right\}}^{\alpha -1}$$

(1)

In the uplink system of ground-to-satellite laser communication, $\alpha$ is the shape parameter related to the receiving aperture, $\beta$ is the shape parameter of the scintillation index, and $\eta$ is the proportional parameter associated with the irradiation intensity. The expressions for these parameters are given as [25]:

$$\alpha =3.931{\left(\frac{D_R}{{\rho }_0}\right)}^{-0.519}$$

$$\beta ={\left(\alpha {\sigma }_I^2\right)}^{\frac{-6}{11}}$$

$$\eta =\frac{1}{\alpha \mathsf{\Gamma }\left(1+\frac{1}{\beta }\right)g\left(\alpha ,\beta \right)}$$

(2)

$${\rho }_0={\left(1.46C_n^2{\left(2\pi /\lambda \right)}^{2}L\right)}^{-3/5}$$

(3)

$$g\left(\alpha ,\beta \right)={\displaystyle {\displaystyle \sum }_{j=0}^{\infty }}\frac{{\left(-1\right)}^j{\left(j+1\right)}^{-\left(1+\beta \right)/\beta }}{j!\mathsf{\Gamma }\left(\alpha -j\right)}$$

(4)

where $\lambda$ is the wavelength of the Gaussian beam, $L$ is the length of the FSO link, $C_n^2$ is the refractive index structure constant, $D_R$ is the receiving aperture, and ${\sigma }_I^2$ is the scintillation index of the uplink non-Kolmogorov turbulence, which is defined as follows [26]:

$$\begin{array}{l}{\sigma }_I^2=4{\pi }^2{k}^{2}A\left(a\right){\beta }_0{u}^{2-a}{\displaystyle \underset{h_0}{\overset{H}{{\displaystyle \int }}}}{C}_n^2\left(h\right){\displaystyle {\displaystyle \sum }_{n=1}^{\infty }}\frac{{\left[\mathsf{\Lambda }{\sigma }_{pe}\left(1-\frac{h-h_0}{H-h_0}\right)\right]}^{2n}}{n!}{\left(\frac{k_L}{u}\right)}^{2n+2-a}\times \\ \hspace{1em}\hspace{1em}\left\{\frac{\mathsf{\Gamma }\left(\frac{a}{2}-n-1\right)}{\mathsf{\Gamma }\left(\frac{a}{2}\right)}+ \frac{\mathsf{\Gamma }\left(n+1-\frac{a}{2}\right)}{\mathsf{\Gamma }\left(n+1\right)}{\left\{{\left(\frac{k_L}{u}\right)}^2\left[\frac{u^2}{k_l{}^2}+\frac{\mathsf{\Lambda }\left(H-h_0\right){\left(1-\frac{h-h_0}{H-h_0}\right)}^2}{k}\right]\right\}}^{\frac{a}{2}-n-1}\right\}dh+\\ \hspace{1em}\hspace{1em} {\pi }^2{k}^{2}A\left(a\right) {\beta }_0{u}^{2-a}{\displaystyle \underset{h_0}{\overset{H}{{\displaystyle \int }}}}{C}_n^2\left(h\right){\left(\frac{k_L}{u}\right)}^{2-a}\mathsf{\Gamma }\left(1-\frac{a}{2}\right)\times Re\left\{\begin{array}{l}{\left\{{\left(\frac{k_L}{u}\right)}^2\left[\frac{u^2}{k_l{}^2}+\frac{\mathsf{\Lambda }\left(H-h_0\right){\left(1-\frac{h-h_0}{H-h_0}\right)}^2}{k}\right]\right\}}^{\frac{a}{2}-1}\\ -{\left\{{\left(\frac{k_L}{u}\right)}^2\left[\begin{array}{l}\frac{u^2}{k_l{}^2}+\frac{\mathsf{\Lambda }\left(H-h_0\right){\left(1-\frac{h-h_0}{H-h_0}\right)}^2}{k}+\\ i\frac{\left(H-h_0\right)\left(1-\frac{h-h_0}{H-h_0}\right)\left[1- \overline{\mathsf{\Theta }} \left(1-\frac{h-h_0}{H-h_0}\right)\right]}{k}\end{array}\right]\right\}}^{\frac{a}{2}-1}\end{array}\right\}dh\end{array}$$

(5)

where $a$ is the power law of the spectrum, $u$ is the anisotropy factor, $H$ is the receiver’s height, and $h_0$ is the height of the transmitter. ${\sigma }_{pe}$ is the pointing error caused by the light-speed drift.

According to the Markov approximation and geometric optics approximation of laser propagation in atmospheric turbulence, the angle of arrival fluctuation of laser propagation in the atmosphere obeys Rayleigh distribution. Its probability density expression is as follows [27]:

$$f_{\theta }\left(\theta \right)=\frac{\theta }{{\delta }_{\theta }^2}exp\left(-\frac{\theta }{2{\delta }_{\theta }^2}\right)$$

(6)

In summary, considering the influence of light intensity scintillation, beam drift, and the angle of arrival fluctuation and using $f_{\gamma }\left(\gamma \right)=\frac{1}{2\sqrt{\gamma \overline{\gamma }}}{f}_u\left(\sqrt{\gamma /\overline{\gamma }}\right)$ transformation [28], the closed expression of the $\gamma$ probability density function of the EW distribution under the combined action of the three is:

$$f_{\gamma }\left(\gamma \right)=\frac{1}{2\sqrt{\gamma \overline{\gamma }}}{\displaystyle {\displaystyle \sum }_{i=1}^{\infty }}{w}_i\frac{\alpha \beta }{\eta }{\left(\frac{\sqrt{\gamma }}{\eta \sqrt{\overline{\gamma }}}\right)}^{\beta -1}exp\left[-{\left(\frac{\sqrt{\gamma }}{<I>\eta \sqrt{\overline{\gamma }}}\right)}^{\beta }\right]\times {\left\{1-exp\left[-{\left(\frac{\sqrt{\gamma }}{<I>\eta \sqrt{\overline{\gamma }}}\right)}^{\beta }\right]\right\}}^{\alpha -1}$$

(7)

where $w_i$ is the i’th Gaussian coefficient of the angle of arrival fluctuations, and $<I>$ is the average received light intensity.

3. Performance Analysis

For the communication system, BER is an important index to measure the communication performance of the system. In the uplink, the bit error rate of the system using hexagonal quadrature amplitude modulation (HQAM) and cross quadrature amplitude modulation (XQAM) can be approximately expressed as [19]:

$$P={\displaystyle \underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}}{f}_{\gamma }\left(\gamma \right)P_e\left(\gamma \right)d\gamma$$

(8)

$P_e\left(\gamma \right)$ is the error probability expression of XQAM and HQAM, which can be expressed as:

$$P_{XQAM}\left(\gamma \right)=\left(4-\frac{2}{M}-\frac{2}{N}\right)Q\left(\tau \sqrt{\gamma }\right)-\left(4-\frac{4}{M}-\frac{4}{N}\right)Q^2\left(\tau \sqrt{\gamma }\right)$$

(9)

$$P_{HQAM}\left(\gamma \right)=K_{NN}Q\left(\sqrt{\xi \gamma }\right)+\frac{2}{3}{K}_{NN}{Q}^2\left(\sqrt{\frac{2\xi \gamma }{3}}\right)-2K_{CNN}Q\left(\sqrt{\xi \gamma }\right)Q\left(\sqrt{\frac{\xi \gamma }{3}}\right)$$

(10)

In order to simplify the analysis, the expression part of $Q^2\left(\right)$ can be ignored, so $P_{XQAM}\left(\gamma \right)$ and $P_{HQAM}\left(\gamma \right)$ can be approximately expressed as [29]:

$$P_{HQAM}\left(\gamma \right)=K_{NN}Q\left(\sqrt{\xi \gamma }\right)$$

(11)

$$P_{XQAM}\left(\gamma \right)=\left(4-\frac{2}{M}-\frac{2}{N}\right)Q\left(\tau \sqrt{\gamma }\right)$$

(12)

In the ground–HAP–satellite uplink, the average bit error rate of the system can be expressed as [16]:

$$P_{BER}=P_{g-h}+P_{h-s}-2P_{g-h}{P}_{h-s}$$

(13)

where $P_{g-h}$ and $P_{h-s}$ represent the bit error rate of the ground–HAP link and HAP–satellite link, respectively:

$$\begin{array}{c}{P}_{g-h\left(HQAM\right)}={\displaystyle \int \frac{exp\left(-\gamma \right)}{\sqrt{\gamma }}\frac{1}{2\sqrt{\overline{\gamma }}}{\displaystyle {\displaystyle \sum }_{i=1}^{\infty }}{w}_i\frac{{\alpha }_1{\beta }_1}{{\eta }_1}{\left(\frac{\sqrt{\gamma }}{\eta \sqrt{\overline{\gamma }}}\right)}^{{\beta }_1-1}exp\left[\gamma -{\left(\frac{\sqrt{\gamma }}{<I>\eta \sqrt{\overline{\gamma }}}\right)}^{{\beta }_1}\right]\times {\left\{1-exp\left[-{\left(\frac{\sqrt{\gamma }}{<I>\eta \sqrt{\overline{\gamma }}}\right)}^{{\beta }_1}\right]\right\}}^{{\alpha }_1-1}{K}_{NN}Q\left(\sqrt{\xi \gamma }\right)d}\gamma \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_{m}g\left(a_m\right)\hfill \end{array}$$

(14)

$$g\left(a_m\right)=K_{NN}Q\left(\sqrt{\xi a_m}\right)\frac{{\alpha }_1{\beta }_1}{2{\eta }_1\sqrt{\gamma }}{\left(\frac{\sqrt{a_m}}{\sqrt{\gamma }<I>{\eta }_1}\right)}^{{\beta }_1-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\gamma }<I>{\eta }_1}\right)\right]}^{{\beta }_1}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\gamma }<I>{\eta }_1}\right)}^{{\beta }_1}}\right)}^{{\alpha }_1-1}$$

(15)

$$H_m=\frac{\mathsf{\Gamma }\left(n+1/2\right)a_m}{n!{\left(n+1\right)}^2{\left[L_n^{-0.5}\left(a_m\right)\right]}^2}$$

(16)

According to (14)–(16), the error rate of the ground–HAP link’s HQAM can be determined as:

$$P_{g-h\left(HQAM\right)}={\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_m{K}_{NN}Q\left(\sqrt{\xi a_m}\right)\frac{{\alpha }_1{\beta }_1}{2{\eta }_1\sqrt{\overline{\gamma }}}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)\right]}^{{\beta }_1}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1}}\right)}^{{\alpha }_1-1}$$

(17)

Similarly, it can be concluded that:

$$P_{g-h\left(XQAM\right)}={\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_m{K}_{CN}Q\left(\tau \sqrt{a_m}\right)\frac{{\alpha }_1{\beta }_1}{2{\eta }_1\sqrt{\overline{\gamma }}}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)\right]}^{{\beta }_1}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1}}\right)}^{{\alpha }_1-1}$$

(18)

$$P_{h-s\left(HQAM\right)}={\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_m{K}_{NN}Q\left(\sqrt{\xi a_m}\right)\frac{{\alpha }_2{\beta }_2}{2{\eta }_2\sqrt{\overline{\gamma }}}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)\right]}^{{\beta }_2}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2}}\right)}^{{\alpha }_2-1}$$

(19)

$$P_{h-s\left(XQAM\right)}={\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_m{K}_{CN}Q\left(\tau \sqrt{a_m}\right)\frac{{\alpha }_2{\beta }_2}{2{\eta }_2\sqrt{\overline{\gamma }}}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)\right]}^{{\beta }_2}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2}}\right)}^{{\alpha }_2-1}$$

(20)

where $K_{CN}=\left(4-\frac{2}{M}-\frac{2}{N}\right),{\alpha }_1,{\beta }_1,{\eta }_1$ and ${\alpha }_2,{\beta }_2,{\eta }_2$ are the parameters of the ground–HAP and HAP–satellite links, respectively.

Finally, the average bit error rate closed expression of the system is obtained by bringing Equations (17)–(20) into Equation (13):

$$\begin{array}{l}{P}_{BER\left(HQAM\right)}={\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_m\frac{K_{NN}Q\left(\sqrt{\xi a_m}\right)}{2\sqrt{\overline{\gamma }}}\left(\begin{array}{l}\frac{{\alpha }_1{\beta }_1}{{\eta }_1}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>\eta }\right)\right]}^{{\beta }_1}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>\eta }\right)}^{{\beta }_1}}\right)}^{{\alpha }_1-1}+\\ \frac{{\alpha }_2{\beta }_2}{{\eta }_2}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)\right]}^{{\beta }_2}}\times {\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2}}\right)}^{{\alpha }_2-1}\end{array}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}-{\left({\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_m\frac{K_{NN}Q\left(\sqrt{\xi a_m}\right)}{\sqrt{\overline{\gamma }}}\right)}^2\left(\begin{array}{l}\frac{{\alpha }_1{\beta }_1}{{\eta }_1}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)\right]}^{{\beta }_1}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1}}\right)}^{{\alpha }_1-1}\times \\ \frac{{\alpha }_2{\beta }_2}{{\eta }_2}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)\right]}^{{\beta }_2}}\times {\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2}}\right)}^{{\alpha }_2-1}\end{array}\right)\end{array}$$

(21)

$$\begin{array}{l}{P}_{BER\left(XQAM\right)}={\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_m\frac{K_{CN}Q\left(\sqrt{\xi a_m}\right)}{2\sqrt{\overline{\gamma }}}\left(\begin{array}{l}\frac{{\alpha }_1{\beta }_1}{{\eta }_1}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)\right]}^{{\beta }_1}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1}}\right)}^{{\alpha }_1-1}+\\ \frac{{\alpha }_2{\beta }_2}{{\eta }_2}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)\right]}^{{\beta }_2}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2}}\right)}^{{\alpha }_2-1}\end{array}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}-{\displaystyle {\displaystyle \sum }_{m=1}^n}{H}_m\frac{K_{CN}Q\left(\sqrt{\xi a_m}\right)}{\sqrt{\overline{\gamma }}}\left(\begin{array}{l}\frac{{\alpha }_1{\beta }_1}{{\eta }_1}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)\right]}^{{\beta }_1}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_1}\right)}^{{\beta }_1}}\right)}^{{\alpha }_1-1}\times \\ \frac{{\alpha }_2{\beta }_2}{{\eta }_2}{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2-1}{e}^{a_m-{\left[-\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)\right]}^{{\beta }_2}}{\left(1-e^{-{\left(\frac{\sqrt{a_m}}{\sqrt{\overline{\gamma }}<I>{\eta }_2}\right)}^{{\beta }_2}}\right)}^{{\alpha }_2-1}\end{array}\right)\end{array}$$

(22)

4. Simulation Results and Analysis

Based on the above theoretical analysis and formula derivation, the performance of the G-H-S laser communication system was simulated and analyzed under the EW distributed channel model, and the accuracy of the numerical results was verified via Monte Carlo simulation. Due to the use of a non-Kolmogorov turbulence model in the stratosphere, the influence of turbulence on the stratosphere is relatively small. Therefore, for this article, we conducted analysis under weak turbulence conditions. In weak turbulence, the structural constant of atmospheric refractive index is 7.5 × 10⁻¹⁷ [16]. The specific parameters of the G-H-S laser communication system shown in

Table 1. Simulation parameter selection of G-H-S laser communication system.

System Parameters	Symbol	Value
Height of satellite ground station	H	$3600 \mathrm{km}$
Height of the transmitter from the ground	${\mathrm{h}}_0$	$100 \mathrm{m}$
Wind speed	$v$	$21 \mathrm{m}/\mathrm{s}$
Light wavelength	$\lambda$	$1.55 \mathrm{um}$
Atmospheric structure constant of refractive index	$C_n^2$	7.5 × 10−17
Receiving diameter	D	$0.2 \mathrm{m}$
Zenith angle	$\zeta$	30°
anisotropic factor	u	1 and 3
Height of HAP	Hp	20 km
FSO link length from ground transmitter to HAP	L1	40 km
FSO link length from HAP to satellite	L2	7160 km
Inclination angle of HAP to the ground	ζ1	60°
Inclination angle of HAP to the satellite Transmitter beam radius	ζ2 ω0	30° 0.1 m

were selected.

Figure 2a,b show the variation in the SNR of HQAM, XQAM, RQAM, and QAM with BER at different anisotropy factors of u = 1 and u = 3, respectively. The results show that the BER decreases not only with the increase in SNR but also with the increase in the anisotropy factor. As can be seen below, the bit error rate of the G-H-S system under four modulation schemes gradually decreases. When the SNR is the same, the G-H-S system with HQAM modulation has the lowest BER. When the BER is the same, the SNR of the G-H-S system modulated by HQAM is the lowest. Moreover, the BER of G-H-S and G-S systems decrease monotonically with increased SNR. When the SNR is small, the difference between the BER of G-H-S and G-S systems is small. As the SNR increases, the difference between them increases. The lower the SNR, the more severe the interference the signal is subjected to and the larger the BER of the system. The G-H-S and G-S lines in the figure have a slow downward trend when the SNR is low. The higher the SNR, the less interference the signal is subjected to and the lower the error rate of the system. Therefore, the G-H-S and G-S lines in the figure show a significant downward trend when the SNR is high. The G-H-S system with a HAP is less affected by turbulence and weather, so its bit error rate drops faster. Therefore, the two lines of the G-H-S and G-S systems using QAM are relatively close when the SNR is low, and the difference between them gradually increases when the SNR is large. The G-S system has a higher BER. For example, when the SNR is 22 dB and u = 1, the BER of the G-H-S and G-S systems are 0.47 and 0.83, respectively. When the SNR is 70 dB and u = 1, the BERs of G-H-S and G-S systems are 2.17 × 10⁻⁶ and 3.23 × 10⁻⁵, respectively. However, with the increase in anisotropy factor u, the influence of turbulence on the propagating laser beam will be weakened, and the BER of the system will be further reduced. To achieve the same BER 10⁻⁷, when the anisotropy factor u = 1, the SNR ratio of the G-H-S system modulated by HQAM is 70 dB. Compared with the G-H-S system with HQAM modulation when u = 3, the required SNR is increased by 20 dB. Therefore, the G-H-S system with HQAM modulation can achieve better communication performance in the ground–satellite uplink.

Figure 3a,b show the variation in the zenith angle of HQAM, XQAM, RQAM, and QAM with BER at different anisotropy factors of u = 1 and u = 3, respectively. The results show that the BER of the system not only increases with the increase in the zenith angle but also decreases with the increase in the anisotropy factor. In ground–satellite laser communication, the zenith angle is an essential physical quantity that can change atmospheric turbulence parameters. As can be seen below, the BER of the four modulation schemes all increase with the increase in the zenith angle and decrease with the increase in the anisotropy factor at the same zenith angle. For example, when u = 1 and the zenith angle is 22°, the BERs of HQAM, XQAM, RQAM, and QAM are 2.97 × 10⁻⁴, 7.67 × 10⁻⁴, 2.02 × 10⁻³, and 3.65 × 10⁻³, respectively. When u = 3, and the zenith angle is 22°, the BERs of HQAM, XQAM, RQAM, and QAM are 2.05 × 10⁻⁵, 6.09 × 10⁻⁵, 2 × 10⁻⁴, and 3.87 × 10⁻⁴, respectively. However, the BER of HQAM modulation is always lower than that of XQAM, RQAM, and QAM. Moreover, the BER of the G-H-S and G-S systems increases monotonically with the increase in the zenith angle, which indicates that a high zenith angle has a more severe influence on atmospheric turbulence than a low zenith angle. Regarding trends, when the zenith angle is small, the difference in bit error rate between the two is the largest, and the distance between the two lines is large. As the zenith angle increases, the BER of the G-H-S system shows a greater upward trend than that of G-S. The difference between them gradually decreases, and the two lines are closer but do not overlap. For example, when u = 1 and the zenith angle is 10°, the BERs of the G-H-S and G-S systems are 1.8 × 10⁻⁴ and 7.1 × 10⁻³, respectively. When u = 1 and the zenith angle is 37°, the BERs of the G-H-S and G-S systems are 0.08 and 0.1, respectively. Therefore, it is better to use a HAP to assist ground–satellite uplink and adopt HQAM modulation.

Figure 4a,b show the variation in the receiving aperture of HQAM, XQAM, RQAM, and QAM with BER at different anisotropy factors of u = 1 and u = 3, respectively. The results show that the BER of the system decreases not only with the increase in the receiving aperture but also with the increase in the anisotropy factor, mainly because the rise of the aperture will increase the power of the incident light and lead to a decrease in the BER. As can be seen from Figure 4a,b, the BER of the four modulation schemes decreases with the increase in the acceptance aperture and decreases with the increase in the anisotropy factor under the same acceptance aperture. For example, when u = 1 and the receiving aperture is 1 m, the BERs of HQAM, XQAM, RQAM, and QAM are 1.16 × 10⁻², 2.84 × 10⁻², 6.76 × 10⁻², and 1.17 × 10⁻¹, respectively. When u = 3 and the receiving aperture is 1 m, the BERs of HQAM, XQAM, RQAM, and QAM are 5.93 × 10⁻⁴, 1.61 × 10⁻³, 4.64 × 10⁻³, and 8.62 × 10⁻³, respectively. However, when u = 3 and the BER of the G-H-S system is 10⁻³, the receiving apertures required for HQAM, XQAM, RQAM, and QAM are 0.8 m, 1 m, 1.2 m, and 1.4 m, respectively. Therefore, under the same communication performance, the receiving aperture required by HQAM is relatively tiny. Moreover, the BER of the G-H-S and G-S systems decreases monotonically with the increase in receiving aperture. Regarding trends, the initial BER distance between the two is similar but does not overlap. As the receiving aperture increases and the incident light power increases, the receiving intensity of the optical signal increases. The BER of the two gradually decreases, and the BER of the G-H-S system decreases faster, leading to a gradual increase in the difference in bit error rate between the two. When u = 3 and the receiving aperture is 0.8 m, the BERs of the G-H-S system and G-S system under QAM modulation are 2.1 × 10⁻² and 3.9 × 10⁻³, respectively. The communication performance of the G-H-S system is superior to that of the traditional G-S system. In the uplink, a small receiving aperture can reduce the influence of beam distortion on system performance, minimize transmission cost, and effectively avoid the problems of high manufacturing cost and complex processing caused by large aperture reception.

Figure 5a,b show the variation in the transmit radius of HQAM, XQAM, RQAM, and QAM with BER at different anisotropy factors of u = 1 and u = 3, respectively. The results show that the BER of the system not only decreases first and then increases with the increase in the emission radius but also decreases with the increase in the anisotropy factor. When the system reaches the optimal transmission radius, the performance of the HQAM modulation scheme is the best, and the BER is lower with the increase in the anisotropy factor. For example, when u = 1, the BERs of HQAM, XQAM, RQAM, and QAM at the optimal transmission half a catty are 8.54 × 10⁻⁸, 5.12 × 10⁻⁷, 3.7 × 10⁻⁶, and 2.16 × 10⁻⁵, respectively. When u = 3, the BERs of HQAM, XQAM, RQAM, and QAM at the optimal transmission half a catty are 5.03 × 10⁻⁹, 4.15 × 10⁻⁸, 2.6 × 10⁻⁷, and 5.68 × 10⁻⁷, respectively. However, compared with the system using HAP, the BER of the G-S system is higher. When u = 1, the BERs of the G-H-S and G-S systems under QAM modulation are 5.59 × 10⁻⁶ and 1.7 × 10⁻⁵, respectively. Therefore, the G-H-S system has better communication performance, and HQAM modulation has a lower bit error rate and the best transmission aperture in a more comprehensive flat range. In practical application, the radius of the emission beam may change. It will not be kept at the optimal value; the more extensive the emission radius range, the more accessible the laser beam is to control the system.

Figure 6a,b show the variation in the beam divergence angles of HQAM, XQAM, RQAM, and QAM with BER at different anisotropy factors of u = 1 and u = 3, respectively. The results show that the BER of the system not only decreases first and then increases with the increase in the divergence angle but also decreases with the increase in the anisotropy factor. As can be seen from the Figure 6a,b, all four modulation methods have the best beam divergence angle to minimize the BER. When the system reaches the optimal beam divergence angle, the performance of the HQAM modulation scheme is the best, and the BER is lower with the increase in the anisotropy factor. For example, when u = 1, the BERs of HQAM, XQAM, RQAM, and QAM at the optimal beam divergence angle are 1.91 × 10⁻⁷, 1.04 × 10⁻⁶, 5.59 × 10⁻⁶, and 1.19 × 10⁻⁵, respectively. When u = 3, the BERs of HQAM, XQAM, RQAM, and QAM at the optimal beam divergence angle are 5.03 × 10⁻⁹, 4.15 × 10⁻⁸, 2.6 × 10⁻⁷, and 2.48 × 10⁻⁶, respectively. Moreover, when the system BER reaches the minimum, the optimal beam divergence angles of HQAM, XQAM, RQAM, and QAM are 55 × 10⁻⁵ rad, 51 × 10⁻⁵ rad, 46 × 10⁻⁵ rad, 45 × 10⁻⁵ rad, respectively, and the beam divergence angle of HQAM is the largest. Therefore, obtaining the best beam divergence angle by HQAM modulation is easier. However, compared with the quasi-stationary aircraft system, the BER of the G-S system is higher. For example, when u = 1, the BERs of the G-H-S and G-S systems at the optimal beam divergence angle are 3.9 × 10⁻⁵ and 1.6 × 10⁻⁴, respectively. When u = 3, the BERs of G-H-S and G-S systems at the optimal beam divergence angle are 4.54 × 10⁻⁶ and 2.1 × 10⁻⁵, respectively. So, the performance of the G-H-S system is the best. In communication systems, the beam divergence angle is challenging to compress, and a large beam divergence angle is easier to obtain.

Figure 7a,b show the variation in the scintillation index of HQAM, XQAM, RQAM, and QAM with BER at different anisotropy factors of u = 1 and u = 3, respectively. The results indicate that the bit error rate of the system not only increases with the increase in scintillation index but also decreases with the increase in anisotropy factor. From Figure 7a,b, it can be seen that the error rate of the four modulation schemes increases with the increase in the scintillation index, and the scintillation index decreases with the increase in the anisotropy factor. When u = 1 and the scintillation index is 0.2, the BERs of HQAM, XQAM, RQAM, and QAM are 2.57 × 10⁻⁴, 9.84 × 10⁻⁴, 1.52 × 10⁻³, and 3.17 × 10⁻³. When u = 3 and the scintillation index is 0.2, the BER of HQAM, XQAM, RQAM, and QAM are 2.18 × 10⁻⁵, 6.33 × 10⁻⁵, 2 × 10⁻⁴, and 3.86 × 10⁻⁴. Therefore, when the scintillation index is the same, the BER using HQAM is relatively small. At the same time, the bit error rates of the G-H-S and G-S systems increase monotonically with the increase in the scintillation index. Regarding trends, the initial BER difference between the two is relatively large, but as the scintillation index increases, the laser beam is more affected by the intensity scintillation. The BER of the two gradually increases, and the difference in error rate gradually decreases. However, the BER of the G-H-S system is always lower than that of the G-S system. When u = 3 and the flicker index is 0.2, the bit error rate of the G-H-S system under QAM modulation is 3.86 × 10⁻⁴; the bit error rate of G-S system is 1.16 × 10⁻³. Obviously, the communication performance of the G-H-S system is more superior. In the uplink, the light intensity scintillation has a significant impact on the propagation of laser beams.

5. Conclusions

This paper studied the HAP-assisted ground–satellite uplink laser communication system under an anisotropic non-Kolmogorov turbulence model; hexagonal quadrature amplitude modulation (HQAM) and cross quadrature amplitude modulation (XQAM) techniques were adopted. Considering the influence of light intensity scintillation, beam drift, and the angle of arrival fluctuation on atmospheric turbulence, the closed expression of BER of the ground–HAP–satellite (G-H-S) uplink is derived. Concomitantly, the relationship between BER and zenith angle, receiving aperture, signal-to-noise ratio (SNR), beam divergence angle, and transmitter beam radius under different anisotropy factor u values was simulated and analyzed and compared with the modulation technology used in the satellite-to-ground laser system and the traditional ground–satellite (G-S) system without HAP.

The simulation results showed that the BER of the HAP-assisted ground–satellite (G-S) system under an anisotropic non-Kolmogorov turbulence model is lower and decreases with the increase in the anisotropy factor. Concomitantly, in the case of the same communication performance, compared with QAM, RQAM, and XQAM, the ground–HAP–satellite (G-H-S) system using HQAM modulation can obtain better communication performance. For the same BER, the average transmit power required by HQAM is less than the power needed for the other three modulation schemes, which is beneficial in reducing the system power consumption and making the temperature control of the terminal laser easier. However, HQAM achieves a larger zenith angle, improves the coverage area of a single satellite, and can better control the antenna angle. Moreover, HQAM has the optimal transmitting aperture radius with the most extensive flat range, which can reduce the difficulty of beam control. In addition, HQAM has a smaller receiving aperture, which is conducive to reducing transmission costs. A smaller receiving aperture increases ground mobility and the flexibility of the laser network. Regarding the optimal beam divergence angle, HQAM is easier to obtain the optimal beam divergence angle than the other three modulation schemes. At the same time, HAP is used to connect communication between the ground and satellites. Due to the flexible deployment of HAP, it can be used as both a communication relay and for meteorological forecasting. Due to the influence of turbulence and weather in ground satellite communication, the HAP can be monitored in the atmosphere to obtain detailed meteorological data and ensure the quality of ground satellite communication. In summary, the HAP-assisted ground–satellite uplink studied under the anisotropic non-Kolmogorov turbulence model and the application of HQAM modulation to the ground–HAP–satellite (G-H-S) system can effectively optimize system performance and reduce the cost of satellite–ground laser communication.

This design focuses on the ground–HAP–satellite uplink. In previous work, our team studied the satellite–HAP–ground downlink, as well as the ground–satellite uplink and satellite–ground downlink. The modulation techniques and turbulence models used in previous work were MSK, GMSK, and isotropic Kolmogorov turbulence models, respectively. The modulation techniques and turbulence models used this time were HQAM/XQAM and anisotropic non-Kolmogorov turbulence models, respectively. However, this study did not consider HAP hover fluctuations, which can also have a certain impact on the performance of the entire system. It is hoped that improvements can be made in future work.