Optimized Design of Plasma Metamaterial Absorber Based on Machine Learning
Abstract
1. Introduction
2. Materials and Methods
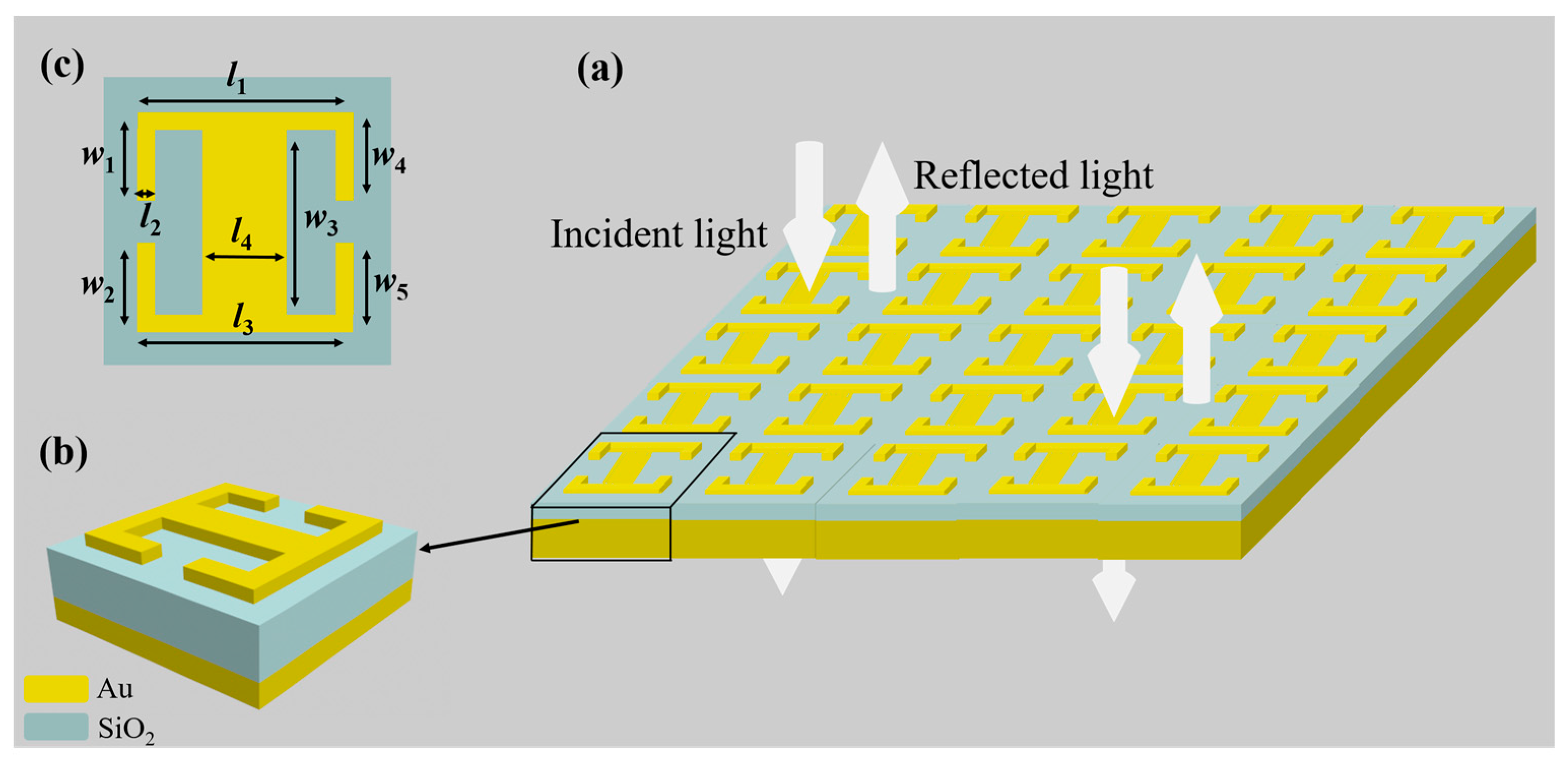
2.1. FDTD Model Building
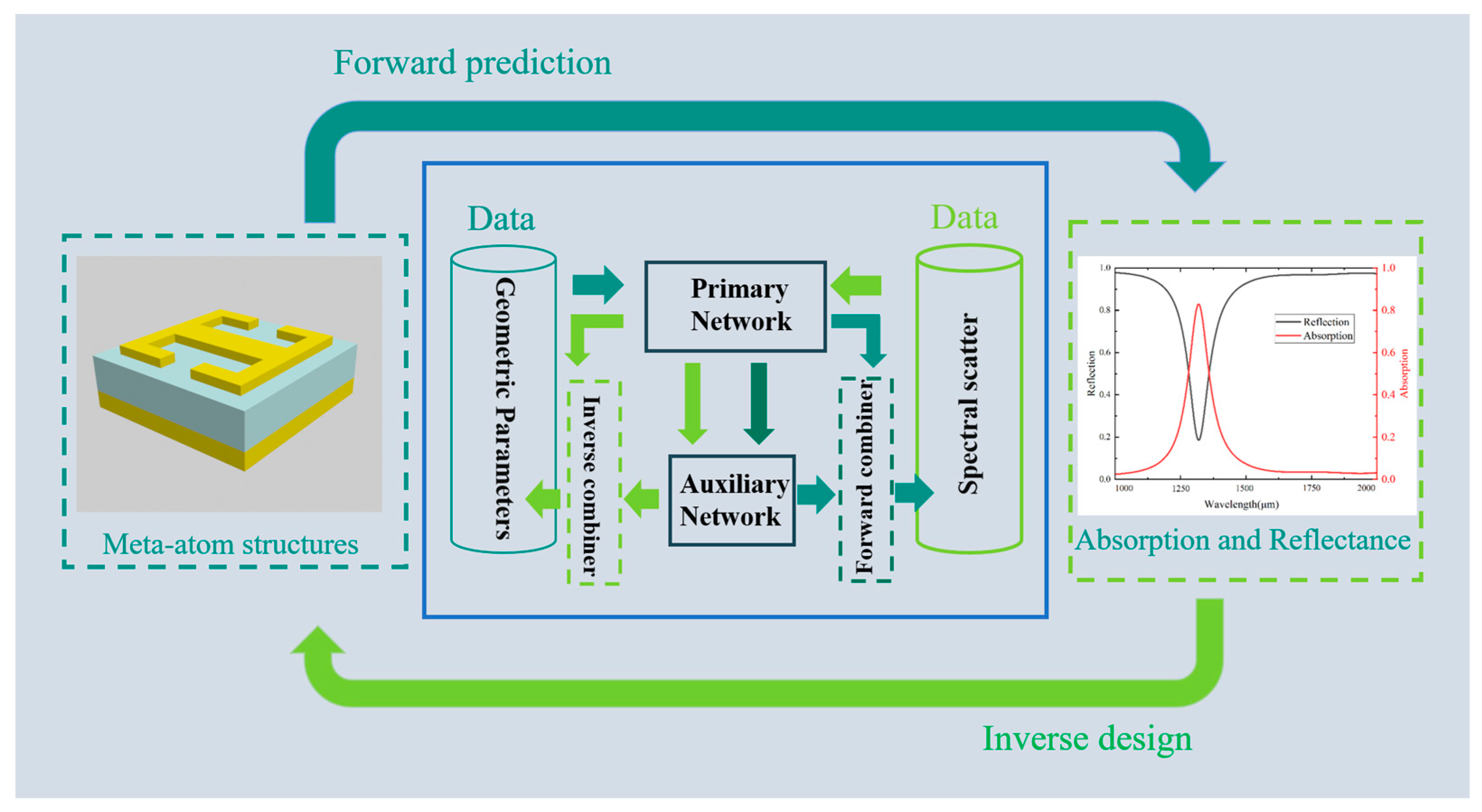
2.2. Forward Prediction and Inverse Design
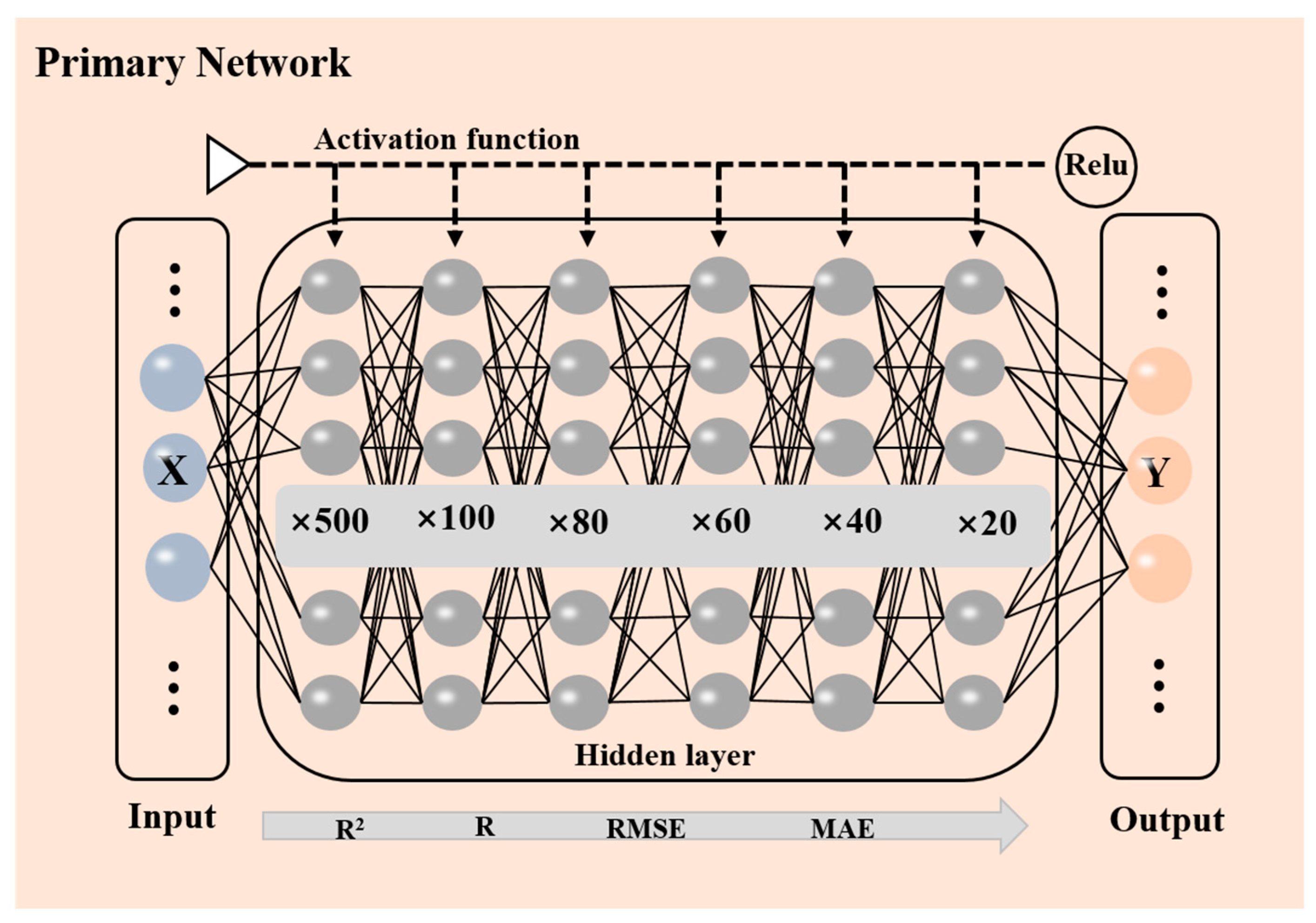
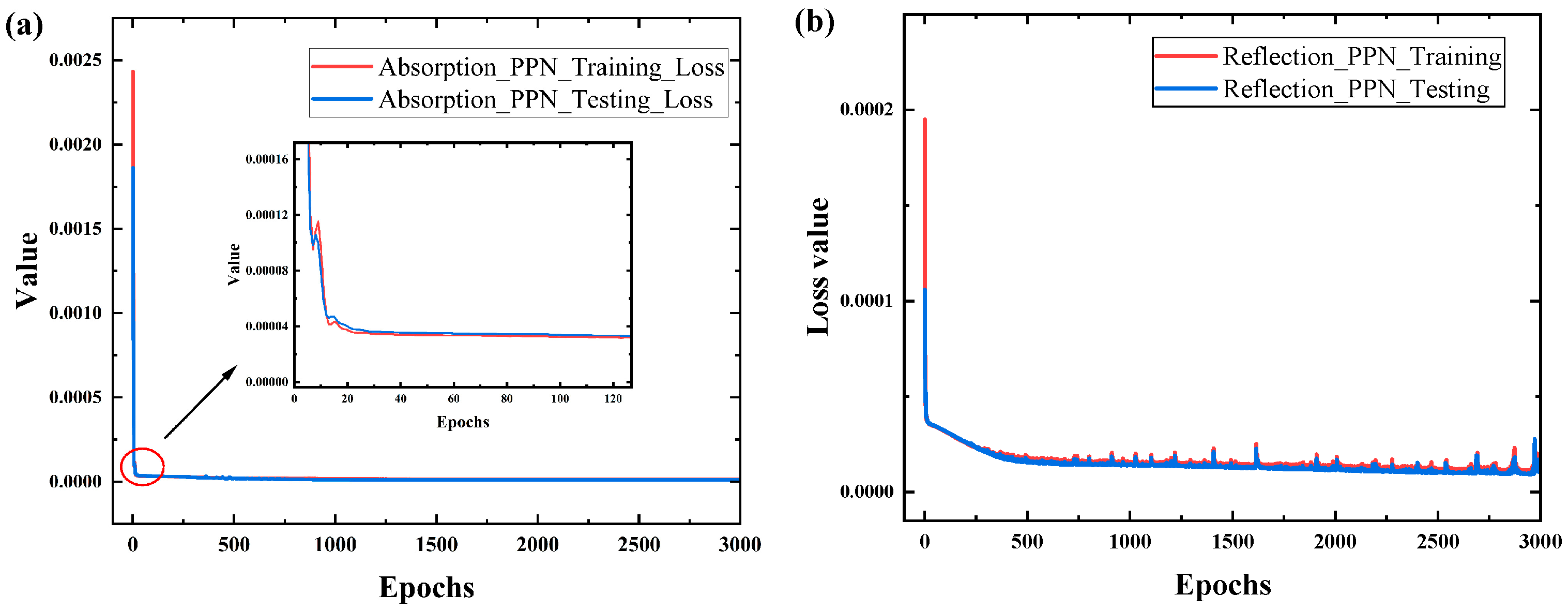
2.3. Primary Prediction Network
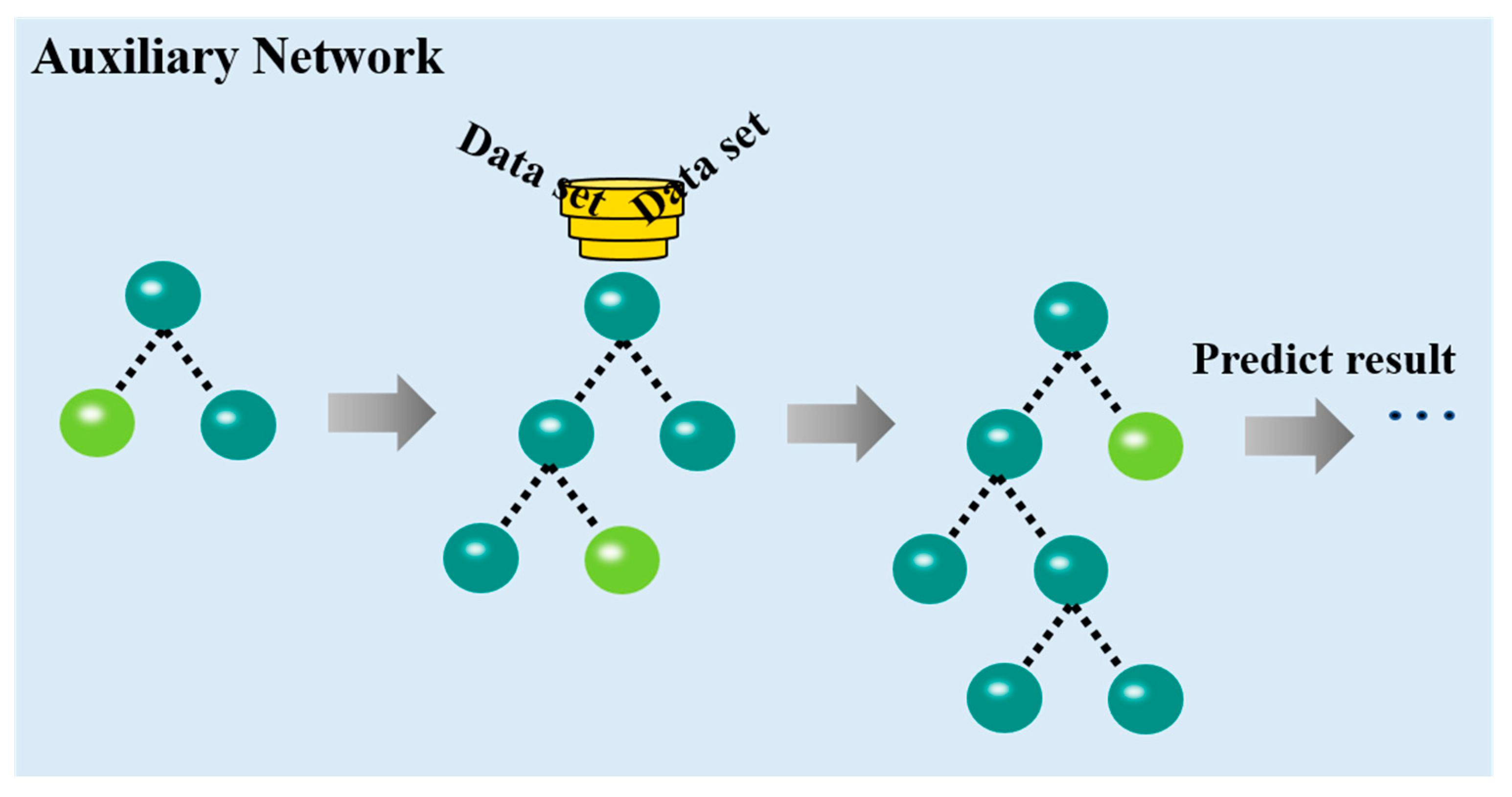
2.4. Auxiliary Prediction Network
3. Results and Discussion
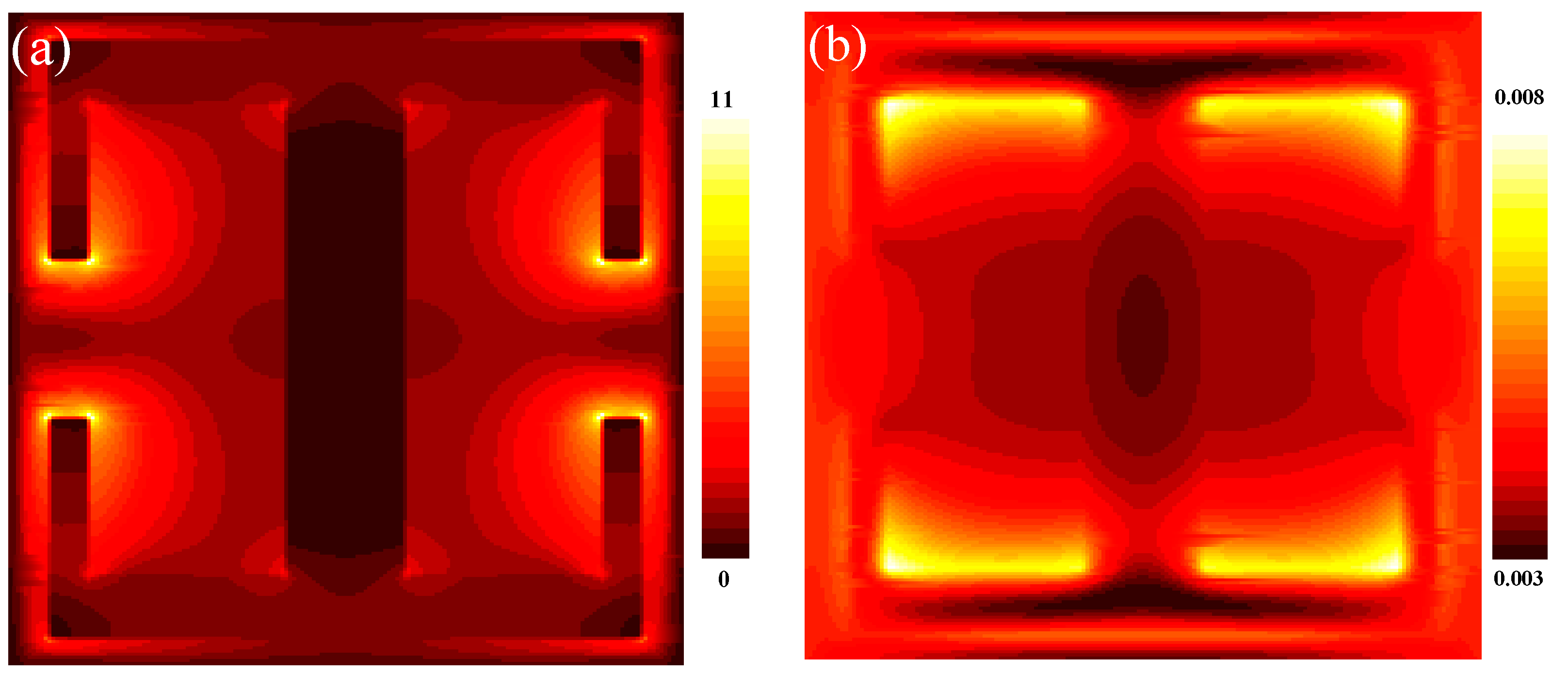
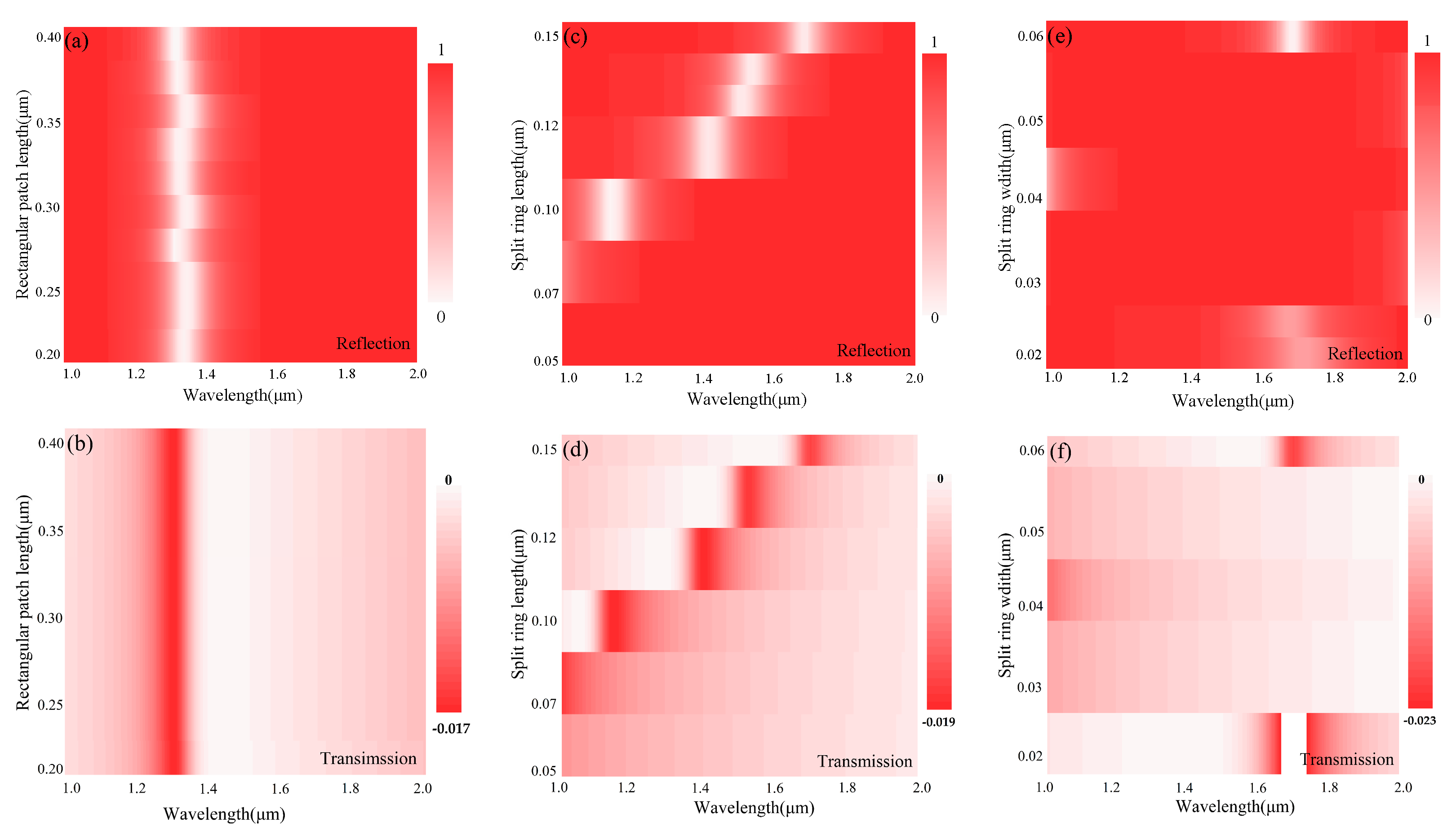
3.1. FDTD Simulation
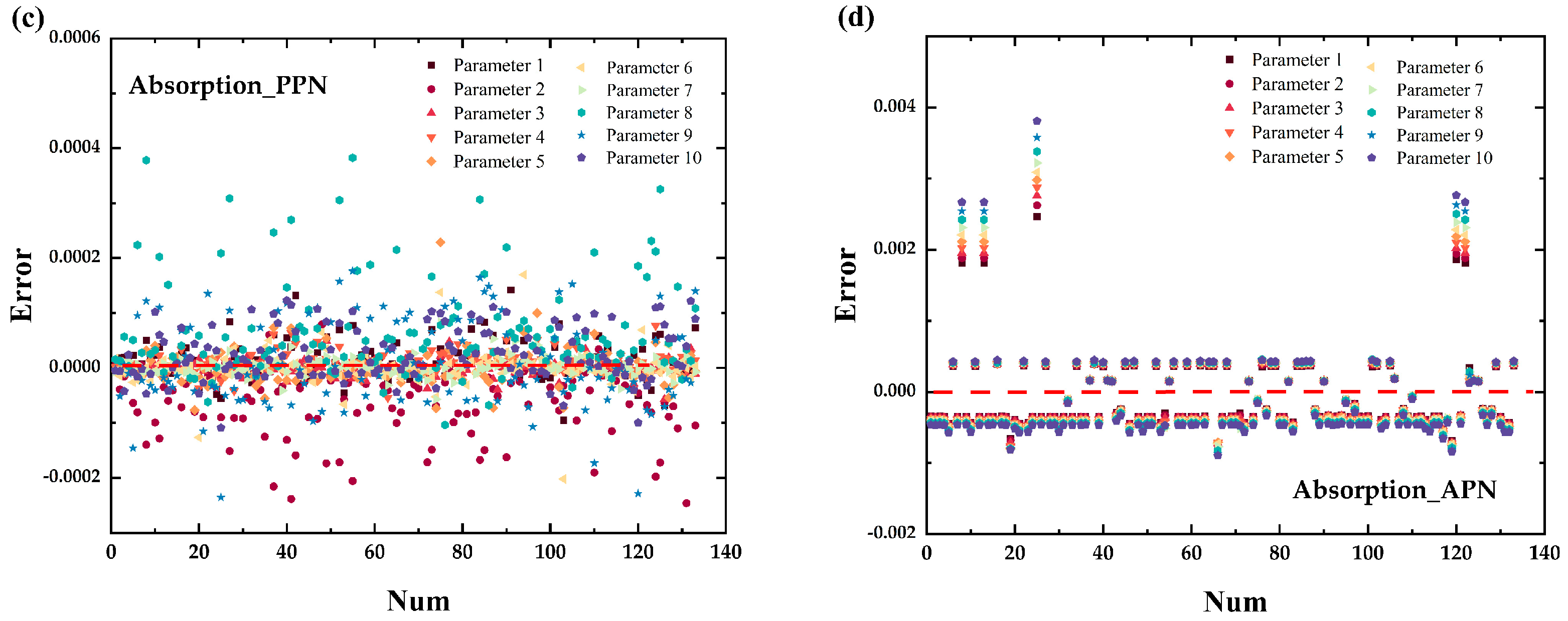
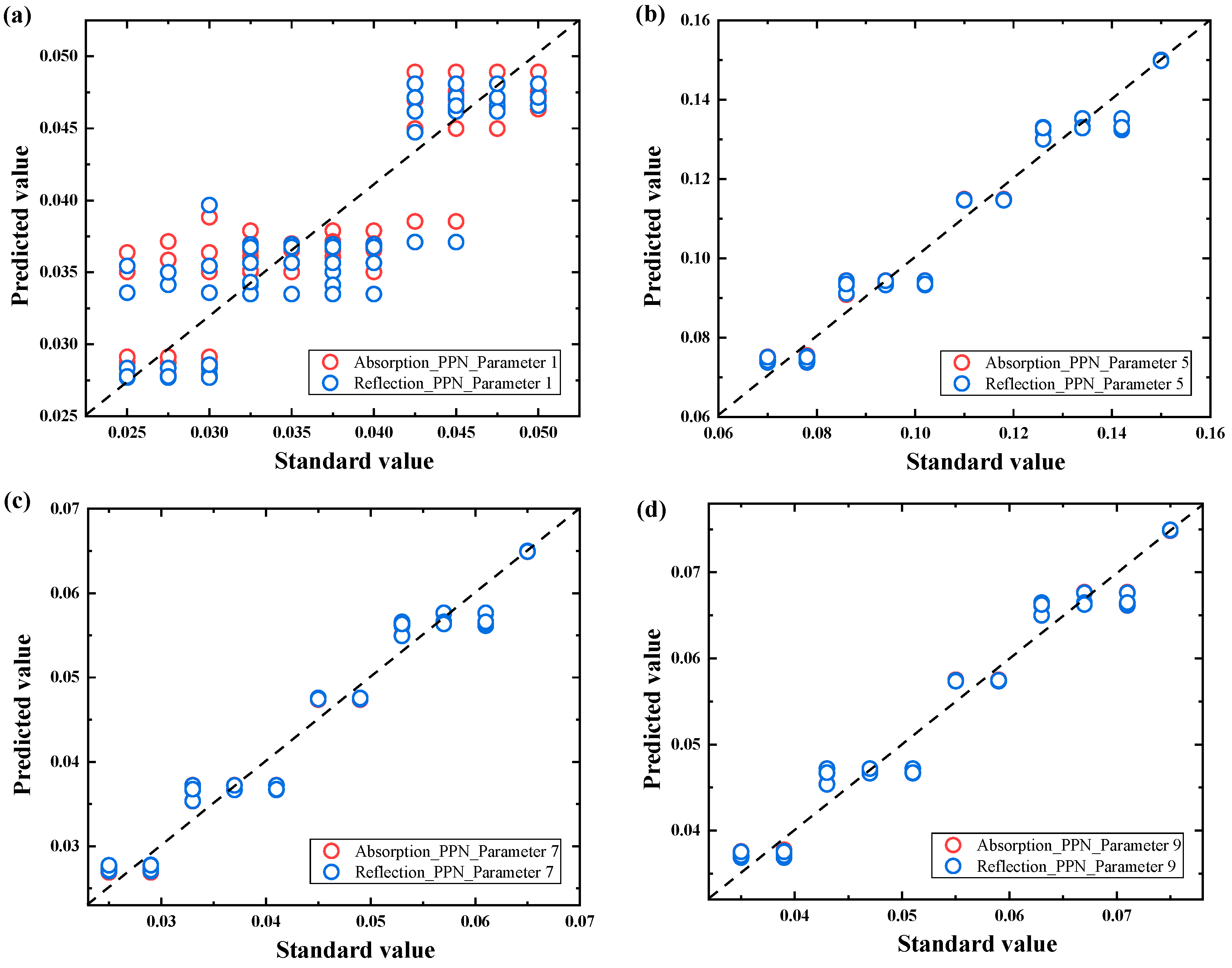
3.2. Forward Prediction
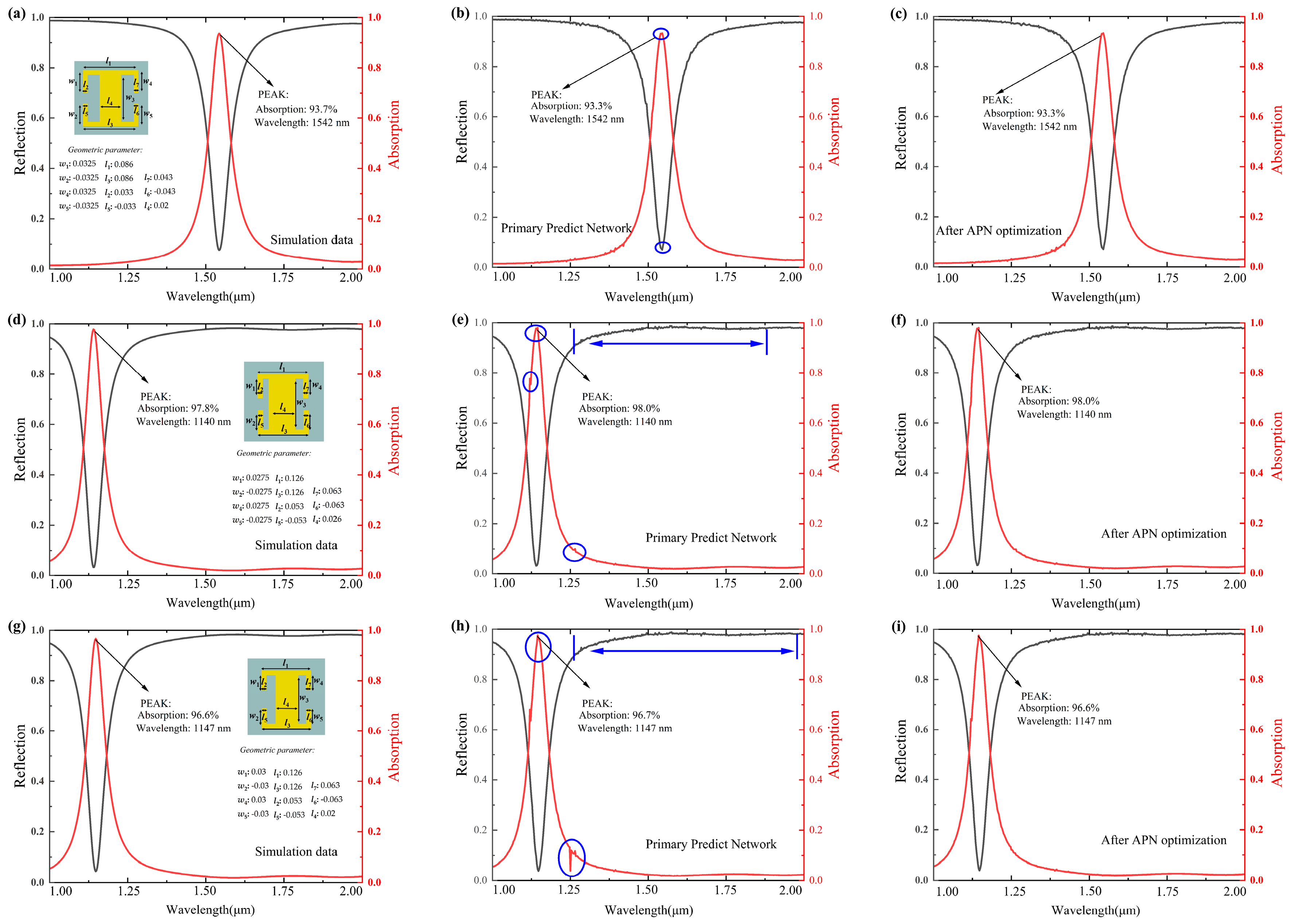
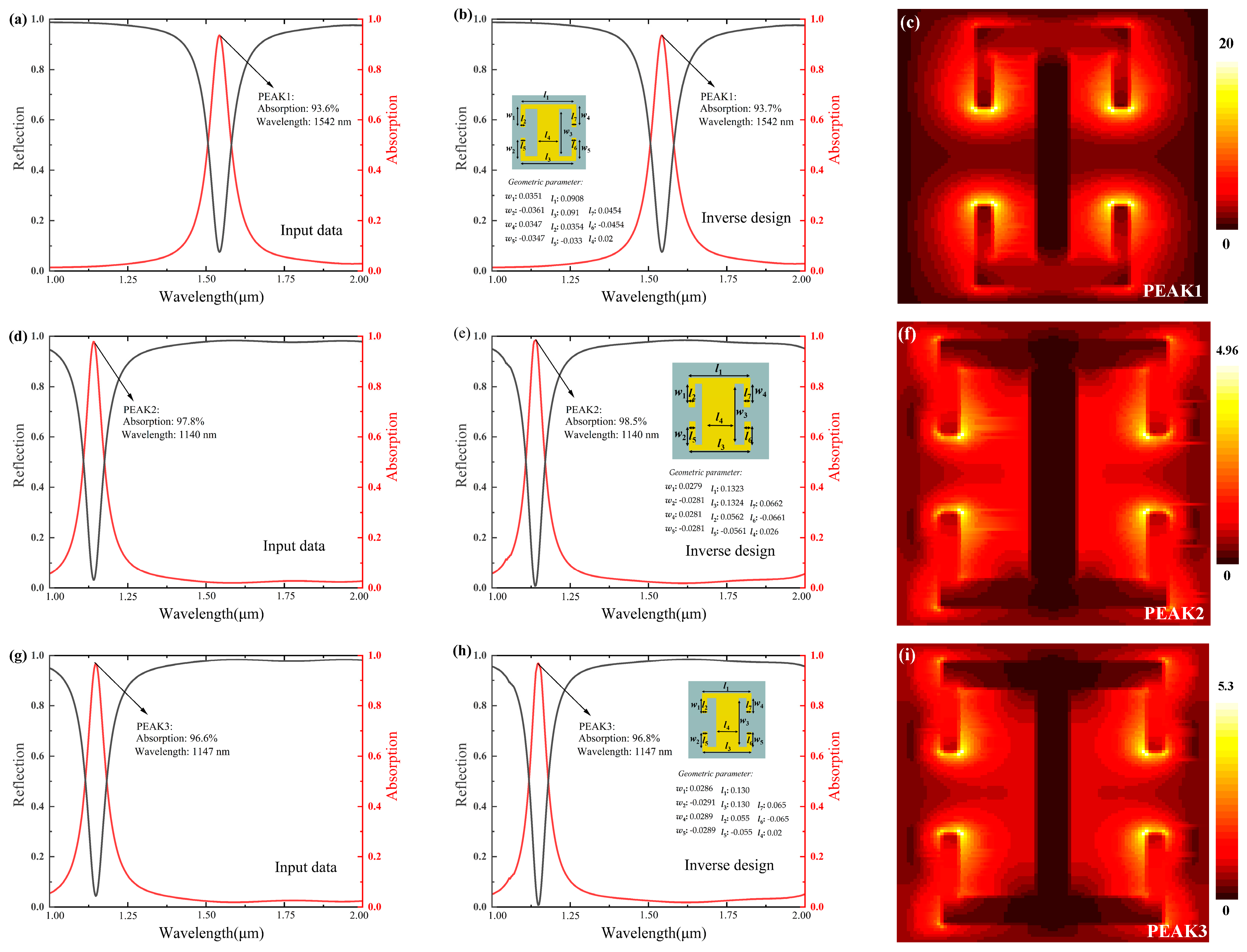
3.3. Inverse Design
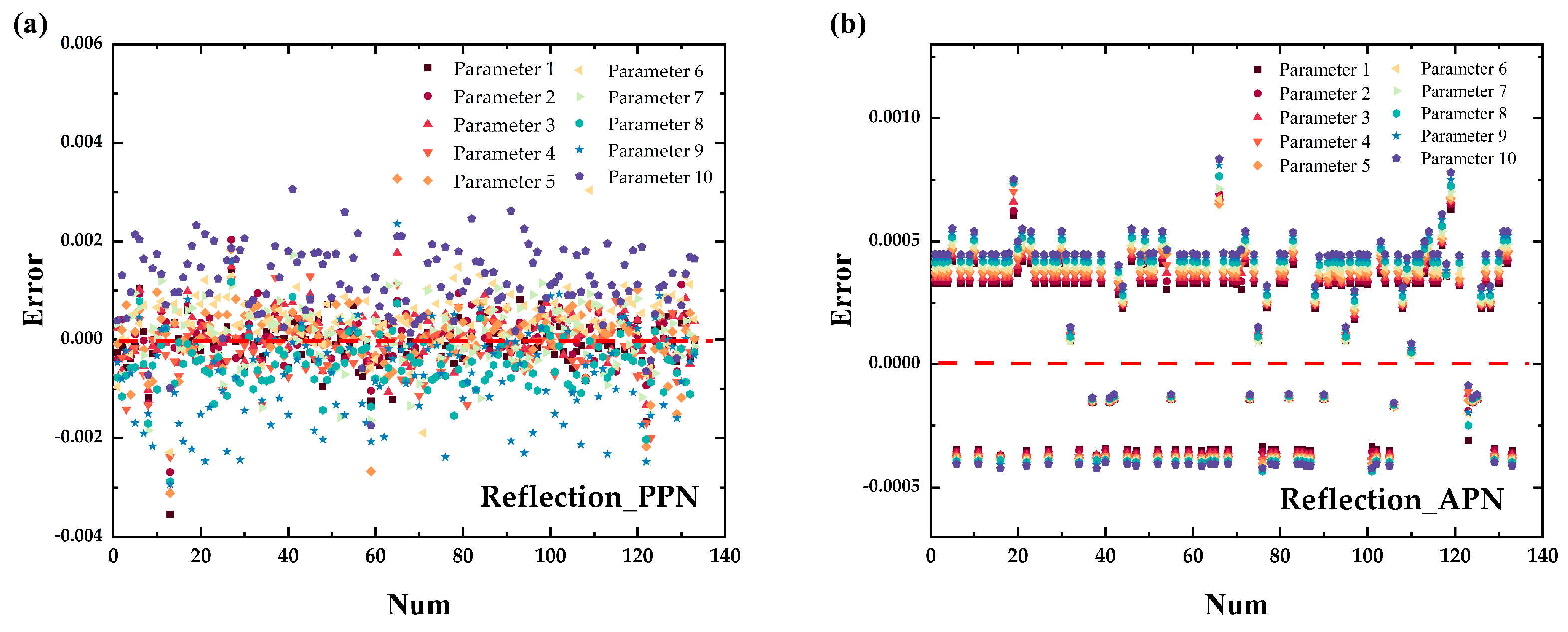
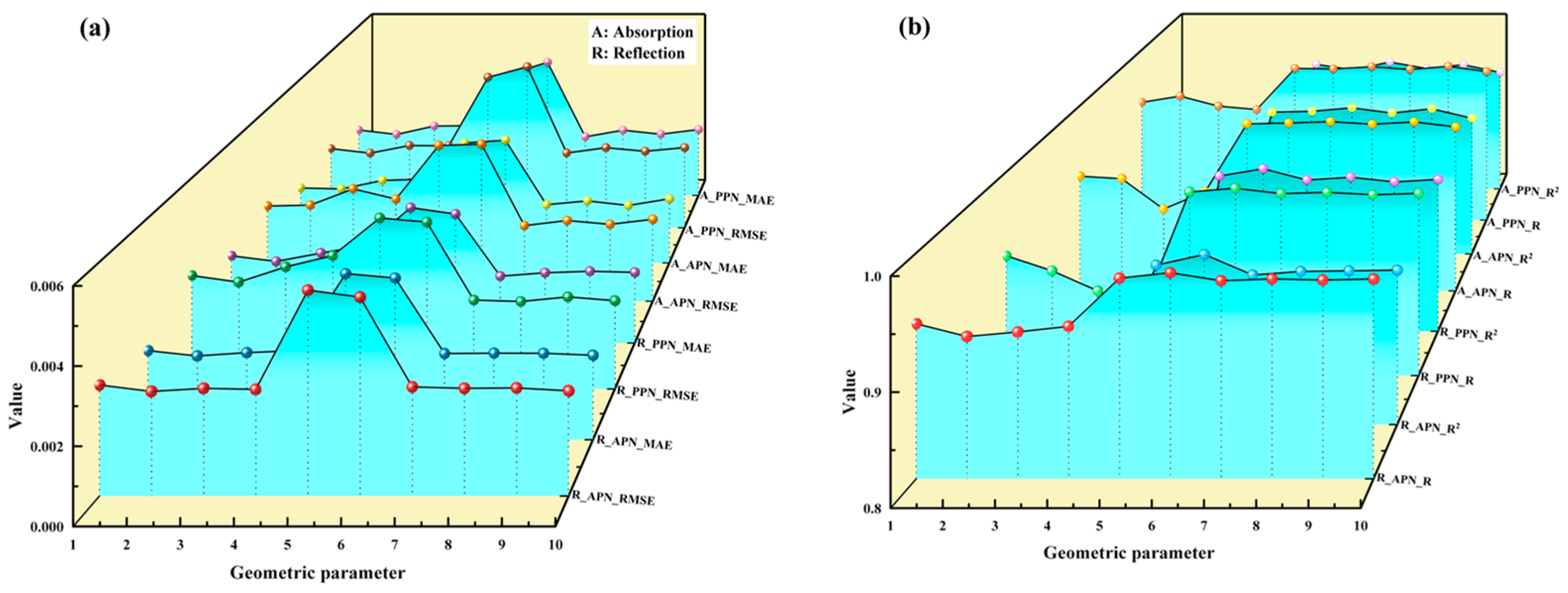
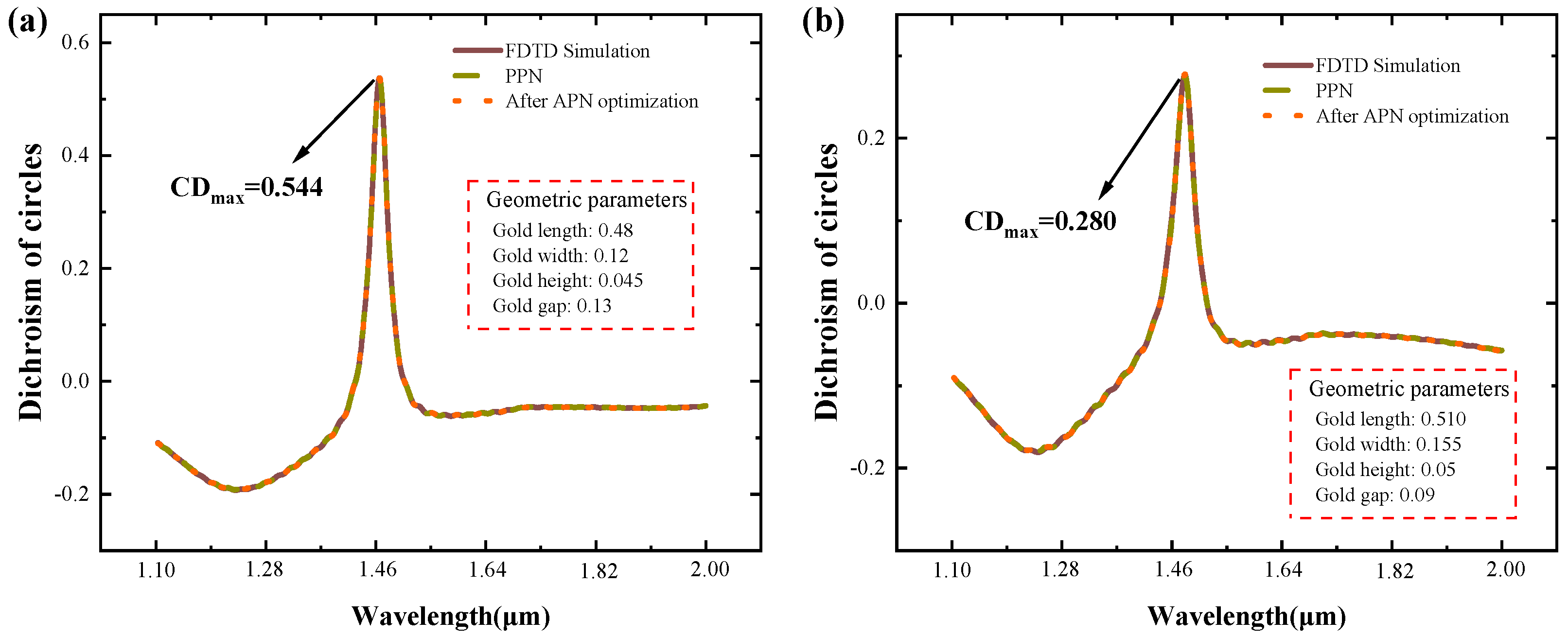
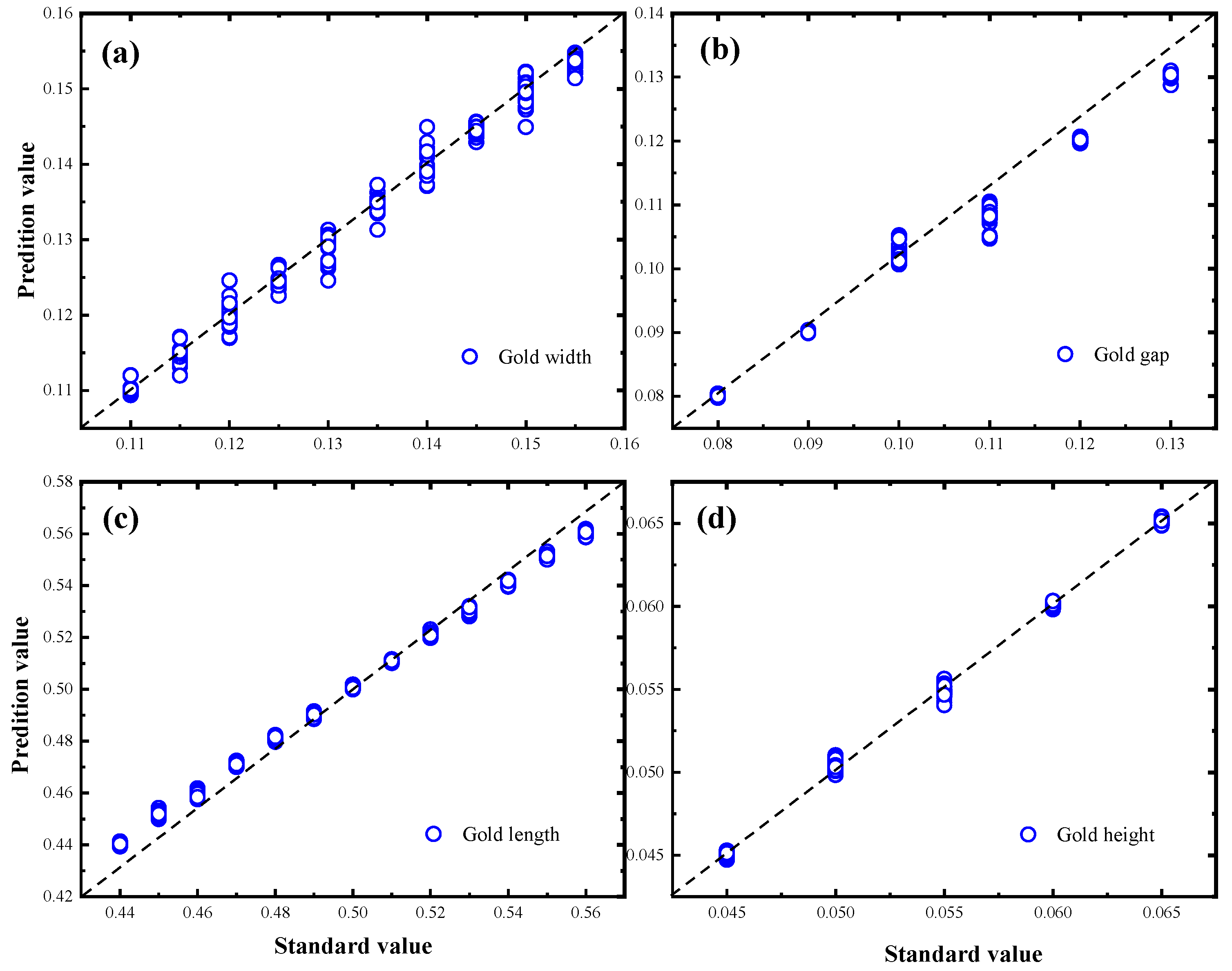
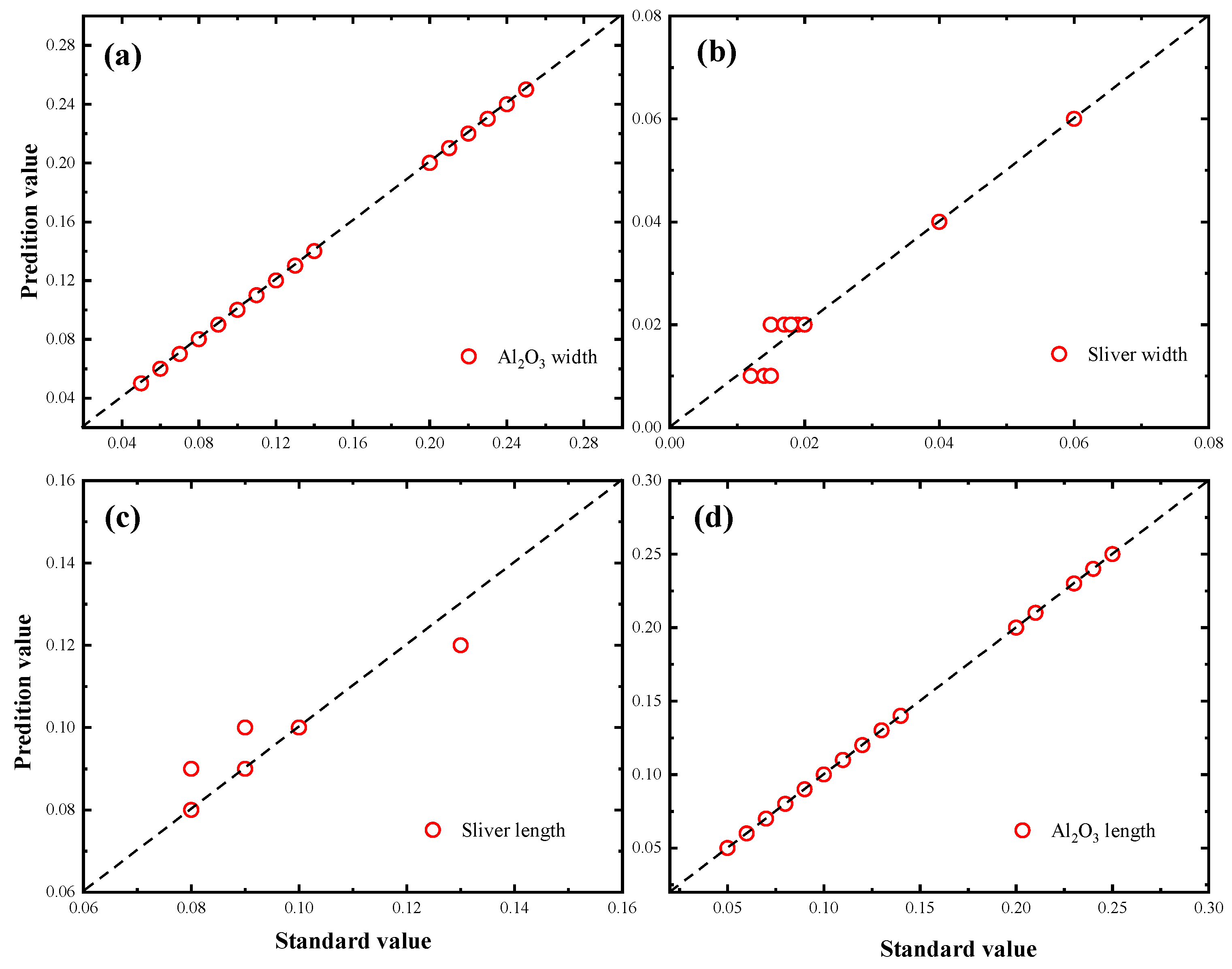
3.4. Design Framework Validation
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, Y.; Koshelev, K.; Zhang, F.; Lin, H.; Lin, S.; Wu, J.; Jia, B.; Kivshar, Y. Bound states in the continuum in anisotropic plasmonic metasurfaces. Nano Lett. 2020, 20, 6351–6356. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.W.; Nebabu, T.; Mikkelsen, M.H. Control of Nanoscale Heat Generation with Lithography-Free Metasurface Absorbers. Nano Lett. 2022, 22, 5151–5157. [Google Scholar] [CrossRef]
- Ghaedizadeh, A.; Shen, J.; Ren, X.; Xie, Y.M. Tuning the performance of metallic auxetic metamaterials by using buckling and plasticity. Materials 2016, 9, 54. [Google Scholar] [CrossRef] [PubMed]
- Al-Ketan, O.; Al-Rub, R.K.A. Multifunctional mechanical metamaterials based on triply periodic minimal surface lattices. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- Yang, M.; Sheng, P. Sound absorption structures: From porous media to acoustic metamaterials. Annu. Rev. Mater. Res. 2017, 47, 83–114. [Google Scholar] [CrossRef]
- Lai, R.; Shi, P.; Yi, Z.; Li, H.; Yi, Y. Triple-band surface plasmon resonance metamaterial absorber based on open-ended prohibited sign type monolayer graphene. Micromachines 2023, 14, 953. [Google Scholar] [CrossRef]
- Chen, Z.; Cai, P.; Wen, Q.; Chen, H.; Tang, Y.; Yi, Z.; Wei, K.; Li, G.; Tang, B.; Yi, Y. Graphene Multi-Frequency Broadband and Ultra-Broadband Terahertz Absorber Based on Surface Plasmon Resonance. Electronics 2023, 12, 2655. [Google Scholar] [CrossRef]
- Li, Y.; Yu, G.; Liang, B.; Zou, X.; Li, G.; Cheng, S.; Cheng, J. Three-dimensional ultrathin planar lenses by acoustic metamaterials. Sci. Rep. 2014, 4, 6830. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef]
- Liang, S.; Xu, F.; Li, W.; Yang, W.; Cheng, S.; Yang, H.; Chen, J.; Yi, Z.; Jiang, P. Tunable smart mid infrared thermal control emitter based on phase change material VO2 thin film. Appl. Therm. Eng. 2023, 2023, 121074. [Google Scholar] [CrossRef]
- Chen, T.; Li, S.; Sun, H. Metamaterials application in sensing. Sensors 2012, 12, 2742–2765. [Google Scholar] [CrossRef]
- Eslami, S.; Gibbs, J.; Mark, A.G.; Lee, T.C.; Jeong, H.-H.; Kim, I.; Fischer, P. Parallel fabrication of wafer-scale plasmonic metamaterials for nano-optics. In Advanced Fabrication Technologies for Micro/Nano Optics and Photonics VIII; SPIE: Bellingham, WA, USA, 2015; pp. 115–122. [Google Scholar]
- Zhou, Y.; Zheng, H.; Kravchenko, I.I.; Valentine, J. Flat optics for image differentiation. Nat. Photonics 2020, 14, 316–323. [Google Scholar] [CrossRef]
- Pahlevaninezhad, H.; Khorasaninejad, M.; Huang, Y.-W.; Shi, Z.; Hariri, L.P.; Adams, D.C.; Ding, V.; Zhu, A.; Qiu, C.-W.; Capasso, F. Nano-optic endoscope for high-resolution optical coherence tomography in vivo. Nat. Photonics 2018, 12, 540–547. [Google Scholar] [CrossRef]
- Zheng, Y.; Yi, Z.; Liu, L.; Wu, X.; Liu, H.; Li, G.; Zeng, L.; Li, H.; Wu, P. Numerical simulation of efficient solar absorbers and thermal emitters based on multilayer nanodisk arrays. Appl. Therm. Eng. 2023, 230, 120841. [Google Scholar] [CrossRef]
- Qin, F.; Chen, J.; Liu, J.; Liu, L.; Tang, C.; Tang, B.; Li, G.; Zeng, L.; Li, H.; Yi, Z. Design of high efficiency perovskite solar cells based on inorganic and organic undoped double hole layer. Sol. Energy 2023, 262, 111796. [Google Scholar] [CrossRef]
- Wu, F.; Shi, P.; Yi, Z.; Li, H.; Yi, Y. Ultra-broadband solar absorber and high-efficiency thermal emitter from uv to mid-infrared spectrum. Micromachines 2023, 14, 985. [Google Scholar] [CrossRef]
- Sheokand, H.; Ghosh, S.; Singh, G.; Saikia, M.; Srivastava, K.V.; Ramkumar, J.; Ramakrishna, S.A. Transparent broadband metamaterial absorber based on resistive films. J. Appl. Phys. 2017, 122, 105105. [Google Scholar] [CrossRef]
- Zhou, Y.; Kravchenko, I.I.; Wang, H.; Zheng, H.; Gu, G.; Valentine, J. Multifunctional metaoptics based on bilayer metasurfaces. Light: Sci. Appl. 2019, 8, 80. [Google Scholar] [CrossRef]
- Ren, H.; Fang, X.; Jang, J.; Bürger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 2020, 15, 948–955. [Google Scholar] [CrossRef]
- Rundo, F.; Trenta, F.; di Stallo, A.L.; Battiato, S. Machine learning for quantitative finance applications: A survey. Appl. Sci. 2019, 9, 5574. [Google Scholar] [CrossRef]
- Goodell, J.W.; Kumar, S.; Lim, W.M.; Pattnaik, D. Artificial intelligence and machine learning in finance: Identifying foundations, themes, and research clusters from bibliometric analysis. J. Behav. Exp. Financ. 2021, 32, 100577. [Google Scholar] [CrossRef]
- Callahan, A.; Shah, N.H. Machine learning in healthcare. In Key Advances in Clinical Informatics; Elsevier: Amsterdam, The Netherlands, 2017; pp. 279–291. [Google Scholar]
- Chen, P.-H.C.; Liu, Y.; Peng, L. How to develop machine learning models for healthcare. Nat. Mater. 2019, 18, 410–414. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Chaturvedi, S.; Akhter, S. Weather forecasting using machine learning algorithm. In Proceedings of the 2019 International Conference on Signal Processing and Communication (ICSC), Noida, India, 7–9 March 2019; pp. 171–174. [Google Scholar]
- Scher, S.; Messori, G. Predicting weather forecast uncertainty with machine learning. Q. J. R. Meteorol. Soc. 2018, 144, 2830–2841. [Google Scholar] [CrossRef]
- Ma, W.; Liu, Z.; Kudyshev, Z.A.; Boltasseva, A.; Cai, W.; Liu, Y. Deep learning for the design of photonic structures. Nat. Photonics 2021, 15, 77–90. [Google Scholar] [CrossRef]
- Ma, W.; Cheng, F.; Liu, Y. Deep-learning-enabled on-demand design of chiral metamaterials. ACS Nano 2018, 12, 6326–6334. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, D.; Rodrigues, S.P.; Lee, K.-T.; Cai, W. Generative model for the inverse design of metasurfaces. Nano Lett. 2018, 18, 6570–6576. [Google Scholar] [CrossRef]
- Surden, H. Machine learning and law. Wash. L. Rev. 2014, 89, 87. [Google Scholar]
- Qiu, J.; Wu, Q.; Ding, G.; Xu, Y.; Feng, S. A survey of machine learning for big data processing. EURASIP J. Adv. Signal Process. 2016, 2016, 67. [Google Scholar] [CrossRef]
- Hou, Z.; Tang, T.; Shen, J.; Li, C.; Li, F. Prediction network of metamaterial with split ring resonator based on deep learning. Nanoscale Res. Lett. 2020, 15, 83. [Google Scholar] [CrossRef]
- Jiang, L.; Li, X.; Wu, Q.; Wang, L.; Gao, L. Neural network enabled metasurface design for phase manipulation. Opt. Express 2021, 29, 2521–2528. [Google Scholar] [CrossRef]
- Gu, L.; Xie, S.; Zhang, Y.; Huang, Y.; He, Y.; Liu, H.; Wei, Z.; Guo, J. Plasmonic Metamaterial Absorbers Design Based on XGBoost and LightGBM Algorithms. Plasmonics 2022, 17, 2037–2047. [Google Scholar] [CrossRef]
- Han, C.; Zhang, B.; Wang, H.; Ding, J. Metamaterial perfect absorber with morphology-engineered meta-atoms using deep learning. Opt. Express 2021, 29, 19955–19963. [Google Scholar] [CrossRef]
- Catal, C. Performance evaluation metrics for software fault prediction studies. Acta Polytech. Hung. 2012, 9, 193–206. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Wang, W.; Lu, Y. Analysis of the mean absolute error (MAE) and the root mean square error (RMSE) in assessing rounding model. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; p. 012049. [Google Scholar]
- Wang, D.-N.; Li, L.; Zhao, D. Corporate finance risk prediction based on LightGBM. Inf. Sci. 2022, 602, 259–268. [Google Scholar] [CrossRef]
- Li, J. Monthly housing rent forecast based on lightgbm (light gradient boosting) model. Int. J. Intell. Inf. Manag. Sci. 2018, 7, 3–9. [Google Scholar]
- Li, W.; Coppens, Z.J.; Besteiro, L.V.; Wang, W.; Govorov, A.O.; Valentine, J. Circularly polarized light detection with hot electrons in chiral plasmonic metamaterials. Nat. Commun. 2015, 6, 8379. [Google Scholar] [CrossRef]
- Hao, J.; Zhou, L.; Qiu, M. Nearly total absorption of light and heat generation by plasmonic metamaterials. Phys. Rev. B 2011, 83, 165107. [Google Scholar] [CrossRef]




| Parameters | Meaning | Effects of Modeling | Value |
|---|---|---|---|
| num_boost_round | The number of iterations | Improve accuracy | 3000 |
| learning_rate | Converge the objective function to the minimum | Improve accuracy | 0.0001 |
| keep_prob | Probability of retaining a hidden layer | Prevent overfitting | 0.8 |
| hidden layer | Feature extraction and representation learning | Improve accuracy | 6 |
| Parameters | Meaning | Effects of Modeling | Value |
|---|---|---|---|
| num_boost_round | The number of iterations | Improve accuracy | 3000 |
| bagging_fraction | The ratio of data used in each iteration | Prevent overfitting | 1 |
| feature_fraction | Randomly select certain parameters to build the tree in the iteration | Reduce overfitting | 1 |
| bagging_freq | Bagging times | Prevent overfitting | 5 |
| learning_rate | Converge the objective function to the minimum | Improve accuracy | 0.01 |
| num_leaves | Number of leaf nodes | Prevent overfitting | 31 |
| max_depth | Maximum depth of tree | Reduce overfitting | 50 |
| verbose | Control the level of approach verbosity | Increase efficiency | 10 |
| Value | Average Performance Metrics | ||||
|---|---|---|---|---|---|
| Name | RMSE | MAE | R | R2 | |
| Reflection PPN | 0.010 | 0.006 | 0.996 | 0.989 | |
| Reflection APN | 0.002 | 0.001 | 0.999 | 0.999 | |
| Absorption PPN | 0.010 | 0.006 | 0.996 | 0.989 | |
| Absorption APN | 0.001 | 0.001 | 0.999 | 0.999 | |
| Value | Average Performance Metrics | ||||
|---|---|---|---|---|---|
| Name | RMSE | MAE | R | R2 | |
| Reflection PPN | 0.003 | 0.003 | 0.945 | 0.870 | |
| Reflection APN | 0.003 | 0.003 | 0.957 | 0.902 | |
| Absorption PPN | 0.003 | 0.003 | 0.952 | 0.890 | |
| Absorption APN | 0.003 | 0.003 | 0.962 | 0.906 | |
| Value | Average Performance Metrics | ||||
|---|---|---|---|---|---|
| Name | RMSE | MAE | R | R2 | |
| Forward_Test1 | 0.016 | 0.010 | 0.997 | 0.994 | |
| Forward_Test2 | 0.001 | 0.001 | 0.999 | 0.999 | |
| Inverse_Test3 | 0.001 | 0.001 | 0.998 | 0.996 | |
| Inverse_Test4 | 0.001 | 0.001 | 0.994 | 0.980 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, L.; Liu, H.; Wei, Z.; Wu, R.; Guo, J. Optimized Design of Plasma Metamaterial Absorber Based on Machine Learning. Photonics 2023, 10, 874. https://doi.org/10.3390/photonics10080874
Gu L, Liu H, Wei Z, Wu R, Guo J. Optimized Design of Plasma Metamaterial Absorber Based on Machine Learning. Photonics. 2023; 10(8):874. https://doi.org/10.3390/photonics10080874
Chicago/Turabian StyleGu, Leilei, Hongzhan Liu, Zhongchao Wei, Ruihuan Wu, and Jianping Guo. 2023. "Optimized Design of Plasma Metamaterial Absorber Based on Machine Learning" Photonics 10, no. 8: 874. https://doi.org/10.3390/photonics10080874
APA StyleGu, L., Liu, H., Wei, Z., Wu, R., & Guo, J. (2023). Optimized Design of Plasma Metamaterial Absorber Based on Machine Learning. Photonics, 10(8), 874. https://doi.org/10.3390/photonics10080874







