Mode Selection Method in Spherical Optical Cavities with Thin Metal Film

Abstract

A new method for the selection of the radial modes of a spherical microresonator by the quality factor, based on the effect of absorption in a thin metal film deposited on a sphere together with a dielectric layer, is proposed. The method was proved by numerical simulation on the example of the second and third radial modes $T{E}_{l,l,q}$, $l$ = 455, $q$ = 2, 3 selection in 80 μm radius quartz microsphere with 5 nm thick nickel film. The structure of the metal-dielectric coating was determined using analytical formulas in such a way that the metal film was placed at the node of the selected mode E-field distribution. The finite element method was used to refine the calculation, optimizing the position of the film in terms of obtaining the maximum quality factor. As a result, it was shown that the selected mode could have a relatively high quality factor ($Q$~10⁷), while the other radial modes are significantly suppressed ($Q$~10³). In addition, it is shown that selection is carried out by the mode index number ($l$) simultaneously with selection by the radial index.

1. Introduction

Spherical microresonators are multiple beam interference devices that have sufficiently high characteristics in terms of the degree of filtering and nonlinear conversion of radiation. The study and application of spherical resonators have been actively developed in recent years. In particular, two areas of their application can be distinguished. One of them is sensory applications related to measurements of physical quantities: temperature, refractive index, pressure, chemical and biological analytes, etc. [1,2]. Another area of application is nonlinear optics: generation in active materials of the second and third harmonics, Mandelstam–Brillouin scattering and Raman scattering, four-wave mixing, and mode selection in lasers [3,4,5,6].

The application of spherical microcavities is associated with a very large number of excited modes, which can complicate experimental work. Indeed, three integer indices $lmq$ ($\left|m\right|\le l$) for each of the two polarizations ($TE$, $TM$) are needed to describe modes in spherical resonators. For each mode with polar index $l$, $2l+1,$ more modes can potentially be excited along the azimuthal index $m$ (taking into account the sign), and for each of them $q$ more radial indices, where $q$ is determined from the dispersion equation. For a quartz sphere with a diameter of 160 μm and telecommunication wavelength ($\lambda$ ≈ 1550 nm) $l$~10³, radial modes with a relatively high quality factor $q$~10, the result is a total number of modes to be about 10⁷. In practice, several methods are used to reduce this number to the level of about 10². However, even this amount can significantly complicate the experiment and applications. In this sense, the development of mode selection methods in spherical resonators is of interest from the point of view of reducing the total number of modes and selecting the required ones. By mode selection, in this case, we mean selection by quality factor, i.e., in terms of losses. At the moment, there are several methods of mode selection in spherical resonators.

The value of the polar index $l$ in the first approximation is determined by the free spectral range of resonator $l\approx 2\pi an/\lambda$, where $\lambda$ is the wavelength of the excited mode, $a$ is the radius of the resonator, and $n$ is its refractive index. Due to the very close to parallel incidence of the light wave mode on the resonator boundary, a distinctive property of this type of resonator is spectral broadband, i.e., the possibility of excitation of a plurality of high-quality longitudinal modes with different $l$, separated by the free spectral range. In an ideal unperturbed spherical resonator, not all modes with different $l$ have the same quality factor; their quality factor increases with $l$ since the angle of incidence on the interface and the scattering of the light wave decrease. However, this Q-factor selection is quite spectrally broadband and is of little practical importance. Modes with a specific index $l$ can be easily picked out by excitation of the microresonator with a laser having a narrow line width. However, in this case, due to the non-optimal coupling of the exciter and microcavity, modes with different index $l$ (for example, higher radial modes) can be excited. In spherical microcavity with a high quality factor (~10⁸), it is possible to select one fundamental mode with distinguished index $l$ for reflection under certain matching conditions with thinned fiber [7].

If the azimuth index $m$ differs from $l$ in the polar direction, i.e., perpendicular to the direction of propagation, the mode has multiple maxima, the number of which depends on the value of $l-m$, and the transverse dimensions of the mode increase. These modes degenerate in frequency, i.e., an ideal spherical resonator should not be spectrally different from the fundamental mode; however, in real resonators, in which some asphericity is always present, their frequencies slightly differ, which can lead to the appearance of closely spaced parasitic resonances. To limit the number of modes by index $m$, a geometric factor is used. The most common method is to reduce the transverse size of the excitation region, for example, using a thinned fiber or a focused Gaussian beam. In this case, modes with smaller indices $m$ are not excited due to the decrease in overlap integral with the exciting radiation. The other geometric method is to deform the sphere. For example, flattening the sphere from the poles leads to both a transverse decrease in the size of the mode and to the splitting of eigenfrequencies and, thus, suppression of the excitation of higher azimuthal modes, which in the limit leads to the formation of a disk resonator. This method is used in integrated optical devices [8] and mushroom-shaped resonators [9] or resonators with mechanically machined sharp edges [10]. Another method, similar to a disk resonator, is associated with the fabrication of a Q-selected region in a cylindrical resonator by etching its surface in the form of a Bragg structure, which results in the selection of high-Q mode and high back reflection [11]. Modes can also be selected by choosing the location of spatial excitation with a thinned fiber, which is used in bottle-type resonators [12]. The authors of [13] have demonstrated a method where the separation of the mode frequency by the azimuthal number occurs due to the influence of the eccentricity of the liquid microsphere.

The radial index $q$ is determined from the dispersion equation and numerically coincides with the number of its root. Higher radial modes can be excited in a spherical resonator if the exciting element (for example, a thinned fiber) is imperfectly matched to the required resonator mode, which is fundamental in most cases, i.e., $TE/T{M}_{l,l,1}$. It is quite difficult to fulfill such a matching condition experimentally; therefore, spurious resonances also arise in the radial index. Radial modes have different quality factors, and as the index increases, the Q-factor decreases since radiative losses increase. For selection by the radial index, the method of a dielectric layer with a high refractive index deposited on a reference sphere with a low refractive index is used [14]. In this case, the mode is mainly concentrated in this layer, and the excitation of higher radial modes may not occur. The method of the layer with a lower refractive index makes it possible to optimize the coupling with the optical exciter and improve the quality factor of the resonator since the mode does not propagate in that layer (or a negligibly small part of its energy propagates). In that case, parasitic losses in the resonator, for example, from touching the resonator boundary with thinned fiber, are significantly reduced. The combination of layers with high and low refractive indices makes it possible to vary the characteristics of the refractive index sensor by effectively moving the mode to one of the layers [15]. In fact, the above methods exploit the effect of total internal reflection (waveguiding) for mode selection but do not use absorption since it is assumed that the dielectric layers have minimal ohmic losses. It is obvious that any absorption is intuitively perceived as the cause of a decrease in the quality factor of the resonator. However, absorbing metal layers are used for sensor applications in the sense of plasmon resonances in microspheres coated with gold film [16] or metal-dielectric-metal structures [17,18], while the quality factor of such resonators is significantly reduced.

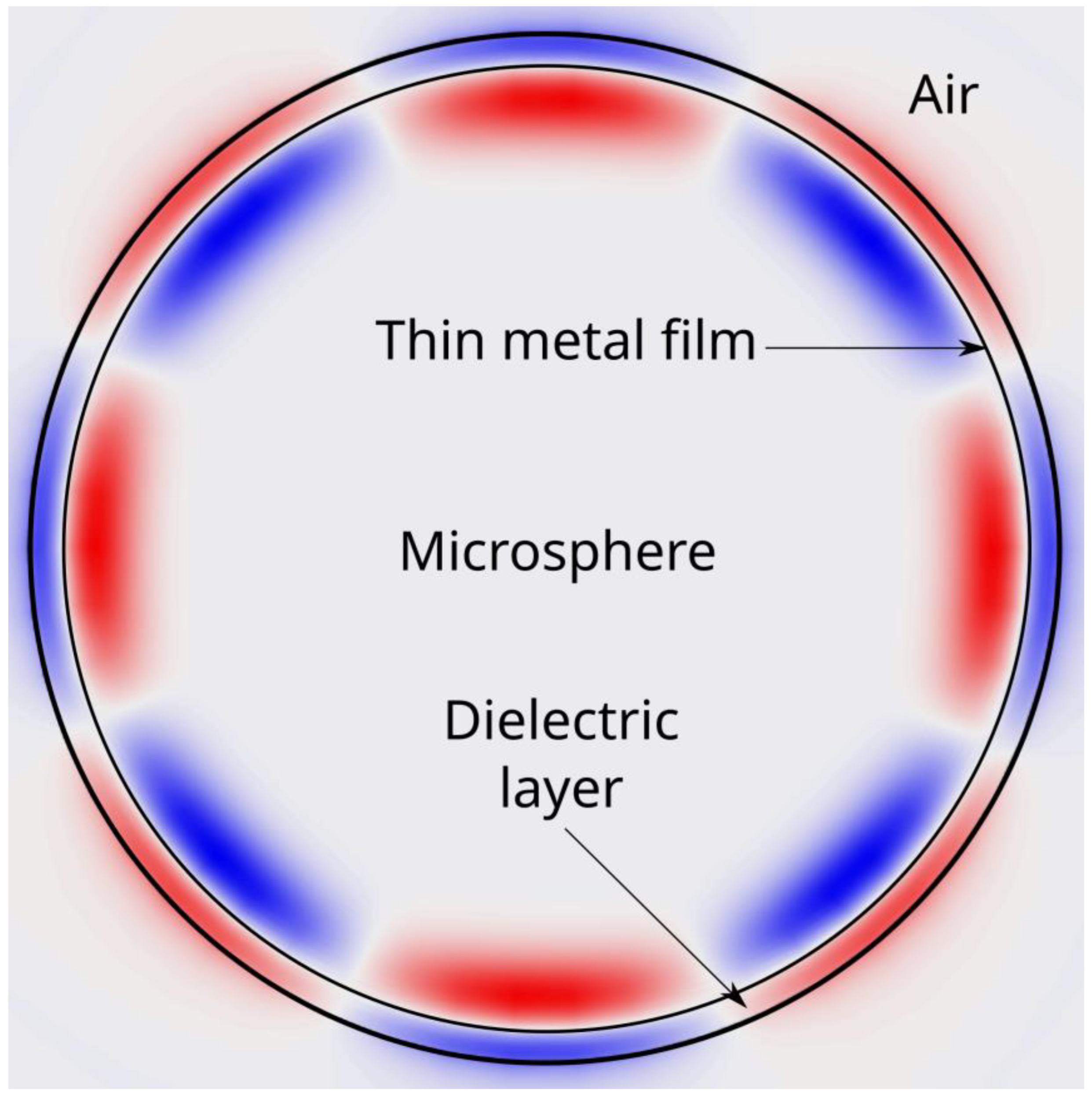
In this paper, using analytical formulas and numerical simulation, we study the thin metal film method for radial mode selection of spherical microresonators, which was previously used for mode selection in Fabry–Perot-like resonators [19,20]. The essence of the method is to place a metal (or any other absorbing structure) in the node of a standing electromagnetic wave, where round-trip losses will be minimal. Schematically, this is shown in Figure 1.

The microsphere is covered with two layers: thin metal film and dielectric overlayer. In this case, the film thickness should be much smaller than the wavelength ($<\lambda /20$); for other modes, the nodes of which spatially do not coincide with the position of the film, it will lead to significant losses and degradation of Q-factor. Since the radial modes of spherical resonators have minima in the radial direction, they turn out to be convenient for Q-selection. In this case, it is possible to obtain relatively high quality factors for the selected mode and low ones for the other modes. As an example, Q-selection of the second and third radial modes ($T{E}_{l,l,2}$ and $T{E}_{l,l,3}$) of a quartz spherical microresonator with a diameter of 160 μm [21] using thin nickel film and quartz layer will be considered.

2. Materials and Methods

It is necessary to determine the structure of two-layer metal-dielectric coating, i.e., set the thickness of the dielectric layer and the metal film. It is intuitively clear that for the selected mode, the metal film should be located close to the zero of the electric field of the unperturbed resonator mode (without the film). Analytical expression for the fields of the $T{E}_{lmq}$ mode is the following [22]:

$$\begin{gathered} \mathit{E}=\frac{A{\varphi }_l\left(kr\right)}{kr\sqrt{l(l+1)}}\left({\frac{im}{sin\theta }Y}_{lm}\left(\theta ,\phi \right){\mathbf{i}}_{\mathit{\theta }}-\frac{\partial Y_{lm}(\theta ,\phi )}{\partial \theta }{\mathbf{i}}_{\phi }\right), \\ \mathit{H}=\frac{-iA}{k_{0}rc\sqrt{l(l+1)}}\left(l\left(l+1\right)Y_{lm}\left(\theta ,\phi \right)\frac{{\varphi }_l\left(kr\right)}{kr}{\mathbf{i}}_{\mathit{r}}+\frac{\partial Y_{lm}(\theta ,\phi )}{\partial \theta }{{\varphi }_l^{\prime }(kr)\mathbf{i}}_{\theta }+{\frac{im}{sin\theta }Y}_{lm}\left(\theta ,\phi \right){\varphi }_l^{\prime }(kr){\mathbf{i}}_{\phi }\right) \end{gathered}$$

(1)

where $\mathit{E}$, $\mathit{H}$ are the vectors of the electric and magnetic fields, respectively, $A$ is the normalization constant, $c$ is the speed of light, $k_{0q}=2\pi /{\lambda }_q$ is the wave vector, $k_q=k_{0q}n$, ${\lambda }_q$ is the wavelength of the $q$-th mode, $n$ is the refractive index of the sphere medium, $\theta$ is polar angle, $\phi$ is azimuth angle, ${\mathbf{i}}_{\mathit{r},\theta ,\phi }$ are orts of the spherical coordinate system, $Y_{lm}\left(\theta ,\phi \right)$ is the angular spherical function, ${\varphi }_l\left(x\right)$ are the Riccati–Bessel functions, and the stroke means the derivative with respect to the argument. Inside the sphere ${\varphi }_l\left(x\right)=x{j}_l\left(x\right)$, outside: ${\varphi }_l\left(x\right)=x{h}_l\left(x\right)$, where $h_l\left(x\right)=j_l\left(x\right)+i{y}_l\left(x\right)$, $j_l\left(x\right)$ and $y_l\left(x\right)$ are spherical Bessel functions of the first and second kind, respectively. Taking into account the boundary conditions for the field components on $\theta$ and $\phi$, from (1) the coefficients of the fields $A_i$ inside and $A_e$ outside the sphere are determined, and dispersion equation is obtained, the numbers of roots of which determine the index $q$:

$$n\frac{j_l^{\prime }\left(k_{q}a\right)}{j_l\left(k_{q}a\right)}=\frac{h_l^{\prime }\left(k_{0q}a\right)}{h_l\left(k_{0q}a\right)}$$

(2)

where $a$ is the radius of the sphere. Determining the wavelengths ${\lambda }_q$ corresponding to $q$-th roots (2), one can analytically calculate the mode fields $T{E}_{l,m,q}$.

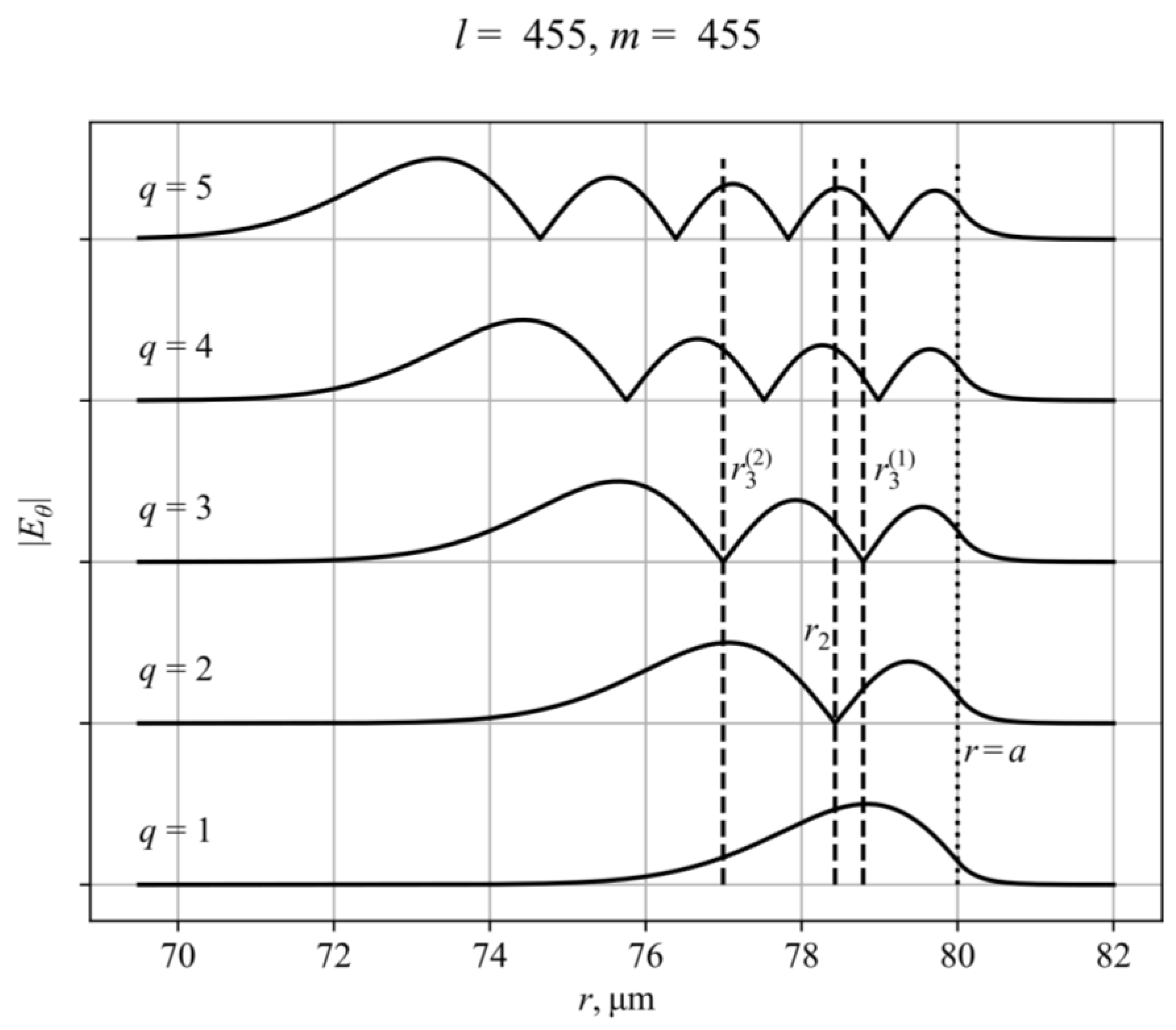
The figure (Figure 2) shows the radial distribution of the field $\left|{\mathit{E}}_{\theta }\right|$ for $\theta =\pi /2$ of the first 5 radial modes of quartz sphere with diameter of $2a$ = 160 μm for $l$ = 455 (components $\left|{\mathit{E}}_r\right|$ and $\left|{\mathit{E}}_{\phi }\right|$ are negligible). Wavelengths of eigenmodes are the following: ${\lambda }_1$ = 1549.311 nm, ${\lambda }_2$ = 1514.419 nm, ${\lambda }_3$ = 1486.624 nm, ${\lambda }_4$ = 1462.731 nm, and ${\lambda }_5$ = 1441.204 nm. From (1), the positions of zeros of the $r_q$ mode along the radius are determined by the zeros of the function ${\varphi }_l\left(k_q{r}_q\right)$ = 0 inside the sphere; the same radii correspond to zeros of $\phi$-component of the Umov–Poynting vector tangential to the film surface. The dashed line shows the radius $r_2$ = 78.429 µm, which is the zeroth approximation of the film position for mode selection with $q$ = 2, as well as $r_3^{\left(1\right)}$ = 78.789 µm for the third mode with $q$ = 3 in the first minimum. In addition, the question of selection of the third mode in the second minimum of the field $r_3^{\left(2\right)}$ = 76.993 μm is of interest.

For a spherical resonator, the position of the zeros of the selected mode can be obtained from analytical expressions, which somewhat simplifies the task. For a sphere with a two-layer coating, exact analytical formulas can be written, but in this case, the expressions for both the mode fields and the dispersion equation become much more complicated. However, this problem can be solved numerically using the finite element method. This is especially true for resonator shapes other than spherical, which cannot be accurately described by analytical formulas. Analytical consideration also makes it possible to validate the reliability of the numerical calculation and the adequacy of the selected parameters of the numerical model. Further simulation was carried out by the finite element method using the COMSOL Multiphysics 6.0 software package (Wave Optics Module).

Q-factor is the relation of energy accumulated in the cavity to the round-trip losses multiplied by angular frequency. Losses in the cavity can have different natures: radiative losses, Rayleigh scattering, material absorption, and others. Most of them are negligibly small. The total Q-factor is determined as $Q_{total}^{-1}=Q_1^{-1}+Q_2^{-1}+Q_3^{-1}+\cdots$, where $Q_i$ (i = 1, 2, 3…) state for a single loss source. The COMSOL estimates Q-factor using the relation $Q=\omega /2\left|\delta \right|$, where ω is eigenfrequency and δ is damping in time, obtained from numerical solution [23].

For example, for the modes of the unperturbed resonator, the wavelengths of eigenmodes were confirmed, and the Q-factors were also calculated: ${\widehat{Q}}_1$ = 1.2 × 10²⁰, ${\widehat{Q}}_2$ = 2.4 × 10¹⁹, ${\widehat{Q}}_3$ = 4.5 × 10¹⁷, ${\widehat{Q}}_4$ = 8.6 × 10¹⁵, ${\widehat{Q}}_5$ = 1.2 × 10¹⁶. The Q-factors are very large since the calculation was idealized and did not take into account other sources of losses (scattering, intrinsic absorption, etc.), which are present in real devices and significantly reduce the resulting Q-factor to the level < 10¹⁰⁻¹¹. There is a tendency to decrease the quality factor by about an order of magnitude from the radial number due to increase in radiative losses.

3. Results

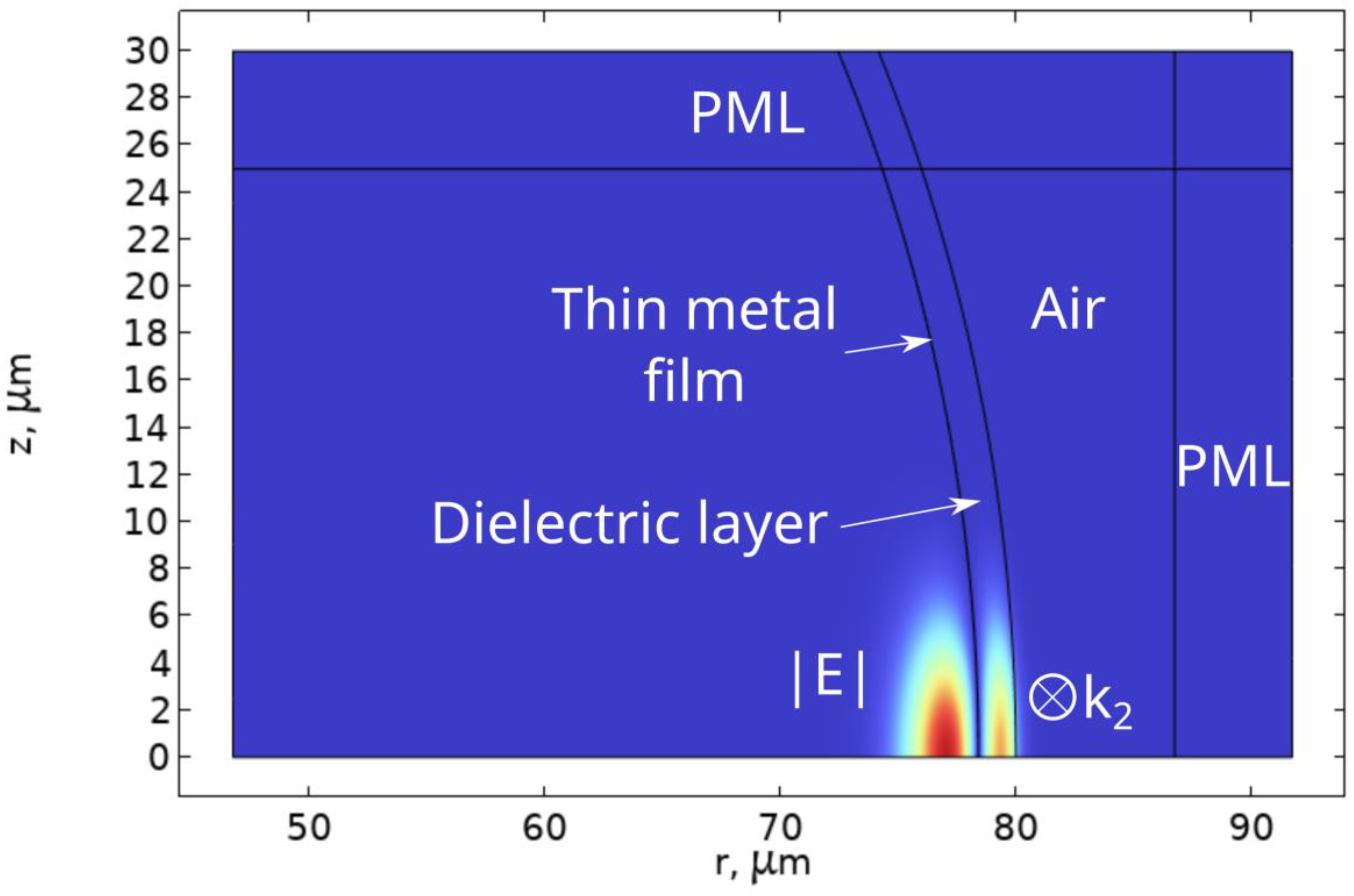
Figure 3 shows the calculated geometry of the model: the symmetry axis is $r$ = 0 in 2D axisymmetric mode, the boundary condition of Perfect Electric Conductor is added in the $z$ = 0 plane to select only $T{E}_{l,l,q}$-polarized modes and reduce the computational domain. The fused silica sphere has a radius $a$ = 80 µm; the refractive index is given by the Sellmeier function [24] $n_{Si{O}_2}(\lambda )=\sqrt{1+\frac{0.696166{\lambda }^2}{{\lambda }^2-0.004679}+\frac{0.407946{\lambda }^2}{{\lambda }^2-0.013512}+\frac{0.897479{\lambda }^2}{{\lambda }^2-97.934003}}$; the refractive index of the nickel film is $n_{Me}\left(\lambda \right)=\sqrt{1+\frac{1.405475·{10}^7{\lambda }^2}{{\lambda }^2+8.794777·{10}^6}+\frac{5.{530745\lambda }^2}{{\lambda }^2+0.388456}}$; and the extinction coefficient $k_{Me}\left(\lambda \right)=\sqrt{1+\frac{1.{582130\lambda }^2}{{\lambda }^2-0.669663}+\frac{310.{081886\lambda }^2}{{\lambda }^2+10.828637}}$ ($\lambda$ is in micrometers) is determined by approximation of data for bulk nickel in the wavelength range of 1–2 µm [25]. There is air outside the sphere $n_{air}$ = 1. The computational area of 40 × 25 µm starts from the coordinate $r$ = 42.5 µm, and Perfectly Matched Layers are placed in the $+z$ and $+r$ directions to suppress the reflection from the boundaries. In the region of silica and air, a triangular computational mesh was generated with the maximum grid size $\lambda /8n$, where $n$ is the refractive index of the material in the region. In the metal film, the mesh is rectangular and has five nodes in the radial direction, and the nodes are matched with adjacent areas at boundaries. In perfectly matched layers, the mesh is also rectangular and has 10 elements in the corresponding direction. In the described model, it is necessary to use an iterative process to search for eigenmodes for a given polar index $l$ since the dispersion of the refractive index is not taken into account in the calculation but is assumed to be constant at the wavelength in the vicinity of which the calculation is performed. To determine the eigenmodes of a resonator with a thin metal film, the wavelength of the corresponding mode obtained from analytical formulas for the unperturbed resonator is used as the zeroth approximation ${\lambda }_q^{\left[0\right]}$. Further, after finding the first approximation for the wavelength ${\lambda }_q^{\left[1\right]}$, the latter must be substituted into the calculation again so that the refractive index is calculated for the new wavelength. Thus, several iterations of the calculation of eigenmodes should be carried out until the difference in wavelengths becomes negligible $\left|{\lambda }_q^{\left[p\right]}-{\lambda }_q^{[p-1]}\right|$ < 1 pm, where $p$ is the iteration number (two or three iterations are usually sufficient). The thickness of the metal film directly affects the absorption losses in the resonator and the nature of the mode selection. Investigation of the dependence of the degree of selection on the film thickness may be the subject of a separate study. For example, the thickness of the nickel film was taken as 5 nm from the point of view of the availability of technological fabrication by vacuum deposition and the introduction of small losses for the selectable mode. From the experimental point of view, it should be taken into account that the optical properties of thin metal films with thicknesses less than 20 nm strongly depend on the conditions of their formation since they may not yet have a continuous surface but may consist of islands with a high degree of capacitive component, which determines its anomalous optical properties, which differs from those for bulk metal.

The obtained preliminary values of the radii $r_2$ and $r_3^{\left(\mathrm{1,2}\right)}$ for an unperturbed resonator are not optimal from the point of view of the maximum quality factor since, when a thin film is added, the spatial distribution of eigenmodes is deformed both from the point of view of the spatial distribution and values of wavelengths ${\lambda }_q$. The parameters of modes that differ from the selected one are more affected due to the larger overlap integral over the film cross-sectional area and the mode field. Therefore, it is necessary to optimize the position of the film along the radius for the selected mode. In our case, the film position was varied in the range from $r_q$ − 5 nm to $r_q$ + 5 nm with a step of 0.5 nm (q = 2, 3). 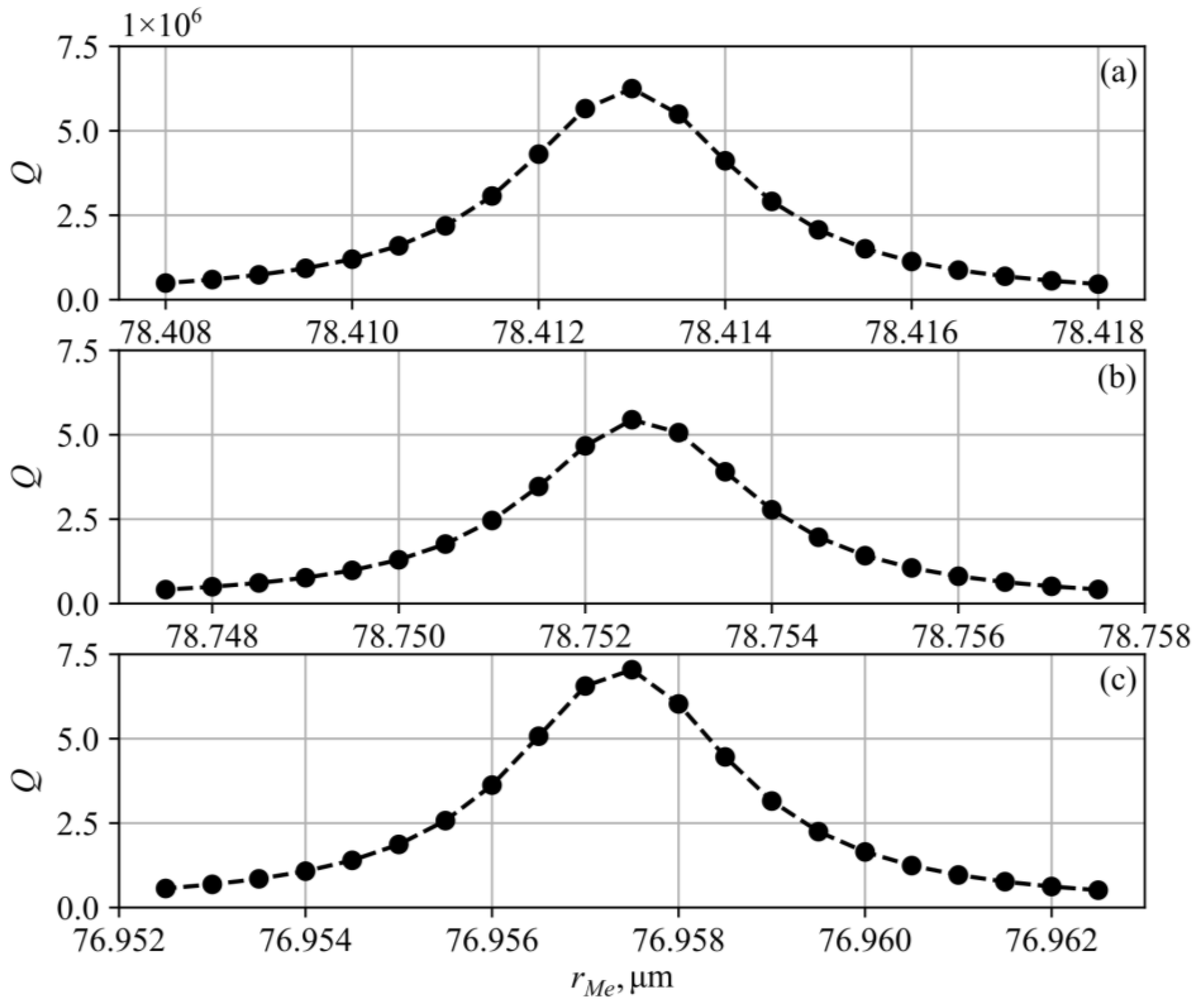Figure 4a shows the dependence of the calculated Q-factor for the $T{E}_{l,l,2}$ mode on the radial position of the film $r_{Me}$. The maximal quality factor $Q_2$ = 6.25∙10⁶ is achieved at $r_2$ = 78.413 μm and ${\lambda }_2$ = 1514.392 nm and a decrease in the Q-factors by order of magnitude corresponds to the shift of film position approximately by its own thickness relative to the optimal radius. Similar results are obtained for both zeros of the $T{E}_{l,l,3}$ mode: $r_3^{\left(1\right)}$ = 78.7525 µm, $Q_3^{\left(1\right)}$ = 5.44∙10⁶, ${\lambda }_3^{\left(1\right)}$ = 1486.617 nm (Figure 4b), $r_3^{\left(2\right)}$ = 76.9575 µm, $Q_3^{\left(2\right)}$ = 7.04∙10⁶, and ${\lambda }_3^{\left(2\right)}$ = 1486.616 nm (Figure 4c).

Next, for the film to be in the optimal position, it is necessary to calculate the quality factors of other modes; for example, this was carried out for the first five radial modes. As follows from Figure 5, Q-factors drop significantly for indices other than the selectable mode in all three cases. Moreover, for the case of the second zero of the third mode, the quality factor of the first (main) mode is an order of magnitude greater than for the other two cases. This happens because the radius $r_3^{\left(2\right)}$ is the smallest one; thus, the film is located in the region of smaller values of the fundamental mode electric field and introduces less loss. In this case, it is more advantageous to suppress the fundamental mode at the radius that is closest to its field maximum for the unperturbed case.

An interesting question is whether there are such modes in which zeros coincide with the zero of the selected mode with an accuracy of 5 nm in order to obtain relatively high Q-factors for them. It is likely that there is some higher mode for which the film will be close to one of its zeros, and such a mode will have a significant quality factor. This question is related to the properties of the zeros of the Riccati–Bessel functions ${\varphi }_l\left(x\right)$. Therefore, it can be argued that, on the one hand, the method with one absorbing film at least significantly reduces the number of excited radial modes but does not guarantee the suppression of all higher modes. On the other hand, a possible higher selectable mode will have a rather high index $q$ and its radiative losses would be significant.

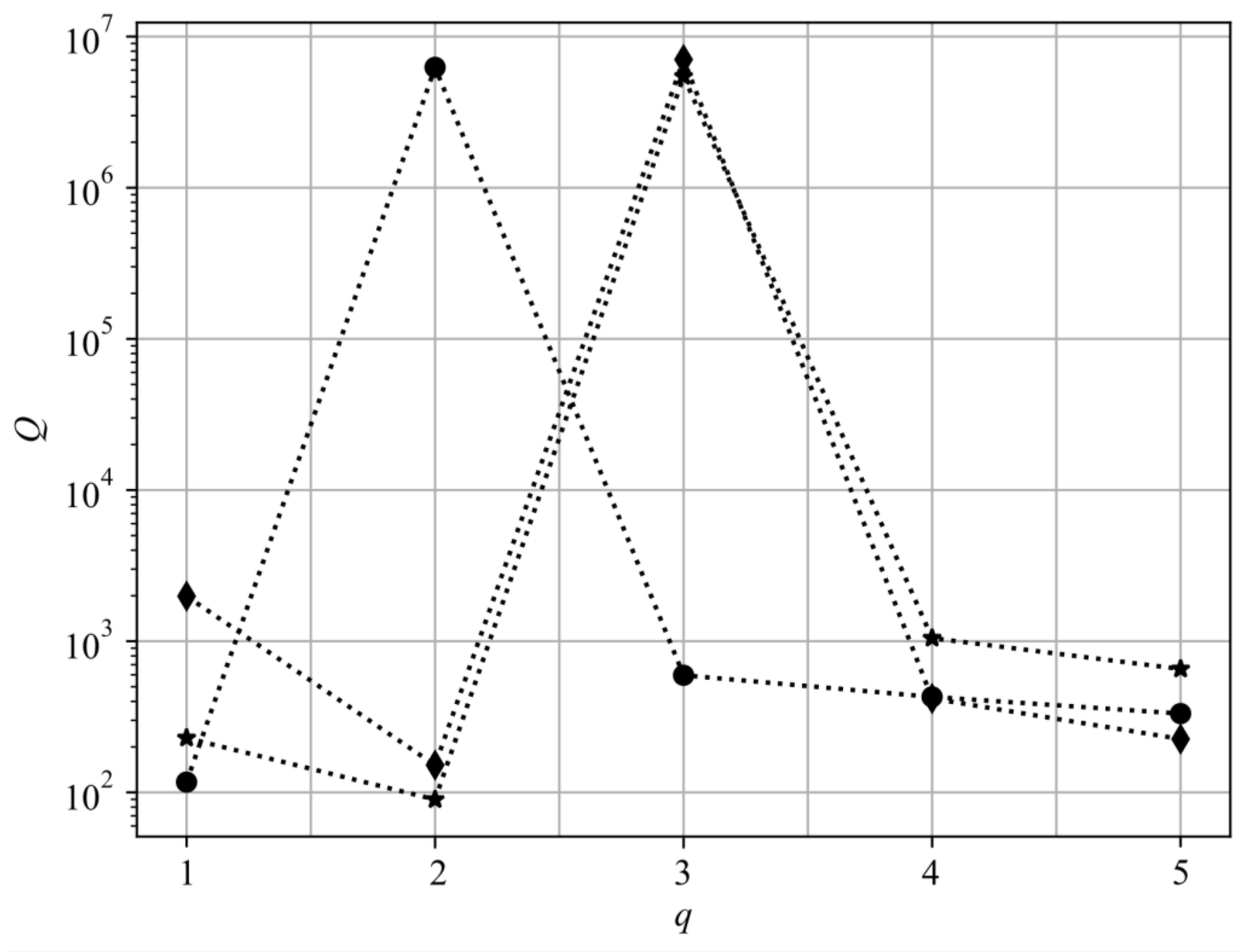
In addition to the radial index, the thin metal film also selects modes with polar indices different from $l$ = 455. Selection becomes possible because the position of the mode node depends on the wavelength since it presents in the argument of Equations (1) and (2). Figure 6 shows the dependencies of the quality factors of selected modes on the index $l$. The difference in wavelengths between neighboring indices approximately equals the free spectral range (≈3.2 nm), which is equivalent to the spectral range for the $T{E}_{l,l,2}$ mode from 1483.26 nm ($l$ = 465) to 1546.81 nm ($l$ = 445), in which the zero of the electric field $r_2$ moves by 40 nm. The quality factor in this range changes hundreds of times. For the $T{E}_{l,l,3}$ mode, the spectral range is from 1456 nm ($l$ = 465) to 1517 nm ($l$ = 445), and the first and second zeros shift by 30.5 nm and 90 nm, respectively, which determines the different slopes of their characteristics.

4. Discussion

The features of the proposed selection method include the absorption of the energy of undesirable modes in the thin metal film, which will lead to the heating of materials and change in the parameters of microsphere eigenmodes, especially in cases of high excitation power and low efficiency of coupling to the selected mode. In this sense, the question of whether it is possible to reduce the thermal load by analogy with the metal-diffraction structure method in a fiber-reflective interferometer [26] or to use a non-absorptive diffractive structure remains open. The essential difference, in this case, is that the energy does not propagate perpendicular to the surface of the absorbing (scattering) structure but is tangential to it.

One of the options for the experimental implementation of the method is to fabricate the film and the outer layer by vacuum deposition. However, here several technological problems arise that need to be overcome. The high reproducibility of thin metal film formation with desired optical properties and dielectric layer are among them. We suppose that this could be carried out using magnetron sputtering with a low deposition rate (down to nm/min) and rapid sphere rotation. Moreover, the curvature radius of the microsphere should be constant along the propagation direction in order to prevent the drift of the node’s position. Otherwise, it will lead to a decrease in the Q-factor. Another problem may be related to the quality of the dielectric coating, but this technological problem can also be solved by a suitable method of deposition.

The proposed structure can be used as a high-sensitivity sensor. For example, the metal film can absorb external radiation, thus heating the whole microsphere and changing the propagation condition. A similar effect will arise in the external alternating magnetic field because of surface currents in the thin film.

The work demonstrates the selection of only higher radial modes since they have at least one local minimum of the field ${\mathit{E}}_{\mathit{\theta }}\left(r\right)$. For the fundamental mode, this method is inapplicable due to the absence of local minima and the placement of the film at a large distance from the surface of the sphere, where the field of the fundamental mode already drops significantly, will lead to a decrease in absorption for higher modes. Apparently, high-quality selection of the fundamental mode can be carried out by a metal film with a gap placed at the radius of nonzero values of the higher radial modes.

This method, apparently, will provide selection and different absorption for higher modes by the index $m$ ($l-\left|m\right|\ne 0$) of the pseudospherical resonator since the zeros of the field of these modes are shifted relative to the zeros of the selected mode.

It is assumed that based on the method presented in this paper, similar methods can be developed for other known types of axisymmetric resonators other than spherical ones.

5. Conclusions

In this paper, we propose a new method for selecting the radial modes of a spherical resonator by the quality factor based on the effect of absorption in a thin metal film deposited on a sphere together with a dielectric layer. The demonstration of the method was carried out on the example of the selection of the second and third radial modes $T{E}_{l,l,q}$, $l$ = 455, $q$ = 2, 3 in a quartz microsphere with a diameter of 160 μm with 5 nm thick nickel film. The structure of the metal-dielectric coating was determined using analytical formulas in such a way that the metal film was placed at the node of the selected mode field. A refinement calculation was performed using the finite element method, optimizing the position of the film from the point of view of the maximum quality factor. As a result, it was shown that the selected mode could have a relatively high quality factor ($Q$~10⁷), while the other radial modes are significantly suppressed ($Q$~10³). In addition, it is shown that simultaneously with radial modes, selection is carried out for longitudinal modes.