Abstract
In practical applications, the independent scattering approximation (ISA) is widely used to analyze light transfer in nanoparticle systems. However, the traditional independent scattering criterion is obtained under the assumption that the host medium surrounding particles is nonabsorbing, and thus may be invalid in certain circumstances. In this work, to explore the applicability of the ISA for small particles in absorbing host media, we calculate the extinction efficiency of particle clusters by direct solutions of macroscopic Maxwell equations. Using the far-field and distance-independent definitions of extinction, the computational efficiency multi-sphere method is applied for particle clusters in absorbing host, and its accuracy is verified with the discrete dipole approximation method. It is well known that for small particles, the dependent scattering in transparent host always enhances the extinction of the cluster and the criterion for the ISA is nearly independent of the particle refractive index and particle size. We show, however, that when the host medium is absorbing, the dependent scattering between particles can lead to a decreased or even negative extinction, and thus the ISA criterion depends on the particle refractive index, size, and host medium absorption index. In this result, the generalized criteria for absorbing host media may differ significantly from the conventional ones for transparent host media. The results can provide guidance in solving problems related to light transfer in nanoparticle systems, particularly in the presence of absorption in the host medium.
1. Introduction
The phenomenon of radiative (light) transfer in nanoparticle systems is ubiquitous and plays a vital role in numerous applications, including climate science, ocean optics, remote sensing, biomedicine, color paints, solar energy utilization and radiative cooling [1,2,3,4,5,6,7,8,9,10,11,12]. Accurate prediction of the radiative properties of nanoparticle systems is central to such applications. An approximate method based on the radiative transfer equation (RTE) is one of the most used methods for calculating the radiative properties of nanoparticle systems [13,14]. Prior to solving the RTE, the scattering properties of particles should be determined. Most works usually calculate the scattering properties of particles based on the independent scattering approximation (ISA) [1,2,15,16]. Under the ISA, the scattering properties of an individual particle in the nanoparticle system are independent of the other particles [1,2]. While the ISA predictions are accurate when the interparticle separation is sufficiently large, they may deviate significantly from the actual properties when particles are in close proximity [2,15,17]. Therefore, the main task of the radiative property calculation is to decide whether the ISA is applicable for the specific practical problem at hand [18].
So far, plenty of works have been conducted to investigate the applicability conditions of the ISA (independent scattering criterion) [2,19,20]. Tien and coworkers [21,22,23] established a regime map for deciding whether dependent scattering can be neglected over a wide range of size parameters and volume fractions based on theoretical analysis and experimental research. Their results suggest that the ISA is satisfied if the clearance-to-wavelength ratio is larger than 0.5 (or the particle volume fraction is less than 0.006). Quirantes et al. [24] used the T-matrix method to calculate scattering cross sections of two-sphere clusters and used the results to determine the maximum distance required to produce interparticle light scattering interaction. Hohmann et al. [25] investigated the effects of multiple and dependent scattering on the Mueller matrix by comparing results of a polarization-sensitive radiative transfer solution to the Maxwell theory. Mishchenko et al. [26] studied the applicability conditions of the RTE based on comparisons of the experimentally measured Stokes reflection matrix for suspensions of microscopic latex particles in water with solutions of the vector RTE. Galy et al. [15] proposed a new criterion for the scattering cross section and the asymmetry factor based on electromagnetic scattering calculation of particle systems with up to eight spherical particles. However, previous studies typically assumed that particles are embedded in the nonabsorbing (transparent) host medium, neglecting the effect of host medium absorption on particle scattering [15,16,18,27,28].
Cases where the absorption of the host medium cannot be neglected are frequently encountered in practical applications. Examples include light scattering by cloud particles surrounded by water vapor in the atmosphere, light scattering by particles in polymers, biomedicine, and many others [4,29,30]. Neglecting host medium absorption can result in errors, because the host medium absorption nullifies the validity of many scattering quantities that are well defined for the nonabsorbing host medium [31]. To obtain appropriate scattering properties for absorbing host media, various approaches have been proposed from different perspectives. One widely used approach is based on the asymptotic form of the scattered field in the far-field zone [32,33,34]. Another widely used approach is based on the integration of the field on the surface of the particle [35,36]. Mishchenko [37,38,39] has developed an alternative approach using the vector volume integral equation, where the far-field extinction cross section and scattering matrix represent observable quantities and can be applied to the RTE. Using the above or other approaches, the optical properties of individual spherical particles [31,40,41,42,43,44,45,46,47,48] and individual aspherical [49,50,51,52] particles have been studied with consideration of the effect of host medium absorption on particle scattering. Additionally, light transfer in the nanoparticle system, which consists of monodisperse or polydisperse spheres randomly dispersed in an absorbing host medium, has also been investigated based on the RTE and the ISA [29,30,53]. However, the independent scattering criterion used in these studies is derived for nonabsorbing host media, and thus may be invalid for absorbing host media. Recently, multiple scattering of light by spherical particles embedded in absorbing host media has been investigated using the statistical approach, and several numerical examples have been presented to illustrate the spectral transmittance and reflectance of thin films containing a two-dimensional array of spherical particles [54].
Many aspects of light scattering by particles in absorbing host media have been studied; however, little work has focused on the effects of host medium absorption on the independent scattering criterion. Considering the widespread use of the ISA (and the RTE) and the presence of absorption in the host medium in many applications, it is necessary to explore the applicability conditions of the ISA for absorbing host media. In this paper, we aim at providing a comprehensive analysis of the applicability conditions of the ISA for absorbing host media. To accomplish this objective, we must obtain the scattering properties of a cluster of nanoparticles considering both the host medium absorption and dependent scattering effects. Using the far-field and distance-independent definitions of extinction [37] and the multi-sphere method (MSM) [55], we can obtain the scattering properties that take these two effects into account simultaneously. Note that the MSM is one of the most efficient numerically exact methods for solving the macroscopic Maxwell equations, which can take into account the interactions between particles. Although the MSM is typically used for nonabsorbing host media, it can be used for absorbing host media with appropriate modifications of the definition of the scattering quantities. With the help of the above methods, we first investigate the extinction properties of a cluster of particles embedded in absorbing host media considering the dependent scattering effect. Then, the effects of host medium absorption on the applicability conditions of the ISA are analyzed. Various factors, including particle refractive index, particle radius, and host medium absorption index, are discussed.
2. Methodology
In this section, we describe the MSM for the absorbing host medium and the cluster models for investigating the independent scattering criterion. The MSM has been well established, and several codes, such as the GMM code [56], the MSTM code [57], the FaSTMM code [58], and the CELES code [59], are freely available. The main idea of the MSM is to expand the scattered fields from all the spheres into a single expansion written about the origin of the cluster. This procedure is based on the addition theorem for vector spherical wave functions, which allows a scattered field from one sphere to be represented as an exciting field in another sphere [55]. It should be noted that to account for the host medium absorption effect, the far-field scattering quantities need to be redefined. In this work, the definition given by Mishchenko [37,60] is adopted because the corresponding scattering quantities can be applied to the RTE.
2.1. Expansion of the Scattered Field
We consider the model of a cluster consisting of nonoverlapping spheres embedded in an absorbing host medium with known complex refractive index . Each sphere is characterized by its radius and complex refractive index , for . The central point of the cluster serves as the origin of the primary coordinate system and the central point of the sphere serves as the origin of the coordinate system, as shown in Figure 1.
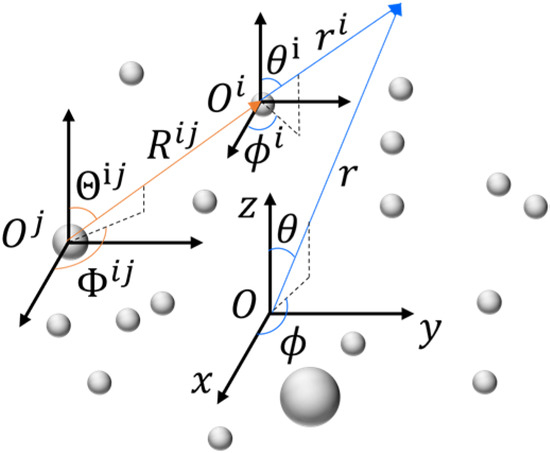
Figure 1.
Illustration of the coordinate systems. The central point of the cluster serves as the origin of the primary coordinate system, and the central point of the () sphere () serves as the origin of the () coordinate system. is the distance from to , and and are the directions from to .
According to the MSM, the scattered field of the cluster can be represented by the superposition of scattered fields from each of the spheres in the cluster [55]
The scattered field of the sphere can be expanded in terms of vector spherical wave functions about its origin as
where is the truncation order [61], is the complex wavenumber in the host medium, is the wavelength in a vacuum, and and are the scattering expansion coefficients for sphere . and represent the vector spherical wave functions and are given by [62]
where , , and . In addition, , and denote the spherical Bessel function, the spherical Hankel function of the first kind, and the associated Legendre function, respectively [1,63,64]. In a similar fashion, the vector spherical harmonic expansion of the incident field is written about the origin of the sphere as [55]
where and are the incident expansion coefficients about the origin . Using the above equations and the addition theorem for vector spherical wave functions, the scattered field of the cluster as a whole can be expanded about the origin of the cluster as [55]
where and are the scattering expansion coefficients of the cluster as a whole in the primary coordinate system. Note that the complex-valued wavevector does not affect the form of the formulas and [65]. Thus, the expressions of the fields for an absorbing medium do not differ from those for a nonabsorbing medium, except that the refractive index of the host medium is complex-valued.
2.2. Far-Field Extinction and Scattering of Sphere Clusters
As shown in Figure 2, we assume the incident light propagates along the axis, and the plane containing the scattering direction (or ) and the incident direction (or ) defines the scattering plane.
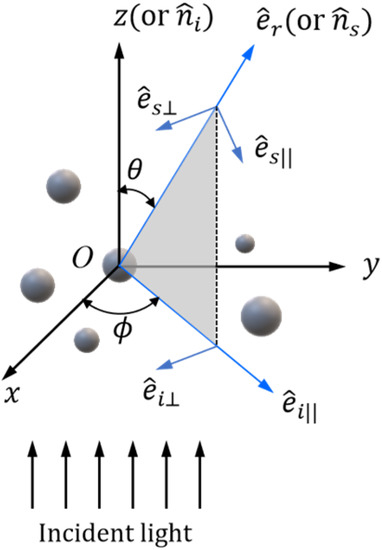
Figure 2.
Schematic of light scattering by particles when the incident direction is along the axis. The scattering plane contains the scattering direction (or ) and the incident direction (or ). The scattered field is resolved into components parallel () and perpendicular () to the scattering plane, respectively.
Following these conventions, the incident electric field is resolved as [1,64]
Similarly, the scattered field in the far-field region is resolved as [64]
or as
where and . Note that the wavenumber is complex for the absorbing host medium. The relation between the scattered and incident fields can be represented by a amplitude scattering matrix [64]
With the elements of the amplitude scattering matrix known, the optical quantities of interest can be derived from them.
Using Mishchenko’s definition [37,60], the far-field and distance-independent extinction and scattering cross sections and the scattering phase function are written as
where is the real part of the complex wavenumber in the absorbing host medium, Im represents the imaginary part of the argument, and the asterisk denotes the complex conjugate. Taking the extinction cross section as an example, the explicit expressions for incident -polarized and -polarized lights are written as
where the subscripts and on (or ) denote the arguments calculated for incident -polarized and -polarized lights, respectively, and Re represents the real part of the argument. The formulas reduce to the conventional formulas in a nonabsorbing host medium [61]. For incident unpolarized light, the extinction cross section is simply given by , and the corresponding extinction efficiency factor is given by , while is the effective volume-equivalent-sphere radius. For monodispersed spheres, we have .
2.3. Nanoparticle Cluster Model for Investigating the Independent Scattering Criterion
Similar to previous studies [15,16,18,27], the model of an imaginary spherical volume filled with randomly distributed identical spheres (see Figure 3) is used to explored the effect of host medium absorption on the scattering properties of a nanoparticle cluster. By keeping the particle radius fixed while scaling all particle coordinates, the clusters with different average interparticle clearances (or particle volume fraction ) are obtained. The average clearance is calculated based on the relative positions of particles.

Figure 3.
Spherical volume elements filled with 27 and = 100 randomly distributed identical spheres.
If the interactions between particles can be neglected, the total extinction cross section of the -sphere cluster is equal to times the corresponding single-particle extinction cross section . Therefore, in the independent scattering regime, the value of the nondimensional extinction cross section
must be equal to unity [27]. In practical applications, the independent scattering regime is usually considered to be reached when the extinction of the cluster deviates less than 5% from the summation of extinction by the individual particles (the value of locates between 0.95 and 1.05). In this work, the ratio of average interparticle clearance to wavelength is used to determine the ISA criterion, and the ISA is considered to be applicable when 0.95 1.05.
First, we investigate the extinction properties of sphere cluster embedded in absorbing host media with different particle radii and particle numbers for both fixed and random orientations. Then, the impact of host medium absorption on the applicability conditions of the ISA is analyzed, considering the effects of the particle refractive index and particle radius.
3. Validation
In this section, we validate the MSM by comparing it with the discrete dipole approximation (DDA) method [50,51] for absorbing host media. The extinction efficiency factor and the scattering phase function are used for validation in this work, because these two parameters represent observable quantities in the absorbing host medium. The clusters composed of = 2, 3 and 8 spheres are considered. The complex refractive indices of the spheres and the host medium are = 1.5 and , respectively. The incident light propagates along the axis, and the wavelength in a vacuum is λ = 2 μm. Figure 4a–d shows the extinction efficiency factors of two-sphere clusters, calculated by the MSM and the DDA method, as a function of the ratio of interparticle clearance to the radius of sphere 1, . represents the total number of discretized sub-volumes of the multiple-sphere cluster. Different numbers of discretized sub-volumes are used to ensure the accuracy of the DDA results. As shown, the extinction efficiency factors obtained by the MSM coincide very well with those obtained by the DDA method. Figure 4e,f shows the extinction efficiency factors of three-sphere and eight-sphere clusters as a function of sphere radius . Some minor differences are observed for large radius, but the differences become smaller with increasing the number of the discretized sub-volumes .
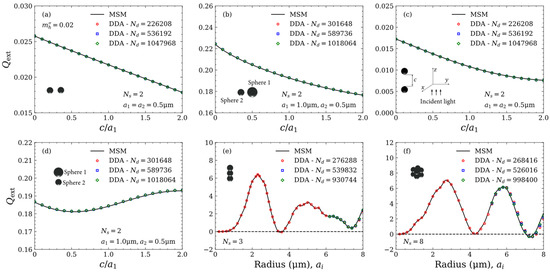
Figure 4.
Comparison of MSM and DDA method extinction efficiency factors for (a–d) two-sphere clusters with different ratios of interparticle clearance to radius of sphere 1, , and (e) three-sphere and (f) eight-sphere clusters with different sphere radii . The complex refractive indices of the spheres and the host medium are 1.5 and , respectively. is the number of the discretized sub-volumes.
Figure 5 compares the scattering phase functions calculated by the MSM and DDA method. It is seen that the MSM results are also in good agreement with the DDA results. In addition, the running times of the MSM and the DDA ( 526,016) method for calculating the scattering properties of the eight-sphere cluster ( 5.0 μm) are 0.463 s and 2423 s, respectively. Note that the calculations are performed on a 64-bit Windows 10 operating system with an Intel Xeon 6144 CPU using one core. Obviously, MSM is much more efficient in calculating particle clusters than the DDA method.
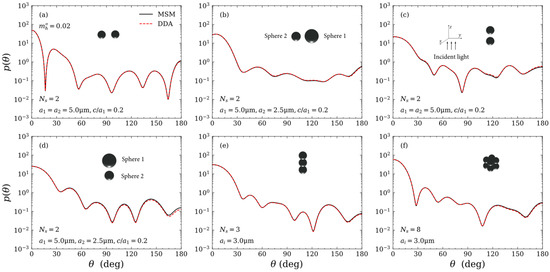
Figure 5.
Comparison of MSM and DDA method scattering phase functions for (a–d) two-sphere clusters, (e) three-sphere cluster and (f) eight-sphere cluster. The complex refractive indices of the particles and the host medium are 1.5 and , respectively.
4. Results and Discussion
4.1. Extinction Properties of Sphere Clusters Embedded in Absorbing Host Media
In this subsection, we will investigate the effect of the host medium absorption on the extinction properties of multiple-sphere clusters. Figure 6 depicts the extinction efficiency factors of two-sphere clusters at a fixed orientation versus the ratio of interparticle gap to sphere radius with 0.2, 1.0 and 2.0 μm, respectively. The incident light propagates (a)–(c) perpendicularly to and (d)–(f) along the line connecting the centers of the two spheres. The complex refractive indices of the particle and the host medium are 1.59 and with 0.0, 0.001, 0.01 and 0.02, respectively. The incident wavelength is λ = 2 μm. For comparison, the extinction efficiency factors of the single sphere with radius equal to the cluster components are listed in Table 1. As shown, with enhancing the absorption of the host medium, the extinction efficiency factor of the single sphere decreases at 0.2 and 1.0 μm, but increases at 2.0 μm. A similar trend is found for the two-sphere cluster. In addition, for the case of 0.2 μm and 0.01 and 0.02, the extinction efficiency factor is negative for the single sphere, but may become positive for the two-sphere cluster. This phenomenon can be understood from the negative extinction and the dependent scattering effects. The concept of extinction in an absorbing host medium is the difference between two readings of a well-collimated detector in the absence and in the presence of particles [40,41]. Therefore, under the conditions where the particle is less attenuated than the host medium, the extinction efficiency factor of the particle is negative [45,66]. However, the dependent scattering effects may enhance the extinction of light by particles, so that the host medium can be less attenuated than the two-sphere cluster. As a consequence, the extinction efficiency factor is no longer negative. On the other hand, it is found in Figure 6f that when 0.02, the amplitude of the interference oscillations increases exponentially with increasing . This phenomenon has been observed and discussed in previous studies of individual particles [40,41]. For a nonabsorbing particle embedded in an absorbing host medium, the exponentially increasing amplitude of the oscillations with increasing particle size is due to the fact that the directly transmitted light is no longer subject to the exponential attenuation over the path length given by the particle diameter [40,41]. With this explanation, the exponential increase in the amplitude of the oscillations of two-sphere clusters can also be understood.
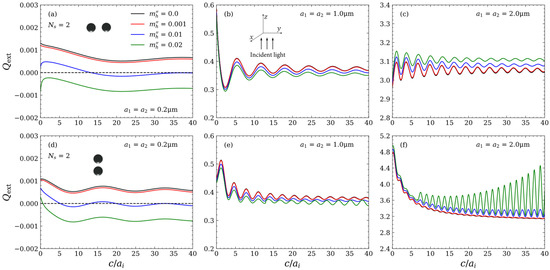
Figure 6.
The extinction efficiency factors of two-sphere clusters versus the ratio of interparticle gap to sphere radius with 0.2, 1.0 and 2.0 μm, respectively. The incident light (λ = 2 μm) propagates (a–c) perpendicularly to and (d–f) along the line connecting the centers of the two spheres. The complex refractive indices of the particle and the host medium are = 1.59 and with 0.0, 0.001, 0.01 and 0.02, respectively.

Table 1.
The extinction efficiency factors of the single particle with 0.2, 1.0 and 2.0 μm, respectively. The complex refractive indices of the particle and the host medium are = 1.59 and with 0.0, 0.001, 0.01 and 0.02, respectively.
Considering that the complex refractive index of a material typically varies with the wavelength, we also investigate the extinction efficiency factors of randomly oriented silica (SiO2) clusters embedded in polyethylene (PE), as presented in Figure 7a–d for different particle numbers , and in Figure 7d–f for different particle radii . The complex refractive indices of SiO2 and PE are taken from [67] and [68], respectively. The particle volume fraction is fixed at 0.1. The extinction efficiency factors presented in the figures are averaged over 132 different orientations and 10 different configurations to obtain random-orientation averaging results. In practical applications, particles with radii in the order of a few nanometers to micrometers may be used [6,69]; however, we only focus on small particles with radii ranging from 40 to 160 nm. In addition, we consider the wavelength range of 3–12 µm because it is especially useful for designing functional coatings, and the resonance peak of SiO2 is also in this wavelength range [70,71]. As demonstrated in Figure 7, within the wavelength range of 3.0–8.0 μm, the host medium absorption can lead to negative extinction, which significantly deviates from the results for the nonabsorbing host medium. In contrast, within the wavelength range of 8.0–12.0 μm, the effect of host medium absorption on can be neglected due to the extremely small values of and the strong absorption of the particle. Moreover, the comparison between the clusters with different particle radii (see Figure 7d–f) reveals that the differences caused by neglecting the host medium absorption become more pronounced as the particle radius increases from 40 to 160 nm. Notably, the changes in the extinction will, in turn, affect the applicability conditions of the ISA, as we shall discuss in the following section.
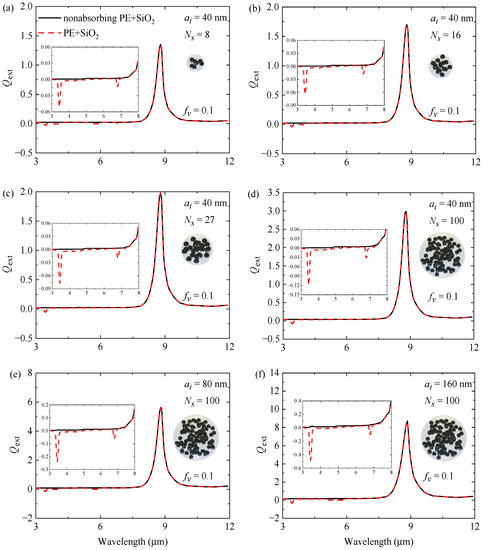
Figure 7.
The extinction efficiency factors of SiO2 nanoparticle clusters embedded in PE and its nonabsorbing counterpart with different particle numbers and particle radii . Each cluster consists of identical particles with a particle volume fraction of 0.1. (a) 8 and 40 nm, (b) 16 and 40 nm, (c) 27 and 40 nm, (d) 100 40 nm, (e) 100 and 80 nm, and (f) 100 and 160 nm. The results are averaged over 132 different orientations and 10 different configurations.
4.2. Effect of Host Medium Absorption on the Dependent Scattering between Particles
In this subsection, we investigate the effect of host medium absorption on the applicability conditions of the independent scattering approximation (ISA). The ISA is widely used in many analyses involving particles [2]. Similar to previous studies [15,16,18,27], we use the model of a small volume filled with monodisperse spherical particles to investigate the applicability conditions of the ISA. Each cluster consists of = 27 identical particles. The complex refractive index of the host medium is with ranging from 0.0 to 0.01, and the incident wavelength is λ = 4.0 μm, unless otherwise specified. Note that the value of 1.5154 is selected as the refractive index (real part of the complex refractive index) of polyethylene (PE) at λ = 4.0 μm. The particle radius ranges from 40 to 160 nm, which is small compared to the incident wavelength.
Figure 8 presents the color images of the nondimensional extinction cross section as functions of relative refractive index and the ratio of average interparticle clearance to wavelength , with varying from 0.8 to 2.0, and varying from 0.055 to 4.91. The particle radius is 40 nm, and the particle absorption index (imaginary part of the complex refractive index) is 0.0. The white regions in the images represent the value of lying between 0.95 and 1.05, indicating that the ISA is satisfied. It should be noted that Figure 8 does not encompass the instance where the complex refractive index of the host medium is equal to that of the particle ( = 1.0 and 0.0). As seen in Figure 8a, when the host medium is nonabsorbing ( 0.0), the particle refractive index has a negligible impact on and the applicability conditions of ISA. This observation agrees with previous results and can be attributed to the fact that for small particles, the phase shift is negligible and the scattering is isotropic [15]. Moreover, when particles are close to each other, the values of are always greater than 1.0, suggesting that the interactions between particles enhance the particle extinction. In contrast, when the host medium is absorbing, as illustrated in Figure 8b–d, the values of can be greater than 1.0, less than 1.0, or even negative (cause by the negative extinction), depending on . This means that the interactions between particles may decrease particle extinction ( 1.0), which differs significantly from that observed in nonabsorbing host media. Meanwhile, it is found that as decreases from 2.0 to 0.8, may display a sharp transition from a value of greater than 1.0 to a value of less than 0.0 (negative value). For example, when 0.001 and 0.055 (see Figure 8c), the values of at 1.56 and 1.58 are −396.84 and 113.04, respectively. When 0.01 and 0.055 (see Figure 8d), the value of is 15.95 at 1.66, but decreases to −123.29 at 1.64.
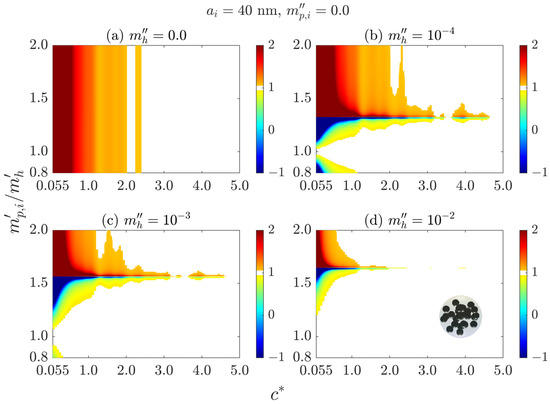
Figure 8.
Color images of the nondimensional extinction cross sections of 27-sphere clusters versus and the ratio of average interparticle clearance to wavelength . The results are averaged over 132 different orientations and 10 different configurations. The radius of the particle is 40 nm, and the incident wavelength is λ = 4.0 μm. The complex refractive index of the host medium is with (a) 0.0, (b) 0.0001, (c) 0.001 and (d) 0.01. The white regions represent the ISA being satisfied ().
The change in will inevitably affect the critical that makes the ISA applicable (0.95 1.05). To better illustrate the effect of host medium absorption on the ISA criterion, we also plot the nondimensional extinction cross section as a function of the ratio of average interparticle clearance to wavelength for 40 nm, 1.38, 2.1216 and 3.0308 ( 0.911, 1.4 and 2.0), and (a) 0.0, (b) 0.0001, (c) 0.001 and (d) 0.01, respectively, as shown in Figure 9. The blue region indicates that the ISA is satisfied for all the three considered. Two dashed lines corresponding to 0.95 and 1.05, respectively, are also plotted for comparison. As expected, when the host medium is nonabsorbing (see Figure 9a), the particle refractive index has little impact on the critical . In this case, the ISA is applicable regardless of the particle refractive index, provided that 2.52. Nevertheless, it can be seen from Figure 9b–d that when the host medium is absorbing, the ISA criterion is correlated with particle refractive index , and even a minor change in the host medium absorption index may result in considerable changes in the critical . For instance, when 1.38 ( 0.911), the criteria ensuring that the ISA is accurate within 5 percent are approximately 2.52, 0.61, 0.22 and 0.055, for 0.0, 0.0001, 0.001 and 0.01, respectively. When 3.0308 ( 2.0), the criteria are approximately 2.52, 2.1, 1.64 and 0.66, for 0.0, 0.0001, 0.001 and 0.01, respectively. We note that when 1.38 and 3.0308, the critical decreases with the increase in , which agrees with the traditional view that absorption suppresses dependent scattering [29]. However, when 2.1216 ( 1.4), as increases from 0.0 to 0.0001, the critical increases from 2.52 to 4.1. The larger critical means that the intensity attenuation in the absorbing host is not the only factor to influence the dependent scattering.
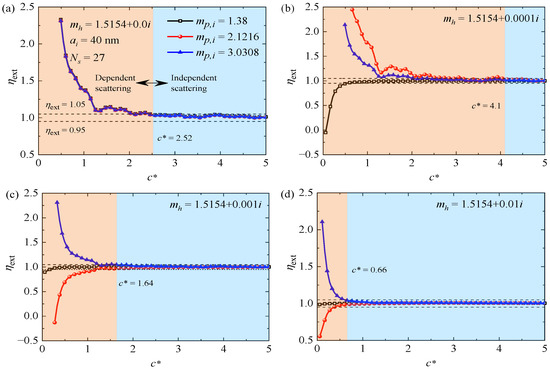
Figure 9.
The nondimensional extinction cross section of 27-sphere cluster versus the ratio of average interparticle clearance to wavelength with incident wavelength of λ = 4.0 μm, particle radius of 40 nm, and particle refractive index of 1.38, 2.1216 and 3.0308 ( 0.911, 1.4, and 2.0), respectively. The complex refractive index of the host medium is with (a) 0.0, (b) 0.0001, (c) 0.001 and (d) 0.01. The blue region indicates that the ISA is satisfied for all the three considered. The results are averaged over 132 different orientations and 10 different configurations.
The preceding discussions have shown that the host medium absorption can either decrease or increase the critical . This is reasonable because host medium absorption can affect the applicability conditions of the ISA from two perspectives. On the one hand, the intensity of light is attenuated as it travels through an absorbing medium. In this regard, the host medium absorption suppresses the dependent scattering and thereby renders the ISA applicable at smaller . On the other hand, the host medium absorption also influences the extinction efficiency factor of individual particles (or particle clusters), which, in turn, affects the critical . These two different effects result in the dependence of the critical on particle refractive index in an absorbing host medium. Although the variation in the critical with is complex. It can be seen from Figure 8 and Figure 9 that in regimes where the value of changes from larger than 1.0 to less than 0.0 (negative), a larger may be required to ensure the accuracy of the ISA.
We also investigate particle clusters with different particle radii. The color images of the nondimensional extinction cross sections as functions of and the ratio of average interparticle clearance to wavelength are illustrated in Figure 10 for 80 nm and in Figure 11 for 160 nm. It is obvious that both the nondimensional extinction cross section and the critical are almost independent of the particle refractive index when the host medium is nonabsorbing, but are correlated with the particle refractive index when the host medium is absorbing. A comparison among particles with different radii demonstrates that in absorbing host media, the particle radius has significant impacts on both and the critical . Furthermore, when the host medium is absorbing, it may need a larger to ensure the accuracy of the ISA in regimes where the value of changes from larger than 1.0 to less than 0.0, which is similar to that observed for the case of 40 nm.
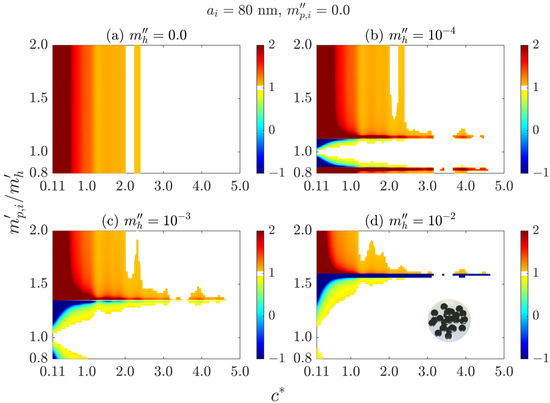
Figure 10.
Color images of the nondimensional extinction cross sections of 27-sphere clusters versus and the ratio of average interparticle clearance to wavelength . The results are averaged over 132 different orientations and 10 different configurations. The radius of the particle is 80 nm, and the incident wavelength is λ = 4.0 μm. The complex refractive index of the host medium is with (a) 0.0, (b) 0.0001, (c) 0.001 and (d) 0.01. The white regions indicate that the ISA is satisfied (0.95 1.05).
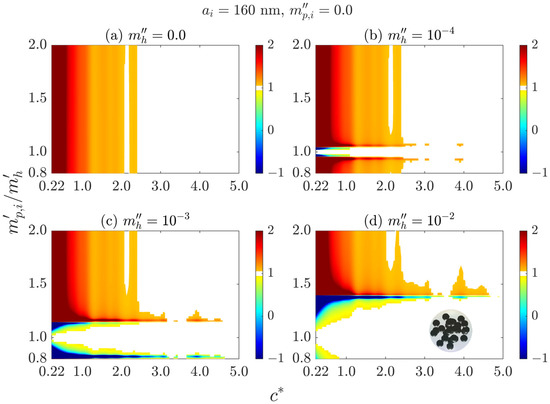
Figure 11.
As in Figure 10, but for 160 nm. is the ratio of average interparticle clearance to wavelength.
Overall, in absorbing host media, the applicability conditions of the ISA are affected by the particle radius , particle refractive index (or ) and host medium absorption index , making it difficult to establish an accurate and comprehensive criterion of ISA based only on limited calculation results. However, for all the cases considered in Figure 8, Figure 9, Figure 10 and Figure 11, the criteria 2.52 for nonabsorbing host media and 4.8 for absorbing host media ensure that the accuracy of the ISA is kept within 5 percent.
Additionally, to illustrate the effect of host medium absorption on the ISA criterion in practical applications, we also investigate the case of silica (SiO2) particles embedded in polyethylene (PE) and its nonabsorbing counterpart. Three incident wavelengths of λ = 3.35, 5.0 and 10.0 μm are considered. The nondimensional extinction cross sections of multiple-sphere clusters composed of 27 identical particles as a function of the ratio of average interparticle clearance to wavelength are presented in Figure 12. The radii of the particles are 40, 80 and 160 nm, respectively. The results for particles embedded in PE are calculated using the actual complex refractive indices, whereas the results for particles embedded in nonabsorbing PE are calculated by assuming 0.0.
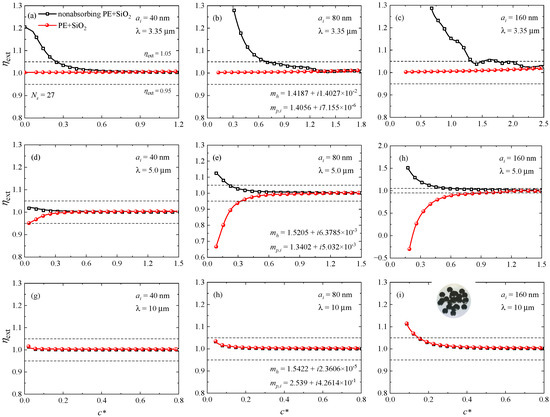
Figure 12.
The nondimensional extinction cross sections of 27-sphere SiO2 clusters embedded in PE and its nonabsorbing counterpart versus the ratio of average interparticle clearance to wavelength . The results are averaged over 132 different orientations and 10 different configurations. The incident wavelengths are (a–c) λ = 3.35 μm, (d–f) λ = 5.0 μm, and (g–i) λ = 10.0 μm. The incident wavelengths are λ = 3.35, 5.0 and 10.0 μm, respectively. The particle radii are 40, 80 and 160 nm.
When λ = 3.35 μm, the host medium exhibits strong absorption with 0.014027, and the value of is 0.9908. According to above discussions, under this condition, the strong absorption of the host medium should significantly suppress the interaction between particles, allowing the ISA to be applicable for very small values of . As a result, the critical for nonabsorbing host media should also be larger than the critical for absorbing host media. These assertions are confirmed by the results depicted in Figure 12a–c. It can be seen from Figure 12a–c that the values of always locate between 0.95 and 1.05, suggesting that the accuracy of the ISA is always kept within 5 percent.
When λ = 5.0 μm, the values of and are 0.0063785 and 0.8814, respectively. From Figure 12d–f, it can be easily observed that the values of can be less than 1.0 or less than 0.0, which will no doubt affect the applicability conditions of the ISA. Therefore, the applicability conditions of the ISA must be carefully considered in this case. These observations are consistent with the above finding that in this regime, the interactions between particles may result in a decreased or even negative particle extinction cross section.
When λ = 10.0 μm, the host medium exhibits extremely weak absorption with 0.000023606 and a value of = 1.6463. We can thus expect that the effects of host medium absorption on and the applicability conditions of the ISA are negligible. These predictions are supported by the observations in Figure 12g–i, where the values of obtained for nonabsorbing host media are almost identical to those obtained for absorbing host media and the ISA criteria for nonabsorbing host media can be regarded as the criteria for absorbing host media.
It is also found from Figure 12 that in nonabsorbing host media, the critical changes with and , which is inconsistent with our previous conclusion that the ISA criteria for nonabsorbing host media are independent of particle radius and particle refractive index. This discrepancy stems from the fact that the absorption index of SiO2 particle is nonzero at the wavelengths considered. The issue of the effect of particle absorption on ISA criteria is beyond the scope of the present work. Interested readers can refer to Ma et al. [16] for detailed discussions.
In summary, for small particles, the host medium absorption has a significant impact on the dependent scattering between particles. The generalized criteria for absorbing host media depend on the particle refractive index, size, and the host medium absorption index and may differ significantly from the conventional ones for nonabsorbing host media. Moreover, since it is impossible to encompass all factors, many relevant factors, such as polydispersity, spatial distributions and large particles, are not considered in this paper. These factors may also affect applicability conditions of the ISA. For example, the effects of host medium absorption on dependent scattering between particles are different for small particles and large particles (see Supplementary Materials, Figure S1). Thus, a lot of work remains to be done to establish an accurate and comprehensive criterion applicable to both absorbing and nonabsorbing host media.
5. Conclusions
The aim of this paper was to investigate the extinction properties and the applicability conditions of the independent scattering approximation (ISA) for multiple nanoparticles embedded in absorbing host media. The multi-sphere method (MSM) is employed to simultaneously consider the effects of host medium absorption and dependent scattering.
First, the effects of host medium absorption on the extinction properties of particles are investigated with consideration of the dependent scattering effect. The results for two-sphere clusters at a fixed orientation indicate that enhancing the absorption of the host medium has a more pronounced effect where the incident light propagates along the line connecting the centers of the two spheres. Moreover, the results for randomly oriented multiple-sphere silica clusters (with particle radius ranging from 40 to 160 nm and particle volume fraction of 0.1) embedded in polyethylene suggest that the host medium absorption can lead to negative extinction within the wavelength range of 3.0–8.0 μm, which differs significantly from the results for nonabsorbing host media.
Then, the effects of host medium absorption on the interactions between (nonabsorbing) particles and the applicability conditions of the ISA are investigated for a wide range of parameters. The particle radius ranges from 40 to 160 nm, which is small compared to the incident wavelength. The ratio of particle refractive index to medium refractive index ranges from 0.8 to 2.0, and the host medium absorption index ranges from 0 to 0.01. When the host medium is nonabsorbing, the nondimensional extinction cross section and the ISA criteria are almost independent of the particle refractive index and particle radius, and the interactions between particles always enhance particle extinction. In contrast, when the host medium is absorbing, the nondimensional extinction cross section and the ISA criteria correlate with particle size, particle refractive index and host medium absorption index, and the interactions between particles may suppress particle extinction and even lead to negative extinction. Moreover, it is found that in regimes where the value of changes from larger than 1.0 to less than 0.0 (negative), a larger (the ratio of interparticle clearance to wavelength) may be required to ensure the accuracy of the ISA, which is inconsistent with the traditional view that absorption suppresses the dependent scattering. In this result, the criteria for absorbing host media differ significantly from the conventional ones for transparent host media. Specifically, for all the cases considered in this work, the criteria 2.52 for nonabsorbing host media and 4.8 for absorbing host media ensure that the accuracy of the ISA is kept within 5 percent.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/photonics10070782/s1, Figure S1: The nondimensional extinction cross section of 27-sphere cluster versus the ratio of average interparticle clearance to wavelength with incident wavelength of λ = 4.0 μm, particle radius of 500, 750 and 1000 nm, and particle refractive index of 1.38, 2.1216 and 3.0308 ( 0.911, 1.4, and 2.0). The complex refractive index of the host medium is with 0.0, and 0.001. (a) 500 nm, 0.0, (b) 500 nm, 0.001, (c) 750 nm, 0.0, (d) 750 nm, 0.001, (e) 1000 nm, 0.0, and (f) 1000 nm, 0.001. The blue region represents that the ISA is satisfied for all the three considered. The results are averaged over 132 different orientations and 10 different configurations.
Author Contributions
Conceptualization, J.Z., S.Z. and L.L.; methodology, J.Z. and S.Z.; software, J.Z.; investigation, J.Z., S.Z. and L.L.; data curation, J.Z., S.Z. and L.L.; writing—original draft preparation, J.Z.; writing—review and editing, J.Z., S.Z. and L.L.; supervision, S.Z. and L.L.; funding acquisition, S.Z. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant 52076123) and the China Postdoctoral Science Foundation (grant 2021M691906).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time, but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Howell, J.R.; Mengüc, M.P.; Siegel, R. Thermal Radiation Heat Transfer; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Theobald, D.; Yu, S.; Gomard, G.; Lemmer, U. Design of Selective Reflectors Utilizing Multiple Scattering by Core–Shell Nanoparticles for Color Conversion Films. ACS Photonics 2020, 7, 1452–1460. [Google Scholar] [CrossRef]
- Gentle, A.R.; Smith, G.B. Radiative Heat Pumping from the Earth Using Surface Phonon Resonant Nanoparticles. Nano Lett. 2010, 10, 373–379. [Google Scholar] [CrossRef] [PubMed]
- Schertel, L.; Siedentop, L.; Meijer, J.-M.; Keim, P.; Aegerter, C.M.; Aubry, G.J.; Maret, G. The Structural Colors of Photonic Glasses. Adv. Opt. Mater. 2019, 7, 1900442. [Google Scholar] [CrossRef]
- Yalçın, R.A.; Blandre, E.; Joulain, K.; Drévillon, J. Colored Radiative Cooling Coatings with Nanoparticles. ACS Photonics 2020, 7, 1312–1322. [Google Scholar] [CrossRef]
- Hwang, V.; Stephenson, A.B.; Barkley, S.; Brandt, S.; Xiao, M.; Aizenberg, J.; Manoharan, V.N. Designing angle-independent structural colors using Monte Carlo simulations of multiple scattering. Proc. Natl. Acad. Sci. USA 2021, 118, e2015551118. [Google Scholar] [CrossRef]
- Boutghatin, M.; Assaf, S.; Pennec, Y.; Carette, M.; Thomy, V.; Akjouj, A.; Djafari Rouhani, B. Impact of SiO2 Particles in Polyethylene Textile Membrane for Indoor Personal Heating. Nanomaterials 2020, 10, 1968. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, J.; Wu, X.; Huang, M. Numerical analysis of light reflection and transmission in poly-disperse sea fog. Opt. Express 2020, 28, 25410–25430. [Google Scholar] [CrossRef]
- Ma, L.; Hu, L.; Jia, C.; Wang, C.; Liu, L. Quantitative Evaluation of the Phase Function Effects on Light Scattering and Radiative Transfer in Dispersed Systems. Photonics 2022, 9, 584. [Google Scholar] [CrossRef]
- Ma, L.; Hu, K.; Wang, C.; Yang, J.-Y.; Liu, L. Prediction and Inverse Design of Structural Colors of Nanoparticle Systems via Deep Neural Network. Nanomaterials 2021, 11, 3339. [Google Scholar] [CrossRef]
- Fei, T.; Lin, L.; Li, X.; Yang, J.-Y.; Zhao, J.; Liu, L. Modeling Effect of Bubbles on Time-Dependent Radiation Transfer of Microalgae in a Photobioreactor for Carbon Dioxide Fixation. Photonics 2022, 9, 864. [Google Scholar] [CrossRef]
- Mishchenko, M.I. Electromagnetic Scattering by Particles and Particle Groups: An Introduction; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Penttilä, A.; Markkanen, J.; Väisänen, T.; Räbinä, J.; Yurkin, M.A.; Muinonen, K. How much is enough? The convergence of finite sample scattering properties to those of infinite media. J. Quant. Spectrosc. Radiat. Transf. 2021, 262, 107524. [Google Scholar] [CrossRef]
- Galy, T.; Huang, D.; Pilon, L. Revisiting independent versus dependent scattering regimes in suspensions or aggregates of spherical particles. J. Quant. Spectrosc. Radiat. Transf. 2020, 246, 106924. [Google Scholar] [CrossRef]
- Ma, L.; Zhai, J.; Wang, C. Investigation of the single scattering approximation through direct electromagnetic scattering simulation. OSA Contin. 2021, 4, 2496–2509. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, C.Y.; Wang, B.X. Effect of nanoparticle aggregation on the thermal radiation properties of nanofluids: An experimental and theoretical study. Int. J. Heat Mass Transfer 2020, 154, 119690. [Google Scholar] [CrossRef]
- Aoyu, Z.; Fuqiang, W.; Ziming, C.; Huaxu, L.; Xuhang, S. Radiative property investigation of dispersed particulate medium with the consideration of non-uniform particle size distribution and dependent scattering effects. Int. J. Heat Mass Transfer 2022, 186, 122488. [Google Scholar] [CrossRef]
- Kokhanovsky, A. Springer Series in Light Scattering: Volume 1: Multiple Light Scattering, Radiative Transfer and Remote Sensing; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Kokhanovsky, A.A. Optics of Light Scattering Media: Problems and Solutions; Springer: London, UK, 2001. [Google Scholar]
- Cartigny, J.D.; Yamada, Y.; Tien, C.L. Radiative Transfer With Dependent Scattering by Particles: Part 1—Theoretical Investigation. J. Heat Transfer 1986, 108, 608–613. [Google Scholar] [CrossRef]
- Yamada, Y.; Cartigny, J.D.; Tien, C.L. Radiative Transfer With Dependent Scattering by Particles: Part 2—Experimental Investigation. J. Heat Transfer 1986, 108, 614–618. [Google Scholar] [CrossRef]
- Drolen, B.L.; Tien, C.L. Independent and dependent scattering in packed-sphere systems. J. Thermophys. Heat Transfer 1987, 1, 63–68. [Google Scholar] [CrossRef]
- Quirantes, A.; Arroyo, F.; Quirantes-Ros, J. Multiple Light Scattering by Spherical Particle Systems and Its Dependence on Concentration: A T-Matrix Study. J. Colloid Interface Sci. 2001, 240, 78–82. [Google Scholar] [CrossRef]
- Hohmann, A.; Voit, F.; Schäfer, J.; Kienle, A. Multiple scattering of polarized light: Influence of absorption. Phys. Med. Biol. 2014, 59, 2583. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, M.I.; Goldstein, D.H.; Chowdhary, J.; Lompado, A. Radiative transfer theory verified by controlled laboratory experiments. Opt. Lett. 2013, 38, 3522–3525. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, M.I.; Liu, L.; Videen, G. Conditions of applicability of the single-scattering approximation. Opt. Express 2007, 15, 7522–7527. [Google Scholar] [CrossRef] [PubMed]
- Yalcin, R.A.; Lee, T.; Kashanchi, G.N.; Markkanen, J.; Martinez, R.; Tolbert, S.H.; Pilon, L. Dependent Scattering in Thick and Concentrated Colloidal Suspensions. ACS Photonics 2022, 9, 3318–3332. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Dlugach, J.M. Multiple scattering of polarized light by particles in an absorbing medium. Appl. Opt. 2019, 58, 4871–4877. [Google Scholar] [CrossRef]
- Ma, L.X.; Xie, B.W.; Wang, C.C.; Liu, L.H. Radiative transfer in dispersed media: Considering the effect of host medium absorption on particle scattering. J. Quant. Spectrosc. Radiat. Transf. 2019, 230, 24–35. [Google Scholar] [CrossRef]
- Ivanenko, Y.; Gustafsson, M.; Nordebo, S. Optical theorems and physical bounds on absorption in lossy media. Opt. Express 2019, 27, 34323–34342. [Google Scholar] [CrossRef]
- Mundy, W.C.; Roux, J.A.; Smith, A.M. Mie scattering by spheres in an absorbing medium. J. Opt. Soc. Am. 1974, 64, 1593–1597. [Google Scholar] [CrossRef]
- Chýlekt, P. Light scattering by small particles in an absorbing medium. J. Opt. Soc. Am. 1977, 67, 561–563. [Google Scholar] [CrossRef]
- Quinten, M.; Rostalski, J. Lorenz-Mie Theory for Spheres Immersed in an absorbing host medium. Part. Part. Syst. Charact. 1996, 13, 89–96. [Google Scholar] [CrossRef]
- Sudiarta, I.W.; Chylek, P. Mie-scattering formalism for spherical particles embedded in an absorbing medium. J. Opt. Soc. Am. A 2001, 18, 1275–1278. [Google Scholar] [CrossRef]
- Fu, Q.; Sun, W. Mie theory for light scattering by a spherical particle in an absorbing medium. Appl. Opt. 2001, 40, 1354–1361. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, M.I. Electromagnetic scattering by a fixed finite object embedded in an absorbing medium. Opt. Express 2007, 15, 13188–13202. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, M.I. Multiple scattering by particles embedded in an absorbing medium. 1. Foldy—Lax equations, order-of-scattering expansion, and coherent field. Opt. Express 2008, 16, 2288–2301. [Google Scholar] [CrossRef]
- Mishchenko, M.I. Multiple scattering by particles embedded in an absorbing medium. 2. Radiative transfer equation. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 2386–2390. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Videen, G.; Yang, P. Extinction by a homogeneous spherical particle in an absorbing medium. Opt. Lett. 2017, 42, 4873–4876. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Dlugach, J.M. Scattering and extinction by spherical particles immersed in an absorbing host medium. J. Quant. Spectrosc. Radiat. Transf. 2018, 211, 179–187. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Dlugach, J.M. Plasmon resonances of metal nanoparticles in an absorbing medium. OSA Contin. 2019, 2, 3415–3421. [Google Scholar] [CrossRef]
- Peck, R.L.; Brolo, A.G.; Gordon, R. Absorption leads to narrower plasmonic resonances. J. Opt. Soc. Am. B 2019, 36, F117–F122. [Google Scholar] [CrossRef]
- Zhai, J.; Ma, L.; Xu, W.; Liu, L. Effect of host medium absorption on the radiative properties of dispersed media consisting of optically soft particles. J. Quant. Spectrosc. Radiat. Transf. 2020, 254, 107206. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, W.; Liu, L. Scattering by a charged sphere embedded in an absorbing medium. J. Quant. Spectrosc. Radiat. Transf. 2020, 246, 106908. [Google Scholar] [CrossRef]
- Khlebtsov, N.G. Extinction, absorption, and scattering of light by plasmonic spheres embedded in an absorbing host medium. Phys. Chem. Chem. Phys. 2021, 23, 23141–23157. [Google Scholar] [CrossRef] [PubMed]
- Peck, R.; Khademi, A.; Ren, J.; Hughes, S.; Brolo, A.G.; Gordon, R. Plasmonic linewidth narrowing by encapsulation in a dispersive absorbing material. Phys. Rev. Res. 2021, 3, 013014. [Google Scholar] [CrossRef]
- Zhang, S.; Dong, J.; Zhang, W.; Luo, M.; Liu, L. Extinction by plasmonic nanoparticles in dispersive and dissipative media. Opt. Lett. 2022, 47, 5577–5580. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, W.; Dong, J.; Liu, L. Optical theorem of an infinite circular cylinder in weakly absorbing media. Phys. Rev. A 2022, 105, 023516. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, W.; Liu, L. Discrete dipole approximation method for electromagnetic scattering by particles in an absorbing host medium. Opt. Express 2021, 29, 7690–7705. [Google Scholar] [CrossRef] [PubMed]
- Yurkin, M.A.; Moskalensky, A.E. Open-source implementation of the discrete-dipole approximation for a scatterer in an absorbing host medium. J. Phys. Conf. Ser. 2021, 2015, 012167. [Google Scholar] [CrossRef]
- Khlebtsov, N.G. Extinction and scattering of light by nonspherical plasmonic particles in absorbing media. J. Quant. Spectrosc. Radiat. Transf. 2022, 280, 108069. [Google Scholar] [CrossRef]
- Wang, C.C.; Ma, L.X. Effect of host medium absorption on polarized radiative transfer in dispersed media. Appl. Opt. 2019, 58, 7157–7164. [Google Scholar] [CrossRef]
- Loiko, N.A.; Miskevich, A.A.; Loiko, V.A. Optical characteristics of a monolayer of identical spherical particles in an absorbing host medium. J. Opt. Soc. Am. A 2023, 40, 682–691. [Google Scholar] [CrossRef]
- Hergert, W.; Wriedt, T. The Mie Theory: Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Xu, Y. Electromagnetic scattering by an aggregate of spheres. Appl. Opt. 1995, 34, 4573–4588. [Google Scholar] [CrossRef]
- Mackowski, D.W.; Mishchenko, M.I. A multiple sphere T-matrix Fortran code for use on parallel computer clusters. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2182–2192. [Google Scholar] [CrossRef]
- Markkanen, J.; Yuffa, A.J. Fast superposition T-matrix solution for clusters with arbitrarily-shaped constituent particles. J. Quant. Spectrosc. Radiat. Transf. 2017, 189, 181–188. [Google Scholar] [CrossRef]
- Egel, A.; Pattelli, L.; Mazzamuto, G.; Wiersma, D.S.; Lemmer, U. CELES: CUDA-accelerated simulation of electromagnetic scattering by large ensembles of spheres. J. Quant. Spectrosc. Radiat. Transf. 2017, 199, 103–110. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Yang, P. Far-field Lorenz–Mie scattering in an absorbing host medium: Theoretical formalism and FORTRAN program. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 241–252. [Google Scholar] [CrossRef]
- Mackowski, D.W. Calculation of total cross sections of multiple-sphere clusters. J. Opt. Soc. Am. A 1994, 11, 2851–2861. [Google Scholar] [CrossRef]
- Mackowski, D.W. Calculation of the Scattering Properties for a Cluster of Spheres. User Guide Accompanying the SCSMFO.FOR Code. 1999. Available online: ftp://ftp.eng.auburn.edu/pub/dmckwski/scatcodes/scsmfo.ps (accessed on 5 June 2023).
- Mackowski, D.W. Analysis of radiative scattering for multiple sphere configurations. Proc. Math. Phys. Eng. Sci. 1991, 433, 599–614. [Google Scholar]
- Tsang, L.; Kong, J.A.; Ding, K.H. Scattering of Electromagnetic Waves: Theories and Applications; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists; Academic Press: Boston, MA, USA, 2013. [Google Scholar]
- Bohren, C.F.; Gilra, D.P. Extinction by a spherical particle in an absorbing medium. J. Colloid Interface Sci. 1979, 72, 215–221. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- David, M.; Disnan, D.; Lardschneider, A.; Wacht, D.; Hoang, H.T.; Ramer, G.; Detz, H.; Lendl, B.; Schmid, U.; Strasser, G.; et al. Structure and mid-infrared optical properties of spin-coated polyethylene films developed for integrated photonics applications. Opt. Mater. Express 2022, 12, 2168–2180. [Google Scholar] [CrossRef]
- Chen, M.; Pang, D.; Chen, X.; Yan, H. Investigating the effective radiative cooling performance of random dielectric microsphere coatings. Int. J. Heat Mass Transfer 2021, 173, 121263. [Google Scholar] [CrossRef]
- Baneshi, M.; Maruyama, S.; Komiya, A. Infrared Radiative Properties of Thin Polyethylene Coating Pigmented With Titanium Dioxide Particles. J. Heat Transfer 2009, 132, 023306. [Google Scholar] [CrossRef]
- Wang, G.-H.; Zhang, Y.; Zhang, D.-H.; Fan, J.-P. Design and calculation of low infrared transmittance and low emissivity coatings for heat radiative applications. Int. J. Miner. Metall. Mater. 2012, 19, 179–184. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).