The Design of Large Curved Waveguide Based on Sunflower Graded Photonic Crystal
Abstract
1. Introduction
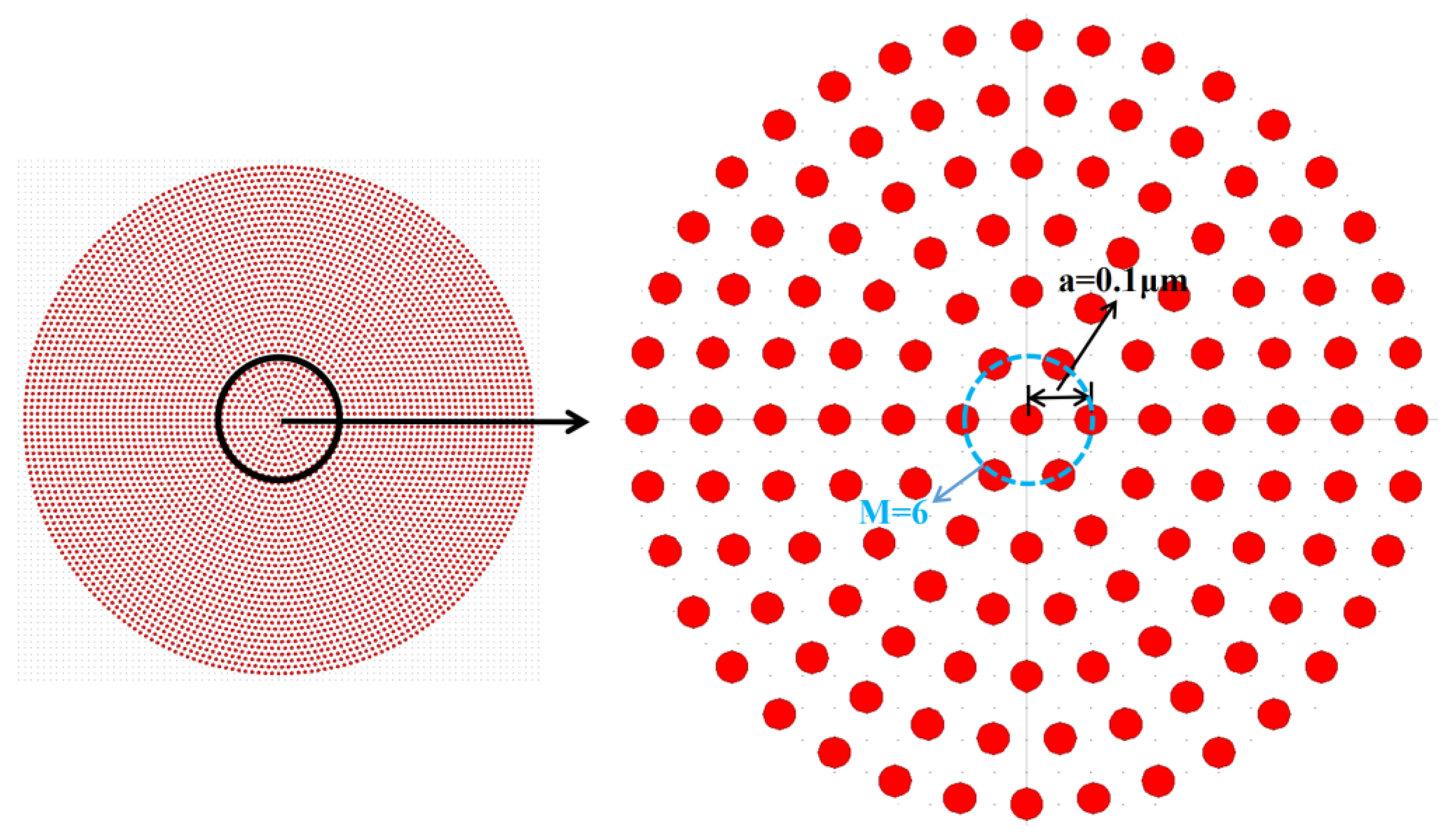
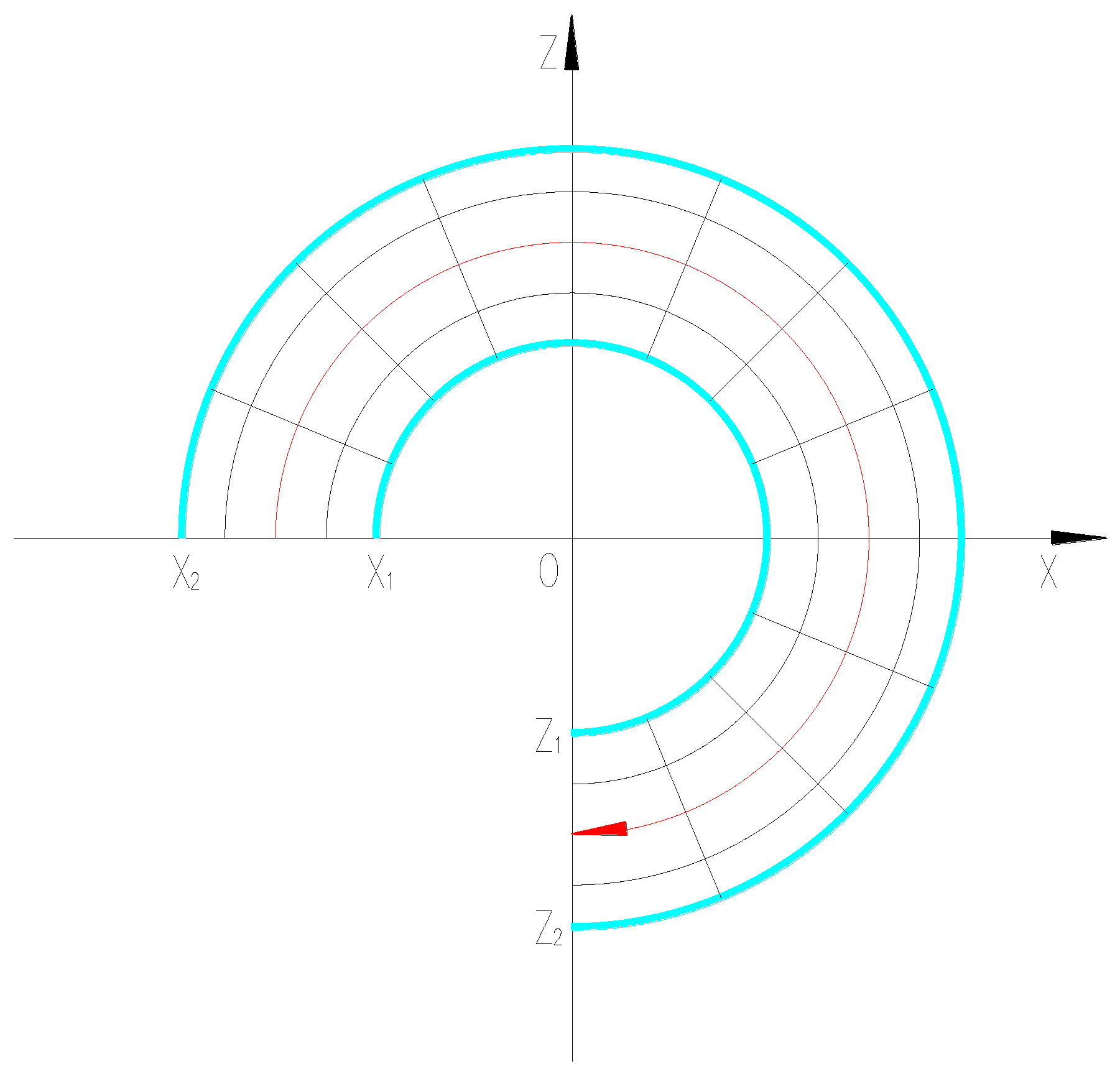
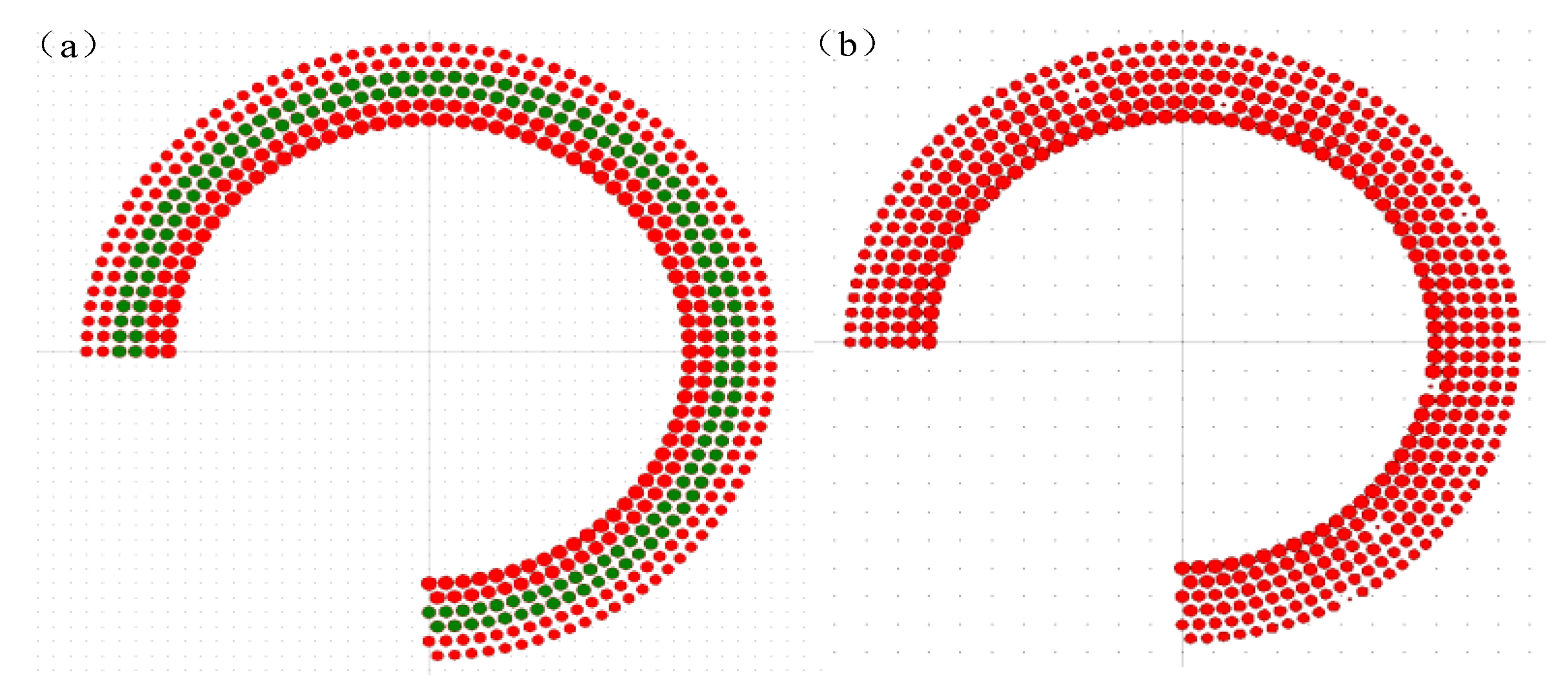
2. The Principle of the Design
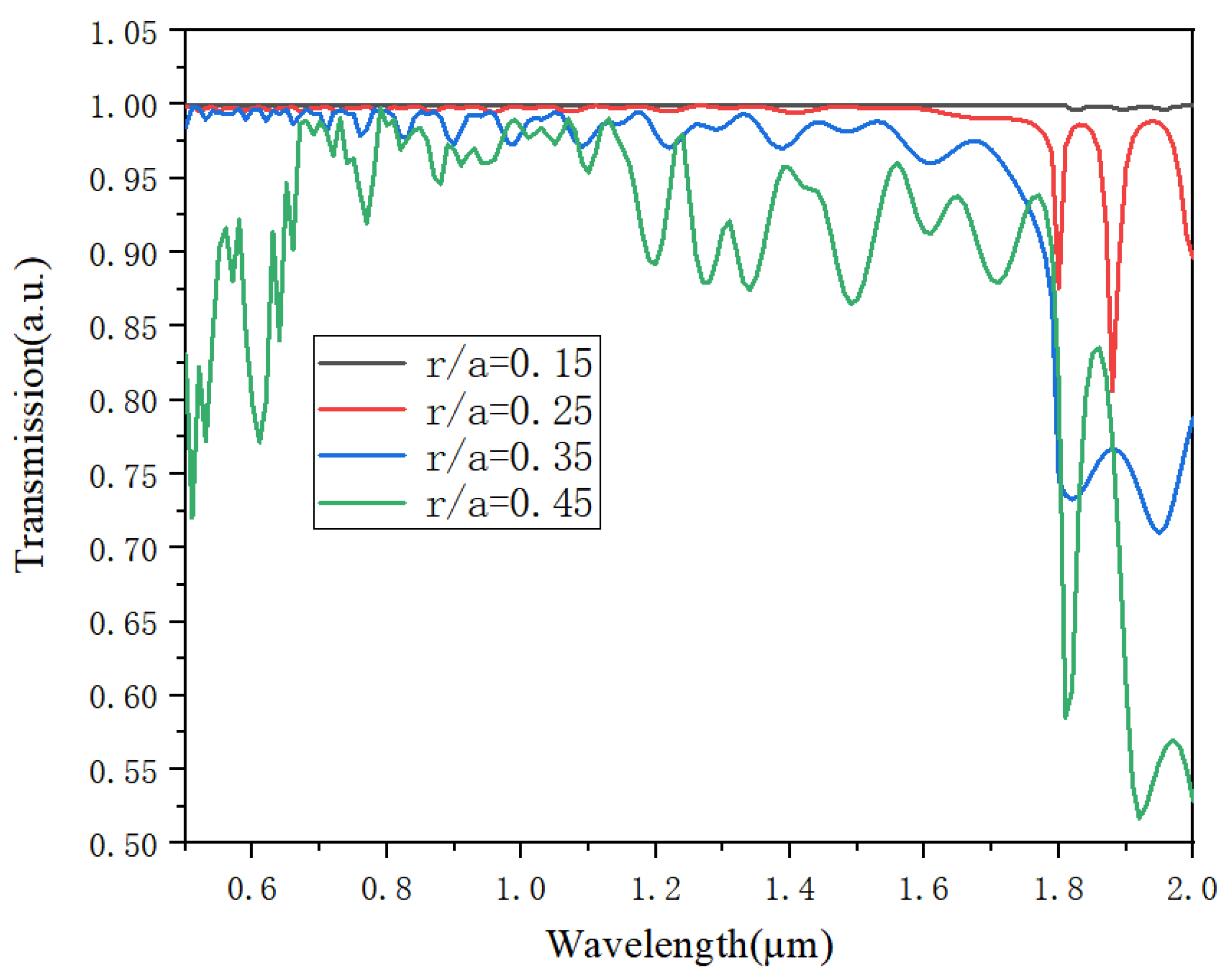
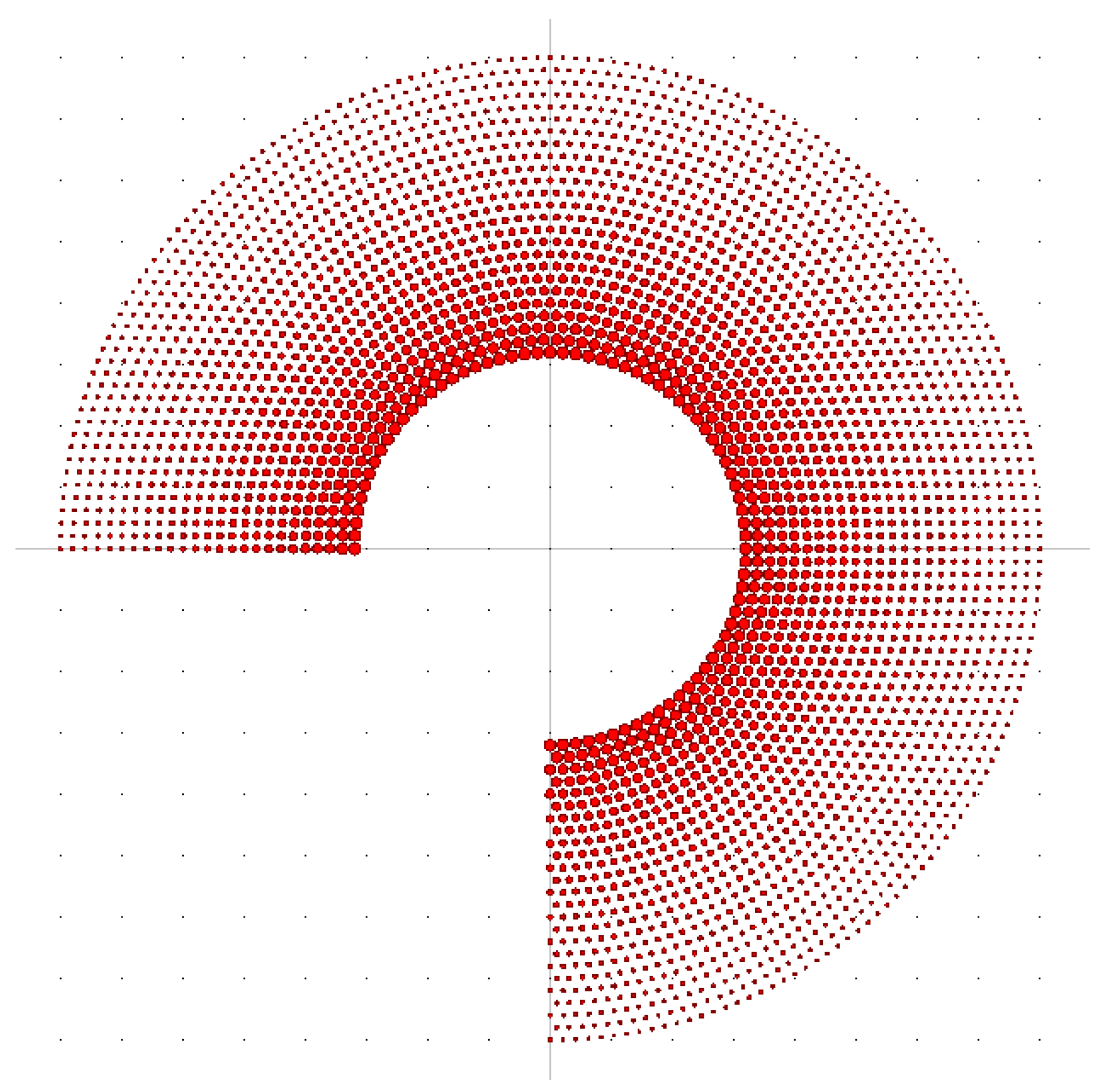
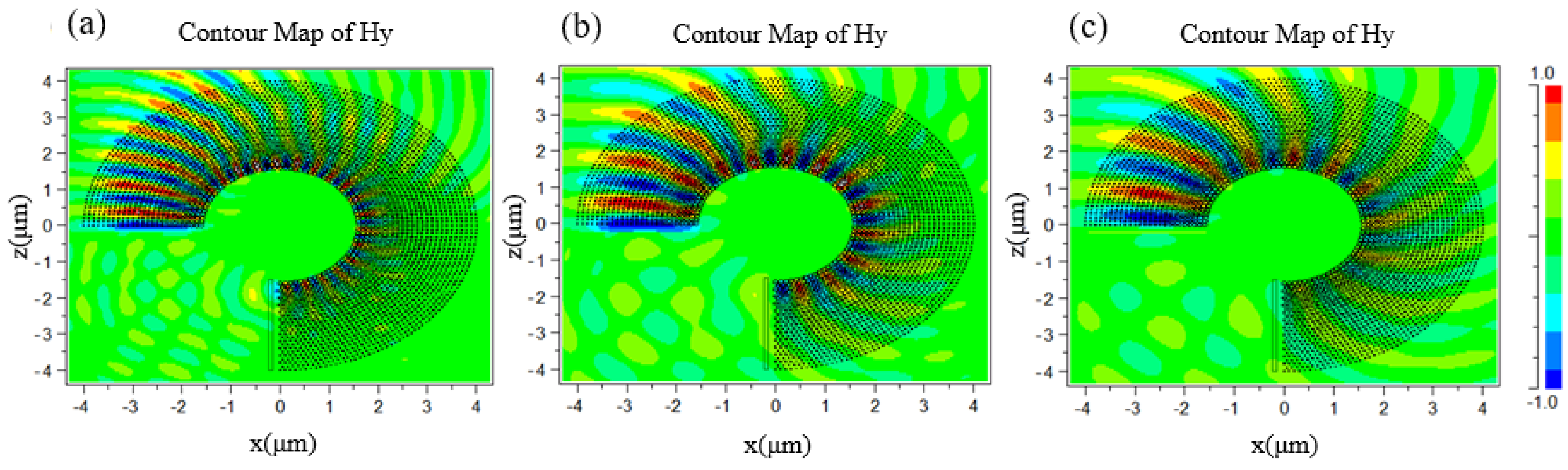
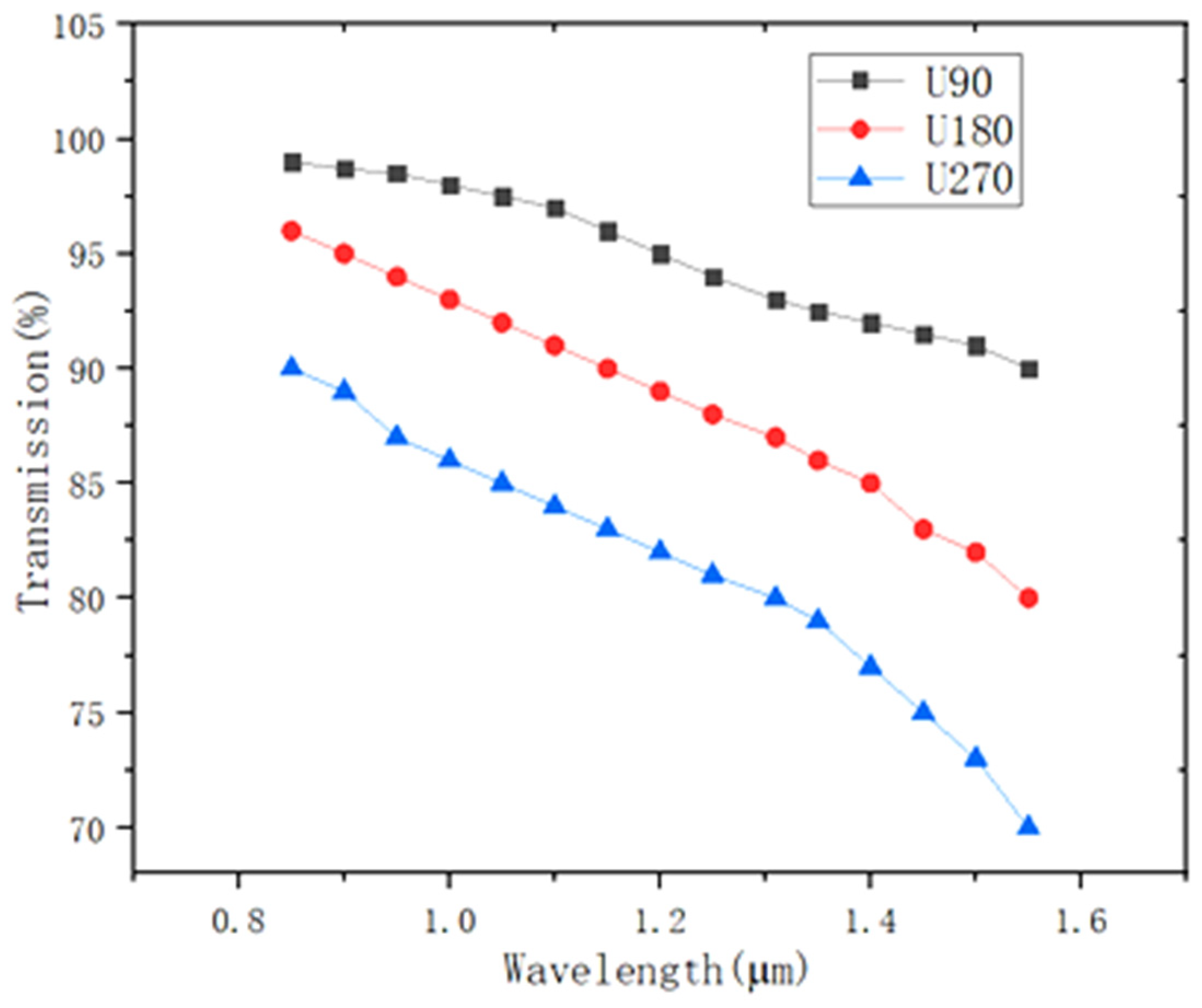
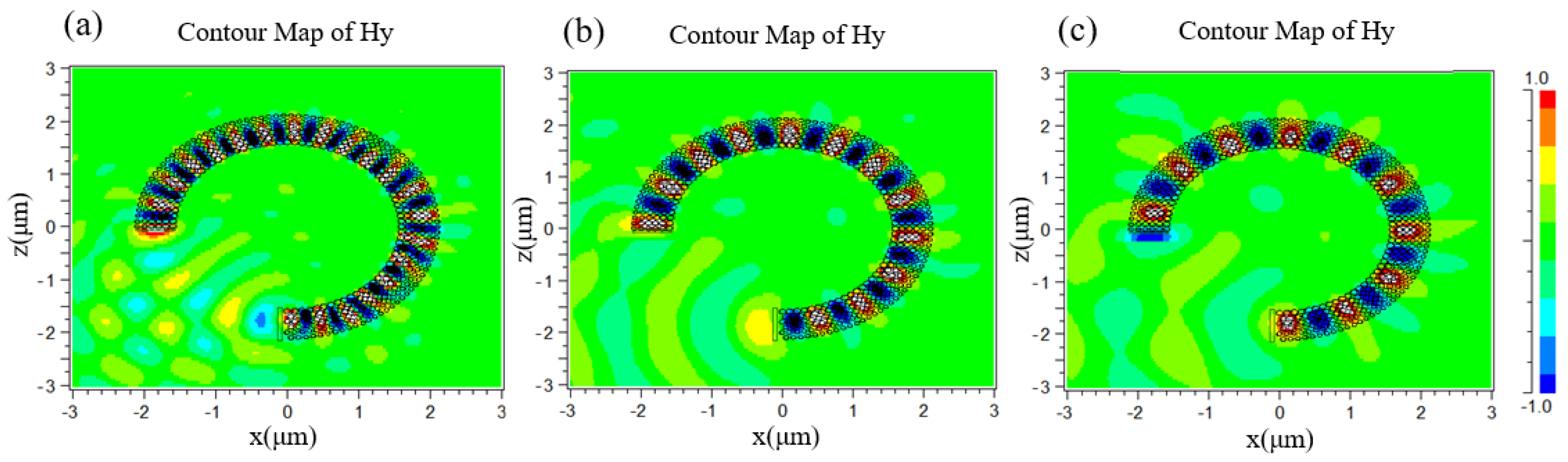
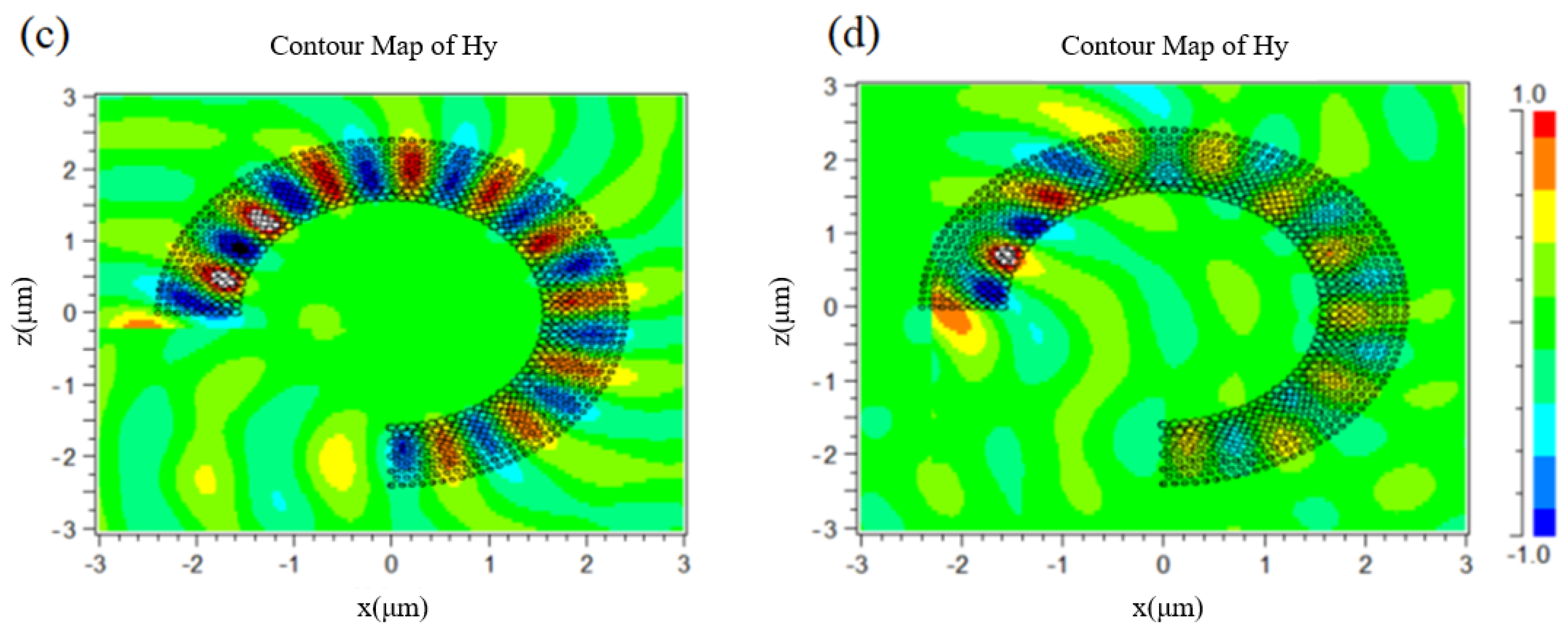
3. The Simulation of Large Curved Waveguide
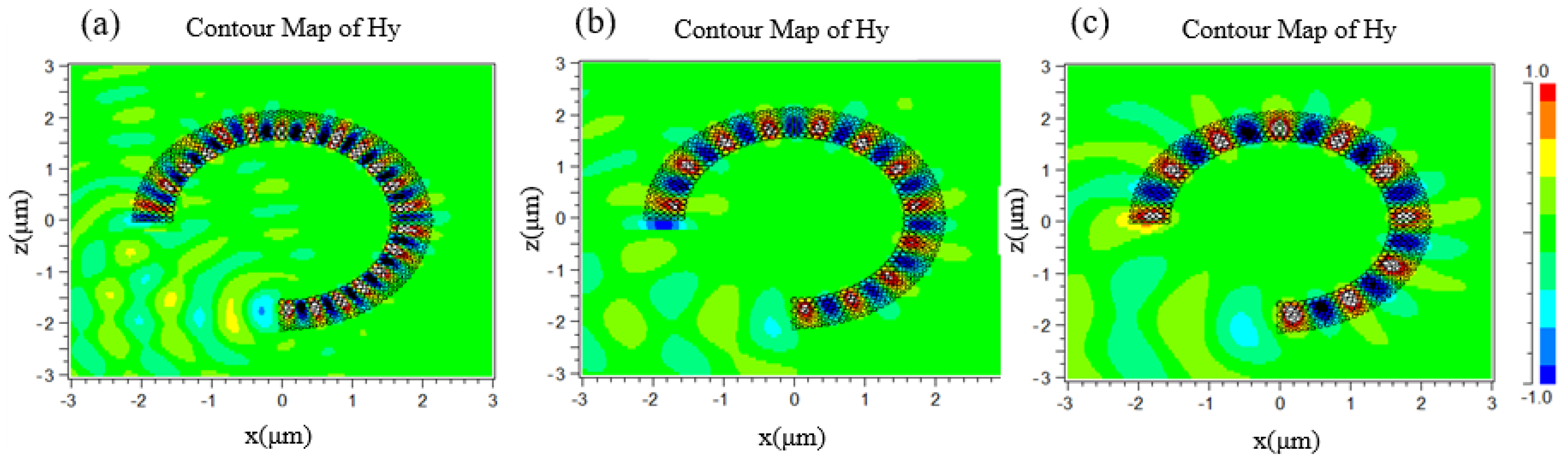
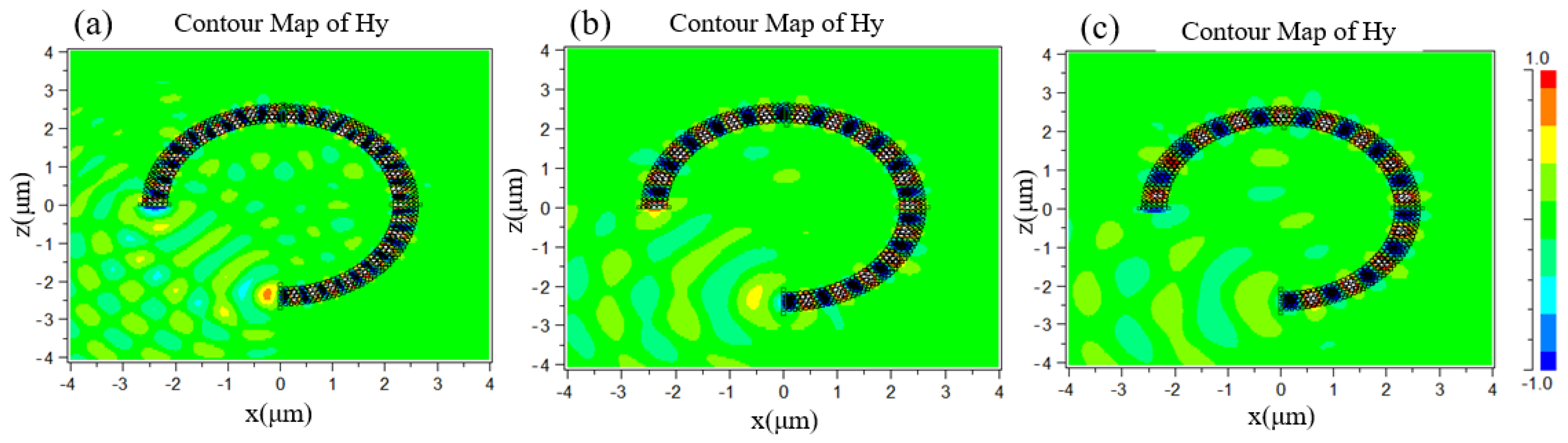
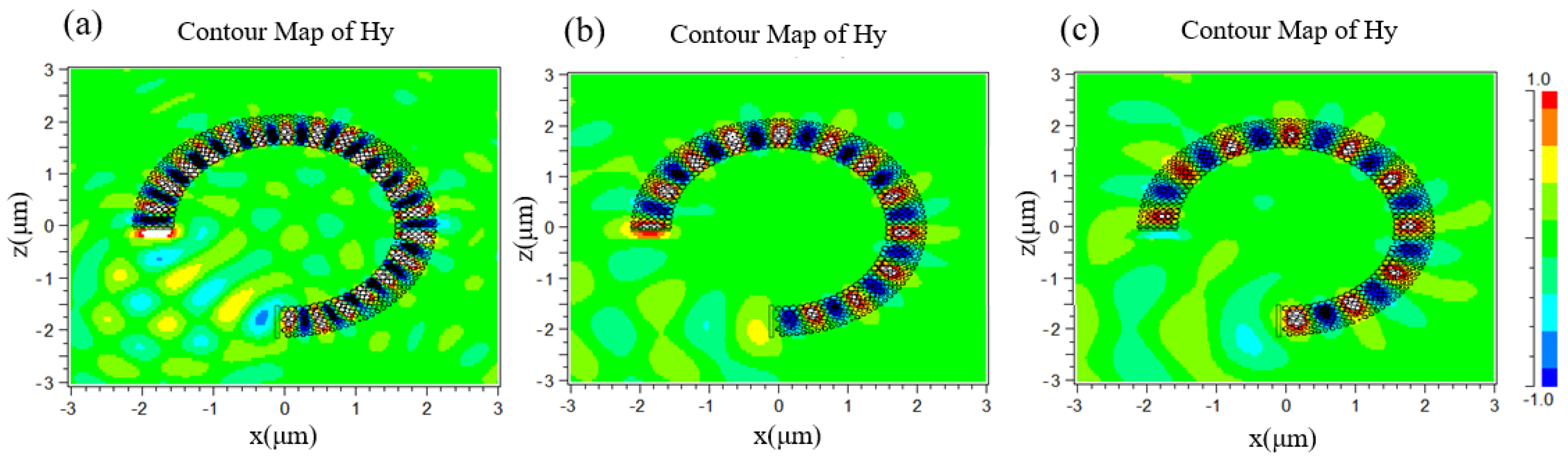
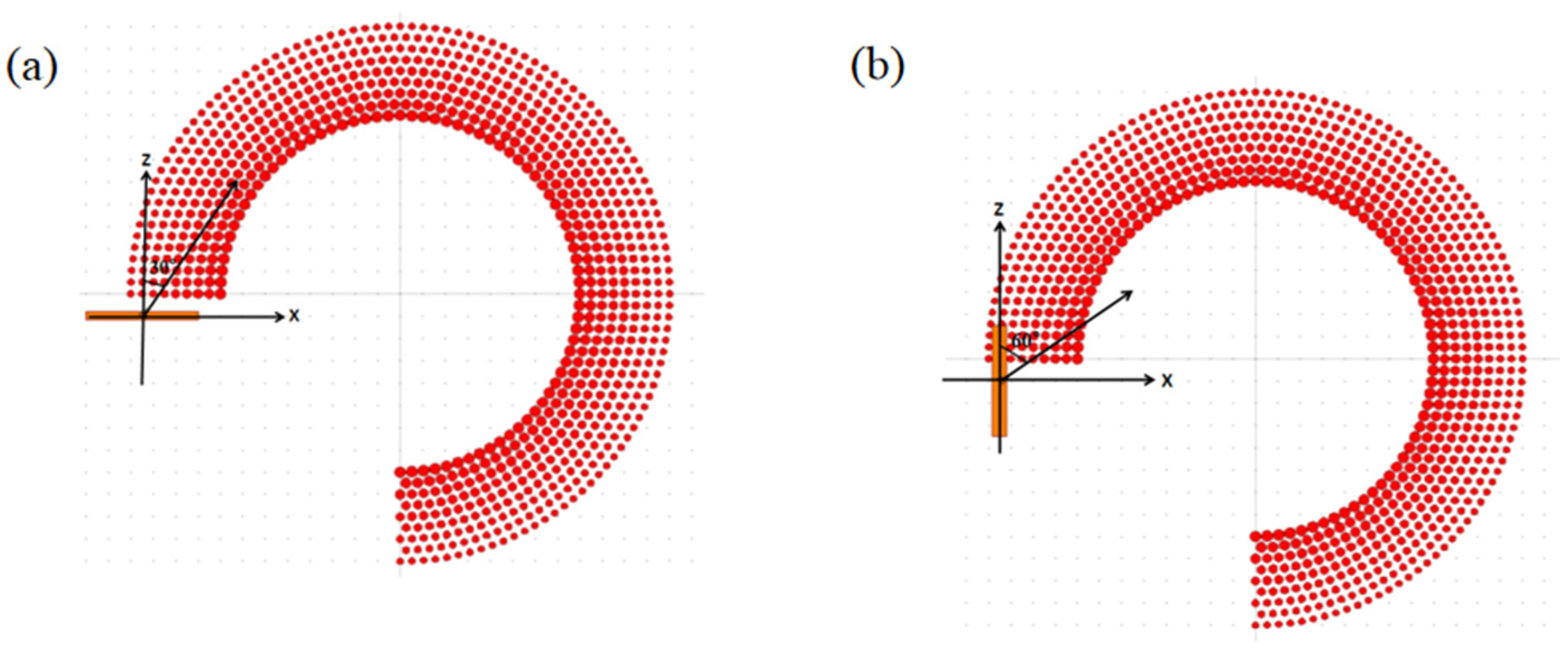
4. Robustness Analysis
5. Application Prospect Analysis and Prospect
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2488. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2061. [Google Scholar] [CrossRef] [PubMed]
- Centeno, E.; Cassagne, D. Graded photonic crystals. Opt. Lett. 2005, 30, 2278–2280. [Google Scholar] [CrossRef] [PubMed]
- Centeno, E.; Cassagne, D.; Albert, J.-P. Mirage and superbending effect in two-dimensional graded photonic crystals. Phys. Rev. B 2006, 73, 235119. [Google Scholar] [CrossRef]
- Vasić, B.; Gajić, R. Self-focusing media using graded photonic crystals: Focusing, fourier transforming and imaging, directive emission, and directional cloaking. J. Appl. Phys. 2011, 110, 0531031–0531038. [Google Scholar] [CrossRef]
- Russell, P.S.J.; Birks, T.A. Hamiltonian optics of nonuniform photonic crystals. J. Light. Technol. 1999, 17, 1982. [Google Scholar] [CrossRef]
- Jiao, Y.; Fan, S.; Miller, D.A.B. Designing for beam propagation in periodic and nonperiodic photonic nanostructures: Extended Hamiltonian method. Phys. Rev. E 2004, 70, 036612. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Qin, L.; Chen, Y.; Jia, P.; Chen, C.; Liang, L.; Chen, H.; Zhang, X.; Ning, Y. Research progress and application of curved waveguides. Chin. Opt. 2017, 10, 18. [Google Scholar]
- Mei, Z.L.; Cui, T.J. Experimental realization of a broadband bend structure using gradient index metamaterials. Opt. Express 2009, 17, 18354–18363. [Google Scholar] [CrossRef]
- Vasić, B.; Isić, G.; Gajić, R.; Hingerl, K. Coordinate transformation based design of confined metamaterial structures. Phys. Rev. B 2009, 79, 085103. [Google Scholar] [CrossRef]
- Vasić, B.; Isić, G.; Gajić, R.; Hingerl, K. Controlling electromagnetic fields with graded photonic crystals in metamaterial regime. Opt. Express 2010, 18, 20321–20333. [Google Scholar] [CrossRef]
- Scheuer, J.; Yariv, A. Circular photonic crystal resonators. Phys. Rev. E 2004, 70, 036603. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.; Scheuer, J.; Yariv, A. Optimization of circular photonic crystal cavities-beyond coupled mode theory. Opt. Express 2005, 13, 9272–9279. [Google Scholar] [CrossRef]
- Li, D.; Pu, S.; Zhao, Y.; Li, Y.; Hao, Z.; Han, Z. Sensing properties of symmetrical side-polished photonic crystal fiber based on surface plasmon resonance. Opt.-Int. J. Light Electron Opt. 2020, 224, 165662. [Google Scholar] [CrossRef]
- Pu, S.; Bai, X.; Wang, L. Temperature dependence of photonic crystals based on thermoresponsive magnetic fluids. J. Magn. Magn. Mater. 2011, 323, 2866. [Google Scholar] [CrossRef]
- Kamau, S.; Hassan, S.; Alnasser, K.; Zhang, H.; Cui, J.; Lin, Y. Broadband Absorption in Patterned Metal/Weakly-Absorbing-Spacer/Metal with Graded Photonic Super-Crystal. Photonics 2021, 8, 114. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling Electromagnetic Fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Li, Z.-W. Study on the Regulation of Electromagnetic Wave by Artificially Structured Metasurface and One-Dimensional Photonic Crystal. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2016. [Google Scholar] [CrossRef]
- Savotchenko, S.E. Surface waves in a linearly graded-index and an intensity-dependent index layered structure. J. Opt. Soc. Am. A 2022, 39, 1210–1217. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.; Sale, O.; Lowell, D.; Hurley, N.; Lin, Y. Holographic Fabrication and Optical Property of Graded Photonic Super-Crystals with a Rectangular Unit Super-Cell. Photonics 2018, 5, 34. [Google Scholar] [CrossRef]
- Badri, S.H.; Gilarlue, M.M. Low-index contrast waveguide bend based on truncated Eaton lens implemented by graded photonic crystals. J. Opt. Soc. Am. B 2019, 36, 1288–1293. [Google Scholar] [CrossRef]
- Zhang, H.; Qian, L.; Wang, C.; Ji, C.-Y.; Liu, Y.; Chen, J.; Lu, C. Topological rainbow based on graded topological photonic crystals. Opt. Lett. 2021, 46, 1237–1240. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Qiu, M. High-Q microcavities realized in a circular photonic crystal slab. Photonics Nanostruct.-Fundam. Appl. 2005, 3, 134–138. [Google Scholar] [CrossRef]
- Xiao, S.; Qiu, M. Study of transmission properties for waveguide bends by use of a circular photonic crystal. Phys. Lett. A 2005, 340, 474–479. [Google Scholar] [CrossRef]
- Sun, X.H.; Wu, Y.L.; Liu, W.; Hao, Y.; Jiang, L.-D. Luneburg lens composed of sunflower-type graded photonic Crystals. Opt. Commun. 2014, 315, 367–373. [Google Scholar] [CrossRef]
- David, L.; Safaa, H.; Murthada, A.; Hurley, N.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-crystals using an integrated spatial light modulator and reflective optical element laser projection system. Appl. Opt. 2017, 56, 9888. [Google Scholar]
- Hurley, N.; Kamau, S.; Alnasser, K.; Philipose, U.; Cui, J.; Lin, Y. Laser Diffraction Zones and Spots from Three-Dimensional Graded Photonic Super-Crystals and Moiré Photonic Crystals. Photonics 2022, 9, 395. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, K.; Wang, S.; Chen, D.; Sun, X. Focusing characteristics of graded photonic crystal waveguide lens based on interference lithography. Opt. Eng. 2021, 60, 077102. [Google Scholar] [CrossRef]
- Taylor, H.F. Power loss at directional change in dielectric waveguides. Appl. Opt. 1974, 13, 642–647. [Google Scholar] [CrossRef] [PubMed]
- Neumann, E.G. Curved Dielectric Optical Waveguide with Reduced Transition Losses. Microw. Antennas Propag. 1982, 129, 278–280. [Google Scholar] [CrossRef]
- Smit, M.K.; Pennings, E.C.M.; Blok, H. A normalized approach to the design of low-loss optical wave-guide bends. J. Light. Technol. 1993, 11, 1737–1742. [Google Scholar] [CrossRef]
- Fan, G.; Sang, W.; Liu, X.; Zhen, Z. Silicon waveguide racetrack resonators with 1.5 μm radius using junction offsets. Microw. Opt. Technol. Lett. 2012, 54, 1470–1471. [Google Scholar] [CrossRef]
- Ladouceur, F.; Labeye, P. A new general-approach to optical wave-guide path design. J. Light. Technol. 1995, 13, 481–492. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224–227. [Google Scholar] [CrossRef]
- Liu, R.; Ji, C.; Mock, J.J.; Chin, J.Y.; Cui, T.J.; Smith, D.R. Broadband Ground-Plane Cloak. Science 2009, 323, 366–369. [Google Scholar] [CrossRef]



| ρ (µm) | n | r (µm) |
|---|---|---|
| 1.6 | 3.125 | 0.047963 |
| 1.7 | 2.941176471 | 0.047943 |
| 1.8 | 2.777777778 | 0.04492 |
| 1.9 | 2.631578947 | 0.042192 |
| 2 | 2.5 | 0.039716 |
| 2.1 | 2.380952381 | 0.037453 |
| 2.2 | 2.272727273 | 0.035376 |
| 2.3 | 2.173913043 | 0.033458 |
| 2.4 | 2.083333333 | 0.031679 |
| 2.5 | 2 | 0.030022 |
| 2.6 | 1.923076923 | 0.028472 |
| 2.7 | 1.851851852 | 0.027016 |
| 2.8 | 1.785714286 | 0.025644 |
| 2.9 | 1.724137931 | 0.024345 |
| 3 | 1.666666667 | 0.023111 |
| 3.1 | 1.612903226 | 0.021935 |
| 3.2 | 1.5625 | 0.02081 |
| 3.3 | 1.515151515 | 0.01973 |
| 3.4 | 1.470588235 | 0.01869 |
| 3.5 | 1.428571429 | 0.017684 |
| 3.6 | 1.388888889 | 0.016707 |
| 3.7 | 1.351351351 | 0.015755 |
| 3.8 | 1.355789474 | 0.014832 |
| 3.9 | 1.282051282 | 0.013906 |
| 4 | 1.25 | 0.013 |
| ρ (µm) | n | r (µm) |
|---|---|---|
| 1 | 3 | 0.04582 |
| 1.1 | 2.727 | 0.0411 |
| 1.2 | 2.5 | 0.03711 |
| 1.3 | 2.308 | 0.03369 |
| 1.4 | 2.143 | 0.0307 |
| 1.5 | 2 | 0.02805 |
| ρ (µm) | n | r (µm) |
|---|---|---|
| 2.2 | 3.182 | 0.04893 |
| 2.3 | 3.043 | 0.04656 |
| 2.4 | 2.917 | 0.04438 |
| 2.5 | 2.8 | 0.04236 |
| 2.6 | 2.692 | 0.04049 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Liu, H.; Sun, X.; Zhang, F. The Design of Large Curved Waveguide Based on Sunflower Graded Photonic Crystal. Photonics 2023, 10, 781. https://doi.org/10.3390/photonics10070781
Liu W, Liu H, Sun X, Zhang F. The Design of Large Curved Waveguide Based on Sunflower Graded Photonic Crystal. Photonics. 2023; 10(7):781. https://doi.org/10.3390/photonics10070781
Chicago/Turabian StyleLiu, Wei, Hechao Liu, Xiaohong Sun, and Fan Zhang. 2023. "The Design of Large Curved Waveguide Based on Sunflower Graded Photonic Crystal" Photonics 10, no. 7: 781. https://doi.org/10.3390/photonics10070781
APA StyleLiu, W., Liu, H., Sun, X., & Zhang, F. (2023). The Design of Large Curved Waveguide Based on Sunflower Graded Photonic Crystal. Photonics, 10(7), 781. https://doi.org/10.3390/photonics10070781





