Abstract
Silicon photonics (SiPh) has emerged as a promising technology for photonic integrated circuits (PICs). One of the basic components in SiPh is the directional coupler (DC), which plays an important role in signal monitoring with the requirement of low wavelength dependence and low loss. This paper proposes a broadband and low-loss DC designed for signal power tapping on the 3 μm silicon-on-insulator (SOI) waveguide platform. By utilizing the advantages of multi-micron waveguides and replacing one of the straight waveguides with an optimized arc-shaped waveguide in the coupling region, the proposed DC enhances spectral stability and improves transmission with negligible loss. Experimental evidence indicates that the proposed DC showcases a minimal variation in the tapping ratio. From 1470 nm to 1630 nm, the largest deviation away from the tapping ratio at 1550 nm is 1.433%. Additionally, the device exhibits a low excess loss of −0.27 dB. These results suggest that the proposed device is well-suited to reliable signal power tapping and monitoring, particularly within PICs.
1. Introduction
Silicon photonics (SiPh) has gained prominence as one of the leading technologies for integrated photonics, with a diverse range of applications in high-performance computing [,], optical communications [], and optical sensors []. The key advantage of SiPh lies in its compatibility with standard complementary metal oxide semiconductor (CMOS) technology, resulting in cost-effective mass production. The directional coupler (DC) is a fundamental and widely employed building block in SiPh, serving as a power splitter to construct complex devices, such as Mach–Zehnder interferometers (MZIs) [], wavelength division multiplexers (WDMs) [], optical switches [], and electro-optics modulators []. In optical communication and sensing, the DC is commonly used to construct waveguide taps to extract a portion of the light signal traveling along a primary waveguide. These taps serve monitoring purposes, allowing for the precise measurement of the light signal’s characteristics at a specific location []. However, coupled mode theory [,] demonstrates that the coupling efficiency of conventional DCs with parallel waveguides sections is highly dependent on the propagation constants. This leads to a varying amplitude of the coupling power with the operating wavelength, resulting in strong wavelength dependence, which is unfavorable for signal power tapping and monitoring applications. In the past two decades, researchers have made significant efforts in developing broadband DCs [,,,]. Adiabatic directional couplers [] have demonstrated promising broadband operation, using tapered waveguides for achieving adiabatic transitions; however, they have the disadvantage of large footprints. Another approach [] involves the use of sub-wavelength grating (SWG) structures to enhance the coupling strength and reduce device size while maintaining broadband operation. However, achieving this requires high fabrication accuracy to control the dimensions of waveguides. Additionally, broadband MZI-based couplers [] which integrate MZI structures into DCs still have challenges in terms of their larger footprints compared to conventional DCs on the same SiPh platform. Consequently, the development of DCs with broadband characteristics, low loss, and high fabrication tolerance continues to be a topic that requires further exploration.
The 3 μm silicon-on-insulator (SOI) optical waveguide platform, also referred to as the thick-SOI platform, has emerged as a highly successful option for SiPh fabrication over the last ten years [,]. This platform has demonstrated exceptional performance in key components such as etched diffraction grating (EDG) [], arrayed waveguide grating (AWG) [], Ge photodetectors [], and electro absorption modulators (EAMs) []. Additionally, these key building blocks have been successfully monolithically integrated [,]. In contrast to the majority of SiPh waveguide platforms that utilize sub-micron top silicon waveguide layers, the 3 μm SOI waveguide platform presents significant advantages for the design of ultra-wideband, low-loss, and high-fabrication-tolerance photonic integrated circuits (PICs). The multi-micron waveguide core of the thick-SOI platform boasts significantly lower effective index sensitivity, making it particularly well-suited for applications that require spectral stability []. Meanwhile, the larger dimensions enable complete confinement of the optical mode field, reducing sensitivity to variations in waveguide shape and resulting in negligible propagation loss of approximately −0.1 dB/cm []. Another notable advantage of the thick-SOI platform is its wavelength independence and robust performance across a wide range of waveguide dimensions for single-mode operation. This behavior arises from the efficient leakage of higher-order modes into the slab modes of rib waveguides, as long as the relative waveguide dimensions are well controlled. These characteristics substantially enhance the potential of the 3 μm SOI waveguide platform as an attractive choice for developing broadband, low-loss, and fabrication-tolerant SiPh devices and systems.
In this work, we present a DC for tapping signal power on the 3 μm SOI waveguide platform. The device exhibits broadband and low-loss characteristics by leveraging the platform’s effective index insensitivity and low-loss transmission. By replacing one of the two straight waveguides in the conventional coupling region with an arc-shaped waveguide, the device achieves an effectively shortened coupling length, thus reducing its sensitivity to wavelength as expected by the coupled mode theory. The proposed DC is characterized over a broad wavelength range of 1470 nm to 1630 nm, resulting in minimal fluctuations in the tapping ratio within the range of −1.373% to 1.433% when compared to its value at 1550 nm, and a low excess loss (EL) level of −0.27 dB. These results indicate that our design can serve as a fundamental component for various applications that require stable power tapping and monitoring.
2. Principle and Device Structure
The schematic diagram of a conventional DC is presented in Figure 1. The DC is composed of two symmetric arms that have a uniform width of W. Each arm comprises a straight waveguide of length LC and two S-bends, functioning as the input and output ports, respectively. Power exchange occurs between the two straight waveguides, and thus, the term coupling length is applicable to describe the length of the straight waveguide. In addition, the parts of the S-bends adjacent to the straight waveguides also contribute to coupling, meaning that the effective coupling length is greater than LC. A cross-sectional view of the coupling region is shown in Figure 1b. Careful design of the rib waveguide height H, slab thickness h, gap size G, and W is required to achieve the desired coupling strength.
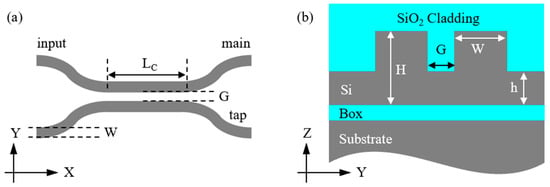
Figure 1.
(a) Top view of a conventional DC. (b) Cross-sectional schematic of rib waveguides in the coupling region.
Based on the coupled mode theory or the supermode solution method, the DC’s splitting ratio correlates with the mode effective index in each arm or the effective indices of the supermodes supported by the two waveguides. However, the presence of mode dispersion constrains the operating bandwidth. In this study, we applied the Lumerical finite difference eigenmode (FDE) solver to determine the effective indices of two sets of supermodes in the coupling region, which corresponded to diverse design parameters and represented the distinct single-mode configurations on the 220 nm SOI waveguide platform and the thick-SOI platform, respectively. In Figure 2a, the effective indices of supermodes are plotted against the wavelength λ. The blue lines illustrate the design based on the 3 μm SOI waveguide platform, with dimensions of H = 3 μm, h = 1.8 μm, G = 2.2 μm, and W = 2.6 μm, while the red lines correspond to the design based on the 220 nm SOI waveguide platform, with dimensions of H = 220 nm, h = 70 nm, G = 150 nm, and W = 450 nm. The solid and dashed lines in each color represent the effective refractive indices of symmetric and antisymmetric modes, denoted by ns_eff and nas_eff, respectively. Within the wavelength range of 1470 nm to 1630 nm, the ns_eff shifts by 0.1447 for the 220 nm waveguide-based design, whereas for the 3 μm waveguides, the shift is only 0.0031. Similarly, the nas_eff shifts by 0.1841 and 0.0032 for the 220 nm and 3 μm waveguides, respectively. The comparisons confirm that the ns_eff and nas_eff remain almost unaffected by wavelength on the 3 μm SOI waveguide platform, which is important in extending the bandwidth of the DC. Moreover, the difference between ns_eff and nas_eff, represented by Δneff, is also examined. As shown in the insert of Figure 2a, within the wavelength range of 1470 nm to 1630 nm, the Δneff for 3 μm waveguides is remarkably lower (i.e., nearly two orders of magnitude) compared with 220 nm waveguides. This finding reiterates the lower wavelength sensitivity of the thick-SOI platform.
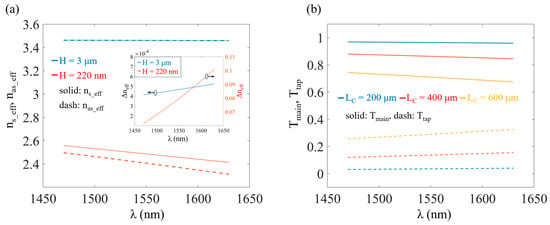
Figure 2.
(a) Simulation results of the relationship between the ns_eff (solid lines) and nas_eff (dash lines) and λ in the coupling region of typical DC designs on the 3 μm SOI waveguide platform and the 220 nm SOI waveguide platform. The blue lines correspond to the structure with design parameters H = 3 μm, h = 1.8 μm, G = 2.2 μm and W = 2.6 μm, while the red lines represent the structure with H = 220 nm, h = 70 nm, G = 150 nm and W = 450 nm. The insert exhibits the relationship between Δneff and λ for designs based on both platforms. (b) Simulated Tmain and Ttap as functions of λ for the design based on the 3 μm SOI waveguide platform when the LC values are 200 μm, 400 μm, and 600 μm, respectively.
The transmission of the DC can be expressed as []:
where Tmain and Ttap represent the transmission of the main and tap ports, respectively. To investigate the impact of varying wavelengths on the transmission, we calculated the derivative of Ttap with respect to wavelength:
where Δng = Δneff − λ·dΔneff/dλ. It is noteworthy that for the sine function’s argument lying between 0 and π/2, the right-hand side of Equation (3) monotonically decreases with LC. Therefore, Ttap’s sensitivity to wavelength can be effectively minimized by employing a relatively small LC value. To achieve the above, it is necessary for the 3 μm SOI waveguide platform-based coupling region mentioned earlier to have an LC value of less than approximately 820 μm, meeting the sine function’s argument’s requirements by being smaller than π/2. Figure 2b illustrates the transmission as a function of wavelength for LC values of 200 μm, 400 μm, and 600 μm. The results demonstrate that DCs with shorter coupling lengths exhibit a substantial level of splitting ratio stability. Additionally, the decrease in LC leads to a corresponding decrease in Ttap, preventing excessive power coupling from the main-path waveguide, which is advantageous for signal power monitoring applications.
To obtain a shorter coupling length, we propose a DC design presented in Figure 3a (the SiO2 cladding has been omitted for clarity), where the tap waveguide in the coupling region is designed as an arc shape. Two typical waveguide profiles, rib and strip, are employed in the DC (see Figure 3b for their cross-sectional views). The rib waveguide has a height of 3 μm and a slab thickness of 1.8 μm, whereas the strip waveguide shares the same height but has a significantly thinner slab of only 0.2 μm. The reduced slab thickness in the strip waveguide promotes its lateral mode confinement, leading to a decrease in the bend radius and a more compact device footprint. Furthermore, Figure 3a,b illustrate that the main path exclusively consists of the rib waveguide, whereas the tap path incorporates the rib profile in the coupling and straight regions, and utilizes the strip waveguide for the curved segment. A comprehensive description of the tap waveguide is provided in Figure 3c, revealing its adoption of a mirrored structure with four designated regions on each side, where each region serves a distinct function. Region I is an arc-shaped waveguide designed for tapping signals, with R and θ denoting its radius and angle, respectively. The geometric diagram of the coupling region reveals a progressively increased gap between the arc-shaped and main waveguides with an increase in distance from the mirror plane. This phenomenon leads to a gradual decline in the coupling strength, resulting in weak coupling in regions that are further from the mirror plane. In other words, in contrast to the conventional DC with two parallel straight waveguides, the power transfer of our proposed design takes place only in the area where the two waveguides are in close proximity. As a result, the effective coupling length is reduced, which considerably decreases the wavelength sensitivity, as apparent from Equation (3). Region II secures the mode converter [,] with a length L of 350 μm, achieving a low-loss transition between the rib waveguide and the strip waveguide. Region III features an S-bend that employs a pair of Euler bends [,,] to provide an efficient transition between straight and curved waveguides, reducing mode mismatches, bend loss, and bend radii. In our design, the starting radius RS1 of the Euler bend connected to the straight waveguide is 1500 μm, and the other radius RS2 connected to the curved waveguide is 150 μm. Region IV comprises both the identical mode converter employed in Region II and a segment of the rib waveguide. Its objective is to facilitate the guidance of the tapped signal towards the tap port. The rib waveguide is designed to maintain a straight configuration, thereby enabling the tapped signal to reach the edge of the sample chip where the DC is located. Thanks to its efficient edge-coupling capability with lensed fibers, the rib waveguide greatly facilitates the straightforward connection of the DC to the optical link during subsequent testing procedures. Finally, both the main and tap waveguides in the proposed DC have a width W of 2.6 μm for single-mode operation, while the gap size G between the two waveguides along the mirror plane is also defined.
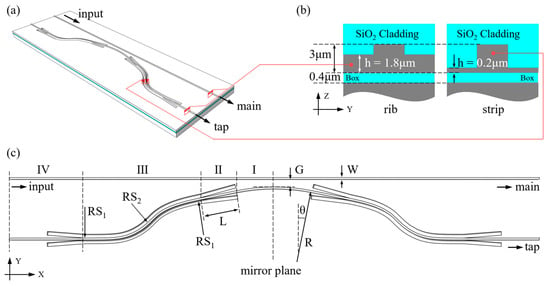
Figure 3.
(a) Perspective view of the proposed DC for signal power tapping. The SiO2 cladding has been omitted for better visualization. (b) Cross-sectional views of the rib waveguide and the strip waveguide. (c) The schematic for the DC with labelled design parameters.
The tapping ratio S and the excess loss EL of the device are defined as follows:
S is set as 4%. The effective coupling length of the proposed DC is ensured to stay below 820 μm, as determined by the limitations of the sine function’s argument in Equation (3). To achieve this, we initially set R to 7000 μm and θ to approximately 3.6 degrees. The eigenmode expansion (EME) solver in Lumerical is utilized to optimize the design parameters, with a cell step size of 0.5 μm for accuracy. The simulation results at a fixed G of 2 μm and at a wavelength of 1550 nm are presented in Figure 4a,b, depicting the variation of S and EL with θ for three Rs, namely 7500 μm, 7000 μm, and 6500 μm. The results from all three values of R indicate that an increase in θ leads to an increase in S, but it is also accompanied by an increased level of device loss. In addition, varying R can also affect S, but our primary interest lies in the trend of increasing R, which results in a decrease in device loss. Moreover, as R grows, the shape of the curved waveguide approaches that of the straight waveguide, and this leads to an increase in the effective coupling length of the coupling region. As previously discussed, this consequence results in a narrower bandwidth, which is undesirable for the device’s performance. By taking all of these factors into account, we selected optimal values of R = 7000 μm and θ = 3.7 degrees to maintain low EL and large operating bandwidth, with a tapping ratio of 4% for the device. Figure 4c displays the simulation results concerning the entirety of the coupling region, along with the normalized electric field distribution on the cross-sections at its endpoints (indicated by white dashed lines). This visualization enables clear observation of the power coupling, revealing that a minor fraction is transferred into the tap waveguide, with the main path effectively preserving the majority of the power.
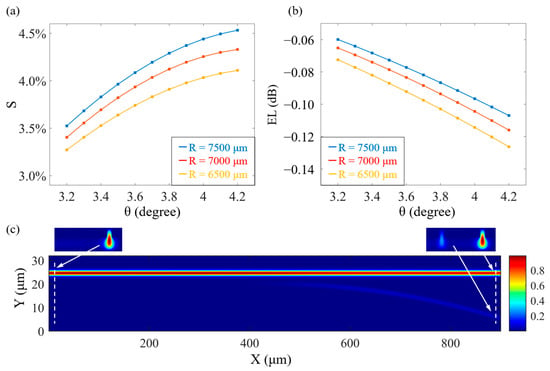
Figure 4.
Simulated results of (a) S and (b) EL as a function of θ for different values of R. (c) Visual representation of power transfer within the coupling region, with the electric field distribution on the cross-sections which are depicted by white dashed lines.
The relationship between S (blue line) and EL (red line) as a function of G is aptly depicted in Figure 5a. It is evident that adjusting G provides a way to regulate the device’s tapping ratio. However, it must be kept in mind that reducing G would also elevate the level of loss. This is due to the fact that a narrower gap results in more energy coupling into the tap waveguide, leading to increased loss as a result of mode mismatch and waveguide bending in the curved section. Additionally, a smaller G, while enhancing coupling strength, amplifies the wavelength dependence of the device []. To achieve a desired S of 4% while considering these factors, we set G to 2 μm. Figure 5b presents the simulated performance of our proposed design, indicating a maximum deviation of S from its value at 1550 nm of 0.6272% across the wavelength range of 1470 nm to 1630 nm, and the largest EL is at −0.0977 dB. These results demonstrate that our designed DC offers low-loss characteristics and a wide operational bandwidth, making it appropriate for wavelength-insensitive signal power tapping and monitoring applications.
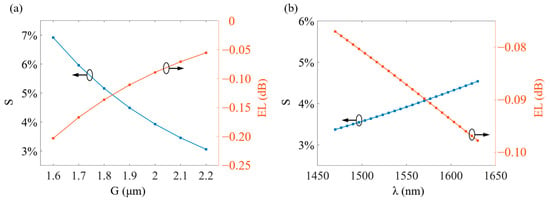
Figure 5.
(a) Simulated results of S (blue line) and EL (red line) as a function of G at λ = 1550 nm. (b) Calculated S (blue line) and EL (red line) as a function of λ for the proposed DC with the following design parameters: R = 7000 μm, θ = 3.7 degrees, and G = 2 μm.
We proceeded to investigate the proposed DC’s tolerance to fabrication errors arising from deviations in waveguide geometry, which most often impact the width W and height H of the rib waveguides as specified in Figure 1b. The calculated variations in S as a function of wavelength for different waveguide geometry deviations are shown in Figure 6. In Figure 6a, various Ws ranging from 2.54 μm to 2.66 μm are introduced, with a maximum deviation of ±0.06 μm. The changes in S resulting from these waveguide profiles remained within ±1% over a wide wavelength range from 1470 nm to 1630 nm. A notable point is that the device’s wavelength sensitivity increases with decreasing W, since narrow waveguides have a higher sensitivity of the effective refractive index of the fundamental mode to the wavelength. In Figure 6b, we introduced fabrication errors of up to ±0.04 μm in the waveguide height and observed changes in S ranging from −0.73% to +0.71% across the entire optical band. These results indicate the excellent fabrication reliability of our proposed DC.
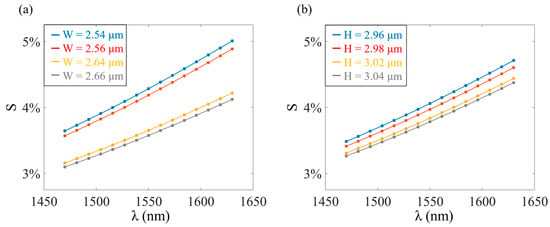
Figure 6.
Simulated results of S varying with λ for different (a) Ws and (b) Hs representing the fabrication errors in the waveguide’s width and height.
3. Experimental Results and Discussion
Several DCs with different values of G were fabricated on an SOI wafer comprising a 3 µm top silicon layer and a 0.4 µm buried silicon dioxide (BOX) layer, and reference straight waveguides were also fabricated on the same wafer. The fabrication process involved deep-ultraviolet (DUV) photolithography followed by dry etching. To minimize transmission loss, the etching process was optimized to smoothen the sidewalls of the waveguide. Thereafter, a cladding layer was deposited using plasma-enhanced chemical vapor deposition (PECVD), with a 2.2 µm SiO2 layer and a 0.7 µm silicon nitride layer. Further details about the fabrication process can be found in []. The scanning electron microscope (SEM) image in Figure 7a shows the desired sidewall steepness of waveguides. However, it should be noted that the rib waveguide had a profile of W = 2.77 µm, H = 3.27 µm and h = 1.97 µm, reflecting errors of approximately 0.17 µm, 0.27 µm and 0.17 µm for waveguide width, height, and slab thickness, respectively. The impact of these errors on the splitting ratio of the device will be discussed later. The top-view optical microscope image of the devices with a range of G from 2.2 µm to 1.6 µm is displayed in Figure 7b. The length of the coupling region for all devices is 903.45 μm, with an overall footprint of 125 × 2825.65 μm2.
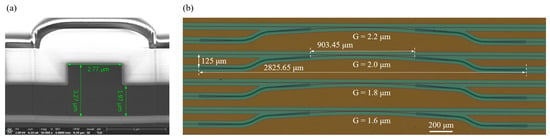
Figure 7.
Fabricated devices. (a) Scanning electron microscope image of the cross-section of the rib waveguide. (b) Optical microscope image of devices with G values of 2.2 µm, 2.0 µm, 1.8 µm, and 1.6 µm, respectively.
The signal originating from the tunable laser source (Keysight 8164B) was edge-coupled into the DC using a lensed fiber with a spot size of 2.5 ± 0.25 µm. Subsequently, the output signal was captured through another lensed fiber and measured using a power meter (Keysight N7744A). It is noteworthy that each interface between the fiber and waveguide introduces a coupling loss of approximately −1.53 dB. Prior to entering the DC, the signal was passed through a polarization synthesizer (Keysight N7786B) to selectively excite only the TE mode. The final transmission results were then normalized using the reference waveguide’s outcomes. In Figure 8a, normalized splitting ratios from 1470 nm to 1630 nm for different gap sizes are demonstrated. For the design focused on obtaining a 96%/4% splitting ratio, a tapping ratio of 5.753% at 1550 nm (red dash line) was attained, displaying a variation of −1.373% to 1.433% throughout the entire spectrum. Similarly, other designs with distinct gap sizes exhibit minor S deviations concerning wavelength, indicating broadband features. It should be noted that all devices yield higher S than the results calculated at 1550 nm illustrated in Figure 5a. Such difference can be attributed to the larger dimensions of the fabricated waveguides in W and h compared to the initial design. This leads to a narrower gap and a stronger coupling strength of the DC, resulting in an increased coupling ratio. To test this hypothesis, we updated the simulation model’s geometric features according to the SEM figure presented in Figure 7a. The findings from subsequent simulations, presented in Figure 8b, showed good alignment between the recalculated results (blue dashed line) and the experimental results (red dots), presenting evidence that fabricated errors can be quantified for the tapping ratio. The fabrication errors in W and h also contribute to the rise in device losses, driven by the corresponding increase in the coupling ratio. Compared to the main waveguide, the curved shape of the tap waveguide leads to higher radiation losses. Additionally, the mode overlap loss occurs in the tap path due to the mode mismatch between straight and curved waveguides. The higher coupling ratio signifies a greater amount of power coupled into the tap waveguide. However, this power experiences higher losses in comparison to the main waveguide, leading to an elevated level of excess loss in the device. Experimental results for EL are provided in Figure 9, which displays measured values of −0.17 dB, −0.27 dB, −0.42 dB, and −0.68 dB at 1550 nm, respectively, when the gap size reduces from 2.2 µm to 1.6 µm. It is worth noting that in comparison to Figure 5a, the experimental ELs of the four devices exhibit varying degrees of increase. These increments are partly due to deviations in waveguide dimensions and partly due to sidewall roughness, which is not captured in the EL simulation results. Nonetheless, since all waveguides on the same chip possess similar sidewall roughness, comparing the relative relationship of ELs for different gap sizes remains meaningful. Figure 9 verifies our previous prediction that as the gap narrows, the corresponding excess loss increases. In the forthcoming fabrication process, we will employ finer masks to achieve waveguides with precise widths and enhance the photolithography process to improve the quality of the etching profile. Additionally, we will opt for more conservative values for the bending radius in order to minimize radiation losses and mode mismatch within the tap waveguide, effectively mitigating the excess loss of the design.
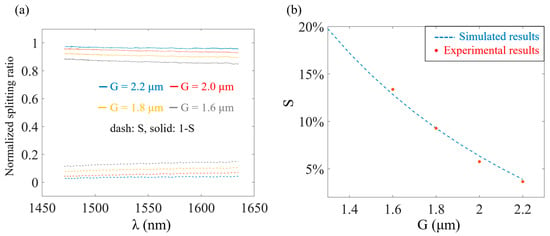
Figure 8.
(a) Normalized splitting ratio of DCs with different Gs. (b) Comparison of simulated and experimental results for the tapping ratio after updating waveguide dimensions based on SEM image.
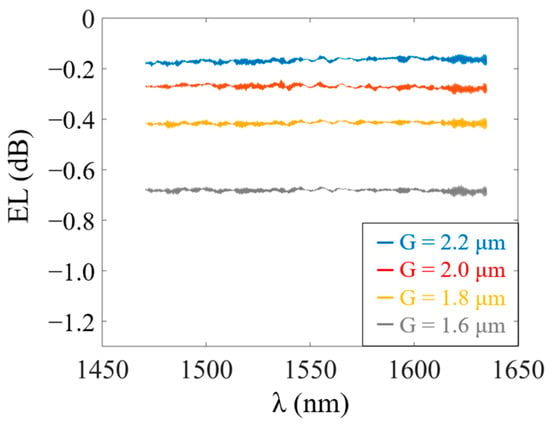
Figure 9.
Measured excess loss of DCs with different Gs.
Despite significant fabrication variations, our proposed DC maintains notable wavelength stability and low-loss characteristics, making it highly suitable for applications such as SiPh transmitter chips that require signal power tapping and monitoring. Table 1 provides a summary of the comparison between our demonstrated DC and state-of-the-art broadband power splitters. Compared to other devices, our design exhibits a wider bandwidth covering the S, C, and L bands, with significantly low excess loss. The outstanding performance can be attributed to two key factors—firstly, the curved-straight waveguide coupling region design, and secondly, the inherent advantages of the 3 µm SOI waveguide platform, including low wavelength sensitivity, low losses, and high fabrication tolerance. In the future, these advantages could be further exploited to produce DCs with arbitrary splitting ratios, promoting their application in large-scale SiPh integrated systems.

Table 1.
Comparison of performance with reported power splitters and this work.
4. Conclusions
We have designed and experimentally demonstrated a broadband DC with low-loss characteristics based on the 3 µm SOI waveguide platform for signal power tapping. The coupling region of the DC consists of a straight waveguide and an arc-shaped waveguide that reduce the effective coupling length while maintaining efficient power splitting for tapping. The shortened coupling length and the wavelength insensitivity of the 3 µm waveguide ensure stable tapping ratios over a wide wavelength range. Experimental results demonstrate that for our design with a target splitting ratio of 96%/4%, the tap ratio variation remains within −1.373% to 1.433% from 1470 nm to 1630 nm. Additionally, the device features low excess loss of only −0.27 dB at 1550 nm. Various designs with different gap sizes were fabricated, tested, and matched well with our simulation results. Moreover, the calculated results illustrate that the proposed device exhibits significant robustness against fabrication imperfections. Given the recent advancements in SiPh industrialization, the demonstrated low-loss DC with wide bandwidth capabilities can be extensively applied in on-chip power sensing, among other areas.
Author Contributions
Conceptualization, A.W. and D.L.; methodology, D.L.; software, D.L.; validation, L.W., C.L., A.L. and R.W.; formal analysis, D.L.; resources A.W.; data curation, R.W.; writing—review and editing, D.L.; supervision, A.W.; project administration, R.W.; funding acquisition, A.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Key Research and Development Program of China under Grant 2021YFB2206502, in part by the National Natural Science Foundation of China under Grant 62275259, in part by the Program of Shanghai Academic Research Leader under Grant 22XD1404300, and in part by the Youth Innovation Promotion Association CAS under Grant 2021232.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Relevant data are available from the authors upon reasonable request.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Orlandin, M. Analysis of Silicon Photonics Neuromorphic Networks. Master’s Thesis, Politecnico di Torino, Torino, Italy, 2023. [Google Scholar]
- Pai, S.; Sun, Z.; Hughes, T.W.; Park, T.; Bartlett, B.; Williamson, I.A.D.; Minkov, M.; Milanizadeh, M.; Abebe, N.; Morichetti, F.; et al. Experimentally Realized in Situ Backpropagation for Deep Learning in Photonic Neural Networks. Science 2023, 380, 398–404. [Google Scholar] [CrossRef]
- Shi, T.; Su, T.-I.; Zhang, N.; Hong, C.; Pan, D. Silicon Photonics Platform for 400G Data Center Applications. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; p. M3F.4. [Google Scholar]
- Wade, J.H.; Alsop, A.T.; Vertin, N.R.; Yang, H.; Johnson, M.D.; Bailey, R.C. Rapid, Multiplexed Phosphoprotein Profiling Using Silicon Photonic Sensor Arrays. ACS Cent. Sci. 2015, 1, 374–382. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Xu, H.; Tan, Y.; Shi, Y.; Dai, D. Silicon Photonic Filters. Microw. Opt. Technol. Lett. 2021, 63, 2252–2268. [Google Scholar] [CrossRef]
- Horst, F.; Green, W.M.J.; Assefa, S.; Shank, S.M.; Vlasov, Y.A.; Offrein, B.J. Cascaded Mach-Zehnder Wavelength Filters in Silicon Photonics for Low Loss and Flat Pass-Band WDM (de-)Multiplexing. Opt. Express 2013, 21, 11652. [Google Scholar] [CrossRef]
- Tu, X.; Song, C.; Huang, T.; Chen, Z.; Fu, H. State of the Art and Perspectives on Silicon Photonic Switches. Micromachines 2019, 10, 51. [Google Scholar] [CrossRef] [PubMed]
- Anwar, N.; Themistos, C.; Rahman, B.M.A.; Grattan, K.T.V. Design Considerations for an Electrooptic Directional Coupler Modulator. J. Light. Technol. 1999, 17, 598–605. [Google Scholar] [CrossRef]
- Hsu, S.-H. Polarization-Dependent Loss Compensation on Silicon-Wire Waveguide Tap by Complex Refractive Index of Metals. Opt. Lett. 2009, 34, 1798–1800. [Google Scholar] [CrossRef]
- Yariv, A. Coupled-Mode Theory for Guided-Wave Optics. IEEE J. Quantum Electron. 1973, 9, 919–933. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Photonics: Optical Electronics in Modern Communications; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Mao, D.; Wang, Y.; El-Fiky, E.; Xu, L.; Kumar, A.; Jaques, M.; Samani, A.; Carpentier, O.; Bernal, S.; Alam, M.S.; et al. Adiabatic Coupler with Design-Intended Splitting Ratio. J. Light. Technol. 2019, 37, 6147–6155. [Google Scholar] [CrossRef]
- Yun, H.; Chrostowski, L.; Jaeger, N.A.F. Ultra-Broadband 2 × 2 Adiabatic 3 DB Coupler Using Subwavelength-Grating-Assisted Silicon-on-Insulator Strip Waveguides. Opt. Lett. 2018, 43, 1935–1938. [Google Scholar] [CrossRef]
- Hsu, S.-H. Signal Power Tapped with Low Polarization Dependence and Insensitive Wavelength on Silicon-on-Insulator Platforms. J. Opt. Soc. Am. B 2010, 27, 941–947. [Google Scholar] [CrossRef]
- Sattari, H.; Takabayashi, A.Y.; Zhang, Y.; Quack, N. Silicon Photonic Broadband Suspended Directional Coupler. In Proceedings of the 2019 International Conference on Optical MEMS and Nanophotonics (OMN), Daejeon, Republic of Korea, 28 July–1 August 2019; pp. 214–215. [Google Scholar]
- Rickman, A. The Commercialization of Silicon Photonics. Nat. Photon 2014, 8, 579–582. [Google Scholar] [CrossRef]
- Streshinsky, M.; Ding, R.; Liu, Y.; Novack, A.; Galland, C.; Lim, A.E.-J.; Lo, P.G.-Q.; Baehr-Jones, T.; Hochberg, M. The Road to Affordable, Large-Scale Silicon Photonics. Opt. Photonics News 2013, 24, 32–39. [Google Scholar] [CrossRef]
- Feng, D.; Qian, W.; Liang, H.; Kung, C.-C.; Fong, J.; Luff, B.J.; Asghari, M. Novel Fabrication Tolerant Flat-Top Demultiplexers Based on Etched Diffraction Gratings in SOI. In Proceedings of the 2008 5th IEEE International Conference on Group IV Photonics, Sorrento, Italy, 17–19 September 2008; IEEE: Cardiff, UK, September, 2008; pp. 386–388. [Google Scholar]
- Bhat, S.; Harjanne, M.; Sun, F.; Cherchi, M.; Kapulainen, M.; Hokkanen, A.; Delrosso, G.; Aalto, T. Low Loss Devices Fabricated on the Open Access 3 μm SOI Waveguide Platform at VTT. In Proceedings of the 21st European Conference on Integrated Optics, Ghent, Belgium, 24–26 April 2019. [Google Scholar]
- Aalto, T.; Vehmas, T.; Kapulainen, M.; Heimala, P.; Delrosso, G.; Sun, F.; Gao, F. (Invited) Monolithic Ge Integration on the 3 Μm SOI Platform for 40 GHz Photodiodes. ECS Trans. 2020, 98, 303–313. [Google Scholar] [CrossRef]
- Feng, D.; Liao, S.; Liang, H.; Fong, J.; Bijlani, B.; Shafiiha, R.; Luff, B.J.; Luo, Y.; Cunningham, J.; Krishnamoorthy, A.V.; et al. High Speed GeSi Electro-Absorption Modulator at 1550 Nm Wavelength on SOI Waveguide. Opt. Express 2012, 20, 22224. [Google Scholar] [CrossRef]
- Aalto, T.; Harjanne, M.; Vehmas, T.; Karppinen, M.; Sitomaniemi, A.; Malacarne, A.; Neumeyr, C.; Bauwelinck, J. Transceivers for 400G Based on Hybrid Integrated Thick SOI and III/V Chips. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; pp. 1–3. [Google Scholar]
- Feng, D.; Qian, W.; Liang, H.; Luff, B.J.; Asghari, M. High-Speed Receiver Technology on the SOI Platform. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 3800108. [Google Scholar] [CrossRef]
- Zilkie, A.J.; Srinivasan, P.; Trita, A.; Schrans, T.; Yu, G.; Byrd, J.; Nelson, D.A.; Muth, K.; Lerose, D.; Alalusi, M.; et al. Multi-Micron Silicon Photonics Platform for Highly Manufacturable and Versatile Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 8200713. [Google Scholar] [CrossRef]
- Aalto, T.; Cherchi, M.; Harjanne, M.; Bhat, S.; Heimala, P.; Sun, F.; Kapulainen, M.; Hassinen, T.; Vehmas, T. Open-Access 3-μm SOI Waveguide Platform for Dense Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 8201109. [Google Scholar] [CrossRef]
- Wang, Y.; Bhat, S.; Tessema, N.; Kraemer, R.; Napoli, A.; Delrosso, G.; Calabretta, N. Ultrawide-Band Low Polarization Sensitivity 3-μm SOI Arrayed Waveguide Gratings. J. Light. Technol. 2022, 40, 3432–3441. [Google Scholar] [CrossRef]
- Cherchi, M.; Ylinen, S.; Harjanne, M.; Kapulainen, M.; Aalto, T. Dramatic Size Reduction of Waveguide Bends on a Micron-Scale Silicon Photonic Platform. Opt. Express 2013, 21, 17814–17823. [Google Scholar] [CrossRef]
- Bogaerts, W.; Selvaraja, S.K. Compact Single-Mode Silicon Hybrid Rib/Strip Waveguide with Adiabatic Bends. IEEE Photonics J. 2011, 3, 422–432. [Google Scholar] [CrossRef]
- Bahadori, M.; Nikdast, M.; Cheng, Q.; Bergman, K. Universal Design of Waveguide Bends in Silicon-on-Insulator Photonics Platform. J. Light. Technol. 2019, 37, 3044–3054. [Google Scholar] [CrossRef]
- Xu, D.-X.; Densmore, A.; Waldron, P.; Lapointe, J.; Post, E.; Delâge, A.; Janz, S.; Cheben, P.; Schmid, J.H.; Lamontagne, B. High Bandwidth SOI Photonic Wire Ring Resonators Using MMI Couplers. Opt. Express 2007, 15, 3149–3155. [Google Scholar] [CrossRef]
- Zhou, Y.; Lv, D.; Bi, D.; Wu, L.; Wang, R.; Ma, S.; Zhang, E.X.; Fleetwood, D.M.; Wu, A. Radiation-Hardened Silicon Photonic Passive Devices on a 3 μm Waveguide Platform under Gamma and Proton Irradiation. Opt. Express 2022, 30, 16921–16930. [Google Scholar] [CrossRef]
- Katzman, M.; Piasetzky, Y.; Rubin, E.; Barenboim, B.; Priel, M.; Erew, M.; Zadok, A.; Suchowski, H. Robust Directional Couplers for State Manipulation in Silicon Photonic-Integrated Circuits. J. Light. Technol. 2022, 40, 7634–7639. [Google Scholar] [CrossRef]
- Lu, Z.; Yun, H.; Wang, Y.; Chen, Z.; Zhang, F.; Jaeger, N.A.F.; Chrostowski, L. Broadband Silicon Photonic Directional Coupler Using Asymmetric-Waveguide Based Phase Control. Opt. Express 2015, 23, 3795–3808. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lu, Z.; Ma, M.; Yun, H.; Zhang, F.; Jaeger, N.A.F.; Chrostowski, L. Compact Broadband Directional Couplers Using Subwavelength Gratings. IEEE Photonics J. 2016, 8, 7101408. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, Y.; Sheng, Z.; Gan, F. Ultra-Broadband, Compact Arbitrary Ratio Power Splitters Enabled by Adiabatic Sub-Wavelength Grating. Photonics 2023, 10, 578. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).