Abstract
A self-homodyne coherent (SHC) transmission system that has a good prospect in terms of short-reach interconnections can simplify digital signal processing (DSP) and reduce the power consumption of laser diodes. However, the polarization control of the carrier becomes a pivotal part of these systems, and different from the traditional polarization control on a certain state of polarization (SOP), it only needs to lock the two polarization lights after the polarization beam splitter (PBS) in a state of equal power. Half-wave plates or Mach–Zehnder interferometers can accomplish the above goals. In order to evaluate the performance of these polarization control structures in the SHC system, we modeled them on the basis of theoretical analysis. Furthermore, a variable-step greedy linear descent (GLD) algorithm is proposed to solve the power fluctuation problem caused by the accelerated change of SOP near the pole of the Poincaré sphere. The simulation results indicate that the variable-step GLD algorithm can effectively improve the tracking ability of the polarization control loop up to approximately 1.5 times of the GLD algorithm and the gradient descent (GD) algorithm.
1. Introduction
Considering the issues of cost and complexity, data centers (DCs) have traditionally adopted the intensity modulation direct detection (IMDD) system. However, this scheme only uses the optical signal amplitude information for encoding, which greatly limits improving transmission efficiency [1]. With the explosive growth of network traffic, DCs face increasing pressure as IMDD systems struggle to improve the transmission bit rate to 200 Gbit/s. Therefore, establishing a simple efficient, and low-power interconnected optical network is extremely significant in this era of explosive data growth. The traditional coherent optical transmission system can make full use of all dimensions of the optical signal to transmit information and has been used in long-dual transmission, but it is not suitable for DCs due to its high cost and complexity.
From the perspective of reducing power consumption and cost, the self-homodyne coherent optical communication system (SHC) is very attractive for the next-generation DC. In the SHC scheme, the modulated signal and local oscillator (LO) come from the same laser at the origin, and they are transmitted to the coherent receiver through the fiber. This method can eliminate the influence of laser frequency offset and minimize the impact caused by the linewidth of the laser. So a large linewidth laser with low power consumption can be used at the transceiver [2]. However, in the SHC optical communication system, random polarization state rotation will occur in LO transmission through optical fiber, and the rotated LO may experience power attenuation in a certain polarization state (such as the X polarization state), which cannot guarantee successful demodulation by the coherent receiver [3]. Therefore, the integrated coherent receiver (ICR) in the SHC system should be tailored for DC. To confront the polarization fading of LO, a polarization diversity coherent receiver (PDCR) using an automatic polarization controller (APC) [4,5,6,7] or complementary PDCR [8] is deployed. The complementary PDCR structure composed of three hybrids is more complicated compared with APC. Meanwhile, compared to the traditional polarization controller which through cascaded waveplates or equivalent waveplates caused by electro-optical effects controls the input light to any state of polarization (SOP) [9,10], the role of polarization control in the SHC system is to prevent the LO power from fading. Therefore, a simple, low-power automatic feedback polarization control loop can accomplish the goal of outputting equal powers of two orthogonal polarization states of light. There are two types of APC structures: waveplate-type polarization controllers (PC) and Mach–Zehnder interferometer (MZI) control loops. In this paper, these two types of APC structures are studied for the LO polarization control in the SHC system. Additionally, a robust and efficient optimization algorithm is crucial for practical applications of a polarization control system. Commonly used algorithms include the gradient descent (GD) algorithm, simulated annealing algorithm, and swarm iterative algorithm [11,12,13,14]. Due to the simplified polarization control goal in the SHC system, the control algorithm can also be predigested. On the base of theoretical analysis and derivation of the control principle, the polarization control of the GD algorithm and greedy linear descent (GLD) algorithm are realized. According to this simplified polarization control objective, a variable-step GLD algorithm is proposed to automatically adapt an arbitrary input polarization state into the target location. Meanwhile, it is demonstrated that it has better tracking ability than GD and GLD algorithms.
2. Polarization Control Structure Furthermore, Principle
Due to the influence of the optical fiber link, the delivered LO undergoes random polarization state rotation in SHC systems, which results in LO power fluctuation on two polarizations. To ensure that both received polarization signals can be obtained with stable and equal amounts of LO light, an APC is required in the front end of the receiver for the LO branch [15], as shown in Figure 1. Different from traditional APC that needs to lock the input polarization to a certain point from the perspective of the Poincaré sphere, the APC in SHC system only needs to lock to a ring, which can be realized by using a half-wave plate (HWP) or MZI, respectively. In the following section, their structures and operating principles will be studied and analyzed in detail.
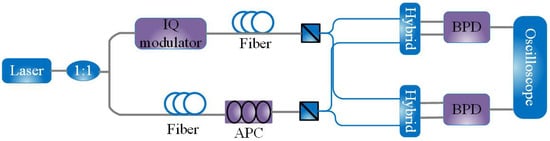
Figure 1.
The SHC transmission system.
2.1. Waveplate-Based Polarization Control Structure
Figure 2 depicts the structure of the waveplate-based polarization controller. The received LO of any SOP can be seen as rotation of elliptical polarized light in the laboratory coordinate system as
where can be expressed as
where , , , correspond to amplitude and phase of X polarization and Y polarization, respectively. Assuming that the laboratory coordinate is its main axis coordinates, then , is ellipticity, there are and . For the convenience of analysis, we only consider variables that are affected by changes in SOP, so Equation (1) can be simplified as:
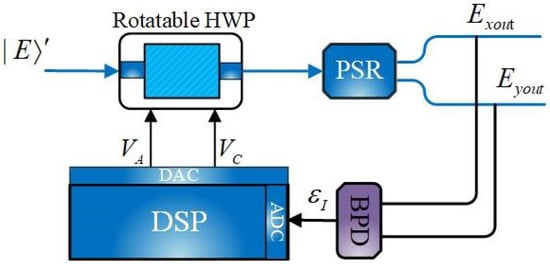
Figure 2.
Waveplate-type polarization control structure. (polarization splitter–rotator (PSR), balanced photodetector (BPD), analog-to-digital conversion (ADC), and digital-to-analog conversion (DAC)).
Since the control target is here to obtain equal power of LO light for two polarizations rather than control to a certain SOP as precise as the target of traditional APC, it can be realized by using only one stage of HWP in theory [5,16]. It is known that HWP is a phase-fixed-angle-adjustable PC, which is expressed in Jones matrix as
where represents the tunable azimuth of HWP, which can be adjusted according to the input driving voltage , . The received LO controlled by rotatable HWP can then be expressed as:
After detected by BPD, the feedback error signal is obtained:
The DSP module is used to minimize the feedback signal by and adjust the azimuth of HWP. It can be seen from Equation (6) that should meet to be in order to keep it at the minimum value. Figure 3 illustrates the transition process of the SOP of the input LO through an HWP. are stokes parameters that can visually describe the SOP of light on the Poincare sphere. refers to the difference in intensity of the light after passing through the horizontal and vertical polarizers. is the difference in intensity of the light after passing through ±45° polarizers. is the difference in intensity of the light after passing through a quarter-wave-plate (QWP) and ±45° polarizers. From the perspective of Poincaré sphere, the control target is the ring . The SOP of input light can be assumed to be set at point A which will be rotated around the axis to reach the target ring.
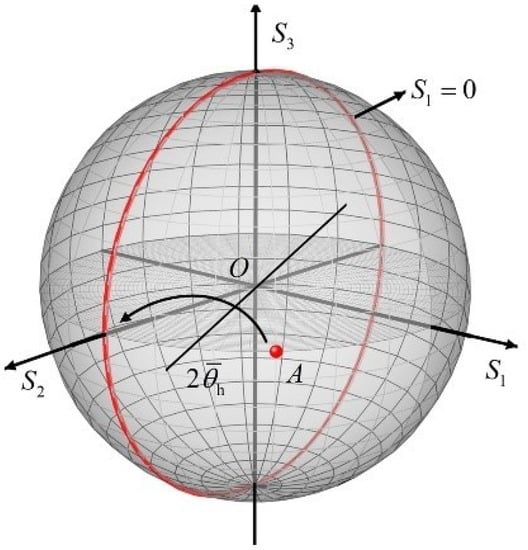
Figure 3.
The trajectory controlled by HWP on Poincaré ball.
2.2. Mach–Zehnder Interferometer-Based Polarization Control Structure
An alternative polarization control structure is composed of a PSR and a tunable MZI, as shown in Figure 4. The two output ports of the PSR are connected to an MZI incorporating two phase shifters and two couplers [17,18], which can be expressed as
where , represents the phase of the first-stage and second-stage phase shifter, respectively. The first-stage is used to rotate the input polarization around axis on the Poincaré ball to avoid going beyond its boundary, which has only two choices 0 or .
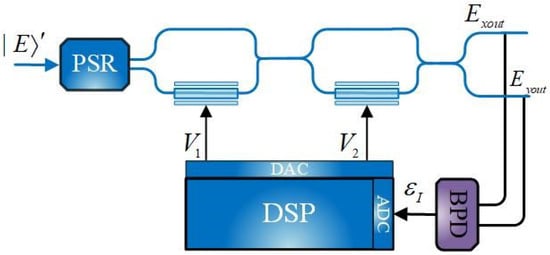
Figure 4.
The control structure based on MZI.
The second-stage is used to rotate the polarization of light around the axis. By changing the phases of them, the SOP of the output two paths of light can be changed accordingly, and achieve the purpose of controlling the output power of the two paths of light to be equal. Regardless of tracking speed, an MZI can rotate the input LO of any SOP to the target position.
Here, the photoelectric field of input LO can also be denoted as Equation (3). After being controlled by a two-stage MZI controller, the two output polarized lights can be represented as
where , , , and .
The power difference between these two polarized lights can be obtained by using a BPD. The output of BPD under the prerequisite of or is:
Similarly, a DSP module exports , decided by , through minimizing originating from BPD. After the minimum state is locked, has:
When stabilizing the polarization state of the input light, only the second-stage phase shifter needs to be tuned in most cases. However, when the second-stage phase shifter reaches its voltage bound, it needs to be reset with the help of the first-stage phase shifter. From Equations (11) and (12), we can conclude , so we can flip the tunable direction of by shifting to 0 or . If gradually increases to its limit value, shifting can gradually decrease so that is always working within its working voltage range [19]. The change process of the polarization state through MZI from the perspective of the Poincaré sphere is shown in Figure 5. It is supposed that the SOP of the input light of the PC can be represented by point A. After passing through the polarization control loop, point A is rotated around the axis to the target ring. Point A will make omissions to when is shifted between 0 and , which reverses the change direction of .
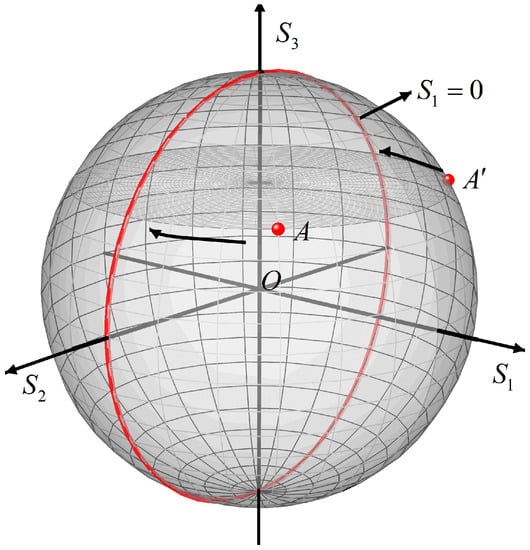
Figure 5.
The trajectory controlled by MZI on Poincaré ball.
2.3. Comparisons of These Two Control Structures
There are several other pivotal factors of polarization control devices that play a significant role in the control process of SOP. We provide a comparison of some performance parameters between the two types of PC in the table to illustrate the differences between them as Table 1. The PC consists of MZI based on thin-film lithium niobate (LN) has a more compact footprint, lower optical insertion loss, shorter response time, and lower half-wave voltage compared to the HWP-type PC. However, HWP can rotate endlessly to accomplish endless polarization manage. The PC based on MZI requires a reset process to ensure endless and stable polarization control, which may subjoin the complexity of DSP. These polarization control structures are promising to be further integrated with ICR. Nanofabrication technology is gradually mature. Integrated photonics that can modulate optical signals will lead to better performance of polarization controllers. Polarization controllers combining these technologies will have an ultra-compact size, enabling a high degree of integration and flexibility. Furthermore, it will have negative group velocity and anti-reflection and anti-scattering properties, which can realize precise manipulation and modulation of light [20].

Table 1.
Some parameters of PC based on HWP or MZI.
3. Polarization Control Algorithm
In the process of accomplishing polarization control, the control algorithm is a key part. An effective tracking method should have fast convergence and stable output results. The most commonly used and simple control algorithms are the GD and GLD algorithms.
The traditional polarization control method which locks to a fixed SOP typically utilizes the GD algorithm, which first calculates the gradient of the feedback signal, and then updates the HWP or phase shifter accordingly [22,23]. The gradient of the GD method is obtained by adding a perturbation and finding the secant. Different Poincaré sphere trajectories and state of polarization change rates (RSOP) lead to different azimuth-changing velocities of the LO. When the azimuth angle (phase) of HWP (phase shifter) cannot keep up with the azimuth variation of input LO, the feedback signal will fall into an uncontrolled area. In the event of the above situation, there will be a large error in the calculation of the gradient, which leads to fluctuations in the SOP of the output optical signal.
Considering the simplification of the control loop in the SHC system, the DSP optimization equation in this control system is simpler. On this basis, the GLD algorithm may be better suited to control injected SOP of the PC. The flow of the variable-step GLD algorithm in MZI-structure PC is shown in Figure 6. represents the input feedback signal of the DSP module, while and represent the azimuth of the first and second phases of the phase shifter, respectively. The updated formula of MZI is as Equation (13). The method of shifting is shown in Equation (14). The initial value of n is set to 1. When or , .
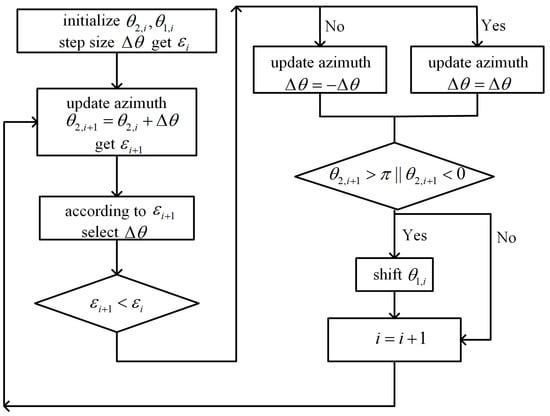
Figure 6.
Flow of the variable-step greedy algorithm.
When the feedback signal value converges, the algorithm stops tracking. Then DSP continues to judge the value of the feedback signal and to track once the feedback signal is out of control. To elevate tracking ability and improve the convergence speed, a variable-step GLD algorithm can be used, that is, when the SOP of LO is far from the target position, select a larger step size for tracking, and if it is near target position, select a smaller one for tracking. The criteria for step selection are based on the feedback signal, which will be discussed in the next section.
This method can not only ensure high precision of the signal after control but also improve the ability to track a larger RSOP. In the HWP architecture, the only difference is that and reset are not required.
4. System Algorithm Simulation Furthermore, Analysis
According to the control theories and control algorithms discussed above, a simulation system shown in Figure 7 is fabricated based on the Simulink platform.
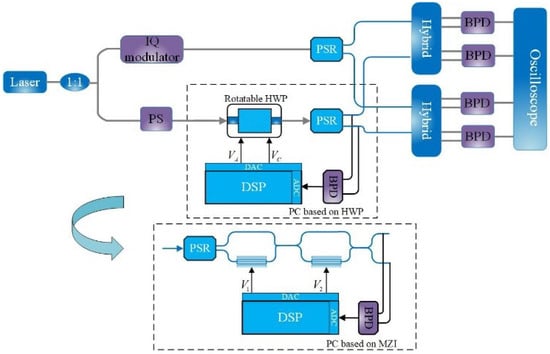
Figure 7.
Structure of the simulated system.
The LO and modulated signal originate from the same laser. The light is split into two branches by a splitter and then one is modulated into a 28 Gbaud, 16 QAM signal for transmission, and the other is transmitted as an LO. The polarization scrambler (PS) is used to simulate the impact of the random polarization disturbance caused by the optical fiber link on LO. The composition of PS consists of three QWPs, one HWP, and three QWPs [24]. The rotation rate of the HWP represents the RSOP of LO. The sampling rate and main frequency clock of the DSP module are 65 MHz and 250 MHz, respectively. The control algorithm takes about 15 cycles of the main frequency, mainly depending on the number of operations. Meanwhile, the waiting loop delay is set to around 80 cycles of the main frequency considering the response of DA, AD, and photoelectric devices. Before the receiver, LO scrambled by the PS is controlled using a PC based on HWP or MZI to produce two output lights with orthogonal polarization states and equal power. The insertion losses of HWP and MZI are set to 2.5 dB and 1 dB, respectively. After PC, the output LO together with modulated optical signal injects into the coherent receiver. Note that the system structure does not consider the transmission mismatch length of the two optical signals. Table 2 gives some simulation parameters.

Table 2.
Key parameters of PC system simulation.
The laser generates light with a linear SOP, and arbitrary SOP change of the LO which has random power attenuation can be obtained after PS. Since LO and the modulated signal originate from the same laser, frequency offset compensation is not required in the DSP process, and the process of phase recovery can also be simplified. The power of these two output lights is equal, but the phase error between the controlled LO and signal changes slowly. Figure 8 shows the constellation plots for RSOP of 10 krad/s and 100 krad/s without carrier phase recovery (CPR), both under the condition that the LO is fully controlled to . It can be seen that the change rate of phase error increases with the increase in RSOP. To compensate for the tight phase error, we use simplified blind phase search (BPS) for CPR. It uses a fixed phase for phase compensation within a certain period of time. The fixed phase is updated periodically. Considering the mismatch length, the phase error can be compensated together with the phase error caused by the mismatch length.
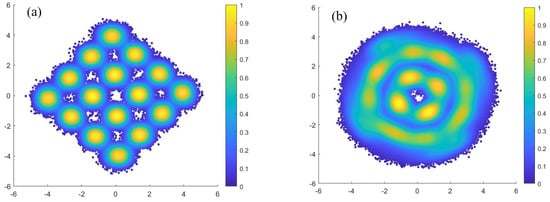
Figure 8.
Constellation without CPR under different RSOP (a) 10 krad/s (b) 100 krad/s.
In the case where the feedback signal is not fully controlled, the normalized amplitude of the feedback signal will appear bumpy. To characterize the worst-case communication quality, we measured the bit error rate (BER) at the largest bump, which is called the worst-BER in this paper. Figure 9 shows the worst-BER of the GLD algorithm with different steps in case of different RSOP under the PC based on HWP. In the step variation range of 2°–5°, a smaller step corresponds to higher control accuracy but weaker control ability, correspondingly a larger step corresponds to poorer control accuracy but stronger control ability. As depicted in Figure 9, even when the feedback signal is fully controlled within the 5 krad/s–50 krad/s range, the worst-BER remains high under the 5° step due to poor control precision. Conversely, the LO is out of control at 30 krad/s under the 3° step due to weak control ability. Figure 9 shows that the 4° step offers the best overall performance in terms of the worst-BER. Therefore, we selected a step of 4° for the GLD algorithm. The fluctuation of a fully controlled normalized signal will not exceed −0.348 dB. Therefore, when the normalized feedback signal exceeds −0.348 dB, a larger step size is selected in variable-step GLD algorithms for tracking. Additionally, we chose a 2° step and a 5° step for the variable-step GLD algorithm to ensure both control accuracy and control ability.
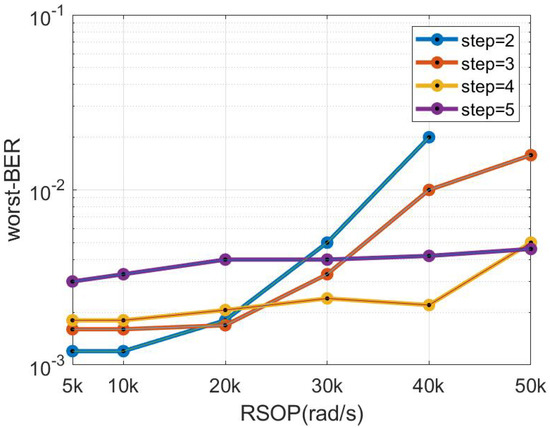
Figure 9.
The worst−BER versus RSOP with different steps.
Similarly, in the MZI structure, the GLD algorithm uses a step of 5°, and the steps of the variable-step GLD algorithm vary between 4° and 8°, respectively.
We also give the tracking process of the MZI structure employing the GD algorithm, GLD algorithm, and variable-step GLD algorithm under 18 krad/s. The azimuth of scrambled LO and the phase changes of the phase shifter under three algorithms are visual in Figure 10. Figure 11 accordingly expresses the tracking process of the feedback signal with these algorithms. From these figures, it is evident that the phase of MZI varies with the azimuth of input LO as in Equation (12), and the feedback signal remains stable. When the azimuth of LO changes rapidly, the variable phase cannot keep up with it. Furthermore, the updating direction is misjudged, leading to the bumpy of the feedback signal. The above situation is more probable to happen with GD and GLD algorithms. It can be seen that the feedback signal controlled by the variable-step GLD algorithm experiences the smallest bumpy, and the angle of the feedback signal tracks LO with higher accuracy. This observation suggests that the variable-step GLD algorithm exhibits the best tracking ability among the three algorithms.
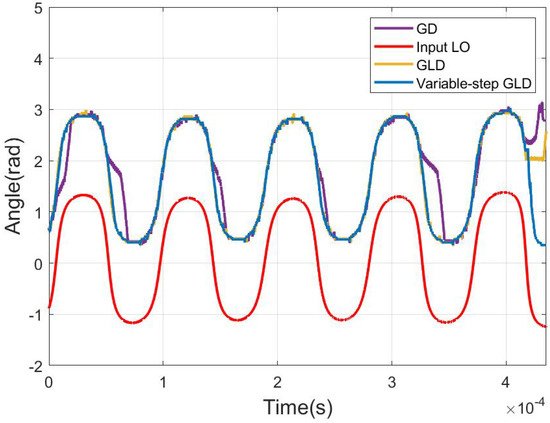
Figure 10.
Angle tracking process under different algorithms.
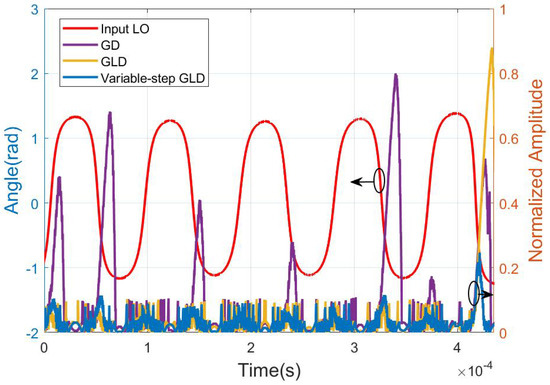
Figure 11.
Feedback signal tracking process under different algorithms.
Figure 12 presents the measured worst-BER under different RSOP in different algorithms of HWP polarization control structure. The BER threshold before 7% overhead hard-decision forward error correction (HD-FEC) is used. As shown in the figure, the GD algorithm and GLD algorithm can control RSOP up to 30 krad/s, while the variable-step GLD algorithm can control the RSOP up to 50 krad/s under the pre-FEC BER threshold. Compared with the first two algorithms, the variable-step GLD algorithm effectively improves the tracking speed. It should be noted that phase drift and power fluctuations may slightly affect the tracking results.
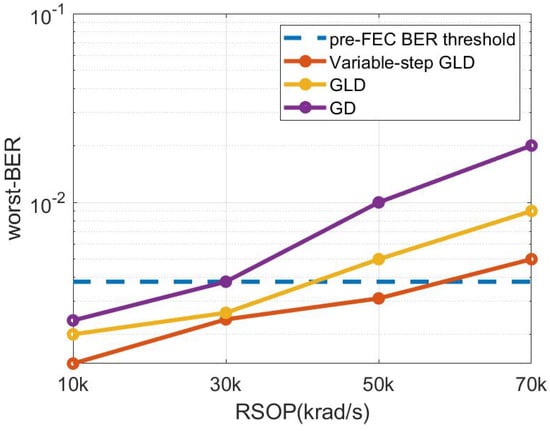
Figure 12.
The worst-BER under different algorithms.
Figure 13 displays the schematic diagram of the Poincaré sphere and feedback signal normalized amplitude after the scrambled and controlled LO of the variable-step GLD algorithm under the HWP structure at different RSOP. As the RSOP increases, the azimuth of input LO near the pole changes faster than other areas of the Poincaré sphere, resulting in the HWP or phase update rate fail to keep up with the azimuth angle change, and the feedback signal is more likely to fall into an uncontrolled area. The situation that the PC output LO is away from will exacerbate on the pole of the Poincaré sphere.
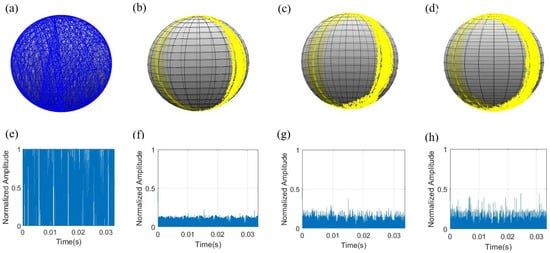
Figure 13.
(a) Poincaré sphere of input random SOP. (b–d) Poincaré sphere after control under 30 krad/s, 50 krad/s, 70 krad/s. (e) Input feedback signal of PC. (f–h) Feedback signal after control under 30 krad/s, 50 krad/s, 70 krad/s.
In order to accurately analyze the effectiveness of the polarization tracking scheme in the optical fiber transmission scenario, the 28G baud, 16QAM standard single-mode fiber (SSMF) transmission system is established. The transmission length of the fiber is 40 km, and its loss is dB/m. The dispersion and polarization mode dispersion (PMD) coefficients of the fiber are ps/nm and s/, respectively. The BER of GLD, variable-step GLD algorithms under back-to-back (BTB) system and single mode fiber (SSMF) system are compared as shown in Figure 14. The BER of BTB and SSMF is slightly different, and the control speed is also presumably no difference. No matter under BTB or SSMF system, variable-step GLD algorithm has better tracking ability and more precise convergence compared to GLD algorithm.
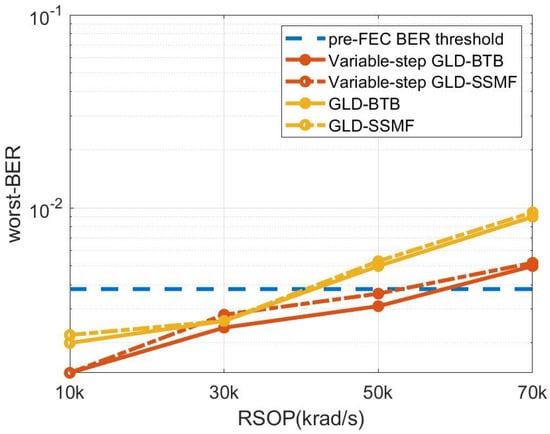
Figure 14.
The worst-BER of GLD, variable-step GLD algorithm under different RSOP in BTB and SMF systems.
The tracking ability is not only related to the polarization control algorithm but also affected by the control loop bandwidth, DA/AD sampling rate, DSP processing rate, and other factors. The control loop bandwidth has a significant effect on the control speed. To show the relationship between the control loop conditions and tracking speed more clearly, we simulated the control situation under different loop delays and obtained the maximum controllable RSOP, as shown in Figure 15. As the loop delay becomes longer, the control capability of these control structures is also weakened. Increasing the bandwidth of the control loop can significantly improve its tracking capability. The tracking ability of the MZI structure is weaker than that of HWP structure under the same loop delay owing to the reset in MZI structure. To sum up, the hardware speed of MZI can be faster, but its control algorithm is more complex than that of HWP in the SHC system.
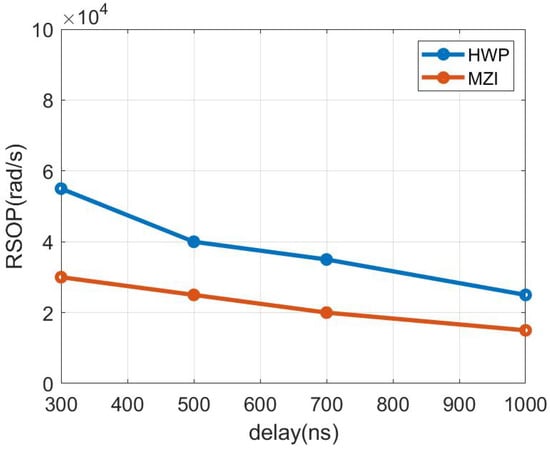
Figure 15.
The maximum SOP that can be controlled at different update rates.
5. Conclusions
The control theories and structure of two polarization control structures in the homologous SHC optical communication systems are discussed, one is mainly composed of an HWP, and the other is based on an MZI. Furthermore, in terms of polarization control algorithms, an effective improvement compared with GLD and GD algorithms in tracking ability is achieved here with the proposed variable-step GLD algorithm. At the same time, we give the controllable RSOP under different update rates of HWP or phase shifter to illustrate the influence of the loop situation on tracking ability. The further improvement of tracking capability mainly depends on improving the physical performance of PC, as well as proposing new tracking algorithms. Advanced photonic integrated circuit technology will provide new possibilities for the development of polarization controllers.
Author Contributions
Methodology, Q.F. and X.Z.; Software, Q.F.; Validation, R.L., Y.G., S.W. and F.L.; Formal analysis, Q.F.; Investigation, R.L., S.W. and F.L.; Resources, Y.G. and S.W.; Data curation, Y.G.; Writing—original draft, Q.F.; Writing—review & editing, X.Z.; Visualization, R.L. and K.L.; Supervision, X.Z. and K.L.; Project administration, X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 62171022), Beijing Natural Science Foundation (Grant No. 4222009), Guangdong Basic and Applied Basic Research Foundation (Grant No. 2021B1515120057), the Scientific and Technological Innovation Foundation of Shunde Graduate School, USTB (Grant No. BK19AF005).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Perin, J.K.; Shastri, A.; Kahn, J.M. Coherent data center links. J. Light. Technol. 2020, 39, 730–741. [Google Scholar] [CrossRef]
- Gui, T.; Wang, X.; Tang, M.; Yu, Y.; Lu, Y.; Li, L. Real-time demonstration of homodyne coherent bidirectional transmission for next-generation data center interconnects. J. Light. Technol. 2021, 39, 1231–1238. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, Y.; Li, Y.; Bai, Q.; Liu, X.; Jin, B. Polarization Fading Suppression for Optical Fiber Sensing: A Review. IEEE Sens. J. 2022, 22, 8295–8312. [Google Scholar] [CrossRef]
- Ito, M.; Okawa, K.; Suganuma, T.; Fukui, T.; Kato, E.; Tanemura, T.; Nakano, Y. Efficient InGaAsP MQW-based polarization controller without active-passive integration. Opt. Express 2021, 29, 10538–10545. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zeng, Y.; Liao, R.; Shen, L.; Zhao, C.; Wu, H.; Tang, M. Half-Wave-Plate based Adaptive Polarization Controller. In CLEO: QELS_Fundamental Science, Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 9–14 May 2021; Optica Publishing Group: Washington, DC, USA, 2021; p. JW1A-49. [Google Scholar]
- Noe, R.; Heidrich, H.; Hoffmann, D. Endless polarization control systems for coherent optics. J. Light. Technol. 1988, 6, 1199–1208. [Google Scholar] [CrossRef]
- Madsen, C.K.; Oswald, P.; Cappuzzo, M.; Chen, E.; Gomez, L.; Griffin, A.; Kasper, A.; Laskowski, E.; Stulz, L.; Wong-Foy, A. Reset-free integrated polarization controller using phase shifters. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 431–438. [Google Scholar] [CrossRef]
- Ji, H.; Li, J.; Li, X.; Dong, S.; Xu, Z.; Su, Y.; Shieh, W. Complementary polarization-diversity coherent receiver for self-coherent homodyne detection with rapid polarization tracking. J. Light. Technol. 2022, 40, 2773–2779. [Google Scholar] [CrossRef]
- Zheng, Z.; Lu, L.; Li, C.; Wang, W.; Zhang, S.; Fan, L.; Zhang, T.; Zuo, T.; Liu, L.; Lau, A.P.T.; et al. High speed, low voltage polarization controller based on heterogeneous integration of silicon and lithium niobate. In Proceedings of the Optical Fiber Communication Conference, Washington, DC, USA, 6–11 June 2021; p. Th1A-12. [Google Scholar]
- Heismann, F. Analysis of a reset-free polarization controller for fast automatic polarization stabilization in fiber-optic transmission systems. J. Light. Technol. 1994, 12, 690–699. [Google Scholar] [CrossRef]
- Garcia, J.D.; Amaral, G.C. An optimal polarization tracking algorithm for Lithium-Niobate-based polarization controllers. In Proceedings of the 2016 IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM), Rio de Janeiro, Brazil, 10–13 July 2016; pp. 1–5. [Google Scholar]
- Su, R.; Liu, Y.; Yang, B.; Ma, P.; Wang, X.; Zhou, P.; Xu, X. Active polarization control of a 1.43 kW narrow linewidth fiber amplifier based on SPGD algorithm. J. Opt. 2017, 19, 045802. [Google Scholar] [CrossRef]
- Sha, Z.; Feng, H.; Shi, Y.; Zeng, Z. Polarization control for dual mach-zehnder fiber vibration sensor using simulated annealing. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar]
- Hou, Q.; Yuan, X.; Zhang, Y.; Zhang, J. Endless polarization stabilization control for optical communication systems. Chin. Opt. Lett. 2014, 12, 110603. [Google Scholar]
- Puttnam, B.J.; Luís, R.S.; Delgado Mendinueta, J.M. Self-homodyne detection in optical communication systems. Photonics 2014, 1, 110–130. [Google Scholar] [CrossRef]
- Gui, T.; Cao, J.; Chen, X.; Zheng, K.; Yuan, S.; Fang, X.; Lei, Y.; Zhan, Q.; Wang, D.; Sui, Q.; et al. Real-time Single-Carrier 800 Gb/s DP-64QAM Demonstration using Bi-Directional Self-homodyne Coherent Transceivers with 200 krad/s Endless Active Polarization Controller. In Proceedings of the Optoelectronics and Communications Conference, Hong Kong, China, 3–7 July 2021; p. T5A-5. [Google Scholar]
- Wang, X.; Zeng, Y.; Liao, R. High-performance polarization management devices based on thin-film lithium niobate. In Proceedings of the 2021 Optical Fiber Communications Conference and Exhibition (OFC), Online, 6–10 June 2021; pp. 1–3. [Google Scholar]
- Lin, Z. Endless polarization stabilization control for optical communication systems. Light. Sci. Appl. 2022, 11, 93. [Google Scholar] [CrossRef] [PubMed]
- Martinelli, M.; Martelli, P.; Pietralunga, S.M. Polarization stabilization in optical communications systems. J. Light. Technol. 2006, 24, 4172–4183. [Google Scholar] [CrossRef]
- Sirmaci, Y.D.; Barreda Gomez, A.; Pertsch, T.; Schmid, J.H.; Cheben, P.; Staude, I. All-dielectric Huygens’ meta-waveguides for resonant integrated photonics. Laser Photonics Rev. 2023, 17, 2200860. [Google Scholar] [CrossRef]
- Polarization Controllers—EOSPACE, INC. Available online: https://www.eospace.com/polarization-controller (accessed on 18 May 2023).
- Ma, M.; Shoman, H.; Tang, K.; Shekhar, S.; Jaeger, N.A.; Chrostowski, L. Automated control algorithms for silicon photonic polarization receiver. Opt. Express 2020, 28, 1885–1896. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lu, L.; Gao, W.; Li, X.; Chen, J.; Zhou, L. Silicon non-blocking 4 × 4 optical switch with automated polarization adjustment. Chin. Opt. Lett. 2021, 19, 101302. [Google Scholar] [CrossRef]
- Novoptel: Polarization Scramblers: Technology at Work. Available online: https://novoptel.de/Scrambling/Scrambling_en.php (accessed on 26 June 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).