Post Optical Freeform Compensation Technique for Machining Errors of Large-Aperture Primary Mirror
Abstract
1. Introduction
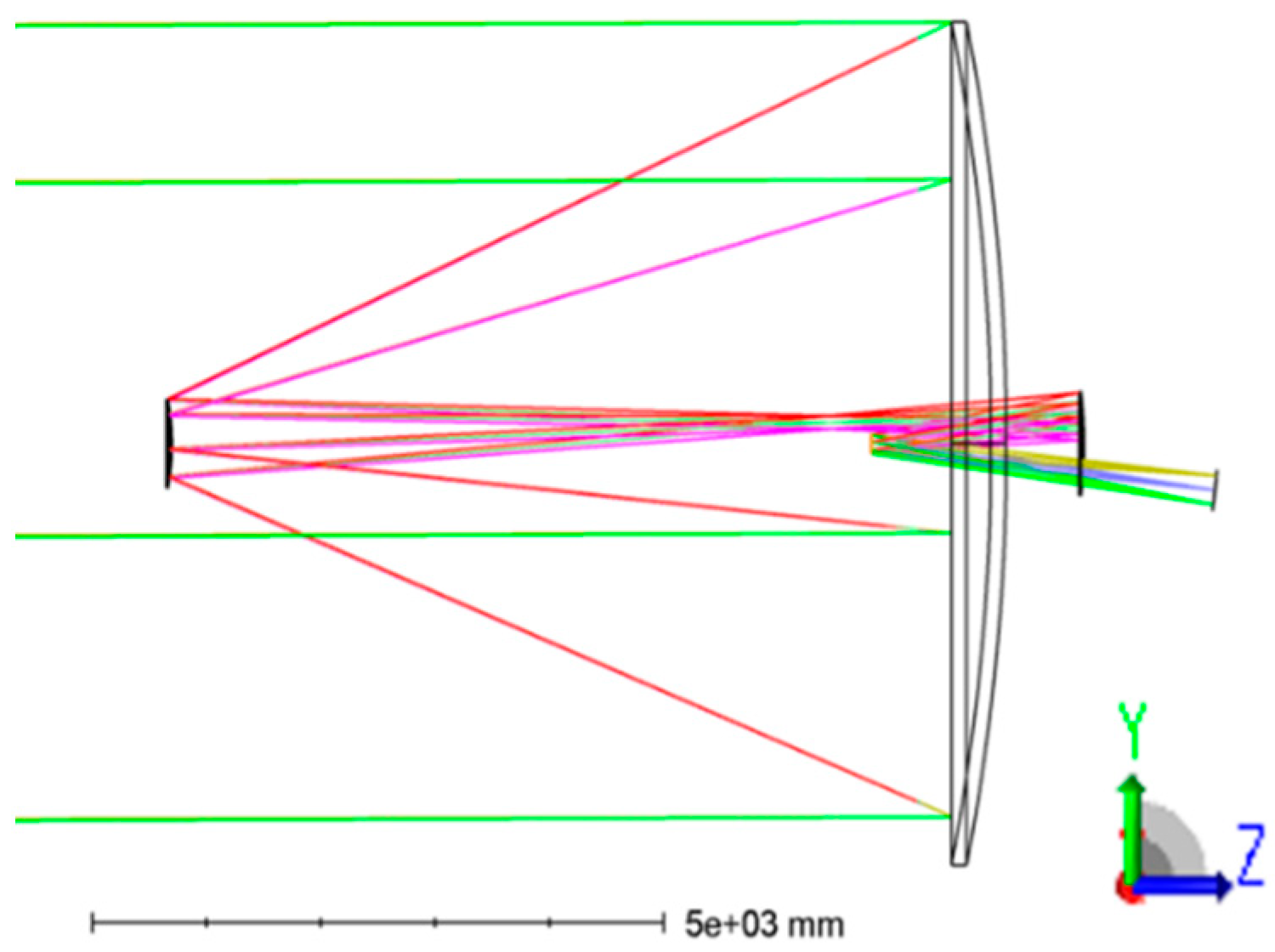
2. Analysis of Correction Ability of Different Compensation Methods
2.1. Pose Compensation for Machining Errors of Primary Mirror
- (1)
- Pose compensation in R–C optical system
- (2)
- Pose compensation in three-mirror optical system
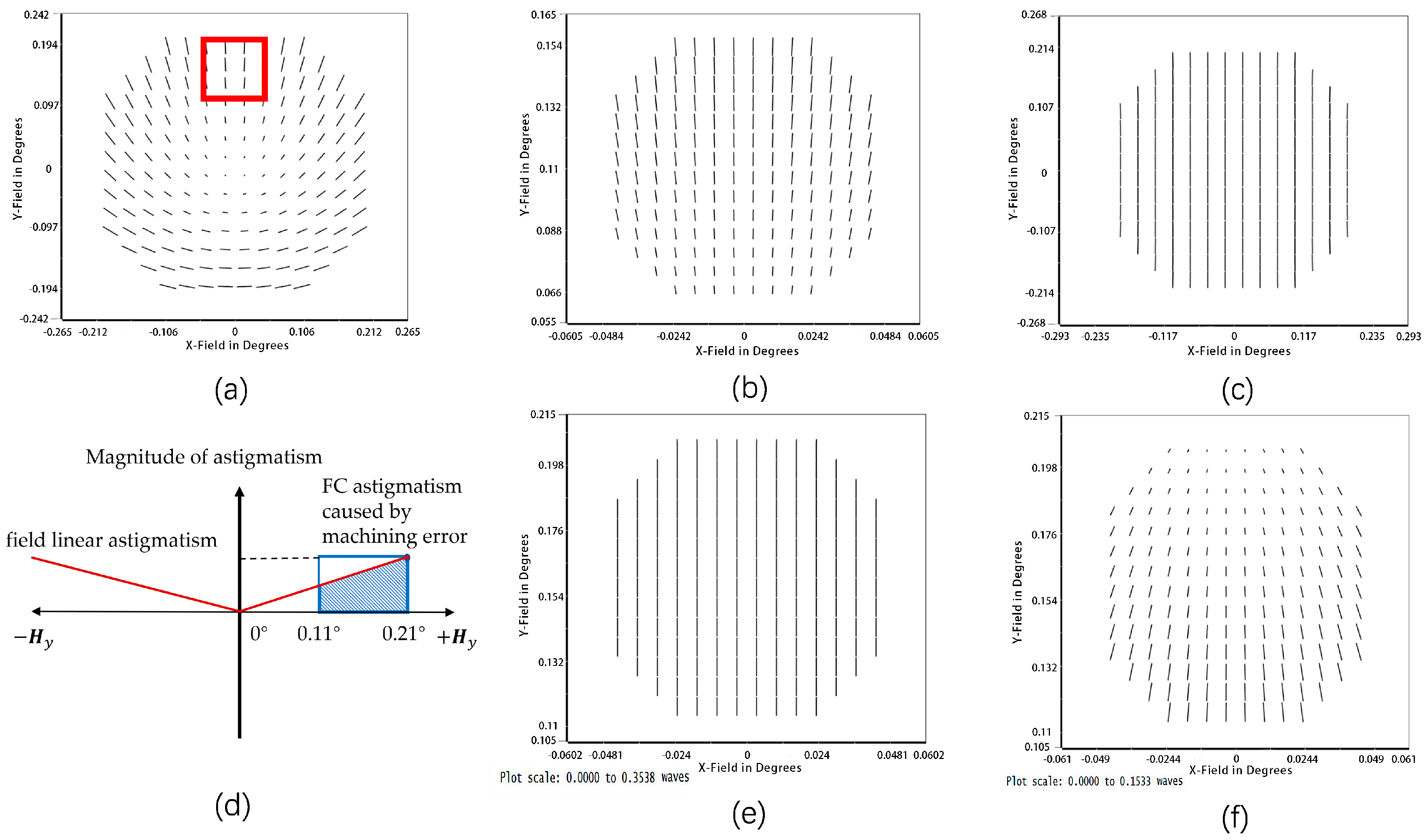
2.2. Freeform Compensation for Machining Errors of Primary Mirror
3. Combination of Freeform Compensation and Pose Compensation
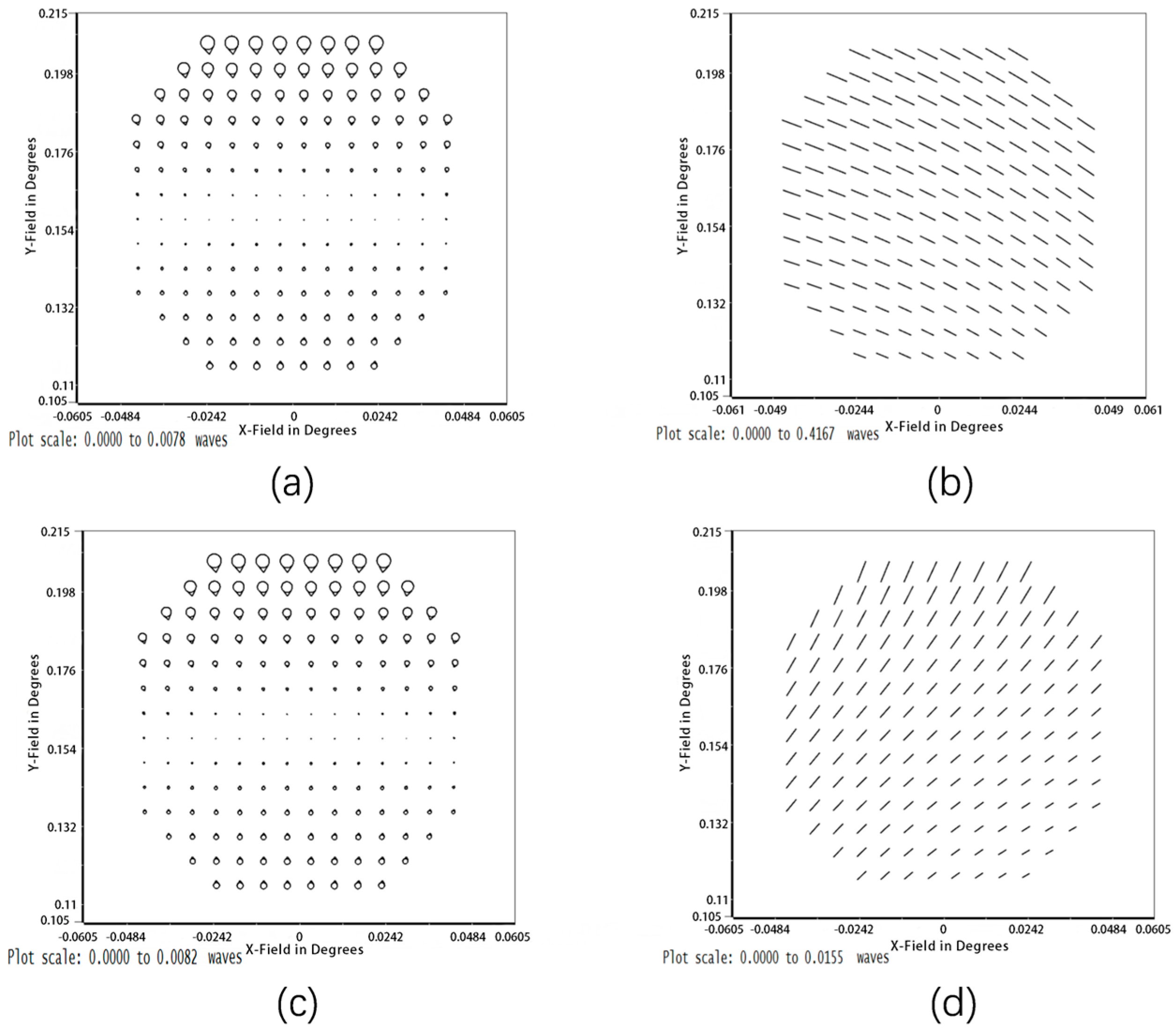
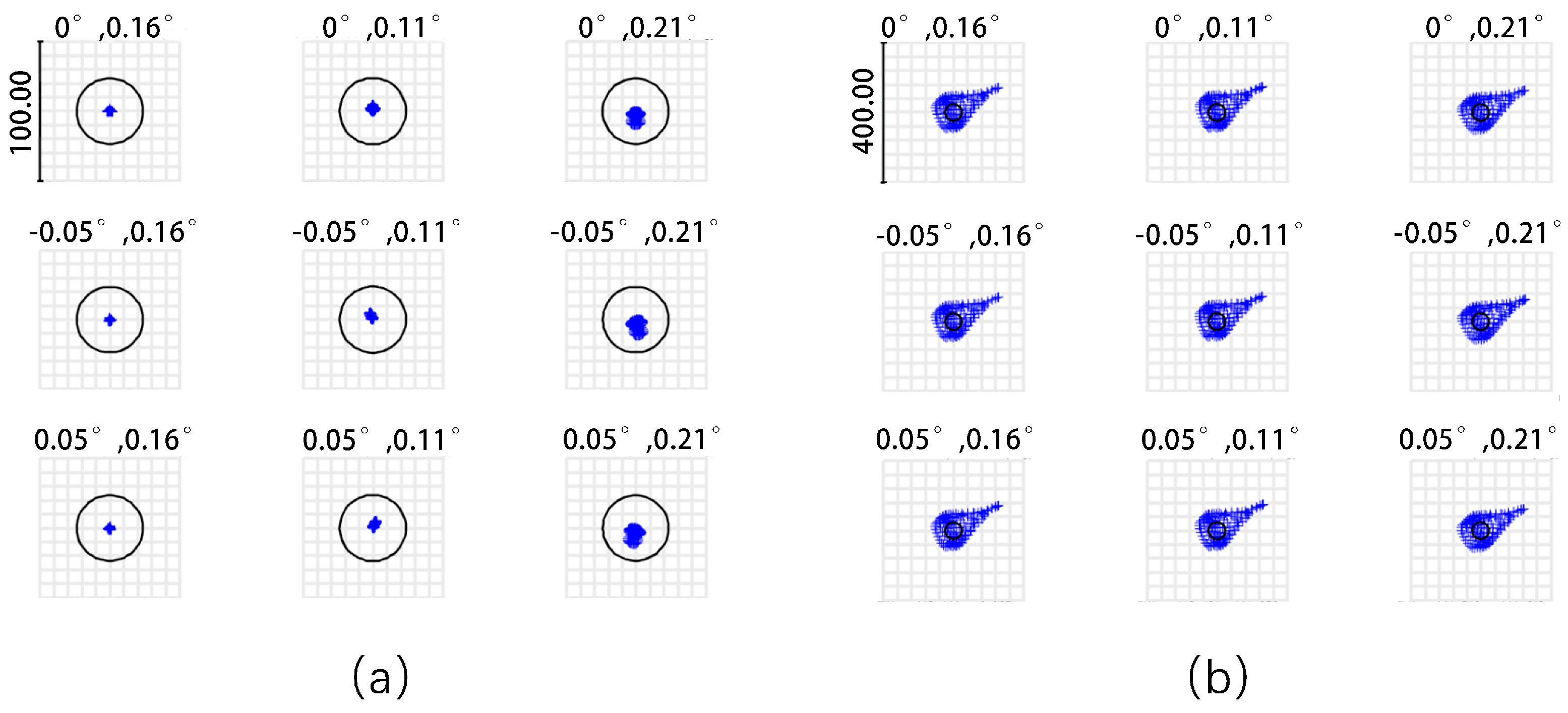
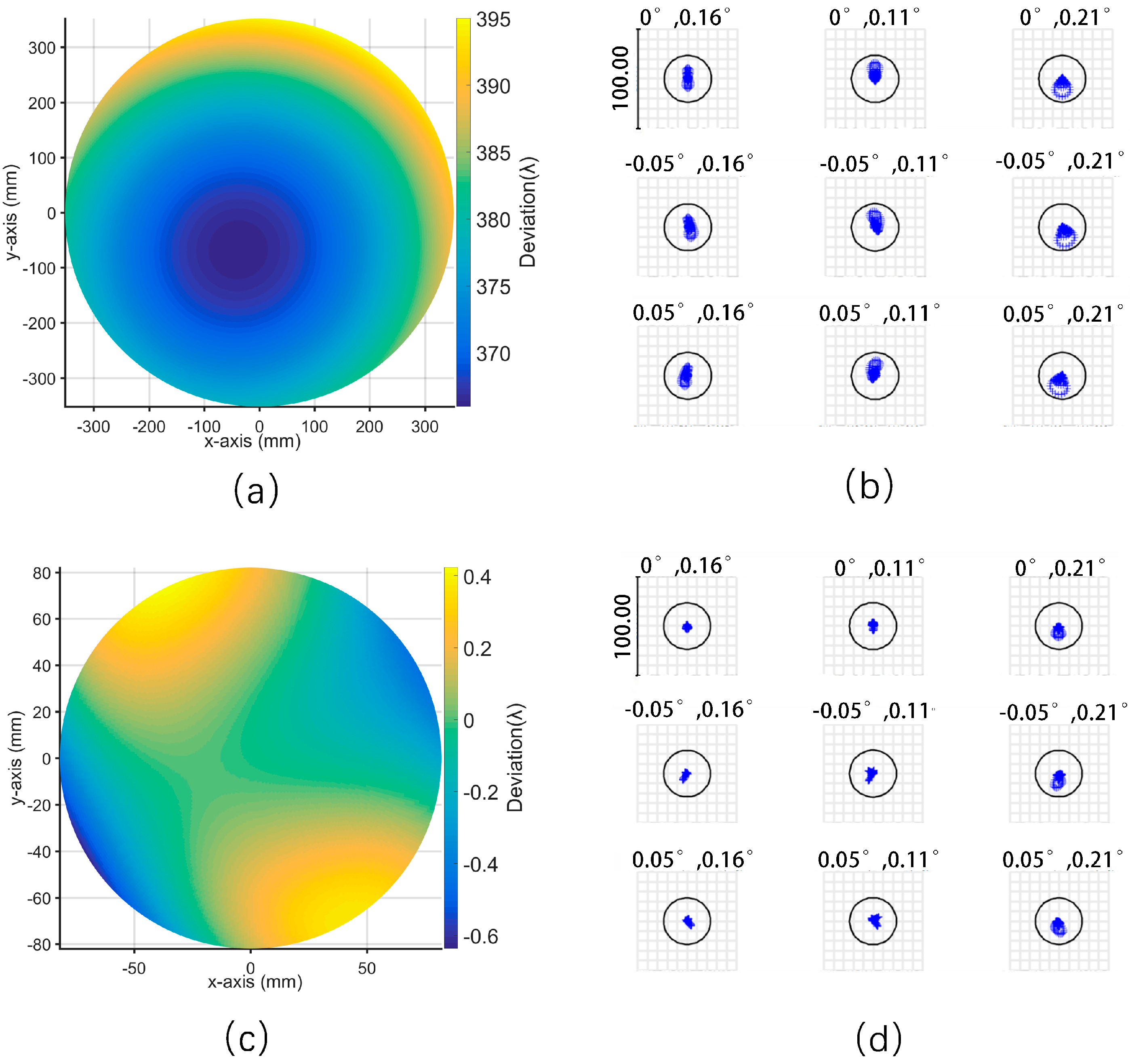
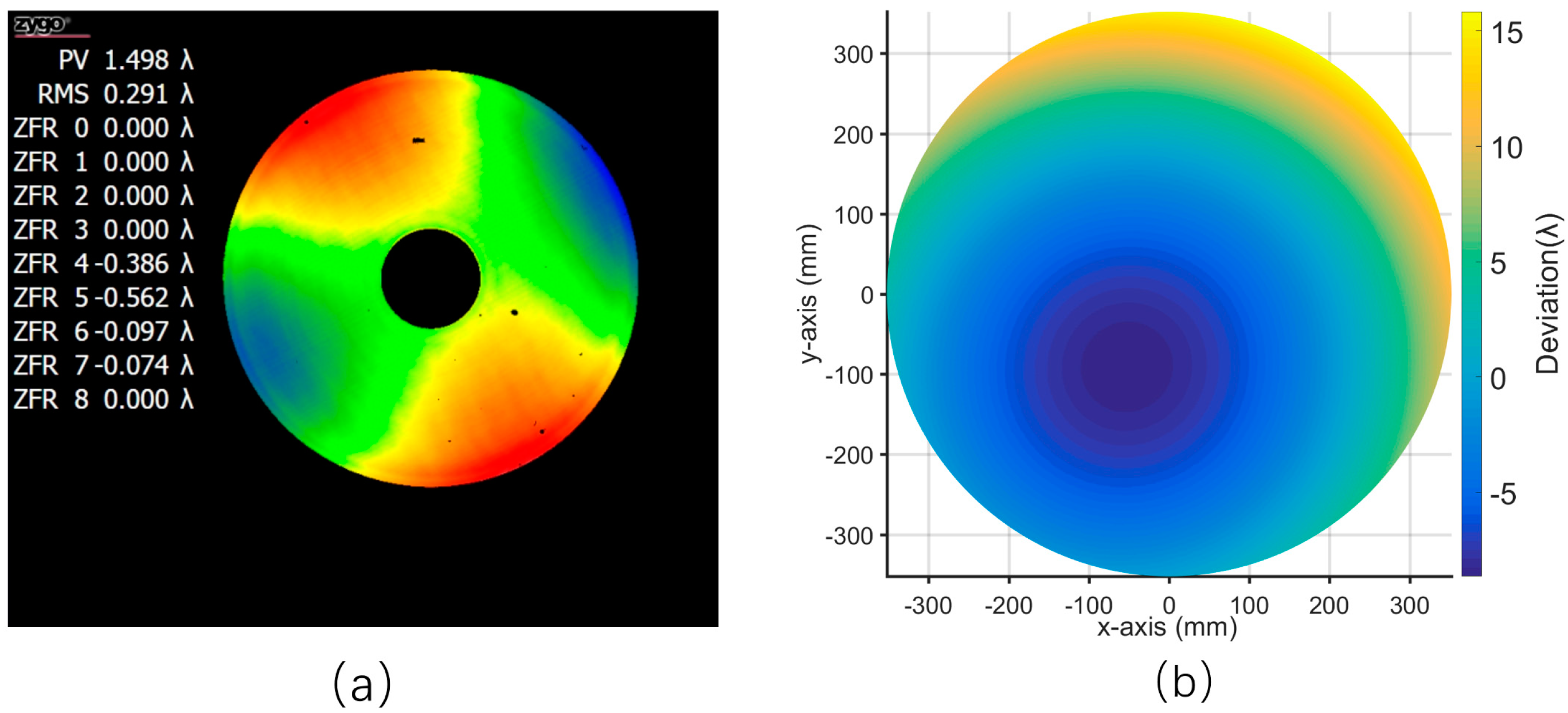
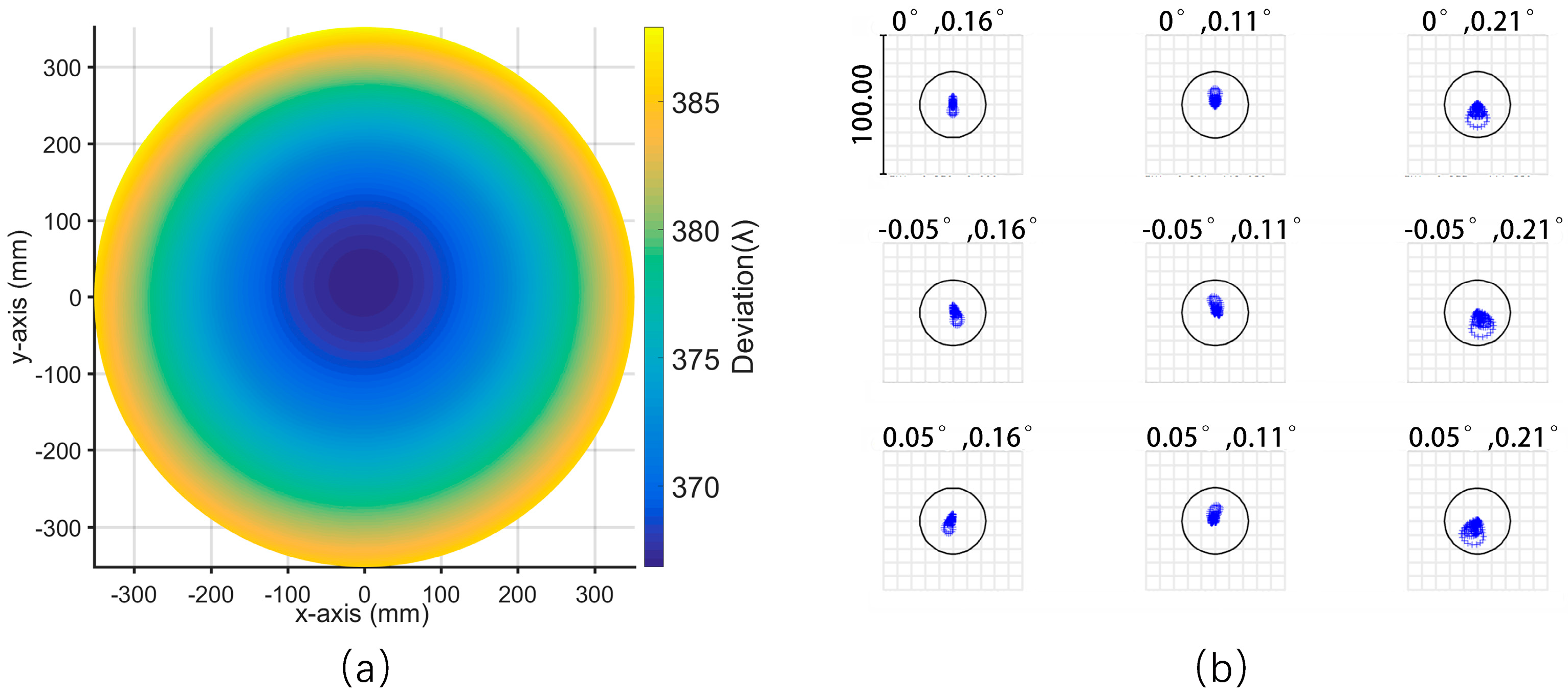
3.1. Compensate for Specific Machining Errors
3.2. Compensate for Multiple Machining Errors
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bougoin, M.; Lavenac, J. From Herschel to Gaia: 3-meter class SiC space optics. In Proceedings of the Optical Manufacturing and Testing IX, San Diego, CA, USA, 22–24 August 2011; pp. 248–257. [Google Scholar]
- Young, E.; Becklin, E.; Marcum, P.; Roellig, T.L.; De Buizer, J.M.; Herter, T.L.; Güsten, R.; Dunham, E.W.; Temi, P.; Andersson, B.-G.; et al. Early science with SOFIA, the stratospheric observatory for infrared astronomy. Astrophys. J. Lett. 2012, 749, L17. [Google Scholar] [CrossRef]
- Trumper, I.; Hallibert, P.; Arenberg, J.W.; Kunieda, H.; Guyon, O.; Stahl, H.P.; Kim, D.W. Optics technology for large-aperture space telescopes: From fabrication to final acceptance tests. Adv. Opt. Photonics 2018, 10, 644–702. [Google Scholar] [CrossRef]
- Cole, G.C.; Garfield, R.; Peters, T.; Wolff, W.; Johnson, K.; Bernier, R.; Kiikka, C.; Nassar, T.; Wong, H.A.; Kincade, J.; et al. An overview of optical fabrication of the JWST mirror segments at Tinsley. Space Telesc. Instrum. I Opt. Infrared Millim. 2006, 6265, 253–261. [Google Scholar]
- Kim, D.W.; Burge, J.H.; Davis, J.M.; Martin, H.M.; Tuell, M.T.; Graves, L.R.; West, S.C. New and improved technology for manufacture of GMT primary mirror segments. In Proceedings of the Conference on Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II, Edinburgh, UK, 26 June–1 July 2016. [Google Scholar]
- Geyl, R.; Leplan, H.; Ruch, E. Advanced space optics development in freeform optics design, ceramic polishing, rapid and extreme freeform polishing. In Proceedings of the International Conference on Space Optics—ICSO 2016, Biarritz, France, 18–21 October 2016; SPIE: Bellingham, WA, USA, 2017; Volume 10562. [Google Scholar]
- Xie, X.; Yang, B.; Zhou, L.; Song, C.; Hu, H. A large size ion beam figuring system for 1.2 m astronomical telescopes fabrication. In Proceedings of the Conference on Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation II, Edinburgh, UK, 26 June–1 July 2016. [Google Scholar]
- Thompson, K. Description of the third-order optical aberrations of near-circular pupil optical systems without symmetry. J. Opt. Soc. Am. A 2005, 22, 1389–1401. [Google Scholar] [CrossRef] [PubMed]
- Schmid, T.; Rolland, J.P.; Rakich, A.; Thompson, K.P. Separation of the effects of astigmatic figure error from misalignments using Nodal Aberration Theory (NAT). Opt. Express 2010, 18, 17433–17447. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Angel, R.; Mangus, J.D.; Rodney, G.A.; Shannon, R.R.; Spoelhof, C.P. The Hubble Space Telescope Optical Systems Failure Report; NASA Report; National Aeronautics and Space Administration: Champaign, IL, USA, 1990. [Google Scholar]
- Feinberg, L.D.; Geithner, P.H. Applying HST lessons learned to JWST. In Proceedings of the Space Telescopes and Instrumentation 2008: Optical, Infrared, and Millimeter, Marseille, France, 23–28 June 2008; pp. 209–217. [Google Scholar]
- Thompson, K.P.; Rodgers, J.M.; Kestner, B. Compensating lens designs and testing of the COSTAR optics. In Proceedings of the International Optical Design Conference, Rochester, NY, USA, 6–9 June 1994; p. TSO. 284. [Google Scholar]
- Rolland, J.P.; Davies, M.A.; Suleski, T.J.; Evans, C.; Bauer, A.; Lambropoulos, J.C.; Falaggis, K. Freeform optics for imaging. Optica 2021, 8, 161–176. [Google Scholar] [CrossRef]
- Zhong, Y.; Gross, H. Initial system design method for non-rotationally symmetric systems based on Gaussian brackets and Nodal aberration theory. Opt. Express 2017, 25, 10016–10030. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhu, J. Design Method of Freeform Off-Axis Multi-Mirror Optical Systems. Photonics 2022, 9, 534. [Google Scholar] [CrossRef]
- Fuerschbach, K.; Rolland, J.P.; Thompson, K. Extending nodal aberration theory to include mount-induced aberrations with application to freeform surfaces. Opt. Express 2012, 20, 20139–20155. [Google Scholar] [CrossRef] [PubMed]
- Fuerschbach, K.; Rolland, J.P.; Thompson, K. Theory of aberration fields for general optical systems with freeform surfaces. Opt. Express 2014, 22, 26585–26606. [Google Scholar] [CrossRef] [PubMed]
- Bauer, A.; Schiesser, E.M.; Rolland, J.P. Starting geometry creation and design method for freeform optics. Nat. Commun. 2018, 9, 1756. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Chen, L.; Li, X.; Yuan, Q.; Gao, Z. Review of optical freeform surface representation technique and its application. Opt. Eng. 2017, 56, 110901. [Google Scholar] [CrossRef]
- Thompson, K.P.; Schmid, T.; Cakmakci, O.; Rolland, J.P. Real-ray-based method for locating individual surface aberration field centers in imaging optical systems without rotational symmetry. J. Opt. Soc. Am. A 2009, 26, 1503–1517. [Google Scholar] [CrossRef] [PubMed]
- Feinberg, L.D.; Keski-Kuha, R.; Atkinson, C.; Texter, S.C. Use of a pathfinder optical telescope element for James Webb Space Telescope risk mitigation. In Proceedings of the Space Telescopes and Instrumentation: Optical, Infrared, and Millimeter Wave, San Diego, CA, USA, 27 June–2 July 2010; pp. 1347–1355. [Google Scholar]
- Contos, A.R.; Acton, D.S.; Barto, A.A.; Burns, L.A.; Contreras, J.; Dean, B.; Elliott, E.; Feinberg, L.; Hansen, K.; Hardy, B.; et al. Verification of the James Webb Space Telescope (JWST) wavefront sensing and control system. In Proceedings of the Space Telescopes and Instrumentation: Optical, Infrared, and Millimeter, Marseille, France, 23–28 June 2008; pp. 256–268. [Google Scholar]
- Huang, C.; Xie, Y.; Mao, X. Freeform surface compensation design for machining error of primary mirror. In Proceedings of the Symposium on Novel Photoelectronic Detection Technology and Application, Hefei, China, 21–23 April 2023. [Google Scholar]

| Additional Aberration Contributions | Types of the Additional Aberrations |
|---|---|
| Field asymmetric, field-linear (FAFL) astigmatism, FC astigmatism | |
| FC coma |
| Zernike Terms | Aberration Contributions | Types of the Aberrations |
|---|---|---|
| Z5/Z6 | FC astigmatism, tilt | |
| Z7/Z8 | FC coma, FAFL astigmatism, and focal plane tilt | |
| Z9 | Spherical aberration, coma, defocus, astigmatism, and distortion |
| Terms | Zernike Polynomial | Coefficients |
|---|---|---|
| Z5 | −2.44261 × 10−4 | |
| Z6 | −3.55634 × 10−4 | |
| Z7 | −6.13816 × 10−5 | |
| Z8 | −4.68270 × 10−5 | |
| Z9 | −4.00117 × 10−5 |
| Pose Variation | ||||
|---|---|---|---|---|
| Compensation value | 0.0190 | 0.0147 | 1.1500 × 10−4 | −1.5200 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Li, J.; Cai, Z.; Yu, J.; Xie, Y.; Mao, X. Post Optical Freeform Compensation Technique for Machining Errors of Large-Aperture Primary Mirror. Photonics 2023, 10, 768. https://doi.org/10.3390/photonics10070768
Huang C, Li J, Cai Z, Yu J, Xie Y, Mao X. Post Optical Freeform Compensation Technique for Machining Errors of Large-Aperture Primary Mirror. Photonics. 2023; 10(7):768. https://doi.org/10.3390/photonics10070768
Chicago/Turabian StyleHuang, Cheng, Jinpeng Li, Zhaohan Cai, Jiadong Yu, Yongjun Xie, and Xianglong Mao. 2023. "Post Optical Freeform Compensation Technique for Machining Errors of Large-Aperture Primary Mirror" Photonics 10, no. 7: 768. https://doi.org/10.3390/photonics10070768
APA StyleHuang, C., Li, J., Cai, Z., Yu, J., Xie, Y., & Mao, X. (2023). Post Optical Freeform Compensation Technique for Machining Errors of Large-Aperture Primary Mirror. Photonics, 10(7), 768. https://doi.org/10.3390/photonics10070768




