1. Introduction
The technology of electro-optical devices is growing and requires new materials to work with in order to expand the possibilities that are currently available. The research of suitable materials for that purpose increases, therefore, in parallel. Zinc Oxide, ZnO, is a well-known wide-bandgap semiconductor of the II–VI semiconductor group. It is intrinsically
n-type due to oxygen vacancies or zinc interstitial defects [
1]. This semiconductor has several favorable properties, including good transparency, high electron mobility, a wide bandgap, and strong room-temperature luminescence. It is a classic material with respect to combining optical and electrical properties. Indeed, it has been used not only as a transparent conductor [
2] for liquid crystal displays but also as a light emitter [
3,
4] in light emitting diodes and as junction material in transparent thin-film transistors [
5], not to mention its use as an energy-saving or heat-protecting window coating. The ZnO bandgap is about 3.37 eV at room temperature and can be tuned in the range from 3 to 4 eV by alloying with magnesium or cadmium oxides. The current most important limitation of its industrial large scale use comes from the difficulty in achieving a
p-doped specimen due to the low solubility of
p-type dopants and their compensation by abundant
n-type impurities. Anyway, recent findings can open the route to its use in industry as anode material for lithium-ion batteries [
6]. The technological relevance of ZnO is therefore blooming as an “evergreen” material.
In order to improve the quality and performance of existing devices (or, better yet, to build new and most performative ones), knowledge of fundamental parameters such as intrinsic carrier lifetime, scattering rate, and recombination mechanisms is crucial. Nevertheless, the dynamics of charge carriers in bulk ZnO have not been sufficiently investigated so far. Among others, two works are of particular interest for us here: Refs. [
1,
7]. In both cases, the ZnO charge carrier dynamics have been measured by time-resolved Terahertz (THz) spectroscopy (TRTS). The TRTS technique has been used quite extensively [
8] so far in order to investigate the ultrafast dynamics of photo-induced charge carriers in a large variety of different materials, both in condensed and soft matter systems. Covering the energy range from a few to about 100 meV, THz radiation is sensitive to the response of charge quasiparticles, e.g., free carriers, polarons, and excitons. The distinct spectral signatures of these different quasiparticles in the THz range allow their discrimination and characterization using pulsed THz radiation. Moreover, using a Pump-Probe scheme, it is possible to monitor the nonequilibrium ultrafast evolution of carriers and low-energy excitations in the picosecond time-scale [
9]. All these unique features made possible the direct observation of an “early stage” of the carrier dynamics, as in the exciton formation in ZnO wafers [
7]. In general, the dynamical spectral information can be analyzed by means of appropriate models in order to infer the carrier density and mobility as a function of time. Two aspects are of particular interest in the specific case of ZnO pumped with two-photon absortion of sub-bandgap photons. First, the photoconductivity can probe electrons as well as holes because they are always created with perfect balancing, and this can overcome the problem of
p-doping of ZnO. Moreover, the number of photogenerated carriers can be much higher than the defect or impurity charge population, so to directly access their intrinsic behavior, and because the electron-hole pairs are created out of valence and conduction band states, they have similar effective masses, compared with the case of single-photon absorption in which the holes are left in low-mobility midgap states [
1]. Second, the possibility of two-photon absorption processes (which are so strong in ZnO to achieve naked-eye visible photo-luminescence under illumination with sub-bandgap photons) ensures a quite homogeneous excitation of the sample along its thickness. A gradient in the transverse profile of the excitation energy is indeed difficult to model and may lead to artifacts in the results due to uncorrect data analysis [
8,
10]. Baxter and Schmuttenmaer indeed attempted to pump the ZnO with near IR photons (800 nm), but they could not achieve a significant photo-induced absorption, mainly because of the low energy and relatively large time duration of their laser pulses.
In this manuscript, we present optical Pump-THz Probe measurements on bulk 500
m thick ZnO
samples. We measured the material dielectric function in the 0.5–3 THz range at different time-delays after photo-excitation with sub-bandgap photons at very high Pump fluences, which allowed us to completely saturate the absorption by the sample. We were able to measure up to the point in which the sample turns completely opaque, so that only a minor fraction of the incident THz pulse could be transmitted and detected. Our laser fluence is as high as 80 mJ/cm
, which means two orders of magnitude larger than that achieved in Ref. [
1] at the same photon frequency. This extreme regime is interesting for observing many-body relaxations, such as for instance the Auger effect. Our results are consistent with those obtained with one-photon low-fluence absorption by Baxter and Schmuttenmaer and represent an extension of the cited work, up to complete saturation.
2. Materials and Methods
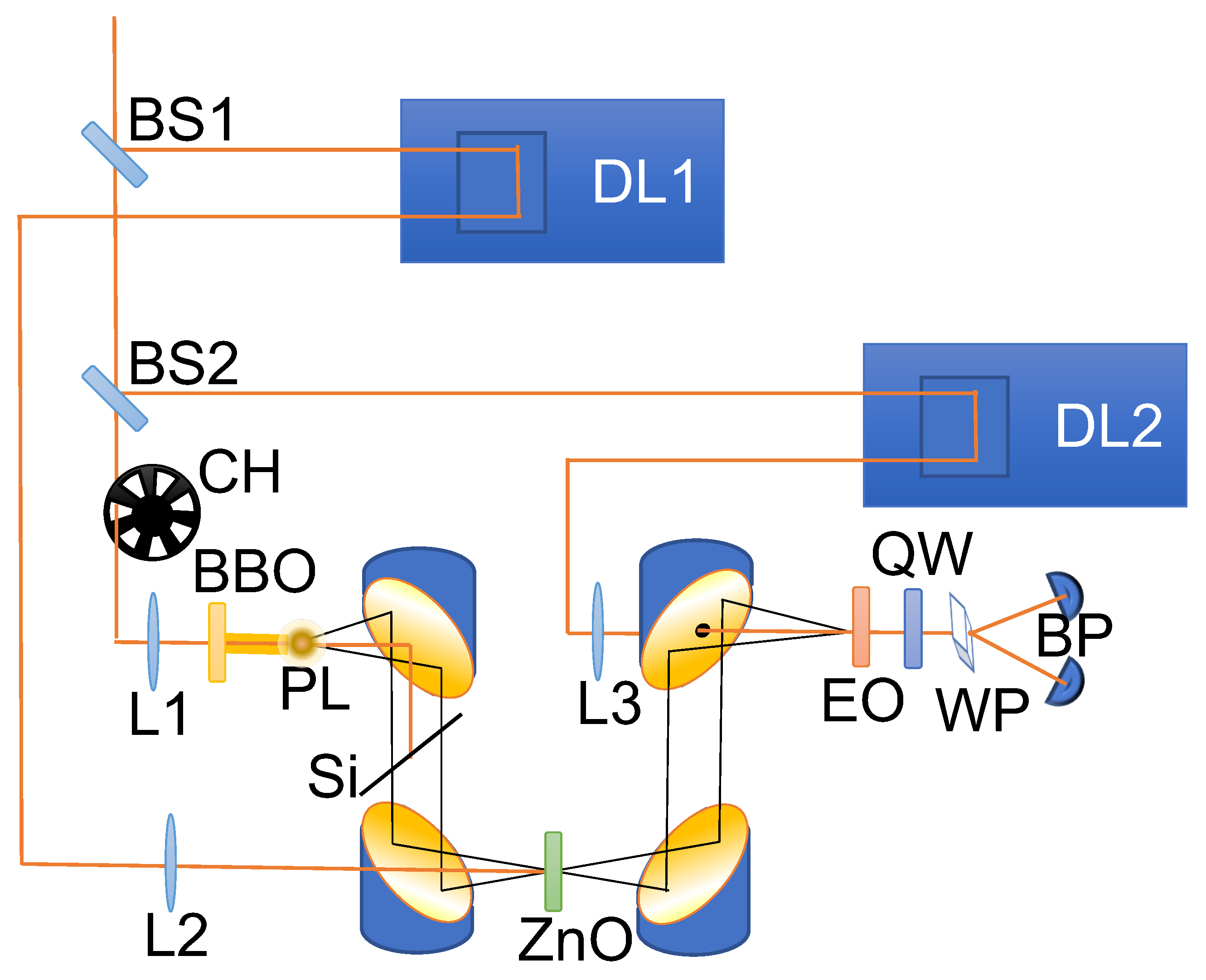
The experimental setup is a standard Optical Pump/THz Probe setup, where the THz pulses are provided by four-wave mixing in air [
11,
12].
Figure 1 illustrates the schematic representation of the experimental setup. A regenerative amplified femtosecond laser system (Coherent Legend) is utilized, emitting optical pulses with a central wavelength of 800 nm and a duration of 35 fs. The laser operates at a power of 3.8 W with a repetition rate of 1 kHz. To generate and detect THz radiation, the laser beam is split into two portions using a 5–95% beamsplitter. The stronger portion serves as the pump for generating THz radiation, while the weaker portion acts as the probe for detecting the THz radiation.
In the pump path, the beam is focused by a lens with a focal length of 200 mm. A Beta Barium Borate (BBO) crystal is positioned between the lens and its focus to generate second harmonic light from the fundamental pump beam. At the focal point, THz pulses are generated through a four-wave mixing process, combining the fundamental wave with its second harmonic. The generated THz light is then collected and collimated by a parabolic mirror. To block the pump beam and its second harmonic, a silicon wafer is employed.
The THz beam is focused on the sample using a second parabolic mirror. Subsequently, a third parabolic mirror collects and collimates the transmitted THz beam. Finally, the THz beam is focused onto a 1 mm thick ZnTe crystal for detection using Electro-Optical Sampling (EOS) [
13]. This detection process involves the probe beam, which first passes through a series of optical elements for power and polarization control. It is then directed by a retroreflector mounted on an adjustable delay line to vary its temporal delay in relation to the pump. Ultimately, the probe beam is focused by a lens onto the ZnTe crystal and spatially overlapped with the THz beam. The presence of the THz beam modulates the birefringence of the ZnTe crystal and, consequently, alters the ellipticity of the probe beam. The change in ellipticity is measured using a combination of a Wollaston prism and a pair of balanced photodiodes.
A second beam-splitter separates the beam that is employed to produce the THz radiation from the beam that is used as an optical Pump. A mechanical chopper—synchronized with the laser—blocks every second Pump pulse to perform the measurement of the Pump ON and OFF THz waves in parallel. The Pump optical pulse is sent with a small incident angle of about
with respect to the surface normal direction. The Pump spot size was set to double the THz focal spot size (diameter < 1 mm) in order to obtain a homogeneous in-plane distribution of the photo-excited charge density in the THz-probed region. For the same reason, the Pump pulse wavelength was kept equal to the native 800 nm wavelength of the Ti:Saphhire laser (1.5 eV): at this wavelength, ZnO is very transparent [
14], and this ensures that the photo-induced charge excitation will be provided exclusively by two- or three-photon absorption so as to obtain a constant depth-profile of the charge density, which in turn avoids (as already mentioned above) data-analysis artifacts [
10]. Furthermore, by employing this approach, potential issues arising from the existence of residual and exceedingly weak post-pulses are effectively circumvented. The reason behind this lies in the non-linear nature of two- and three-photon absorption processes, which intensify the distinction between the primary pulse and the subsequent pulses to the extent that the latter exert a negligible influence on the sample photo-excitation. On the other hand, the disadvantage of this method is that one cannot precisely predict the photo-excited carrier density, which can be anyway inferred
by performing a Drude model fit procedure, as explained in the following.
The samples used in the present work are commercial both side polished ZnO crystals of 500 m thickness. This thickness ensures that we can discriminate the first main pulse from the following ones, thus simplifying the data analysis.
3. Results and Discussion
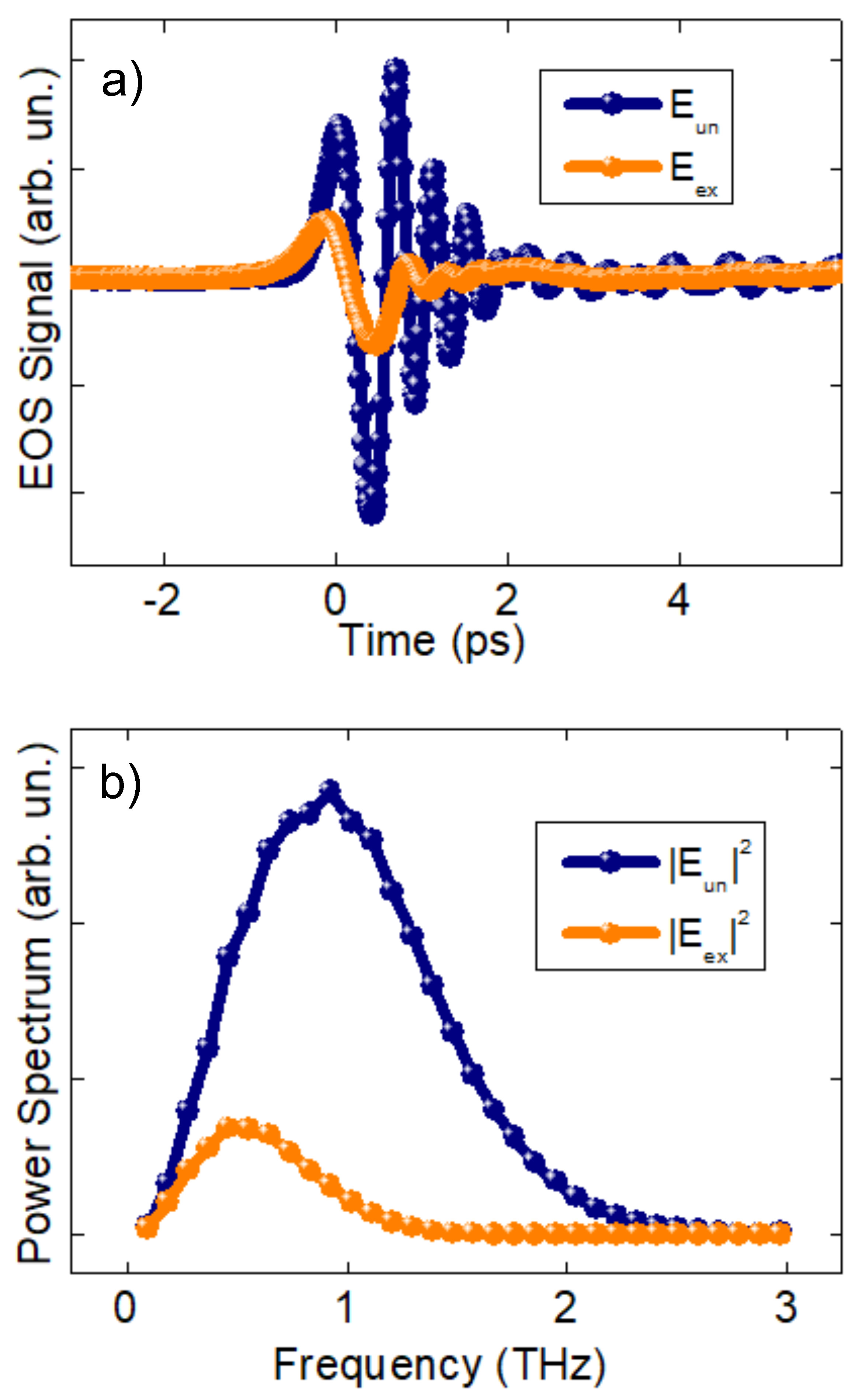
Figure 2 shows an example of the transmitted THz waveforms at 120 ps Pump-Probe delay with an optical Pump pulse applied (
where
stays for excited) and not applied (
where
stays for unexcited). These measurements have been taken actually within the same experimental run, by means of the mechanical chomechanicalp er, and then separated by selecting every second pulse from the following one. The effect of the optical pumping is dramatic: the THz transmittivity is reduced by more than
already at 40 mJ/cm
fluence, which is half of the maximum fluence investigated. The difference between excited and unexcited sample transmittivity is even more evident when comparing the Power Spectra of the same waveforms (
Figure 2b). Let us now turn our attention to the behavior of the THz waveforms at different Pump-Probe time delays.
Figure 3a shows the normalized integrated power spectra of all waveforms as a function of the delay. The normalization highlights that the time the system takes to recover from the unexcited state is not the same for every Pump fluence. In particular, this characteristic time clearly increases as the Pump fluence increases. This behavior is uncommon and unexpected because many body effects, such as bimolecular recombination [
15] and Auger recombination [
16] usually shorten the recombination times at high excitation fluences. We will come back on this important point in the following.
Figure 3b shows the percentage of maximum absorption of each curve, which is obtained a few picoseconds after pumping. The behavior is strongly saturated, showing that the excitation has reached a point at which the sample has an almost metallic behavior and absorbs/reflects more than 90% of the THz radiation. According to ref. [
10], we analyzed our THz spectra in order to extract the photoinduced changes in the relative-permittivity function
under the assumption of homogeneous spatial excitation of the sample and for delay times much longer than the THz pulse duration itself (∼1 ps). We have analyzed the results in terms of a simple linear relationship between the photo-induced relative-permittivity variation
and the measured ratio of excited and unexcited waveforms (Equation (6) in Ref. [
10]):
where the measured static index of refraction
was found to be flat and featureless and to have no significant imaginary part,
m is the sample thickness,
c is the speed of light and
is the measured photo-induced transmittivity (
t) change.
One example is shown in
Figure 4, where real and imaginary parts of
are shown. For the static spectra of the relative permittivity, we refer to
Figure 3 of ref. [
17]. We do not observe significant changes in the photoexcited spectral shape for different delays after
, a part of an overall scale factor due to charge recombination. The data are well approximated by a simple free-charge Drude model:
where
is the high-frequency dielectric constant,
is the scattering time,
is the squared plasma frequency,
N is the carrier density, and
is the carrier effective mass given by
. The fact that the Drude model provides a reasonably good fit for the relative permittivity function means that the simple picture of non-interacting charges (electron-hole gas) is still valid in this extreme regime. Anyway, minor deviations from the fit curves are observed, indicating the possible presence of interactions. A refined model that accounts for these interactions is anyway not required to capture the main physical finding, i.e., the behavior of the characteristic time with Pump fluence, which is clearly visible already in the bare data (
Figure 3). Therefore, these deviations from the standard Drude model will be discussed elsewhere.
The scattering time was found to be constant during the decay, and its value is about 10 fs, which is in a quite good agreement with the room temperature values found in doped specimens, such as, for instance, 6–16 fs of Al-doped ZnO [
18] and about one order of magnitude smaller than the low temperature and low excitation values [
1,
7] in intrinsic samples. As already mentioned, it is difficult to know in advance the photoinduced charge density
N by direct absorption measurement, and therefore it is not possible to estimate the charge effective masses. On the contrary, it is possible to roughly estimate the charge density induced by the strong laser pulse once the effective mass value is known. One should mention that, when carriers are excited to large excess energies, the values of electron and hole effective masses can be significantly altered [
1]. Anyway, for a simple order of magnitude estimation, we will use the value of
found on doped specimens [
19,
20], and we infer the charge density to be about
m
, which is, as expected, much higher than a typical doping charge concentration. Similarly, we can also estimate the combined carrier mobility to be
cm
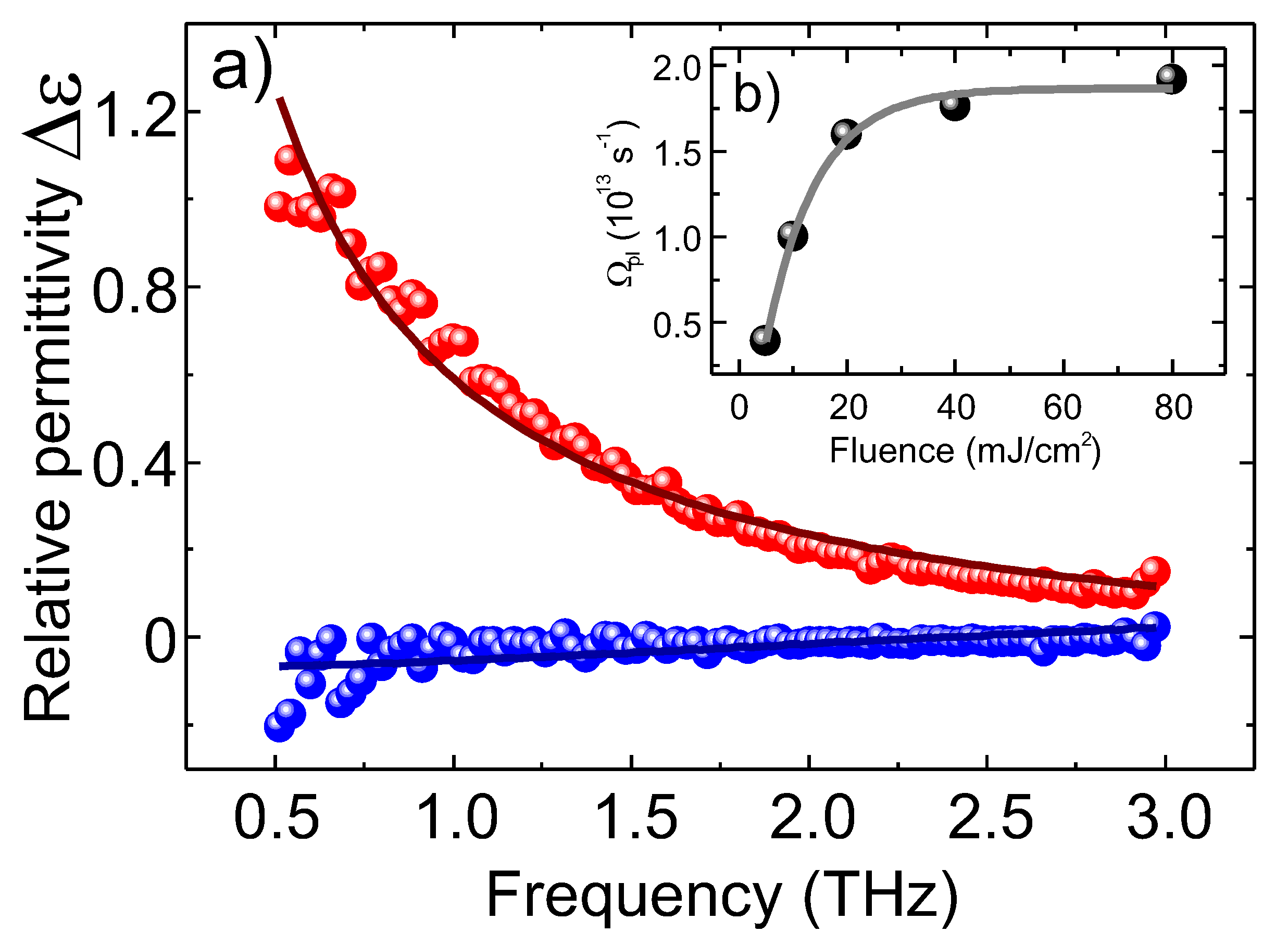
/Vs. In the hypothesis that the effective mass does not change drastically during the decay, we can use the decay of the normalized squared plasma frequency
, shown in
Figure 5a, as an estimation of the carrier density decay time
, shown in
Figure 5b. The decay, as already mentioned, is well-approximated by a single exponential function, and the behavior of
scales roughly linearly with the pump fluence.
4. Conclusions
In conclusion, this article presents the results of optical pump-terahertz probe measurements on bulk ZnO samples. The study aims to improve the understanding of the fundamental parameters and dynamics of charge carriers in ZnO, which are crucial for enhancing the quality and performance of electro-optical devices. By employing time-resolved terahertz spectroscopy, we have investigated the ultrafast dynamics of photo-induced charge carriers in ZnO and analyzed their behavior under sub-bandgap photon excitation.
The experimental results demonstrate the significant impact of optical pumping on the transmittivity of terahertz radiation through the ZnO samples. The transmittivity is dramatically reduced upon photoexcitation, indicating the transition of the sample to an almost metallic behavior. The absorption of terahertz radiation increases to more than 90% at high pump fluences, indicating a saturated excitation state. By analyzing the photoinduced changes in the dielectric function, we confirm the validity of a simple Drude model for the behavior of non-interacting charges (electron-hole gas) in this extreme excitation regime.
One notable finding is the observation that the characteristic time for the system to recover from the unexcited state increases with higher pump fluences. This behavior, contrary to expectations based on many-body effects, provides valuable insights into the relaxation dynamics of photoexcited charge carriers in ZnO. The scattering time is determined to be approximately 10 fs, consistent with room temperature values in doped specimens. The estimated charge density and combined carrier mobility suggest the presence of a high-density carrier population and their efficient mobility within the sample.
Overall, this study contributes to the understanding of charge carrier dynamics in ZnO and provides valuable insights into its potential applications in electro-optical devices. The observed behavior of charge carriers under sub-bandgap photon excitation highlights the possibility of photoinducing a high-density carrier population with high mobility and opens up possibilities for further investigations and improvements in the design and performance of optoelectronic devices utilizing this material.