Optimal I–V Curve Scan Time for a GaAs Laser Power Converter
Abstract
1. Introduction
2. Materials and Methods
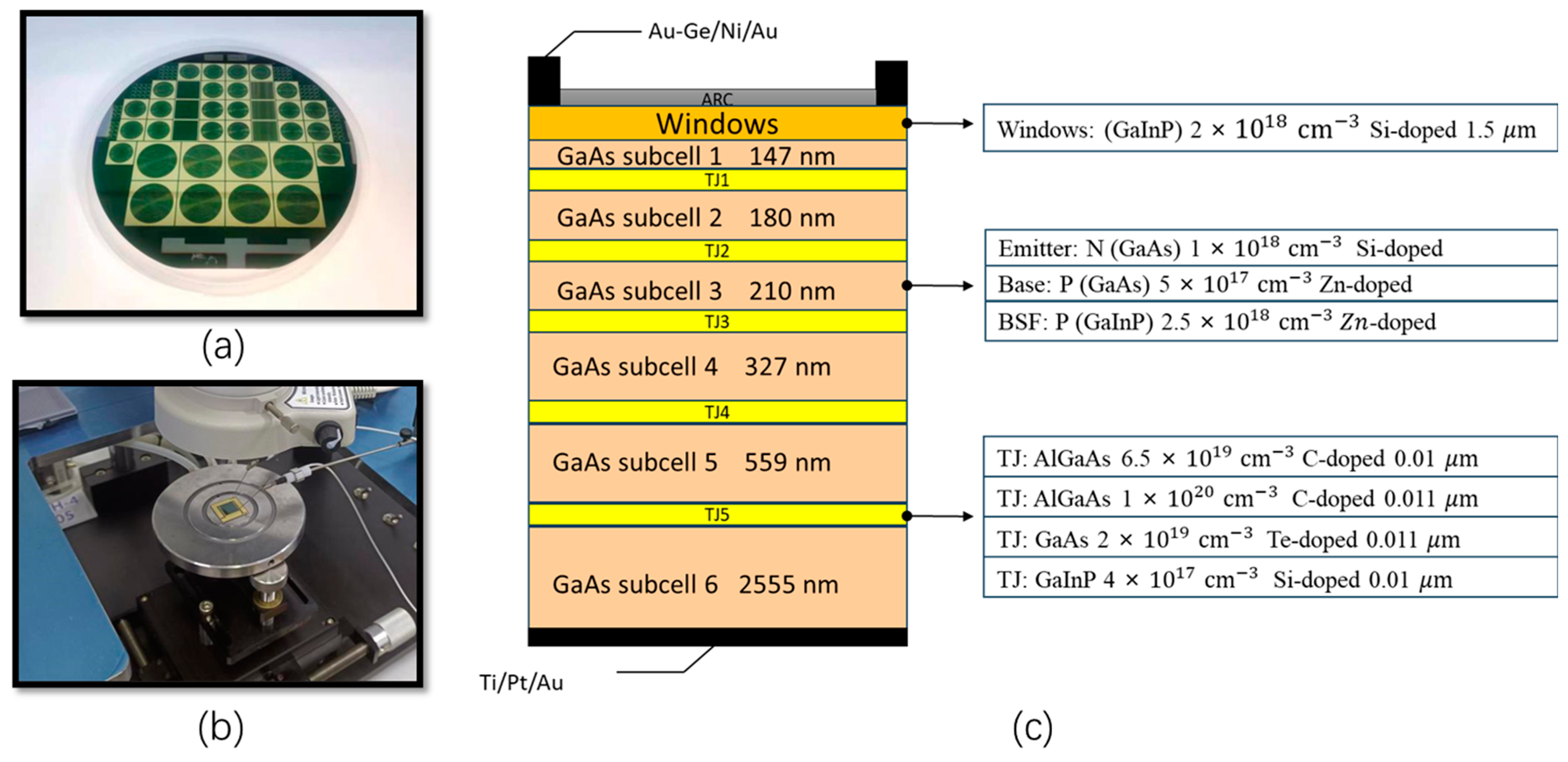
2.1. Structure of the GaAs LPC
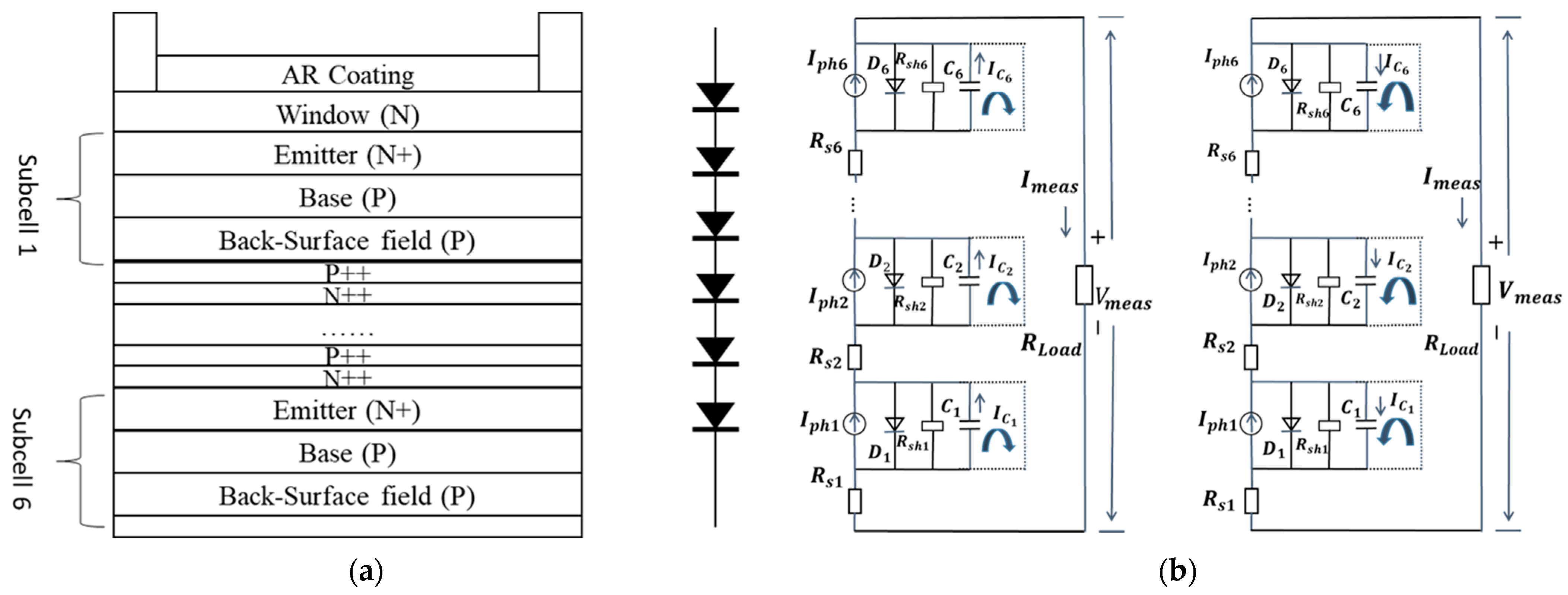
2.2. Modeling and Analysis of the Multijunction LPC
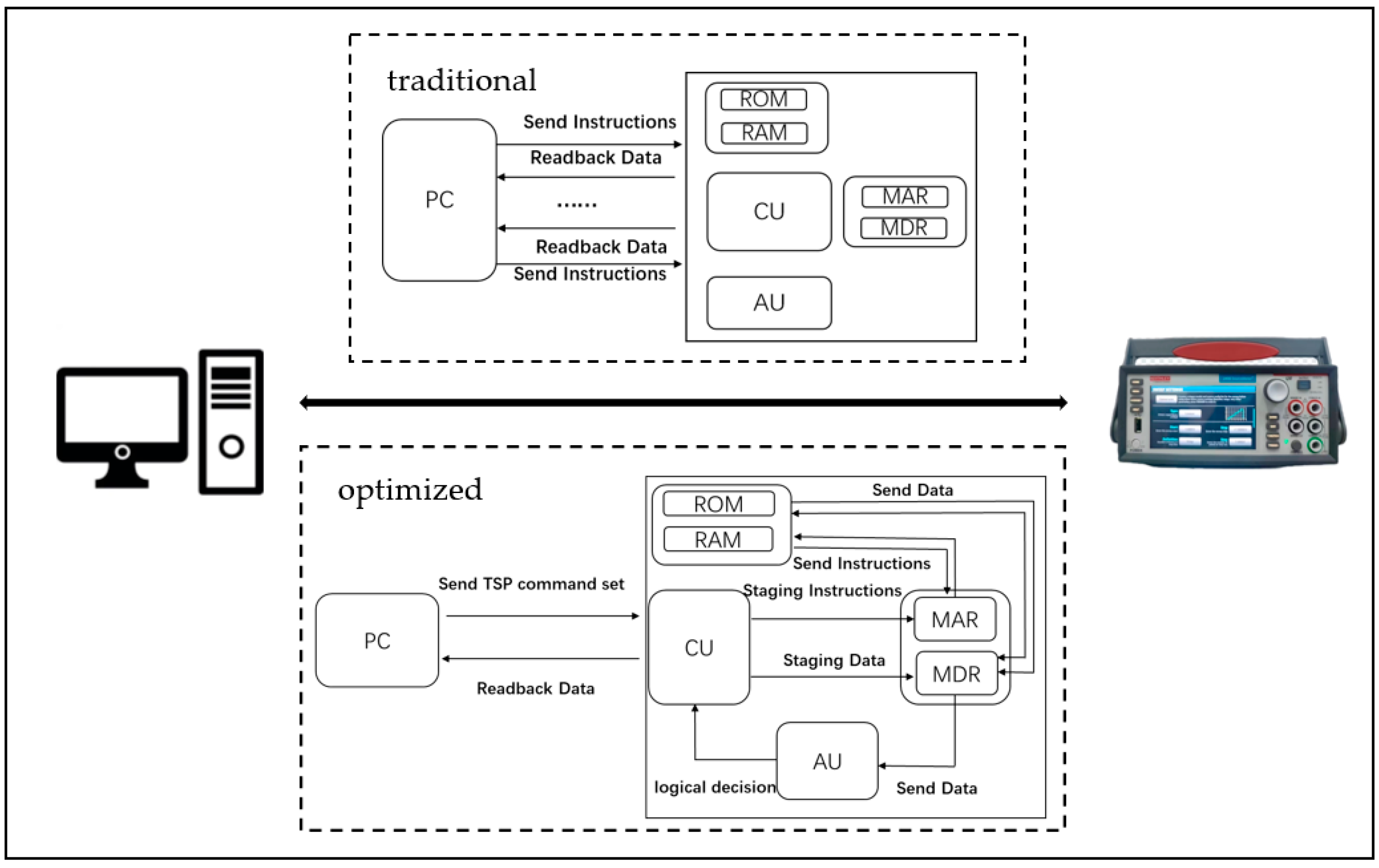
2.3. Optimization of the Acquisition System
3. Results
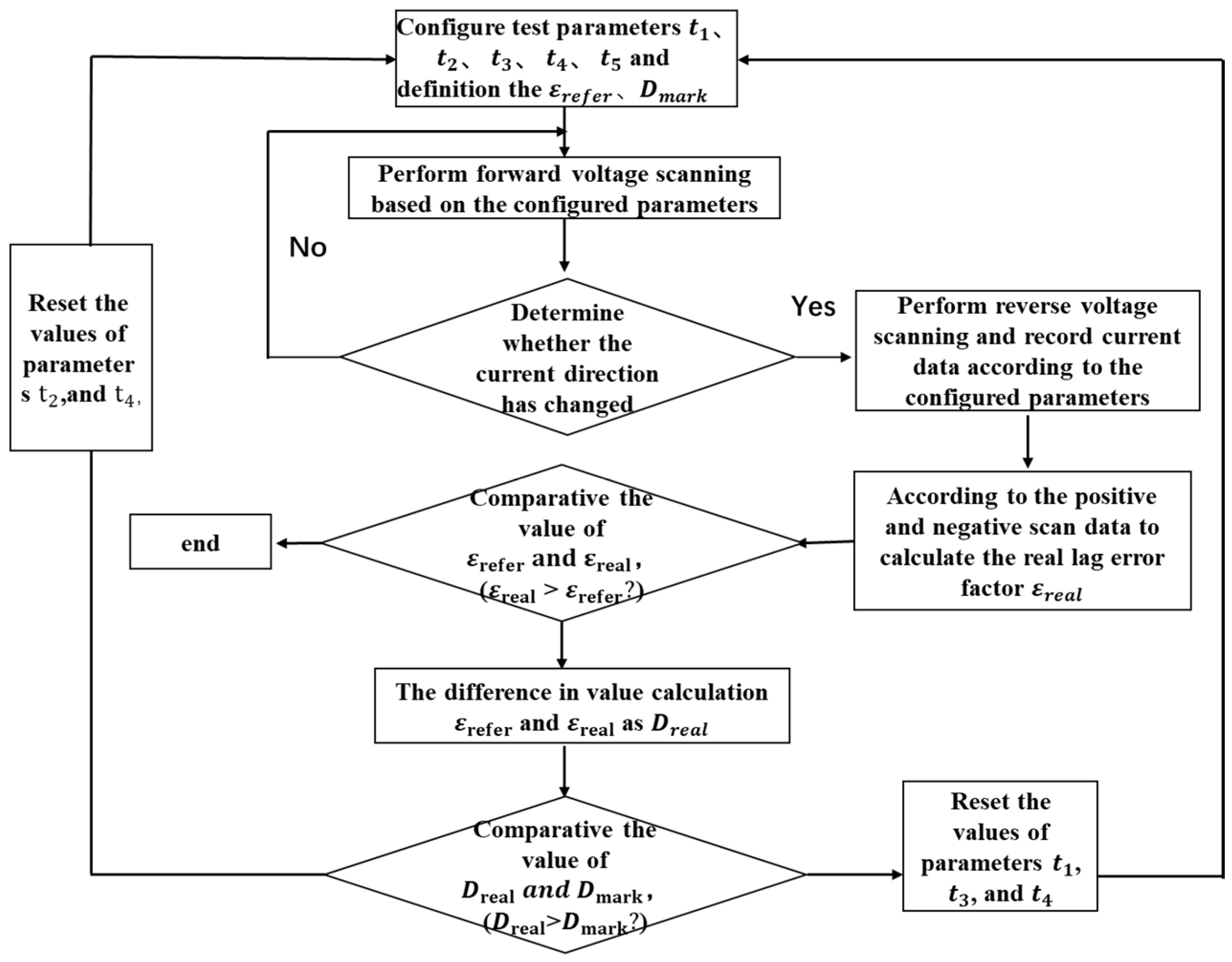
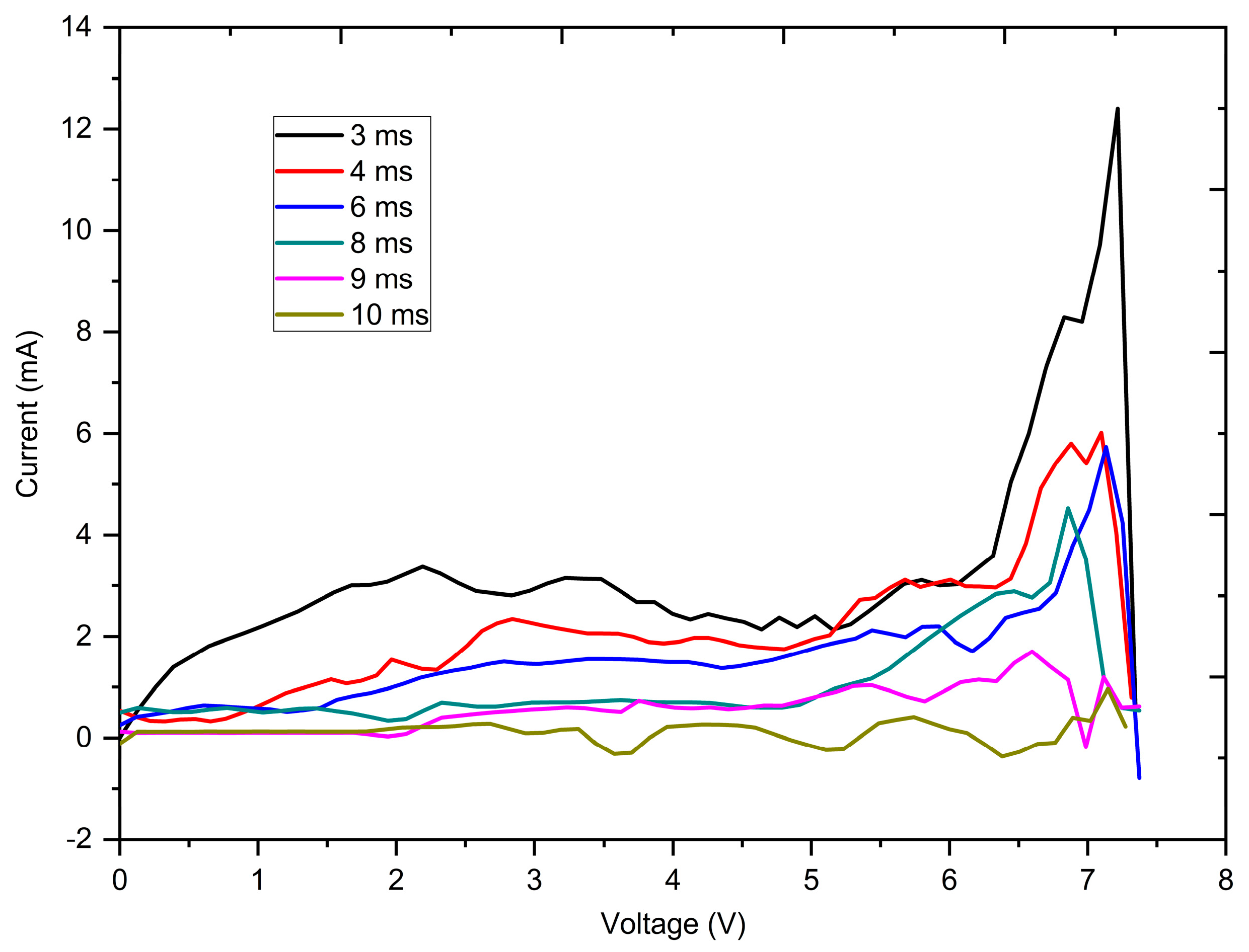
3.1. Test System and Optimized Algorithm
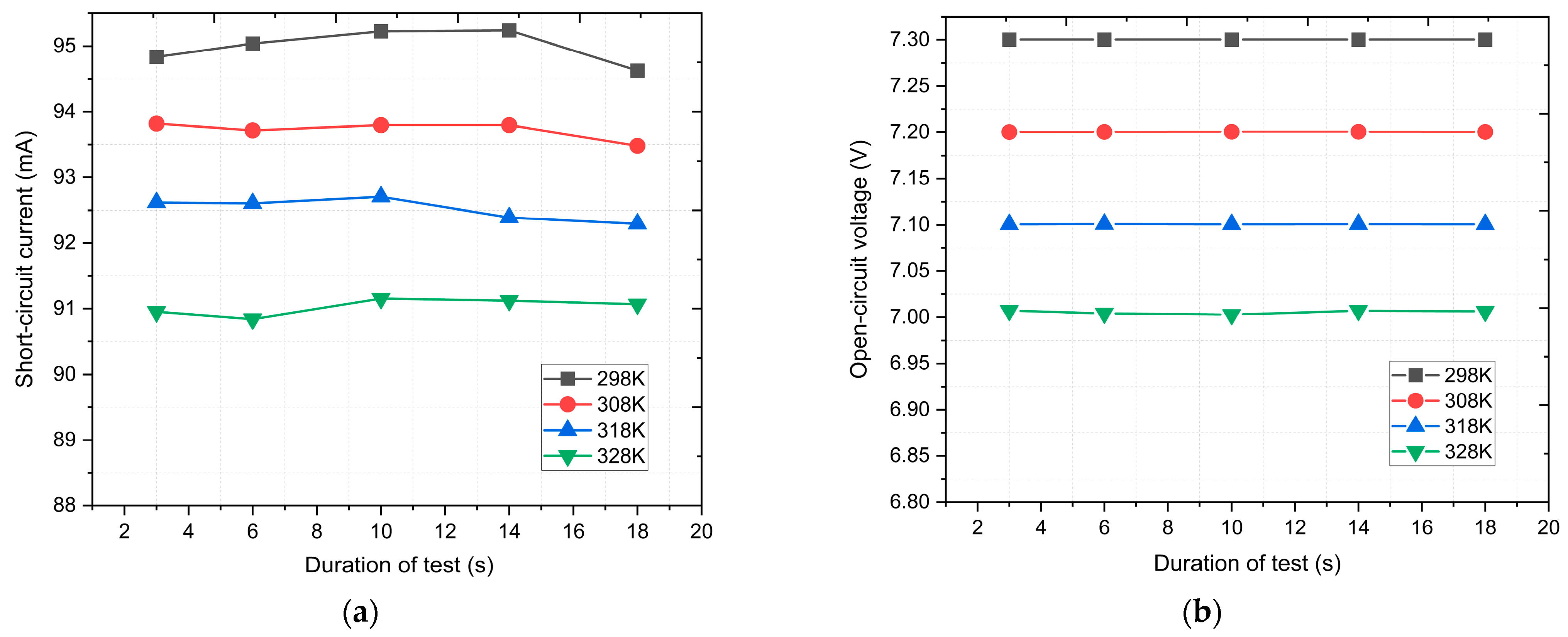
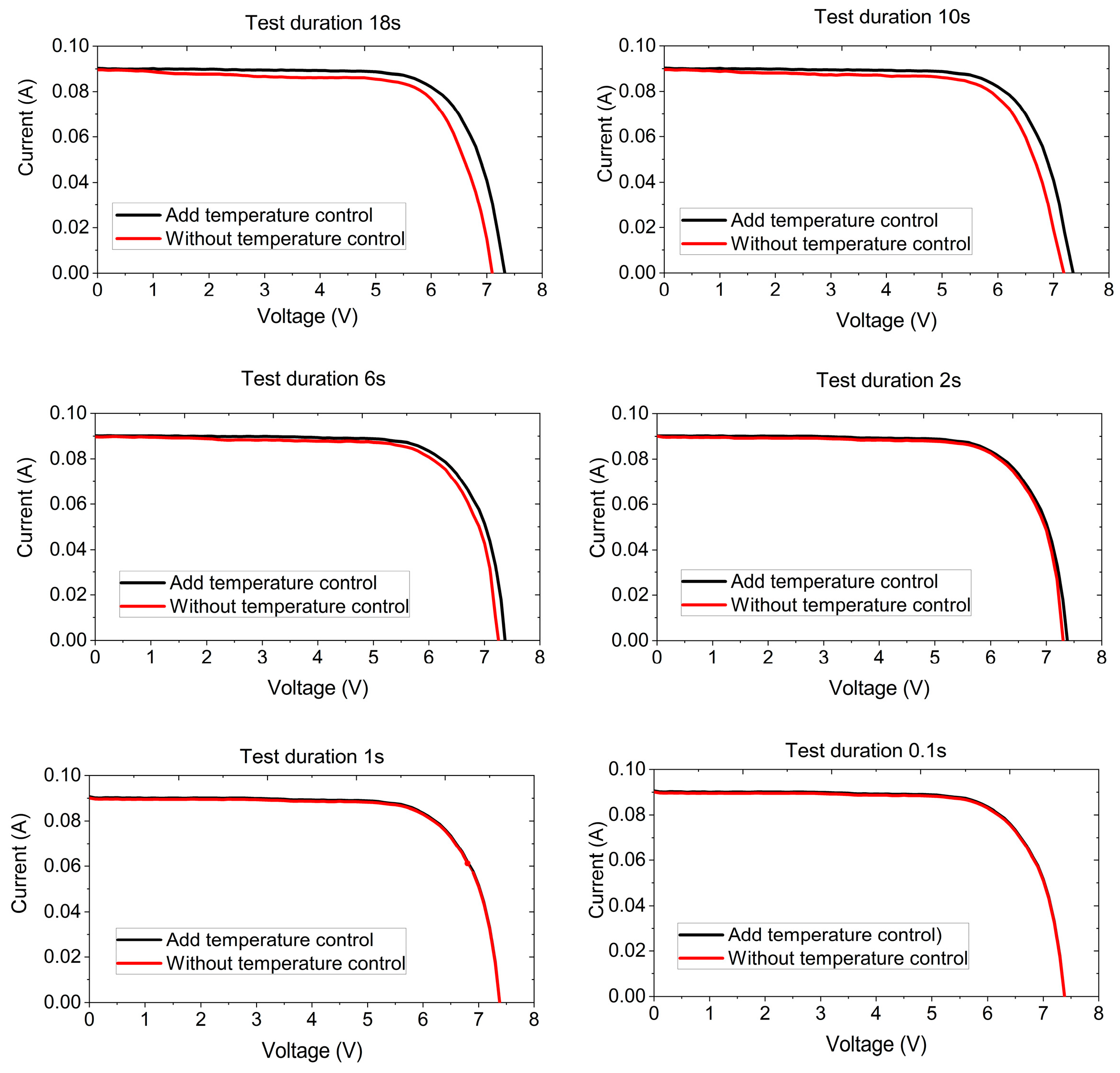
3.2. Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wojtczuk, S.J. Long-wavelength laser power converters for optical fibers. In Proceedings of the 26th IEEE Photovoltaic Specialists, Anaheim, CA, USA, 29 September–3 October 1997. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, S.; Ren, H.; Li, S.; Han, P. Energy band adjustment of 808 nm GaAs laser power converters via gradient doping. J. Semicond. 2021, 42, 032701. [Google Scholar] [CrossRef]
- Fafard, S. High-Efficiency and High-Power Multijunction InGaAs/InP Photovoltaic Laser Power Converters for 1470 nm Photonics. Photonics 2022, 9, 438. [Google Scholar] [CrossRef]
- Zhao, Y.; Liang, P.; Ren, H.; Han, P. Enhanced efficiency in 808 nm GaAs laser power converters via gradient doping. AIP Adv. 2009, 9, 105206. [Google Scholar] [CrossRef]
- Oliva, E.; Dimroth, F. GaAs converters for high power densities of laser illumination. Prog. Photovolt. 2008, 16, 289–295. [Google Scholar] [CrossRef]
- Olsen, L.C.; Huber, D.A. High efficiency monochromatic GaAs solar cells. In Proceedings of the 22th IEEE Photovoltaic Specialists, Las Vegas, NV, USA, 7–11 October 1991. [Google Scholar] [CrossRef]
- Nandon, S. InAlGaAs/InP-Based laser photovoltaic converter at 1070 nm. IEEE Electron Device Lett. 2016, 37, 1154–1157. [Google Scholar] [CrossRef]
- Shan, T.; Qi, X. Design and optimization of GaAs photovoltaic converter for laser power beaming. Infrared Phys. Technol. 2015, 71, 144–150. [Google Scholar] [CrossRef]
- Reichmuth, S.K. On the temperature dependence of dual-junction laser power converters. Prog. Photovolt. Res. Appl. 2017, 25, 67–75. [Google Scholar] [CrossRef]
- Walker, A.W. Optimal laser wavelength for efficient laser power converter operation over temperature. Appl. Phys. Lett. 2016, 108, 241104. [Google Scholar] [CrossRef]
- Mau, S.; Krametz-Proc, T. Influence of solar cell capacitance on the measurement of I-V-curves of PV-modules. In Proceedings of the 20th European Photovoltaic Solar Energy Conference, Barcelona, Spain, 6–10 June 2005. [Google Scholar]
- Sinton, R.A. A solution to the problem of accurate flash-testing of high-efficiency modules. In Proceedings of the 21th European Photovoltaic Solar Energy Conference, Munchen, Germany, 4–8 September 2006. [Google Scholar]
- Friesen, F.; Ossenbrink, H.A. Capacitance effects in high-efficiency cell. Sol. Energy Mater Sol. Cells 1997, 48, 77–83. [Google Scholar] [CrossRef]
- Granek, F. Advanced system for calibration and characterization of solar cells. Opto-Electron. Rev. 2004, 12, 57–67. [Google Scholar]
- Roth, T.; Wichmann, D. In-depth analysis of transient errors of inline IV measurements. Energy Procedia 2011, 8, 82–87. [Google Scholar] [CrossRef]
- Edler, A.; Schlemmer, M. Understanding and overcoming the influence of capacitance effects on the measurement of high efficiency silicon solar cells. Energy Procedia 2012, 27, 267–272. [Google Scholar] [CrossRef]
- Kojima, H.; Iwamoto, K. Accurate and rapid measurement of high-capacitance PV cells and modules using a single short pulse light. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference, Denver, CO, USA, 8–13 June 2014. [Google Scholar]
- Herman, M. Optimal I-V curve scan time of solar cells and modules in light of irradiance level. Int. J. Photoenergy 2012, 2012, 151452. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, Y. Effects of I-V measurement parameters on the hysteresis effect and optimization in high-capacitance PV module testing. IEEE J. Photovolt. 2018, 8, 710–718. [Google Scholar] [CrossRef]
- Moreno-Romero, P.M. Voltage scanning speed determination and current voltage curves of different types of perovskite solar cells. IEEE J. Photovolt. 2022, 12, 611–617. [Google Scholar] [CrossRef]
- Gopalan, S.; Lautenschlager, P. Temperature dependence of the shifts and broadenings of the critical points in GaAs. Phys. Rev. B 1987, 35, 5578–5584. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Guan, C.; Chu, W.; Zhou, Y.; Zhou, R.; Yao, Y. Optimal I–V Curve Scan Time for a GaAs Laser Power Converter. Photonics 2023, 10, 762. https://doi.org/10.3390/photonics10070762
Zhang Y, Guan C, Chu W, Zhou Y, Zhou R, Yao Y. Optimal I–V Curve Scan Time for a GaAs Laser Power Converter. Photonics. 2023; 10(7):762. https://doi.org/10.3390/photonics10070762
Chicago/Turabian StyleZhang, Yihao, Chenggang Guan, Wenxiu Chu, Yikai Zhou, Ruling Zhou, and Yucheng Yao. 2023. "Optimal I–V Curve Scan Time for a GaAs Laser Power Converter" Photonics 10, no. 7: 762. https://doi.org/10.3390/photonics10070762
APA StyleZhang, Y., Guan, C., Chu, W., Zhou, Y., Zhou, R., & Yao, Y. (2023). Optimal I–V Curve Scan Time for a GaAs Laser Power Converter. Photonics, 10(7), 762. https://doi.org/10.3390/photonics10070762




