Proposal for Optomagnonic Teleportation and Entanglement Swapping
Abstract
1. Introduction
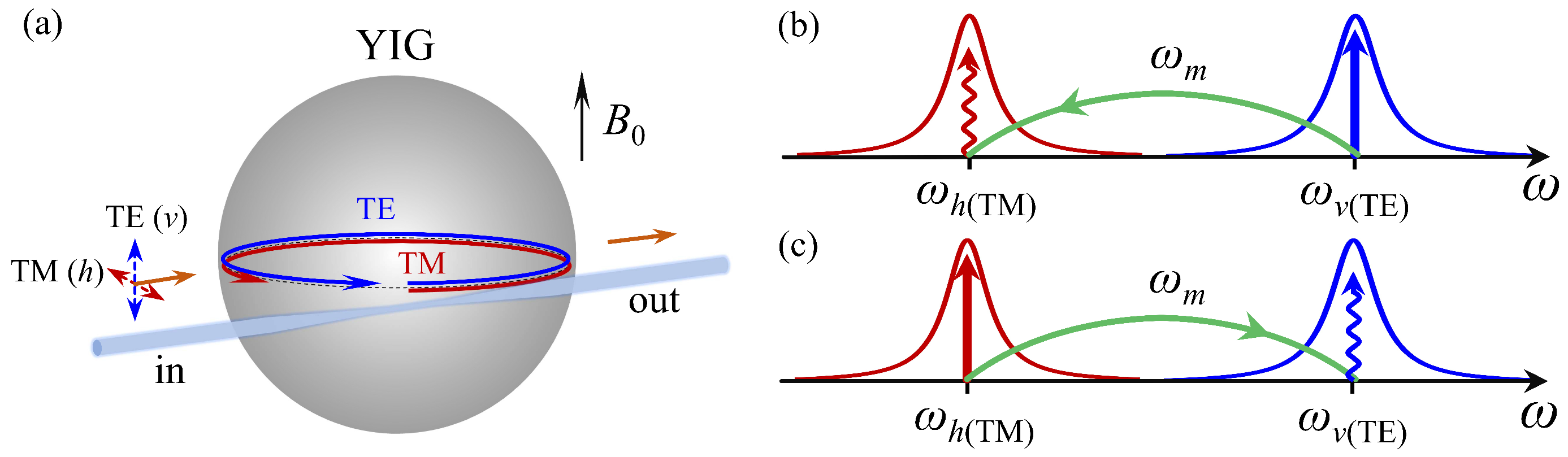
2. Optomagnonic Interaction
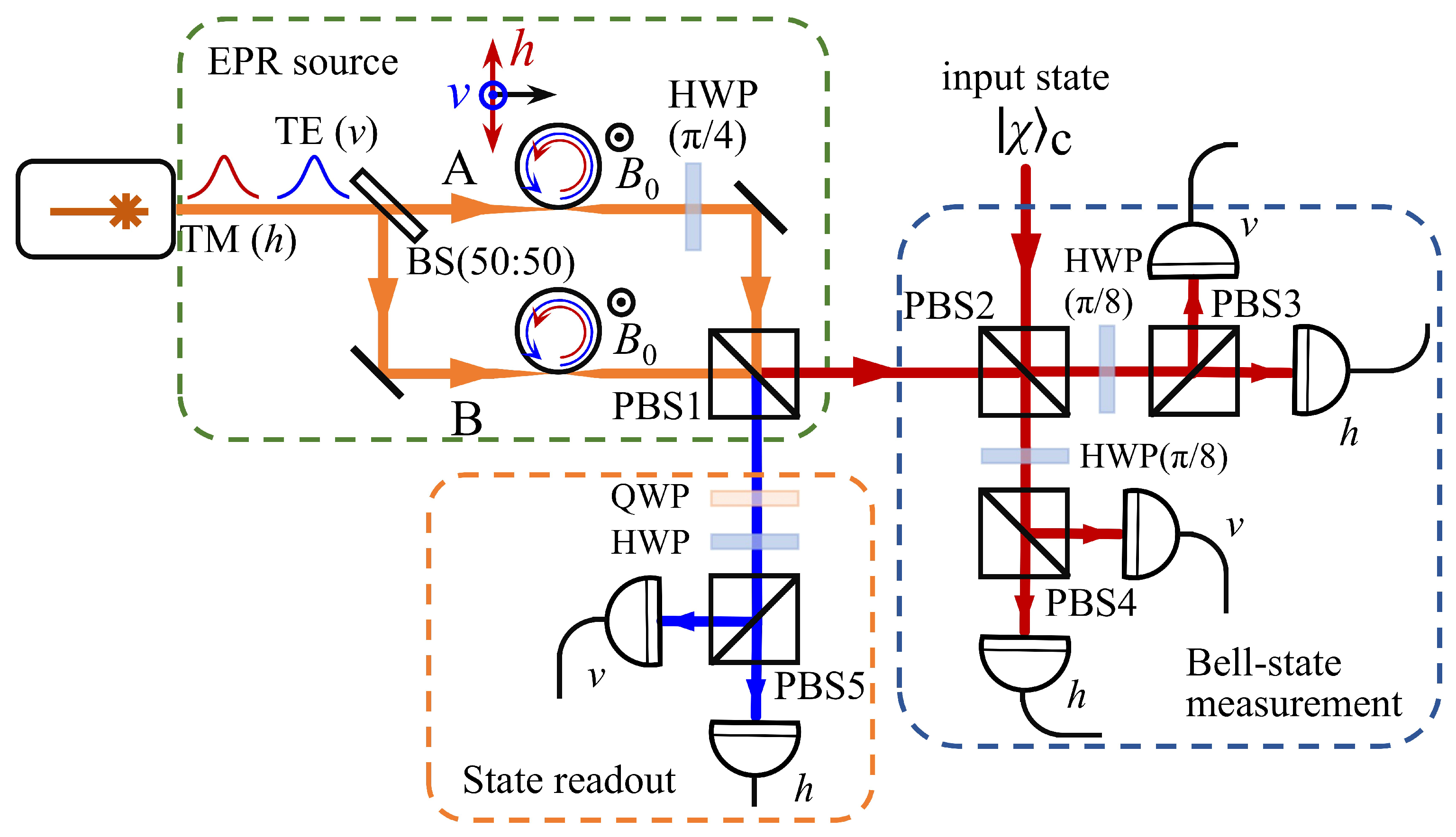
3. Optomagnonic Quantum Teleportation
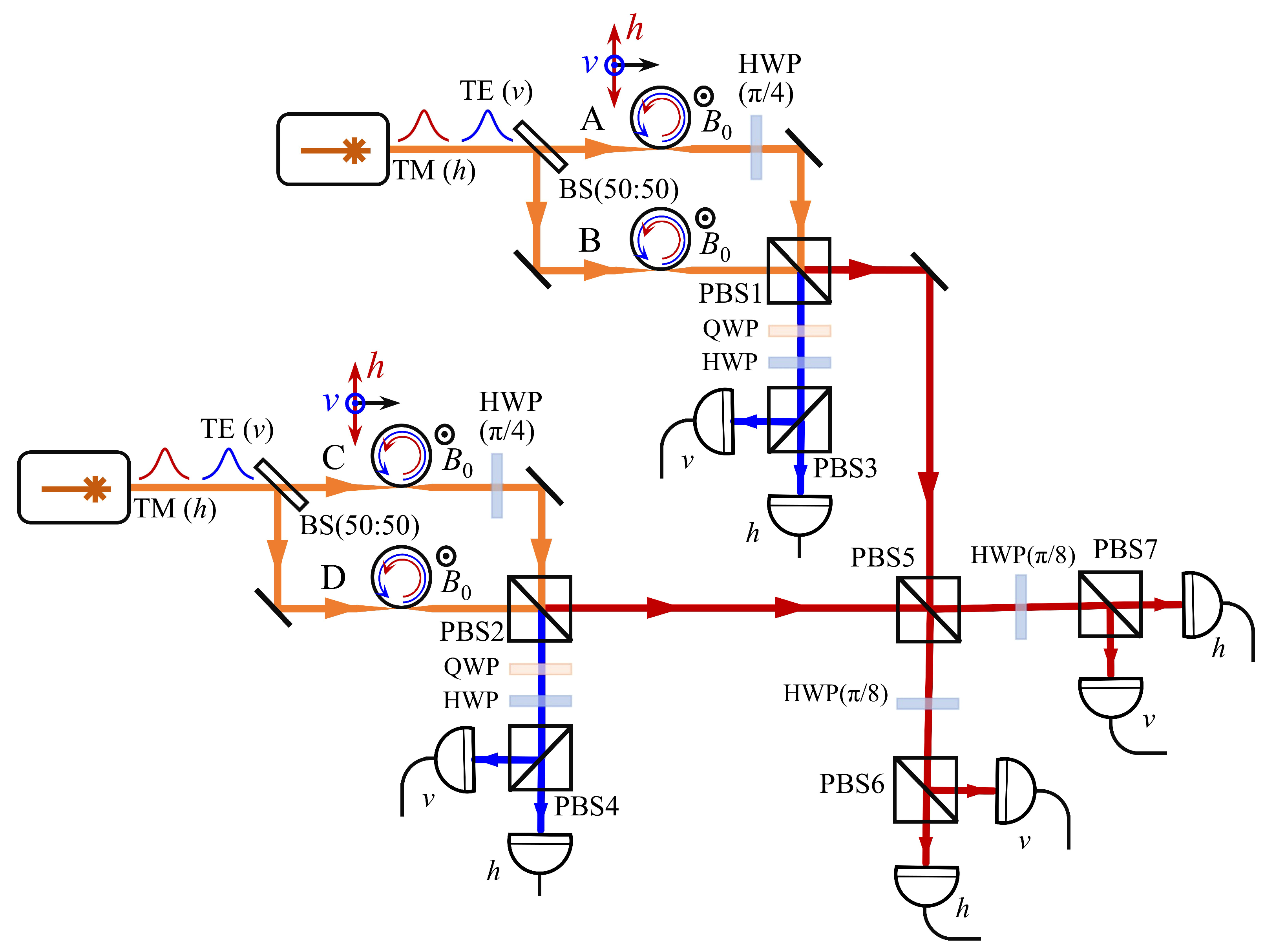
4. Optomagnonic Entanglement Swapping
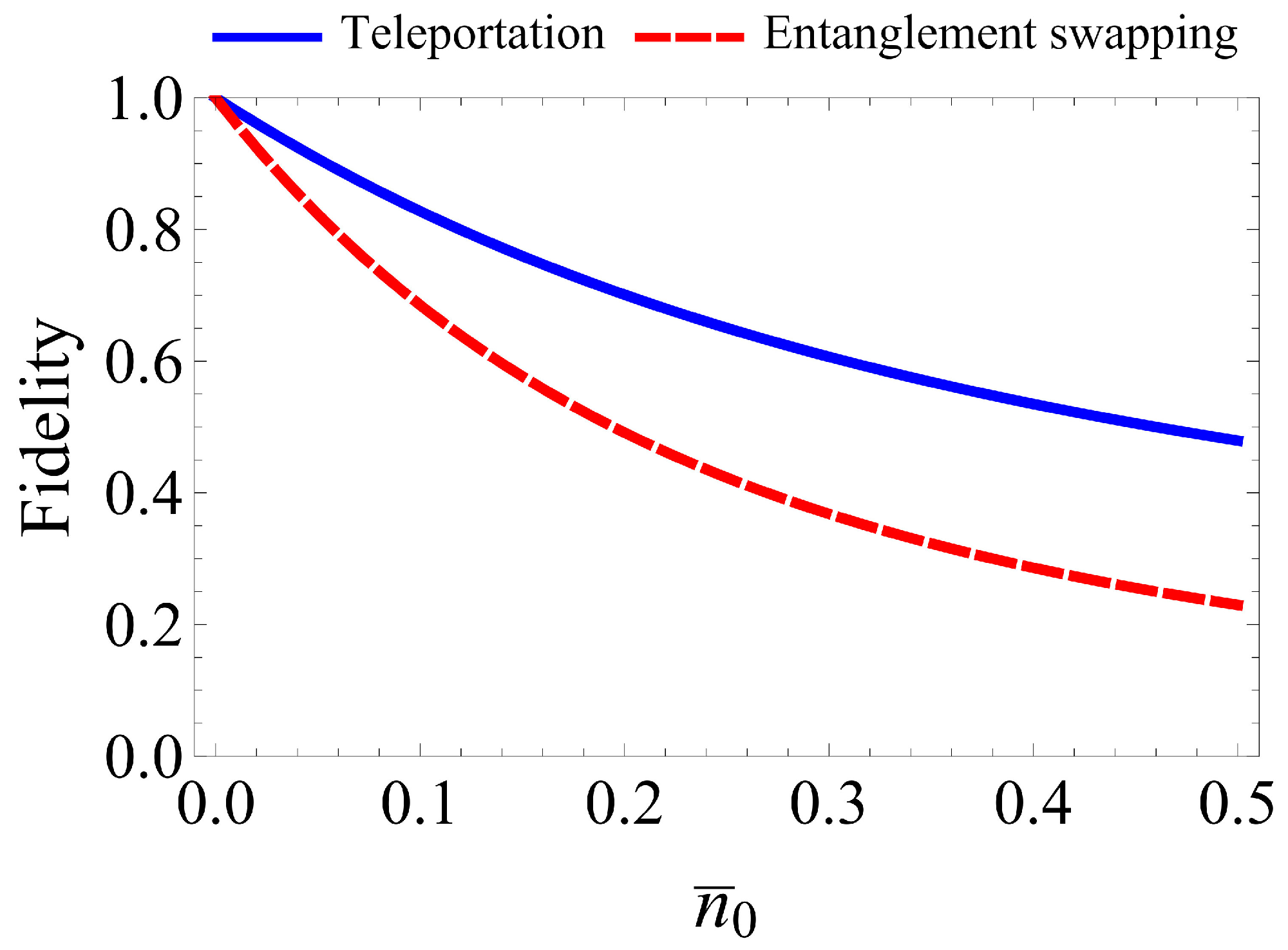
5. Effect of Magnonic Thermal Excitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.-W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Pan, J.-W.; Bouwmeester, D.; Weinfurter, H.; Zeilinger, A. Experimental Entanglement Swapping: Entangling Photons That Never Interacted. Phys. Rev. Lett. 1998, 80, 3891–3894. [Google Scholar] [CrossRef]
- Lombardi, E.; Sciarrino, F.; Popescu, S.; De Martini, F. Teleportation of a Vacuum-One-Photon Qubit. Phys. Rev. Lett. 2002, 88, 070402. [Google Scholar] [CrossRef]
- Marcikic, I.; de Riedmatten, H.; Tittel, W.; Zbinden, H.; Gisin, N. Long-distance teleportation of qubits at telecommunication wavelengths. Nature 2003, 421, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Knill, E.; Laflamme, R. Complete quantum teleportation using nuclear magnetic resonance. Nature 1998, 396, 52–55. [Google Scholar] [CrossRef]
- Barrett, M.D.; Chiaverini, J.; Schaetz, T.; Britton, J.; Itano, W.M.; Jost, J.D.; Knill, E.; Langer, C.; Leibfried, D.; Ozeri, R.; et al. Deterministic quantum teleportation of atomic qubits. Nature 2004, 429, 737–739. [Google Scholar] [CrossRef]
- Riebe, M.; Häffner, H.; Roos, C.F.; Hänsel, W.; Benhelm, J.; Lancaster, G.P.T.; Körber, T.W.; Becher, C.; Schmidt-Kaler, F.; James, D.F.V.; et al. Deterministic quantum teleportation with atoms. Nature 2004, 429, 734–737. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-A.; Chen, S.; Yuan, Z.-S.; Zhao, B.; Chuu, C.-S.; Schmiedmayer, J.; Pan, J.-W. Memory-built-in quantum teleportation with photonic and atomic qubits. Nat. Phys. 2008, 4, 103–107. [Google Scholar] [CrossRef]
- Bao, X.-H.; Xu, X.-F.; Li, C.-M.; Yuan, Z.-S.; Lu, C.-Y.; Pan, J.-W. Quantum teleportation between remote atomic-ensemble quantum memories. Proc. Natl. Acad. Sci. USA 2012, 109, 20347–20351. [Google Scholar] [CrossRef]
- Steffen, L.; Salathe, Y.; Oppliger, M.; Kurpiers, P.; Baur, M.; Lang, C.; Eichler, C.; Puebla-Hellmann, G.; Fedorov, A.; Wallraff, A. Deterministic quantum teleportation with feed-forward in a solid state system. Nature 2013, 500, 319–322. [Google Scholar] [CrossRef]
- Hou, P.-Y.; Huang, Y.-Y.; Yuan, X.-X.; Chang, X.-Y.; Zu, C.; He, L.; Duan, L.-M. Quantum teleportation from light beams to vibrational states of a macroscopic diamond. Nat. Commun. 2016, 7, 11736. [Google Scholar] [CrossRef]
- Fiaschi, N.; Hensen, B.; Wallucks, A.; Benevides, R.; Li, J.; Mayer Alegre, T.P.; Gröblacher, S. Optomechanical quantum teleportation. Nat. Photonics 2021, 15, 817–821. [Google Scholar] [CrossRef]
- Sangouard, N.; Simon, C.; de Riedmatten, H.; Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 2011, 83, 33–80. [Google Scholar] [CrossRef]
- Gottesman, D.; Chuang, I.L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 1999, 402, 390–393. [Google Scholar] [CrossRef]
- Huebl, H.; Zollitsch, C.W.; Lotze, J.; Hocke, F.; Greifenstein, M.; Marx, A.; Gross, R.; Goennenwein, S.T. High Cooperativity in Coupled Microwave Resonator Ferrimagnetic Insulator Hybrids. Phys. Rev. Lett. 2013, 111, 127003. [Google Scholar] [CrossRef]
- Tabuchi, Y.; Ishino, S.; Ishikawa, T.; Yamazaki, R.; Usami, K.; Nakamura, Y. Hybridizing Ferromagnetic Magnons and Microwave Photons in the Quantum Limit. Phys. Rev. Lett. 2014, 113, 083603. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, C.L.; Jiang, L.; Tang, H.X. Strongly Coupled Magnons and Cavity Microwave Photons. Phys. Rev. Lett. 2014, 113, 156401. [Google Scholar] [CrossRef]
- Osada, A.; Hisatomi, R.; Noguchi, A.; Tabuchi, Y.; Yamazaki, R.; Usami, K.; Sadgrove, M.; Yalla, R.; Nomura, M.; Nakamura, Y. Cavity Optomagnonics with Spin-Orbit Coupled Photons. Phys. Rev. Lett. 2016, 116, 223601. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, N.; Zou, C.-L.; Tang, H.X. Optomagnonic Whispering Gallery Microresonators. Phys. Rev. Lett. 2016, 117, 123605. [Google Scholar] [CrossRef]
- Haigh, J.A.; Nunnenkamp, A.; Ramsay, A.J.; Ferguson, A.J. Triple-Resonant Brillouin Light Scattering in Magneto-Optical Cavities. Phys. Rev. Lett. 2016, 117, 133602. [Google Scholar] [CrossRef] [PubMed]
- Osada, A.; Gloppe, A.; Hisatomi, R.; Noguchi, A.; Yamazaki, R.; Nomura, M.; Nakamura, Y.; Usami, K. Brillouin Light Scattering by Magnetic Quasivortices in Cavity Optomagnonics. Phys. Rev. Lett. 2018, 120, 133602. [Google Scholar] [CrossRef] [PubMed]
- Zhu, N.; Zhang, X.; Han, X.; Zou, C.-L.; Zhong, C.; Wang, C.-H.; Jiang, L.; Tang, H.X. Waveguide cavity optomagnonics for microwave-to-optics conversion. Optica 2020, 7, 1291–1297. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, C.L.; Jiang, L.; Tang, H.X. Cavity magnomechanics. Sci. Adv. 2016, 2, e1501286. [Google Scholar] [CrossRef]
- Li, J.; Zhu, S.-Y.; Agarwal, G.S. Magnon-Photon-Phonon Entanglement in Cavity Magnomechanics. Phys. Rev. Lett. 2018, 121, 203601. [Google Scholar] [CrossRef]
- Yu, M.; Shen, H.; Li, J. Magnetostrictively Induced Stationary Entanglement between Two Microwave Fields. Phys. Rev. Lett. 2020, 124, 213604. [Google Scholar] [CrossRef]
- Potts, C.A.; Varga, E.; Bittencourt, V.; Kusminskiy, S.V.; Davis, J.P. Dynamical Backaction Magnomechanics. Phys. Rev. X 2021, 11, 031053. [Google Scholar] [CrossRef]
- Shen, R.C.; Li, J.; Fan, Z.-Y.; Wang, Y.-P.; You, J.Q. Mechanical Bistability in Kerr-modified Cavity Magnomechanics. Phys. Rev. Lett. 2022, 129, 123601. [Google Scholar] [CrossRef]
- Tabuchi, Y.; Ishino, S.; Noguchi, A.; Ishikawa, T.; Yamazaki, R.; Usami, K.; Nakamura, Y. Coherent coupling between a ferromagnetic magnon and a superconducting qubit. Science 2015, 349, 405–408. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Tabuchi, Y.; Ishino, S.; Noguchi, A.; Ishikawa, T.; Yamazaki, R.; Nakamura, Y. Resolving quanta of collective spin excitations in a millimeter-sized ferromagnet. Sci. Adv. 2017, 3, e1603150. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Wolski, S.P.; Tabuchi, Y.; Kono, S.; Usami, K.; Nakamura, Y. Entanglement-based single-shot detection of a single magnon with a superconducting qubit. Science 2020, 367, 425–428. [Google Scholar] [CrossRef]
- Wolski, S.P.; Lachance-Quirion, D.; Tabuchi, Y.; Kono, S.; Noguchi, A.; Usami, K.; Nakamura, Y. Dissipation-Based Quantum Sensing of Magnons with a Superconducting Qubit. Phys. Rev. Lett. 2020, 125, 117701. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Gu, X.-K.; Li, H.-K.; Weng, Y.-C.; Wang, Y.-P.; Li, J.; Wang, H.; Zhu, S.-Y.; You, J.Q. Quantum control of a single magnon in a macroscopic spin system. Phys. Rev. Lett. 2023, 130, 193603. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Tabuchi, Y.; Gloppe, A.; Usami, K.; Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 2019, 12, 070101. [Google Scholar] [CrossRef]
- Yuan, H.Y.; Cao, Y.; Kamra, A.; Duine, R.A.; Yan, P. Quantum magnonics: When magnon spintronics meets quantum information science. Phys. Rep. 2022, 965, 1–74. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Tyberkevych, V.; Kwok, W.-K.; Hoffmann, A.; Novosad, V. Hybrid magnonics: Physics, circuits, and applications for coherent information processing. J. Appl. Phys. 2020, 128, 130902. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.-P.; Wu, W.-J.; Zhu, S.-Y.; You, J.Q. Quantum Network with Magnonic and Mechanical Nodes. Phys. Rev. X Quantum 2021, 2, 040344. [Google Scholar] [CrossRef]
- Sharma, S.; Blanter, Y.M.; Bauer, G.E.W. Optical Cooling of Magnons. Phys. Rev. Lett. 2018, 121, 087205. [Google Scholar] [CrossRef] [PubMed]
- Bittencourt, V.A.S.V.; Feulner, V.; Kusminskiy, S.V. Magnon heralding in cavity optomagnonics. Phys. Rev. A 2019, 100, 013810. [Google Scholar] [CrossRef]
- Sun, F.-X.; Zheng, S.-S.; Xiao, Y.; Gong, Q.; He, Q.; Xia, K. Remote Generation of Magnon Schrödinger Cat State via Magnon-Photon Entanglement. Phys. Rev. Lett. 2021, 127, 087203. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.-J.; Wang, Y.-P.; Wu, J.-Z.; Li, J.; You, J.Q. Remote magnon entanglement between two massive ferrimagnetic spheres via cavity optomagnonics. Phys. Rev. A 2021, 104, 023711. [Google Scholar] [CrossRef]
- Xie, H.; Shi, Z.-G.; He, L.-W.; Chen, X.; Liao, C.-G.; Lin, X.-M. Proposal for a Bell test in cavity optomagnonics. Phys. Rev. A 2022, 105, 023701. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Xiong, H. Magnon laser based on Brillouin light scattering. Opt. Lett. 2020, 45, 5452–5455. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Jia, X.; Lu, X.-H.; Xiong, H. PT-symmetric magnon laser in cavity optomagnonics. Phys. Rev. A 2022, 105, 053705. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Wang, B.; Xiong, H.; Wu, Y. Magnon-induced high-order sideband generation. Opt. Lett. 2018, 43, 3698–3701. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.-X.; You, C.; Wang, B.; Xiong, H.; Wu, Y. Phase-mediated magnon chaos-order transition in cavity optomagnonics. Opt. Lett. 2019, 44, 507–510. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Li, Y.-Q. Optomagnonic frequency combs. Photonics Res. 2022, 10, 2786–2793. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Peng, J.; Xiong, H. Generation of magnonic frequency combs via a two-tone microwave drive. Phys. Rev. A 2023, 107, 053708. [Google Scholar] [CrossRef]
- Xie, H.; He, L.-W.; Shang, X.; Lin, G.-W.; Lin, X.-M. Nonreciprocal photon blockade in cavity optomagnonics. Phys. Rev. A 2022, 106, 053707. [Google Scholar] [CrossRef]
- Liang, Z.; Li, J.; Wu, Y. All-optical polarization-state engineering in quantum cavity optomagnonics. Phys. Rev. A 2023, 107, 033701. [Google Scholar] [CrossRef]
- Sharma, S.; Blanter, Y.M.; Bauer, G.E.W. Light scattering by magnons in whispering gallery mode cavities. Phys. Rev. B 2017, 96, 094412. [Google Scholar] [CrossRef]
- Pantazopoulos, P.A.; Stefanou, N.; Almpanis, E.; Papanikolaou, N. Photomagnonic nanocavities for strong light-spin-wave interaction. Phys. Rev. B 2017, 96, 104425. [Google Scholar] [CrossRef]
- Osada, A.; Gloppe, A.; Nakamura, Y.; Usami, K. Orbital angular momentum conservation in Brillouin light scattering within a ferromagnetic sphere. New J. Phys. 2018, 20, 103018. [Google Scholar] [CrossRef]
- Haigh, J.A.; Lambert, N.J.; Sharma, S.; Blanter, Y.M.; Bauer, G.E.W.; Ramsay, A.J. Selection rules for cavity-enhanced brillouin light scattering from magnetostatic modes. Phys. Rev. B 2018, 97, 214423. [Google Scholar] [CrossRef]
- Duan, L.-M.; Lukin, M.D.; Cirac, J.I.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413–418. [Google Scholar] [CrossRef]
- Riedinger, R.; Hong, S.; Norte, R.A.; Slater, J.A.; Shang, J.; Krause, A.G.; Anant, V.; Aspelmeyer, M.; Gröblacher, S. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature 2016, 530, 313–316. [Google Scholar] [CrossRef]
- Riedinger, R.; Wallucks, A.; Marinković, I.; Löschnauer, C.; Aspelmeyer, M.; Hong, S.; Gröblacher, S. Remote quantum entanglement between two micromechanical oscillators. Nature 2018, 556, 473–477. [Google Scholar] [CrossRef]
- Li, J.; Wallucks, A.; Benevides, R.; Fiaschi, N.; Hensen, B.; Alegre, T.P.M.; Gröblacher, S. Proposal for optomechanical quantum teleportation. Phys. Rev. A 2020, 102, 032402. [Google Scholar] [CrossRef]
- Żukowski, M.; Zeilinger, A.; Horne, M.A.; Ekert, A.K. “Event-ready-detectors” Bell experiment via entanglement swapping. Phys. Rev. Lett. 1993, 71, 4287–4290. [Google Scholar] [CrossRef]
- Azuma, K.; Tamaki, K.; Lo, H.-K. All-photonic quantum repeaters. Nat. Commun. 2015, 6, 6787. [Google Scholar] [CrossRef]
- Buterakos, D.; Barnes, E.; Economou, S.E. Deterministic Generation of All-Photonic Quantum Repeaters from Solid-State Emitters. Phys. Rev. X 2017, 7, 041023. [Google Scholar] [CrossRef]
- Li, C.-L.; Fu, Y.; Liu, W.-B.; Xie, Y.-M.; Li, B.-H.; Zhou, M.-G.; Yin, H.-L.; Chen, Z.-B. All-photonic quantum repeater for multipartite entanglement generation. Opt. Lett. 2023, 48, 1244–1247. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.-K.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef]
- Xie, Y.-M.; Lu, Y.-S.; Weng, C.-X.; Cao, X.-Y.; Jia, Z.-Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.-L.; Chen, Z.-B. Breaking the Rate-Loss Bound of Quantum Key Distribution with Asynchronous Two-Photon Interference. Phys. Rev. X Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Massar, S.; Popescu, S. Optimal Extraction of Information from Finite Quantum Ensembles. Phys. Rev. Lett. 1995, 74, 1259–1263. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Zuo, X.; Qian, H.; Li, J. Proposal for Optomagnonic Teleportation and Entanglement Swapping. Photonics 2023, 10, 739. https://doi.org/10.3390/photonics10070739
Fan Z, Zuo X, Qian H, Li J. Proposal for Optomagnonic Teleportation and Entanglement Swapping. Photonics. 2023; 10(7):739. https://doi.org/10.3390/photonics10070739
Chicago/Turabian StyleFan, Zhiyuan, Xuan Zuo, Hang Qian, and Jie Li. 2023. "Proposal for Optomagnonic Teleportation and Entanglement Swapping" Photonics 10, no. 7: 739. https://doi.org/10.3390/photonics10070739
APA StyleFan, Z., Zuo, X., Qian, H., & Li, J. (2023). Proposal for Optomagnonic Teleportation and Entanglement Swapping. Photonics, 10(7), 739. https://doi.org/10.3390/photonics10070739




