Confocal Single-Pixel Imaging

Abstract

Obtaining depth-selective images requires gating procedures such as spatial, nonlinear, or coherence gating to differentiate light originating from different depths of the volume of interest. Nonlinear gating requires pulsed excitation sources and excitation probes, limiting easy usage. Coherence gating also requires broadband sources and interferometry requiring specialized stable setups. Spatial gating can be used both for fluorescence and reflection geometry and various light sources and thus has the least requirements on hardware, but still requires the use of a pinhole which makes it difficult to use for photography or widefield imaging schemes. Here, we demonstrate that we can utilize a single digital micromirror device (DMD) to simultaneously function as a dynamic illumination modulator and automatically synchronized dynamic pinhole array to obtain depth-sectioned widefield images. Utilizing the multiplexed measurement advantage of single-pixel imaging, we show that the depth and ballistic light gating of the confocal single pixel imaging scheme can be utilized to obtain images through glare and multiple scattering where conventional widefield imaging fails to recover clear images due to saturation or random scattered noise.

1. Introduction

Optical imaging has become an essential part of everyday life and holds valuable information as can be seen in the impact of high-quality cameras embedded in smartphones. The same holds true when we increase the resolution aimed to look at smaller structures in both industry and in the life sciences [1,2]. High resolution optical imaging enables the imaging of the subcellular organelles making up individual cells and enables nondestructive inspection of industrial products en masse. These examples illustrate the strength of optical imaging in fast and easy high-resolution imaging of superficial layers of various objects. However, when trying to look through multiple layers of objects or inside deep structures, optical imaging faces difficulties associated with depth selectivity and multiple scattering of light.

Since optical sensors detect the intensity of light disregarding the direction or whether the light is converging or diverging, cameras cannot differentiate light originating from different depths of the sample or whether the light has undergone multiple scattering. In other words, to differentiate ballistic photons that originate from specific depths of the sample and obtain depth-selective imaging, we need to add specific gating mechanisms such as spatial, nonlinear, or coherence gating into an optical system. Nonlinear gating requires the use of expensive pulsed laser sources and cannot be used for non-excitable targets [3]. Coherence gating requires broadband sources and interferometry and cannot be used for fluorescence [4]. Spatial gating does not have limitations on light source selection and can be applied for both reflection and fluorescence imaging [5]. Spatial gating, however, requires the use of a pinhole which restricts use in widefield imaging such as photography. Conventional confocal microscopy also suffers from reduced signal-to-noise ratios when applied to thick scattering samples as the amount of ballistic light is exponentially reduced as a function of sample thickness. Due to the importance of 3D imaging, advances in developing different methods to realize depth selectivity is still ongoing; for example, realizing unconventional optical geometries that incorporate orthogonal illumination and detection paths as in lightsheet microscopy [6], and encoding depth information based on high spatial frequency contrast of specially designed illumination patterns such as in structured illumination microscopy [7,8].

Whereas absorption of light reduces the energy of the propagating light without changing its direction, the propagation direction of light is altered whenever it meets a refractive index mismatch. In other words, we can overcome absorption by simply using wavelengths that are not absorbed by the specific target of interest [9]. However, overcoming multiple scattering is a much more difficult problem since refractive index mismatch among different structures exist for all wavelengths. To overcome optical aberrations and multiple scattering due to the refractive index inhomogeneity, the field of adaptive optics [10,11,12,13] and wavefront shaping [14,15,16,17,18,19] is gaining popularity, where wavefront distortions that are accumulated during the transport of light through complex media are actively compensated. Originally developed for astronomy [20], adaptive optics and wavefront shaping have been shown to be equally effective in correcting for optical distortions due to complex media, especially for thick biological tissues. While actively compensating for the distortions has been shown to be effective for various microscopy methods such as confocal [21], multiphoton [22,23,24,25], lightsheet [26,27], and optical coherence tomography [28,29], its application requires the additional design and setup of complex hardware and measurement algorithms that are out of reach for most small research groups. Adaptive optics is also fundamentally limited by the optical memory effect which restricts the effective imaging field of view that can benefit from the complex phase correction [30,31,32] and requires an extended amount of measurements when trying to correct for distortions due to multiple scattering where Shack–Hartmann wavefront sensors fail to operate.

In a simpler approach, single-pixel imaging [33] has been shown to be less sensitive to multiple scattering in comparison with conventional widefield imaging. Conventional widefield imaging relies on the combination of 2D sensors (camera) and a lens with respective distances between the sample of interest, the lens, and sensor satisfying the imaging condition. In contrast, single-pixel imaging does not require the imaging condition to be satisfied between the sample of interest and the detector. Rather, the entirety of the light that is scattered or emitted from the sample is simply integrated onto a single-pixel photodetector, removing the spatial information in detection. In such a scheme, the spatial information about the sample is not directly measured on the detection side and therefore must be obtained in a different manner. Single-pixel imaging satisfies this requirement by illuminating the sample with known 2D patterns. In other words, the spatial degree of freedom is imposed onto the illumination rather than the detector. By simply summing the illuminated patterns that are weighted with their respective measured intensities after interacting with the sample, we can obtain the 2D image of the object as in traditional imaging. Since the requirements on the sensors is less than conventional imaging and only a single-pixel sensor is required rather than a multitude array of 2D pixels, the detection of light in exotic ranges such as deep infra-red becomes possible where cheap camera solutions do not exist.

This unique geometry where the information relays between the sample and detector only requires the delivery of total intensity without any spatial information has allowed demonstrations where the insertion of turbid media between the sample and detector has negligible effects in image reconstruction quality. The initial demonstration showed this in transmission geometry where there was no disturbance along the illumination source to sample path and the disturbance was solely distributed along the sample to detector path [34,35]. As previously discussed, the scattering of light in the detection path does not compromise image reconstruction. However, this approach required a clear path between the illumination source to the sample which is a severe constraint limiting practical applications. Recently, it was shown that the application of temporal focusing can reduce this constraint by utilizing the longer center wavelength as well as the broader bandwidth that is used for multiphoton excitation and the required ultrafast pulsewidth of the excitation source [36]. This approach, however, requires expensive amplifiers to increase the maximum peak power while reducing the pulse repetition rate to realize multiphoton excitation over a wide field of view which only a limited number of well-funded labs have access to.

Here, we describe the use of a double path single-pixel imaging geometry which we call confocal single-pixel imaging to reduce the deleterious effects of multiple scattering and simultaneously gate ballistic photons at specific depths to automatically obtain depth selectivity. The required hardware for confocal single-pixel imaging is identical to conventional single-pixel imaging, minimizing the costs and complexity of the setup. The only difference is that the target light after interacting with the sample is redirected to the DMD in a double pass geometry to utilize individual mirrors of the DMD as both illuminating and detecting confocal pinholes. Utilizing this simple setup, we demonstrate that we can dynamically change single-pixel imaging characteristics from conventional widefield imaging to depth-selective imaging. In contrast to confocal microscopy, our method can be easily applied to macroscopic photography utilizing standard camera lenses which we demonstrate can be utilized to obtain depth-selective widefield imaging resistant to glare as well as imaging through complex structures that induce multiple scattering.

2. Materials and Methods

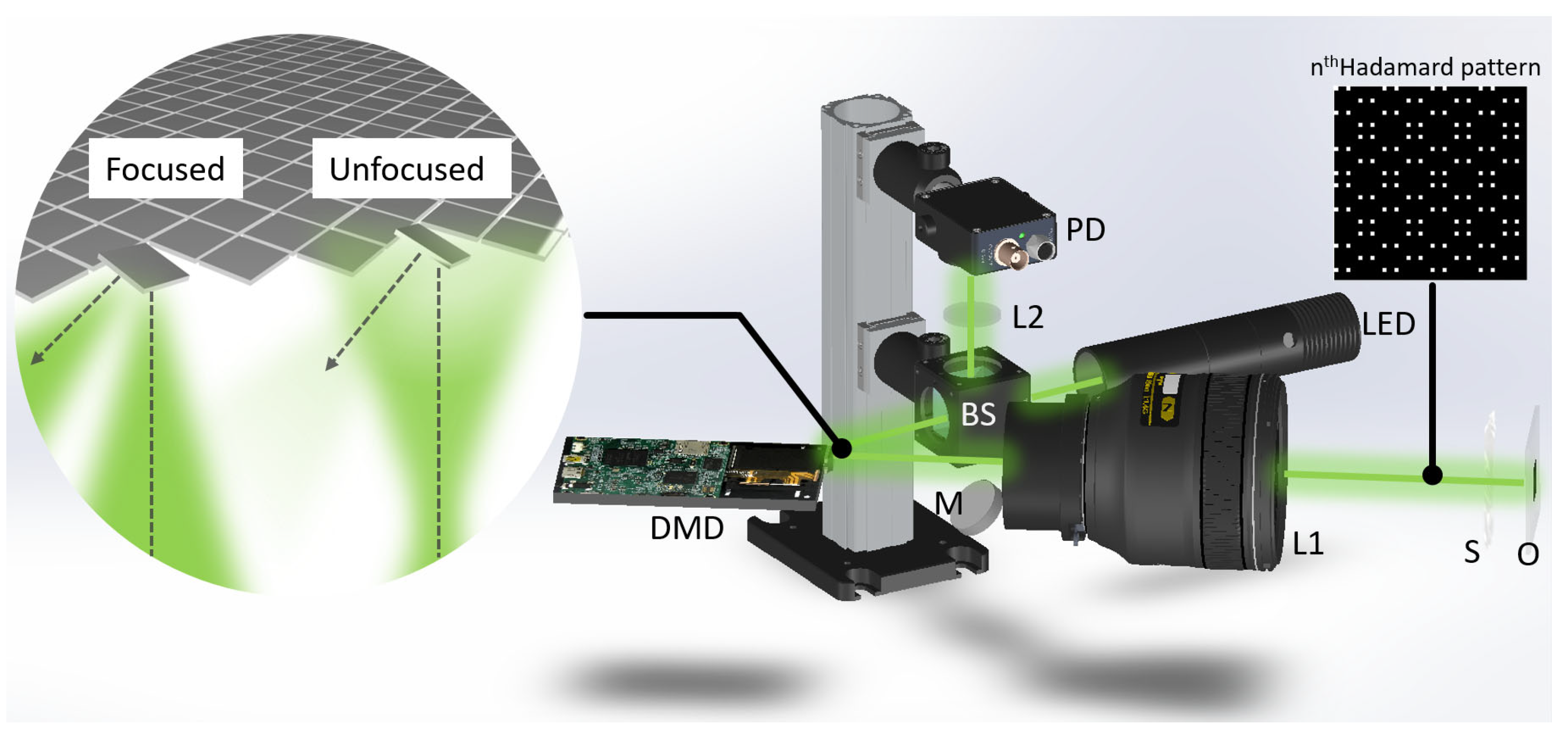
Our imaging setup (Figure 1) consists of just a LED light source (Thorlabs, Newton, NJ, USA, MWWHL4), a DSLR macrolens (Nikkor, f/2.8, focal length 105 mm) for both illumination and detection of light to and from the sample, a DMD to control the illumination patterns as well as the confocal gating array (Texas Instruments, Dallas, TX, USA, DLP LightCrafter), a photodiode detector (Thorlabs, PDA100A-EC), and a lens to focus light onto the photodiode. The DMD had a 7.6 µm micromirror pitch distance and a total of 608 × 684 pixels. The mirrors can be tilted to ±12° for independent binary amplitude modulation of each pixel. Using a HDMI connection port, image commands could be updated at 60 Hz. Using 3-color 8-bit dynamic range images, the actual refresh rate of binary patterns could be controlled at a 1440 Hz refresh rate. The DMD surface is simply aligned to be conjugate to the target sample depth using the DSLR macrolens. This alignment automatically aligns the reflected light from the targeted depth back onto the DMD. Due to the double pass geometry, the setup is alignment free and the same mirror segments of the DMD are used for both illumination and detection paths. Since each mirror of the DMD defines the spatial coordinates on the target sample plane, the illumination can be actively turned on or off on an individual pixel basis. The illuminated light that reaches the target is then scattered and reflected back to the same mirror of origin. Other scattered light that has been scattered from different depths or scattered by multiple scattering does not pass through the confocal gating and is removed from the image reconstruction process. A final lens simply integrates the total reflected light into a photodiode. While we demonstrate our method by measuring the scattered light from the sample in a brightfield imaging geometry, the same setup can be easily adapted to be used for other schemes such as fluorescence imaging.

In conventional confocal microscopy, decreasing the pinhole size results in an enhancement of depth selectivity and resolution while reducing the signal-to-noise ratio due to the lower detection throughput. This is also the same for spinning disk confocal microscopy where many pinholes are used in parallel. Although the signals are measured through multiple pinholes simultaneously, the light passing through each pinhole is individually measured and the reduction of pinhole size results in a decrease in signal-to-noise ratio for the respective pinhole. In comparison, single-pixel imaging utilizes multiplexed measurements where the signal collected from all areas across the field of view are integrated and processed together. This results in the so called Fellgett’s advantage and we can utilize the light collection efficiency of the entire system as a whole.

To take advantage of the multiplexed detection and increase the depth-sectioning efficiency of confocal ghost imaging, we tested several design parameters for optimal results. Since we are utilizing single-pixel imaging reconstruction algorithms, it is advantageous to use orthogonal illumination patterns. When illuminating the sample with orthogonal 2D patterns, we only need to illuminate the sample with M = N measurements where N is the number of definable pixels on the sample plane. In short, we just need to take exactly the same number of measurements as there are degrees of freedom in the field of view that we want to measure. The use of nonorthogonal illumination patterns requires M >> N measurements which makes the imaging process inefficient. In this approach, compressive sensing can be applied to reduce the number of measurements by utilizing the sparsity of natural images [37].

The spacing between adjacent micromirrors has been decided with consideration of the diffraction limit:

Rayleigh diffraction limit = 0.61 λ/NA

in which λ is the wavelength and NA is the numerical aperture of the optical system. Here, the minimum spacing corresponds to the diffraction limit of the optical system, and as the spacing between the two micromirrors increases, the confocal gating efficiency increases. However, as the spacing increases, the light throughput and SNR of acquired images decrease, so an appropriate value of the spacing should be selected under the trade-off relationship. Since the diffraction limit of the system configuration is 1.12 µm, the effective size of the pinhole has been chosen to be 1.95 µm which can be realized by grouping the 576 by 576 active pixels of DMD into macropixels of 6 by 6 pixels to make 96 by 96 effective pixels. The minimal spacing between adjacent macropixels is 11.7 µm which is far enough to eliminate the out-of-focus lights. The value of spacing keeps altering depending on which pattern will be illuminated. The confocal orthogonal illumination/pinhole patterns were generated by simply redistributing standard Hadamard basis patterns by changing the minimal spacing (Figure 2). As the illumination basis is still uniform, theoretically we only require the same number of measurements as the number of pixels in the measured image. Since light intensity cannot be negative, we measured an identical set of conjugate patterns where the 1 and 0 intensity mirror positions were reversed resulting in a measurement number of 2 × N, where N is the number of pixels of the obtained image.

In detail, each confocal orthogonal pattern (96 by 96) has been generated by reshaping a vectorized Hadamard matrix (256 by 256). The reshaped pattern is spread out over the large size matrix (561 by 561) which is then zero padded to match with the size of the DMD (683 by 607). Before spreading out, the diameter of the multiplexed pinholes and space between pinholes should be determined considering the system’s diffraction limit. The Hadamard pattern is composed of 1 and −1, and is realized by displaying two complementary patterns consecutively and subtracting the second measurement since light intensity cannot be negative. The patterns are streamed live onto the DMD, which updates the displayed pattern at a refresh rate of 1440 Hz. The analog voltage signal measured from a single-pixel detector is then captured by a data acquisition (DAQ) card (National Instruments, Austin, TX, USA, PCIe-6321), synchronized with the DMD. For image acquisition, the signal values corresponding to each complementary pattern set are subtracted to generate a single Hadamard pattern as previously discussed. All the patterns displayed are given weights defined by the measured light intensity reflecting off the object. Summation of all the weighted patterns reconstructs the object. In short, several sub-regions assigned based on the confocal principle are imaged through the conventional single-pixel imaging method, filling out the FOV with a multiplexed raster scanning method.

where O is the reconstructed image in a Cartesian coordinate system, (x, y); S_i is the signal measured with the theoretical Hadamard pattern I_i; N is the number of modes of SPI which is also identical to the number of pixels in the I_i; and m is the iteration number for the raster scanning across the total FOV and O_m will be retrieved at every iteration. Using orthogonal illumination patterns, we need the same number of measurements as the number of pixels of the image. To generate Hadamard patterns with +1 and −1 values, we need twice as many measurements resulting in 18,432 measurements to acquire a 96 by 96 pixel image. Based on the system refresh rate of 1440 Hz, the current image measurement time is 12.8 s. The image reconstruction is simply summations of the weighted patterns which can be implemented in real time. If needed, the number of measurements can be reduced by employing compressive sensing into the reconstruction process [37].

3. Results

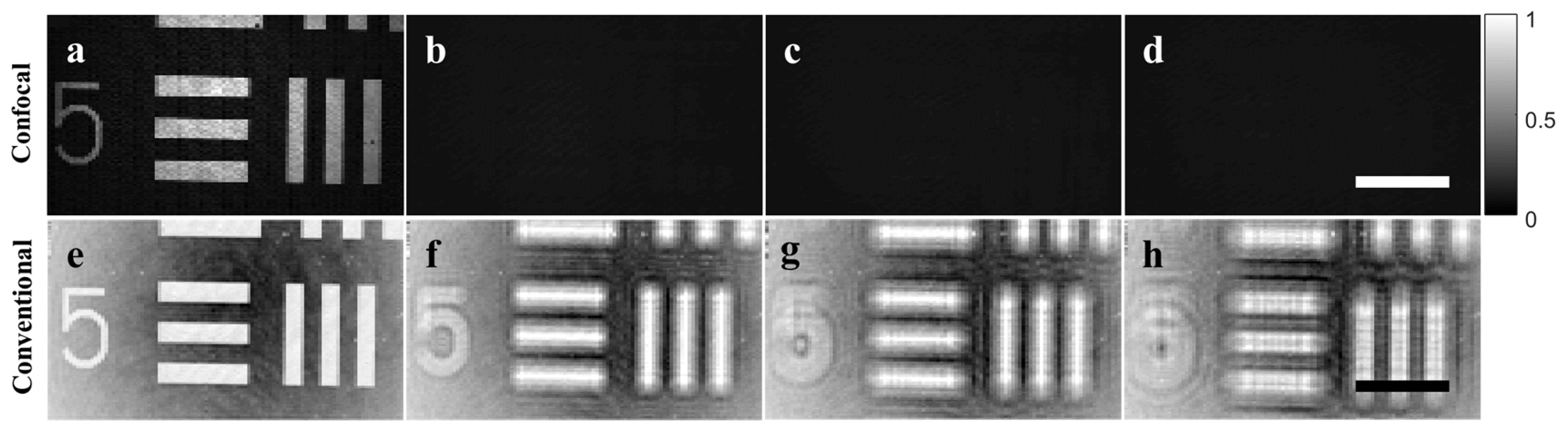
We verified the depth-sectioning capabilities for widefield imaging using confocal single-pixel imaging (Figure 3). Using a USAF target as the target object, depth sectioning was clearly observed using the confocal orthogonal basis illumination patterns for extended objects, where the entire USAF target within the field of view disappeared from the detection range as soon as the target was moved in the axial direction. In contrast, using conventional Hadamard basis illumination patterns, out of focus blurred images persisted to be measured with increased blurring as a function of axial misplacement. As both imaging modalities can be realized using a single setup, we can also modulate different parts of the field of view simultaneously, for instance, some regions of interest (ROI) via conventional widefield imaging, and some ROIs via spatially gated imaging if needed. Comparing the axial PSF for conventional confocal imaging, confocal single-pixel imaging, and conventional single-pixel imaging, we found the z-PSF FWHM to be 1, 1.07, and 1.40, respectively, normalized to the performance of conventional confocal imaging. The depth sectioning performance of confocal single-pixel imaging is therefore comparable to that of conventional confocal imaging.

To demonstrate further applications, we employed confocal single-pixel imaging to obtain widefield images through severe glare (Figure 4). Glare was generated by placing a Petri dish in front of the USAF target. Using conventional imaging, the severe glare reflected off from out-of-plane refractive index mismatch overwhelmed the signal from the actual target of interest causing saturation and compromising quantitative imaging across the field of view (Figure 4a). In comparison, confocal single-pixel imaging effectively removed the glare originating from different depths and successfully measured the target without glare artifacts (Figure 4b). To compare the image quality enhancement from glare suppression, we defined the signal-to-background ratio of our images by choosing a part of the object that should not have signal as the background, and the signal of a constant area of the object of interest as the true signal. Comparing the regions outlined below, we found the signal-to-background ratio in conventional widefield imaging to be 1.2559 whereas the signal-to-background ratio in confocal single-pixel imaging was 3.3685, clearly demonstrating the enhancement in contrast due to glare suppression.

We finally tested confocal single-pixel imaging for imaging through scattering layers (Figure 5). For further applications, we demonstrate the possibility of our confocal SPI system using various illumination wavelengths that normally cannot be imaged using conventional cameras. Using various illumination sources, we could observe that broadband sources suffered least from speckle artifacts in the recovered image, while longer wavelengths suffered less from image aberrations and displayed sharper contrast through scattering [32]. Consequently, our multiplexed confocal regime will continue to extract more informative light with a higher SNR from deeper and scattering tissue compared to conventional SPI and confocal systems.

The feasibility of confocal SPI through scattering media has been demonstrated with broadband visible light in Figure 5. Within the length of the mean free path, the broadband illumination provided lower speckle contrast than infra-red light. For the visibility of the speckle, we placed a single layer of Scotch tape (reduced scattering cross section ${\mu }_s^{\prime }$~3 cm⁻¹ [38]) and optimized the distance between the layer and the target (Figure 5a–c), while speckle tolerant imaging was achieved using broadband LED illumination (Figure 5d–f), showing higher contrast than that with conventional widefield imaging (Figure 5g–i).

4. Discussion and Conclusions

Although various gating mechanisms have been demonstrated to be effective in microscopy, their direct applications to various scales spanning from microscopic to macroscopic levels is currently difficult. For example, nonlinear microscopy which relies on high peak pulse powers is not effective for macroscopic imaging since obtaining the high flux for larger effective pixel sizes will require more powerful laser sources with prohibitive costs. Similar restrictions hold for other laser scanning microscopy techniques such as confocal and optical coherence tomography since telecentric scan lenses used to translate angle tilt of light to spatial shift typically have short focal lengths along with the limited scan angles of scan mirrors which limit the achievable high quality scan range. In this regard, we have demonstrated confocal single-pixel imaging which utilizes conventional camera lenses for widefield depth-selective macroscopic imaging. Using DMDs which can dynamically modify illumination patterns in a double path geometry, we obtained automatic spatial gating with the same individual mirrors acting as both the illuminator as well as detector. To realize efficient spatial gating using 2D DMDs, we developed confocal orthogonal illumination patterns which only require the exact same number of measurements as the obtained image pixel resolution.

While our current demonstration utilized brightfield epi-reflection imaging and realized removal of glare artifacts and multiple scattering background noise, the same principle can be used for various applications such as fluorescence and phase imaging. Removing glare may find applications in long range surveillance where looking through windows on a sunny day or looking inside deep waters through surface reflections is required. Macroscopic imaging through turbid media will also find valuable use in various applications such as imaging through fog or turbulence as well as biomedical imaging.