Dynamic Tunable Deflection of Radiation Based on Epsilon-Near-Zero Material

Abstract

Epsilon-near-zero nanoantennas can be used to tune the far-field radiation pattern due to their exceptionally large intensity-dependent refractive index. In this study, we propose a hybrid optical antenna based on indium tin oxide (ITO) to enable optical tuning of the deflection of radiation, specifically a hybrid structure antenna of ITO and dielectric material, which makes the deflection angle changes 17${}^{\circ }$ as incident intensities increase. Moreover, by employing an array of ITO or hybrid nanodisks, we can enhance the unidirectionality of the radiation pattern, resulting in a needle-like shape with an angular beam width $\alpha <$ 8${}^{\circ }$ of the main lobe. The deflection angle of the radiation pattern response with the needle-like lobe paves the way for further studies and applications in beam steering and optical modulation where dynamic control of the nanoantennas is highly desirable.

1. Introduction

Optical antennas have drawn much attention in the field of photonics due to their potential applications. The role of the antenna is to receive and transmit signals. Different from radio frequency (RF) microwave antennas, optical antennas manipulate and control optical radiation on the subwavelength scale.The optical responses of antennas are predominantly influenced by the geometry and surrounding environment. Traditionally, a direct method to achieve the tuning effect could be realized by reshaping the geometry of antennas, such as laser ablating [1]. However, this method is not reversible. In addition, various approaches for dynamical manipulation of the beam steering and reversible tuning can be achieved via optical [2,3], external input [4], electrical [5], chemical [6], thermal [7], magneto-optical [8,9], and even mechanical tuning [10]. In comparison, optical tuning offers additional advantages such as fast response time and reversible processes. The intensity of the incident light decides the induced electric and magnetic multipole moments [11]. Several antenna structures have been proposed to increase the field enhancement factor of the antenna and to adjust its resonance characteristics, aiming to provide an effective way to process optical information and adjust the spectrum or far-field radiation response [12,13]. The study of radiation control of optical antennas is of great significance in the research fields of ultra-diffraction limit imaging, new optical probes, and propagation control of nanoscale optical information [14,15,16,17,18]. To control the far-field radiation of an optical antenna, its optical properties must be dynamically modulated. In recent years, indium tin oxide (ITO) as an epsilon-near-zero (ENZ) material has been reported. ITO can obtain an intensity-dependent refractive index at ultra-high speed in the spectral region where the real part of the permittivity is small. The ITO inspires new concepts for beam steering. This change of refractive index is reversible and its response time is femtoseconds experimentally [19].

We conducted a theoretical investigation into the modulation of the far-field radiation of the optical nano-antenna utilizing ENZ material. Initially, we examined the radiation pattern of a single ITO nanoparticle and demonstrated that it can be altered by increasing the incident intensity. To further enhance the control over the deflection angle of the radiation pattern, we propose a hybrid structure comprising ITO and dielectric nanodisk. This hybrid structure exploits the remarkable Kerr effect of ENZ materials. Additionally, we explored the directional scattering properties of nanodisks arranged in a one-dimensional (1D) chain, observing how the intensity of the laser can influence these properties.

2. Materials and Methods

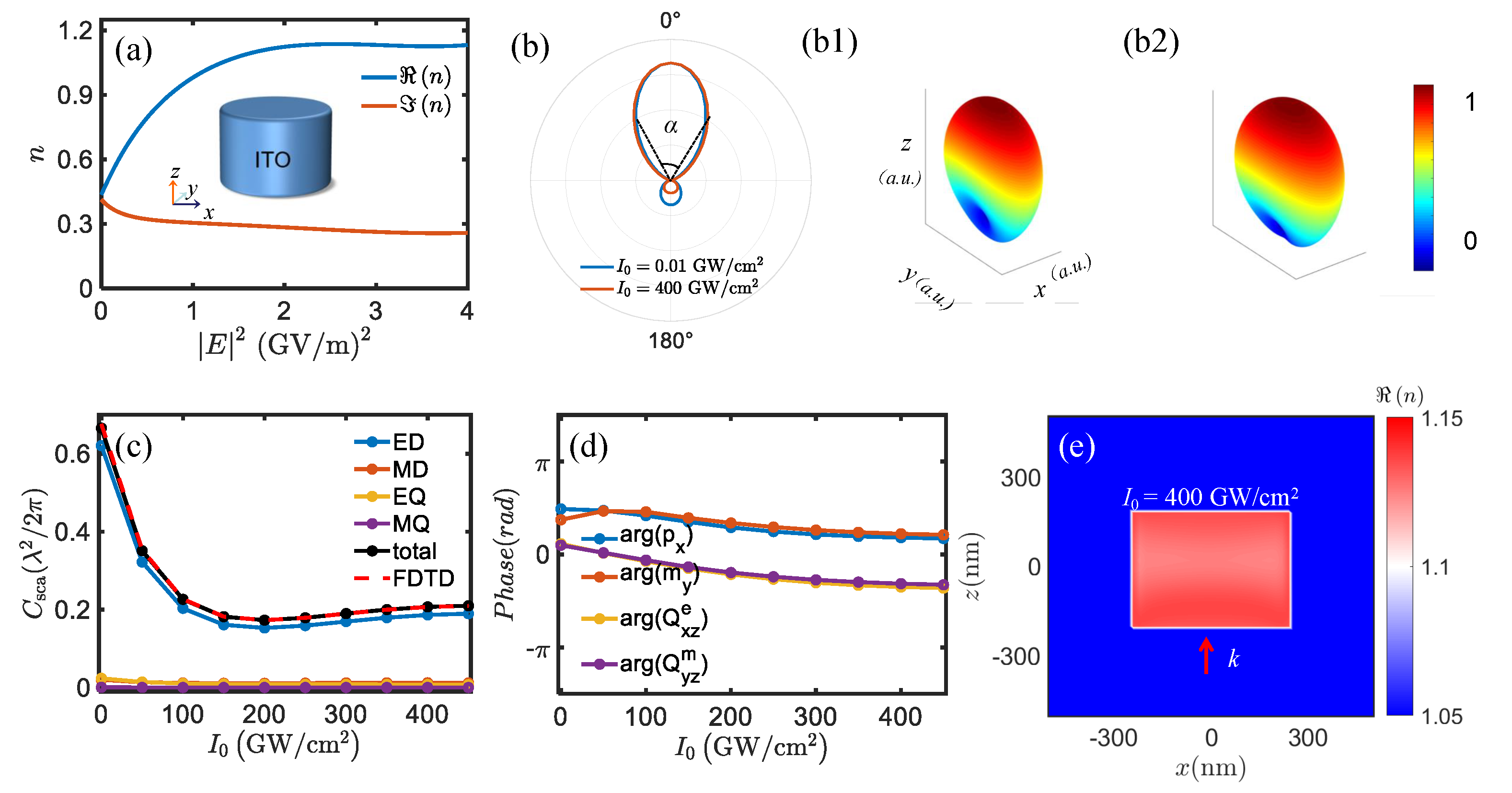
The proposed structure, consisting of a three-dimensional (3D) ITO disk with a height (H) of 400 nm and diameter (D) of 600 nm, is schematically shown in the inset of Figure 1a. The nonlinear material, composed of ITO, is illuminated by a plane wave with an electric field ${\mathbf{E}}_{\mathrm{inc}}\left(\mathbf{r},\omega \right)=(E_0/2)e^{i\left(\mathbf{k}·\mathbf{r}-\omega t\right)}{\mathbf{e}}_x+\mathrm{c}.\mathrm{c}.$, where $\left|\mathbf{k}\right|=2\pi /\lambda$ is the wavenumber, $\omega$ is the angular frequency, $E_0$ denotes the amplitude of the incident field, and c.c. signifies the complex conjugate. $I_0=\frac{1}{2}c{\epsilon }_0{\left|E_0\right|}^2$ is the free-space intensity of the incident plane wave. The intensity-dependent refractive index of ITO, denoted as $n_{{}_{\mathrm{NL}}}\left(\mathbf{r},\omega \right)$, is approximately equal to the square root of the nonlinear permittivity ${\epsilon }_{{}_{\mathrm{NL}}}\left(\mathbf{r},\omega \right)$, where $n_{{}_{\mathrm{NL}}}\left(\mathbf{r},\omega \right)$ is given by [20,21]

$$n_{{}_{\mathrm{NL}}}\left(\mathbf{r},\omega \right)\approx \sqrt{{\epsilon }_{\mathrm{L}}+\stackrel{3}{\sum _{j=1}}{c}_{2j+1}{\chi }^{(2j+1)}\left(\omega \right){\left|\frac{\mathbf{E}\left(\mathbf{r},\omega \right)}{2}\right|}^{2j}},$$

(1)

where, ${\chi }^{\left(3\right)}\left(\omega \right)$, ${\chi }^{\left(5\right)}\left(\omega \right)$, and ${\chi }^{\left(7\right)}\left(\omega \right)$ are the third-order, fifth-order, and seventh-order nonlinear susceptibilities (refer to Table 1 in Ref. [21]) of ITO, respectively. The degeneracy factors are given by $c_3=3,c_5=10,c_7=35$ [20]. The electric field inside the ITO is denoted by $\mathbf{E}\left(\mathbf{r},\omega \right)$. The real part of the dielectric constant $\epsilon$ of ITO is zero at 1240 nm, which is the ENZ wavelength ${\lambda }_{ENZ}$ [16,21]. As per the relationship between the refractive index and permittivity ($n=\sqrt{\epsilon }$), a change of $\Delta \epsilon$ in the permittivity $\epsilon$ leads to a change of $\Delta n$. Consequently, ITO exhibits strong nonlinear optical properties when the permittivity becomes small. Figure 1a illustrates the intensity-dependent refractive index of a single ITO at ${\lambda }_{ENZ}$ [16,21]. The change in the real part of the refractive index with intensity is approximately 0.72, while the linear refractive index is 0.4.

The optical response of the radiation pattern can be described using the multipole expansion of the induced displacement current ${\mathbf{J}}_{NL}(r,\omega )=-i\omega \left[{ϵ}_{NL}(\mathbf{r},\omega )-{ϵ}_0\right]\mathbf{E}(\mathbf{r},\omega )$ [11,22]. The excited multipole can be obtained by the induced nonlinear displacement current ${\mathbf{J}}_{NL}$. The multipole expansion, introduced by [11,22], is given as follows:

$$\begin{array}{cc}\hfill p_{\alpha }& =-\frac{1}{i\omega }\left\{\int d^3\mathbf{r}{J}_{\alpha ,\mathrm{NL}}{j}_0\left(kr\right)\right.\hfill \\ \hfill & \left.+\frac{k^2}{2}\int d^3\mathbf{r}\left[3\left(\mathbf{r}·{\mathbf{J}}_{\mathrm{NL}}\right)r_{\alpha }-r^2{J}_{\alpha ,\mathrm{NL}}\right]\frac{j_2\left(kr\right)}{{\left(kr\right)}^2}\right\},\hfill \\ \hfill m_{\alpha }& =\frac{3}{2}\int d^3\mathbf{r}{\left(\mathbf{r}\times {\mathbf{J}}_{\mathrm{NL}}\right)}_{\alpha }\frac{j_1\left(kr\right)}{kr},\hfill \\ \hfill Q_{\alpha \beta }^{\mathrm{e}}& =-\frac{3}{i\omega }\left\{\int d^3\mathbf{r}\left[3\left(r_{\beta }{J}_{\alpha ,\mathrm{NL}}+r_{\alpha }{J}_{\beta ,\mathrm{NL}}\right)-2\left(\mathbf{r}·{\mathbf{J}}_{\mathrm{NL}}\right){\delta }_{\alpha \beta }\right]\right.\hfill \\ \hfill & \frac{j_1(kr}{kr}+2k^2\int d^3\mathbf{r}[5r_{\alpha }{r}_{\beta }(\mathbf{r}·{\mathbf{J}}_{\mathrm{NL}})-(r_{\alpha }{J}_{\beta ,\mathrm{NL}}+r_{\beta }{J}_{\alpha ,\mathrm{NL}})r^2\hfill \\ \hfill & -r^2(\mathbf{r}·{\mathbf{J}}_{\mathrm{NL}}){\delta }_{\alpha \beta }\left]\frac{j_3\left(kr\right)}{{\left(kr\right)}^3}\right\},\hfill \\ \hfill Q_{\alpha \beta }^m& =15\int d^3\mathbf{r}\left\{r_{\alpha }{\left(\mathbf{r}\times {\mathbf{J}}_{\mathrm{NL}}\right)}_{\beta }+r_{\beta }{\left(\mathbf{r}\times {\mathbf{J}}_{\mathrm{NL}}\right)}_{\alpha }\right\}\frac{j_2\left(kr\right)}{{\left(kr\right)}^2},\hfill \end{array}$$

(2)

where $\alpha ,\beta \in x,y,z$, $p_{\alpha }$, $m_{\alpha }$, $Q_{\alpha \beta }^e$, and $Q_{\alpha \beta }^m$ are the electric dipole (ED), magnetic dipole (MD), electric quadrupole (EQ), and magnetic quadrupole (MQ) multipole moments, respectively. $j_n\left(kr\right)$ is the nth spherical Bessel function. The total scattering cross-section can be calculated using the following expression [11,22]:

$$\begin{array}{ccc}\hfill C_{\mathrm{sca}}& =& \frac{k^4}{6\pi {\epsilon }_0^2{\left|E_0\right|}^2}\left[\sum _{\alpha }\left({\left|p_{\alpha }\right|}^2+{\left|\frac{m_{\alpha }}{c}\right|}^2\right)\right.\hfill \\ & & \left.+\frac{1}{120}\sum _{\alpha ,\beta }\left({\left|k{Q}_{\alpha \beta }^e\right|}^2+{\left|\frac{k{Q}_{\alpha \beta }^m}{c}\right|}^2\right)\right],\hfill \end{array}$$

(3)

which is the contribution of each multipole moment (marked ’total’ in Figure 1c and Figure 2c). The far field corresponding to the radiation pattern ($\propto {\left|\mathbf{E}\right|}^2$) in space is

$$\begin{array}{ccc}\hfill \mathbf{E}& \approx & \frac{k^2}{4\pi \epsilon }{p}_x\frac{e^{ikr}}{r}\left(-sin\phi \widehat{\phi }+cos\theta cos\phi \widehat{\theta }\right)\hfill \\ & -& \frac{k^2}{4\pi \epsilon }\frac{\sqrt{{\epsilon }_r}{m}_y}{c}\frac{e^{ikr}}{r}\left(sin\phi cos\theta \widehat{\phi }-cos\phi \widehat{\theta }\right)\hfill \\ & -& \frac{k^2}{4\pi \epsilon }\frac{ik{Q}_e}{6}\frac{e^{ikr}}{r}\left(-sin\phi cos\theta \widehat{\phi }+cos2\theta cos\phi \widehat{\theta }\right)\hfill \\ & -& \frac{k^2}{4\pi \epsilon }\frac{ik{Q}_m}{6c}\frac{e^{ikr}}{r}\left(-sin\phi cos2\theta \widehat{\phi }+cos\theta cos\phi \widehat{\theta }\right),\hfill \end{array}$$

(4)

where, r, $\theta$, and $\phi$ represent the spherical coordinates. k is the wavenumber, and c is the speed of light.

3. Results

We utilized the finite difference time domain (FDTD) to analyze the two-dimensional (2D) far-field radiation patterns at $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ and $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$, respectively. For the simulations, periodic boundary conditions are employed along the x and y axes, while perfectly matched layers (PMLs) were used along the z axis. A single plane wave source at 1240 nm was employed for normal incidence. To ensure accurate results, the mesh size is optimized after conducting a converging test. The corresponding three-dimensional (3D) radiation patterns are presented in Figure 1(b1,b2). The changes observed in the scattering cross-section in Figure 1c can be attributed to the contribution of different multipole moments, as described by Equation (2). At an incident intensity of $I_0=400$ $\mathrm{GW}/{\mathrm{cm}}^2$, the main lobe width of the radiation pattern slightly increases compared to $I_0=0.01$ $\mathrm{GW}/{\mathrm{cm}}^2$. This variation is due to the different electric field distributions associated with distinct local electromagnetic modes within the ITO structure, which can be calculated using an iteration method. The refractive index, $n=n(\mathbf{r}$) (see Figure 2d), has varying effects on each multipole moment. The enhanced forward scattering is achieved when the oscillating dipole and quadrupole modes are in phase [23]. Therefore, the induced ED, MD, and MQ moments (normalized to ${\lambda }^2/2\pi$) interfere constructively (destructively) in the forward direction. Consequently, the antenna exhibits a nearly unidirectional radiation pattern with small backscattering, known as generalized Kerker effect [23]. Hence, the observed slight differences in the backward radiation pattern are entirely due to the varying induced electric and magnetic multipole moments calculated by Equation (2) (see Figure 1c). Importantly, the scattering cross-section calculated using FDTD demonstrates excellent agreement with the results obtained from the multipole expansion described in Equation (3). The findings highlight the advantageous capabilities of an ENZ-based antenna in controlling the radiation pattern ($\propto {\left|\mathbf{E}\right|}^2$). Here, $\mathbf{E}$ is calculated by Equation (4). When both electric/magnetic dipole and quadrupole coexist, the so-called generalized Kerker condition can be expressed as

$$\begin{array}{c}\hfill c{p}_x-m_y+\frac{ik}{6}c{Q}_{xz}^e-\frac{ik}{6}{Q}_{yz}^m.\end{array}$$

(5)

The phase can be obtained using arg($p_x$), arg($m_y$), arg($Q_{ze}^x$), and arg($Q_{zm}^y$). When dipole and quadrupole oscillate in phase (i.e., “+”), they constructively interfere with each other and the resulting scattering pattern will be strongly enhanced along the forward direction. As the intensity increases, ED and MD almost oscillate in phase (red solid line), which satisfies the Kerker effect. Likewise, EQ and MQ nearly meet the generalized Kerker effect. Since the phase difference between the dipole and the quadrupole modes (red dashed line) is about 0.4$\pi$ (see Figure 1d), the backscattering is maximally suppressed (see Figure 1(b1,b2)). Therefore, the far-field radiation of this nanoantenna exhibits almost unidirectionally forward scattering. Different local electromagnetic modes have different electric field distributions, and the distribution in the ITO is not uniform; it can be calculated using the $iteration$ method. The refractive index $n=n\left(\mathbf{r}\right)$ (see Figure 1e) will eventually have different effects on each multipole.

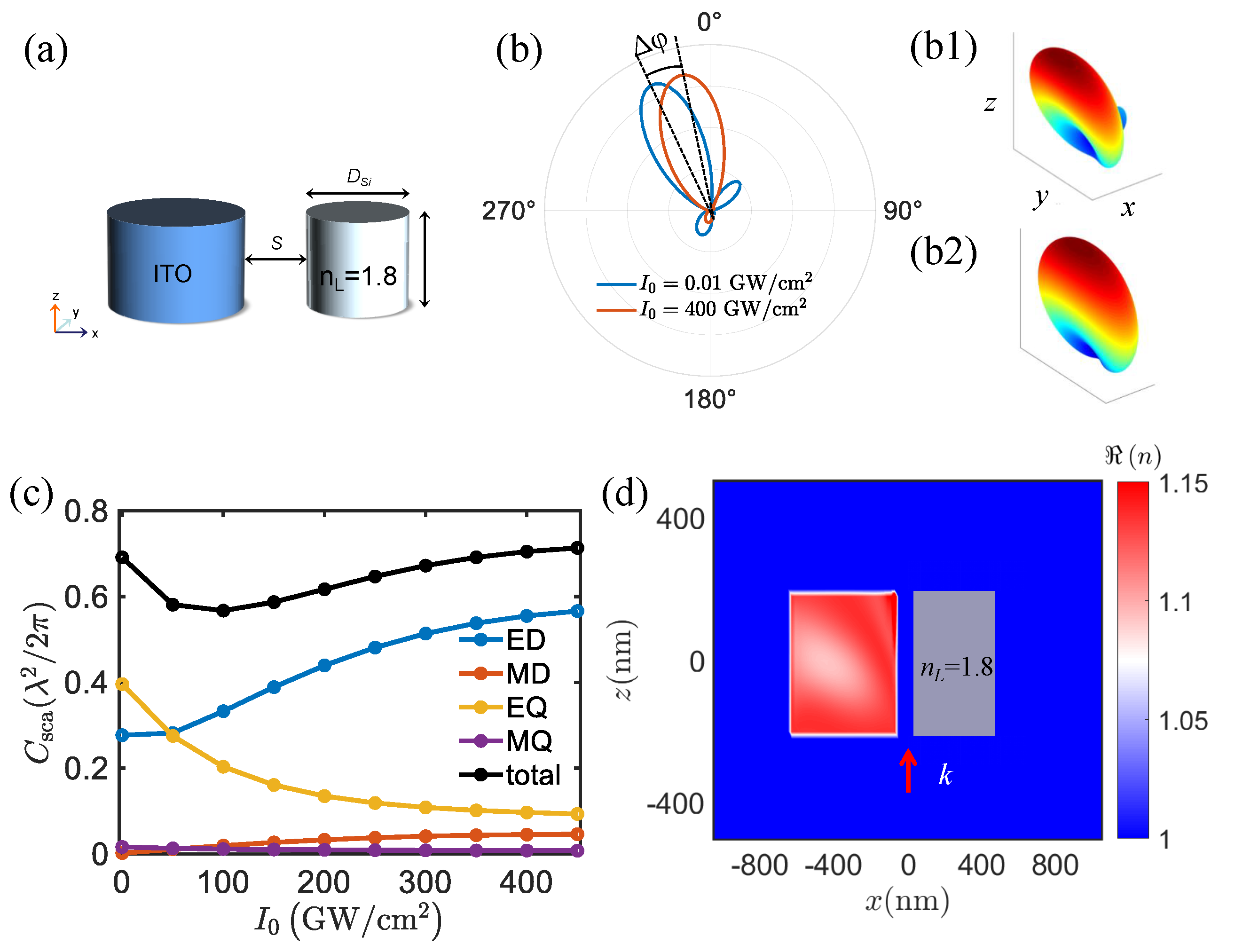
The utilization of high-refractive-index dielectric materials with low loss in antenna design results in a strong electromagnetic response and a significant large scattering cross-section [13,24]. To further enhance control over the scattering properties of ITO antennas, we propose a nonlinear antenna composed of both ENZ and lossless dielectric materials. By incorporating a high-refractive-index material ($n_L$=1.8) and ITO nanodisks, a hybrid antenna is created to dynamically adjust the deflection and beamwidth angle of the radiation pattern. The optimized configuration consists of ITO ($D_{ITO}=600$ nm, $H_{ITO}=400$ nm) and dieletric material ($D_L=400$ nm, $H_L=400$ nm) with a separation distance of 100 nm, as depicted in Figure 2a. The dispersion angle in the $xz$ plane, denoted as $\Delta \phi$, is illustrated in Figure 2b. When the incident intensity gradually increases from $I_0=0.01$ $\mathrm{GW}/{\mathrm{cm}}^2$ to $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$, the radiation main lobe undergoes noticeable deflection, and the deflection angle $\Delta \varphi$ is ${16}^{\circ }$. The corresponding 3D radiation patterns calculated using Equation (4) are presented in Figure 2(b1,b2). The varying intensities lead to a difference in the multipole moments, resulting in intensity-dependent magneto-electric coupling (see Figure 2c). Specifically, as the intensity increases, the contribution of the ED moment gradually increases, while the EQ moment decreases. The MD and MQ remain constant in the scattering cross-section. The induced ED, MD, EQ, and MQ moments interfere constructively (destructively), thereby altering the radiation pattern, as observed in Figure 2b. In comparison with other methods of adjusting the angle size [25], our approach offers the advantage of achieving the deflection angle solely by changing the light intensity, with a maximum change of ${17}^{\circ }$ in the deflection angle. Additionally, in Figure 2d, we present the real part of the refractive index of the hybrid antenna in the $xz$-plane when $I_0=400$ $\mathrm{GW}/{\mathrm{cm}}^2$. The refractive index is position-dependent, influenced by the nonuniform electric field distribution within the antenna and the coupling effect between ITO and linear dielectric material.

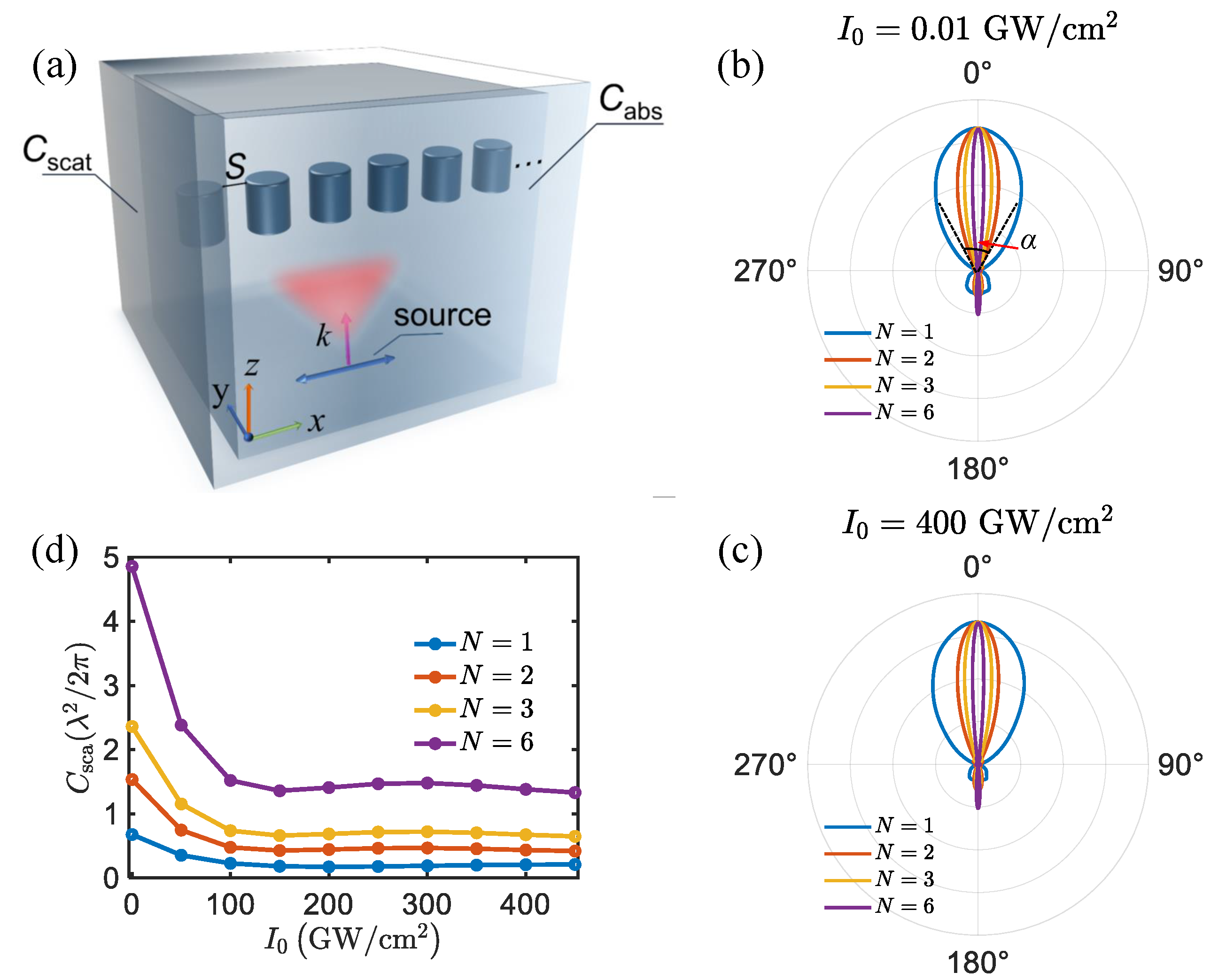
Figure 3a schematically illustrates a linear chain of ITO disks aligned along the x-axis. The normalized radiation patterns for different quantities of ITO disks are presented in Figure 3b and c at $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ and $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$, respectively. As the number of ITO disks increases, the width of the main lobe in radiation decreases. This trend is observed in both cases. Specifically, the angular beamwidth of the main lobe, denoted as $\alpha$, decreases from ${61.75}^{\circ }$ to $8^{\circ }$. This reduction indicates reduced energy leakage in the undesired directions, attributed to the constructive interference among dominant multipolar moments. The sharp angular beamwidth $\alpha$ of the main lobe signifies improved scattering directivity. Further increasing the number of ITO disks does not yield significant changes in the radiation pattern. The main lobe progressively achieves a high level of directivity, with ($\alpha$ approaching $3^{\circ }$) as more pairs of nanodisks are added. Consequently, the scattering cross-section increases with the the number of ITO disks, as demonstrated in Figure 3d.

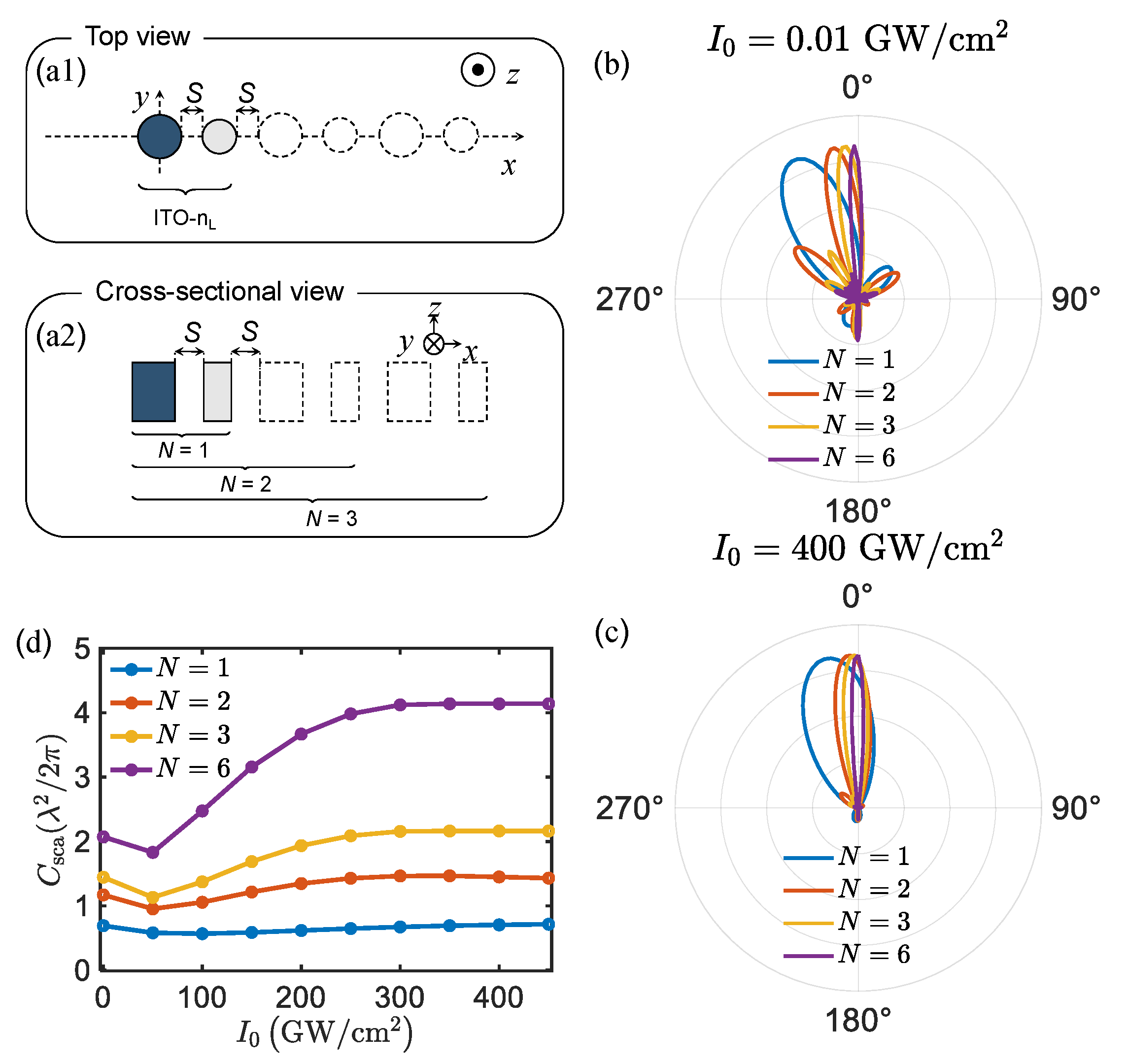
Finally, the influence of the number of hybrid structures on the radiation pattern is investigated, schematically illustrated in Figure 4(a1,a2). The radiation patterns are shown in Figure 4b,c at $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ and $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$ in the XZ plane, respectively. The deflection of 3D radiation patterns is prominent in the XZ plane. A larger deflection is apparent for $I_0=0.01$$\mathrm{GW}/{\mathrm{cm}}^2$ when compared to $I_0=400$$\mathrm{GW}/{\mathrm{cm}}^2$. The deflection starts lowering for intensities larger than $0.01$$\mathrm{GW}/{\mathrm{cm}}^2$. Here, we only pay attention to the variation in the XZ plane. For $N=1,2,3$, and 6, the deflection angle $\Delta \phi$ in the $xz$ plane is ${16}^{\circ },6^{\circ }$, ${4.5}^{\circ }$, and ${1.5}^{\circ }$ from $I_0=0.01$ $\mathrm{GW}/{\mathrm{cm}}^2$ to $I_0=400$ $\mathrm{GW}/{\mathrm{cm}}^2$, respectively. The main lobe angular beamwidth $\alpha$ is significantly reduced as N increases. When $N\ge 2$, the influence on its deflection angle is reduced. To realize a practical application, at least six groups of hybrids are to be integrated into one design after simulation. Generally, the radiation pattern response, such as the main lobe and deflection angle, of the finite structure will sustain a tunable response comparable to that of the ideal periodic structure. Therefore, it is possible to form micro-scale units with the proposed d design. Significantly, when adding the hybrid group, the variation in the deflection angle gradually becomes smaller as the input intensity increases. The scattering cross-section will increase as the number of hybrid antennas increases, as shown in Figure 4d. The 400 $\mathrm{GW}/{\mathrm{cm}}^2$ is very high and difficult to achieve practically. In fact, the refractive index does not change much after the intensity exceeds 100 $\mathrm{GW}/{\mathrm{cm}}^2$.

4. Conclusions

In conclusion, we have presented a novel approach for achieving an active control over the deflection angle of the radiation pattern using ENZ material. Initially, we investigated the influence of incident light intensity on the radiation pattern of a single ITO structure, leveraging its strong Kerr effect. By comparing the results with the single ITO case, we then proposed a structured hybrid nano-antenna that exhibits distinct radiation patterns, accompanied by a dispersion angle of ${17}^{\circ }$ as the light intensity increases. Furthermore, as the number of ITO or hybrid antenna groups is increased, the width of the radiation main lobe decreases, offering potential application in light beam directivity control. Notably, the addition of hybrid antenna groups leads to a reduction in the deflection angle as the intensity increases. These actively tunable nanoantennas introduce a new degree of freedom for controlling the far-field radiation pattern based on the significant Kerr effect of ENZ materials.