A Polarimetric Fiber Ring Laser Incorporating a Coupled Optoelectronic Oscillator and Its Application to Magnetic Field Sensing

Abstract

A novel configuration for a polarimetric fiber ring laser incorporating a coupled optoelectronic oscillator (COEO) is proposed and experimentally demonstrated, and its application to magnetic field sensing is studied. The COEO-based polarimetric fiber ring laser has two mutually coupled loops: the fiber ring laser loop and the OEO loop. In the fiber ring laser loop, longitudinal modes break up into orthogonal polarization modes because of birefringence. The frequency of the polarization mode beat (PMB) signals is determined by the cavity birefringence. In the OEO loop, a microwave signal with its frequency equal to the PMB signal is generated. By feeding the oscillation mode to modulate the optical loop, mode-locking can be achieved, rendering the mode spacing of the laser equal to the frequency of the oscillating OEO mode. We can estimate the birefringence variation by measuring the oscillating frequency of the COEO. To validate the proposed sensing system, a circular birefringence change is introduced in a magneto-optic crystal via the Faraday rotation effect. Then, the magnetic field sensing is implemented. Such configuration can achieve single longitudinal oscillation and realize high-speed and high-precision measurements.

1. Introduction

Fiber laser sensors have received extensive interest owing to their unique merits of high sensitivity, compact size, low cost, and immunity to electromagnetic interference [1,2]. They have greatly contributed to the development of various sensing applications, such as temperature [3,4], strain [5,6], pressure [7,8], acoustic wave [9,10], magnetic field [11,12], and so on. Based on the operation principle, the fiber laser sensor can be categorized into two types: wavelength encoding fiber laser sensor and polarimetric fiber laser sensor. The former one is to transfer the measurand into a corresponding change in the laser wavelength. The sensing information can be obtained by monitoring the wavelength shift. In this category, the optical spectrum analyzer is employed mostly to interrogate the sensing information. The high resolution is achieved at the sacrifice of the interrogation speed. The latter one depends on the polarization mode beat signals (PMB) which are generated from two orthogonal polarization modes. When the physical parameters vary, the beat frequency shifts since the perturbation will induce the change in cavity birefringence. Compared with the former one, the information extraction of the latter one is much easier and simpler due to the conversion of the sensing signal from the optical domain to the radiofrequency (RF) domain. The expensive wavelength interrogation equipment is replaced by a photodetector (PD) and high-speed electrical processing equipment. The interrogation resolution and speed are greatly improved. In 1993, the polarimetric fiber laser sensor was firstly proposed [5]. During recent years, polarimetric fiber laser sensors have been widely adopted to measure many physical measurands, for instance, temperature change [13], twist [14], magnetic field [15], and so on. However, one of the main drawbacks with these polarimetric fiber laser sensors is that the multiple oscillation laser mode output causes instability of the PMB signal and is not appropriate for multiplexing. Single-longitudinal mode operation by reducing the cavity length can significantly improve the stability of the output signal [13]. An ultra-short polarimetric fiber laser (8.4 mm) achieves a stable single-longitudinal oscillation. Another difficulty is the wavelength selection component. The lasing wavelength is selected by using a fiber Bragg grating (FBG), which is easily influenced by the environmental disturbance.

Recently, the fiber optical sensors combining microwave photonics (MWP) have attracted extensive research, contributing to new potentials in various sensing applications [16]. Optoelectronic oscillator-based sensors have been regarded as one of the most promising techniques to realize high resolution and resolution measurement, which have been used for temperature sensing [17], stress sensing [18], distance measurement [19], frequency measurement [20], magnetic field sensing [21], and so on. A coupled optoelectronic oscillator (COEO) is a combination of an OEO and a mode-locked laser sharing one electro-optical modulator. The COEO can be regarded as a mode-locked laser, which is improved by the OEO loop [22]. The OEO loop generates microwave oscillation. While the laser loop produces short optical pulses at the rate of the OEO oscillation frequency. Due to the coupling, the low-noise characteristic of the OEO loop can be transferred to the laser loop. The COEO can generate high-frequency microwave signals and optical pulses with high quality simultaneously [23,24], which is suitable for high precision measurement. An effective RF Q factor exceeding 10⁶ at 10 GHz has been reported [25,26]. The optical pulse can be adopted to accomplish dynamic measurement. A polarimetric fiber ring laser incorporating a COEO can resolve the above mentioned problem about the instability induced by multiple frequency components and wavelength selection component. Up to now, there is little literature on polarimetric fiber ring laser based on COEO and its application with regard to sensing. Among the various physical quantities that can be measured through monitoring the change in the birefringence, the magnetic field is an important parameter in navigation, disaster forecast, data storage, medical facilities and national defense [16]. Traditional electronic techniques, such as Hall-effect sensors [27], anisotropic magneto-resistive sensors [28], superconducting quantum interference device magnetometers [29] and so on, have the drawbacks of bulky structure, complicated operation, and high cost limit in the application field, especially some measurements in small spaces. The popular technique to implement optical fiber magnetic sensors is using material coating [11], such as magneto-optical material [30,31] and magnetic fluid [32,33]. Transferring the interrogation from the optical domain to the microwave domain can improve interrogation resolution and speed.

In this paper, we have proposed and experimentally demonstrated a polarimetric fiber ring laser incorporating a COEO and its application to magnetic field sensing. The proposed system has two mutually coupled loops: the fiber ring laser loop and the OEO loop. In the laser loop, cavity birefringence would generate orthogonal polarization modes, which determine the frequency of polarization mode beat signals (PMB). In the OEO loop, a microwave signal, the frequency of which is equal to the PMB signal, is also generated. By feeding the oscillation mode to modulate the optical loop, mode-locking can be achieved. Such a configuration can achieve single longitudinal oscillation. The instability of the PMB signal can be solved. Due to the coupling, the low noise characteristic of the OEO loop can be transferred to the laser loop. The high spectrum purity and high stability of the generated microwave signal can be used to implement high speed and high-resolution magnetic field sensing with high stability and accuracy. The proposed scheme can be applied to other sensors, such as temperature and refractive index sensors. Moreover, the COEO can generate optical pulse, the pulse period of which is influenced by the sensing parameters. The system can also be used in dynamic measurement.

2. Materials and Methods

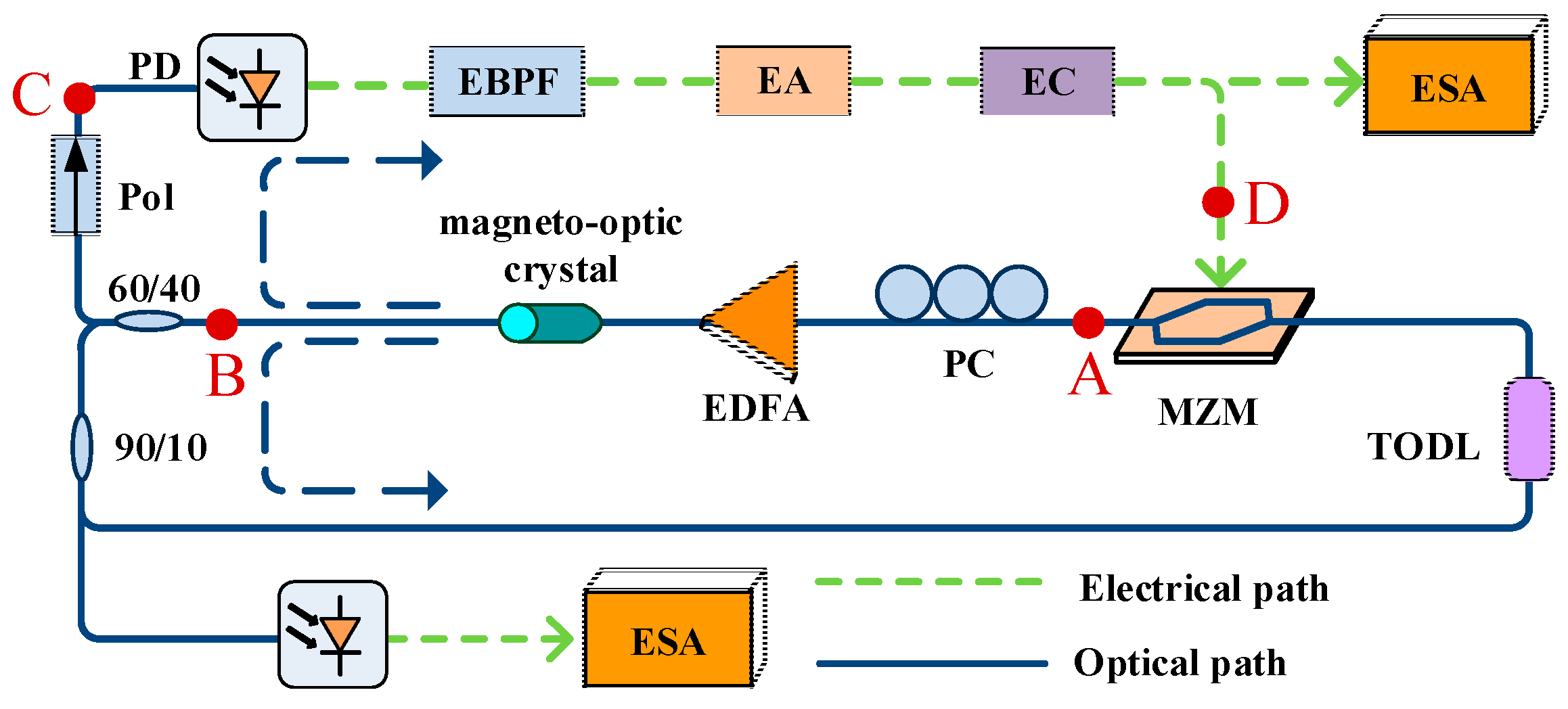
The schematic diagram of the proposed polarimetric fiber ring laser incorporating a COEO is demonstrated in Figure 1. As can be seen, the system has two feedback loops: the mode-locked laser loop and the OEO loop. A path consisting of a Mach-Zehnder modulator (MZM), a magneto-optic crystal, and an erbium-doped fiber amplifier (EDFA) is shared by two loops. The fiber laser loop contains an MZM, an EDFA, a magneto-optic crystal, a polarization controller (PC), a tunable optical delay line (TODL), a 60/40 optical coupler (OC) and a 90/10 OC. The MZM is polarization-dependent, which supports intensity modulation only along one polarization direction. The PC is placed to adjust the polarization state of light. The TODL is used to improve mode-locking efficiency by tuning the length of two loops to match.

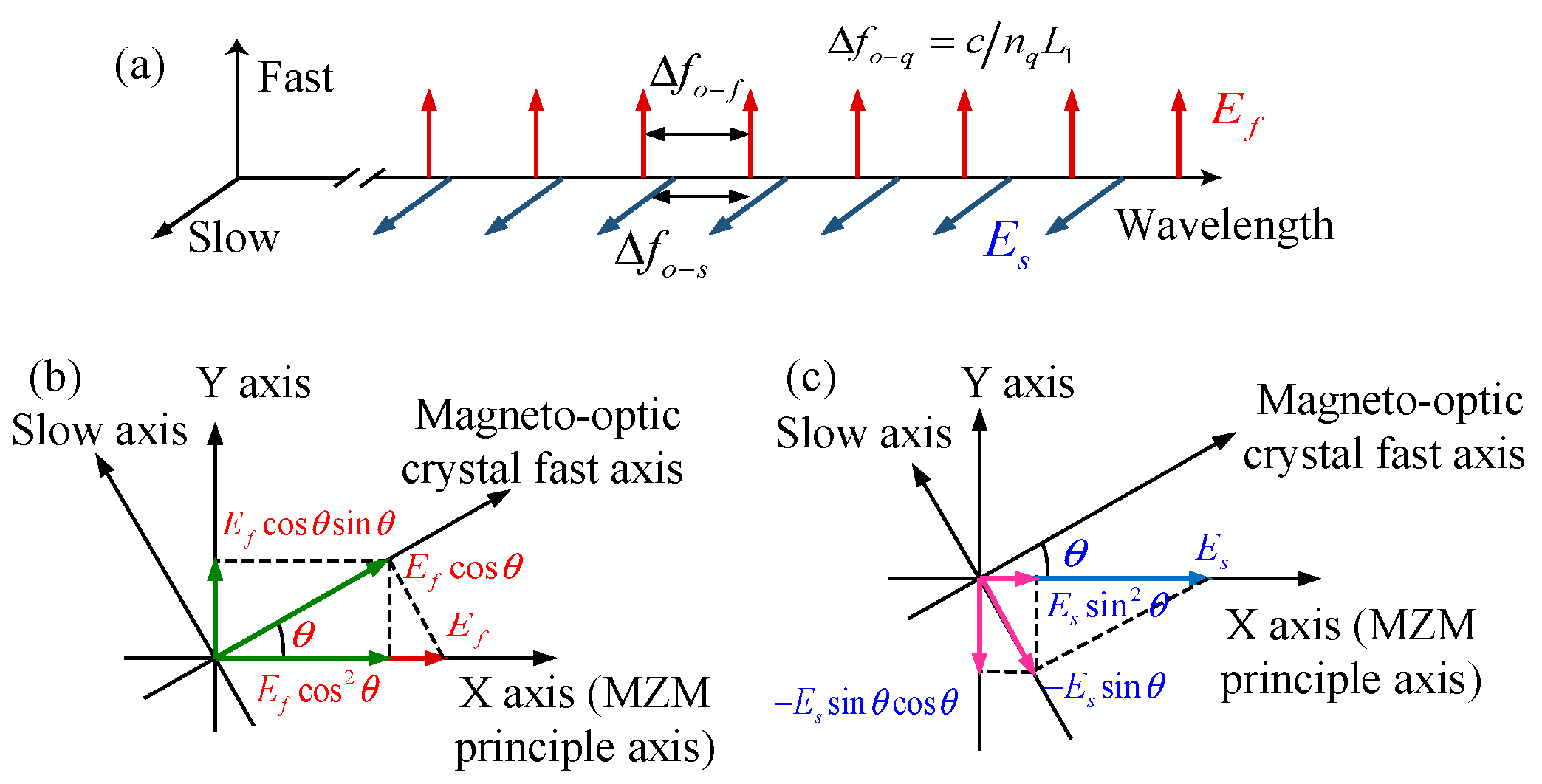
The magneto-optic crystal introduces additional birefringence into the cavity, rendering the refractive index along the two principal axes slightly different. The same longitudinal mode breaks up into two eigenpolarization modes, as shown in Figure 2a. The optical field of the orthogonal polarization modes are $E_f$ and $E_s$ (the slow and fast axes are determined by the magneto-optic crystal). The mode spacing is

$$\Delta f_{o-q}=\frac{c}{n_q{L}_1},\hspace{1em}q=f,s$$

(1)

where c is the speed of light in vacuum; n_q is the refractive index of the fast/slow axis; and L₁ is cavity length of the laser loop.

Suppose that the light at point A in Figure 1 is the summation of the orthogonal polarization modes, it can be expressed by a Jones vector. Since the MZM is a polarization dependent device, only the x-axis (the principal axis of the MZM) can be modulated. The light along the y-axis, which will suffer much more loss, cannot be mode-locked. Therefore, the components in the Jones vector along the y-axis can be ignored. The optical field at point A can be described as

$$E_A=\left[\begin{array}{c}{E}_f\\ 0\end{array}\right]+\left[\begin{array}{c}{E}_s\\ 0\end{array}\right]$$

(2)

The light is linearly polarized and sent to the magneto-optic crystal. The polarization direction of the incident light (along x-axis of the MZM) oriented at an angle of $\theta$ with respect to the fast axis of the magneto-optic crystal by adjusting the PC. As seen from Figure 2b, for the light $E_f$, they can be divided into two orthogonal components according to the slow and fast axes of the magneto-optic crystal. One is along the fast axis of the magneto-optic crystal, which is still satisfied with the resonant condition. The other component that is projected to the slow axis is not satisfied and fades away. For the light $E_s$, the component that is projected to the slow axis of the magneto-optic crystal remains and the component projected to the fast axis vanishes as shown in Figure 2c. Therefore, the optical field after the magneto-optic crystal at point B is expressed as

$$E_B=\left[\begin{array}{c}{\cos }^2\theta E_f\\ \cos \theta \sin \theta E_f\end{array}\right]+\left[\begin{array}{c}{\sin }^2\theta E_s\\ -\sin \theta \cos \theta E_s\end{array}\right]$$

(3)

The OEO loop is formed by an MZM, an EDFA, a magneto-optic crystal, a polarizer (Pol), a photodetector (PD), an electrical band pass filter (EBPF), an electrical amplifier (EA) and an electrical coupler (EC). The light extracted from the laser loop via 60/40 OC is sent to the PD through a Pol. The principal axis of the Pol has an angle of $\varphi =\theta -\pi /4$ relative to the principal axis of the MZM, as shown in Figure 3. The signal after the Pol at the point C is given by

$$E_C=\left[\begin{array}{cc}\cos \left(-\varphi \right)& -\sin \left(-\varphi \right)\\ 0& 0\end{array}\right]E_B\left|{}_{\varphi =\theta -\pi /4}\right.=\frac{\sqrt{2}}{2}\cos \theta E_f+\frac{\sqrt{2}}{2}\sin \theta E_s$$

(4)

After converting the optical signal to the electrical signal by the PD, the ac component of the photo current at point D is

$$I_{PD}=\Re {\left|E_C\right|}^2=\frac{1}{2}\Re \sin 2\theta E_f{E}_s$$

(5)

where $\Re$ is the responsibility of the PD.

The optical signals $E_f$ and $E_s$ are a series of longitudinal modes, which can be expressed as

$$\begin{array}{l}{E}_f=\left|E_f\right|\cos \left({\displaystyle \sum _{N=0}^{\infty }N2\pi \Delta f_{o-f}t}\right)\\ E_s=\left|E_s\right|\cos \left({\displaystyle \sum _{M=0}^{\infty }M2\pi \Delta f_{o-s}t}\right)\end{array}$$

(6)

Applying Equation (6) to Equation (5), the photo current can be rewritten as

$$I_{PD}=\frac{1}{4}\Re \left|E_f{E}_s\right|\sin 2\theta \cos \left[2\pi {\displaystyle \sum _{N,M=0}^{\infty }\left(N\Delta f_{o-f}-M\Delta f_{o-s}\right)t}\right]$$

(7)

As seen from Equation (7), the frequency of the detected microwave signal is the frequency of the polarization mode beat (PMB) signal which is generated by multi-longitudinal modes of different polarization directions. Equation (7) can be written as

$$I_{PD}=\frac{1}{4}\Re \left|E_f{E}_s\right|\sin 2\theta \cos \left(2\pi f_{PMB}t\right)$$

(8)

The same longitudinal mode breaks up into two eigenpolarization modes because of the cavity birefringence shown in Figure 4a. After optical-to-electrical conversion, the longitudinal modes will beat. Seen from Figure 4b, the beating signals can be classified into linear mode beat signals (LMB), which are generated from the same polarization, and PMB signals. The frequency of the LMB $f_{LMB}$ can be given by

$$f_{LMB}=\frac{\left(N-M\right)c}{n_0{L}_1}=\frac{pc}{n_0{L}_1}$$

(9)

where $p$ is the mode number; $n_0$ is the average refractive index.

For lasers with a sufficiently small birefringence, the frequency of PMB can be described as [2,11,14]

$$f_{PMB}=f_{LMB}\pm q{v}_B=f_{LMB}\pm \frac{qcB}{n_0^2{L}_1}$$

(10)

where $v_B=cB/n_0^2{L}_1$; $q$ is the mode number; $B=n_f-n_s$ is birefringence of the cavity, and $n_f$ and $n_s$ are the refractive indices of the fast and slow axis. The interval of the same order LMB and PMB is $v_B$.

As analyzed above, the oscillating mode frequencies that existed in the OEO loops are the frequencies of PMB. Due to the EBPF, some beating signals will be filtered according to the center frequency and bandwidth of the EBPF. Because of the mode competition in the OEO loop, the mode which achieves the largest gain will oscillation which is demonstrated in Figure 4c. When this oscillation mode is fed to drive the MZM to modulate the gain of the laser loop, mode-locking is achieved. The mode-locking renders the mode spacing of the laser equal to the frequency of the oscillating OEO mode, which is the frequency of the PMB signal shown in Figure 4d. By adopting an appropriate center frequency of the EBPF to match the bandwidth of the PD, single-longitudinal oscillation can be obtained. Owing to the mode-locking, the neighboring modes of the laser have a fixed-phase difference. Their beating signals are all in phase. Hence, the OEO oscillation mode will obtain more power from the laser, and the oscillation is enhanced, as shown in Figure 4e.

Since the LMB is generated from the same polarization longitudinal modes, the frequency of the LMB is independent on the cavity birefringence change. Equations (8)–(10) show that the frequency of the detected RF signal is proportional to the cavity birefringence $B$. Therefore, any perturbation resulting in the birefringence change can be detected by discriminating the oscillation frequency shift. The frequency shift is

$$\Delta f_{osc}=\pm \frac{qcB}{n_0^2{L}_1}$$

(11)

When a magnetic field is applied to the magneto-optic crystal, a weak circular birefringence is induced into the laser through the Faraday effect. Normally, there exists an intrinsic linear birefringence in the cavity. The resultant birefringence of the association of the linear and the circular birefringence is an elliptical birefringence, which is

$$\Omega =\sqrt{{\alpha }^2+{\beta }^2}$$

(12)

When the circular birefringence $\alpha$ is much smaller than the linear birefringence $\beta$, Equation (12) can be approximated to

$$\Omega \approx \beta +\frac{{\alpha }^2}{2\beta }$$

(13)

By applying Equation (13) to Equation (11), the frequency shift $\Delta f_{osc}$ can be related the elliptical birefringence as

$$\Delta f_{osc}=\frac{qc}{n_0^2{L}_1}\left(\beta +\frac{{\alpha }^2}{2\beta }\right)$$

(14)

The circular birefringence induced by the magnetic field can be described as [12]

$$\alpha =2VH$$

(15)

where $H$ is the magnetic field, and $V$ is the Verdet constant.

Equation (11) can be rewritten as

$$\Delta f_{osc}=\frac{qc}{n_0^2{L}_1}\left(\beta +\frac{2}{\beta }{V}^2{H}^2\right)$$

(16)

As can be seen, when the circular birefringence induced by the magnetic field is much smaller than the linear birefringence, the frequency shift is proportional to the square of the magnetic field. However, if the dominant birefringence is the circular birefringence, the frequency shift will be linearly proportional to the magnetic field as

$$\Delta f_{osc}=\frac{qc}{n_0^2{L}_1}\left(VH+\frac{1}{2VH}{\beta }^2\right)$$

(17)

According to Equations (16) and (17), the sensitivity depends on the mode order $q$. The sensitivity can be enhanced by adopting a higher frequency. Moreover, the COEO can generate an optical pulse and RF signal simultaneously, which have a relationship of $T_{osc}=1/f_{osc}$. The magnetic field can also be evaluated from the optical pulse period. In the time domain, the optical pulse period can give not only the strength but also the time information. Therefore, the proposed scheme can be used in the dynamic magnetic field measurement. This part of the study will be performed in our future work.

3. Results

An experiment based on the setup shown in Figure 1 is carried out. The device parameters are as follows: The MZM has a 10 GHz bandwidth and a half-wave voltage of 4.1 V (JDSU X5). The bandwidth of the PD is 2 GHz (CETC). The center frequency and bandwidth of the EF are 942.5 MHz and 40 MHz (Spectrum C942.5-40-6SS). The tunable range of TODL is 300 ps (VDL-001-35-33-SS-FC/PC). The element of magneto-optic crystal is Bismuth substituted Rare-earth Iron Garnet single crystal. The diameter and the length are 4 mm and 25 mm, respectively. The Saturated magnetic field is 700 Oe.

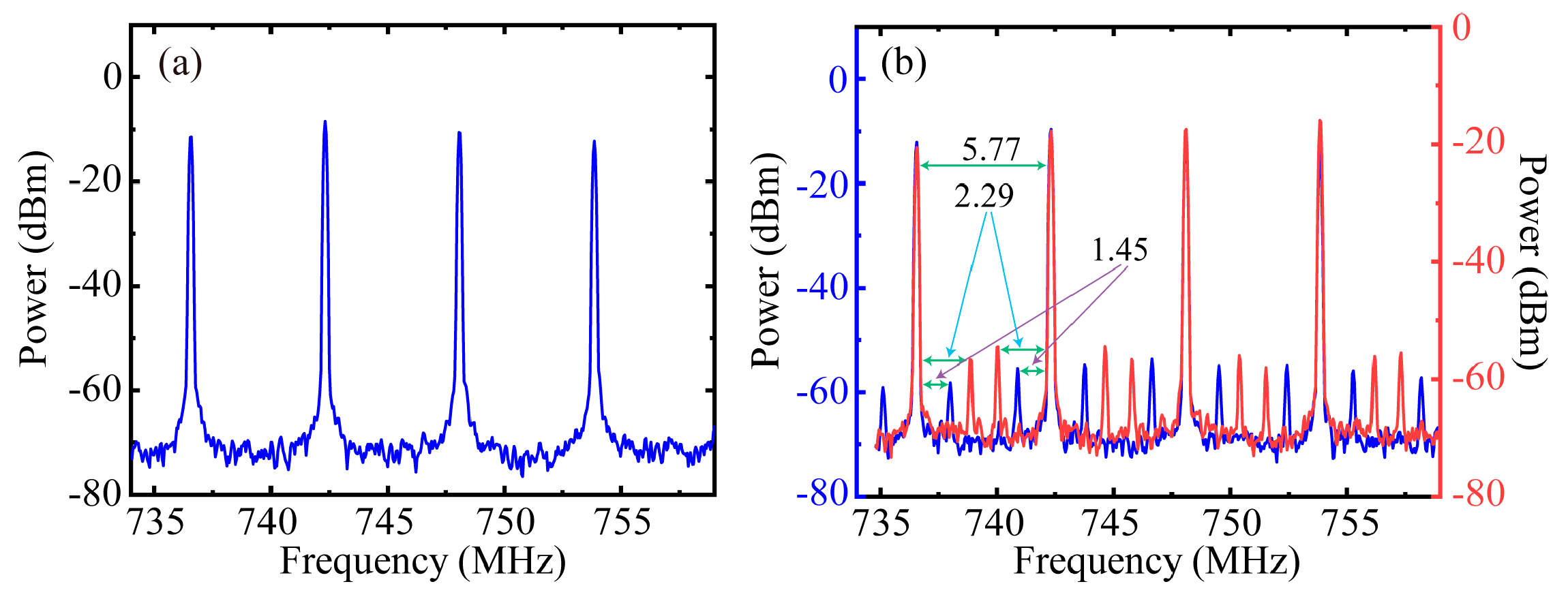
We first study the performance of the polarimetric fiber ring laser without COEO, which acts as a tradition polarimetric fiber laser. The measured RF spectra of the laser beating signals is demonstrated in Figure 5. Because of the cavity birefringence, the same longitudinal mode breaks up into two eigenpolarization modes which are orthogonal. When there is no Pol placed before the PD, only the modes of the same polarization can beat. Hence, there are five different longitudinal modes, which are LMB signals. The mode spacing is 5.77 MHz in Figure 5a, which is consistent with the laser longitudinal mode interval formula (Equation (1), $L\approx 34 \mathrm{m}$). When the Pol is inserted in front of the PD, new beat signals appeared, which are the PMB signals, as seen in Figure 5b, $v_B=1.45 \mathrm{MHz}$. When the magnetic field is applied to the magneto-optic crystal, the frequencies of the PMB signals vary, $v_B=2.99 \mathrm{MHz}$. Since the applied magnetic field increases the cavity birefringence $B$, $v_B$ shifts to a larger frequency. While the frequencies of the LMB signals have no relationship with the birefringence, they remain unchanged, which is in agreement with the theoretical analysis. As seen from Figure 5, the output of the polarimetric fiber ring laser without COEO is multiple oscillation laser modes which will cause instability of the PMB signal and is not appropriate for multiplexing.

Then, we investigate the performance of the polarimetric fiber ring laser incorporating the COEO. We firstly study the output of the laser. Since mode-locking is achieved, we can achieve the optical pulses shown in Figure 6a via a digital sampling oscilloscope. The measured pulse period is 1.08 ns, and the pulse width is 22.49 ps. The optical spectrum of the pulses measured has a bandwidth of 0.378 nm which is shown in Figure 6b. For comparison, we measure the optical spectrum of the laser without optoelectronic oscillation. The bandwidth is 0.108 nm. As can be seen, the spectrum has been broadened effectively. This is because of the oscillation mode of the OEO, which is feeding back to the MZM to modulate the gain of the laser loop. Once the mode-locking is achieved, all the oscillating modes in the ring laser are forced in phase and the mode spacing of the laser changes to the frequency of the oscillating OEO mode. The OEO oscillation mode will obtain more power from the laser, and the oscillation is enhanced. Hence, the optical spectrum will be broadend and the optical pulse is obtained.

Figure 7a shows the RF signal by detecting the optical pulses. Compared with Figure 4, we can know that the polarimetric fiber ring laser incorporating COEO has achieved single longitudinal oscillation. This is because of the mode spacing of the laser change to the frequency of the oscillating OEO mode, which is a multiple of the natural mode spacing of the laser. Since the center frequency of the EF and the bandwidth of the PD are 942.5 MHz and 2 GHz, only one oscillation mode be can retained. The signal frequency is 956.04 MHz. The supermode suppression ratio is 31 dB. The measured electrical spectrum of the RF signal from the OEO loop is demonstrated in Figure 7b. The signal frequency is 959.493 MHz. The sidemode suppression ratio of the RF signal is 47 dB. The sidemode suppression ratio is high. This is becausethe two feedback loops of COEO can guarantee the high quality of the generated microwave signal. There is no need to place a long length fiber to increase the Q value. The length of the optoelectronic cavity is relatively short (~27 m) and the mode spacing is large (~7.4 MHz). Owing to the narrow bandwidth of EBPF, the sidemodes can be easily removed which increase the sidemode suppression ratio. The RF signal from the OEO loop is adopted as the tracking signal on account of it havingthe higher sidemode suppression ratio.

We explore the capacity of the magnetic sensor. The magnetic field strength is from 0 to 640.7 Oe. The measured frequency responses of the COEO under different magnetic field strengths are demonstrated in Figure 8a. With the increment of magnetic field strength, the oscillation frequency shifts toward a lower frequency, which is in agreement with Equation (11). Figure 8b depicts the measured oscillation frequency as a function of the magnetic field strength. The frequency shift is proportional to the square of the magnetic field, which coincides with Equation (16). Because the dominant birefringence is the linear birefringence, the circular birefringence is very small. The frequency shift is proportional to the square of the magnetic field. The R² coefficient of determination is 0.997, indicating that the regression line fits the data well. We also study the accuracy of the magnetic sensor. Figure 8c illustrates the measured magnetic field as a function of the applied magnetic field and the measured errors. The maximum error is 10.8 Oe.

The stability of the oscillation frequency is a critical parameter for high-precision measurement. Hence, we set the proposed sensor to operate at room temperature for a period of 120 min. The frequency is recorded for 120 min with a step of 5 min, which is shown in Figure 9. The maximum frequency drift of the COEO is within ±145 Hz, which corresponds to a measurement error of ± 1.44 Oe.

4. Discussion

As seen from Figure 8, the sensitivity is not high, which is mainly due to the low Verdet constant of the magneto-optic crystal. Therefore, magneto-optic crystal or active fibers with a high Verdet constant can greatly improve the sensitivity. According to Equation (16), the sensitivity is undermined by the large intrinsic linear birefringence inside the laser cavity. The intrinsic birefringence can be artificially lowered [12] so that the sensitivity can be enhanced and tuned. Furthertmore, the sensitivity depends on the mode order $q$ of the oscillation frequency. The sensitivity can be enhanced by adopting a higher frequency.

The system stability may be affected by the environmental perturbations which cause the mode hopping in the laser cavity as well as the oscillating frequency. To solve the problem, several methods can be adopted to suppress the supermodes, such as narrowband filters [34], a nonlinear polarization rotation effect [35], unpumped erbium-doped fiber [36], and so on.

For fiber-optic magnetic field sensors, the problem of cross sensitivity is always desired to be solved, such as stress, vibrations, temperature and so on, but frequently difficult to realize. For magneto-optic crystal, the size of which is small (the diameter and the length are 4 mm and 25 mm), the same problem still exists. However, small size means that the implementation of disturbance-immune packages can be fairly easy. Moreover, because of single longitudinal oscillation, multiplex can be exploited for multiparameter measurements by multiplexing several sensors for measurement. The problem of cross-sensitivity among measurands is automatically solved via matrix manipulations in mathematics. Therefore, the proposed method is flexible and agile, which has great potential in many applications.

5. Conclusions

In conclusion, a novel configuration for a polarimetric fiber ring laser incorporating a COEO is proposed and experimentally demonstrated, and its application to magnetic field sensing is studied. With the magnetic field applied to the magneto-optic crystal, an additional birefringence is introduced into the cavity through the Faraday rotation effect, which affects the frequency of the PMB signal. The oscillation frequency of the COEO is equal to the frequency of the PMB signal. By feeding the output signal of the COEO to modulate the laser, single-mode oscillation can be achieved. Moreover, we can estimate the magnetic field by measuring the oscillating frequency of the COEO. Since the fundamental concept of this COEO-based sensor is transforming the additional birefringence into the oscillation frequency shift, the proposed scheme can be applied to other sensors with high speed and high resolution, such as torsion sensors, refractive index sensors, and so on. The proposed scheme has potential application for dynamic magnetic field sensing.