High-Efficiency Second-Harmonic Generation Using Quasi-Bound State in LiNbO₃ Metasurface

Abstract

We numerically demonstrated a high-efficiency second-harmonic generation (SHG) using quasi-bound state in the continuum (quasi–BIC) in thin film LiNbO₃ (TFLN) metasurface. The TFLN possessed exceptionally high second-order nonlinear coefficients, contributing to the enhanced SHG performance. An eccentric cylinder unit cell was presented to achieve high Q–factor resonances associated with the asymmetric parameter introduced. Simulations showed that the high efficiency of the second-harmonic conversion was obtained by using the high Q–factor of the asymmetric dielectric cylinder metasurface, and it achieved a high SHG efficiency of 6.5% at pump intensities as low as 1 MW/cm² at a normal incident. Furthermore, the simulation results indicated that breaking the symmetry through oblique incidence was more effective in achieving a higher Q–factor compared to altering the structural parameters. Specifically, under 1° oblique incidences, the conversion efficiency could reach 1.2% at an incident power of 1 kW/cm². We have proposed a method to achieve a high conversion efficiency of second-harmonic generation in low-refractive-index materials. Our work not only offers theoretical support but also provides valuable insights for the advancement of efficient nonlinear frequency doubling technology, optical communication, and sensing applications.

1. Introduction

Second–harmonic generation (SHG) is a fundamental process in nonlinear optics, exhibiting significant importance in diverse domains such as optical communication, spectroscopy, signal processing, image processing, and laser technology [1,2,3,4,5,6]. Originally observed by Franken et al. [7], SHG involves the nonlinear scattering process where two photons at the fundamental frequency combine to generate a photon with double the frequency [8]. However, conventional SHG techniques rely on complex phase matching utilizing bulk crystals to enhance the weaker nonlinear effects [2], which imposes limitations on its broad applicability. To overcome these limitations, researchers have recently focused on the investigation of nonlinear micro–nano metasurfaces, which obviate the requirement for phase matching and enable device miniaturization and compactness [9,10]. Nevertheless, the reduced dimensions of these micro and nano structures pose challenges in achieving sufficient interaction length between the super-surface and incident light. In such structures, the generation of second-order nonlinear effects heavily relies on the local enhancement of electric and magnetic fields. Addressing this challenge necessitates the exploration of novel techniques to enhance the interaction between light and the metasurface. Researchers are actively pursuing strategies to optimize the efficiency of SHG processes in micro and nano super-surface structures. The advancement of these techniques holds promising prospects for the advancement of nonlinear optics, facilitating the development of highly efficient and compact photonic devices.

So far, a lot of methods to enhance the nonlinear effects by exploring field enhancement were proposed [3]. Plasmonic nanostructures were used to achieve local field enhancement and to enhance the second-order or higher-order nonlinear effects [11,12,13]. However, their energy was only localized near the metal surface and their own losses were high. Therefore, the plasmonic nanostructures were gradually replaced by dielectric materials [14,15]. Nano–antennas and super surfaces made of high refractive index media have appeared, and the concept of cylindrical metasurface structures has been proposed. They can support Mie resonance, which has a strong ability to confine the electric field, and can localize the optical field in the structure without ohmic loss, instead of localizing the energy at the surface as in plasmonic structures. Thus, high refractive index dielectric materials are promising candidates to generate SHG. In addition, there are some interesting ideas, such as integrating a layer of nonlinear 2D materials [16] (e.g., transition metal sulfides (TMDs) [17], layered GaSe [18], etc.) on the waveguide or super-surface structure, which can have between two and three orders of magnitudes higher second-harmonic intensity compared to that without the integrated 2D materials and can be well applied in harmonic converters. In recent years, there has been a surge of interest in bound states in the continuum (BIC) owing to their distinct physical mechanisms [19,20]. Theoretically, BIC states possess an infinite quality factor (Q–factor), which manifests a dark mode with infinite lifetime because there is no radiation channel for radiation leakage with external electromagnetic waves. However, ideal BIC states do not manifest in reality. Consequently, through the deliberate introduction of specific disturbances, such as adjusting the characteristics of the shape, changing the angle at which the light source hits the surface, or incorporating a refractive index imbalance using different materials, it becomes feasible to transform a BIC into a quasi–BIC state characterized by a significantly high Q-factor. Due to its strong confinement capabilities in both electric and magnetic fields, quasi-BIC states exhibit enhanced interactions between light and matter, resulting in extremely narrow linewidths. Building upon this characteristic, the synergy between BIC and the second harmonic offers a promising avenue for enhancing the efficiency of second-harmonic generation (SHG) [21,22]. Simultaneously, various metasurface structures such as dual ellipses, dual rectangles, split ring resonators, and others have been extensively employed in this field.

Lithium niobate (LiNbO₃) possesses exceptional attributes, including negligible loss, a wide band gap, and high second–order nonlinear coefficients. Moreover, significant advancements have been achieved in the fabrication techniques of lithium niobate, enabling precise control over its structural and optical properties. The material exhibits remarkable transparency within the near-infrared to near–ultraviolet spectral range and can facilitate the realization of various efficient nonlinear effects, such as second harmonic generation (SHG), third harmonic generation (THG), sum frequency generation (SFG), difference frequency generation (DFG), among others. Researchers have employed a structure comprising a lithium niobate cylinder combined with a lithium niobate slab for the generation of second harmonic waves. However, low refractive index dielectric materials are seldom utilized in frequency multiplication technology due to their inherent limitations in field confinement and relatively lower conversion efficiency. The introduction of bound states in the continuum (BIC) waveguides offers intriguing possibilities for harnessing the potential of low refractive index materials to achieve high–efficiency SHG, particularly in the presence of Fano resonances [23]. By capitalizing on the exceptional properties of lithium niobate, its transparency, and the unique advantages offered by BIC waveguides, researchers are unveiling new perspectives for the application of low refractive index materials in the realization of highly efficient SHG processes. This research paves the way for the development of advanced photonic devices with enhanced nonlinear optical functionalities, opening doors to a wide range of applications in fields such as integrated optics, nonlinear optics, and quantum photonics.

In this work, we designed a cylinder composed of thin film LiNbO₃ (TFLN) by combining the high Q–factor and strong field enhancement ability of BIC based on theory and numerical simulation. By defining an asymmetric parameter α to describe the eccentricity of the eccentric cylinder, the relationship between the magnetic dipole (MD) resonance and the BIC/quasi–BIC in symmetric and asymmetric distributions was also revealed. Then, we discuss the influence of the asymmetric parameter α and other parameters on the resonance. To quantitatively analyze the contribution of magnetic dipoles to resonance, we had a multipolar decomposition in Cartesian coordinates, and calculated the scattered power of the far-field multipoles. The high efficiency of second-harmonic conversion was obtained by using the high Q–factor of the asymmetric dielectric cylinder metasurface; it achieved a high SHG efficiency of 6.5% at pump intensities as low as 1 MW/cm². Finally, the oblique incident was investigated for the TFLN metasurface. We demonstrated that breaking the symmetry through oblique incidence offers a more straightforward approach to achieving higher Q–factors than modifying the structural parameters. Furthermore, we have proposed utilizing the high–Q factors generated by quasi-bound states in the continuum (quasi–BIC) and the large nonlinear coefficient of TFLN to effectively enhance the efficiency of second-harmonic generation. Our work can provide theoretical support and ideas for the development of efficient nonlinear frequency doubling technology, optical communication, and sensing.

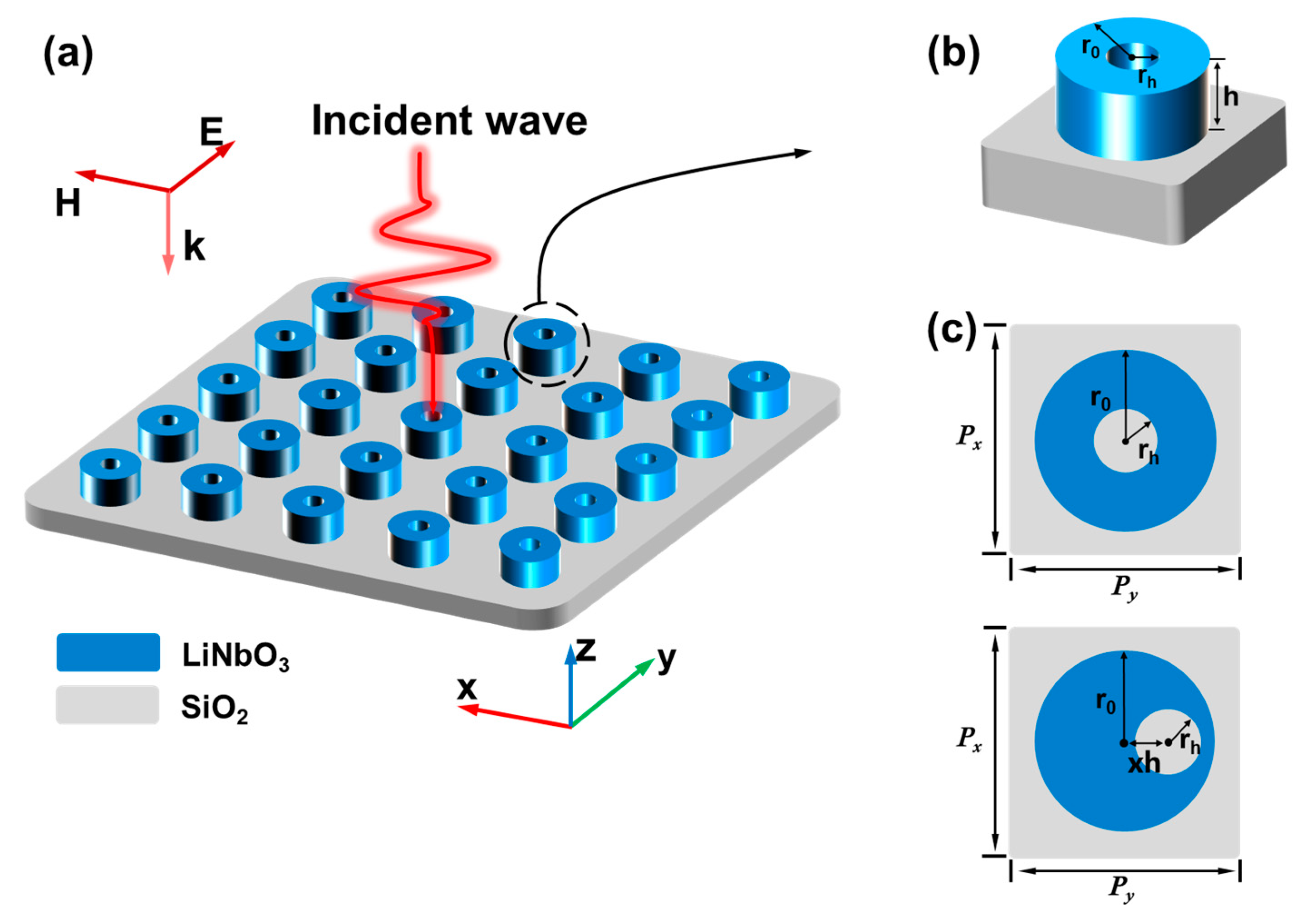
2. Materials and Methods

As shown in Figure 1a, the metasurface was composed of the unit cells with cylinders on a thin film LiNbO₃ (TFLN) deposited silica substrate, where the refractive of silica was nsub = 1.45. The structural parameters of the unit cell are shown in Figure 1b. The lattice constant in the structure was P_x = P_y = P = 700 nm, the outer radius of the cylinder was r₀ = 280 nm, the inner radius of the cylinder was rh = 80 nm, and the height of the cylinder was h = 300 nm. To break the symmetric of this unit cell, an asymmetric parameter α = xh/2r₀ was introduced in this study, where the parameter xh represented the eccentricity of the eccentric cylinder, as shown in Figure 1c. When α = 0, it means that the unit cell is a cylinder and the structure is in a symmetric state in the x–y plane. When α ≠ 0, a symmetry breaking is introduced and the unit cell is an eccentric cylinder, where the inner center is shifted to the right along the y-axis direction. The top view of the unit cell under symmetric and asymmetric states in the x–y plane is shown in Figure 1c, and shows the way the structure breaks symmetry.

The Finite Element Analysis software was used to numerically simulate the spectral response and electromagnetic properties of the proposed metasurface. An y–polarized plane wave propagating along the z-axis was incident on the structure, with periodic boundary conditions in the x and y directions and a perfectly matched layer in the z–direction. To take into account the optical anisotropy of the TFLN [24], the refractive index along the normal optical axis was n_o = 2.2264, and the refractive index along the unusual optical axis was n_e = 2.1506. Aligning the unusual optical axis with the y–axis, we could assume n_o = n_x = n_z = 2.2264 and n_e = n_y = 2.1506.

3. Results and Discussions

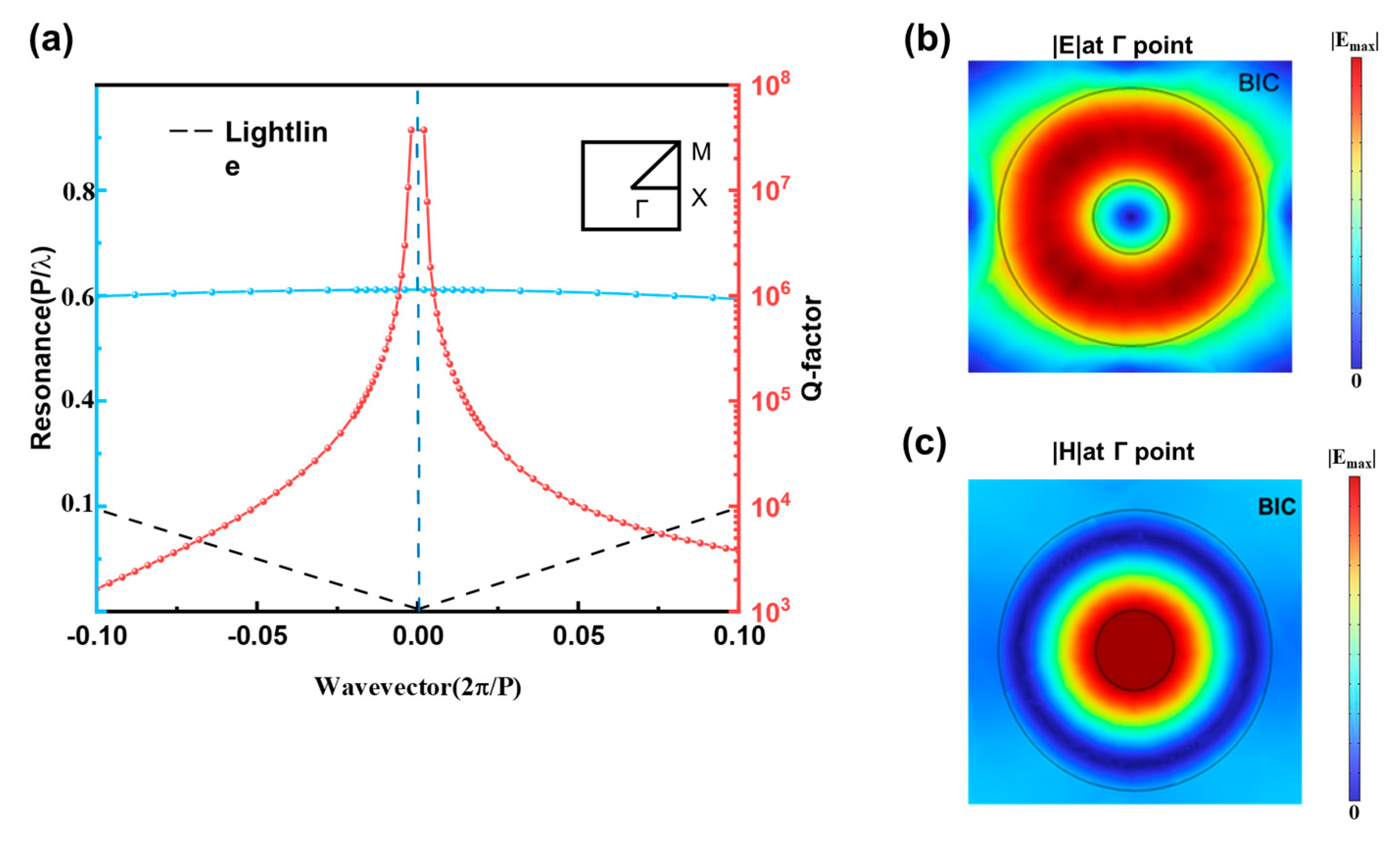
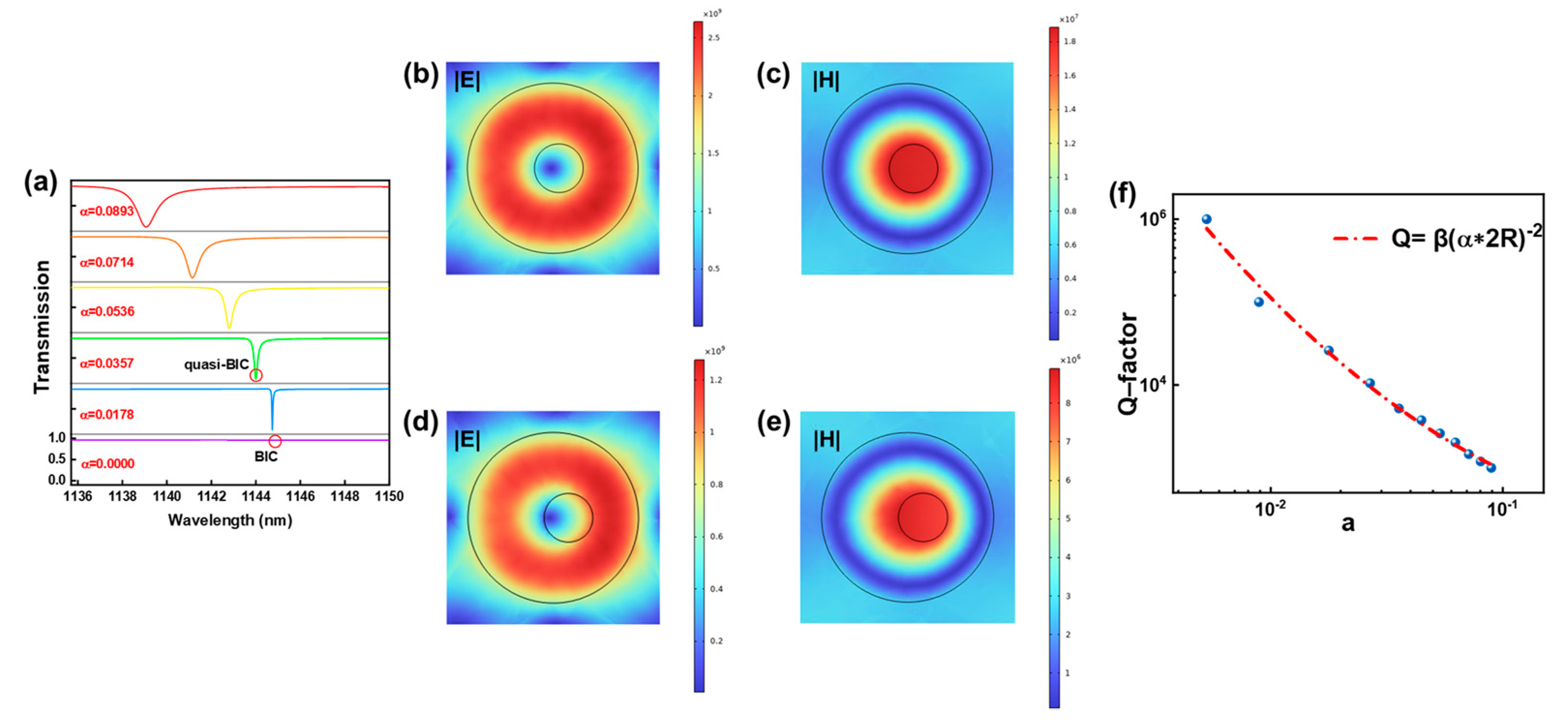
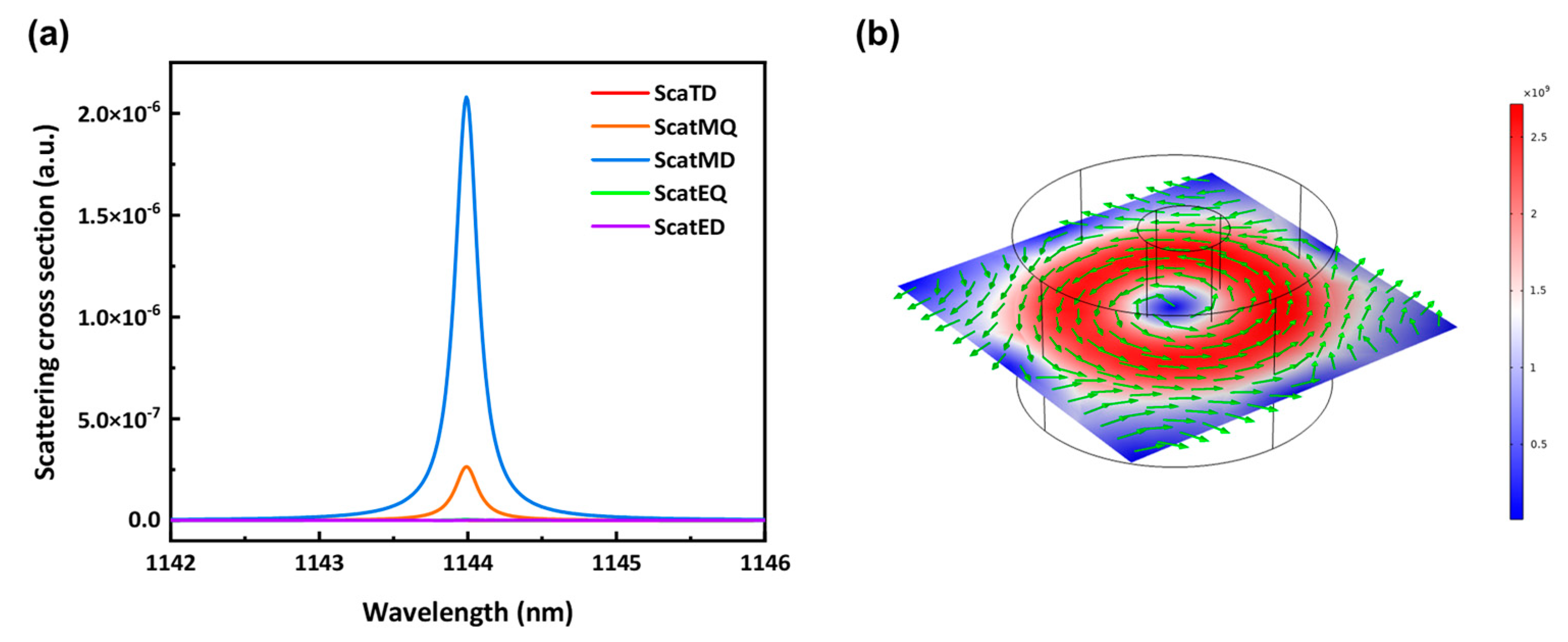
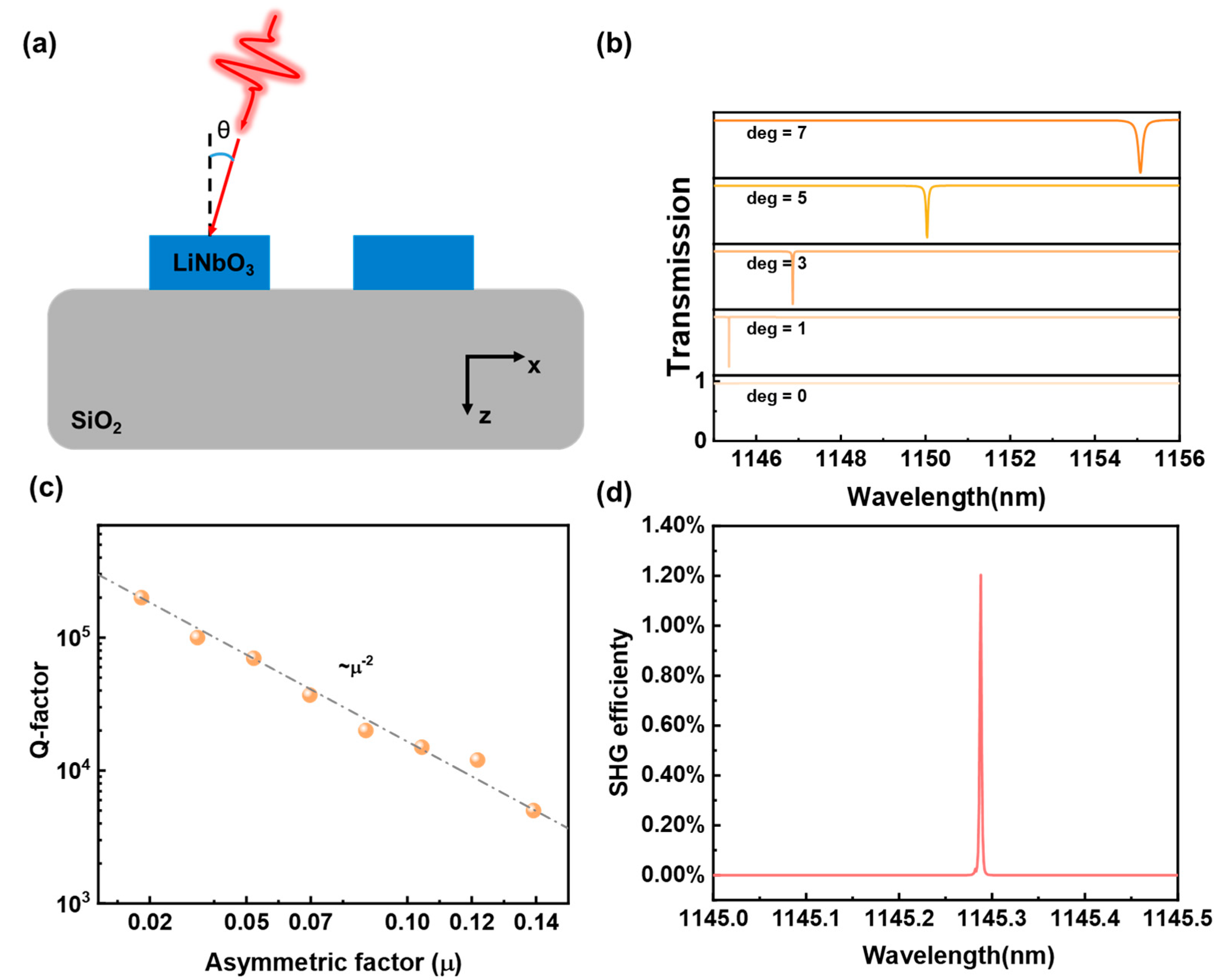
3.1. Characterization of Quasi-BIC by Changing α

To understand the properties of the BIC states that appeared in the structure, we analyzed the eigenmode distribution characteristics near the Γ point and the theoretical values of the Q–factor in the k–space by plotting the energy band diagram. It was obvious that the dispersion curve resonance position lay above the light cone, and the Q–factor tended to infinity near Γ point, as shown in Figure 2a. The resonance position and the variation of the Q–factor indicated that the resonance belonged to the BIC category. Figure 2b,c shows the electric and magnetic field distributions in the BIC state at the Γ point (α = 0) plotted by the eigen analysis method. It could be seen that the electric field energy was all in the TFLN cylinder, and the magnetic field direction was perpendicular to the electric field direction. The electromagnetic field intensity distribution in the BIC state was C₂ symmetric, indicating that the mode belonged to the non-simplex mode in the C_4v system [25,26]. By adjusting α, the BIC was weakly coupled to the far field, which led to partial energy leakage into the surrounding environment, forming a quasi-BIC.

Next, we investigated the effect of asymmetry, the asymmetric parameter α, on the transmission spectrum, as shown in Figure 3a. As α increased, the resonance wavelength was red-shifted, the line width of the resonance peak became wider, and the Q–factor became smaller. When α = 0, the resonance linewidth disappeared and the Q–factor tended to infinity, which indicated that our structure could realize the process from quasi-BIC to true BIC and achieve adjustable BIC. Under the BIC state, the spatial symmetry of the mode made it mismatched with the external radiated waves, which resulted in the mode not being radiated. By introducing symmetry breaking in the structure and constructing radiation channels with free space, the BIC mode was converted to a radiable quasi-BIC with a high Q–factor. In this work, we transformed the BIC to a quasi–BIC with Fano linearity by breaking the inversion symmetry in the structural plane by controlling the eccentricity of the eccentric cylinder. When the eccentricity, xh, increased, it meant that the structural asymmetry increased, leading to an increase in the energy leakage and a decrease in the Q–factor. Therefore, in theory, the smaller the asymmetry parameter, the higher the Q–factor and the narrower the resonance peak. The fitted curve of α versus Q is shown in Figure 3f, which confirms the theory that the Q–factor increased as α decreased and shows that the Q–factor was proportional to α⁻². However, the very narrow resonance had high requirements for the experiment devices. Meanwhile, the small asymmetry parameter would not be conducive to the subsequent processing. Therefore, we chose the case of asymmetric parameter α = 0.0357 for our study. The electromagnetic field diagrams for the cases of α = 0.0357 (resonance wavelength at 1144 nm) and 0.0893 (resonance wavelength at 1139.1 nm) were plotted and compared as shown in Figure 3b–e. It can be seen that as α decreased, the state got closer to the ideal BIC, and the field localization capability was enhanced.

To quantitatively assess the causes of resonance generation, we performed a computational analysis based on the multiple scattering theory [27,28,29]. According to the multipole scattering formula, the contribution of different multipoles to the far-field scattering power can be obtained (including electric dipole (ED), magnetic dipole (MD), circular dipole (TD), electric quadrupole (EQ), and magnetic quadrupole (MQ)) [30]. As shown in Figure 4a, it can be seen that the contribution of the MD to the resonance dominates at the resonance peak. The contribution of MQ was second only to the MD, but an order of magnitude lower than the MD, while the contribution of the ED, EQ and TD to resonance was very small and almost negligible; this means that it was an MD resonance. Figure 4b shows the current direction distribution at the resonant peak in the x–y plane. It can be seen that the current in the cylinder flowed in a counterclockwise direction, forming a circular current distribution, and this current distribution feature further indicated that a typical magnetic dipole resonance mode was generated in the structure as well [31].

Being important parameters of the structure, r₀, rh, and h, shown in Figure 5, had an effect on the resonance performance. The results of the numerical simulations demonstrated that an increase in the large radius r₀ of the cylinder led to a red shift in the resonant frequency, as depicted in Figure 5a. Conversely, an increase in rh was observed to induce a blue shift in the resonance position, as illustrated in Figure 5b. The thickness of the cylinder, however, did not impact the structural symmetry. Nevertheless, an increase in h caused a red shift in the resonance position, as shown in Figure 5c. Consequently, by manipulating the value of h, it became possible to tune the resonance wavelength to a desired position. In summary, the attainment of a wavelength-tunable quasi–BIC state could be accomplished through judicious design choices and the control of structural parameters.

3.2. Second-Harmonic Generation

In this section, we explored the second-harmonic mechanism and the conversion efficiency of the proposed TFLN metasurface.

$$\mathrm{P}(2\mathsf{\omega })\propto {\int }_{\mathrm{V}}{\mathsf{\chi }}^{\left(2\right)}(\mathrm{r},\mathsf{\omega })\left[{\mathrm{E}}_{\mathrm{l}\mathrm{o}\mathrm{c}}\right(\mathrm{r},\mathsf{\omega }){]}^2\mathrm{d}\mathrm{V}$$

(1)

Equation (1) [15] assumes that the second-harmonic power is proportional to second-order nonlinear and harmonic coefficients, the intensity of the pumped light, and the strong interaction of light with matter. At the same time, the BIC in the structure provides for enhanced light–matter interaction, and the very high–quality factor provides for strong field confinement [32,33]. We simulated the nonlinear part of the structure, and the nonlinear polarization matrix of lithium niobate is shown in Equation (2):

$$\left[\begin{array}{c}{\mathrm{P}}_{\mathrm{x}}^{\mathrm{S}\mathrm{H}}\hfill \\ {\mathrm{P}}_{\mathrm{x}}^{\mathrm{S}\mathrm{H}}\hfill \\ {\mathrm{P}}_{\mathrm{x}}^{\mathrm{S}\mathrm{H}}\hfill \end{array}\right]=2{\mathsf{\epsilon }}_0\left[\begin{array}{cccccc}0& 0& 0& 0& {\mathrm{d}}_{22}& {\mathrm{d}}_{31}\\ {\mathrm{d}}_{31}& {\mathrm{d}}_{31}& {\mathrm{d}}_{33}& 0& 0& 0\\ {\mathrm{d}}_{22}& 0& -{\mathrm{d}}_{22}& {\mathrm{d}}_{31}& 0& 0\end{array}\right]\left[\begin{array}{c}{\mathrm{E}}_{\mathrm{x}}^2\hfill \\ {\mathrm{E}}_{\mathrm{y}}^2\hfill \\ {\mathrm{E}}_{\mathrm{z}}^2\hfill \\ 2{\mathrm{E}}_{\mathrm{y}}{\mathrm{E}}_{\mathrm{z}}\hfill \\ 2{\mathrm{E}}_{\mathrm{x}}{\mathrm{E}}_{\mathrm{z}}\hfill \\ 2{\mathrm{E}}_{\mathrm{x}}{\mathrm{E}}_{\mathrm{y}}\hfill \end{array}\right]$$

(2)

where ε₀ is the dielectric constant of the vacuum. We set the second-order nonlinear coefficients to d₃₁ = −3.2 pm/V, d₂₂ = 1.9 pm/V, and d₃₃ = 19.5 pm/V [25], and defined the conversion efficiency of SHG as η = P_SHG/P_in, to describe the ability of the structure to convert the input light into SH light. P_SHG was the outgoing power to produce the second harmonic and Pin was the input power of the pump light. The relationship between α and conversion efficiency is shown in Figure 6a. Combining the relationship between α and Q, we can conclude that as α decreases, the SHG conversion efficiency increases and the Q–factor increases. Therefore, the magnitude of the Q–factor can be an indicator for us to judge the field enhancement as well as the magnitude of the conversion efficiency. The smaller the distance of the wave vector component from the Γ point, the closer to the ideal BIC state and the Q–factor tending towards infinity. Finally, we chose α = 0.0178 (xh = 10 nm) to calculate the conversion SHG efficiency. Figure 6a shows that the frequency doubling wavelength was about 572.4 nm and the conversion efficiency reached 6.5%, where the pumping power was 1 MW/cm² and the incident wavelength was 1144.8 nm. Figure 6b shows that the resonance wavelength appeared to blue shift with a narrowing in the resonance width with α increases. Figure 6c,d shows the electric field distribution at the fundamental frequency field and doubling field respectively in y–z plane with the maximum conversion efficiency. Finally, we verified the dependence of the SHG power on the input pump power with a different offset α in Figure 6e. The resulting fitted relationship satisfied the equation ${\mathrm{P}}_{\mathrm{S}\mathrm{H}\mathrm{G}}=\mathsf{\alpha }{\mathrm{P}}_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}}^{\mathrm{b}}$ [34].

3.3. Characterization of Oblique Incidence

For symmetry-protected BIC, the symmetry could be broken both in real space (changing the structural parameters) and in wave-vector space (making the horizontal wave-vector leave the Γ point) [35,36,37]. On the basis of real space, we studied the case of breaking symmetry in the wave-vector space. The schematic diagram of oblique incidence is shown in Figure 7a. Based on the optimized structural parameters in the previous section, the transmittance spectral profiles were simulated for different incidence angles. Figure 7b shows the optical response of the lithium niobate hollow ring at different incidence angles. From the transmittance plot, it can be seen that with the increase of incidence angle the resonance appeared to red shift with the increase of resonant line width. For each 2° increase in angle, the speed of resonance movement was not equally spaced and showed an increasing trend. In addition, we defined an asymmetry factor, μ = sinθ, where θ respects to the incidence angle. When θ = 0, it corresponded to the BIC state. As an increase of θ, the Q–factor decreased, which indicated the quasi-BIC state. It is interesting that the fit gave an inverse relationship between the Q–factor and the quadratic side of µ, as shown in Figure 7c. Compared with changing the structural symmetry, the method of breaking symmetry by oblique incidence had the advantages of simplicity of operation and cost saving. At the same value of Q–factor, the symmetry broken by oblique incidence was greater. The smallest size that could be processed was 10 nm, limited by the manufacturing process. After computational analysis, we concluded that the Q–factor at a structural offset distance of xh = 10 nm (α = 0.0178) was one order of magnitude lower than that at a rotation angle of 1° of the incident light. It can be seen that for this structure, it was easier to obtain a higher Q–factor by breaking the symmetry through oblique incidence than by changing the structural parameters.

We calculated that when θ was set to 1°, the Q–factor was up to about 2 × 10⁵, and the conversion efficiency could reach 1.2% at an incident power of 1 kW/cm² (three orders of magnitude lower than the previous incident power) as shown in Figure 7d. In addition, we have investigated the conversion efficiency of the second harmonic in recent years as shown in

Table 1. Second-harmonic conversion efficiency research. Where FH is short for fundamental harmonic.

Meta-Atoms	FH Wavelength (nm)	Material	Input Power	Conversion Efficiency
Cylinder [38]	1200–1700	AlGaAs	1 GW/cm2	4 × 10−5
Cylinder [39]	1100–1800	AlGaAs	0.053 GW/cm2	4 × 10−4
Cylinder plus slab [40]	766–786	LiNbO3	0.65 GW/cm2	1.4 × 10−3
Grating [41]	1280–2080	Au	1 GW/cm2	1.2 × 10−5
This work	1100–1200	LiNbO3	1 MW/cm2	6.5×10−2

, and our results have broken the previous records.

4. Conclusions

In conclusion, we have demonstrated the mechanism of SHG enhancement in low–refractive–index materials by combining the high nonlinear coefficients and the zero–loss characteristics of lithium niobate hollow rings with the strong localization capability of BIC. Quasi–BIC resonance was obtained by breaking the super-surface symmetry by changing the magnitude of the asymmetry parameter α. Further, a wavelength–tunable BIC was achieved by varying the super-surface structure parameters, and it was concluded that the structure supports a high-quality factor of MD resonance by multilevel subscattering theory analysis. Finally, we simulated and analyzed the performance of the structure, and the results showed that the structure had high conversion efficiency for second-harmonic generation and could reach 6.5% conversion efficiency at a pumping power of 1 MW/cm². We also showed that it was easier to obtain a higher Q–factor by breaking the symmetry through oblique incidence than by changing the structural parameters, where the conversion efficiency could reach 1.2% at an incident power of 1 kW/cm² with 1° oblique incidences. The innovative data provided a good platform for further development of high-sensitivity sensing and nonlinear frequency transition techniques. The high Q–factors generated by the structure play a vital role in the fields of sensing [42,43,44] and nonlinear frequency conversion. Our findings pave the way for their applications in these domains.