Abstract
In synthetic diamond plates, the intrapulse-correlated dynamics of self-phase modulation and spontaneous nonresonant Raman scattering by center-zone optical phonons were for the first time directly investigated for tightly focused (focusing numerical aperture NA = 0.25) positively chirped visible-range high-intensity laser pulses with variable durations (0.3–9.5 ps) and energies transmitted through the sample. The observed self-phase modulation broadening and modulation of the transmitted light and Stokes Raman spectra for the (sub)picosecond pulse durations indicate the considerable Raman–Kerr contribution to the nonlinear polarization. The latter appears through plasma emission of the optical phonons, which emerges on the (sub)picosecond timescale and dominates at ≈1 ps. Later, this phonon contribution is eventually suppressed in the material due to picosecond-scale electron-lattice thermalization and the related thermally enhanced symmetrical decay of optical phonons into lower-frequency acoustic ones.
1. Introduction
Tightly focused ultrashort laser pulses (pulsewidth ~0.01–10 ps) were revealed as powerful tools for fabricating nano- and micro-optical structures and devices in the volume of transparent solid dielectrics in both pre- and filamentation regimes [1,2]. Key input parameters for direct laser writing in dielectric media include wavelength, duration, peak power, intensity, repetition rate, and total exposure of ultra-short pulses, while the optical characteristics of the final structures serve as output parameters of the technological process. Nevertheless, interactions between ultrashort laser pulses and dielectric materials are predominantly nonlinear, particularly in the filamentation regime [3], providing complex relationships between the input laser parameters and the output characteristics of the inscribed structural features [4,5,6]. Moreover, given the scalability of filament parameters for ultrashort laser pulses, depending on focusing conditions [7], it can be postulated that, in tight-focusing regimes and associated microscale filamentation of ultrashort laser pulses, the defocusing solid-state electron-hole plasma in filaments may approach a near-critical state [8], thereby strongly reflecting and becoming opaque to laser radiation, ultimately altering the fundamental outcomes of the laser inscription process.
In this context, the application of diverse dynamic methods for the acquisition and control of parameters of ultrashort laser pulse interactions with dielectric media holds significant interest, encompassing measurements of intrapulse nonlinear transmission [9], harmonic generation [10], supercontinuum generation [11] (self-steepening and self-phase modulation, SPM [3]), spontaneous [12], and stimulated Raman scattering [13], among others. Chirped ultrashort laser pulses, which exhibit temporal interaction dynamics with the material in the spectral representation [14,15], further pique interest for dynamic diagnostics. Time-resolved acquisition of the “laser-dielectric medium” interaction parameters is crucial also for the reason of nonlinear transient effects—e.g., delayed Raman–Kerr nonlinearity [3], based on the instantaneous optical-phonon-induced nonlinear lattice polarization and considerably affecting the onset parameters for ultrashort-pulse laser filamentation [16,17]. The related instantaneous, spontaneous or stimulated Raman scattering in dielectrics could be nonresonant [12,18], proceeding versus virtual intragap states, or resonant one, when photo-generated dense solid-state electron-hole plasma induces during its relaxation not only postpulse interband photoluminescence, but also intrapulse Raman emission [18]. Hence, a combination of various experimental capabilities, complementarily characterizing ultrafast optical, electronic and lattice processes in dielectric material, is generally required to provide an enlightening view of key underlying physical processes, enable the construction of a comprehensive picture of the phenomenon and the extraction of valuable information on ultrafast nano- and microscale processes within dielectric volumes under the influence of ultrashort laser pulses in a noncontact mode.
Specifically, in diamonds, in the last decade, ultrashort-pulse laser inscription has been utilized for the fabrication of waveguides [19], single-photon sources based on separate optically active color centers [20,21] and photoluminescent encoding [22,23]. Special attention was focused on the identification of laser filamentation regimes at tight (high-NA) focusing as a function of diamond purity [23], laser wavelength, pulsewidth and polarization [17,24] and the arrangement of laser polarization regarding high-symmetry directions in diamond samples [24,25]. Ultrashort-pulse laser filamentation was characterized in terms of electron-hole plasma dynamics, with near-critical plasma working in the material as a defocusing force for the arrest of Kerr self-focusing beam collapse [3]. In this regime, photoluminescence and spontaneous Raman scattering were found to both exhibit a linear dependence on incident laser pulse energy [12,22,23], thus giving useful insights into the correlated optical field, electron-hole plasma and lattice dynamics.
In this investigation, the correlated intra-pulse dynamics of self-phase modulation of laser radiation and spontaneous nonresonant Raman scattering generated in synthetic diamond were explored in pre- and filamentation regimes. By utilizing chirped ultrafast laser pulse techniques for the first time in this context, this study aimed to elucidate the consequent and/or interfering dynamic optical, electronic, electron-phonon and phonon-phonon effects in the material.
2. Materials and Methods
Transmission spectra were examined for a Type IIa synthetic diamond cube (dimensions: 2 × 2 × 2 mm) with six polished opposite facets, employing ultrashort laser pulses at the central 515-nm second harmonic wavelength of a Yb-laser Satsuma (Amplitude Systemes, St. Etienne, France), corresponding to the spectral full-width at the half-maximum of 1.3 nm or ≈63 cm−1. The ultrashort laser pulses were precisely focused within the crystal volume using a micro-objective with a numerical aperture NA = 0.25 to yield the focal spot radius at the 1/e-intensity level ≤2 µm (in the prefilamentation regime, the peak fluence ~2 J/cm2 and peak intensity ~7 TW/cm2 at the 200-nJ threshold pulse energy). The spectral shape was maintained while varying the laser pulse duration through a technique that involved partial positive chirping (incomplete compression of stretched pulses for amplification, radial frequency increasing during the pulse) in the range τ = 0.3–12 ps. Pulse durations were determined using a single-pulse auto-correlator, AA-10DD-12PS (Avesta Project Ltd., Moscow, Russia). Ultrashort laser pulse energy was adjusted using a thin-film transmission attenuator (Standa, Vilnius, Lithuania) in the range E = 50–800 nJ (estimated peak energy density in linear focusing mode: 0.4–7 J/cm2). The transmitted radiation was carefully collected by a fluorite microscope objective (LOMO, St. Petersburg, Russia) with a numerical aperture NA = 0.2 and subsequently guided to the entrance slit of a spectrometer ASP-190 (Avesta Project Ltd., Moscow, Russia). Spectra were accumulated over a 10-s duration at the ultrashort laser pulse repetition rate of 10 kHz, and the sample was moved in steps of 50 µm, using a motorized translation stage for micro-positioning (Standa, Vilnius, Lithuania) after each spectrum acquisition.
Peak power and energy of ultrashort laser pulses were identified as critical parameters for filamentation in synthetic diamond samples. The onset of visible asymmetric elongation of glowing filamentation channels towards laser radiation was observed as a function of increasing laser pulse energy (peak power), as previously reported [17,24,26]. This observation suggested the formation of a nonlinear focus beyond the Rayleigh length (linear focus parameter). For linearly polarized ultrashort laser pulses with a wavelength of 515 nm and varying pulse durations, the threshold energy values were discovered to be in the range of ≈210–230 nJ [17].
3. Results and Discussion
3.1. Self-Phase Modulation Dynamics
The spectra of transmitted ultrashort laser pulses as a function of pulse duration and energy below and above the threshold for filamentation onset (≥200 nJ [17]) are shown in Figure 1a–d. At the minimum duration τ = 0.3 ps, ultrashort laser pulse energy increases above the threshold due to nonlinear SPM [3]. The spectrum significantly broadens in the 500–520 nm range (full width at the noise level), which is more pronounced on the blue wing (Figure 1a). At the longer pulse duration τ = 1.3 ps, the total SPM-related broadening of the laser pulse decreases (full width at the noise level) due to reduced peak ultrashort laser pulse intensity [3,27], becoming strongly shifted to the blue wing and more modulated across the spectrum (Figure 1b). The origins of periodic low-frequency spectral modulation under SPM conditions were discussed in [27,28], while some other effects can be considered too [5]. Subsequently, at the ultrashort laser pulse duration τ = 2.4 ps, the total broadening further decreases (511–517 nm) but becomes more pronounced on the red wing (Figure 1c). Finally, at the maximum duration τ = 9.5 ps and corresponding lower peak intensity, the ultrashort laser pulse line restores a Lorentzian-like shape and slightly homogeneously broadens (full width at the noise level—512–517 nm, Figure 1d) with the minor spectral modulations.
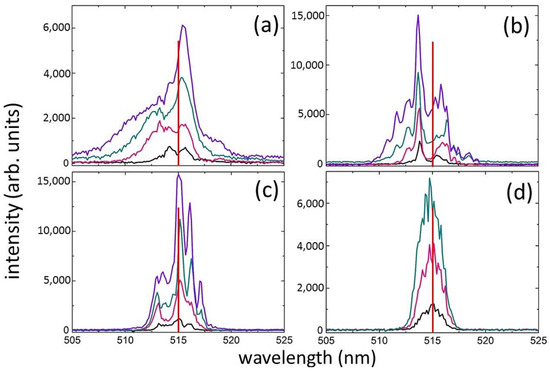
Figure 1.
Spectra of transmitted radiation from positively chirped ultrashort laser pulses with durations of 0.3 (a), 1.3 (b), 2.4 (c) and 9.5 (d) ps and pulse energies of 50 (black), 200 (pink), 400 (green, for 9.5 ps—300 nJ), and 800 (purple) nJ. The vertical red line indicates the central wavelength position of ultrashort laser pulses at 515 nm. The threshold energy for the onset of filamentation is above 200 nJ.
The observed effects demonstrate the change in the spectral width with the increasing ultrashort laser pulse duration and decreasing peak laser intensity, which is one of the key parameters for SPM along with the electronic component of the nonlinear (Kerr) refractive index [3]. Here, the blue-range asymmetry of the SPM broadening can usually be attributed to the possibility of plasma shielding on the trailing edge of the ultrashort laser pulse and its nonlinear self-steepening, typically manifested as a stronger extension of the “blue” SPM wing [29]. Additionally, the same effect is manifested by a “delayed” phonon component of Kerr nonlinearity (Kerr–Raman effect [3]) on the trailing (“blue”) edge of positively chirped ultrashort laser pulses. As a result, such blue-range SPM-based spectral extension is observed even for the bandwidth-limited ultrashort laser pulses with a duration of 0.3 ps, which acquire weak dispersive chirping upon their passage in the diamond [22].
In contrast, broadening switches to the “red” wing for the positively chirped ultrashort laser pulses with the larger τ = 1.3 ps, apparently due to the laser pulse self-steepening at the leading pulse front. Since the common electronic Kerr contribution becomes weaker for the less intense longer pulses, the observed steepening effect could manifest the stronger phonon-based Raman–Kerr contribution on the leading (“red”) edge of the ultrashort laser pulses.
Then, for the ultrashort laser pulses with τ = 2.4 ps, the laser spectrum appears slightly broadened, rather symmetrical and strongly modulated. During such picosecond pulses, due to fast electron-hole plasma thermalization with the crystalline lattice (characteristic time—1–2 ps [2]) and pulsewidth-weakened electronic contribution, the delayed Raman–Kerr nonlinearity could be damped by phonon-phonon anharmonicity at the leading (“red”) edge of the ultrashort laser pulses. Specifically, thermal filling of low-frequency acoustic phonon modes should weaken the lattice polarization based on Raman-active zone-center optical phonons due to the acceleration of their symmetric decay into acoustic phonons [30,31]. Finally, for the long, low-intensity ultrashort laser pulses with τ = 9.5 ps, the electronic Kerr contribution to the nonlinear polarization will be weakly expressed but it holds for the heated or even melted material in the focal region, compared to the negligible Raman–Kerr contribution.
3.2. Raman Scattering Dynamics
Intriguingly, as ultrashort laser pulses propagate through diamond, the generation of Raman signals of zone-center optical phonons occurs with a wave number of approximately 1340 cm−1 (Figure 2a–d). The generation exhibits a spontaneous origin since the initial laser band (width of ≈63 cm−1) and even its SPM-broadened replica (width ≤ 600–700 cm−1, Figure 2 and other figures below) do not contain in their spectra the Stokes wave shifted by 1340 cm−1. Moreover, in our work, the Raman scattering/Raman–Kerr process along with its related SPM process was observed in the high-intensity regime (in the linear focusing regime, peak laser intensity ~10 TW/cm2 at the 200-nJ pulse energy), compared to previous studies, when pronounced Raman and SPM processes occurred in low-intensity, long-pass regimes in fibers [32,33,34]. As a result, strong photoionization is expected in the high-intensity regime [22], making Raman scattering a nonresonant process, while enhanced by plasma emission of optical phonons. Then, the nearly linear (angular slopes in the range of ≈0.8–1.2) dependences of the integrated intensity of the Raman signal on the pulse energy for all these pulsewidths (Figure 3) could evidence the characteristic near-critical dense plasma regime (plasma density ρeh), being very similar to plasma photoluminescence yield Φ at the instantaneous intensity I(t) and pulse peak intensity I0 [23]:
where the consecutive terms in the first rate equation are impact ionization and radiative and Auger recombination with their corresponding coefficients α, β and γ, respectively. The second equation describes the impact ionization balanced in dense electron-hole plasma by Auger recombination (steady state). Then, plasma density could be derived as a function of laser intensity (third equation). Finally, the fourth equation presents PL intensity as a linear function of laser intensity.
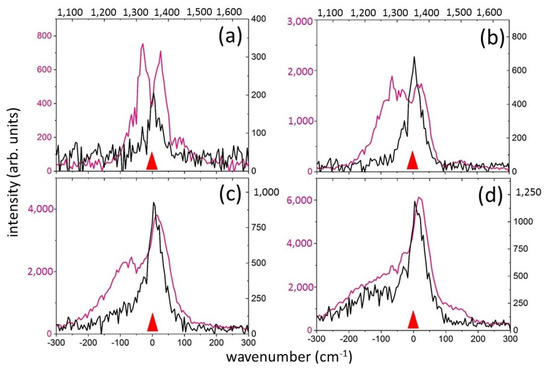
Figure 2.
Comparison of the spectra of transmitted ultrashort laser pulses (pink color, left/bottom axes) and their Raman components (black color, right/top axes) for the pulse duration of 0.3 ps and energies of 50 (a), 200 (b), 400 (c) and 800 (d) nJ. The red triangle indicates the central wavelength position of ultrashort laser pulses—515 nm.
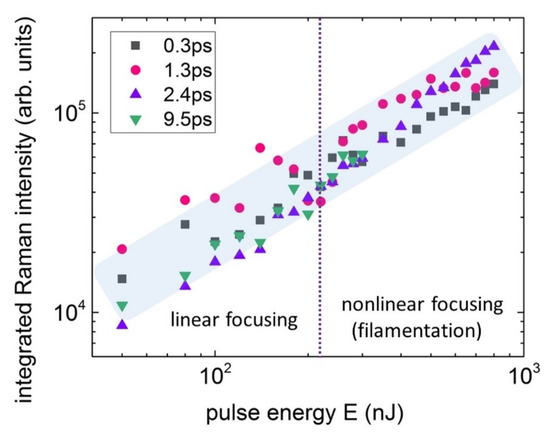
Figure 3.
Dependence of the spectrally integrated intensity of Raman signal on ultrashort laser pulse energy for different pulse durations in linear and nonlinear (filamentation) focusing regimes, separated by a dashed vertical line. The colored band demonstrates the general linear nature of the curves, whose angular slopes vary within the range of 0.8–1.2.
According to this analysis, the rather similar slopes of these curves both in the pre-filamentation and filamentation regimes imply that the dense plasma (as a prerequisite of filamentation due to plasma defocusing arrest of Kerr self-focusing collapse [3]), rather than filamentation, dictates the slope values. On the other hand, this propagation regime in the diamond is quite different from the previously studied one in underdense plasmas for (sub)relativistic ultrashort laser pulses (peak intensities ~10–103 PW/cm2 [15,35,36]).
Specifically, at τ = 0.3 ps, the intensity of the Raman signal is linear with respect to the energy in the sub-filamentation regime, up to 200 nJ (Figure 2a,b), where the half-width of the main Raman peak is approximately equal to 50 cm−1, roughly corresponding to the width of the laser pulse. Moreover, as the energy of ultrashort laser pulses exceeds 200 nJ in the filamentation regime, the increase in the intensity of the Raman signal decelerates, the main peak progressively shifts towards 1360 cm−1 and the width broadens due to the “red” wing following the laser pulse, still maintaining the half-width of the main peak (Figure 2c,d). In this case, the intensity of the Raman signal correlates with the intensity of the laser spectrum predominantly at the “blue” wing (on the tail of ultrashort laser pulses in the SPM regime), while the efficiency of the Raman generation on the “red” wing (the leading pulse front) is notably lower but progressively increases with its earlier onset. Since it is the Raman signal that follows the SPM changes of the laser spectra in the filamentation regime, it is reasonable to suggest the laser spectral brightness dictates the Raman emission during the 0.3-ps laser pulse through electron-hole plasma generation.
For the positively chirped ultrashort laser pulses with the duration τ = 1.3 ps, despite filamentation of the laser pulses manifested as luminescent micro-tracks [6,22,23] and pronounced SPM broadening and modulation of the laser spectrum at energies above 200 nJ (Figure 4), with a very narrow main peak (≈15 cm−1) shifted to ≈1294 cm−1, a linear output of the Raman signal is observed in the entire range of E (Figure 3). At this pulse duration, the SPM broadening and modulation are more pronounced at the “red” wing of the laser band, with its strong modulation starting at the energy E = 50 nJ (Figure 4), apparently due to the laser pulse self-steepening at the leading pulse front. Since the common electronic Kerr contribution becomes weaker for the less intense longer pulses, the observed steepening effect could manifest the stronger phonon-based Raman–Kerr contribution on the leading (“red”) edge of the ultrashort laser pulses. Indeed, the efficient Raman generation is also predominantly realized on the “red” wing, i.e., at the beginning of the chirped ultrashort laser pulses, but almost totally not on the “blue” wing, i.e., it does not completely replicate the laser spectra. At the “red” wing, this may indicate the rapidly increasing Bose-like population of the optical-phonon mode and the rise of the related phonon-based nonlinear polarization with the characteristic 1-ps timescale. In contrast, at the “blue” pulse edge, the optical-phonon Raman mode could be depopulated yet by thermally accelerated symmetric decay of the optical phonons into two lower-frequency counterpropagating acoustic phonons with equal energies (half of the optical phonon energy) and wavenumbers [30,31]. This process is supported by the fast electron-hole plasma thermalization with the crystalline lattice (characteristic time: 1–2 ps [2]). Meanwhile, due to the significant excitation of optical phonons at the beginning of ultrashort laser pulses on (sub)picosecond timescales, the efficiency (integrated intensity) of Raman generation for this pulse duration is considerably higher (both in the prefilamentation and filamentation regimes) than for the shorter pulse with τ = 0.3 ps (Figure 3).
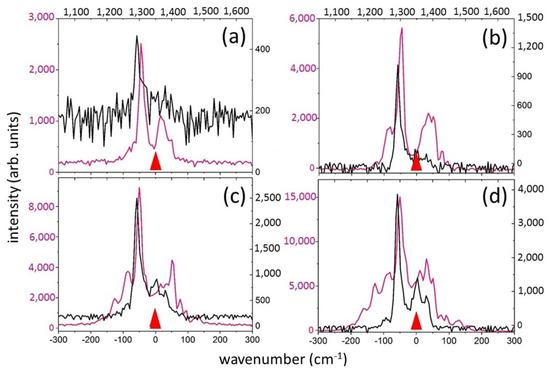
Figure 4.
Comparison of transmitted ultrashort laser pulse spectra (pink color, left/bottom axes) and their Raman components (black color, right/top axes) for pulse duration of 1.3 ps and pulse energies of 50 (a), 200 (b), 400 (c) and 800 (d) nJ. The red triangle indicates the position of the central wavelength of the USP—515 nm.
Moreover, for ultrashort laser pulses with a duration τ = 2.4 ps, the Raman signal spectrum adequately replicates the ultrashort pulse laser spectrum (Figure 5a–d), considering that the latter is moderately symmetrically broadened and modulated by the persisting electronic SPM. Stronger “red”-wing broadening at the lower pulse energies could be assigned to the “delayed” phonon-based nonlinearity, pronounced at the leading pulse edge until its thermal suppression via the symmetrical decay of optical phonons into acoustic modes during the latter portion of the pulse. The centroid of the Raman spectrum lies in the range of 1325–1340 cm−1 (Figure 5), and its spectrally integrated intensity is practically linearly dependent on the ultrashort laser pulse energy (Figure 3). The efficiency (integral intensity) of Raman generation for this pulse duration is significantly lower than for the shorter pulses (Figure 3), except for the filamentation regime. Thus, Raman signal generation in these conditions apparently illustrates its initial contribution to SPM broadening and the following thermalization of the absorbed laser energy in the material for the ultrashort laser pulse duration, exceeding the electron-phonon and phonon-phonon thermalization times (in total ≈ 1–2 ps [2]), possibly even with its melting at a certain instant during the pulse.
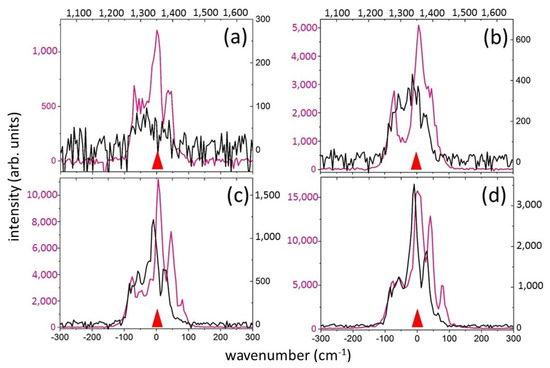
Figure 5.
Comparison of transmitted ultrashort laser pulse spectra (pink color, left/bottom axes) and their Raman components (black color, right/top axes) for pulse duration of 2.4 ps and pulse energies of 50 (a), 200 (b), 400 (c) and 800 (d) nJ. The red triangle indicates the position of the central wavelength of the ultrashort laser pulse—515 nm.
In a similar way, both the spectra of the transmitted laser pulses and the Raman spectra for the pulsewidth τ = 9.5 ps (Figure 6a–d) exhibit broadened (≈100 cm−1) Lorentzian-like and mutually correlating shapes, with the linear dependence of the Raman signal output on the ultrashort laser pulse energy E, overall reflecting the thermalized state of the material. At the same time, the lower efficiency of the spontaneous Raman generation for the pulsewidth (Figure 3) may suggest significant heating and melting of the material in the focal region because of its strong interaction with the ultrashort laser pulses.
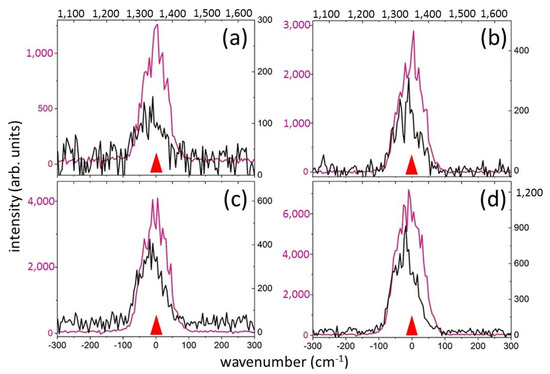
Figure 6.
Comparison of transmitted ultrashort laser pulse spectra (pink color, left/bottom axes) and their Raman components (black color, right/top axes) for pulse duration of 9.5 ps and pulse energies of 50 (a), 100 (b), 200 (c), and 300 (d) nJ. The red triangle indicates the position of the central wavelength of the ultrashort laser pulse—515 nm.
4. Conclusions
In conclusion, in this work, we attempted to elucidate the joint optical, electronic and lattice dynamics during strong excitation and filamentation in bulk diamond, probed by tightly focused, positively chirped high-intensity laser pulses of variable widths (0.3–9.5 ps) with a central wavelength of 515 nm. For this purpose, we performed experimental studies of the spectral broadening and modulation as well as spontaneous nonresonant Raman scattering of the laser pulses in a synthetic diamond. Compared to the previous studies, our research was for the first time performed neither in low-intensity, long-pass regimes of ultrashort laser pulses in fibers nor in relativistic ultrashort laser pulses in focally underdense plasma. In this work, our focus was on the strongly excited diamond with the near-critical electron-hole plasma, supporting both the defocusing arrest of Kerr self-focusing beam collapse prior to filamentation onset and the emission of center-zone optical phonons to build up the Raman–K err contribution to the nonlinear polarization. Indeed, the phonon-based contribution to the nonlinear polarization and resulting self-phase modulation in the laser pulse spectra were observed to establish themselves during the first picosecond. However, at later picosecond times, the delayed Kerr nonlinearity of the lattice polarization and the efficiency of spontaneous Raman generation diminish owing to the anharmonic symmetrical decay of optical phonons into acoustic phonons, thermally enhanced by electron-phonon and phonon-phonon thermalization in diamond (characteristic timescale of ~1–2 ps). Overall, our results indicate the relationship between self-phase modulation of the laser pulses and nonresonant Raman scattering in the electron-hole plasma, as well as the characteristic timescales of spontaneous optical phonon emission and electron-lattice thermalization in diamonds.
Author Contributions
Conceptualization, S.K. and J.C.; methodology, P.D.; software, P.D.; validation, S.K., P.D. and J.C.; formal analysis, S.K.; investigation, P.D.; data curation, J.C.; writing—original draft preparation, S.K.; writing—review and editing, J.C.; visualization, P.D.; supervision, S.K.; project administration, P.D.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation (project No. 21-79-30063); https://rscf.ru/en/project/21-79-30063/ (accessed on 16 April 2023).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sugioka, K.; Cheng, Y. Ultrafast Lasers-Reliable Tools for Advanced Materials Processing. Light Sci. Appl. 2014, 3, 149. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Y.; Wang, L.; Sakakura, M.; Yu, Y.; Shayeganrad, G.; Kazansky, P.G. 100-Layer Error-Free 5D Optical Data Storage by Ultrafast Laser Nanostructuring in Glass. Laser Photonics Rev. 2022, 16, 2100563. [Google Scholar] [CrossRef]
- Couairon, A.; Mysyrowicz, A. Femtosecond Filamentation in Transparent Media. Phys. Rep. 2007, 441, 47–189. [Google Scholar] [CrossRef]
- Canning, J.; Lancry, M.; Cook, K.; Weickman, A.; Brisset, F.; Poumellec, B. Anatomy of a femtosecond laser processed silica waveguide. Opt. Mater. Express 2011, 1, 998–1008. [Google Scholar] [CrossRef]
- Desmarchelier, R.; Poumellec, B.; Brisset, F.; Mazerat, S.; Lancry, M. In the heart of femtosecond laser induced nanogratings: From porous nanoplanes to form birefringence. World J. Nano Sci. Eng. 2015, 5, 115. [Google Scholar] [CrossRef]
- Danilov, P.; Kuzmin, E.; Rimskaya, E.; Chen, J.; Khmelnitskii, R.; Kirichenko, A.; Rodionov, N.; Kudryashov, S. Up/Down-Scaling Photoluminescent Micromarks Written in Diamond by Ultrashort Laser Pulses: Optical Photoluminescent and Structural Raman Imaging. Micromachines 2022, 13, 1883. [Google Scholar] [CrossRef]
- Geints, Y.É.; Zemlyanov, A.A.; Ionin, A.A.; Kudryashov, S.I.; Seleznev, L.V.; Sinitsyn, D.V.; Sunchugasheva, E.S. Peculiarities of Filamentation of Sharply Focused Ultrashort Laser Pulses in Air. J. Exp. Theor. Phys. 2010, 111, 724–730. [Google Scholar] [CrossRef]
- Kudryashov, S.; Rupasov, A.; Kosobokov, M.; Akhmatkhanov, A.; Krasin, G.; Danilov, P.; Lisjikh, B.; Abramov, A.; Greshnyakov, E.; Kuzmin, E.; et al. Hierarchical Multi-Scale Coupled Periodical Photonic and Plasmonic Nanopatterns Inscribed by Femtosecond Laser Pulses in Lithium Niobate. Nanomaterials 2022, 12, 4303. [Google Scholar] [CrossRef]
- Gulina, Y.S.; Kudryashov, S.I.; Smirnov, N.A.; Kuzmin, E.V. High-NA Focusing of Ultrashort Laser Pulses in Bulk of ZnSe. Opt. Spectrosc. 2022, 130, 396. [Google Scholar] [CrossRef]
- Gordienko, V.M.; Mikheev, P.M.; Potemkin, F.V. Generation of Coherent Terahertz Phonons by Sharp Focusing of a Femtosecond Laser Beam in the Bulk of Crystalline Insulators in a Regime of Plasma Formation. JETP Lett. 2010, 92, 502–506. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Samokhvalov, A.A.; Ageev, E.I.; Veiko, V.P. Ultrafast Broadband Nonlinear Spectroscopy of a Colloidal Solution of Gold Nanoparticles. JETP Lett. 2019, 109, 298–302. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Danilov, P.A.; Sdvizhenskii, P.A.; Lednev, V.N.; Chen, J.; Ostrikov, S.A.; Kuzmin, E.V.; Kovalev, M.S.; Levchenko, A.O. Transformations of the Spectrum of an Optical Phonon Excited in Raman Scattering in the Bulk of Diamond by Ultrashort Laser Pulses with a Variable Duration. JETP Lett. 2022, 115, 251–255. [Google Scholar] [CrossRef]
- Kinyaevskiy, I.O.; Kovalev, V.I.; Danilov, P.A.; Smirnov, N.A.; Kudryashov, S.I.; Seleznev, L.V.; Dunaeva, E.E.; Ionin, A.A. Highly Efficient Stimulated Raman Scattering of Sub-Picosecond Laser Pulses in BaWO4 for 10.6-μm Difference Frequency Generation. Opt. Lett. 2020, 45, 2160–2163. [Google Scholar] [CrossRef] [PubMed]
- Chien, C.Y.; La Fontaine, B.; Desparois, A.; Jiang, Z.; Johnston, T.W.; Kieffer, J.C.; Pépin, H.; Vidal, F.; Mercure, H.P. Single-Shot Chirped-Pulse Spectral Interferometry Used to Measure the Femtosecond Ionization Dynamics of Air. Opt. Lett. 2000, 25, 578. [Google Scholar] [CrossRef] [PubMed]
- Faure, J.; Marques, J.R.; Malka, V.; Amiranoff, F.; Najmudin, Z.; Walton, B.; Rousseau, J.P.; Ranc, S.; Solodov, A.; Mora, P. Dynamics of Raman Instabilities Using Chirped Laser Pulses. Phys. Rev. E 2001, 63, 065401. [Google Scholar] [CrossRef]
- Lim, K.; Durand, M.; Baudelet, M.; Richardson, M. Transition from linear-to nonlinear-focusing regime in filamentation. Sci. Rep. 2014, 4, 7217. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Danilov, P.A.; Kuzmin, E.V.; Gulina, Y.S.; Rupasov, A.E.; Krasin, G.K.; Zubarev, I.G.; Levchenko, A.O.; Kovalev, M.S.; Pakholchuk, P.P.; et al. Pulse-Width-Dependent Critical Power for Self-Focusing of Ultrashort Laser Pulses in Bulk Dielectrics. Opt. Lett. 2022, 47, 3487. [Google Scholar] [CrossRef]
- Stevens, T.E.; Kuhl, J.; Merlin, R. Coherent phonon generation and the two stimulated Raman tensors. Phys. Rev. B 2002, 65, 144304. [Google Scholar] [CrossRef]
- Sotillo, B.; Bharadwaj, V.; Hadden, J.P.; Sakakura, M.; Chiappini, A.; Fernandez, T.T.; Longhi, S.; Jedrkiewicz, O.; Shimotsuma, Y.; Criante, L.; et al. Diamond photonics platform enabled by femtosecond laser writing. Sci. Rep. 2016, 6, 35566. [Google Scholar] [CrossRef]
- Chen, Y.C.; Salter, P.S.; Knauer, S.; Weng, L.; Frangeskou, A.C.; Stephen, C.J.; Ishmael, S.N.; Dolan, P.R.; Jonson, S.; Green, B.L.; et al. Laser writing of coherent colour centres in diamond. Nat. Photonics 2017, 11, 77–80. [Google Scholar] [CrossRef]
- Ju, Z.; Lin, J.; Shen, S.; Wu, B.; Wu, E. Preparations and applications of single color centers in diamond. Adv. Phys. X 2021, 6, 1858721. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Danilov, P.A.; Smirnov, N.A.; Stsepuro, N.G.; Rupasov, A.E.; Khmelnitskii, R.A.; Oleynichuk, E.A.; Kuzmin, E.V.; Levchenko, A.O.; Gulina, Y.S.; et al. Signatures of ultrafast electronic and atomistic dynamics in bulk photoluminescence of CVD and natural diamonds excited by ultrashort laser pulses of variable pulsewidth. Appl. Surf. Sci. 2022, 575, 151736. [Google Scholar] [CrossRef]
- Kudryashov, S.; Danilov, P.; Smirnov, N.; Krasin, G.; Khmelnitskii, R.; Kovalchuk, O.; Kriulina, G.; Martovitskiy, V.; Lednev, V.; Sdvizhenskii, P.; et al. “Stealth Scripts”: Ultrashort Pulse Laser Luminescent Microscale Encoding of Bulk Diamonds via Ultrafast Multi-Scale Atomistic Structural Transformations. Nanomaterials 2023, 13, 192. [Google Scholar] [CrossRef] [PubMed]
- Krasin, G.K.; Gulina, Y.S.; Kuzmin, E.V.; Martovitskii, V.P.; Kudryashov, S.I. Polarization-Sensitive Nonlinear Optical Interaction of Ultrashort Laser Pulses with HPHT Diamond. Photonics 2023, 10, 106. [Google Scholar] [CrossRef]
- Kozak, M.; Otobe, T.; Zukerstein, M.; Trojánek, F.; Maly, P. Anisotropy and polarization dependence of multiphoton charge carrier generation rate in diamond. Phys. Rev. B 2019, 99, 104305. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Levchenko, A.O.; Danilov, P.A.; Smirnov, N.A.; Ionin, A.A. IR Femtosecond Laser Micro-Filaments in Diamond Visualized by Inter-Band UV Photoluminescence. Opt. Lett. 2020, 45, 2026. [Google Scholar] [CrossRef]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Grudtsyn, Y.V.; Zubarev, I.G.; Koribut, A.V.; Kuchik, I.E.; Mamaev, S.B.; Mikheev, L.D.; Semjonov, S.L.; Stepanov, S.G.; Trofimov, V.A.; Yalovoi, V.I. Self-Phase Modulation in a Thin Fused Silica Plate upon Interaction with a Converging Beam of down-Chirped Femtosecond Radiation. Quantum Electron. 2015, 45, 415–420. [Google Scholar] [CrossRef]
- Kudryashov, S.; Danilov, P.; Rupasov, A.; Khonina, S.; Nalimov, A.; Ionin, A.; Krasin, G.; Kovalev, M. Energy Deposition Parameters Revealed in the Transition from 3D to 1D Femtosecond Laser Ablation of Fluorite at High-NA Focusing. Opt. Mater. Express 2020, 10, 3291–3305. [Google Scholar] [CrossRef]
- Klemens, P.G. Anharmonic Decay of Optical Phonon in Diamond. Phys. Rev. B 1975, 11, 3206–3207. [Google Scholar] [CrossRef]
- Bulgadaev, S.A.; Levinson, I.B. Combinational scattering induced by strongly unequal-weighted phonons. JETP Lett. 1974, 19, 583–585. (In Russian) [Google Scholar]
- North, T.; Rochette, M. Broadband self-pulsating fiber laser based on soliton self-frequency shift and regenerative self-phase modulation. Opt. Lett. 2012, 37, 2799–2801. [Google Scholar] [CrossRef] [PubMed]
- Uzunov, I.M.; Arabadzhiev, T.N.; Nikolov, S.G. Self-steepening and intrapulse Raman scattering in the presence of nonlinear gain and its saturation. Optik 2022, 271, 170137. [Google Scholar] [CrossRef]
- Kinyaevskiy, I.; Kovalev, V.; Danilov, P.; Smirnov, N.; Kudryashov, S.; Koribut, A.; Ionin, A. Highly efficient transient stimulated Raman scattering on secondary vibrational mode of BaWO 4 crystal due to its constructive interference with self-phase modulation. Chin. Opt. Lett. 2023, 21, 031902. [Google Scholar] [CrossRef]
- Yau, T.W.; Hsu, C.J.; Chu, H.H.; Chen, Y.H.; Lee, C.H.; Wang, J.; Chen, S.Y. Dependence of relativistic self-guiding and Raman forward scattering on duration and chirp of an intense laser pulse propagating in a plasma. Phys. Plasmas 2002, 9, 391–394. [Google Scholar] [CrossRef]
- Jha, P.; Malviya, A.; Upadhyay, A.K. Propagation of chirped laser pulses in a plasma channel. Phys. Plasmas 2009, 16, 063106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).