Scintillation of Computational Ghost Imaging with a Finite Bucket Detector through Atmospheric Turbulence
Abstract
1. Introduction
2. Theory
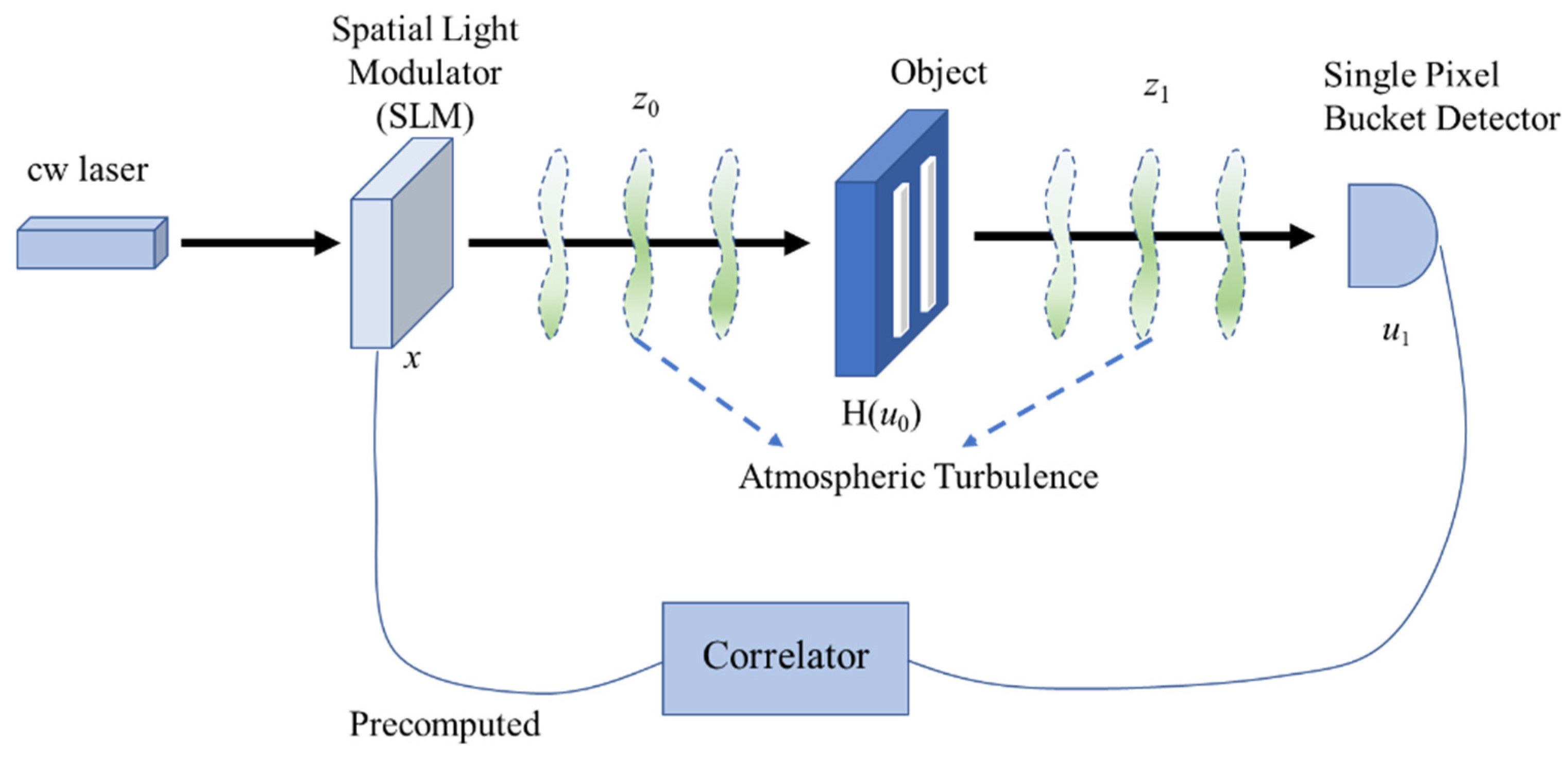
3. Numerical Simulation Model
4. Results
4.1. Influence of the Atmospheric Coherence Length r0
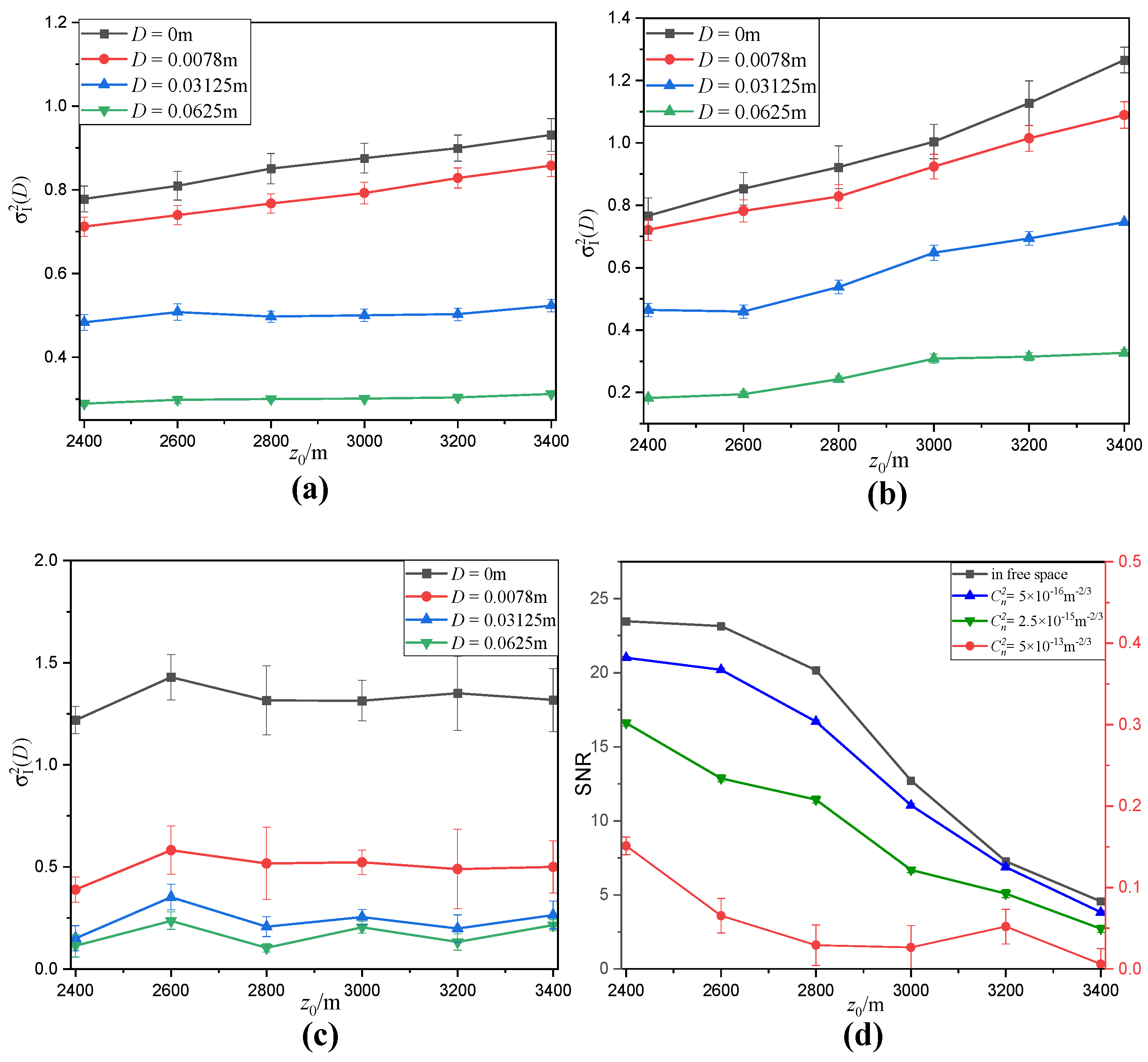
4.2. Influence of the Propagation Distance z0
4.3. Influence of Coherence Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pittman, T.B.; Shih, Y.H.; Strekalov, D.V.; Sergienko, A.V. Optical imaging by means of 2-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429–R3432. [Google Scholar] [CrossRef] [PubMed]
- Bennink, R.S.; Bentley, S.J.; Boyd, R.W. “Two-photon” coincidence imaging with a classical source. Phys. Rev. Lett. 2002, 89, 113601. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Zhai, Y.-H.; Wu, L.-A.; Chen, X.-H. Correlated two-photon imaging with true thermal light. Opt. Lett. 2005, 30, 2354–2356. [Google Scholar] [CrossRef]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Bromberg, Y.; Katz, O.; Silberberg, Y. Ghost imaging with a single detector. Phys. Rev. A 2009, 79, 053840. [Google Scholar] [CrossRef]
- Erkmen, B.I. Computational ghost imaging for remote sensing. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 2012, 29, 782–789. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Han, S. Correlated imaging in scattering media. Opt. Lett. 2011, 36, 394–396. [Google Scholar] [CrossRef]
- Hardy, N.D.; Shapiro, J.H. Reflective ghost imaging through turbulence. Phys. Rev. A 2011, 84, 063824. [Google Scholar] [CrossRef]
- Zhang, P.; Gong, W.; Shen, X.; Han, S. Correlated imaging through atmospheric turbulence. Phys. Rev. A 2010, 82, 033817. [Google Scholar] [CrossRef]
- Cheng, J. Ghost imaging through turbulent atmosphere. Opt. Express 2009, 17, 7916–7921. [Google Scholar] [CrossRef]
- Li, C.; Wang, T.; Pu, J.; Zhu, W.; Rao, R. Ghost imaging with partially coherent light radiation through turbulent atmosphere. Appl. Phys. B Laser Opt. 2010, 99, 599–604. [Google Scholar] [CrossRef]
- Tan, W.; Huang, X.; Nan, S.; Bai, Y.; Fu, X. Ghost imaging through inhomogeneous turbulent atmosphere along an uplink path and a downlink path. OSA Contin. 2020, 3, 1222–1231. [Google Scholar] [CrossRef]
- Liu, X.; Wang, F.; Zhang, M.; Cai, Y. Effects of Atmospheric Turbulence on Lensless Ghost Imaging with Partially Coherent Light. Appl. Sci. 2018, 8, 1479. [Google Scholar] [CrossRef]
- Elsayed, E.E.; Kakati, D.; Singh, M.; Grover, A.; Anand, G. Design and analysis of a dense wavelength-division multiplexed integrated PON-FSO system using modified OOK/DPPM modulation schemes over atmospheric turbulences. Opt. Quantum Electron. 2022, 54, 768. [Google Scholar] [CrossRef]
- Shi, D.; Fan, C.; Zhang, P.; Zhang, J.; Shen, H.; Qiao, C.; Wang, Y. Adaptive optical ghost imaging through atmospheric turbulence. Opt. Express 2012, 20, 27992–27998. [Google Scholar] [CrossRef] [PubMed]
- Ferri, F.; Magatti, D.; Lugiato, L.A.; Gatti, A. Differential Ghost Imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef]
- Sun, B.; Welsh, S.; Edgar, M.P.; Shapiro, J.H.; Padgett, M. Normalized ghost imaging. Opt. Express 2012, 20, 16892–16901. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Sun, B.; Edgar, M.P.; Bowman, R.; Vittert, L.E.; Welsh, S.; Bowman, A.; Padgett, M.J. 3D Computational Ghost Imaging. In Proceedings of the 27th IEEE Photonics Conference (IPC), San Diego, CA, USA, 12–16 October 2014. [Google Scholar]
- Eyyuboğlu, H.; Baykal, Y. Analysis of reciprocity of cos-Gaussian and cosh-Gaussian laser beams in a turbulent atmosphere. Opt. Express 2004, 12, 4659–4674. [Google Scholar] [CrossRef]
- Eyyuboğlu, H.T.; Arpali, C.; Baykal, Y.K. Flat topped beams and their characteristics in turbulent media. Opt. Express 2006, 14, 4196–4207. [Google Scholar] [CrossRef]
- Polynkin, P.; Peleg, A.; Klein, L.; Rhoadarmer, T.; Moloney, J. Optimized multiemitter beams for free-space optical communications through turbulent atmosphere. Opt. Lett. 2007, 32, 885–887. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O. Scintillation index of a stochastic electromagnetic beam propagating in random media. Opt. Commun. 2008, 281, 2342–2348. [Google Scholar] [CrossRef]
- Gu, Y.; Gbur, G. Scintillation of nonuniformly correlated beams in atmospheric turbulence. Opt. Lett. 2013, 38, 1395–1397. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Korotkova, O.; Gbur, G. Scintillation of nonuniformly polarized beams in atmospheric turbulence. Opt. Lett. 2009, 34, 2261–2263. [Google Scholar] [CrossRef] [PubMed]
- Baykal, Y.; Eyyuboğlu, H.T.; Cai, Y. Scintillations of partially coherent multiple Gaussian beams in turbulence. Appl. Opt. 2009, 48, 1943–1954. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Zhu, W.; Rao, R. Numerical investigation on propagation effects of pseudo-partially coherent Gaussian Schell-model beams in atmospheric turbulence. Opt. Express 2009, 17, 3782–3791. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Chen, Y.; Eyyuboglu, H.T.; Baykal, Y. Scintillation index of elliptical Gaussian beam in turbulent atmosphere. Opt. Lett. 2007, 32, 2405–2407. [Google Scholar] [CrossRef] [PubMed]
- Eyyuboğlu, H.T.; Baykal, Y.; Sermutlu, E.; Korotkova, O.; Cai, Y. Scintillation index of modified Bessel-Gaussian beams propagating in turbulent media. J. Opt. Soc. Am. A 2009, 26, 387–394. [Google Scholar] [CrossRef]
- Cai, Y.; Eyyuboğlu, H.T.; Baykal, Y. Scintillation of astigmatic dark hollow beams in weak atmospheric turbulence. J. Opt. Soc. Am. A 2008, 25, 1497–1503. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, Y. Scintillation properties of a rectangular dark hollow beam. J. Mod. Opt. 2009, 56, 502–507. [Google Scholar] [CrossRef]
- Cai, Y. Scintillation properties of non-circular flat-topped beams. J. Opt. A Pure Appl. Opt. 2008, 10, 075003. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, G.; Zhang, Q.; Song, Z. Scintillation Index for Spherical Wave Propagation in Anisotropic Weak Oceanic Turbulence with Aperture Av-eraging under the Effect of Inner Scale and Outer Scale. Photonics 2022, 9, 458. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y. Computational lensless ghost imaging in a slant path non-Kolmogorov turbulent atmosphere. Optik 2012, 123, 1360–1363. [Google Scholar] [CrossRef]
- Shapiro, J.H.; Boyd, R.W. The physics of ghost imaging. Quantum Inf. Process. 2012, 11, 949–993. [Google Scholar] [CrossRef]
- Gatti, A.; Brambilla, E.; Bache, M.; Lugiato, L.A. Ghost imaging with thermal light: Comparing entanglement and classical correlation. Phys. Rev. Lett. 2004, 93, 093602. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef]
- Cai, Y.; Zhu, S.-Y. Ghost imaging with incoherent and partially coherent light radiation. Phys. Rev. E 2005, 71, 056607. [Google Scholar] [CrossRef]
- Ji, X.; Li, X. Directionality of Gaussian array beams propagating in atmospheric turbulence. J. Opt. Soc. Am. A 2009, 26, 236–243. [Google Scholar] [CrossRef]
- Gu, M.; Zhou, J.; Ren, X.; Liao, S. Theoretical investigation on spectral emissivity of thermal control coatings with optical-rough surface. Optik 2019, 181, 44–49. [Google Scholar] [CrossRef]
- Kuga, Y.; Phu, P. Experimental studies of millimeter-wave scattering in discrete random media and from rough surfaces—Summary. J. Electromagn. Waves Appl. 1996, 10, 451–453. [Google Scholar] [CrossRef]
- Xiang, J.; Zhang, X.; Zhang, M.; Yang, S. Generation of infinitely long turbulence phase screen. High Power Laser Part. Beams 2012, 24, 1071–1075. [Google Scholar] [CrossRef]
- Tao, Z.; Ren, Y.; Abdukirim, A.; Liu, S.; Rao, R. Mitigating the effect of atmospheric turbulence on orbital angular momentum-based quantum key distribution using real-time adaptive optics with phase unwrapping. Opt. Express 2021, 29, 31078–31098. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Wu, P.; Tao, Z.; Li, X.; Li, Y.; Rao, R.; Ren, Y. Scintillation of Computational Ghost Imaging with a Finite Bucket Detector through Atmospheric Turbulence. Photonics 2023, 10, 542. https://doi.org/10.3390/photonics10050542
Deng H, Wu P, Tao Z, Li X, Li Y, Rao R, Ren Y. Scintillation of Computational Ghost Imaging with a Finite Bucket Detector through Atmospheric Turbulence. Photonics. 2023; 10(5):542. https://doi.org/10.3390/photonics10050542
Chicago/Turabian StyleDeng, Hanling, Pengfei Wu, Zhiwei Tao, Xinmiao Li, Yanling Li, Ruizhong Rao, and Yichong Ren. 2023. "Scintillation of Computational Ghost Imaging with a Finite Bucket Detector through Atmospheric Turbulence" Photonics 10, no. 5: 542. https://doi.org/10.3390/photonics10050542
APA StyleDeng, H., Wu, P., Tao, Z., Li, X., Li, Y., Rao, R., & Ren, Y. (2023). Scintillation of Computational Ghost Imaging with a Finite Bucket Detector through Atmospheric Turbulence. Photonics, 10(5), 542. https://doi.org/10.3390/photonics10050542




