Particle Swarm Optimized Compact, Low Loss 3-dB Power Splitter Enabled by Silicon Columns in Silicon-on-Insulator
Abstract
1. Introduction
2. Device Schematic and Operation Principle
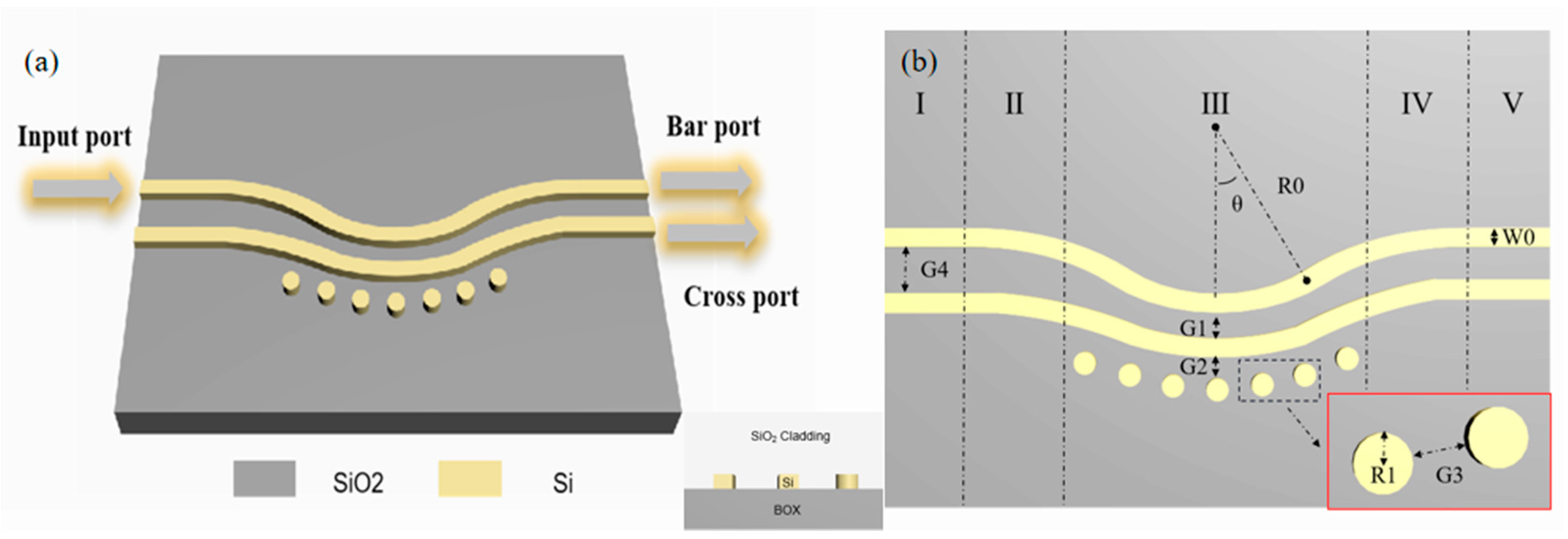
2.1. Device Schematic
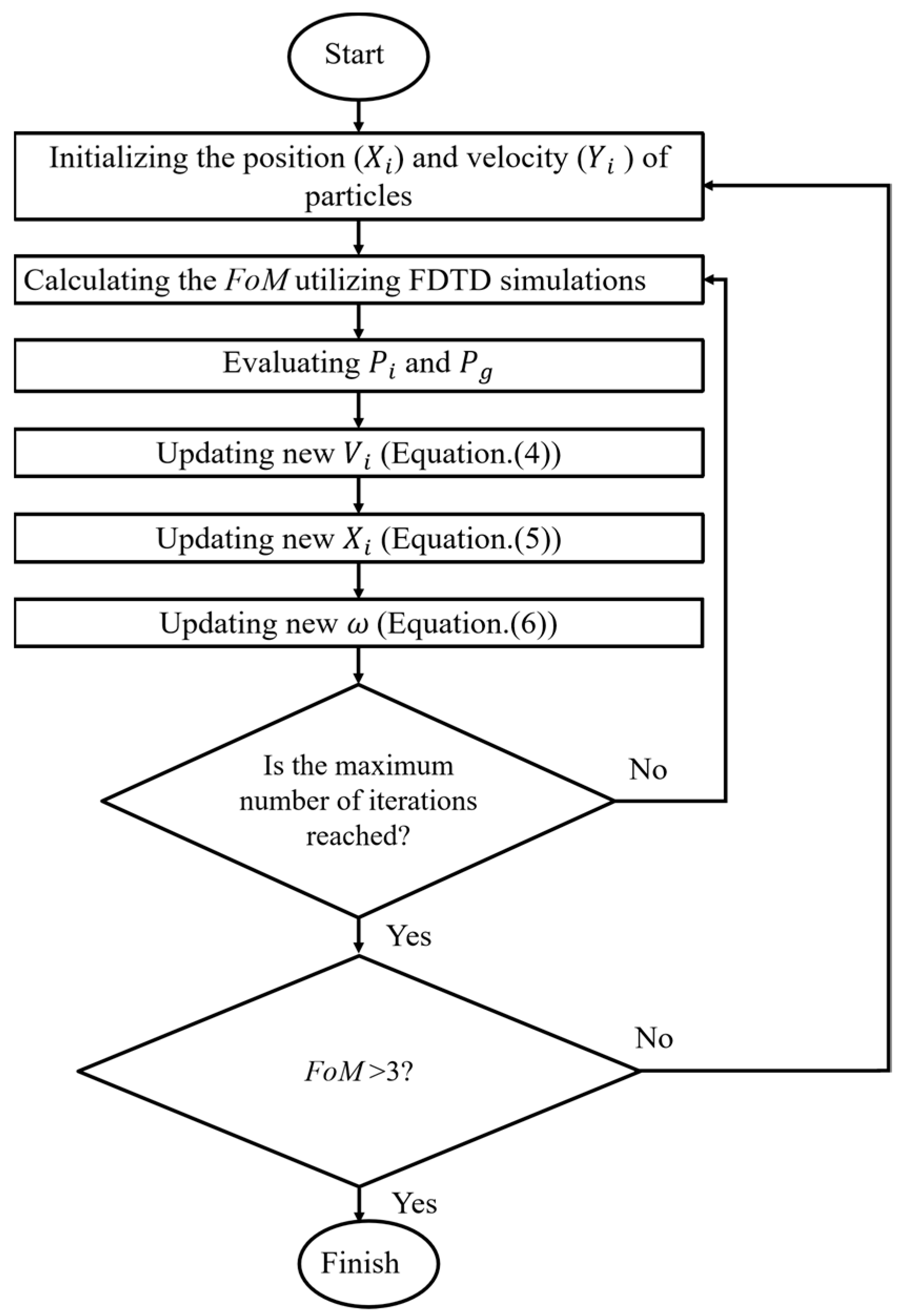
2.2. Mathematical Model
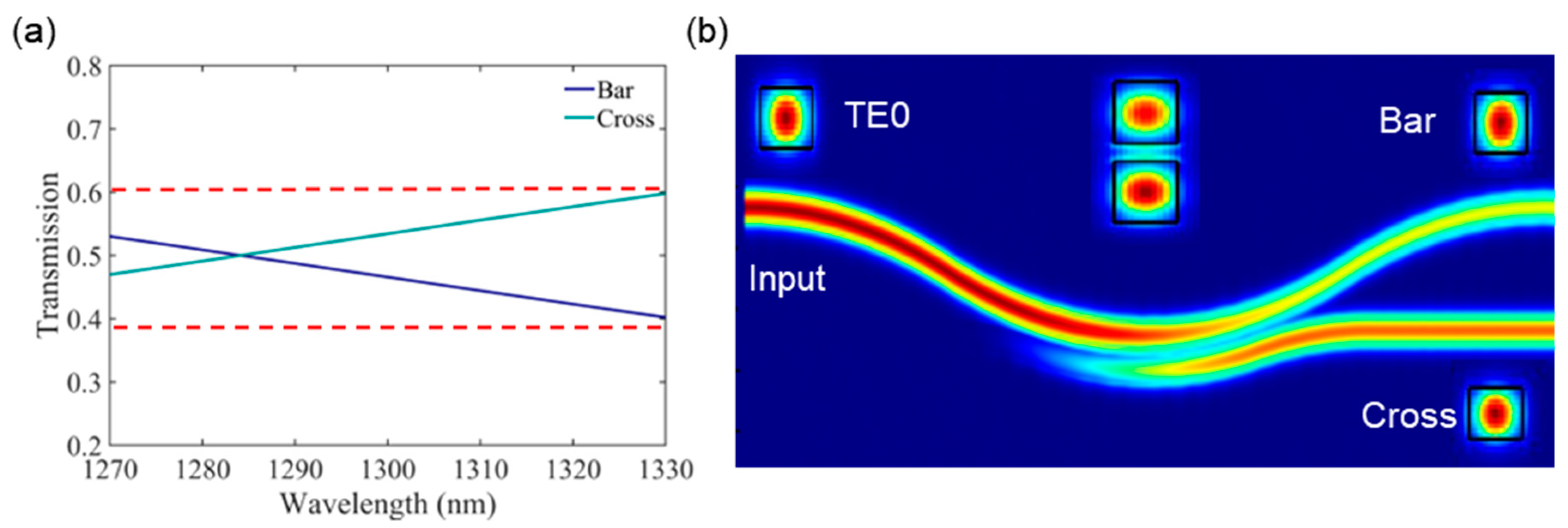
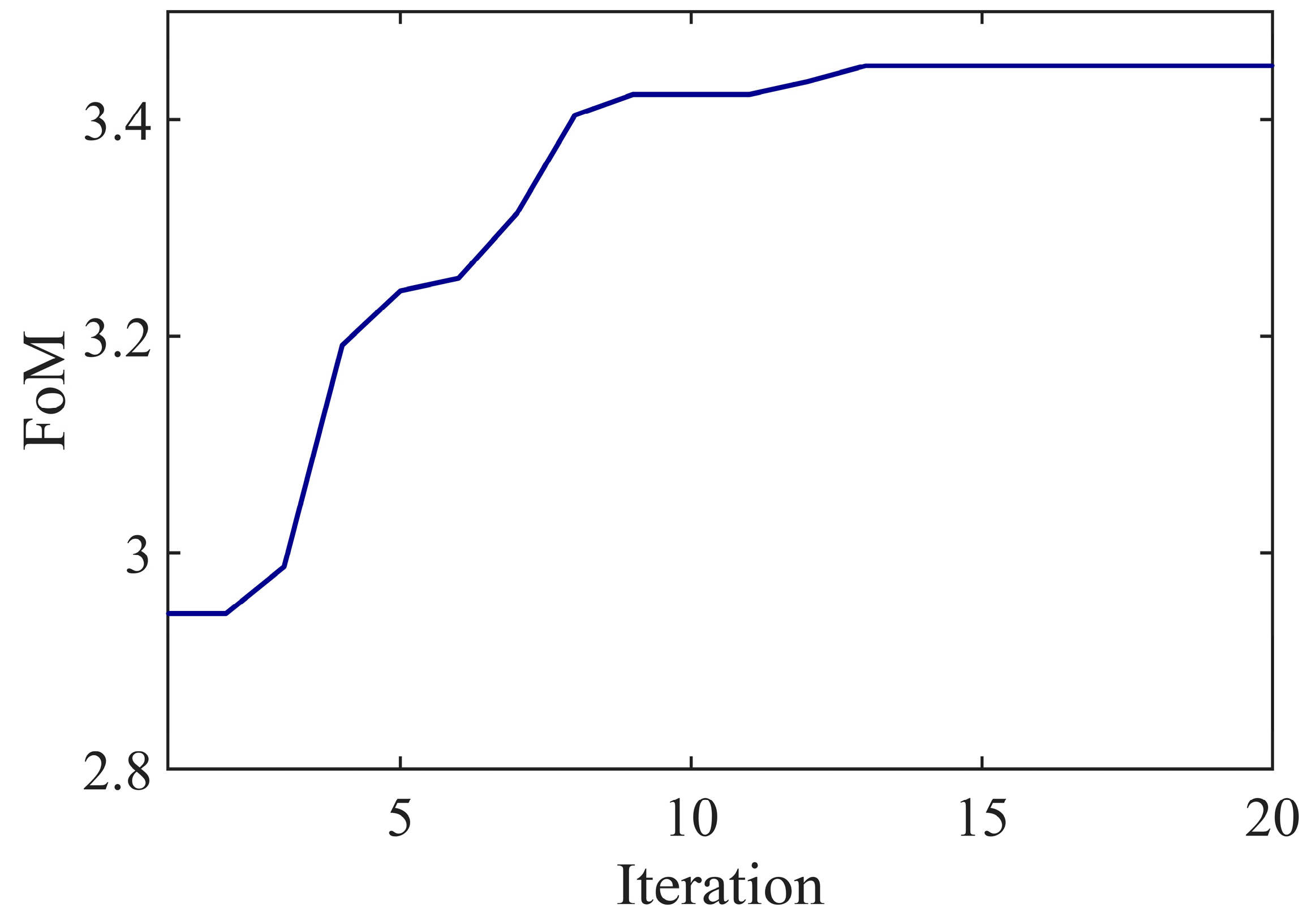
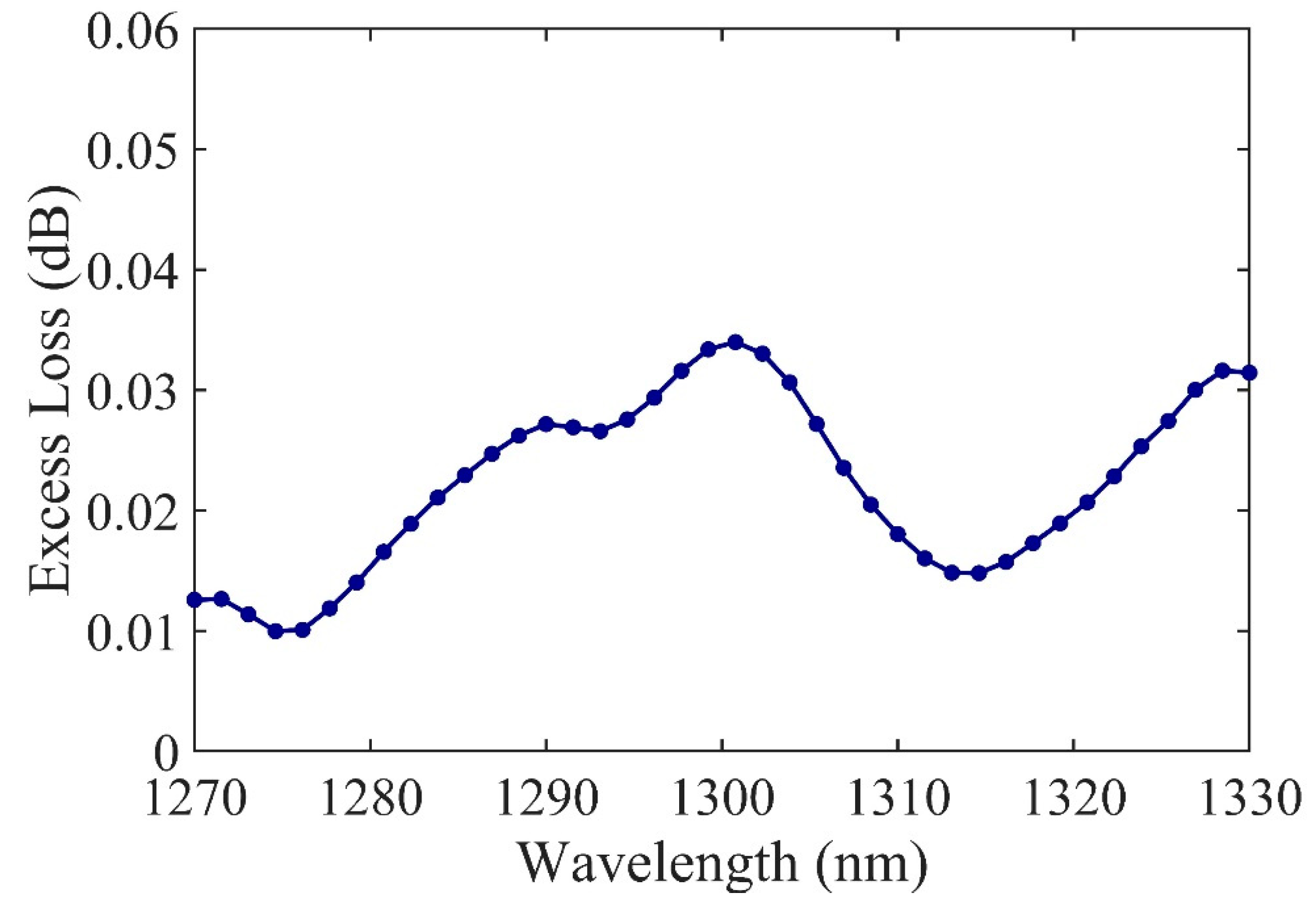
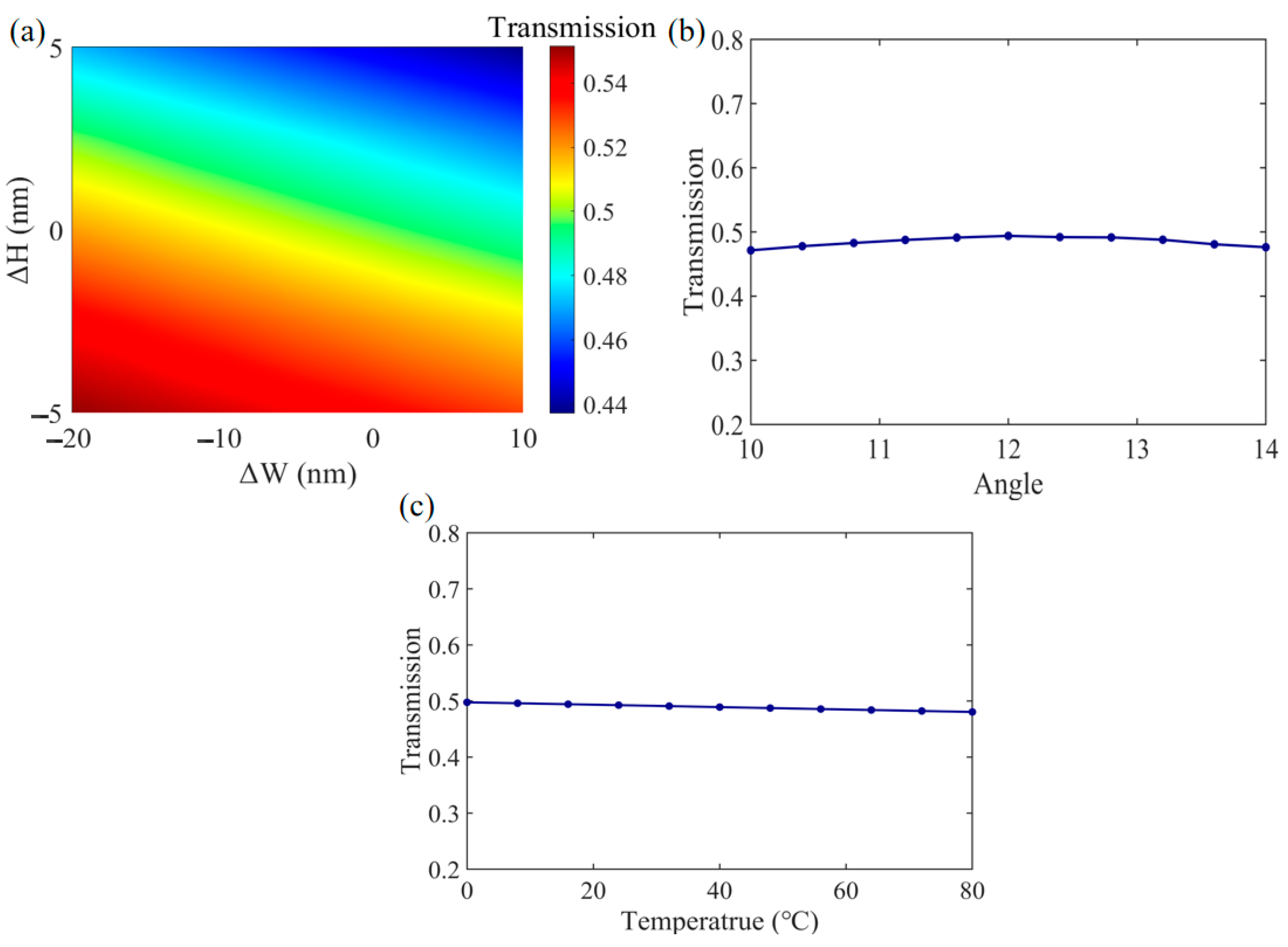
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pitris, S.; Moralis-Pegios, M.; Alexoudi, T.; Ban, Y.; De Heyn, P.; Van Campenhout, J.; Lambrecht, J.; Ramon, H.; Yin, X.; Bauwelinck, J.; et al. O-Band Silicon Photonic Transmitters for Datacom and Computercom Interconnects. J. Light. Technol. 2001, 37, 5140–5148. [Google Scholar] [CrossRef]
- Siew, S.Y.; Li, B.; Gao, F.; Zheng, H.Y.; Zhang, W.; Guo, P.; Xie, S.W.; Song, A.; Dong, B.; Luo, L.W.; et al. Review of Silicon Photonics Technology and Platform Development. J. Light. Technol. 2021, 39, 4374–4389. [Google Scholar] [CrossRef]
- Zhu, J.; Chao, Q.; Huang, H.; Zhao, Y.; Li, Y.; Tao, L.; She, X.; Liao, H.; Huang, R.; Zhu, Z.; et al. Compact, broadband, and low-loss silicon photonic arbitrary ratio power splitter using adiabatic taper. Appl. Opt. 2021, 60, 413–416. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, T.; Zhang, K.; Li, M.; Liu, H.; Li, H.; Niu, P.; Gu, E. Bidirectional grating based interleaved angled MMI for high-uniformity wavelength division (de)multiplexing and surface-normal fiber packaging. Appl. Opt. 2021, 60, 5615–5622. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.F.R.; Choi, J.W.; Sahin, E.; Tan, D.T.H.; Ng, D.K.T. On-chip 1 by 8 coarse wavelength division multiplexer and multi-wavelength source on ultra-silicon-rich nitride. Opt. Express 2019, 27, 23549–23557. [Google Scholar] [CrossRef]
- Xue, X.; Ji, W.; Huang, K.; Li, X.; Zhang, S. Tunable Multiwavelength Optical Comb Enabled WDM-OFDM-PON With Source-Free ONUs. IEEE Photonics J. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Xu, M.; Liu, C.; Subramaniam, S. PODCA: A passive optical data center network architecture. J. Opt. Commun. Netw. 2018, 10, 409–420. [Google Scholar] [CrossRef]
- Totovic, A.; Giamougiannis, G.; Tsakyridis, A.; Pleros, N.; Lazovsky, D. Programmable photonic neural networks combining WDM with coherent linear optics. Sci. Rep. 2022, 12, 5605. [Google Scholar] [CrossRef] [PubMed]
- Moralis-Pegios, M.; Mourgias-Alexandris, G.; Tsakyridis, A.; Giamougiannis, G.; Totovic, A.; Dabos, G.; Passalis, N.; Kirtas, M.; Tefas, A.; Pleros, N.; et al. Neuromorphic Silicon Photonics and Hardware-Aware Deep Learning for High-Speed Inference. J. Light. Technol. 2022, 40, 3243–3254. [Google Scholar] [CrossRef]
- Qing, F.; Jun, F.S.; Tsung-Yang, L.; Hong, C.; Ming, B.Y.; Guo, Q.L.; Dim-Lee, K. Ultralow Power Silicon Photonics Thermo-Optic Switch With Suspended Phase Arms. IEEE Photonics Technol. Lett. 2011, 23, 525–527. [Google Scholar]
- Chu, T.; Yamada, H.; Ishida, S.; Arakawa, Y. Compact 1 × N thermo-optic switches based on silicon photonic wire waveguides. Opt. Express 2005, 13, 10109–10114. [Google Scholar] [CrossRef]
- Heck, M.J.R. Highly integrated optical phased arrays: Photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107. [Google Scholar] [CrossRef]
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LIDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef]
- Thomson, D.J.; Hu, Y.; Reed, G.T.; Fedeli, J.-M. Low Loss MMI Couplers for High Performance MZI Modulators. IEEE Photonics Technol. Lett. 2010, 22, 1485–1487. [Google Scholar] [CrossRef]
- Liao, L.; Samara-Rubio, D.; Morse, M.; Liu, A.; Hodge, D.; Rubin, D.; Keil, U.D.; Franck, T. High speed silicon Mach-Zehnder modulator. Opt. Express 2005, 13, 3129–3135. [Google Scholar] [CrossRef]
- Palmer, R.; Alloatti, L.; Korn, D.; Schindler, P.C.; Baier, M.; Bolten, J.; Wahlbrink, T.; Waldow, M.; Dinu, R.; Freude, W.; et al. Low Power Mach–Zehnder Modulator in Silicon-Organic Hybrid Technology. IEEE Photonics Technol. Lett. 2013, 25, 1226–1229. [Google Scholar] [CrossRef]
- Xu, K.; Liu, L.; Wen, X.; Sun, W.; Zhang, N.; Yi, N.; Sun, S.; Xiao, S.; Song, Q. Integrated photonic power divider with arbitrary power ratios. Opt. Lett. 2017, 42, 855–858. [Google Scholar] [CrossRef] [PubMed]
- Zanzi, A.; Brimont, A.; Griol, A.; Sanchis, P.; Marti, J. Compact and low-loss asymmetrical multimode interference splitter for power monitoring applications. Opt. Lett. 2016, 41, 227–229. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, S.; Galland, C.; Baehr-Jones, T.; Hochberg, M.; Eu-Jin Lim, A.; Lo, G.-Q. A compact and low loss Y-junction for submicron silicon waveguide. Opt. Express 2013, 21, 1310–1316. [Google Scholar] [CrossRef] [PubMed]
- Yamada, H.; Tao, C.; Ishida, S.; Arakawa, Y. Optical directional coupler based on Si-wire waveguides. IEEE Photonics Technol. Lett. 2005, 17, 585–587. [Google Scholar] [CrossRef]
- Lu, Z.; Yun, H.; Wang, Y.; Chen, Z.; Zhang, F.; Jaeger, N.A.F.; Chrostowski, L. Broadband silicon photonic directional coupler using asymmetric-waveguide based phase control. Opt. Express 2015, 23, 3795–3808. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Wang, Y.; Kumar, A.; El-Fiky, E.; Mao, D.; Tamazin, H.; Jacques, M.; Xing, Z.; Saber, M.G.; Plant, D.V. Compact high-performance adiabatic 3-dB coupler enabled by subwavelength grating slot in the silicon-on-insulator platform. Opt. Express 2018, 26, 29873–29885. [Google Scholar] [CrossRef]
- Mao, D.; Alam, M.S.; Zhang, J.; Zhu, M.; Koh, P.; Plant, D.V.; Wang, Y.; El-Fiky, E.; Xu, L.; Kumar, A.; et al. Adiabatic Coupler With Design-Intended Splitting Ratio. J. Light. Technol. 2019, 37, 6147–6155. [Google Scholar] [CrossRef]
- Haus, H.A.; Huang, W. Coupled-mode theory. Proc. IEEE 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Shiratori, R.; Nakata, M.; Hayashi, K.; Baba, T. Particle swarm optimization of silicon photonic crystal waveguide transition. Opt. Lett. 2021, 46, 1904–1933. [Google Scholar] [CrossRef]
- Fu, P.H.; Tu, Y.C.; Huang, D.W. Broadband optical waveguide couplers with arbitrary coupling ratios designed using a genetic algorithm. Opt. Express 2016, 24, 30547–30561. [Google Scholar] [CrossRef]
- Xu, Y.; Xie, T.; Zhang, Z.; Ma, H.; Yang, J. Ultra-compact power splitters with low loss in arbitrary direction based on inverse design method. Photonics 2021, 8, 516. [Google Scholar] [CrossRef]
- Leng, L.; Jin, M.; Lin, Z.; Zhang, C.; Ding, D.; Jiang, W. Ultra-Broadband, Fabrication Tolerant Optical Coupler for Arbitrary Splitting Ratio Using Particle Swarm Optimization Algorithm. IEEE Photonics J. 2020, 12, 1–12. [Google Scholar] [CrossRef]
- Hung, Y.J.; Chen, C.H.; Lu, G.X.; Liang, F.C.; Chung, H.C.; Tseng, S.Y. Compact and robust 2 × 2 fast quasi-adiabatic 3-dB couplers on SOI strip waveguides. Opt. Laser Technol. 2022, 145, 107485. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Z.; Ma, M.; Yun, H.; Zhang, F.; Jaeger, N.A.F.; Chrostowski, L. Compact Broadband Directional Couplers Using Subwavelength Gratings. IEEE Photonics J. 2016, 8, 1–8. [Google Scholar]
- Halir, R.; Maese-Novo, A.; Ortega-Monux, A.; Molina-Fernández, I.; Wangüemert-Pérez, J.G.; Cheben, P.; Xu, D.X.; Schmid, J.H.; Janz, S. Colorless directional coupler with dispersion engineered sub-wavelength structure. Opt. Express 2012, 20, 13470–13477. [Google Scholar] [CrossRef] [PubMed]

| Symbol | Value | Symbol | Value |
|---|---|---|---|
| W0 | 0.45 μm | G2 | 0.11 μm |
| R0 | 55 μm | G3 | 0.11 μm |
| θ | 12.4 | G4 | 1.5 μm |
| G1 | 0.125 μm |
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| c1 | 1.2 | Particle swarms | 500 |
| c2 | 1.4 | G | 20 |
| 1 | D | 22 | |
| 0.4 | rand | [0,1] |
| Symbol | Value (nm) | Symbol | Value (nm) | Symbol | Value (nm) |
|---|---|---|---|---|---|
| R1 | 155.7 | R9 | 263.6 | R17 | 198.8 |
| R2 | 176.3 | R10 | 258.4 | R18 | 209.9 |
| R3 | 254.7 | R11 | 214.1 | R19 | 216.7 |
| R4 | 174.5 | R12 | 218.3 | R20 | 223.4 |
| R5 | 226.2 | R13 | 217.6 | R21 | 262.6 |
| R6 | 255.1 | R14 | 212.3 | R22 | 242.5 |
| R7 | 267 | R15 | 174.5 | ||
| R8 | 243.1 | R16 | 251.6 |
| Reference | Type | Dimension (μm) | Bandwidth (nm) | EL (dB) |
|---|---|---|---|---|
| [17] | QR code MMI | 3.6 | 30 | 0.97 |
| [22] | SWG, ADC | 65 | 100 | <0.2 |
| [23] | Adiabatic tapers | 240 | 100 | 1 |
| [26] | Inverse design, MMI | 2.4 | 30 | 0.69 |
| [3] | Triple waveguides, DC | 80 | 100 | 0.05 |
| [27] | FAQUAD, strip | 53.7 | 75 | N/A |
| This work | Inverse design, DC | 11.9 | 60 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhao, Y.; Zhu, Z.; Liu, H.; Gan, F. Particle Swarm Optimized Compact, Low Loss 3-dB Power Splitter Enabled by Silicon Columns in Silicon-on-Insulator. Photonics 2023, 10, 419. https://doi.org/10.3390/photonics10040419
Liu X, Zhao Y, Zhu Z, Liu H, Gan F. Particle Swarm Optimized Compact, Low Loss 3-dB Power Splitter Enabled by Silicon Columns in Silicon-on-Insulator. Photonics. 2023; 10(4):419. https://doi.org/10.3390/photonics10040419
Chicago/Turabian StyleLiu, Xiang, Yingxuan Zhao, Zijian Zhu, Hongbao Liu, and Fuwan Gan. 2023. "Particle Swarm Optimized Compact, Low Loss 3-dB Power Splitter Enabled by Silicon Columns in Silicon-on-Insulator" Photonics 10, no. 4: 419. https://doi.org/10.3390/photonics10040419
APA StyleLiu, X., Zhao, Y., Zhu, Z., Liu, H., & Gan, F. (2023). Particle Swarm Optimized Compact, Low Loss 3-dB Power Splitter Enabled by Silicon Columns in Silicon-on-Insulator. Photonics, 10(4), 419. https://doi.org/10.3390/photonics10040419





