Modulation of the Multiple Bound States in the Continuum of the All-Dielectric Metasurface
Abstract
1. Instruction
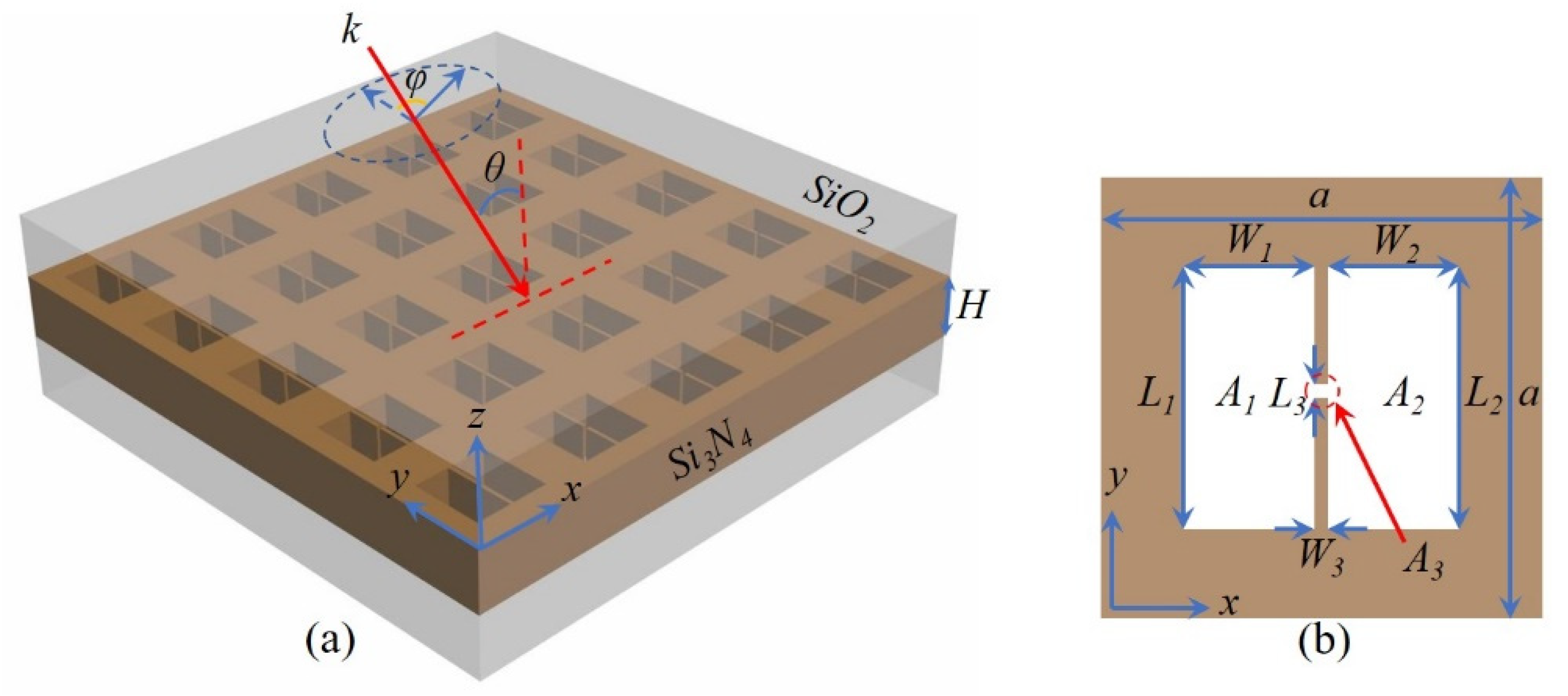
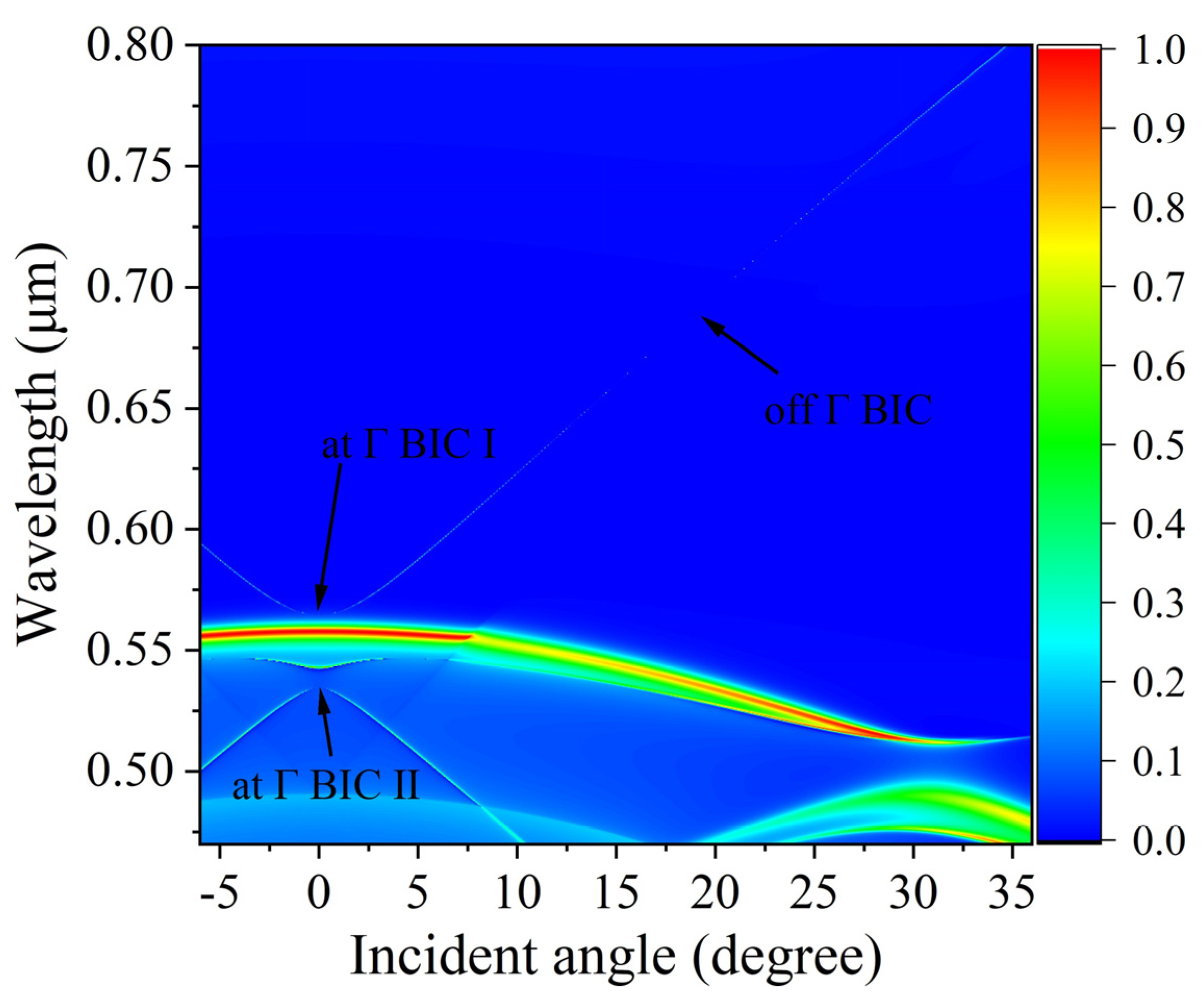
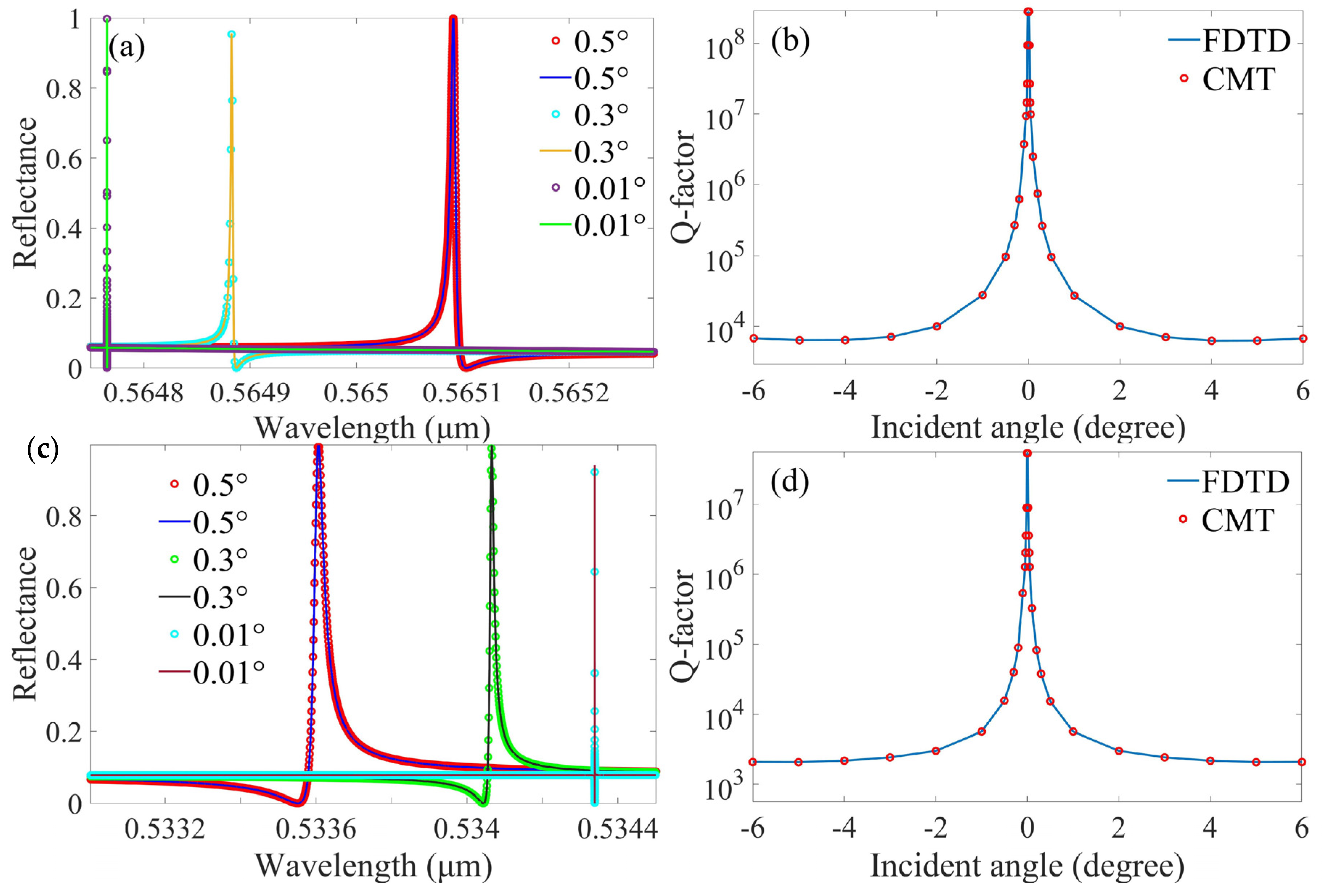
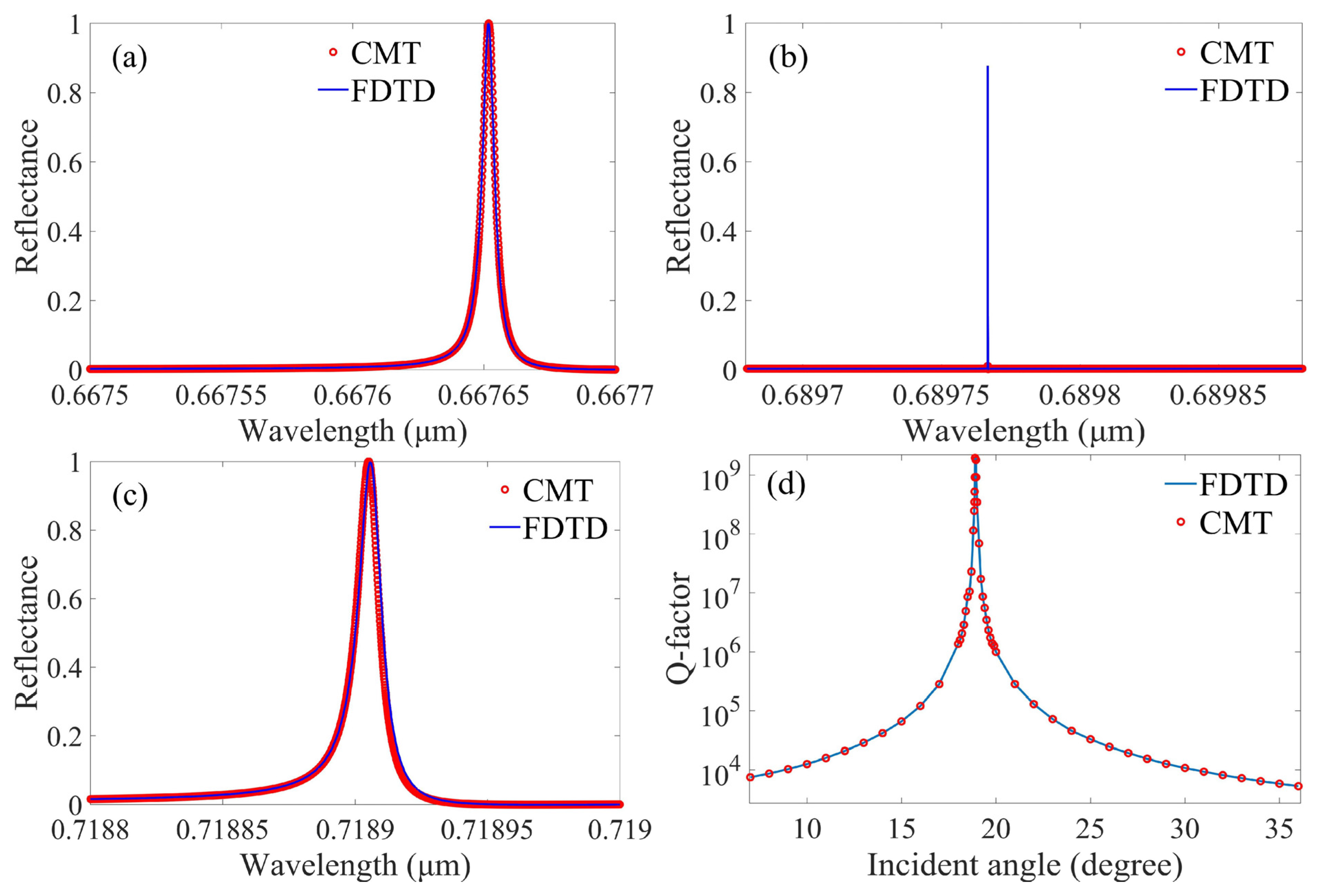
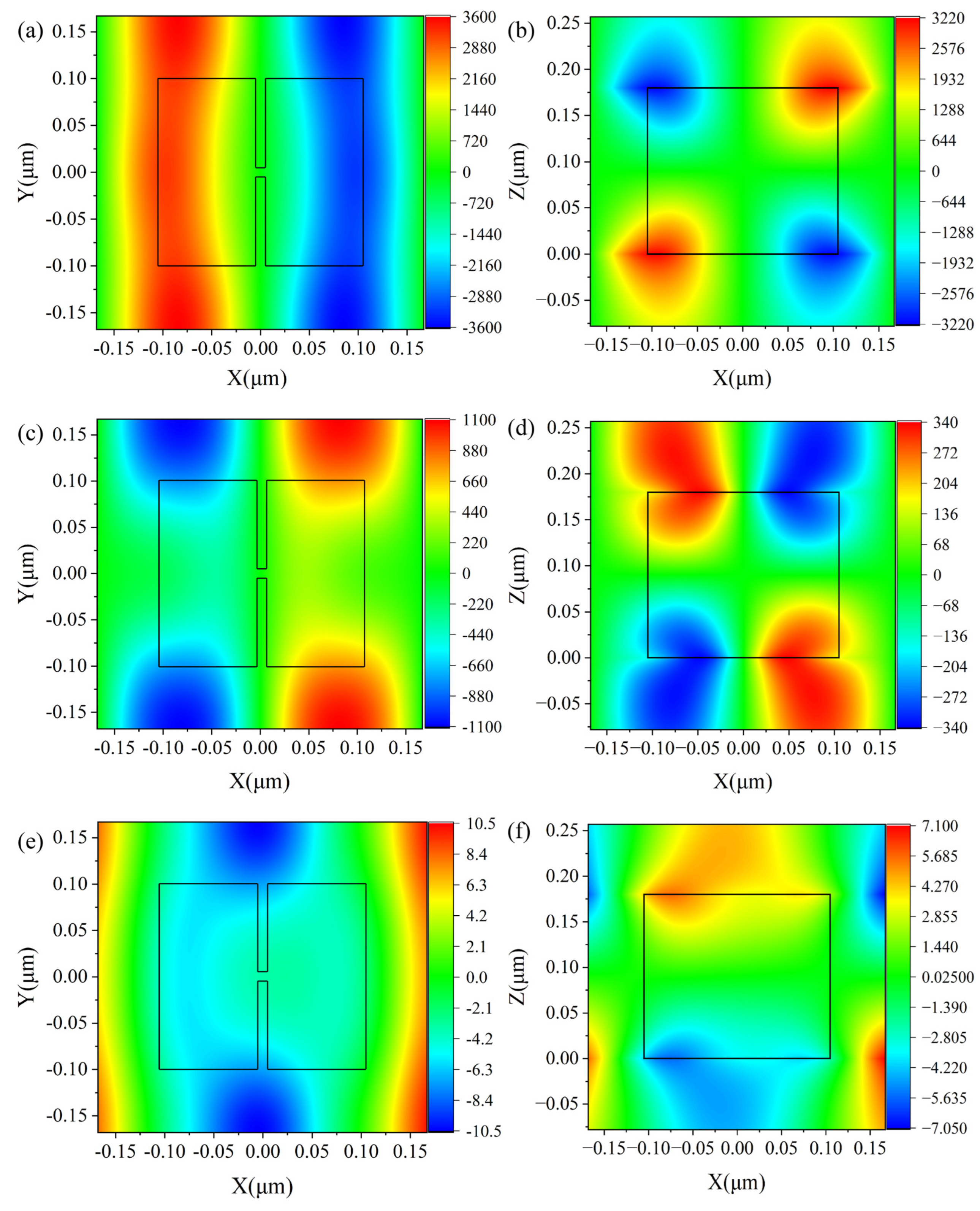
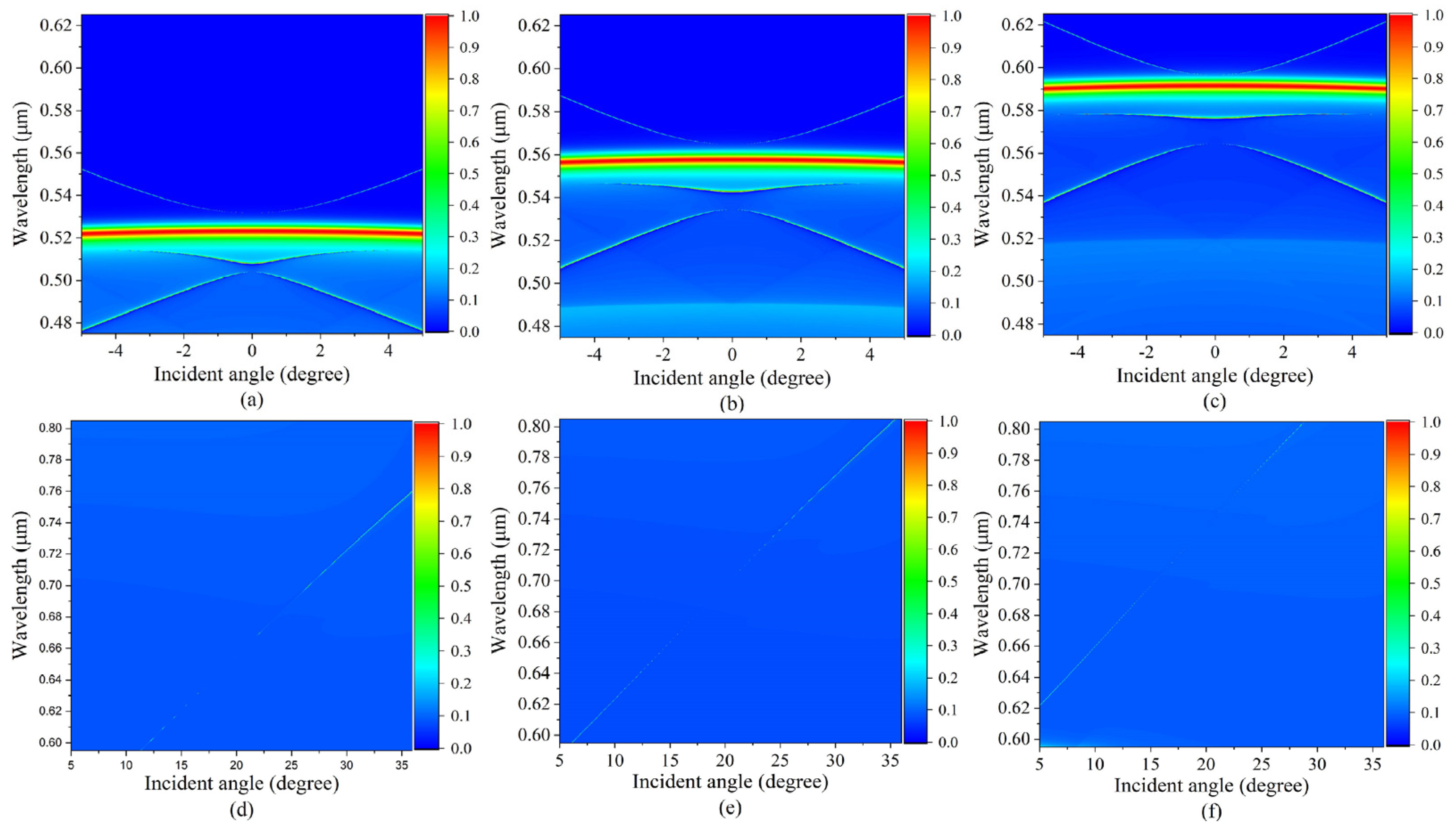
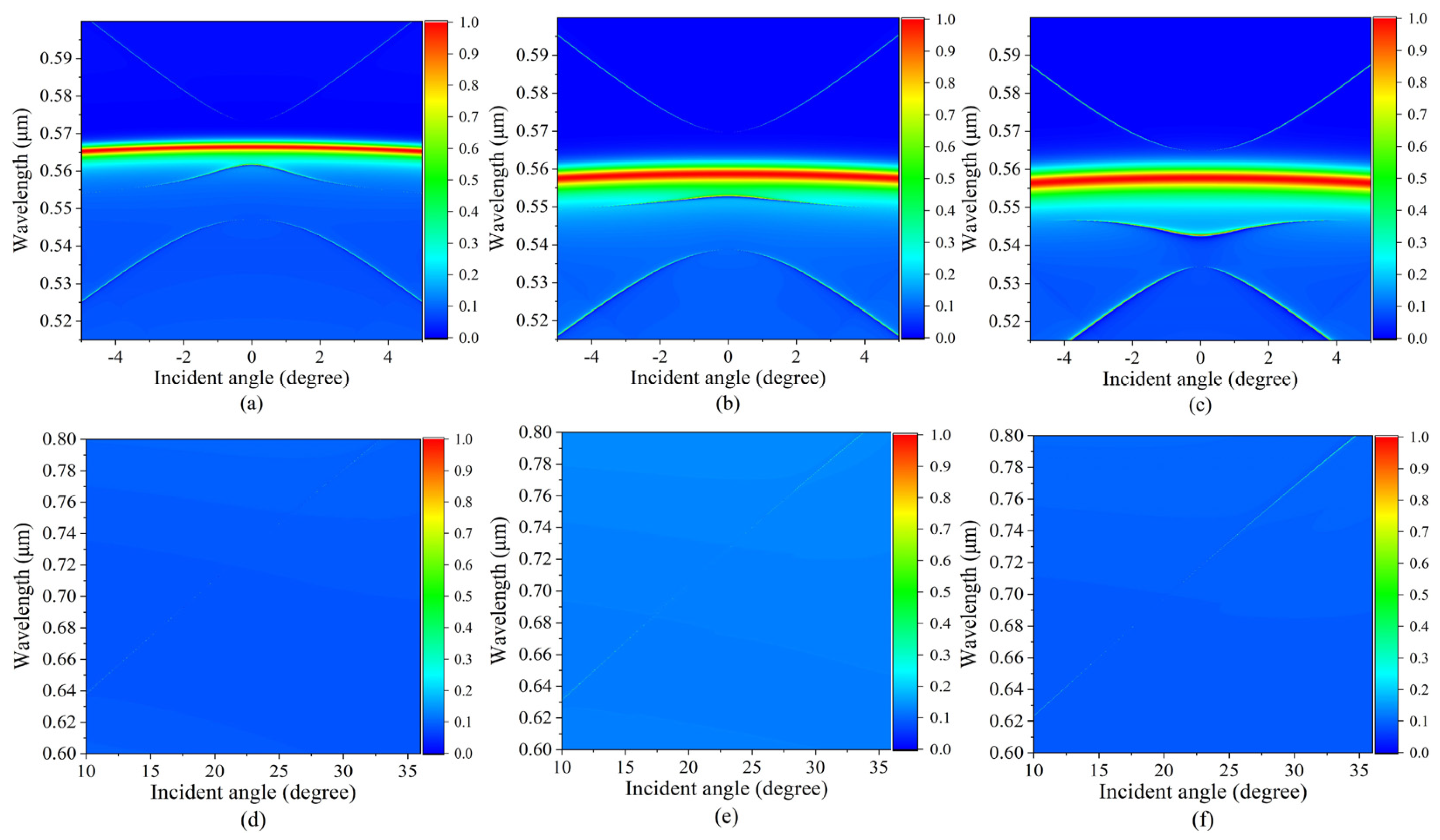
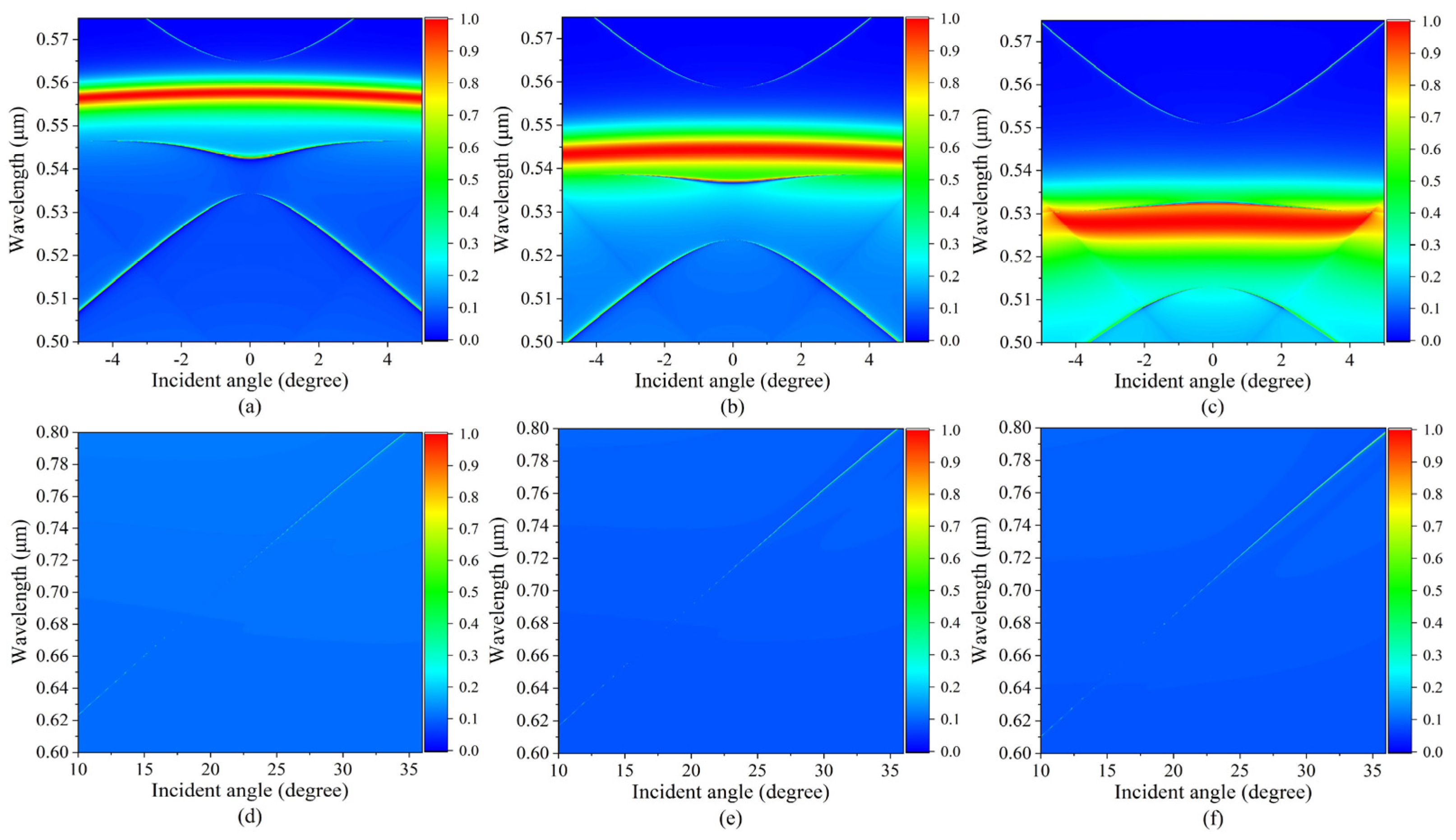
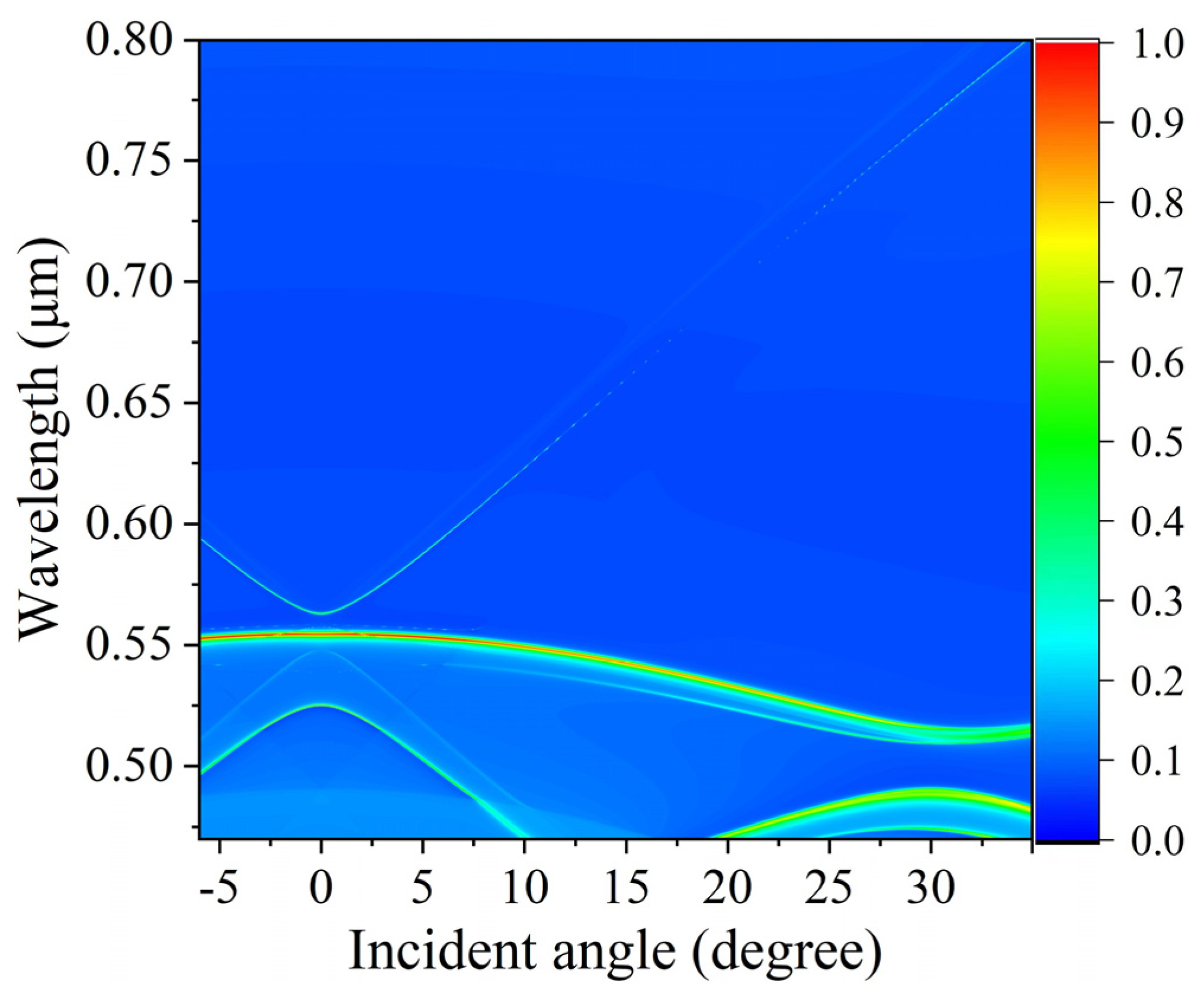
2. Results and Discussions
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ursell, F. Trapping modes in the theory of surface waves. Math. Proc. Camb. Philos. Soc. 1951, 47, 347–358. [Google Scholar] [CrossRef]
- Robnik, M. A simple separable Hamiltonian having bound states in the continuum. J. Phys. A Math. Gen. 1986, 19, 3845–3848. [Google Scholar] [CrossRef]
- Ursell, F. Trapped modes in a circular cylindrical acoustic waveguide. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 435, 575–589. [Google Scholar]
- Evans, D.; Linton, C.; Ursell, F. Trapped mode frequencies embedded in the continuous spectrum. Q. J. Mech. Appl. Math. 1993, 46, 253–274. [Google Scholar] [CrossRef]
- Lee, J.; Zhen, B.; Chua, S.-L.; Qiu, W.; Joannopoulos, J.; Soljačić, M.; Shapira, O. Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs. Phys. Rev. Lett. 2012, 109, 067401. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of trapped light within the radiation continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Sadreev, A.F. Bound states in the continuum in photonic waveguides inspired by defects. Phys. Rev. B 2008, 78, 075105. [Google Scholar] [CrossRef]
- Plotnik, Y.; Peleg, O.; Dreisow, F.; Heinrich, M.; Nolte, S.; Szameit, A.; Segev, M. Experimental Observation of Optical Bound States in the Continuum. Phys. Rev. Lett. 2011, 107, 183901. [Google Scholar] [CrossRef]
- Weimann, S.; Xu, Y.; Keil, R.; Miroshnichenko, A.; Tünnermann, A.; Nolte, S.; Sukhorukov, A.; Szameit, A.; Kivshar, Y.S. Compact Surface Fano States Embedded in the Continuum of Waveguide Arrays. Phys. Rev. Lett. 2013, 111, 240403. [Google Scholar] [CrossRef]
- González, J.W.; Pacheco, M.; Rosales, L.; Orellana, P.A. Bound states in the continuum in graphene quantum dot structures. EPL Europhys. Lett. 2010, 91, 66001. [Google Scholar] [CrossRef]
- Azzam, S.I.; Shalaev, V.M.; Boltasseva, A.; Kildishev, A.V. Formation of Bound States in the Continuum in Hybrid Plasmonic-Photonic Systems. Phys. Rev. Lett. 2018, 121, 253901. [Google Scholar] [CrossRef] [PubMed]
- Sadrieva, Z.; Frizyuk, K.; Petrov, M.; Kivshar, Y.; Bogdanov, A. Multipolar origin of bound states in the continuum. Phys. Rev. B 2019, 100, 115303. [Google Scholar] [CrossRef]
- Kupriianov, A.S.; Xu, Y.; Sayanskiy, A.; Dmitriev, V.; Kivshar, Y.S.; Tuz, V.R. Metasurface Engineering through Bound States in the Continuum. Phys. Rev. Appl. 2019, 12, 014024. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, D.; Joannopoulos, J.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Xu, L.; Rahmani, M.; Ma, Y.; Smirnova, D.A.; Kamali, K.Z.; Deng, F.; Chiang, Y.K.; Huang, L.; Zhang, H.; Gould, S.; et al. Enhanced light–matter interactions in dielectric nanostructures via machine-learning approach. Adv. Photon. 2020, 2, 026003. [Google Scholar] [CrossRef]
- Huang, L.; Xu, L.; Rahmani, M.; Neshev, D.; Miroshnichenko, A.E. Pushing the limit of high-Q mode of a single dielectric nanocavity. Adv. Photon. 2021, 3, 016004. [Google Scholar] [CrossRef]
- Huang, L.; Xu, L.; Woolley, M.; Miroshnichenko, A. Trends in quantum nanophotonics. Adv. Quantum Technol. 2020, 3, 1900126. [Google Scholar] [CrossRef]
- Liu, T.; Qin, M.; Wu, F.; Xiao, S. High-efficiency optical frequency mixing in an all-dielectric metasurface enabled by multiple bound states in the continuum. Phys. Rev. B 2023, 107, 075441. [Google Scholar] [CrossRef]
- Xiao, S.; Qin, M.; Duan, J.; Wu, F.; Liu, T. Polarization-controlled dynamically switchable high-harmonic generation from all-dielectric metasurfaces governed by dual bound states in the continuum. Phys. Rev. B 2022, 105, 195440. [Google Scholar] [CrossRef]
- von Neumann, J.; Wigner, E. Über merkwürdige diskrete Eigenwerte. In The Collected Works of Eugene Paul Wigner: Part A: The Scientific Papers; Springer: Berlin/Heidelberg, Germany, 1993; pp. 291–293. [Google Scholar]
- Watts, M.R.; Johnson, S.; Haus, H.A.; Joannopoulos, J.D. Electromagnetic cavity with arbitrary Q and small modal volume without a complete photonic bandgap. Opt. Lett. 2002, 27, 1785–1787. [Google Scholar] [CrossRef]
- Marinica, D.C.; Borisov, A.G.; Shabanov, S.V. Bound States in the Continuum in Photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef]
- Molina, M.I.; Miroshnichenko, A.E.; Kivshar, Y.S. Surface Bound States in the Continuum. Phys. Rev. Lett. 2012, 108, 070401. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Bloch surface eigenstates within the radiation continuum. Light. Sci. Appl. 2013, 2, e84. [Google Scholar] [CrossRef]
- Linton, C.; McIver, P. Embedded trapped modes in water waves and acoustics. Wave Motion 2007, 45, 16–29. [Google Scholar] [CrossRef]
- Hirose, K.; Liang, Y.; Kurosaka, Y.; Watanabe, A.; Sugiyama, T.; Noda, S. Watt-class high-power, high-beam-quality photonic-crystal lasers. Nat. Photon. 2014, 8, 406–411. [Google Scholar] [CrossRef]
- Wierer, J.J.; David, A.; Megens, M.M. III-nitride photonic-crystal light-emitting diodes with high extraction efficiency. Nat. Photon 2009, 3, 163–169. [Google Scholar] [CrossRef]
- Ganesh, N.; Zhang, W.; Mathias, P.; Chow, E.; Soares, J.A.N.T.; Malyarchuk, V.; Smith, A.D.; Cunningham, B.T. Enhanced fluorescence emission from quantum dots on a photonic crystal surface. Nat. Nanotechnol. 2007, 2, 515–520. [Google Scholar] [CrossRef]
- Zhen, B.; Chua, S.-L.; Lee, J.; Rodriguez, A.W.; Liang, X.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M.; Shapira, O. Enabling enhanced emission and low-threshold lasing of organic molecules using special Fano resonances of macroscopic photonic crystals. Proc. Natl. Acad. Sci. USA 2013, 110, 13711–13716. [Google Scholar] [CrossRef] [PubMed]
- Zhen, B.; Hsu, C.W.; Lu, L.; Stone, A.D.; Soljačić, M. Topological Nature of Optical Bound States in the Continuum. Phys. Rev. Lett. 2014, 113, 257401. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.; Joannopoulos, J.D. Analysis of guided resonances in photonic crystal slabs. Phys. Rev. B 2002, 65, 235112. [Google Scholar] [CrossRef]
- Pacradouni, V.; Mandeville, W.; Cowan, A.; Paddon, P.; Young, J.; Johnson, S. Photonic band structure of dielectric membranes periodically textured in two dimensions. Phys. Rev. B 2000, 62, 4204. [Google Scholar] [CrossRef]
- Yoon, J.W.; Song, S.H.; Magnusson, R. Critical field enhancement of asymptotic optical bound states in the continuum. Sci. Rep. 2015, 5, 18301. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the Fano resonance in optical resonators. J. Opt. Soc. Am. A 2003, 20, 569–572. [Google Scholar] [CrossRef]
- Wu, F.; Luo, M.; Wu, J.; Fan, C.; Qi, X.; Jian, Y.; Liu, D.; Xiao, S.; Chen, G.; Jiang, H.; et al. Dual quasibound states in the continuum in compound grating waveguide structures for large positive and negative Goos-Hänchen shifts with perfect reflection. Phys. Rev. A 2021, 104, 023518. [Google Scholar] [CrossRef]
- Wang, X.; Duan, J.; Chen, W.; Zhou, C.; Liu, T.; Xiao, S. Controlling light absorption of graphene at critical coupling through magnetic dipole quasi-bound states in the continuum resonance. Phys. Rev. B 2020, 102, 155432. [Google Scholar] [CrossRef]
- Hu, Y.; Tong, M.; Hu, S.; He, W.; Cheng, X.; Jiang, T. Spatiotemporal Lineshape Tailoring in BIC-Mediated Reconfigurable Metamaterials. Adv. Funct. Mater. 2022, 32, 2203680. [Google Scholar] [CrossRef]
- Hu, Y.; Xie, S.; Bai, C.; Shen, W.; Yang, J. Multiple photonic bound states in the continuum in an electromagnetically induced transparency metasurface. IEEE Photon. J. 2022, 14, 1–9. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Y.; Lin, Y.; Xiang, J.; Feng, T.; Cao, Q.; Li, J.; Lan, S.; Liu, J. High-Q quasibound states in the continuum for nonlinear metasurfaces. Phys. Rev. Lett. 2019, 123, 253901. [Google Scholar] [CrossRef]
- Xie, S.; Xie, S.; Zhan, J.; Xie, C.; Tian, G.; Li, Z.; Liu, Q. Bound States in the Continuum in a T-Shape Nanohole Array Perforated in a Photonic Crystal Slab. Plasmonics 2020, 15, 1261–1271. [Google Scholar] [CrossRef]
- Xie, S.; Xie, S.; Li, Z.; Tian, G.; Zhan, J.; Liu, Q. Observation of an Optical Bound State in Photonic Crystal Slabs with U-Shape Nanohole Array. Plasmonics 2021, 17, 399–407. [Google Scholar] [CrossRef]
- Li, H.; Zhou, H.; Wei, G.; Xu, H.; Qin, M.; Liu, J.; Wu, F. Photonic spin-selective perfect absorptance on planar metasurfaces driven by chiral quasi-bound states in the continuum. Nanoscale 2023, 15, 6636–6644. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Xu, L.; Powell, D.A.; Padilla, W.J.; Miroshnichenko, A.E. Resonant leaky modes in all-dielectric metasystems: Fundamentals and applications. Phys. Rep. 2023, 1008, 1–66. [Google Scholar] [CrossRef]
- Liu, C.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Zhang, B.; Wu, K. Slow light effect based on tunable plasmon-induced transparency of monolayer black phosphorus. J. Phys. D Appl. Phys. 2019, 52, 405203. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Liu, C.; Wu, K. Absorption and slow-light analysis based on tunable plasmon-induced transparency in patterned graphene metamaterial. Opt. Express 2019, 27, 3598–3608. [Google Scholar] [CrossRef] [PubMed]
- Suh, W.; Wang, Z.; Fan, S. Temporal coupled-mode theory and the presence of non-orthogonal modes in lossless multimode cavities. IEEE J. Quantum Electron. 2004, 40, 1511–1518. [Google Scholar] [CrossRef]
- Li, H.; Wei, G.; Zhou, H.; Xiao, H.; Qin, M.; Xia, S.; Wu, F. Polarization-independent near-infrared superabsorption in transition metal dichalcogenide Huygens metasurfaces by degenerate critical coupling. Phys. Rev. B 2022, 105, 165305. [Google Scholar] [CrossRef]


| BIC | θ | λ0 | γ |
|---|---|---|---|
| at Γ BIC I | 0.01° | 0.5647652 μm | 6 × 106 s−1 |
| 0.3° | 0.5648828 μm | 7 × 109 s−1 | |
| 0.5° | 0.565091 μm | 1.5 × 1010 s−1 | |
| at Γ BIC II | 0.01° | 0.534339 μm | 5 × 107 s−1 |
| 0.3° | 0.534064 μm | 4 × 1010 s−1 | |
| 0.5° | 0.5336022 μm | 9.7 × 1010 s−1 | |
| off Γ BIC | 16° | 0.6676519 μm | 1.2 × 1010 s−1 |
| 19° | 0.6897667 μm | 3.8 × 106 s−1 | |
| 23° | 0.7189055 μm | 1.8 × 1010 s−1 |
| BIC | θ | FWHM | FOM |
|---|---|---|---|
| at Γ BIC I | 0.1° | 3.05 × 10−7 μm | 505,364.83 RIU−1 |
| 0.5° | 7.35 × 10−6 μm | 21,170 RIU−1 | |
| 1° | 2.645 × 10−5 μm | 5986.33 RIU−1 | |
| at Γ BIC II | 0.1° | 1.65 × 10−6 μm | 1198 RIU−1 |
| 0.5° | 3.675 × 10−5 μm | 5301.57 RIU−1 | |
| 1° | 1.116 × 10−4 μm | 1687.87 RIU−1 | |
| off Γ BIC | 16° | 2.41 × 10−5 μm | 12,403.67 RIU−1 |
| 19° | 5.0 × 10−6 μm | 64,472.5 RIU−1 | |
| 23° | 1.8 × 10−6 μm | 195,838 RIU−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Yang, J.; Tian, G.; Shen, W.; Bai, C. Modulation of the Multiple Bound States in the Continuum of the All-Dielectric Metasurface. Photonics 2023, 10, 418. https://doi.org/10.3390/photonics10040418
Xie S, Yang J, Tian G, Shen W, Bai C. Modulation of the Multiple Bound States in the Continuum of the All-Dielectric Metasurface. Photonics. 2023; 10(4):418. https://doi.org/10.3390/photonics10040418
Chicago/Turabian StyleXie, Suxia, Jingcheng Yang, Guang Tian, Weiwei Shen, and Chongjun Bai. 2023. "Modulation of the Multiple Bound States in the Continuum of the All-Dielectric Metasurface" Photonics 10, no. 4: 418. https://doi.org/10.3390/photonics10040418
APA StyleXie, S., Yang, J., Tian, G., Shen, W., & Bai, C. (2023). Modulation of the Multiple Bound States in the Continuum of the All-Dielectric Metasurface. Photonics, 10(4), 418. https://doi.org/10.3390/photonics10040418





