Abstract
In this study, we reconstructed the dynamics of the impact of mid-IR-range (4.6 μm) femtosecond laser pulses on bulk silicon under tight focusing conditions (NA = 0.5). Our experimental results show that under this impact, the deposited energy density (DED) reaches approximately 4 kJ/cm3 (at an energy slightly above the plasma-formation threshold). Initially, the femtosecond pulse energy is absorbed by the laser-induced plasma, with a lifetime of approximately 160–320 fs (depending on the laser pulse energy). The energy transfer from the plasma to the atomic subsystem occurs on a sub-ps timescale, which generates a shock wave and excites coherent phonons on a sub-ps scale. The shift of atoms in the lattice at the front of the shock wave results in a cascade of phase transitions (Si-X => Si-VII => Si-VI => Si-XI => Si-II), leading to a change in the phonon spectra of silicon.
1. Introduction
The field of silicon photonics is a rapidly developing area of research due to the fact that modern microelectronics are primarily based on silicon, making the development of photonic circuits in semiconductors crucial [1,2]. Although generating three-dimensional photonic circuits in dielectrics is relatively easy with ultra-short laser pulses, this technology cannot be adapted for silicon due to its high refractive index, which weakens the effective focusing strength and reduces the laser impact area [3,4,5,6,7]. Silicon’s small band gap (~1.1 eV) and high number of free electrons also limit the use of commercially available lasers [6,7]. Moreover, due to the presence of a sufficiently large number of free electrons, even when exposed to ultra-short laser pulses with a wavelength greater than 1100 nm, microplasma is efficiently generated, which effectively increases the laser impact area, leading to a drop in the deposited energy density (DED) [8]. To overcome these challenges, several approaches have been proposed [9], including the use of nano- and picosecond laser pulses at a wavelength of ~2 μm [10], femtosecond laser pulses at a wavelength of ~4 μm [11], hyperfocusing [6], and an additional pulse to create pre-plasma [12,13]. Among these methods, femtosecond pulses in the mid-IR range (4.6 μm) are the most successful for creating micromodifications in bulk silicon with a single shot. Femtosecond lasers at a ~4.6 μm wavelength offer high-precision processing of silicon with minimal damage to surrounding areas, even inside the volume of the Si sample [11]. This is important for the micro- and nanofabrication of silicon-based devices [1]. The use of femtosecond lasers for silicon processing results in reduced thermal damage compared to longer-pulse-duration lasers. This is due to the shorter pulse duration of femtosecond lasers, which limits the heat-affected zone during processing [3]. Additionally, the laser impact on the material at 4.6 μm could induce several new polymorph phases.
However, little is known about the fundamental processes behind the laser impact on the material, particularly the energy transfer from the electronic to the atomic subsystem, which can lead to irreversible changes in the structural properties of the material. Due to the fundamental complexity of the investigation of laser-induced processes inside semiconductors, this process is monitored during laser ablation when the laser pulse is focused onto the Si surface. In most cases, the energy transfer from laser pulses to Si is performed with ns laser pulses [14,15]. It has been demonstrated that the laser impact on the Si surface can induce several phase transitions to different polymorphs of Si such as β-Sn, Imma, hcp, and other phases [16]. The new phases can be observed by post-mortem analysis [17], during time-resolved X-ray experiments [18], or in optical pump-probe experiments [19,20,21]. However, the dynamics of this phase transition heavily depend on the laser pulse energy and duration.
The energy transport from the laser pulse to the lattice occurs in several stages, including the generation of an electron plasma, energy transfer to the atomic subsystem, and ultra-fast melting and shock-wave generation [22,23]. This leads to the shifting of atoms inside the lattice, resulting in a phase transition and changes in the phonon spectrum [13,24,25]. However, most experiments have been performed near or at the boundary of silicon samples, which can drastically affect the dynamics.
In this study, we experimentally investigated the dynamics of a 160 fs laser pulse with a wavelength of 4.55 μm focused by a reflective objective with NA = 0.5 into bulk silicon. We reconstructed the dynamics of plasma formation and coherent phonon generation to gain insight into the fundamental processes behind laser-induced modifications in silicon.
2. Materials and Methods
In the experiments, the radiation of an Fe:ZnSe laser system (central wavelength of 4.6 µm, pulse duration of 160 fs (FWHM), repetition rate of 10 Hz) was used. For estimating the deposited energy density, we used an experimental setup similar to that described in [26] (see Figure 1). The incoming laser pulse was focused inside a Si sample (2 × 2 × 2 mm high, Tydex Ltd., St. Petersburg, Russia) by a reflective objective (LMM40X-P01, Thorlabs, Newton, USA) with NA = 0.5. The transmitted laser radiation was collimated by an aspheric lens (390037-E, Thorlabs) with NA = 0.85. The sample was mounted onto a motorized XYZ stage (8MT184, Standa, Vilnius, Lithuania) and was shifted from pulse to pulse with a 2.5 μm step. The incoming (Ein) and transmitted (Eout) energies were monitored by a pair of calibrated amplified PbSe photodetectors (PDA20H, Thorlabs). The input and output energies were controlled simultaneously. The laser pulse energy was varied by a half-wave plate and polarizer (WP12LM-IRA, Thorlabs). We obtained the transmitted energy for different input energies, as shown in Figure 2a. The volume of the microplasma was monitored by obtaining its luminescence, as described in [27], using a CCD camera (MindVision ME-GE130GMT). Si has several atomic lines in the near-IR range (1100–1300 nm) and the intensity of their luminescence (1203, 1210, and 1229 nm lines) is proportional to the electron concentration [27]. Therefore, the area where the microplasma is generated can be obtained through microscopy. The deposited energy density (DED = Eabs/Vplasma) is the ratio of the absorbed energy (Eabs = Ein − Eout) to the microplasma volume [8]. Therefore, DED can be calculated by measuring the absorbed energy and plasma volume.
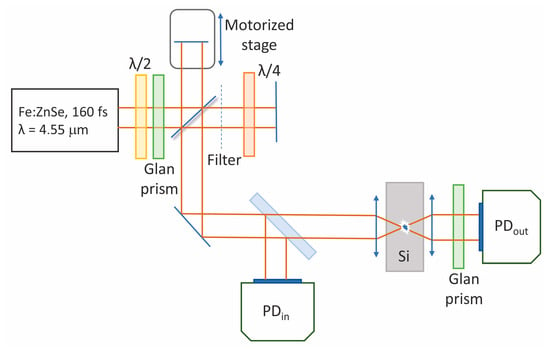
Figure 1.
Experimental setup. The energy of the laser pulse is controlled by a half-wave plate and a Glan prism. The initial laser pulse is split into pump and probe pulses using a Michelson interferometer. The polarization of the pump pulse is orthogonal to the probe pulse. The energy of the laser pulse transmitted through the sample is controlled by a photodetector.
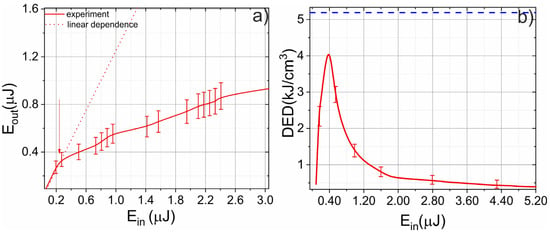
Figure 2.
(a) Dependence of the transmitted energy on the input laser energy. The dashed line indicates the linear dependence and the arrow indicates the plasma-formation threshold. (b) Dependence of deposited energy density (DED) on the input laser energy. The dashed line indicates the threshold of the micromodification formation.
For time-resolved diagnostics of the laser-induced microplasma, we used a Michelson interferometer similar to the one described in [28]. One of the mirrors was placed on the motorized translator (step is 1.25 µm). By varying the optical path, we could control the time delay between the optical pulses in both arms of the interferometer. In one arm of the interferometer, we placed a thin SiO2 plate that decreased the energy of the laser pulse by an order of magnitude. The pulse with lower energy was used as a probe while another pulse was used as a pump. The probe pulse passed through a quarter-wave plate, and on the double path, it changed its polarization to perpendicular with respect to the pump pulse. Therefore, the polarizer placed before the photodetector blocked the pump pulse and transmitted the probe pulse. We monitored the energy of the transmitted pulse and its third harmonic for different time delays, similar to [29]. To suppress the signal from the pump pulse, we placed a polarizer before the photodetector (the polarization of pump and probe pulses is different).
3. Results and Discussion
In the first series of experiments, we measured the plasma-generation threshold, absorbed energy, and deposited energy density (DED). We simultaneously monitored the input and transmitted energy while varying the laser pulse energy, as shown in Figure 2a. At low energies, there was no absorption, because the microplasma was not generated. When the laser pulse energy surpassed the threshold (~250 nJ), the dependence of the transmitted energy on the input energy deviated from linear because the microplasma started to absorb the laser pulse energy (see Figure 2a). We also calculated the DED for a wide range of laser pulse energies, as presented in Figure 2b. The DED was close to zero at energies lower than the threshold because there was no absorption. However, the DED began growing after surpassing the threshold. Initially, the absorbed energy increased faster than the plasma volume; however, by increasing the electron concentration and plasma volume, the microplasma “clamps” the intensity in the focal plane and the DED decreased [8]. The maximum DED was achieved at about 1.6 Eth (Eth is the plasma-formation threshold). At these energy levels, plasma defocusing was not a dominant process and we could efficiently deliver energy to the atomic subsystem from the electronic subsystem [11]. It is important to note that the DED was averaged over the whole microplasma volume and the peak values could be higher. However, the observed DED was lower than the threshold value of micromodification formation and no micromodifications were obtained afterward.
In the next series of experiments, we focused on the dynamics of plasma formation and its relaxation. The time-resolved experiment was performed using a Michelson interferometer (see Section 2). We obtained the signal of the third harmonic generated on the microplasma [30] and coherent phonons [29], as well as the energy of the probe pulse transmitted through the sample. As discussed previously, the laser pulse energy was absorbed in the laser-induced microplasma. Therefore, by varying the time delay between the laser-induced plasma excitation and the generation of the third harmonic by the probe pulse, we obtained the evolution of the microplasma, as presented in Figure 3a.
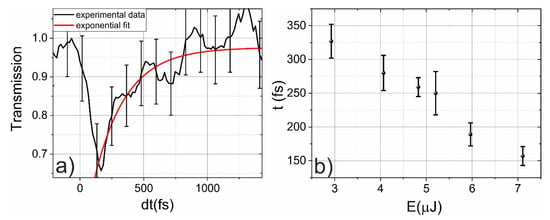
Figure 3.
(a) Dynamics of the change in absorption in the laser-induced plasma. The red line shows exponential fitting. (b) Dependence of plasma relaxation time on the laser pulse energy.
Before the impact of the pump pulse, the transmission was 100%. Then, it rapidly dropped on the laser-pulse-duration timescale (~150 fs) and reached a level of ~65%. Then, the relaxation of the microplasma began. We fit the dynamics of relaxation with an exponential function (1 − (exp(−t/τ))), where τ is the plasma-relaxation time. The dependence of the plasma-relaxation time on the laser pulse energy is presented in Figure 3b. According to [23], the relaxation time of hot electrons in silicon heavily depends on their energy, and electrons with higher energies relax faster. For example, the relaxation time for 3 eV electrons is about 30 fs. This is illustrated in Figure 3b, where the relaxation times of electron plasma decreased from 320 fs in the case of a 3 μJ laser pulse to 160 fs in the case of a 7 μJ laser pulse. It is important to note that in our experiment in the time domain, we were limited by the pulse duration so the relaxation time could be lower than 160 fs.
In the last series of experiments, we retrieved the long-term dynamics of the coherent phonons. This was carried out in an experimental setup similar to the setup used to analyze the dynamics of coherent phonons in transparent dielectrics [31]. In this experiment, a signal of the third harmonic generated by a probe pulse on coherent phonons was recorded, similar to our previous work [20]. By varying the delay between the pump and probe pulses due to the movement of one of the arms in the Michelson interferometer, oscillations were observed in the third harmonic signal. The evolution of the phonon spectrum in silicon was obtained under excitation of the mid-IR laser pulses (see Figure 4) by analyzing this time signal using Fourier analysis with a floating time window.
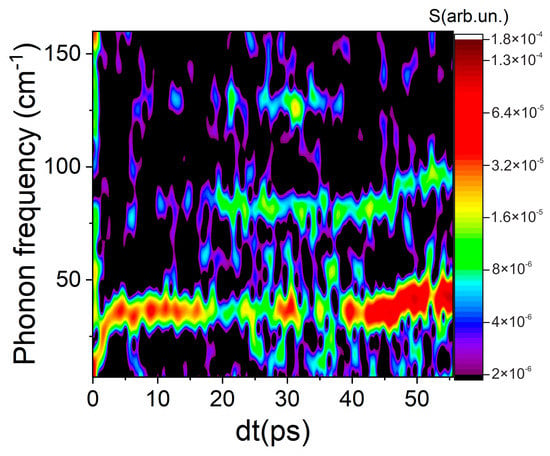
Figure 4.
Intensity map of changes in the frequency of coherent phonons in silicon, depending on the delay between the pump and probe pulses.
The coherent phonons were generated on timescales greater than 300 fs. For lower time delays, a broadband plasma signal on the 2D intensity graph was observed. Then, it vanished and the 38 cm−1 phonon mode appeared. This low-frequency mode was observed under strong anharmonic excitation of the atomic lattice [32]. Based on Figure 4, it is possible to identify the coherent frequencies with the highest amplitudes of the third harmonic signal modulation, namely ~38 cm−1, ~80 cm−1, and ~130 cm−1. Moreover, the phonon frequencies changed over time, as shown in Figure 4. In contrast to magnesium fluoride [20], the frequencies of coherent phonons in silicon are much more difficult to attribute to certain polymorphic phases. This is caused by, firstly, the presence of a large (more than twelve [33]) number of phases observed at high pressures and, secondly, many frequencies (for example, at 130 cm−1) are characteristic of several phases [34]. In addition, the frequencies of phonon vibrations strongly depend on the lattice temperature [34]. However, even in such a non-trivial case, it is possible to analyze the pressure-induced phase transitions in silicon. During the times of electron–phonon interactions (on the order of 150–350 fs in silicon), energy is transferred from the electronic subsystem to the atomic subsystem, which leads to the generation of shock waves. At the front of these shock waves, phase transitions are observed [20,35]. In addition, on the time scales of electron–phonon interactions, coherent phonons are generated. The change in the characteristic frequencies can serve as an indicator of the phase transitions [20,31].
By analyzing the dynamics of the spectrum of coherent phonons, it was possible to determine the characteristic times of changes in the phonon spectrum. In Figure 5, these times are marked with vertical dashed lines. The phase transition from the Imma phase to β-Sn can be easily identified by a smooth disappearance of phonons at a frequency of 130 cm−1, as well as an increase in the phonon frequency from 80 cm−1, which is characteristic of the Imma phase [36], to 100 cm−1, which is characteristic of the β-Sn phase [37]. A similar frequency jump under a pressure variation was noted in [38]. It can also be stated that frequencies in the region of 30 cm−1 are characteristic of the fcc phase, as noted in [36]. In the same work, it was demonstrated that frequencies in the region of 70 cm−1 are characteristic of the cubic phase [36].
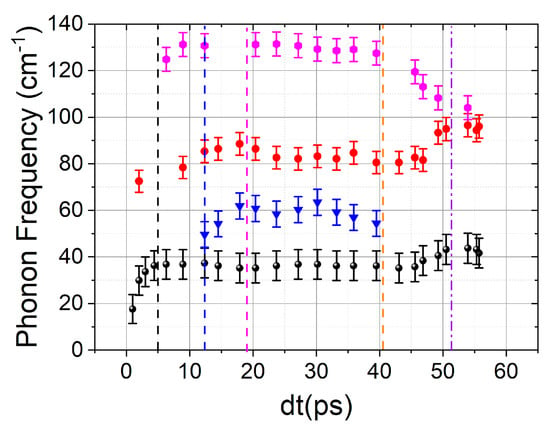
Figure 5.
Dynamics of coherent phonon frequencies in silicon under the impact of a mid-IR femtosecond laser pulse.
However, to identify new phases in silicon, one should pay attention to the time delays when the changes in the phonon spectrum occurred. Because the pressures at which the phase transitions occurred were relatively well-defined, at least for stationary conditions [33], and the pressure at the shock wave front decayed exponentially [39], it was possible to plot the points on axes (time—pressure), where the x-axis represented the delay at which the phase transitions occurred, and the y-axis represented the pressure at which the phase transitions should have occurred. If these points formed an exponential relationship (pressure decay), then the phase change was correctly restored. Figure 6 shows this graph, demonstrating that all points correspond accurately to the exponential decay of pressure. Thus, we can conclude that the shock wave induced by a laser pulse in silicon leads to a cascade of phase transitions and that they occur with decreasing pressure.
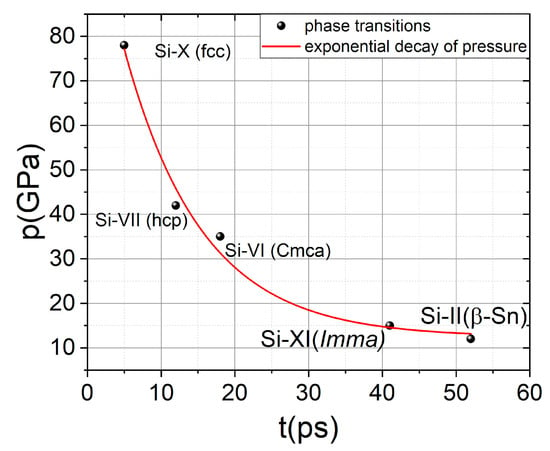
Figure 6.
Dependence of the pressure at which a phase transition can occur on the time delay between the pump and probe pulses. The red line marks the exponential pressure decay.
4. Conclusions
We reconstructed the dynamics of energy transfer from tightly (NA = 0.5) focused femtosecond pulses at a wavelength of 4.6 μm into bulk silicon under extreme deposited energy density (~4 kJ/cm3). Under such high DEDs, the plasma lifetime is around 160–300 fs and during this time, the energy is transferred from the electronic to the atomic subsystem. On the sub-ps time scale, coherent phonons are excited and shock waves are generated due to the energy transfer to the atomic subsystem. At the front of the shock wave, there is a disruption of the atoms in the lattice, which leads to a cascade of phase transitions and distortion of the phonon spectrum.
Author Contributions
Conceptualization, methodology, supervision, funding acquisition, project administration, F.P.; investigation, writing—original draft preparation, and writing—review and editing, F.P., E.M. and N.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded Russian Foundation for Basic Research: 21-32-70021, 19-29-12037, 21-52-50005.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Acknowledgments
The authors thank Gleb Karenkov for helping with the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Leuthold, J.; Koos, C.; Freude, W. Nonlinear silicon photonics. Nat. Photonics 2010, 4, 535–544. [Google Scholar] [CrossRef]
- Bogaerts, W.; Chrostowski, L. Silicon Photonics Circuit Design: Methods, Tools and Challenges. Laser Photonics Rev. 2018, 12, 1700237. [Google Scholar] [CrossRef]
- Schaffer, C.B.; Mazur, E. Laser-induced breakdown and damage in bulk transparent materials induced by tightly focused femtosecond laser pulses. Meas. Sci. Technol. 2001, 12, 1784–1794. [Google Scholar] [CrossRef]
- Fernandez, T.T.; Johnston, B.; Gross, S.; Cozic, S.; Poulain, M.; Mahmodi, H.; Kabakova, I.; Withford, M.; Fuerbach, A. Ultrafast laser inscribed waveguides in tailored fluoride glasses: An enabling technology for mid-infrared integrated photonics devices. Sci. Rep. 2022, 12, 14674. [Google Scholar] [CrossRef] [PubMed]
- Zavedeev, E.V.; Kononenko, V.V.; Konov, V.I. Delocalization of femtosecond laser radiation in crystalline Si in the mid-IR range. Laser Phys. 2016, 26, 016101. [Google Scholar] [CrossRef]
- Chanal, M.; Fedorov, V.Y.; Chambonneau, M.; Tzortzakis, S.; Grojo, D.; Clady, R. Crossing the threshold of ultrafast laser writing in bulk silicon. Nat. Commun. 2018, 8, 773. [Google Scholar] [CrossRef] [PubMed]
- Grojo, D.; Leyder, S.; Delaporte, P.; Marine, W.; Sentis, M.; Utéza, O. Long-wavelength multiphoton ionization inside band-gap solids. Phys. Rev. B-Condens. Matter Mater. Phys. 2013, 88, 195135. [Google Scholar] [CrossRef]
- Mareev, E.I.; Lvov, K.V.; Rumiantsev, B.V.; Migal, E.A.; Novikov, I.D.; Yu, S.S.; Potemkin, F.V. Effect of pulse duration on the energy delivery under nonlinear propagation of tightly focused Cr: Forsterite laser radiation in bulk silicon. Laser Phys. Lett. 2019, 17, 015402. [Google Scholar] [CrossRef]
- Chambonneau, M.; Grojo, D.; Tokel, O.; Ilday, F.Ö.; Tzortzakis, S.; Nolte, S. In-Volume Laser Direct Writing of Silicon—Challenges and Opportunities. Laser Photonics Rev. 2021, 15, 2100140. [Google Scholar] [CrossRef]
- Garcia-Lechuga, M.; Casquero, N.; Wang, A.; Grojo, D.; Siegel, J. Deep Silicon Amorphization Induced by Femtosecond Laser Pulses up to the Mid-Infrared. Adv. Opt. Mater. 2021, 9, 2100400. [Google Scholar] [CrossRef]
- Mareev, E.; Pushkin, A.; Migal, E.; Lvov, K.; Stremoukhov, S. Single-shot femtosecond bulk micromachining of silicon with mid-IR tightly focused beams. Sci. Rep. 2022, 12, 7517. [Google Scholar] [CrossRef] [PubMed]
- Chambonneau, M.; Lavoute, L.; Gaponov, D.; Fedorov, V.Y.; Hideur, A.; Février, S.; Tzortzakis, S.; Utéza, O.; Grojo, D. Competing nonlinear delocalization of light for laser inscription inside silicon with a 2-μm picosecond laser. Phys. Rev. Appl. 2019, 12, 024009. [Google Scholar] [CrossRef]
- Wang, A.; Das, A.; Grojo, D. Temporal-contrast imperfections as drivers for ultrafast laser modifications in bulk silicon. Phys. Rev. Res. 2020, 2, 033023. [Google Scholar] [CrossRef]
- Mcbride, E.E.; Krygier, A.; Ehnes, A.; Galtier, E.; Harmand, M.; Kon, Z. Phase Transition Lowering in Dynamically-Compressed Silicon. Nat. Phys. 2019, 15, 89–94. [Google Scholar] [CrossRef]
- Brown, S.B.; Gleason, A.E.; Galtier, E.; Higginbotham, A.; Arnold, B.; Fry, A.; Granados, E.; Hashim, A.; Schroer, C.G.; Schropp, A.; et al. Direct imaging of ultrafast lattice dynamics. Sci. Adv. 2019, 5, 8044. [Google Scholar] [CrossRef]
- Zeng, Z.; Zeng, Q.; Mao, W.L.; Qu, S. Phase transitions in metastable phases of silicon. J. Appl. Phys. 2014, 115, 103514. [Google Scholar] [CrossRef]
- Gogotsi, Y.; Baek, C.; Kirscht, F. Raman microspectroscopy study of processing-induced phase transformations and residual stress in silicon. Semicond. Sci. Technol. 1999, 14, 936–944. [Google Scholar] [CrossRef]
- Gorman, M.G.; Briggs, R.; McBride, E.E.; Higginbotham, A.; Arnold, B.; Eggert, J.H.; Fratanduono, D.E.; Galtier, E.; Lazicki, A.E.; Lee, H.J.; et al. Direct Observation of Melting in Shock-Compressed Bismuth with Femtosecond X-ray Diffraction. Phys. Rev. Lett. 2015, 115, 095701. [Google Scholar] [CrossRef]
- Wall, S.; Wegkamp, D.; Foglia, L.; Appavoo, K.; Nag, J.; Haglund, R.F.; StäCurrency Signhler, J.; Wolf, M. Ultrafast changes in lattice symmetry probed by coherent phonons. Nat. Commun. 2012, 3, 721. [Google Scholar] [CrossRef]
- Mareev, E.; Potemkin, F. Dynamics of ultrafast phase transitions in MgF2 triggered by laser-induced THz coherent phonons. Sci. Rep. 2022, 12, 6621. [Google Scholar] [CrossRef]
- Pawbake, A.; Bellin, C.; Paulatto, L.; Béneut, K.; Biscaras, J.; Narayana, C.; Late, D.J.; Shukla, A. Pressure-induced phase transitions in Germanium telluride: Raman signatures of anharmonicity and oxidation. Phys. Rev. Lett. 2019, 122, 145701. [Google Scholar] [CrossRef] [PubMed]
- Taylor, L.L.; Scott, R.E.; Qiao, J. Integrating two-temperature and classical heat accumulation models to predict femtosecond laser processing of silicon. Opt. Mater. Express 2018, 8, 648. [Google Scholar] [CrossRef]
- Tanimura, H.; Kanasaki, J.; Tanimura, K.; Sjakste, J.; Vast, N. Ultrafast relaxation dynamics of highly excited hot electrons in silicon. Phys. Rev. B 2019, 100, 035201. [Google Scholar] [CrossRef]
- Zijlstra, E.S.; Walkenhorst, J.; Garcia, M.E. Anharmonic noninertial lattice dynamics during ultrafast nonthermal melting of InSb. Phys. Rev. Lett. 2008, 101, 135701. [Google Scholar] [CrossRef] [PubMed]
- Tsujino, M.; Sano, T.; Ozaki, N.; Sakata, O.; Okoshi, M.; Inoue, N.; Kodama, R.; Hirose, A. Quenching of High-Pressure Phases of Silicon Using Femtosecond Laser-driven Shock Wave. Rev. Laser Eng. 2008, 36, 1218–1221. [Google Scholar] [CrossRef]
- Mareev, E.I.; Rumiantsev, B.V.; Migal, E.; Bychkov, A.S.; Karabutov, A.A.; Cherepetskaya, E.B.; Makarov, V.A.; Potemkin, F.V. A comprehensive approach for characterisation of the deposited energy density during laser-matter interaction in liquids and solids. Meas. Sci. Technol. 2020, 31, 085204. [Google Scholar] [CrossRef]
- Wang, A.; Das, A.; Hermann, J.; Grojo, D. Three-dimensional luminescence microscopy for quantitative plasma characterization in bulk semiconductors. Appl. Phys. Lett. 2021, 119, 041108. [Google Scholar] [CrossRef]
- Migal, E.; Mareev, E.; Smetanina, E.; Duchateau, G.; Potemkin, F. Role of wavelength in photocarrier absorption and plasma formation threshold under excitation of dielectrics by high-intensity laser field tunable from visible to mid-IR. Sci. Rep. 2020, 10, 14007. [Google Scholar] [CrossRef]
- Potemkin, F.V.; Mareev, E.I.; Mikheev, P.M.; Khodakovskij, N.G. Resonant laser-plasma excitation of coherent THz phonons under extreme conditions of femtosecond plasma formation in a bulk of fluorine-containing crystals. Laser Phys. Lett. 2013, 10, 076003. [Google Scholar] [CrossRef]
- Mareev, E.I.; Migal, E.A.; Potemkin, F.V. Ultrafast third harmonic generation imaging of microplasma at the threshold of laser-induced plasma formation in solids. Appl. Phys. Lett. 2019, 114, 031106. [Google Scholar] [CrossRef]
- Potemkin, F.V.; Mareev, E.I.; Mikheev, P.M.; Khodakovskij, N.G. Resonance laser-plasma excitation of coherent terahertz phonons in the bulk of fluorine-bearing crystals under high-intensity femtosecond laser irradiation. Quantum Electron. 2013, 43, 735–739. [Google Scholar] [CrossRef]
- Seres, E.; Seres, J.; Spielmann, C. Time resolved spectroscopy with femtosecond soft-x-ray pulses. Appl. Phys. A Mater. Sci. Process. 2009, 96, 43–50. [Google Scholar] [CrossRef]
- Wippermann, S.; He, Y.; Vörös, M.; Galli, G. Novel silicon phases and nanostructures for solar energy conversion. Appl. Phys. Rev. 2016, 3, 040807. [Google Scholar] [CrossRef]
- Lewis, S.P.; Cohen, M.L. Theoretical study of Raman modes in high-pressure phases of Si, Ge, and Sn. Phys. Rev. B 1993, 48, 3646–3653. [Google Scholar] [CrossRef] [PubMed]
- Mareev, E.I.; Potemkin, F.V. Dynamics of Ultrafast Phase Transitions in (001) Si on the Shock-Wave Front. Int. J. Mol. Sci. 2022, 23, 2115. [Google Scholar] [CrossRef]
- Paul, R.; Hu, S.X.; Karasiev, V.V. Crystalline phase transitions and vibrational spectra of silicon up to multiterapascal pressures. Phys. Rev. B 2019, 100, 144101. [Google Scholar] [CrossRef]
- Domnich, V.; Gogotsi, Y. Phase transformations in silicon under contact loading. Rev. Adv. Mater. Sci. 2002, 3, 1–36. [Google Scholar]
- Gaál-Nagy, K.; Strauch, D. Phonons in the β-tin, Imma, and sh phases of silicon from ab initio calculations. Phys. Rev. B-Condens. Matter Mater. Phys. 2006, 73, 014117. [Google Scholar] [CrossRef]
- Mareev, E.I.; Rumiantsev, B.V.; Potemkin, F.V. Study of the Parameters of Laser-Induced Shock Waves for Laser Shock Peening of Silicon. JETP Lett. 2020, 112, 739–744. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).