Abstract
We propose a scheme for key-space-enhanced chaos secure communication using semiconductor lasers with spectrum-programmable optoelectronic feedback. This feedback consists of multiple parallel optoelectronic feedback loops composed of bandpass filters and radio-frequency amplifiers. The centre frequencies of the filters and gain coefficients of the amplifiers increase the key space. We use 12 parallel filtered feedback loops to analyse the effects of parameter mismatch on the synchronization quality. The simulation result indicates that the key space reaches approximately 2100 at a data rate of 10 Gbit/s, and it can be further enhanced by increasing the number of feedback loops. These results suggest an alternative approach for security-enhanced optical chaos communication.
1. Introduction
Optical chaos communication has attracted considerable attention because of its advantages, such as a high transmission rate, long transmission distance, compatibility with existing fibre networks, and high-level security in physical layer encryption [1,2,3,4,5,6,7,8,9]. In 2005, Argyris et al. implemented a 1 Gbit/s chaos communication field experiment with semiconductor lasers in a 120 km long commercial fibre optic link in Athens [2]. In 2010, Lavrov et al. realised chaos communication with optoelectronic oscillators in a 100 km fibre network in Besancon at a transmission rate of 10 Gbit/s [3]. In 2018, Yi et al. demonstrated chaos communication fibre transmission over 100 km at a bit rate of 30 Gbit/s [5]. In 2020, Wang et al. proposed coherent optical chaos communication in which the data rate was expected to be at least 40 Gbit/s [6]. In 2022, Wang et al. experimentally demonstrated all-optical wideband chaos synchronization and communications based on the mutual injection of semiconductor lasers [10]. In 2023, Li et al. reported and numerically demonstrated an optical chaos communication scheme which allow for broadband chaos generation, high-quality chaos synchronization, and long distance [11]. In 2023, Wang et al. numerically investigated the effects of probabilistic shaping on the performance improvement of coherent optical chaos communication and demonstrated that the decryption bit error ratio of the 16 QAM signal decreases upon increasing the probabilistic shaping factor [12]. The security of optical chaos communication has become important owing to the increase in the transmission speed and distance [13].
In chaos communication, the parameters of authorised transceivers must be matched to achieve chaos synchronization [14,15,16]. In addition, lasers must be selected from the same wafer. Therefore, the synchronization of transceivers is sensitive to parameter mismatch. This implies that it is difficult for an eavesdropper to obtain a parameter-matching laser and build synchronization with legitimate users. Each hardware parameter of a legitimate laser is regarded as a physical key. The key space of the system is defined as the product of the ratio between the entire range of each parameter and the tolerant mismatch range that affords synchronization to decode the message [17]. A larger physical key space implies that it is more difficult for an eavesdropper to crack the system.
A few methods have been proposed to enhance the key space of chaos secure communication. For example, Yi et al. verified that the key space can be significantly improved to 1048 by adding a frequency-dependent group delay module with high-frequency tuning resolution in chaotic optoelectronic oscillation [18]. Wang et al. demonstrated that the key space is enhanced by 244 compared to conventional mirror feedback using external chirped fibre Bragg grating feedback. This is because they time delay signature is suppressed, and new dimensions of the key space are introduced [17,19]. A vertical-cavity surface-emitting laser with common phase-modulated electro-optic feedback has been proposed by Wang et al. to eliminate the time-delay signature and enhance the dimensions of the key space [20]. Gao et al. demonstrated that the key space can be enhanced by 234 by introducing an electro-optic nonlinear transformation hardware module [21]. Wang et al. proposed a key-space-enhanced optical chaos secure communication scheme using a pair of monolithically integrated multi-section semiconductor lasers as transceivers and numerically demonstrated the key space reaches 248 with a data rate of 2.5 Gbit/s [22].
In this paper, we propose a scheme to enhance the key space of chaos secure communication using semiconductor lasers with spectrum-programmable optoelectronic feedback composed of multiple parallel optoelectronic feedback loops. Each feedback loop is composed of a bandpass filter (BPF) and a radio-frequency (RF) amplifier. Chaos synchronization is achieved by driving transceivers with common amplified spontaneous emission (ASE) noise. The effects of the centre frequency mismatch of the BPF and the gain mismatch of the RF amplifier on synchronization are simulated. When the parallel number is 12, the key space of the chaos secure communication system reaches 2100 at a communication rate of 10 Gbit/s.
2. Theoretical Model
The proposed chaos communication system with an enhanced key space is shown in Figure 1. An ASE noise module is applied as the driver, and two parameter-matched distributed-feedback (DFB) lasers with spectrum-programmable optoelectronic feedback are authorised to legitimate users—Alice and Bob. The drive light is divided into two beams and injected into the DFB lasers after filtering and amplification. The output signal of the DFB lasers is detected by a photodetector and divided into two parts, which are fed back to the bias current of the DFB lasers through optoelectronic feedback and spectrum-programmable optoelectronic feedback. The spectrum-programmable optoelectronic feedback consists of multiple parallel optoelectronic filtered feedback loops, each of which comprises a BPF and RF amplifier. The centre frequencies of the BPFs and the gains of the RF amplifiers can be used as additional physical keys of the system to enhance the key space. The DFB lasers of Alice and Bob generate synchronized chaotic signals for secure communication. The message, m(t), is encrypted on the chaos carrier emitted by Alice through chaos masking and then decrypted by Bob by subtracting the chaos carrier.
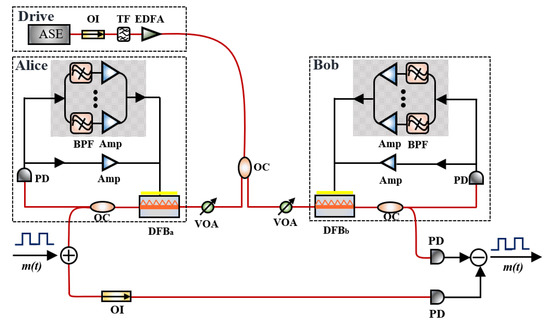
Figure 1.
Schematic of key-space-enhanced secure optical communication using spectrum-programmable optoelectronic feedback. ASE: amplified spontaneous emission; OI: optical isolator; TF: tuneable filter; EDFA: erbium-doped fibre amplifier; OC: optical coupler; VOA: variable optical attenuator; PD: photodetector; BPF: bandpass filter; Amp: amplifier.
The system is simulated using the VPItransmissionMakerTM commercial simulation software. The time delay of the optoelectronic filtered feedback is fixed at 2.55 ns in each feedback loop. The bias currents of the two lasers are both 30 mA, which is 1.5 times the threshold current. In order to provide a certain initial feedback strength, the amplifier gain (G0) in the optoelectronic feedback loop is fixed at 2 dB. The injection strength, kinj, is defined as the ratio of the optical power of the injection to the laser output power. In the simulation, the optical coupling strength of different devices is considered 100%. The two lasers have the same internal parameters, which are listed in Table 1.

Table 1.
Values of parameters used in the simulation.
3. Simulation Results
3.1. Chaos Generation and Synchronization
We investigate the route to broadband chaos in the DFB laser with single optoelectronic filtered feedback to prove the chaos generation of the proposed architecture. The variable strength of the filtered feedback is obtained by tuning the RF amplifier gain (G) in the feedback loop. Figure 2 shows the time series, power spectra, and phase portraits for different RF amplifier gains. The bandwidth and centre frequency of the BPF are B = 2 GHz and f0 = 3 GHz. The laser operates in a steady state for G = 0.4 dB (Figure 2(a1–a3)). The time series shows only minor fluctuations, and the power spectrum almost coincides with the noise floor except for a slight bulge around 2 GHz, which is the characteristic relaxation–oscillation frequency. In addition, an extended dot is observed in the phase portrait. A period-one state is observed at G = 1.5 dB (Figure 2(b1–b3)). The time series shows regular fluctuations, and the fundamental frequency is around the relaxation–oscillation frequency and its harmonics in the corresponding power spectrum. The trajectories of the phase portrait show clear limit cycle features. The laser enters a quasiperiodic state at G = 3.2 dB (Figure 2(c1–c3)). The time series shows irregular fluctuations. The trajectories of the phase portrait are dispersed within a certain range. The laser enters the chaos state at G = 5.6 dB (Figure 2(d1–d3)). The time series shows strong fluctuations, and the corresponding power spectrum continuously covers an extremely broad frequency range. The phase portrait shows a widely scattered distribution over a large area.
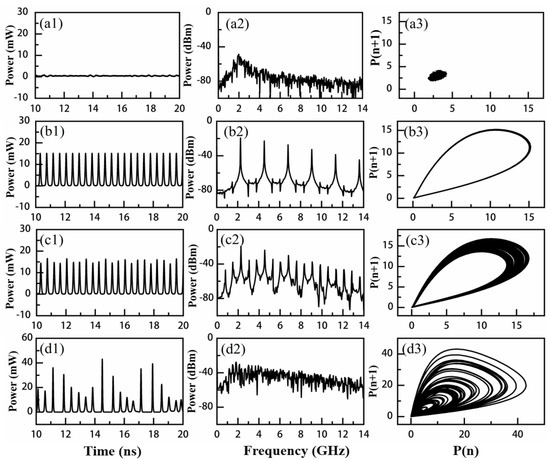
Figure 2.
Time series, power spectrum, and corresponding phase portraits of dynamic states under optoelectronic filtered feedback. (a1–a3) Steady state at G = 0.4 dB; (b1–b3) Regular pulse at G = 1.5 dB; (c1–c3) Quasiperiodic state at G = 3.2 dB; (d1–d3) Chaotic pulsing at G = 5.6 dB.
Next, we investigate the synchronization characteristics of the transceiver. Figure 3a–c illustrate the time series of the driving source and the response lasers of Alice and Bob for an injection strength of kinj = 0.16 and an amplifier gain of G = 20 dB. The chaotic waveforms generated by the response lasers exhibit almost the same profiles. A correlation coefficient of 0.98 is achieved between the output chaotic signals from the two lasers, as shown in Figure 3d, indicating high-quality synchronization. In contrast, the chaotic waveforms output by the response lasers are evidently distinct from the temporal intensity fluctuation of the driving source, and a correlation coefficient of 0.21 is obtained between them, as shown in Figure 3e. Such a low correlation coefficient implies that it is difficult for an eavesdropper to extract the private chaotic encryption signal by tapping the public driving signal.
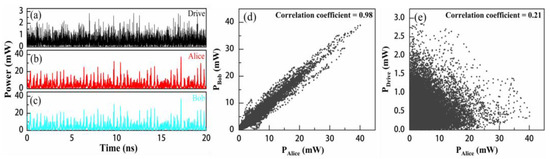
Figure 3.
Time series of (a) drive signal, (b) DFBa, and (c) DFBb; (d) correlation plots of the transceiver; (e) correlation plots of DFBa and drive signal.
Figure 4a,b show the dependence of the chaos synchronization of the response lasers on the injection strength for different amplifier gains and filter widths. As shown in Figure 4a, the correlation coefficient can reach to 0.98 for smaller injection strengths; this reduces the filtered feedback strengths. As shown in Figure 4b, the filtered feedback strengths for different filter widths are almost constant. This clearly shows that the synchronization characteristics have similar evolution trends for different filter widths as the injection strength increases. This implies that excellent synchronization can be obtained under an appropriate injection strength for any amplifier gain or filter width. Figure 4c shows the correlation coefficients for different centre frequencies of the BPF. The filter width is B = 2 GHz, the injection strength is kinj = 0.16, and the filtered feedback strength is constant. At centre frequencies of 1–12 GHz, the correlation coefficient is constant at approximately 0.98, with only minor fluctuations. These results show that the response lasers exhibit similar synchronization characteristics when the filtered feedback strength is fixed, even though the filter width or centre frequency of the BPF may be different.
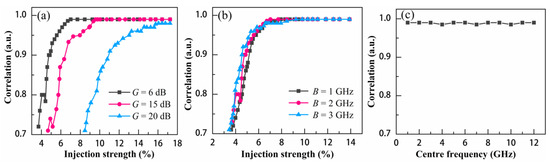
Figure 4.
Correlation coefficient versus injection strength for different (a) amplifier gains and (b) filter widths; (c) correlation coefficient versus centre frequency of filter.
Next, we examine the synchronization tolerance to the parameter mismatch of the response lasers. The parameters for Alice’s laser are maintained and those for Bob’s laser are varied. Figure 5a,b show the correlation performance versus the centre frequency detuning for different centre frequencies and filter widths; the filtered feedback strength is constant. The synchronization between DFBa and DFBb is sensitive to the centre frequency detuning. The mismatch tolerance to the centre frequency of the BPF is in the order of tens of MHz, and the tolerance reduces with the centre frequency (Figure 5a). This is because the detuning of the centre frequency result in a large variation in the filtered feedback strength when it is close to the relaxation–oscillation frequency of the DFB laser. Nevertheless, with the frequency increasing, the chaotic spectrum becomes flatter. Thus, the effects of centre frequency mismatch on feedback strength are limited. However, the tolerances for different filter widths are similar (Figure 5b). Figure 5c shows the effect of the mismatch of the amplifier gain on the correlation for different filter widths. The synchronization performance decreases as the mismatch increases, and a similar trend is observed for different filter widths.
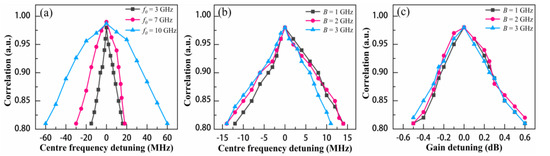
Figure 5.
Correlation coefficient versus (a) centre frequency detuning mismatch for different centre frequencies, (b) centre frequency detuning mismatch for different BPF widths, and (c) amplifier gain detuning for different BPF widths.
3.2. Physical Key Space Analysis
We use multiple filtered feedback loops to significantly enhance the key space. Considering the limitations of the DFB laser output power, 12 parallel filtered feedback loops are used in the emitter and receiver. We have verified that the filter width has a negligible effect on chaos synchronization when the filtered feedback strength is constant. Therefore, in the following simulation, we set the BPF width as B = 2 GHz, the amplifier gain as G = 20 dB, and the centre frequency of the BPFs as f0i = 1.6 + 0.2 × (i − 1) GHz (i = 1–12).
As shown in Figure 6, a data rate of 10 Gbit/s is used as the message for chaos communication, for which the chaos synchronization coefficient is 0.98. Figure 6a–c show the original pseudorandom bit sequence, chaotic carrier, and chaotic carrier with the message, respectively. The message modulation amplitude is adjusted to 0.2, which is defined as the ratio of the mean optical power of the pseudorandom bit sequence to that of the chaotic carrier of the transmitter. Figure 6d,e show a decrypted message and the corresponding eye diagram obtained using chaotic decryption, which is implemented by subtracting the transmitted carrier with the message from the locally generated carrier at the receiver. The message can be clearly distinguished, and the eye diagram is well-opened. The bit error ratio (BER) is calculated as 5.4 × 10−4, which is below the hard-decision forward-error correction (FEC) threshold of 3.8 × 10−3 [23]. Figure 6f shows the effects of the synchronization coefficient on the BER of the decoded message. As the synchronization coefficient decreases to 0.9, the BER increases to a limit of 3.8 × 10−3, below which the decoded message can still be recovered by the FEC processing technique. The message cannot be recovered as the synchronization coefficient decreases further. Therefore, we adopt 0.9 as the synchronization threshold to calculate the critical mismatch of each parameter.
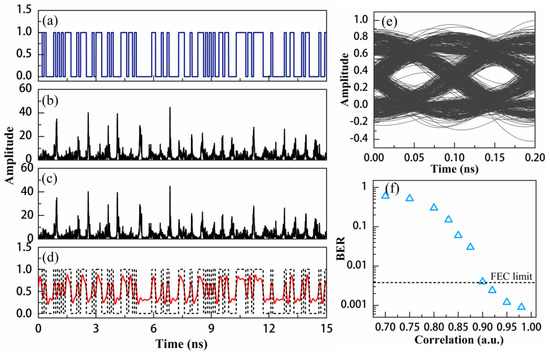
Figure 6.
Time series for (a) original message, (b) chaotic carrier, (c) chaotic carrier with message, and (d) decrypted message. (e) Eye diagrams for decrypted message; (f) BER of decoded message as a function of synchronization coefficient. The message rate is 10 Gbit/s with a modulation amplitude of 0.2.
In optical chaos communication, the key space can be evaluated as follows [17]:
where is the parameter value range in which the laser can generate chaos and is the critical value of parameter mismatch between two chaotic lasers, determined by the synchronization threshold we studied before. “Floor” means rounding down the result to the nearest integer, is the key space of one possible parameter, is the total key space of all possible parameters, and , = 1 means that all parameters are independent or there is only one parameter.
Figure 7 and Figure 8 show the variation in the correlation coefficient with the mismatch of the centre frequency of each BPF and amplifier gain. As shown in Figure 7a–l, we carefully analyse the detuning of the filter centre frequency in each filtered feedback loop, and it can be seen that the chaos synchronization characteristic gradually deteriorates with the expansion of the detuning range. According to Figure 6f, we use 0.9 as the synchronization threshold to calculate the critical mismatch value for each centre frequency. The maximum critical mismatch value is 26 MHz, as shown in Figure 7c. The minimum critical mismatch value is 10 MHz, as shown in Figure 7i. We then systematically analyse the effect of amplifier gain mismatch in each filtered feedback loop on the chaos synchronization, as shown in Figure 8a–l. We can clearly see that the synchronization coefficient is sensitive to the detuning of the amplifier gain, with minimum and maximum critical mismatch values of 0.4 dB and 1.1 dB, respectively, as shown in Figure 8b,e,l. Based on the above analysis, we can conclude that the centre frequency of the BPFs and the gain of the amplifiers can be used as additional key parameters. We calculate the key space by considering the centre frequency with a maximal tuning range of 13 GHz for each BPF within the spectral bandwidth of the chaotic carrier. The maximal tuning range of each amplifier gain was 20 dB. Therefore, according to the Equations (1) and (2), a total key space enhancement of approximately 2100 is expected from the use of 12 parallel optoelectronic filtered feedback loops.
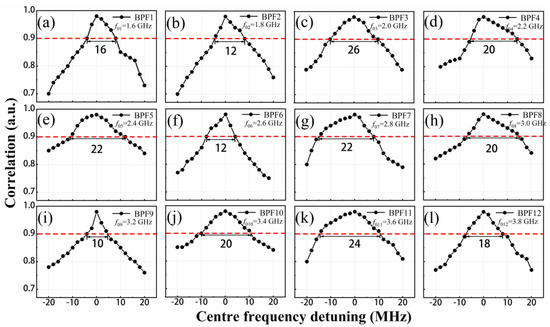
Figure 7.
Effects of mismatch of centre frequency of BPFs on correlation coefficient. The centre frequency of BPFs is (a) 1.6 GHz, (b) 1.8 GHz, (c) 2.0 GHz, (d) 2.2 GHz, (e) 2.4 GHz, (f) 2.6 GHz, (g) 2.8 GHz, (h) 3.0 GHz, (i) 3.2 GHz, (j) 3.4 GHz, (k) 3.6 GHz, (l) 3.8 GHz.
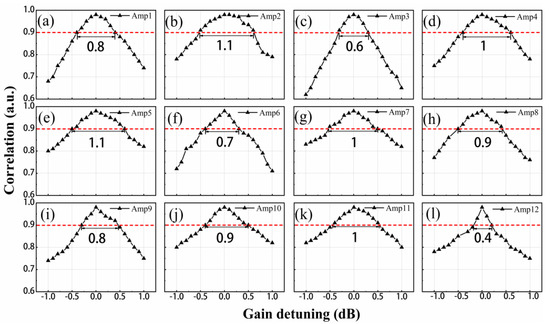
Figure 8.
Effects of mismatch of amplifier gain on correlation coefficient. (a–l) The gain of amplifier is 20 dB.
4. Discussion
Key space enhancement is significantly pursued for high-level security communication. In this paper, we propose and simulate a scheme of key space enhanced chaotic secure communication based on spectrum-programmable optoelectronic feedback. From Figure 7 and Figure 8, we can conclude that the synchronization coefficients are sensitive to the detuning of centre frequencies of the filters and the amplifier gains in the feedback loop. Thus, the centre frequencies of the filters and the gains of the RF amplifiers can be used as additional physical keys of the system to enhance the key space. The simulation results suggest that the proposed scheme can reach a huge key space. In principle, with the increase in the parallel number, the key space will be further enhanced. A tuneable BPF with a frequency response range of 2–18 GHz, a bandwidth of 4 GHz (ADMV8818, ADI) and a variable-gain RF amplifier with a gain range of 18–36 dB (ADL5246, ADI) can be applied to the optoelectronic filtered feedback loop. With the development of integrated circuits, a multichannel and programmable BPF and amplifier can be implemented in a chaos secure communication system. We believe that the proposed scheme can provide a new approach for improving the security of high-speed chaos communication.
5. Conclusions
We numerically demonstrate chaos secure communication with an enhanced key space using semiconductor lasers with spectrum-programmable optoelectronic feedback. Two parameter-matched semiconductor lasers are injected with ASE noise to generate synchronized chaos for secure communication. BPFs with variable centre frequencies and RF amplifiers with variable gains in the feedback loop are used to extend the key space dimensions. The key space is increased to 2100 at a communication rate of 10 Gbit/s using 12 filtered feedback loops, and it can be further enhanced by increasing the parallel number.
Author Contributions
Conceptualization, Y.G., D.W. and A.W.; methodology, Y.G. and D.W.; software, Y.G. and D.W.; validation, L.W.; formal analysis, D.W.; investigation, Y.G. and D.W.; resources, A.W. and Y.W.; data curation, D.W.; writing—original draft preparation, Y.G. and D.W.; writing—review and editing, Y.G., L.W., T.Z., Z.J., P.C. and A.W.; visualization, Y.G. and D.W.; supervision, A.W.; funding acquisition, Y.G. and A.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program of China (2019YFB1803500), the National Natural Science Foundation of China (NSFC) (62035009, 61731014, 61805171, 61927811), the Fund for Shanxi “1331 Project” Key Innovative Research Team, the International Cooperation of Key R&D Program of Shanxi Province (201903D421012), and the Development Fund in Science and Technology of Shanxi Province (YDZJSX2022A010, YDZJSX2021A009).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vanwiggeren, G.D.; Roy, R. Communication with chaotic lasers. Science 1998, 279, 1198–1200. [Google Scholar] [CrossRef] [PubMed]
- Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi-Lodi, V.; Colet, P.; Fischer, I.; García-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef]
- Lavrov, R.; Jacquot, M.; Larger, L. Nonlocal nonlinear electro-optic phase dynamics demonstrating 10 Gb/s chaos communications. IEEE J. Quantum Electron. 2010, 46, 1430–1435. [Google Scholar] [CrossRef]
- Argyris, A.; Grivas, E.; Hamacher, M.; Bogris, A.; Syvridis, D. Chaos-on-a-chip secures data transmission in optical fiber links. Opt. Express 2010, 18, 5188–5198. [Google Scholar] [CrossRef] [PubMed]
- Ke, J.X.; Yi, L.L.; Xia, G.Q.; Hu, W.S. Chaotic optical communications over 100-km fiber transmission at 30-Gb/s bit rate. Opt. Lett. 2018, 43, 1323–1326. [Google Scholar] [CrossRef]
- Wang, L.S.; Mao, X.X.; Wang, A.B.; Wang, Y.C.; Gao, Z.S.; Li, S.S.; Yan, L.S. Scheme of coherent optical chaos communication. Opt. Lett. 2020, 45, 4762–4765. [Google Scholar] [CrossRef]
- Yang, Z.; Ke, J.X.; Zhuge, Q.B.; Hu, W.S.; Yi, L.L. Coherent chaotic optical communication of 30 Gb/s over 340-km fiber transmission via deep leaning. Opt. Lett. 2022, 47, 2650–2653. [Google Scholar] [CrossRef]
- Jiang, L.; Feng, J.C.; Yan, L.S.; Yi, A.L.; Li, S.S.; Yang, H.; Dong, Y.X.; Wang, L.S.; Wang, A.B.; Wang, Y.C.; et al. Chaotic optical communications at 56 Gbit/s over 100-km fiber transmission based on a chaos generation model driven by long short-term memory networks. Opt. Lett. 2022, 47, 2382–2385. [Google Scholar] [CrossRef]
- Gao, Z.S.; Wu, Q.Q.; Liao, L.; Su, B.; Gao, X.L.; Fu, S.N.; Li, Z.H.; Wang, Y.C.; Qin, Y.W. Experimental demonstration of synchronous privacy enhanced chaotic temporal phase en/decryption for high speed secure optical communication. Opt. Express 2022, 30, 31209–31219. [Google Scholar] [CrossRef]
- Xiang, S.; Yang, M.; Wang, J. Chaotic optical communications of 12.5-Gbaud OOK and 10-Gbaud QPSK signals based on mutual injection of semiconductor lasers. Opt. Lett. 2022, 47, 2818–2821. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Zhou, P.; Li, N. Dual-Channel Secure Communication Based on Wideband Optical Chaos in Semiconductor Lasers Subject to Intensity Modulation Optical Injection. Electronics 2023, 12, 509. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.; Mao, X.; Jiang, L.; Li, S.; Sun, Y.; Wang, Y.; Yan, L.; Wang, A. Performance improvement of coherent optical chaos communication using probabilistic shaping. Opt. Lett. 2023, 48, 1008–1011. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Pan, Y.; Yi, A.L.; Feng, J.C.; Pan, W.; Yi, L.L.; Hu, W.S.; Wang, A.B.; Wang, Y.C.; Qin, Y.W.; et al. Trading off security and practicability to explore high-speed and long-haul chaotic optical communication. Opt. Express 2021, 29, 12750–12762. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.F.; Liu, J.M. Open-loop chaotic synchronization of injection-locked semiconductor lasers with gigahertz range modulation. IEEE J. Quantum Electron. 2000, 36, 27–34. [Google Scholar] [CrossRef]
- Ohtsubo, J. Chaos synchronization and chaotic signal masking in semiconductor lasers with optical feedback. IEEE J. Quantum Electron. 2002, 38, 1141–1154. [Google Scholar] [CrossRef]
- Murakami, A.; Ohtsubo, J. Synchronization of feedback-induced chaos in semiconductor lasers by optical injection. Phys. Rev. A 2002, 65, 031802. [Google Scholar] [CrossRef]
- Wang, D.M.; Wang, L.S.; Guo, Y.Y.; Wang, Y.C.; Wang, A.B. Key space enhancement of optical chaos secure communication: Chirped FBG feedback semiconductor laser. Opt. Express 2019, 27, 3065–3073. [Google Scholar] [CrossRef]
- Hou, T.T.; Yi, L.L.; Yang, X.L.; Ke, J.X.; Hu, Y.; Yang, Q.; Zhou, P.; Hu, W.S. Maximizing the security of chaotic optical communications. Opt. Express 2016, 24, 23439–23449. [Google Scholar] [CrossRef]
- Wang, D.M.; Wang, L.S.; Li, P.; Zhao, T.; Jia, Z.W.; Gao, Z.S.; Guo, Y.Y.; Wang, Y.C.; Wang, A.B. Bias current of semiconductor laser: An unsafe key for secure chaos communication. Photonics 2019, 6, 59. [Google Scholar] [CrossRef]
- Wang, H.X.; Lu, T.F.; Ji, Y.F. Key space enhancement of a chaos secure communication based on VCSELs with a common phase-modulated electro-optic feedback. Opt. Express 2020, 28, 23961–23977. [Google Scholar] [CrossRef]
- Gao, Z.S.; Li, Q.H.; Zhang, L.H.; Tang, B.; Luo, Y.; Gao, X.L.; Fu, S.N.; Li, Z.H.; Wang, Y.C.; Qin, Y.W. 32 Gb/s physical-layer secure optical communication over 200 km based on temporal dispersion and self-feedback phase encryption. Opt. Lett. 2022, 47, 913–916. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Wang, Y.; Sun, Y.; Xu, J.; Li, P.; Wang, A.; Qin, Y. Key Space Enhancement in Chaotic Secure Communication Utilizing Monolithically Integrated Multi-Section Semiconductor Lasers. Photonics 2023, 10, 213. [Google Scholar] [CrossRef]
- Argyris, A.; Grivas, E.; Bogris, A.; Syvridis, D. Transmission effects in wavelength division multiplexed chaotic optical communication systems. J. Light. Technol. 2010, 28, 3107–3114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).